1. Introduction
Climate change makes mitigation actions necessary to ensure the adequate conditions of the animals bred due to the increasingly hot microclimate. In dairy cow breeding, coordinated water spraying and fan airflow targeting the animals are used to reduce heat load (‘sprinkling cooling system’), among other available systems [
1,
2,
3], as ascertained by various authors [
4,
5,
6]. In these cooling systems, spray/fan timing is fixed, although there are some attempts to link it, on an empirical basis, to the THI, or to other more- or less-simplified models [
7].
In particular, in [
7], several models to predict the dairy cow’s thermal state using several approaches such as bioclimatic indexes, machine learning or mechanistic modelling are reviewed [
7]. In a recent work, Shu et al. [
8] tested several algorithms through machine learning, and stated that ANN gives the lower error in predicting the physiological responses of dairy cows, allowing a better cooldown decision.
To optimise water and energy consumption, the sprinkling should take place just before the water deposited in the previous spraying on the fur of the cow has completely evaporated—not after, not before. Some researchers have modelled the behaviour of heat exchange with stationary models [
9,
10], also considering latent heat exchange, without giving any indication of the drying time of the fur. Chen et al. in [
11] improved previous works by developing a transient model to predict the drying time of the fur under varying conditions. They also presented a parametric algorithm to directly control a cooling system. In this work, assumptions of some parameters are somewhat uncertain, for example, the fur water content after showering was derived backwards from the findings of other authors.
Other works evaluated the heat exchange characteristics of the fur [
12]. Although the use of sprinkling with ventilation is considered an appropriate practice to reduce heat stress, there are several critical operational aspects to this methodology, such as the flow rate of the sprayer or the duration of shower/water delivery [
12]. Some authors have pointed out that even with low flow rates (1.5 L min
−1 sprayer
−1), a shower of 30/60 s may be sufficient to adequately wet the cow’s fur [
10,
13]. Authors adopted an empirical approach to determine the wetting time, identified as the time the water begins to run off from the abdomen. The same authors warn about the need to avoid wetting the udder to prevent mastitis cases. Due to these reasons, the research did not propose any models to simulate the wetting phase. In fact, Chen et al. [
11], in predicting the wetting phase, declared that it occurs in a few seconds.
Obviously, the diameter distribution of sprinkler droplets also influences wetting, although coarse droplets are preferred to smaller ones as they wet the fur deeper [
14,
15,
16,
17]. In any case, in Arkin et al. [
12] it is reported that fur wets at only 60 percent of the fur’s maximum capacity with normal commercial sprinklers. On the other hand, one aspect considered important enough to be investigated is the duration of the wetting/ventilation cycle as it determines the number of daily showers and, then, given the sprinkler’s flow, global water consumption.
Bouy et al. [
1] gave recommendations to improve the performance of PLF to determine heat stress and the response of animals to various environmental conditions. Then, as water will increasingly become a limited resource [
16], it is desirable to have a sensor to guide the actuation of the nozzles in order to optimise water efficiency.
Most of the models analyzed in [
7] assess the thermal behaviour of animals, but they do not address the estimation of the fur’s drying time, apart from Chen et al. [
11]. Shu et al. [
8], on the other hand, assess the response of cows to the cooling treatment only afterwards, through different predictors of physiological states. Furthermore, most modelling approaches use ambient parameters (Ta, RH) which remain almost unchanged, even after sprinkler activation (apart from a possible increase in RH), which acts on the animal and does not appreciably change the Ta and RH of the ambient air. Therefore, models relying on Ta and RH could continue to indicate a state of stress. Such models, therefore, may be adequate enough to determine when cooling should be performed, but they are not adequate enough to manage the strategy of the cooling system (sprinkler/fan activation timing) apart from, as mentioned above, the model proposed by Chen et al. [
11].
In the present work, an active drying sensor, to be installed in the feeding alley, to emulate cow heat exchange(sensible and latent), cow heat production, and the wetting/drying dynamics of the cow’s coat, thus giving information on the evolution of the drying process and allowing the timing of the sprinkling cooling system (fan velocity, sprinkling timing, etc.) to be managed, was evaluated.
The sensor proposed herein could also be used to assess the heat stress state of the animals, but this aspect was not yet investigated in the present work.
The sensor was evaluated both in a laboratory and in a commercial dairy cow barn equipped with its own cooling system.
2. Materials and Methods
2.1. The Experimental Barn
The commercial barn where the experimentation was carried out houses 110 lactating Holstein cows in a cubicle system. Mean daily milk yield was 29.5 kg d−1 head−1. The field tests were conducted in August 2022.
The barn was equipped with a sprinkling cooling system; showers were arranged 2 m above the feeding alley and 2 m apart. The water flow rate was 1.4 L min−1.The treatment scheme used was nominally 60 s of shower (de facto 67 s) and 300 s of fan; when the shower was on, the fan ran at 10% of its full speed.
Since in the experimentation fur drying was not achieved within 300 s of wetting, the sprinkler near the tested cows was disabled to allow the cows’ fur to fully dry; with this scheme, the sprinkler/fan timing was 1 min/17 min.
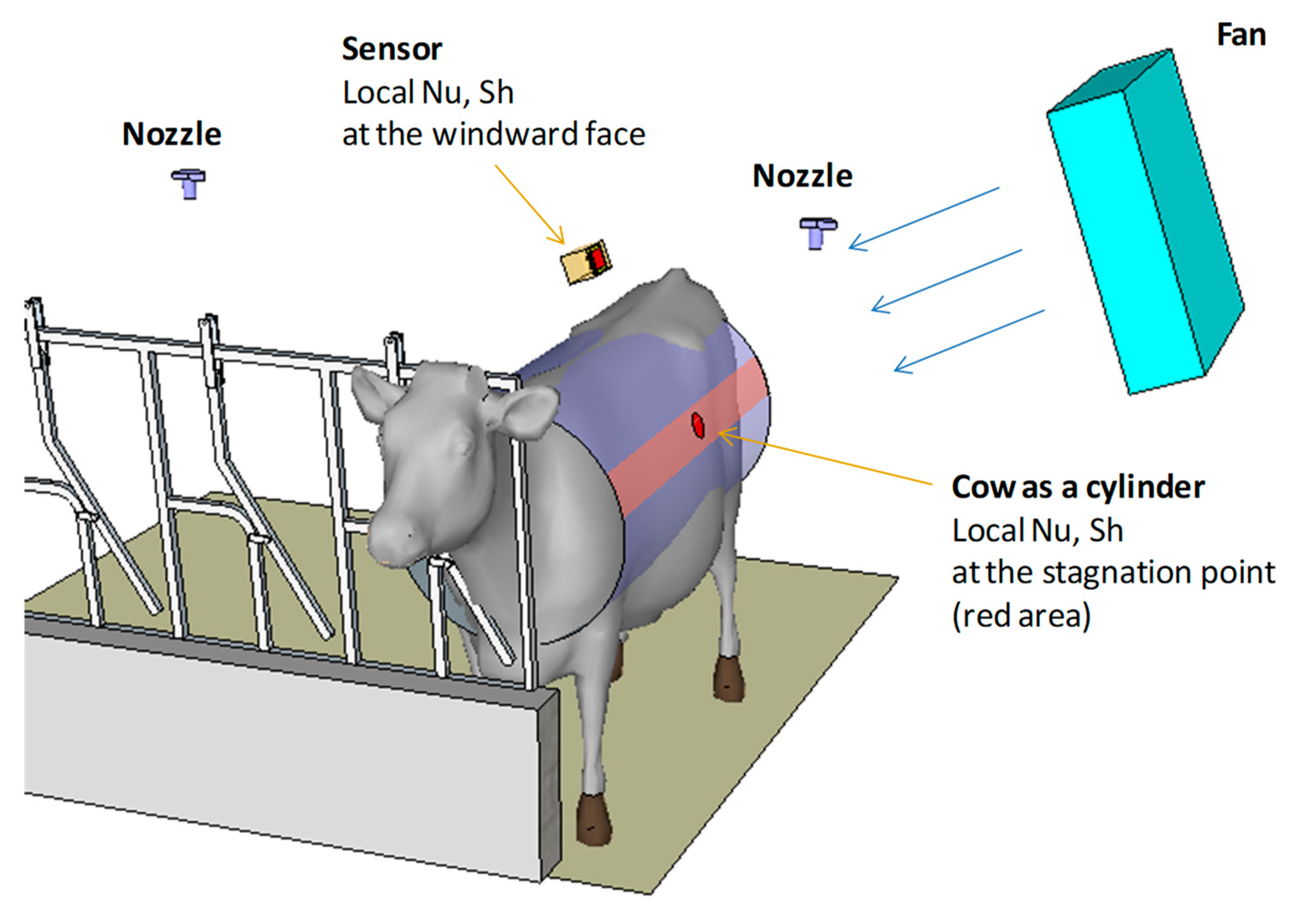
2.2. The Drying Sensor
The drying sensor is an active device acting to simulate cow heat dissipation also considering the contributions of wetted fur. The sensor has been designed to be installed in the manger alley (
Figure 1).
The sensor consists of three layers (
Figure 2): the innermost consists of an aluminum plate (thickness = 0.0005 m) maintained at the cow’s core body temperature of 38.7 °C [
11,
18] by two ceramic-encased heating resistor elements, which were controlled by a purposely designed control system.
A PTFE insulation (second layer) was placed over the aluminum plate to represent the tissue resistance of the cow.
In place of the fur, a third layer of cotton fabric was placed over the insulation. The fabric was fastened by two stainless steel electrodes at their shorter ends, to allow the measurement of the electrical conductivity (EC) of the fabric during drying, after being wetted by the action of the sprinkling (
Figure 2).This allowed for the estimation of the residual water content, and thus the prediction of the drying state of the fabric itself. The residual water content (RWC
t) is calculated by the following equation:
where WC
max, EC
max = the maximum water content and EC of the fabric at the end of spraying, respectively; and EC
t = EC during drying.
A thermal conductive compound was used between the ceramic heating elements and the aluminum plate, and between the aluminum plate and the insulation layer to improve heat transfer; the compound was also used in the junction between the plate and the RTD PT100 sensor.
The resistance of the insulation was also verified through the sensor’s power balance (Equation (2)). The insulation showed a thermal conductivity of λ = 0.20 W m
−1 K
−1 (comparable to the values found in the literature of 0.23–0.25 W m
−1 K
−1)which, for a thickness of 0.0027 m, results in a thermal resistance of 0.0135 m
2 K W
−1. Such resistance is about 4.3 times lower than that used by Chen et al. [
11], and by other authors to represent the cow tissue’s resistance (R
tissue = 0.0585 m
2 K W
−1).
To relate the behavior of the sensor to the drying fur, we need to know the time the fur become dry, and the water content of the fur after the shower. For this reason, a hand-held fur conductivity probe(
Section 2.3), and a field method to assess the fur water content by dubbing (
Section 2.5) were developed.
2.3. The Hand-Held Fur Conductivity Probe
To evaluate the complete drying of the fur, Tresoldi et al. [
14] used a cobalt-chloride-embedded paper to estimate when the fur became dry.
In the current work, the electrical conductivity of the fur was measured. The hand-held conductivity probe (
Figure 3), specially designed, consists of two electrodes, which are pressed against the fur when measurement is performed. To exert controlled pressure and improve the repeatability of the measurement, the electrodes are retractable by a spring, with a pressure of about 7.6 N cm
−2.
During the development of the device, stray currents were detected on the cow due to various unidentified causes; consequently, a capacitor to block the DC component distorting the EC measurements was added (
Figure 4).
2.4. Measuring Circuit of Electrical Conductivity of the Wetted Fabric and Fur
By measuring the electrical conductivity of the wetted fabric, the degree of saturation was evaluated and, thus, the amount of residual water present in the fabric itself was also evaluated.
The measurement circuit works with an alternating square wave current, obtained by two counter-phase oscillating digital outputs (D1, D2,
Figure 4) at 3125 Hz. Frequency does not affect EC measurement within a wide tested range (450–4500 Hz). The acquired EC was the average of 30 readings.
The circuits were calibrated with and without the capacitor, yielding two separate calibration functions, respectively, for the hand EC fur probe, and the EC fabric electrodes of the sensor.
2.5. In-Field Evaluation of the Water Content of the Wetted Fur after Shower
A method was developed to estimate the water content in fur wetted by showers. A 16 cm
2 area of saturated fur, bounded by a mask set on the coat (
Figure 5), was vigorously dabbed repeatedly with three pieces of fabric. A fourth dabbing fabric did not improve the final accuracy of the fur water content estimation.
An initial estimate of the accuracy was evaluated by lab tests with an excised fur; after dabbing, some water was remained in the fur’s internal structure in an almost fixed amount (24.8 gm−2 ± 4.1 g m−2, M ± SD). This means that by using the described method, the error will be smaller than if done on saturated or quasi-saturated fur, which is the case for our estimations (the error was about 9.6%). In any case, the remained fixed amount was added to the quantity of water found by dabbing.
2.6. Instrumentation Used
The sensor is controlled by computer software specifically developed for the present work. It continuously acquired the following: (1) air temperature and air RH (by HTU21D RH/Ta sensor produced by TE Connectivity company (Schaffhausen, Switzerland); Accuracy: RH ± 2%, Ta ± 0.3 °C); (2) the fabric’s electrical conductivity; (3) the aluminum plate’s temperature (TBs); and (4) the hand probe’s measurements of the electrical conductivity of the fur, when applied.
The control system allowed the plate temperature to be constant at the defined value (TBs = 38.7 °C) by controlling the activation of the heating elements according to the temperature of the aluminum plate.
Finally, the control software used for the experimentation allowed for observations to be entered into the log file, which was very useful when inputting fur/fabric spot temperatures measured by the infrared thermometer, and when adding comments to in-field and in-lab experimentation.
Spot measurements were made for air velocity with a hot-wire anemometer (Delta Ohm, model HD9216, Caselle di Selvazzano, Italy), and also for air temperature and humidity (Testo, model 425, Titisee-Neustadt, Germany).
2.7. IR Thermometer vs. Thermocouple Measurements
To measure surface temperature of the fur/fabric during drying, an IR thermometer was used (Fluke 561 HVAC Pro, Everett, WA, USA).To verify the response of the IR thermometer in the presence of water, both on fur and fabric, the surface temperature was compared with a type-K thermocouple measurement.
The difference was about 0.5 °C (infrared > thermocouple), both on white and black fur, with the Fluke IR thermometer set with ε = 0.95.
Gonçalves et al. [
19] showed that different porous materials wetted with water have similar emissivity (Mean = 0.95, SD = 0.2); so, we can assume that we are doing the measurement accurately by setting the IR thermometer with ε = 0.95.
2.8. Theoretical Assumptions
The sensor works with transverse flow, as this condition allows the highest evaporation rate, that is, the shortest drying time (with respect to the parallel flow. At the theoretical level and during field tests, the comparison between the fur and the sensor was done by considering the local Nusselt number and the local Sherwood number, modelling the cow as a cylinder (
Figure 1), as the aptly-named cow-cyl (diameter of the cylinder, D = 0.8 m [
11]).
The local Nusselt number for the cow-cyl was calculated at the stagnation point (around the pink strip area in
Figure 1), obtained by tabulating and interpolating the curves of the graph in [
20] (Figure 7.9) as a function of the Re number (valid for Re = 24 × 10
3− 200 × 10
3; v
a = 0.5–4 m s
−1).
To calculate the local Nusselt number, considering only the downwind face of the sensor (
Figure 1), a square cylinder configuration was considered, using data from Abd-Rabbo et al. [
21] (Figure 10), which was handled the same as in cow-cyl (valid for Re ≈ 2.2 × 10
3− 9.8 × 10
3; v
a = 0.9–4 m s
−1).
The sensor obviously had no geometrical or dynamic similarity when compared to the cow-cyl; so, the output of the sensor has to be interpreted to relate it to the behavior of the drying fur of the cow.
2.9. A Simplified Physical Model to Estimate Fur Drying Time from Sensor Output
Referring to the model proposed by Gebremedhin and Wu [
10], neglecting radiant heat exchange, a code was developed to solve, by iteration, the surface temperature (Ts
s) of the drying surface of the sensor, considering the power balance (
Figure 6):
where Q
s is the total heat loss of the sensor (W m
−2), Q
c is the convective heat flow (W m
−2), and Q
evap is the latent heat flow (W m
−2).
That is:
where R
ins(K m
2 W
−1) is the resistance of the insulation layer, T
Bs represents the core (body) temperature of the sensor (set to 38.7 °C), Ts
s is the surface temperature (°C), T
a is the air temperature (°C), Wa
s is the rate of evaporation of water from the fabric (kg m
−2 s
−1), and J is the latent heat of evaporation of water (J kg
−1).
The thermal resistances of aluminum (RAl_plate) and fabric (Rfabric) were not considered in calculating Qs because their contribution to the global resistance can be considered negligible for the purposes of the simplified model of Equation (3).
Wa
s is obtained by applying Equation (1) to two points of the drying process:
where t
0 represents the beginning time of the drying process, while t
1 can be updated as the drying progresses, allowing a mean Wa
s for a longer period.
When T
Ss was obtained (i.e., the condition of Equation (2) is achieved), the boundary conditions of the sensor were reconstructed, and thus the convective mass transfer coefficient (hm
s, m s
−1) was determined, then the Sherwood number (Sh
s), from which the local Nu
s number for the sensor was calculated, and consequently the convective coefficient of the sensor (hc
s). This allowed the evaluation of Equation (2) at each iteration. For details, see
Appendix A.
From Nus, in the backward direction, Res was calculated and, finally, so too was va. Knowing the va enabled the derivation of the local Nu cow-cyl number and then hc cow-cyl, and the air velocity va (m s−1) of the fan.
Assuming that Ts
s approximates Ts
cow-cyl, and rearranging Equation (3) for the cow, solving for Wa
cow-cyl obtains the rate of evaporation of the fur:
where T
Bcow-cyl is the core body temperature of the cow, hc
cow-cyl (W m
−2 K
−1) is the convective heat coefficient of the cow-cyl, and Ts
cow-cyl is the surface temperature of the cow.
At this point, knowing the initial water content of the fur (W
fur sat, kg m
−2), determined as per
Section 2.5, the drying time (t
dry) was calculated as follows:
2.10. Theoretical Comparison of the Thermal Response of Cow and Sensor—Sensitivity Analysis
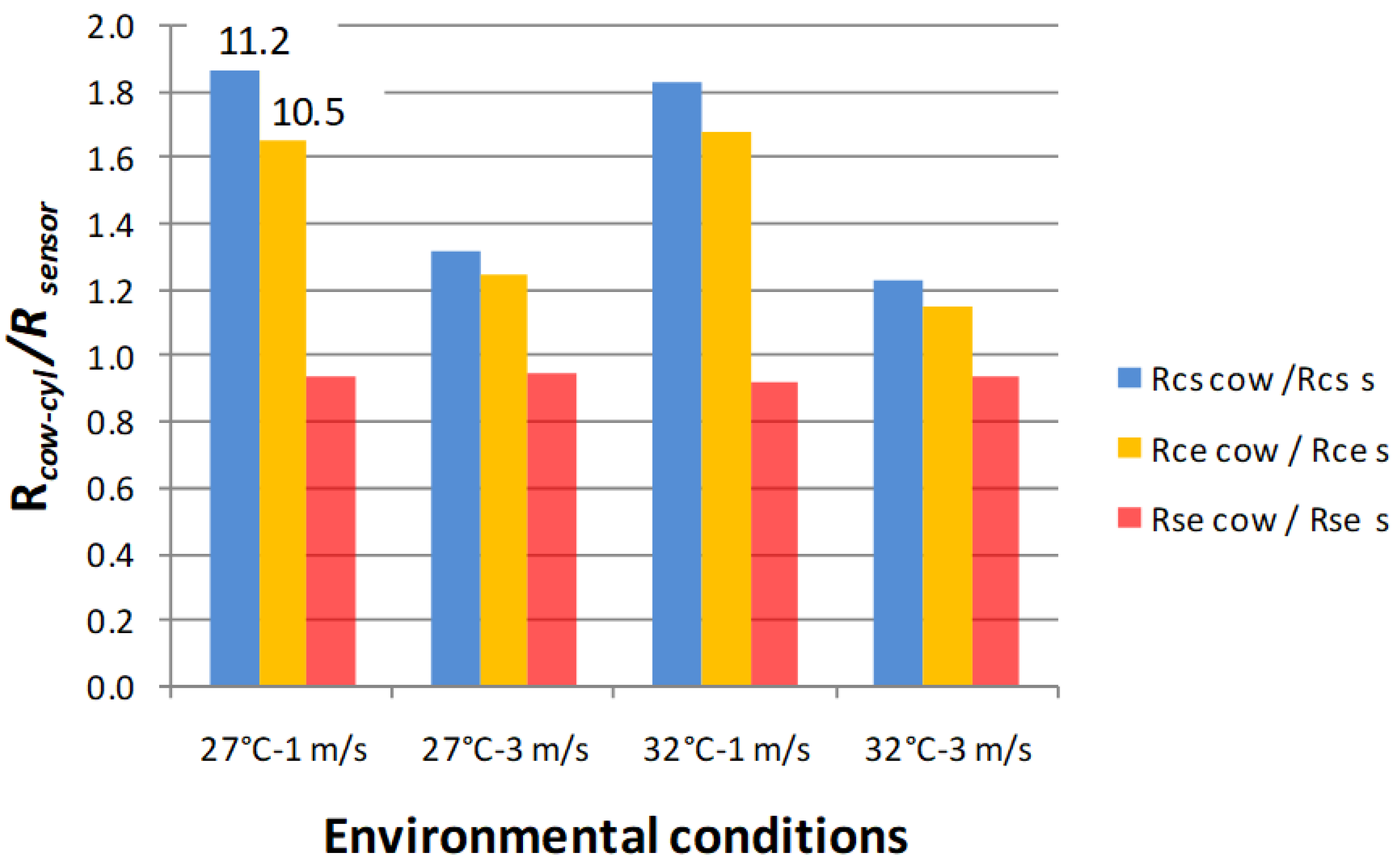
Although the sensor has no similarity with the cow-cyl, by applying the model, as in Equation (3), to the sensor and to the cow, responses were compared from the thermal point of view for two temperatures (27 and 32 °C), and for two va (1.0 and 3.0 m s−1), while RH was 40% for all simulations. The following heat ratios were compared: Qc/Qs, Qc/Qevap, and Qs/Qevap
The tissue and sensor resistances in the simulations were set, respectively, to Rtissue = 0.0585, and Rins = 0.0135 (Rtissue/Rins = 4.3).
Sensitivity analysis was carried out referring to the model by applying Equation (3) to calculate Wacow-cyl. The reference model conditions were: Tscow-cyl = 25 °C, hccow-cyl = 16 W m−2 K−1, and Ta = 32 °C. The introduced error for Tscow-cyl was ranging from 2% to 14%, while for hccow-cyl, the introduced error was higher as its variation affects Wa less, ranging from 10% to 70%.
4. Conclusions
Laboratory tests showed good correlation between the EC of the sensor fabric and its residual water content, allowing the estimation of the drying time. Meanwhile, the sensitivity analysis showed that the sensor adequately represented the heat exchanges of the cow.
The error in estimating the fur drying time (between −11.4% and +14.8%) is considered acceptable for the purpose of the sensor presented in the present work, given the high variability of its boundary conditions, even within the same context (i.e., the same barn). For example, the position of the animal at the manger may result in very different levels of ventilation and wetting of the fur; thus, we might have animals that get very wet during spraying, and receive a low-velocity airflow, or vice versa (high/low combinations with respect to wetting/ventilation might also occur).
The use of the sensor in a barn with a sprinkler/fan cooling system can help reduce energy and water consumption. For example, if applied in the barn used for experimentation, with a wetting cycle of 13.8 min (according to the actual drying time of
Figure 11), about 52 wetting cycles d
−1 are foreseen, given a daily operating time of the cooling system of 12 h. If compared to the current barn setting (wetting cycle of 6 min), there are 120 cycles d
−1. So, the use of the sensor in place of the fixed timing will provide a reduction in cycles and thus a reduced water consumption of about 57%.
Finally, we would like to highlight how the presented sensor could not only contribute to greater water and energy efficiency, but also to the improvement of the welfares of dairy cows.
Future Perspectives
From a precision livestock farming (PLF) perspective, as proposed by Chen et al. [
11], for the theoretical model, the sensor could also be used both to control the timing of the sprays and to modulate the speed of the fans during drying. For example, if the sensor estimates an excessive evaporation rate, the speed of the fans could be reduced, thus preventing the animals from being over-cooled (as well as reducing the operating costs of the cooling system).
The above perspective will require further experimentation.
Furthermore, as previously anticipated, the sensor could also be used to assess the heat stress level of the cows, keeping in mind that this sensor use will require extensive field experimentation.