Abstract
Mine ventilation provides fresh air to underground workers. The dampers can provide a qualified fresh air to each demand workplace by adjusting the air volume, which can ensure workers’ health. However, the powerful impact damage caused by gas explosions in the roadway can lead to deformation and damage to the dampers and even cause the breakdown of the ventilation system. At the same time, the impact effects of gas explosions may cause worker fatalities. For this reason, the dynamic response of gas explosions to dampers and their effects need to be studied. Based on the analysis of the damper construction and the damage characteristics of the gas explosion, ANSYS/LS-DYNA software is used to establish a mathematical-physical model of the damper with ventilation-regulating windows of six different sizes. The reliability of the model is verified by comparing the simulated pressure values with the values calculated by the Sadowski equation. The dynamic response characteristics of the dampers under the gas explosion impact are simulated and the displacement, equivalent stress and effective plastic strain of the dampers are measured. Finally, a theoretical analysis is carried out. The study results show that the displacement of the damper increases gradually from the edge to the center and the deformation is symmetrical in the absence of the ventilation-regulating window. The deformation region below the ventilation-regulating window is more obvious when the ventilation-regulating window is installed. The maximum stress of the damper first appears at the four corners of the damper, the stress of the unit at this position increases with the increase of the side length of the ventilation-regulating window. The stress of the unit in the lower left corner of the ventilation-regulating window first increases and then decreases with the increase of the side length of the ventilation-regulating window, and all the stresses of the units first increase and then decrease, and finally, the stresses basically approach a stable value. From the instantaneous ignition to the completion of the final reaction, the plastic strain gradually increases, but the area of the plastic strain region gradually decreases. The damage and deformation of the damper are basically consistent with the situation of the damper in the explosion accident. The research results can provide some theoretical basis and data support for the damper structure selection, damper location selection and setting of ventilation-regulating window.
1. Introduction
In China, most coal mines are underground [,]. Mine ventilation is necessary for underground coal mining, and requires the installation of appropriate ventilation structures []. However, underground gas explosions generate shock waves and toxic gases with high temperatures, which can disrupt the ventilation system and disturb the airflow. The influx of high temperature and toxic and hazardous gases into the workplace is a major cause of extended injuries and fatalities []. The dampers are an important part of the ventilation system, which guides and controls the airflow in the coal mine. They regulate the airflow and provide qualified airflow to each workplace, thus providing a healthy and hygienic working environment for workers. Therefore, many scholars have carried out a lot of research on dampers being damaged by gas explosions and obtained significant research results [,,,]. For example, Li Chongyi found that gas explosions can cause severe damage to ducts, supports and equipment during their propagation []. Li Feng et al. used experimental methods to study the deformation process of a square plate under impact load; it has been found that the damper deformation under impact loading is mainly a bending deformation [,]. Miao theoretically analyzed the coordinated deformation parameters such as the width of the contact surface of the damper, the maximum bending deflection, the support reaction force and the pivot point displacement, and then proposed a method to effectively promote the coordinated deformation of the dampers []. Gao carried out numerical simulations of the propagation process of gas explosions of different volumes under the condition that the damper was present and not damaged, and the results showed that the maximum value of explosion impact load on the damper and the volume of gas accumulation both have an incremental relation of power function [,]. Xu numerically simulated the damper failure under impact load by LS-DYNA software. The results showed that the trend of stress of the damper with time is consistent with the load application []. Huber studied the stress state of the reverse damper after impact, and found the weak part of the reverse damper, and combined with the relevant factors affecting the strength of the reverse damper, the safety design and strength optimization of the reverse damper were carried out []. Zhang’s research showed that the destruction of the damper has an incentive effect on the gas explosion propagation process []. Liu et al. found that the greater the mass of the blast door is, the higher the explosion overpressure inside the duct is and the longer the time required to open the blast door is, the greater the peak of flame propagation velocity is []. Song calculated the load on the explosion door based on the fan blade damage load and the explosion-proof door’s fly-up height []. Ma et al. used FLUENT software to analyze the safety and reliability of the blast door under the action of a gas explosion, obtained the pressure distribution on the blast door at different moments and its dynamic response law, and finally, proposed measures to optimize the structure of the damper []. Deng explored the influence law of the air door opening and closing dynamic process on mine airflow []. Results indicated that there is a multivariate nonlinear relationship between the abnormal fluctuation time of wind speed data and the inlet wind speed, opening and closing speed, opening and closing angle and the duration of the opening fixed angle before the air door is opened. Zhou’s study showed that the wind speed fluctuation characteristics of the measurement point in front of the dampers better reflected the opening angle of the dampers, and the two were positively correlated []. Liu found that the wind flow field in the roadway is basically unchanged before passing through the ventilation-regulating window, while it becomes abnormally turbulent after the ventilation-regulating window []. Huang’s research found that the number, location and area of the ventilation-regulating window have different effects on the wind flow in the mine []. Ye numerically studied the impact of gas explosions on dampers with different thicknesses, but the effect of the ventilation-regulating window was not considered []. Li Shujuan used FLACS software to numerically analyze the effect of the area and the position of the ventilation-regulating window on the gas explosion and found that the maximum pressure of a gas explosion in front of the damper shows an exponentially decreasing relationship with the area increase of the ventilation-regulating window [].
Therefore, the study on the dynamic response of the damper in the roadway under the action of the gas explosion load can grasp the damage degree of the damper, ensure normal ventilation, and protect the physical and psychological health of workers. In summary, under the action of an intensive gas explosion, a damper is easily deformed or even damaged and cannot be closed. However, a damper is usually equipped with a ventilation-regulating window to improve ventilation efficiency in practice. At present, there is little literature on the damage response characteristics of a damper with a ventilation-regulating window under the impact of a gas explosion. Therefore, in this paper, a damper model with a ventilation-regulating window is established by LS-DYNA software and a numerical simulation is carried out to analyze the dynamic response of the damper with ventilation-regulating windows with different areas under the explosion load. It is expected that the study results can provide some help for the setting of the ventilation-regulating window of a damper.
2. Simulation Methods
2.1. Mathematical Model
In order to carry out the reasonable and effective numerical simulation, according to the actual situation of the problems, the following reasonable assumptions are made for the model: (1) The explosion process is adiabatic, and the heat dissipation in the process of gas explosion propagation is ignored. (2) The inner wall of the roadway is insulated and smooth. The initial concentration of the premixed gas is 9.5% and the gas is evenly distributed. The initial temperature T0 is 25°C and the initial pressure P0 is 0.1 MPa. (3) The intermediate process of reaction is ignored. (4) There is only a heat source of a gas explosion in the roadway. (5) The damage to the original damper structure caused by the ventilation-regulating window is not considered, and the gaps between the joints of the damper structures are ignored. (6) The damper and the roadway will not rotate in all directions.
The destructive effect of the gas explosion is caused by energy exchange. Based on the above assumptions, the governing equations in the process of the gas explosion are as follows:
Mass conservation:
Momentum conservation:
Energy conservation:
Deformation conservation:
Constitutive relation:
Boundary relation:
Initial condition:
Formulas (1)–(7) are control equations for simulating the effects of a gas explosion on the obstacles. Using the weighted residual method, the momentum attenuation equation is obtained as follows:
where, , is virtual speed, using a step-by-step integral, Formula (8) can be written:
Formula (9) is the attenuation form regulated by the momentum-conservation equation, namely, the equation of virtual power. The spatial coordinates of the particle X at any one moment are as follows:
where, is the shape function of node I.
As a result, the displacement X at any point in the unit body is as follows:
where, is the displacement of the node I. Similarly, the velocity, acceleration, deformation rate and virtual velocity at any point in the unit body can be expressed as follows:
The above formulas are written in matrix form and substituted into the virtual power Formula (9), which is as follows:
where, , , is the system quality matrix, which is unconcerned about time, and only needs to be calculated at the initial moment. Formula (13) can obtain the nodal displacement at the current moment, and then obtain the structural strain and stress at the present moment.
2.2. Physical Model and Mesh Discretization
The numerical simulation model shown in Figure 1 is established by using the pre-processing software (LS-Prepost). The length, width and thickness of the dampers are 1.8 m, 1.8 m and 0.05 m, respectively. Two square ventilation-regulating windows with the same area are set, which are axially symmetrical at the center line of the damper. According to the actual situation, the side length of the ventilation-regulating window in this simulation is 0 (without a ventilation-regulating window), 0.2, 0.3, 0.4, 0.5 and 0.6 m, respectively. The whole damper is regarded as a solid steel plate and the damper model is established by the entity unit SOLID164 model. The unit kg-m-s is adopted in the whole modeling process. For the convenience of calculation, a simple and regular damper model is established, which is 1/2 of the solid model, and a symmetric boundary is set on the Y-Z plane. The mesh size is 0.025 m, and the number of elements of the mesh is 5185. The model after mesh generation is shown in Figure 1.
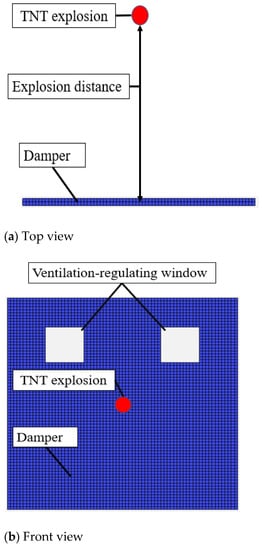
Figure 1.
Two-dimensional diagram of the finite element model.
2.3. Determination of Material Parameters
The nonlinear plastic material model *MAT_PLASTIC_KINEMATIC [,] is adopted for the damper established in this paper. Cowper and Symonds proposed a simple empirical formula between the dynamic limit yield stress and strain rate [,], the influence of strain rate effect on the yield strength of the steel material used in this paper is considered according to the Cowper–Symonds method, and its expression is shown in Formula (14):
where, is the yield strength, ε is the strain rate, K and S are the strain parameters of Cowper Symonds, is the initial yield strength, is different hardening models, is the plastic hardening modulus of steel, is the effective plastic strain.
The material density is 7850 3, the elastic modulus is , the Poisson ratio is 0.25, and the yield stress is .
2.4. Simulation Verification
The *LOAD-BLAST can define an air blast function for the application of pressure loads from the detonation of conventional explosives, which is used in conjunction with the keywords: LOAD_SEGMENT_SET []. So, the *LOAD-BLAST and *LOAD-SEGMENT-SET method combined with the application of a shock wave is applied. According to the filling gas volume in the roadway and TNT equivalent method, the TNT amount calculated at this time is 10 Kg. The response of the damper under explosion shock load is derived by placing TNT at 2.5 m in front of the dampers’ explosion face, which is shown in Figure 1. Parameters of TNT are shown in Table 1 []. Parameters of gas and air are shown in Table 2 [].

Table 1.
Parameters of TNT.

Table 2.
Parameters of gas and air.
The simulated values of the peak pressure of the shock wave on the damper are first calculated by the LS-DYNA software under different operating conditions and then compared with the calculated values o the empirical equation (Sadowski equation) to verify the reliability of the numerical simulation method. In conjunction with the literature [,], the overpressure equation of a shock wave is established by the Sadowski equation. The shock wave overpressure is as follows.
where, is the peak overpressure of the shock wave, MPa; is the scaled distance; R is the distance between the measurement point and the explosion core, m; W is the TNT equivalent, Kg.
The analysis of the theoretical and simulated values under various working conditions is shown in Table 3. The minimum error between the theoretical and simulated values is only 0.57% and the maximum error is not more than 20.265%, and the average error under different working conditions is 9.7%. The verification results show the reliability of the numerical simulation calculation method.

Table 3.
Shock wave overpressure results.
3. Results and Analysis on Numerical Simulation
3.1. Displacement Analysis of the Damper
3.1.1. Displacement Nephogram of the Damper
Figure 2 shows the displacement nephograms of the damper with the ventilation-regulating window with a 0.03 m side length at different times in the z-direction. It can be seen from Figure 2a that only the center of the damper has a circular displacement at this time, but the deformation is very small, only 2.85 × 10−6 m. In Figure 2b, the center deformation rapidly expands to the edge, and there are two shaped deformation regions between the center and the edge of the damper, where the deformation is larger than in other regions. And the deformation below the ventilation-regulating window is more obvious. In Figure 2c, the deformation of the damper reaches the maximum value, and the deformation region moves closer to the center. There is little change in the deformation area of the dampers after 0.01 s. It can be seen from Figure 2 that the deformation of the damper decreases gradually from the center to the edge.
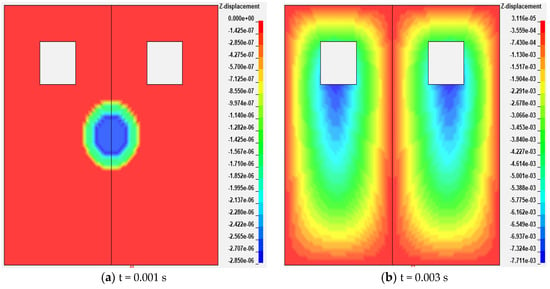
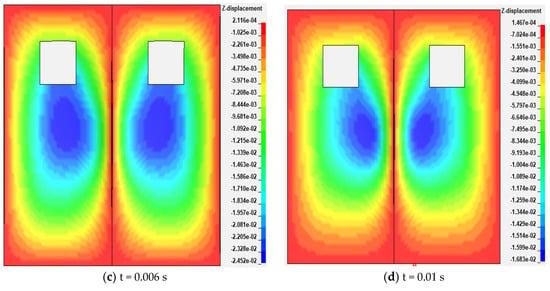
Figure 2.
Displacement nephogram of a damper at different times.
In addition, dampers with ventilation-regulating window side lengths of 0 m, 0.2 m, 0.4 m, 0.5 m and 0.6 m are simulated, respectively. The results show that the damper deformation is symmetrical up and down without the ventilation-regulating window. After the ventilation-regulating window is set, the deformation below the ventilation-regulating window is obviously larger than that in other regions, other changes are similar to the simulation results of the damper with a ventilation-regulating window with aside length of 0.3 m.
3.1.2. Displacement Curve of Time History
As shown in Figure 3, four units are selected on the dampers, A4404 is located at the lower left corner of the ventilation-regulating window, B3837 is located between the edge and the center of the damper, C3781 is located at the center of the damper, and D2557 is located at the upper left corner of the damper. The Schematic diagram of the unit’s location is shown in Figure 3. Figure 4 shows the curve of the Z-displacement of each unit with time. It can be seen from Figure 4 that the displacement of A and B units gradually increases within 0.001–0.006 s. After 0.006 s, the displacement of the damper fluctuates regularly. However, the change range of units C and D are very small.
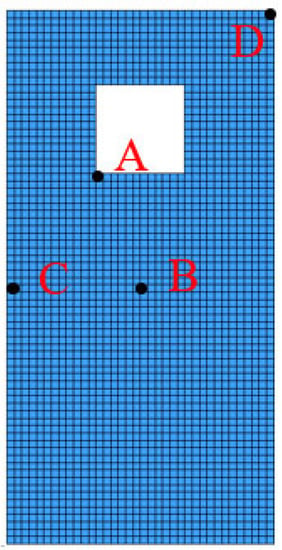
Figure 3.
Schematic diagram of the units’ location.
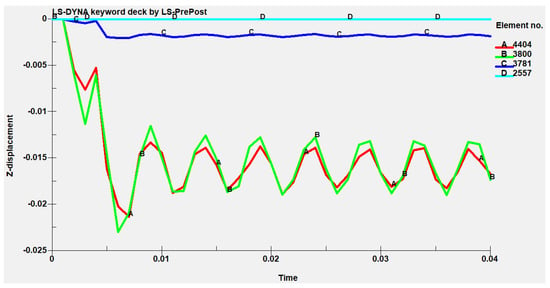
Figure 4.
Time-history displacement curve in Z direction.
From the above analysis, it can be concluded that the maximum displacement value occurs near unit body B. Figure 5 is the displacement curve of the maximum displacement unit on each damper in the Z direction at different times. It can be seen from Figure 5 that there is almost no displacement of each unit body in 0~0.001 ms, and the displacement of each unit body increases within 0.002~0.01 s. When the impact pressure is constant, the maximum displacement of the unit body increases with the increase of the side length of the ventilation-regulating window, and the maximum displacement is 00.3125 m, but none of these dampers have been destroyed.
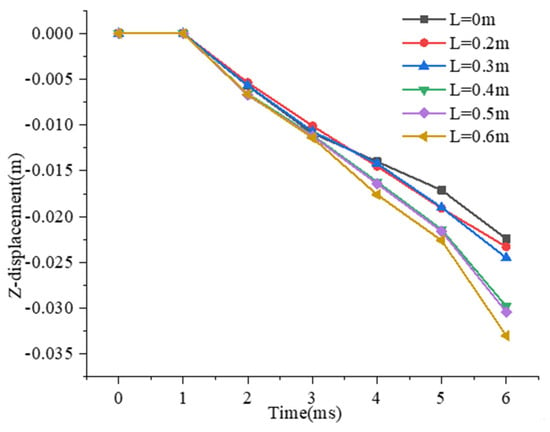
Figure 5.
Time-history displacement curve of the maximum displacement unit in Z direction.
3.2. Analyses of Equivalent Stress
3.2.1. Equivalent Stress Nephogram
The explosion load is applied to the explosion face of the damper with a ventilation-regulating window of 0.03 m in side length. The Vonmises equivalent stress nephogram of the damper is shown in Figure 6. It can be seen from Figure 6 that the maximum stress appears at the four corners and the central region of each damper under the impact load on the explosion face of the damper. The maximum stress value is 234.2 MPa, close to the yield limit of the material (235 MPa), it indicates that the damper is likely to be damaged locally. In addition, when the ventilation-regulating window is not set, the stress distribution of the damper is symmetrical up and down, the maximum stress value is 103.1 MPa, which appears in the four corners of each damper. After the ventilation-regulating window is set, the maximum stress value under the ventilation-regulating window increases with the length of the side length of the ventilation-regulating window; other changes are similar to the simulation results of a damper with a ventilation-regulating window with aside length of 0.3 m.
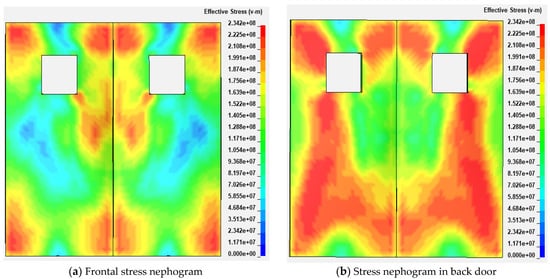
Figure 6.
Stress nephogram in frontal and back door.
3.2.2. Stress Curve of Time History
Figure 7 is the stress curve of four units on the damper with the ventilation-regulating window with 0.03 m in side length in the Z direction at different times. It can be seen from Figure 7 that the maximum stress first appears in the D2557 unit, namely, one corner of the damper, and the maximum stress of the unit body is 79.9 MPa. The maximum stress of unit A4404 is 34 MPa, while the maximum stress of C3781 is 17.2 MPa, and the maximum stress of B3837 is not more than 5 MPa. In Figure 7, the stresses of units A, C and D rapidly decrease to a certain value within 0~0.01 s. Within 0.01~0.04 s, the stresses of the four units fluctuate in a certain range, and the final stresses tend to be of a certain value. The stress of unit A4404 is the maximum at the late stage of the reaction, about 30 MPa, which indicates that the maximum stress appears at the corner of the ventilation-regulating window after 0.01 s. The reason for this phenomenon is that there is a continuous loading effect during the impact of the gas explosion. During the continuous loading of the impact, the stress on the damper gradually increases. But with the increase of time, the loading effect gradually decreases due to the weakening of the subsequent explosion shock, so the stress on the damper also decreases. That is, the stress on the damper shows a tendency to increase first and then decrease.
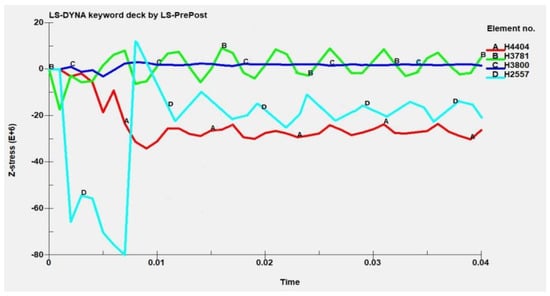
Figure 7.
Stress curve in Z direction.
From the above analysis, it can be concluded that unit D2557 and unit A4404 are stressed greatly. The maximum stress value of units D2557 and A4404 is shown in Figure 8; the curve diagram of the final trend of the stress on the damper changing with the side length of the ventilation-regulating window is also shown in Figure 8. It can be seen from Figure 8 that the maximum stress value and the final stress value of each unit have the same change trend with the increase of the side length of the ventilation-regulating window. The stress of unit D2557 increases with the increase of the area of the ventilation-regulating window, and the stress of unit A4404 increases first and then decreases with the increase of the area of the ventilation-regulating window.
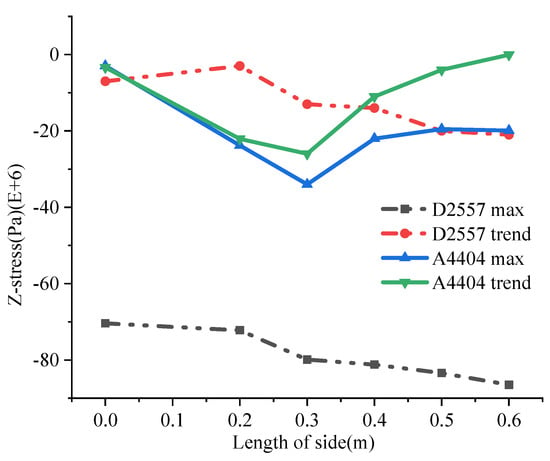
Figure 8.
Stress curve of unit A4404 and D2557 in Z direction.
3.3. Effective Plastic Strain
Figure 9 is the equivalent plastic strain nephogram of the damper with the ventilation-regulating window with 0.03 m in side length at different times. In Figure 9a, the equivalent plastic strain nephogram of the damper presents a Y-shaped strain distribution. In Figure 9b, the equivalent plastic strain of the damper increases with time; the plastic strain is more obvious in the strip region between the center and the edge of the damper. It can be seen from Figure 9c,d that the plastic strain continues to increase; the strain moves to the center and the center forms two small plastic strain regions. It can be seen from Figure 9 that a large plastic strain will appear in the central region of the damper and the four corners of the ventilation-regulating window.
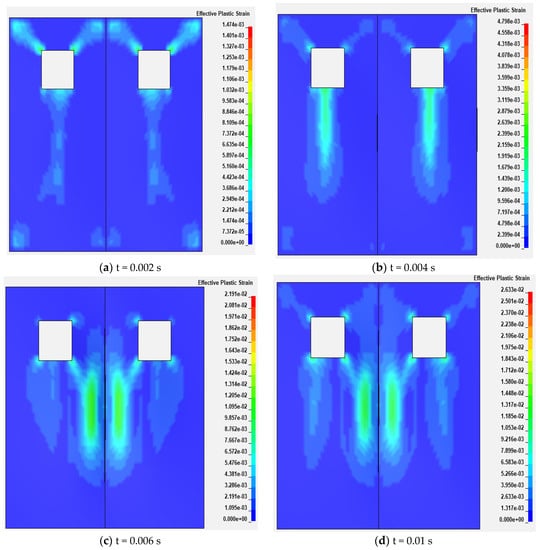
Figure 9.
Effective plastic strain nephogram with 0.03 m in side length at different times.
In addition, the equivalent plastic stress of the damper with a ventilation-regulating window side length of 0 m, 0.2 m, 0.4 m, 0.5 m and 0.6 m are simulated, respectively. Figure 10 is the curve of the plastic strain value of the units in the center area of the damper with time, and Figure 11 is the curve of the plastic strain value of the units in the lower left corner of the ventilation-regulating window with time. It can be seen from Figure 10 and Figure 11 that the plastic strain value gradually increases from instantaneous ignition to 0.01 s, and remains unchanged after 0.01 s. When the ventilation-regulating window is not set, the plastic strain of the damper is finally concentrated in the center position of the damper, and the maximum strain variable is 0.0235. After setting the ventilation-regulating window, the plastic strain value in the central area changes slightly with the edge length of the ventilation-regulating window, but the plastic strain value in the lower left corner of the ventilation-regulating window increases with the length of the ventilation-regulating window. When the side length of the ventilation-regulating window is equal to 0.2 m, the maximum plastic strain value is 0.0375, and when the side length of the ventilation-regulating window is equal to 0.6 m, the maximum plastic strain value is 0.0598.
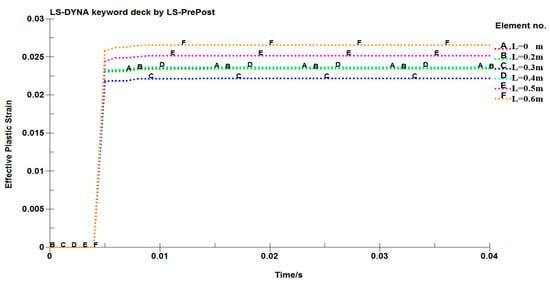
Figure 10.
Curve of the plastic strain value of the units in the center area of the damper with time.
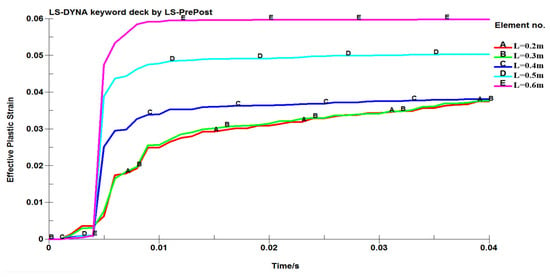
Figure 11.
Curve of the plastic strain value of the units in the lower left corner of the ventilation-regulating window with time.
4. Conclusions
The impact simulation of the damper by a gas explosion were carried out by using ANSYS/LS-DYNA. Under the same conditions, the displacement, equivalent stress and equivalent plastic strain of a damper with six kinds of ventilation-regulating windows (different areas) were numerically simulated; the main conclusions were obtained as follows:
- (1)
- The displacement of the damper increases gradually from the edge to the center. The deformation is symmetrical when the ventilation-regulating window is not set. After the ventilation-regulating window is set, the deformation below the ventilation-regulating window is more obvious. With the increase of the area increase of the ventilation-regulating window, the maximum displacement of the unit body increases, but the damper is not damaged.
- (2)
- The maximum stress first appears at the four corners of the damper. After 0.01 s, the maximum stress appears at the lower left corner of the ventilation-regulating window, where the stress increases first and then decreases with the area increase of the ventilation-regulating window.
- (3)
- The equivalent plastic strain increases gradually from the instantaneous ignition to the final reaction. When the ventilation-regulating window is not set, the plastic strain is mainly concentrated in the central region. After the ventilation-regulating window is set, the region of the plastic strain in the center of the damper decreases gradually, and the plastic strain at the lower left corner of the ventilation-regulating window increases with the area increase of the ventilation-regulating window.
Author Contributions
Conceptualization, Z.J. and Q.Y.; methodology, Z.J. and S.L.; software, Z.J. and S.L.; investigation, Q.Y. and S.L.; writing—original draft preparation, Q.Y. and S.L.; writing—review and editing, Q.Y. and Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
The National Natural Science Foundation Project of China (52174177, 52174178). The project was supported by the Scientific Research Fund of the Hunan Provincial Education Department (20B240).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lin, B.; Ye, Q. Characteristics of Gas Explosion Propagation in Confined Space; China University of Mining and Technology: Xuzhou, China, 2012. [Google Scholar]
- Chen, G.; Dong, H.; Zhang, Q.; Zhao, Y.; Hu, S.; Li, S. Review on the methane- air explosion accidents in the narrow confined space. J. Saf. Environ. 2020, 20, 946–959. [Google Scholar]
- Li, A.; Si, J.; Zhou, X. Experimental Research on Rapid Fire Zone Sealing and Explosion Venting Characteristics of an Explosion Venting Door Using a Large-Diameter Explosion Pipeline. ACS Omega 2021, 6, 27536–27545. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y. Study on the Dynamics Effect of Gas Explosion in the Mine Ventilation Network. Ph.D. Dissertation, Anhui University of Science and Technology, Anhui, China, 2011. [Google Scholar]
- Zhang, H.; Jia, Z.; Ye, Q.; Cheng, Y.; Li, S. Numerical Simulation on Influence of Initial Pressures on Gas Explosion Propagation Characteristics in Roadway. Front. Energy Res. 2022, 10, 913045. [Google Scholar] [CrossRef]
- Ye, Q.; Lin, B.; Jian, C.; Jia, Z. Propagation Characteristics of Gas Explosion in Duct with Sharp Change of Cross Sections. Disa Adv. 2012, 15, 999–1003. [Google Scholar]
- Wan, S.; Yu, M.; Zheng, K.; Xu, Y.; Wang, C.; Yuan, Z. Influence of Side Venting Position on Methane/Air Explosion Characteristics in an End-Vented Duct Containing an Obstacle. Exp. Therm. Fluid. Sci. 2018, 92, 202–210. [Google Scholar] [CrossRef]
- Ye, Q.; Wang, G.G.; Jia, Z.; Zheng, C. Experimental study on the influence of Wall Heat Effect on Gas Explosion and Its Propagation. Appl. Therm. Eng. 2017, 118, 392–397. [Google Scholar] [CrossRef]
- Li, Z. Study on Propagation Characteristics of Gas Explosion under Condition of Additional Cavity. Ph.D. Dissertation, Anhui University of Science and Technology, Anhui, China, 2017. [Google Scholar]
- Cui, G.; Jiang, Z.; Hu, P. Analysis of Deformation and Rupture of Metal Square Plates Subjected to Impulsive Loads. J. Vibr. Shock. 2008, 27, 170–174, 200–201. [Google Scholar]
- Li, F.; He, Z.; Zhang, Y.; Sha, F.; Dong, X.; Liu, Y. Dynamic Response Characteristics and Failure Mechanism of Rectangular Wind Window under Impact Load. J. China Coal Soc. 2020, 45, 3166–3175. [Google Scholar] [CrossRef]
- Gao, J.; Chen, T.; Wang, W.; Wu, Z.; Cai, H. Numerical Simulation Study on Impact Load of Gas Explosion Damper in Tunneling Face. J. Safety. Environ. 2022, 22, 688–694. [Google Scholar]
- Gao, J.; Wang, W.; Wu, Z.; Chen, T.; Cai, H. Research on Impact Load of Damper by Gas Explosion in Mining Face. J. Safety Sci.Tech. 2021, 17, 73–78. [Google Scholar]
- Liu, Z.; Song, W.; Ji, W.; Wen, X. Experimental Study in Effects of Explosion Door Mass in Venting Characteristics of Gas Deflagration. J. Therm. Sci. Tech. 2014, 13, 359–364. [Google Scholar]
- Xu, B.; LI, X. Research on the Structural Failure of Outburst Prevention Air Door According to Coal and Gas Outburst. Min. Res. Dev. 2021, 41, 80–83. [Google Scholar]
- Hu, B. Study on the Mechanism of Two-Phase Flow of Coal and Gas Outburst on the Failure of Reverse Damper. Master’s Thesis, Guizhou University, Guizhou, China, 2022. [Google Scholar]
- Hang, Z. Kinetic Characteristics of Gas Explosion for Complex Structure of Coal Mine. Ph.D. Dissertation, China University of Mining and Technology, Xuzhou, China, 2013. [Google Scholar]
- Song, W.; Sun, Y.; Wang, Y.; Wang, Z. Research on Calculation Methods for Designed Blast Load of Explosion-Proof Doors for Air Shafts of Coal Mine. J. Safety Sc. Tech. 2020, 16, 72–78. [Google Scholar]
- Fan, X. Research on Mine Automatic Resetting Type Flame Proof Door of Ventilation Shaft. Coal Sci.Tech. 2012, 40, 58–61. [Google Scholar]
- Ma, S.; Wen, X. Study on Dynamic Response Characteristics and Structure Optimization of Explosion-Proof Door in Airshaft of Coal Mine. J. Henan Polytech. Univ. Nat. Sci. 2020, 41, 30–34. [Google Scholar]
- Deng, L.; Shang, W.; Liu, J.; Wang, D.; Song, Y. Simulation Experimental Study on the Effect of Air Door Opening and Closing on the Wind Flow Law of Mine. J. Saf. Environ. 2022. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, J.; Deng, L.; Shang, W.; Song, Y. Research on Influence of Dynamic Process of Dampers Opening and Closing on Air Flow in Mine. J. Safety Sc. Tech. 2022, 18, 58–66. [Google Scholar]
- Liu, Y. Study on Flow Characteristics of Adjusting Window in Roadway Based on PIV Experiment. Master’s Thesis, Liaoning Technical University, Liaoning, China, 2017. [Google Scholar]
- Huang, G.; Sun, P.; Lu, Q. Influence of Air Windows on Underground Ventilation System and Its Adjusting and Locating Optimization. J. Safety Sc. Tech. 2014, 10, 160–167. [Google Scholar]
- Ye, Q. Numerical Simulation on Destruction Process of Ventilation Door by Gas Explosion. Procedia Eng. 2018, 211, 934–944. [Google Scholar] [CrossRef]
- Li, S.; Jia, Z.; Ye, Q.; Chen, Y.; Tan, S. Numerical Analysis on Influence of Ventilation-Regulator Window on Gas Explosion. J. Safety Sci. Tech. 2022, 18, 79–84. [Google Scholar]
- Wu, Y. Analysis of dynamic response and continuous collapse of steel frame structure under indoor gas explosion. Master’s Thesis, Northeast Forestry University, Harbin, China, 2012. [Google Scholar]
- Chen, D.; He, X.; Yang, H.; Xiang, G.; Zuo, Z. Influencing Factors Analysis on Numerical Simulation of Ventilation Facilities Caused by Gas Explosion Destruction Status Shock Wave. Saf. Secur. 2021, 42, 36–42. [Google Scholar]
- Li, Y.; Shi, D.; Zhao, Y. Basic Theory and Engineering Practice of ANSYS 11.0/LS-DYNA; China Water Resources and Hydropower Press: Beijing, China, 2011. [Google Scholar]
- Shi, S.; Kang, J.; Wang, M. Engineering Application of ANSYS/LS-DYNA in the Field of Explosion and Shock; China Construction Industry Press: Beijing, China, 2011. [Google Scholar]
- LS-DYNA Keyword User’s Manual, 1st ed.; Livermore Software Technology Corporation: Livermore, CA, USA, 2006.
- Qian, X.; Tian, M.; Shi, T.; Yao, P. Numerical simulation analysis of explosion response of transparent plate. J. Saf. Environ. 2022, 22, 704–711. [Google Scholar]
- Yang, X.; Shi, S.; Cheng, P. Prediction and Numerical Simulation of Overpressure Peak Value of TNT Explosion Shock Wave in Air. Blast 2008, 25, 15–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).