Comparisons on the Local Impact Response of Sandwich Panels with In-Plane and Out-Of-Plane Honeycomb Cores
Abstract
:1. Introduction
2. Geometries
3. Finite Element Model Validation
3.1. The FE Model
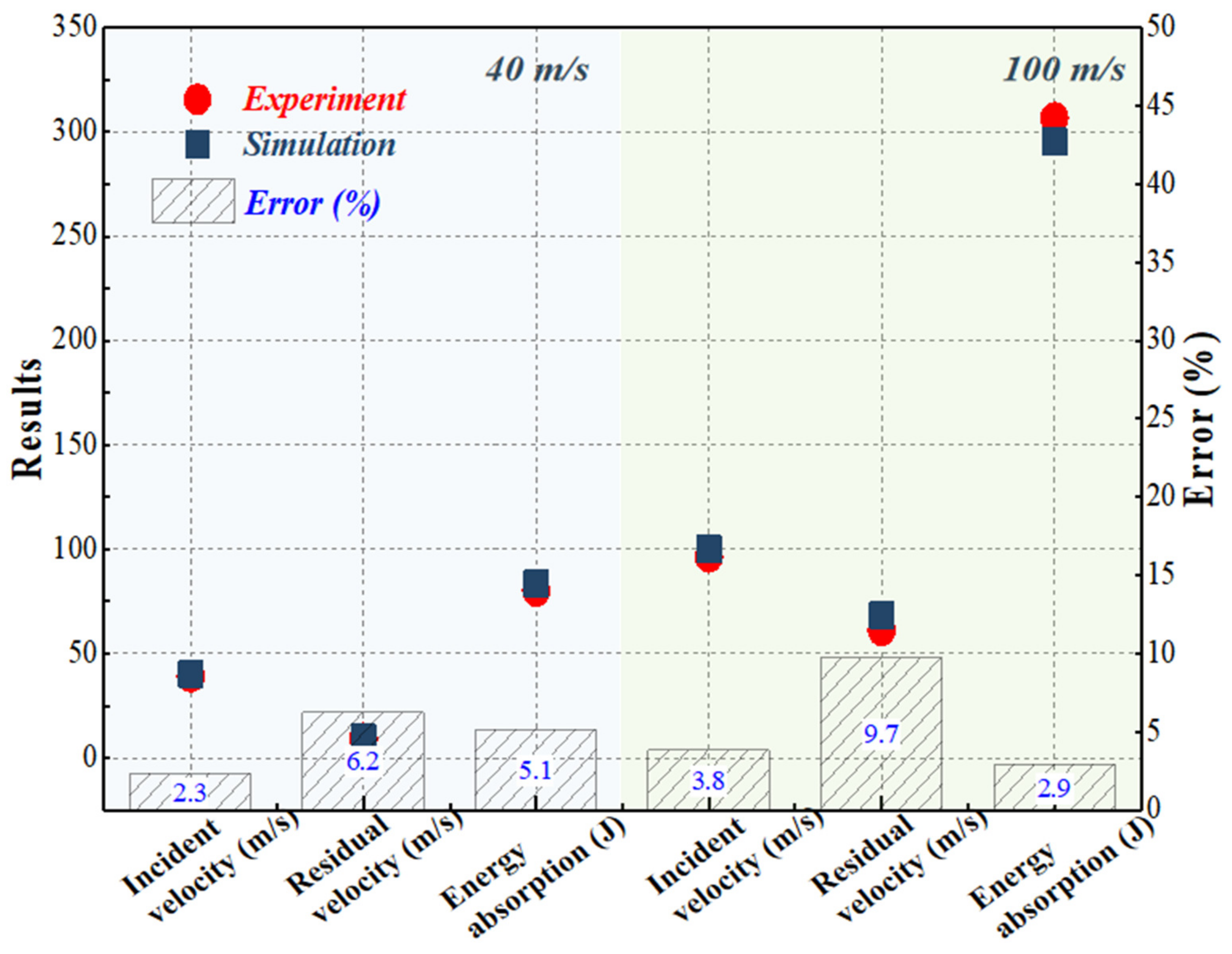
3.2. FE Model Calibration
4. Results and Discussions
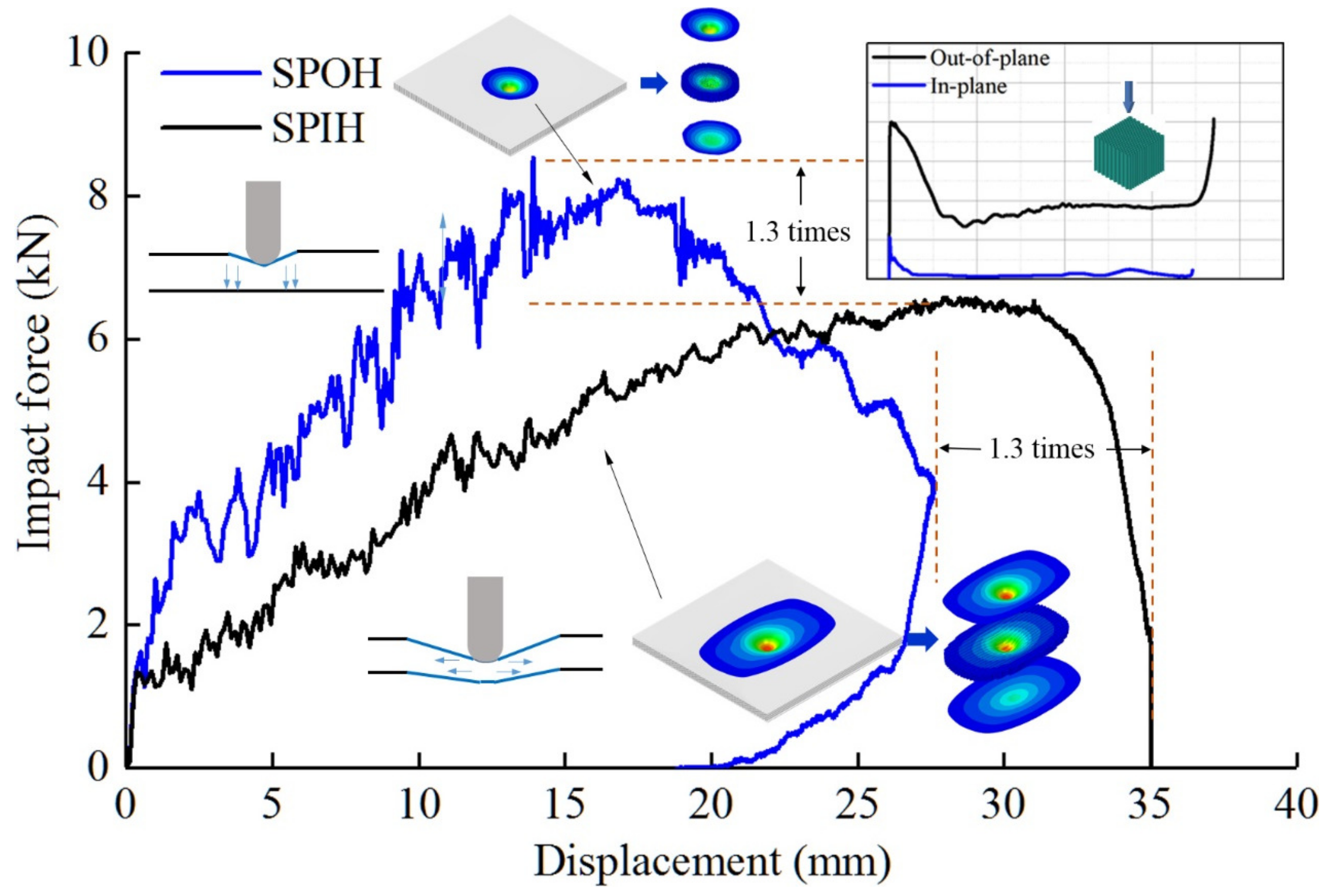
4.1. Comparison between SPIH and SPOH
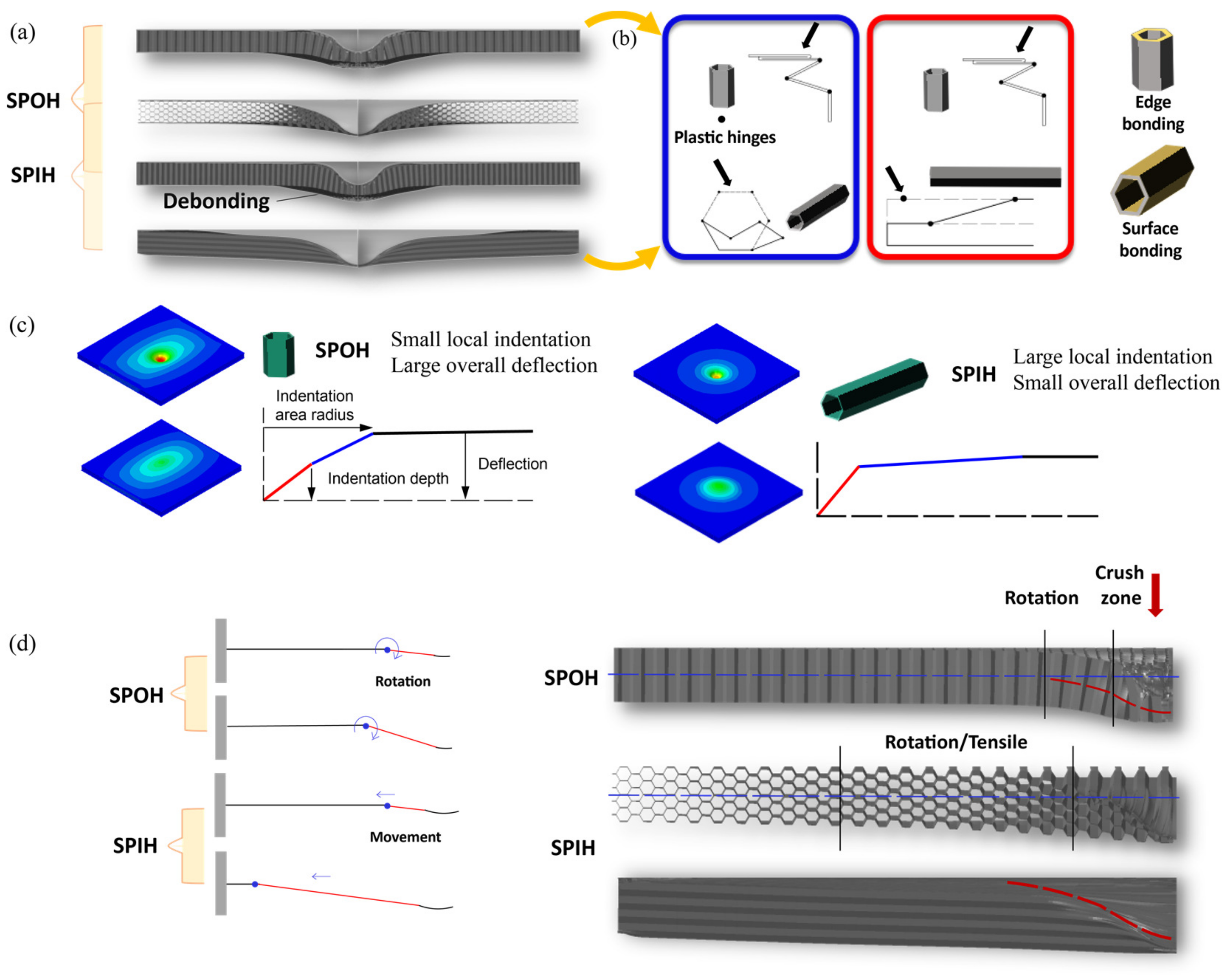
4.1.1. Modes Characterization
4.1.2. Mode-Related Impact Characteristic
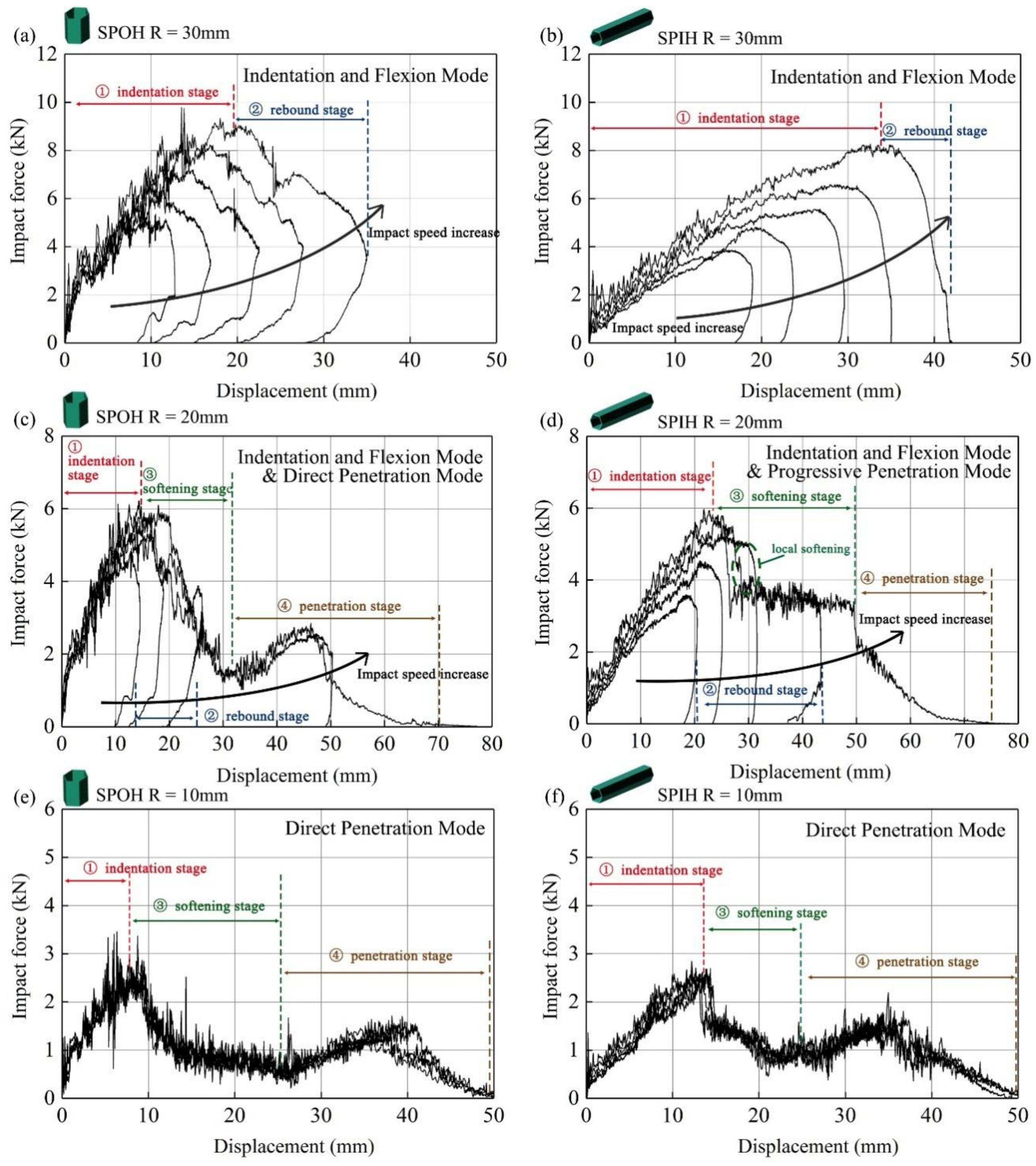
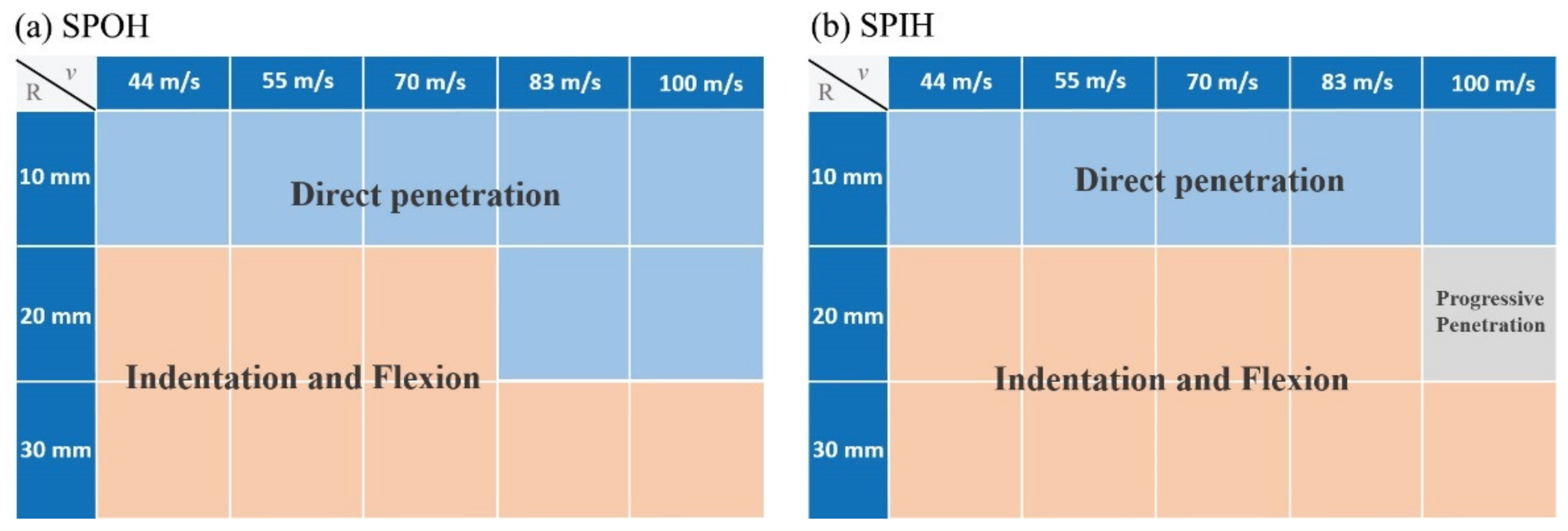
4.2. Effect of Impact Speeds and Impactor Radius
4.2.1. Modes Characterization
4.2.2. Mode-Related Impact Characteristic
5. Gradient Design
5.1. Gradient Design
5.2. Modes Characterization
5.3. Mode-Related Impact Characteristic
6. Conclusions
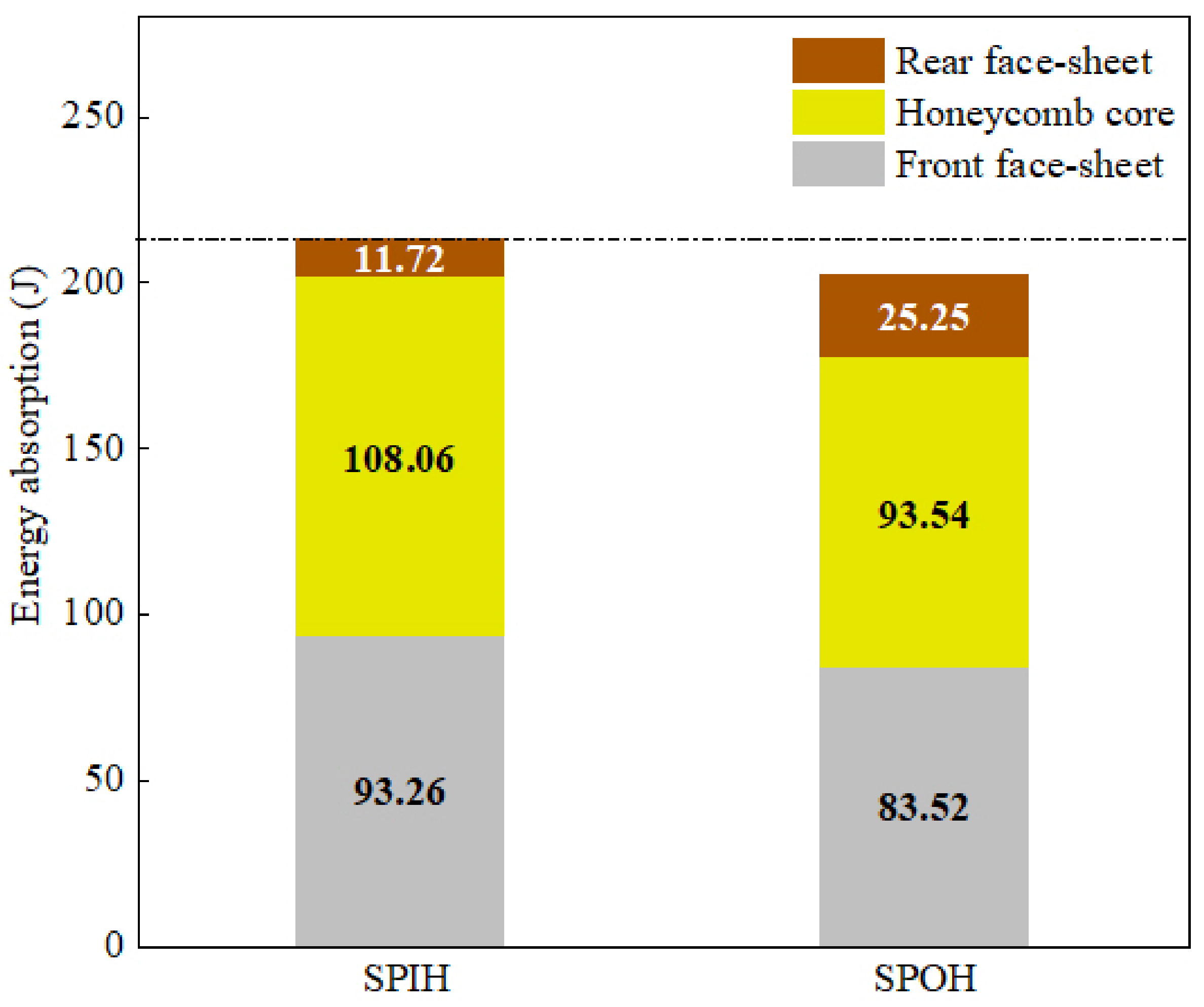
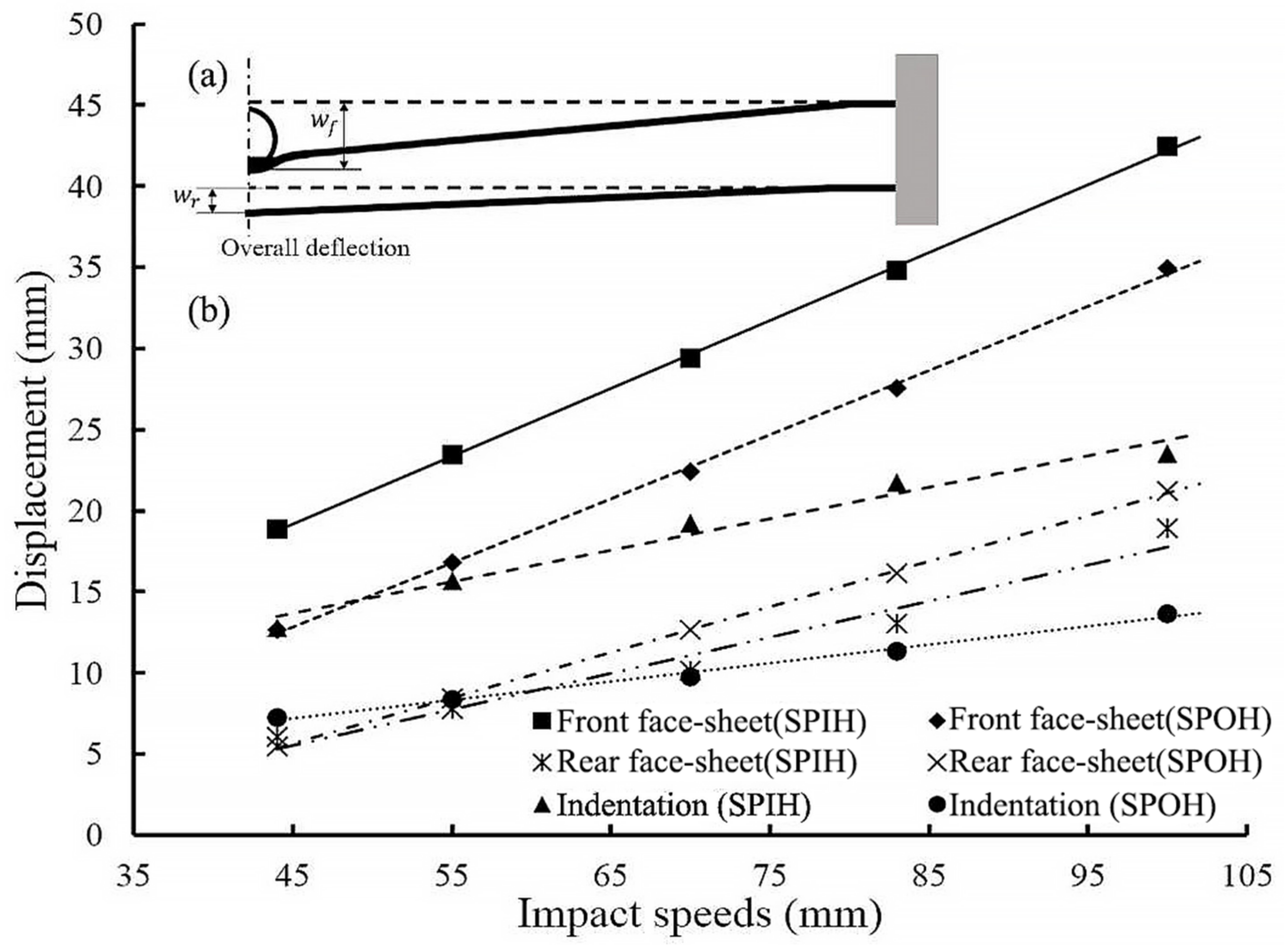
- Compared with SPOH, SPIH shows better energy absorption protection effect under different impact loads. The use of in-plane honeycomb core is not only beneficial to reduce the overall deflection, but also significantly improves the energy absorption. When the sandwich planes are not penetrated (with impact radius 20 mm and impact speed 83 m/s), the maximum displacement of SPIH rear face-sheet is reduced by 30.12% compared with SPOH. When the sandwich panels are penetrated (with impact radius 20 mm and impact speed 83 m/s), the TEA of SPIH is 158.89 J, and the TEA of SPOH is 200.18 J. In contrast, SPIH’s energy absorption increased 59.79%.
- There is an order of magnitude difference between the in-plane strength and the out-of-plane strength of honeycomb. However, under local impact, the difference in impact peak force between SPIH and SPOH is relatively small. When the impact radius is 30 mm and the impact speed is 100 m/s, the peak contact force of SPIH is only 10% less than that of SPOH. It shows that the impact resistance of sandwich panel is not directly determined by the core compression strength. The response mode also has a significant effect.
- The size effect is significant when the sandwich panels are subjected to local impact. A smaller impactor radius is more likely to cause penetration. The indentation flexion mode, direct penetration mode, and progressive penetration mode are three typical characteristic modes. The progressive penetration mode is unique to SPIH, which greatly improves the energy absorption under penetration conditions.
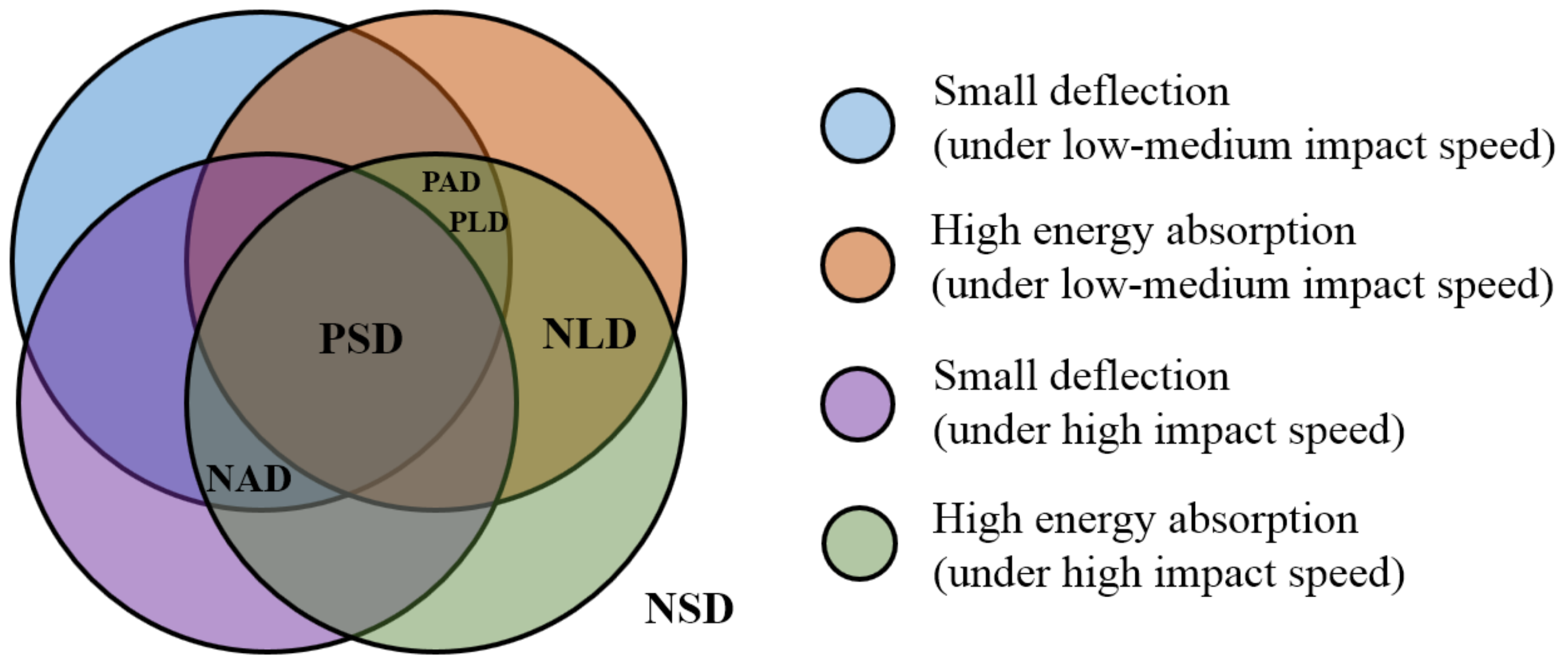
- Through the gradient design of SPIH, the impact resistance characteristics under different load conditions can be optimized. The different gradient schemes enable sandwich panels to perform multiple functions. In general, PSD is recommended to reduce the overall deflection and increase the energy absorption.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Chen, W.; Hao, H.; Wang, Z. In-plane crushing behaviors of hexagonal honeycombs with different Poisson’s ratio induced by topological diversity. Thin-Walled Struct. 2021, 159, 107223. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J. Numerical and theoretical analysis of honeycomb structure filled with circular aluminum tubes subjected to axial compression. Compos. Part B Eng. 2019, 165, 626–635. [Google Scholar] [CrossRef]
- Pydah, A.; Batra, R. Blast loading of bumper shielded hybrid two-core Miura-ori/honeycomb core sandwich plates. Thin-Walled Struct. 2018, 129, 45–57. [Google Scholar] [CrossRef]
- Hou, W.; Shen, Y.; Jiang, K.; Wang, C. Study on mechanical properties of carbon fiber honeycomb curved sandwich structure and its application in engine hood. Compos. Struct. 2022, 286, 115302. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, W.; Lu, Z.; Gu, H.; Li, T.; Zhong, M. Effect of car-body initial dynamic sway on overturning before high-speed trains negotiate wind speed variations. Veh. Syst. Dyn. 2021, 60, 2451–2468. [Google Scholar] [CrossRef]
- Liu, D.; Li, T.; Lu, Z.; Chen, J.; Zhong, M. Experimental–numerical investigation of momentary discomfort in a high-speed train in varying wind speed conditions. Veh. Syst. Dyn. 2020, 60, 1440–1459. [Google Scholar] [CrossRef]
- Tao, Q.; Ren, P.; Shi, L.; Zhao, Z.; Tang, Y.; Ye, R.; Zhang, W.; Cui, J. Energy absorption and impact behavior of composite sandwich panels under high-speed spherical projectile. Int. J. Impact Eng. 2022, 162, 104143. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Hui, D. Blast resistance and parametric study of sandwich structure consisting of honeycomb core filled with circular metallic tubes. Compos. Part B Eng. 2018, 145, 261–269. [Google Scholar] [CrossRef]
- Sun, G.; Chen, D.; Huo, X.; Zheng, G.; Li, Q. Experimental and numerical studies on indentation and perforation characteristics of honeycomb sandwich panels. Compos. Struct. 2018, 184, 110–124. [Google Scholar] [CrossRef]
- Xu, J.; Fu, C.; Fu, Q.; Chen, Y.; Feng, X. Flexible arc-armor inspired by origami. Int. J. Mech. Sci. 2021, 201, 106463. [Google Scholar] [CrossRef]
- Liu, J.; Dong, Z.; Zhu, X.; Sun, W.; Huang, Z. Flexural properties of lightweight carbon fiber/epoxy resin composite sandwiches with different fiber directions. Mater. Res. Express 2022, 9, 10. [Google Scholar] [CrossRef]
- Wang, H.; Ramakrishnan, K.; Shankar, K. Experimental study of the medium speed impact response of sandwich panels with different cores. Mater. Des. 2016, 99, 68–82. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Hao, H.; Yang, Q.; Fang, R. Energy absorption of kirigami modified corrugated structure. Thin-Walled Struct. 2020, 154, 106829. [Google Scholar] [CrossRef]
- Tang, J.; Zhou, Z.; Chen, H.; Wang, S.; Gutierrez, A.; Zhang, C.; Deng, J. Laminate design, optimization, and testing of an innovative carbon fiber-reinforced composite sandwich panel for high-speed train. Polym. Compos. 2021, 42, 5811–5829. [Google Scholar] [CrossRef]
- Xiang, C.; Qin, Q.; Wang, M.; Yu, X.; Chen, S.; Zhang, W.; Xia, Y.; Zhang, J.; Zhao, J.; Wang, T. Low-speed impact response of sandwich beams with a metal foam core: Experimental and theoretical investigations. Int. J. Impact Eng. 2019, 130, 172–183. [Google Scholar] [CrossRef]
- Wang, Z.; Lu, Z.; Yao, S.; Zhang, Y.; Hui, D.; Feo, L. Deformation mode evolutional mechanism of honeycomb structure when undergoing a shallow inclined load. Compos. Struct. 2016, 147, 211–219. [Google Scholar] [CrossRef]
- Liu, J.; Chen, W.; Hao, H.; Wang, Z. Numerical study of low-speed impact response of sandwich panel with tube filled honeycomb core. Compos. Struct. 2019, 220, 736–748. [Google Scholar] [CrossRef]
- Zhang, W.; Yan, L.; Zhao, X.; Su, P.; Lu, T. Enhancement Effect and Energy Absorption of Double-Layer Metallic Lattice Structure Filled with Aluminum Foam. Rare Met. Mater. Eng. 2019, 48, 3911–3916. [Google Scholar]
- Lv, W.; Li, D.; Dong, L. Study on blast resistance of a composite sandwich panel with isotropic foam core with negative Poisson’s ratio. Int. J. Mech. Sci. 2021, 191, 106105. [Google Scholar] [CrossRef]
- Ha, N.; Lu, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Compos. Part B Eng. 2020, 181, 38. [Google Scholar] [CrossRef]
- Felipe, D.; Ferreira, G.; Carlos, A.; Da, C.; Faria, B.; Morais, J. Experimental dynamic analysis of composite sandwich beams with magnetorheological honeycomb core. Eng. Struct. 2018, 176, 231–242. [Google Scholar]
- Xiang, J.; Du, J. Energy absorption characteristics of bio-inspired honeycomb structure under axial impact loading. Mater. Sci. Eng. A 2017, 696, 283–289. [Google Scholar] [CrossRef]
- Peng, H.; Du, J. Energy Absorption Characteristics of Bio-Inspired Honeycomb Column Thin-Walled Structure Under Impact Loading. J. Mech. Behav. Biomed. Mater. 2018, 79, 301. [Google Scholar]
- Zhang, L.; Bai, Z.; Bai, F. Crashworthiness design for bio-inspired multi-cell tubes with quadrilateral, hexagonal and octagonal sections. Thin-Walled Struct. 2018, 122, 42–51. [Google Scholar] [CrossRef]
- Alkbir, M.F.M.; Sapuan, S.M.; Nuraini, A.A.; Ishak, M.R. Fibre properties and crashworthiness parameters of natural fibre-reinforced composite structure: A literature review. Compos. Struct. 2016, 148, 59–73. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, K.; Hou, S.; Han, X.; Ye, L. Multi-objective optimization for designing a composite sandwich structure under normal and 45° impact loadings. Compos. Part B Eng. 2018, 142, 159–170. [Google Scholar] [CrossRef]
- Usta, F.; Türkmen, H.; Scarpa, F. Low-speed impact resistance of composite sandwich panels with various types of auxetic and non-auxetic core structures. Thin-Walled Struct. 2021, 163, 107738. [Google Scholar] [CrossRef]
- Sun, G.; Chen, D.; Wang, H.; Hazell, P.J.; Li, Q. High-velocity impact behaviour of aluminium honeycomb sandwich panels with different structural configurations. Int. J. Impact Eng. 2018, 122, 119–136. [Google Scholar] [CrossRef]
- Sun, G.; Huo, X.; Wang, H.; Hazell, P.J.; Li, Q. On the structural parameters of honeycomb-core sandwich panels against low-speed impact. Compos. Part B Eng. 2021, 216, 108881. [Google Scholar] [CrossRef]
- Zhang, Y.; Zong, Z.; Liu, Q.; Ma, J.; Wu, Y.; Li, Q. Static and dynamic crushing responses of CFRP sandwich panels filled with different reinforced materials. Mater. Des. 2017, 117, 396–408. [Google Scholar] [CrossRef]
- Baran, T.; Ztürk, M. In-plane elasticity of a strengthened re-entrant honeycomb cell. Eur. J. Mech. A Solids 2020, 83, 104037. [Google Scholar] [CrossRef]
- Shen, J.; Ge, J.; Xiao, J.; Liang, J. In-plane impact dynamics of honeycomb structure containing curved reentrant sides with negative Poisson’s ratio effect. Mech. Adv. Mater. Struct. 2020, 29, 1489–1497. [Google Scholar] [CrossRef]
- Ma, Q.; Rejab, R.; Siregar, J.; Guan, Z. A review of the recent trends on core structures and impact response of sandwich panels. J. Compos. Mater. 2021, 55, 2513–2555. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Q.; Chen, W.; Hao, H.; Fang, R.; Cui, J. Dynamic compressive properties of reinforced and kirigami modified honeycomb in three axial directions. Thin-Walled Struct. 2022, 171, 108692. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z.; Shim, V.; Guo, Y.; Wang, Z. In-plane compression of 3D-printed self-similar hierarchical honeycombs—Static and dynamic analysis. Thin-Walled Struct. 2020, 157, 106990. [Google Scholar] [CrossRef]
- Wang, S.; Wang, R.; Xia, Y.; Sun, Z.; You, L.; Zhang, J. Multi-objective aerodynamic optimization of high-speed train heads based on the PDE parametric modeling. Struct. Multidiscip. Optim. 2021, 64, 1285–1304. [Google Scholar] [CrossRef]
- Saurabh, R.; Nikhil, K.; Gaurav, T. A comparative study on the ballistic performance of aramid and aluminum honeycomb sandwich structures. Compos. Struct. 2022, 299, 116048. [Google Scholar]
- Li, Y.; Wu, X.; Xiao, W.; Wang, S.; Zhu, L. Experimental study on the dynamic behaviour of aluminium honeycomb sandwich panel subjected to ice wedge impact. Compos. Struct. 2022, 282, 115092. [Google Scholar] [CrossRef]
- Li, Y.; Lv, Z.; Wang, Y. Blast response of aluminum foam sandwich panel with double V-shaped face plate. Int. J. Impact Eng. 2020, 144, 103666. [Google Scholar] [CrossRef]
- Wang, Z.; Lei, Z.; Li, Z.; Yuan, K.; Wang, X. Mechanical reinforcement mechanism of a hierarchical Kagome honeycomb. Thin-Walled Struct. 2021, 167, 108235. [Google Scholar] [CrossRef]
- He, Q.; Feng, J.; Zhou, H. A numerical study on the in-plane dynamic crushing of self-similar hierarchical honeycombs. Mech. Mater. 2019, 138, 103–151. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, L.; Fu, K. Progressive failure of CFRP tubes reinforced with composite sandwich panels: Numerical analysis and energy absorption. Compos. Struct. 2021, 263, 113674. [Google Scholar] [CrossRef]
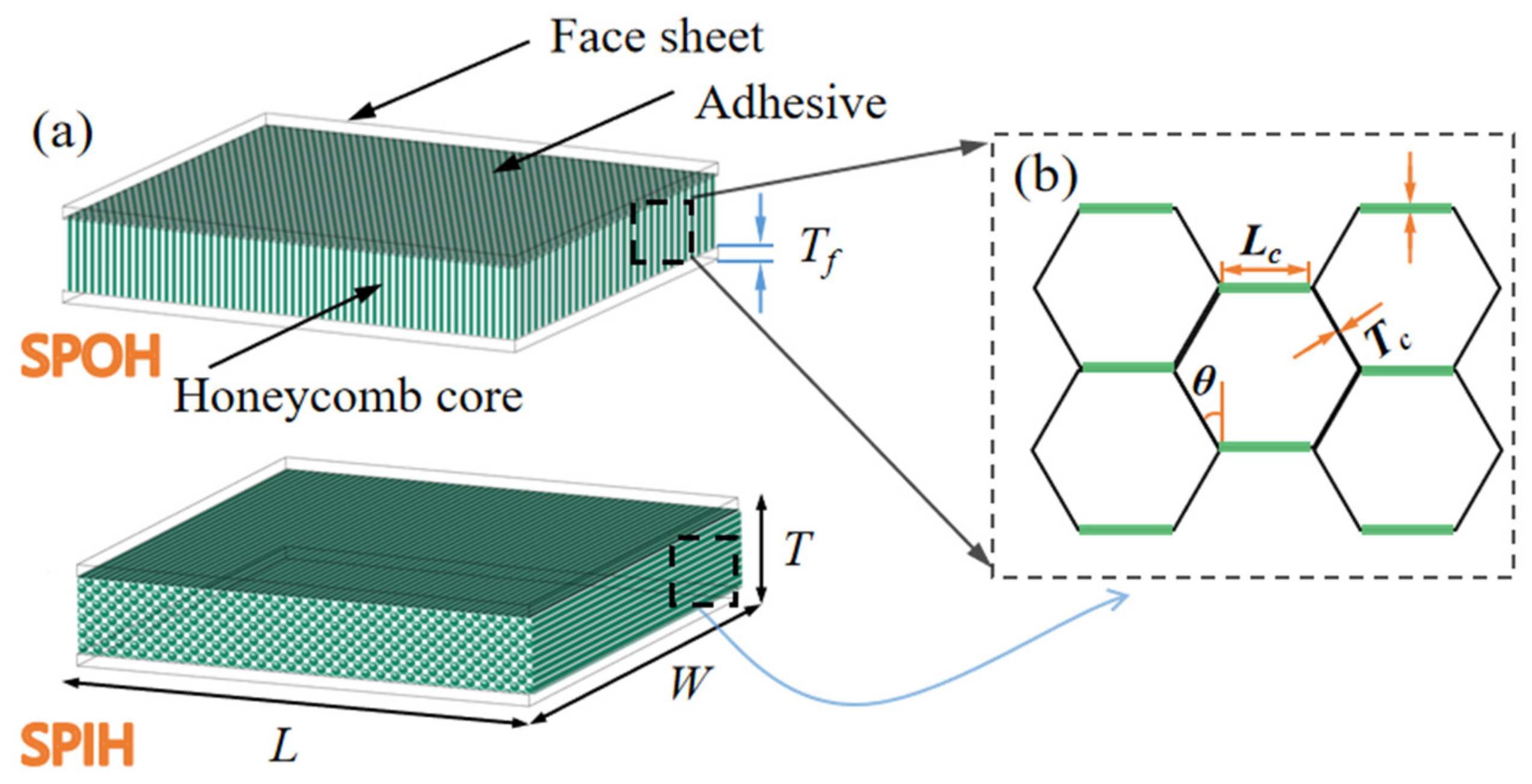
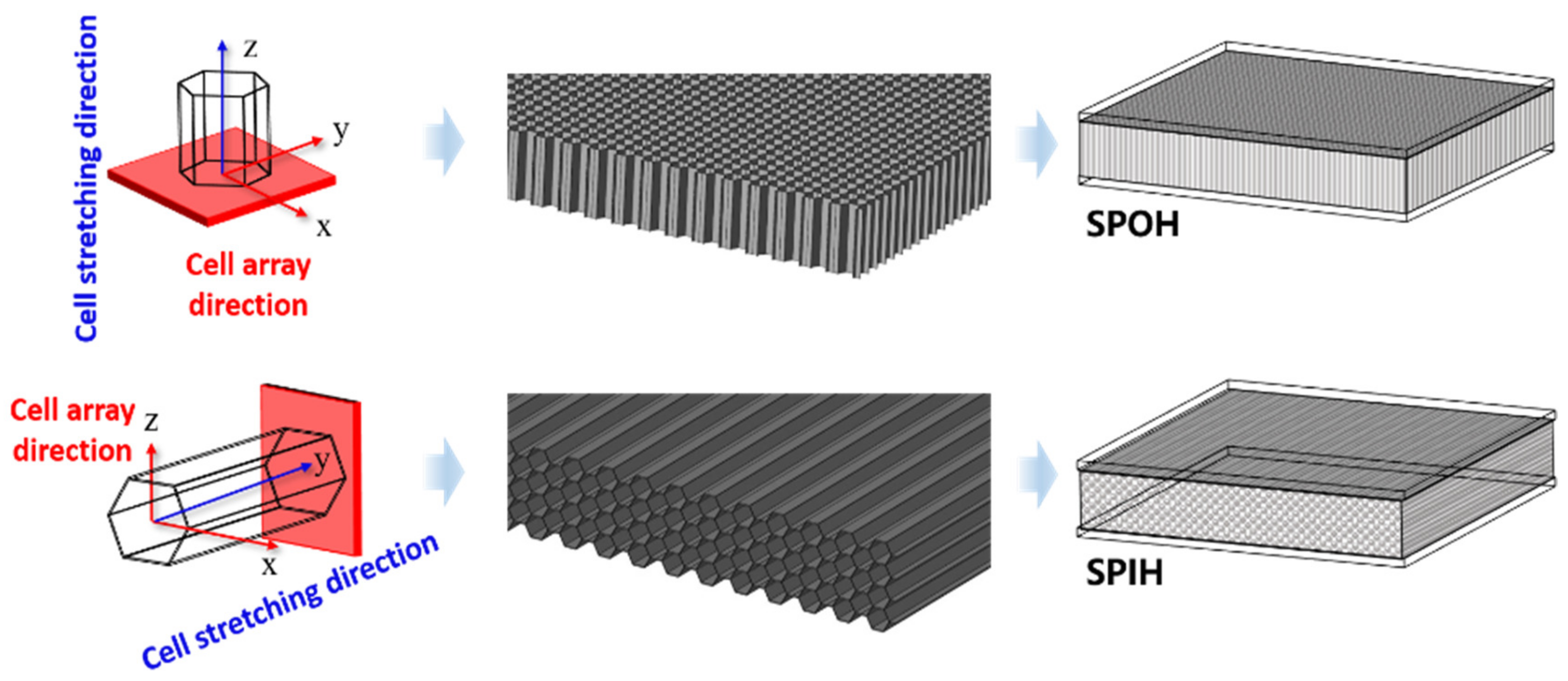



| Component | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Stress (MPa) |
|---|---|---|---|---|
| Honeycomb | 2680 | 67.6 | 0.33 | / |
| Face-sheet | 2680 | 67.6 | 0.33 | / |
| Adhesive | 1500 | 2.5 | 0.3 | 48 |
| Component | A (MPa) | B (MPa) | C | n | |
|---|---|---|---|---|---|
| Honeycomb | 1 | 143 | 0.015 | 0.63 | 1 |
| Face-sheet | 138 | 231 | 0.015 | 0.63 | 1 |
| No. | Specimen | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | SPOH | 15 | 4 | 0.06 | 1 | 250 | 250 | 40 |
| 2 | SPOH | 15 | 4 | 0.06 | 1 | 250 | 250 | 100 |
| Parameters | 24 | 3.46 | 0.06 | 1 | 250 | 250 | 40 | 30 |
| R = 20 mm | R = 30 mm | ||||
|---|---|---|---|---|---|
| 83 m/s | 100 m/s | 44 m/s | 70 m/s | 100 m/s | |
| SPOH | 148.24 J | 158.89 J | 41.24 J | 49.19 J | 49.34 J |
| SPIH | 167.63 J | 200.18 J | 43.63 J | 50.12 J | 51.17 J |
| Increment (%) | 13.08 | 59.79 | 4.66 | 6.62 | 5.02 |
| R = 20 mm | R = 30 mm | ||||
|---|---|---|---|---|---|
| 83 m/s | 100 m/s | 44 m/s | 70 m/s | 100 m/s | |
| SPOH | 15.49 m/s | 30.18 m/s | 8.46 m/s | 27.07 m/s | 44.80 m/s |
| SPIH | no penetrated | 20.32 m/s | 6.91 m/s | 26.90 m/s | 44.59 m/s |
| Reduction (%) | - | 32.67 | 18.32 | 0.63 | 0.47 |
 | Density Gradient | Cell Wall Thickness |
|---|---|---|
| Non-gradient |  | 0.17 mm |
| PLD |  | 0.22–0.12 mm |
| NLD |  | 0.12–0.22 mm |
| PAD |  | 0.22–0.12 mm |
| NAD |  | 0.12–0.22 mm |
| PSD |  | 0.22–0.12 mm |
| NSD |  | 0.12–0.22 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, G.; Lei, Z. Comparisons on the Local Impact Response of Sandwich Panels with In-Plane and Out-Of-Plane Honeycomb Cores. Sustainability 2023, 15, 3437. https://doi.org/10.3390/su15043437
Liu J, Wang G, Lei Z. Comparisons on the Local Impact Response of Sandwich Panels with In-Plane and Out-Of-Plane Honeycomb Cores. Sustainability. 2023; 15(4):3437. https://doi.org/10.3390/su15043437
Chicago/Turabian StyleLiu, Jiefu, Genda Wang, and Ziping Lei. 2023. "Comparisons on the Local Impact Response of Sandwich Panels with In-Plane and Out-Of-Plane Honeycomb Cores" Sustainability 15, no. 4: 3437. https://doi.org/10.3390/su15043437





