An Analytical Solution for Unsteady Aerodynamic Forces on Streamlined Box Girders with Coupled Vibration
Abstract
:1. Introduction
2. Complex Potential
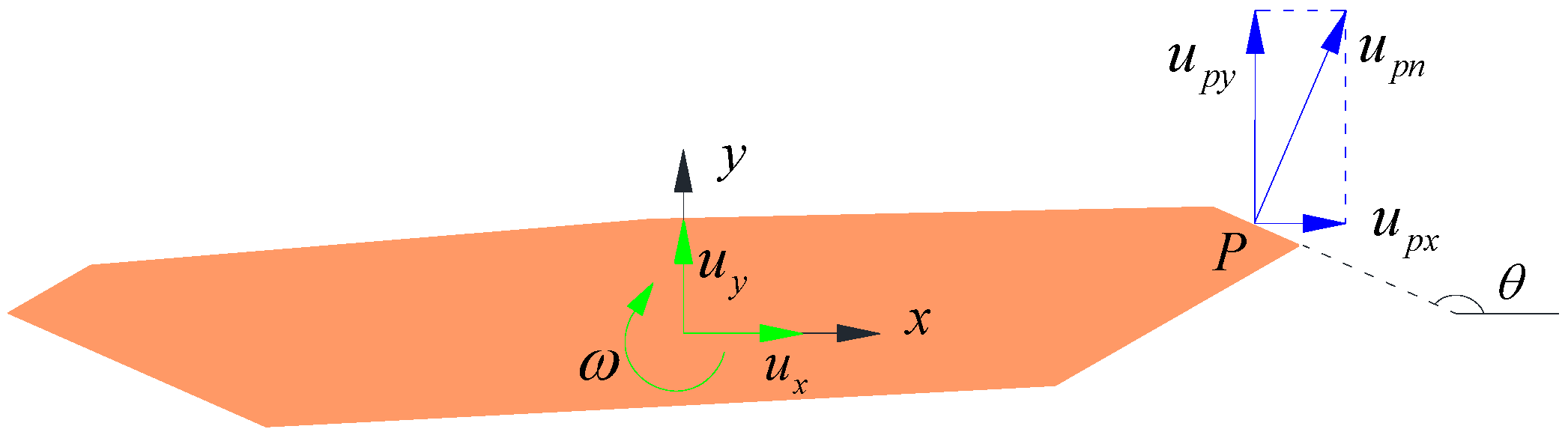
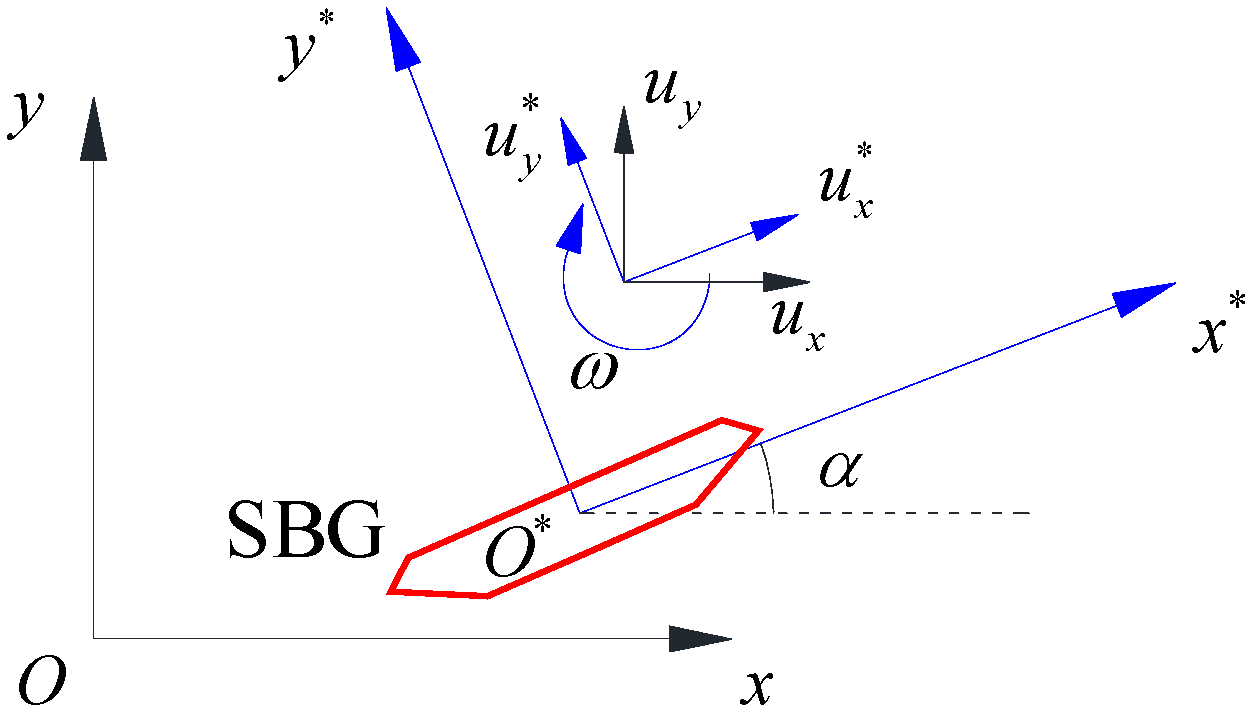
2.1. Stream Function on the Surface of an SBG
2.2. Complex Potential in the Fluid Domain
3. Aerodynamic Forces
3.1. Pressure Function
3.2. Drag Force and Lift Force
3.3. Pitching Moment
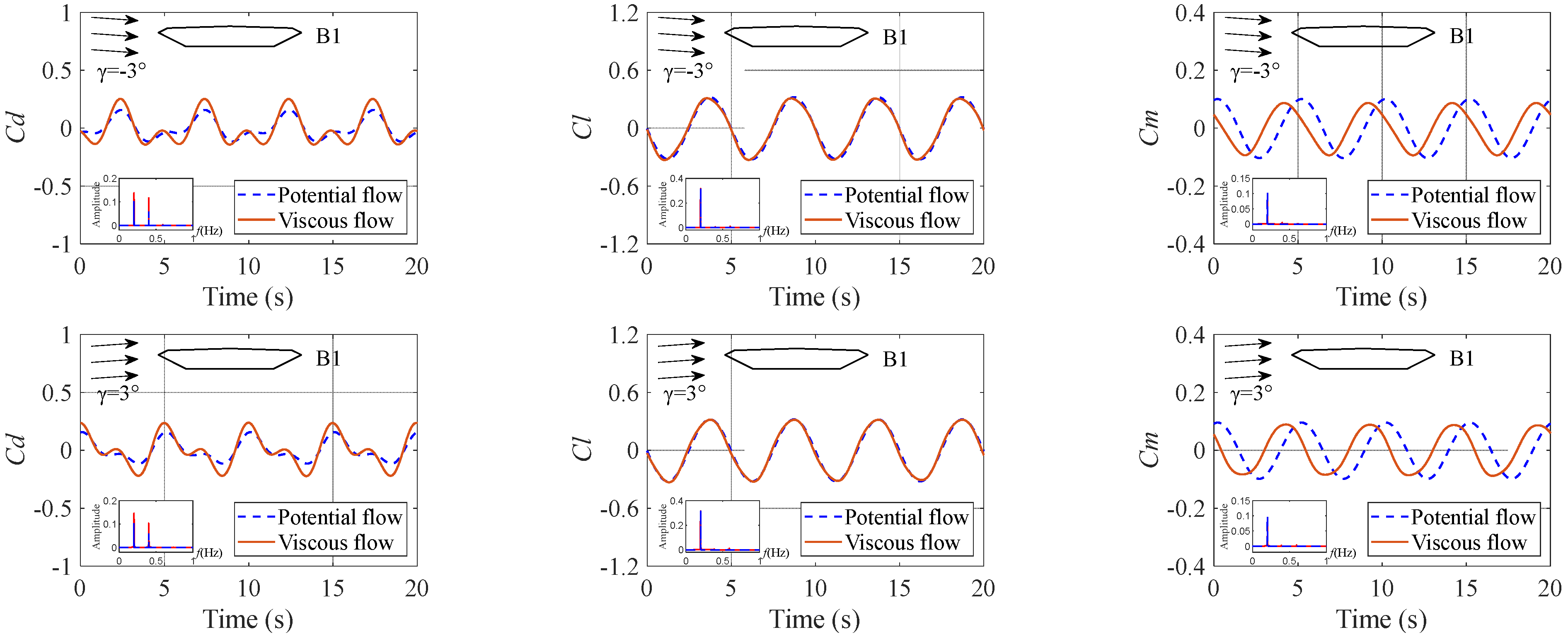
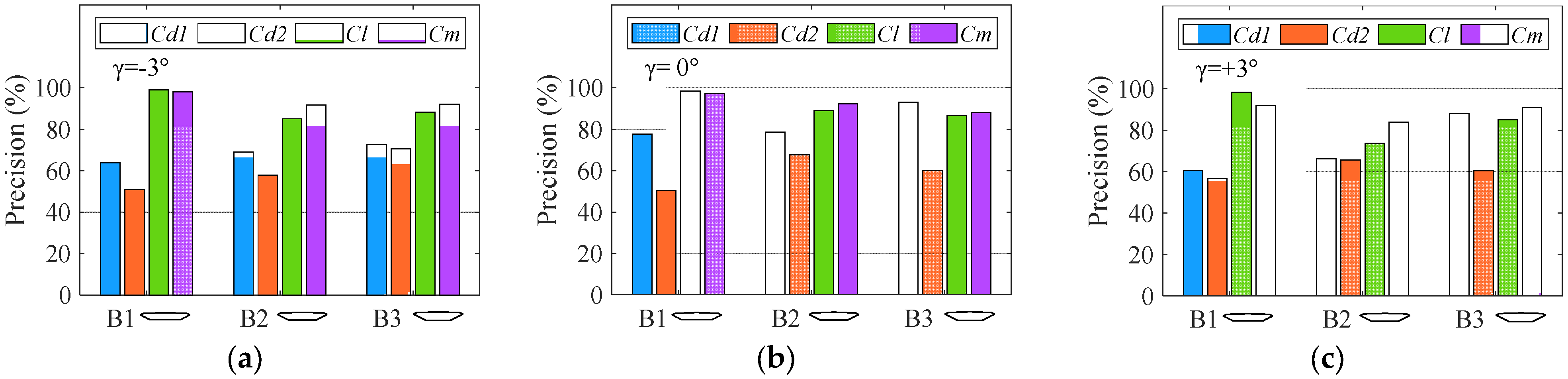
4. Comparison with the Viscous Flow
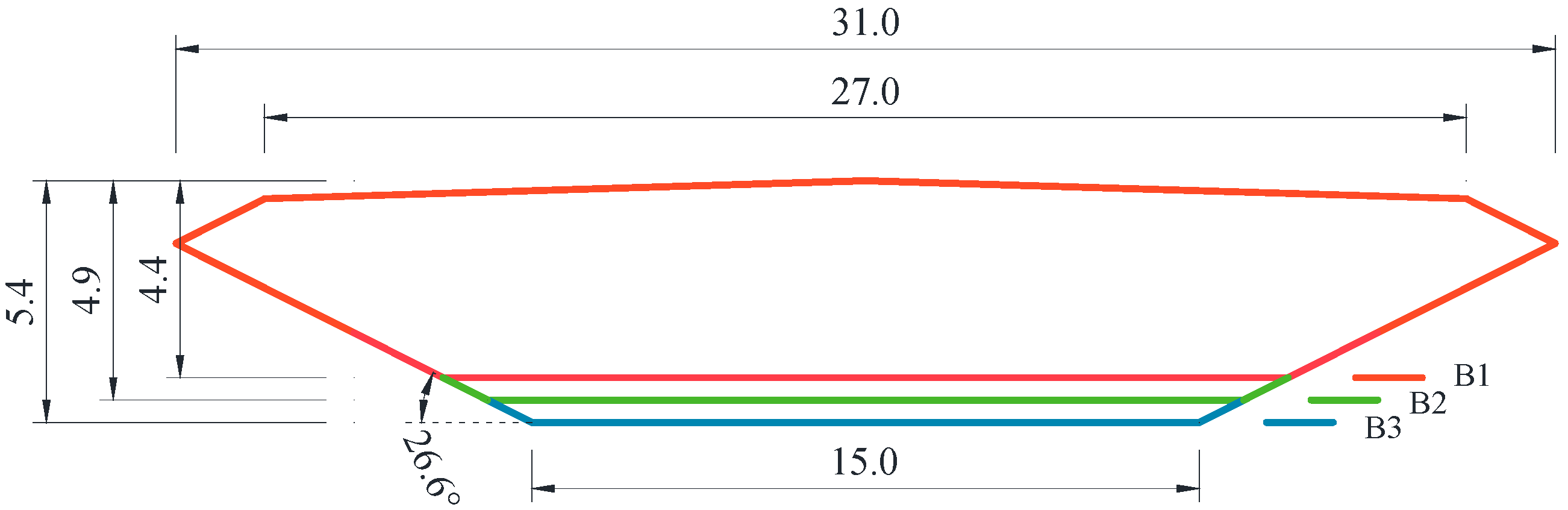
4.1. Numerical Model Verification
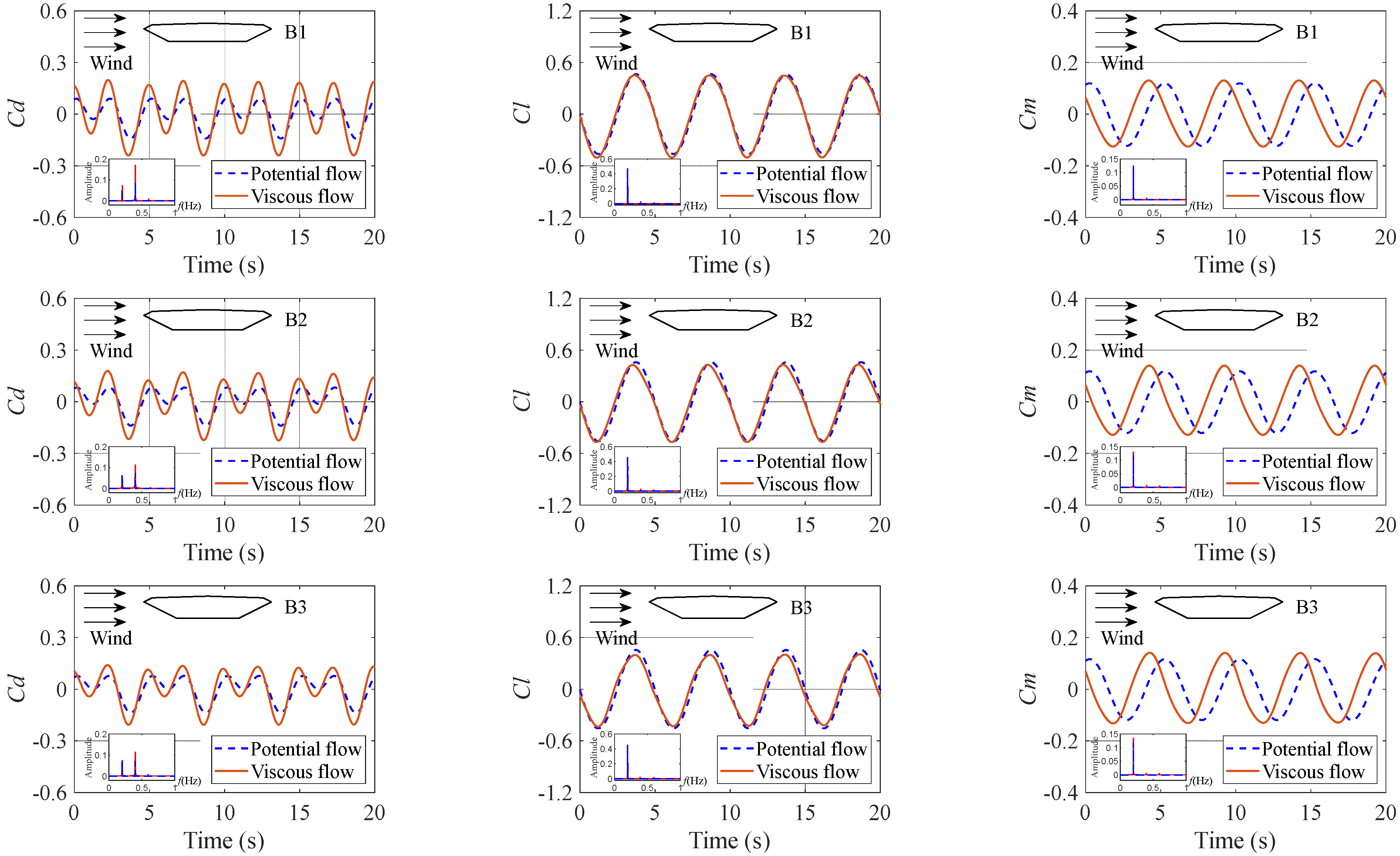
4.2. Aerodynamic Forces Comparative Analysis
5. Conclusions
- (1)
- The proposed analytical solution for the unsteady aerodynamic forces of an SBG with coupled vibration in a potential flow is a function of the SBG’s shape-related parameters and vibration response, providing a convenient and efficient method for calculating the unsteady aerodynamic forces of SBGs.
- (2)
- The analytical drag force successfully reproduced the second-order component, which mainly results from the multiplication of the vertical vibration and pitching vibration velocity terms and plays a significant role in drag force. On the other hand, the first-order frequency component dominates the lift force and pitching moment.
- (3)
- The proposed analytical solution for the drag force in a potential flow yields lower values than that in a viscous flow. Nonetheless, the analytical solution demonstrates high accuracy in predicting the amplitude of the lift force and pitching moment for an SBG at angles of attack of 0° and ±3°. The explicit formulation and satisfactory precision of the analytical solution enable its effective utilization for the rapid estimation of the aerodynamic forces acting on an SBG with coupled vibration.
- (4)
- It is imperative to underscore that the proposed analytical aerodynamic force model may not exhibit a sufficient degree of accuracy when applied to bluff bodies. It is noteworthy that the potential flow theory, which serves as the foundation for this model, is a linearized theory that may not fully capture the intricate nonlinear unsteady aerodynamic forces that manifest at high angles of attack and velocities or during large amplitude vibrations. In the future, there will be a greater focus on a more accurate aerodynamic force model for SBGs. To achieve this, further studies shall be conducted to investigate innovative correction methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Wang, H.; Xu, Z.; Li, J.; Wu, T.; Mao, J. Modeling Multidimensional Multivariate Turbulent Wind Fields Using a Correlated Turbulence Wave Number–Frequency Spectral Representation Method. J. Eng. Mech. 2023, 149, 04023010. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Xu, Z.; Zhang, Y.; Tao, T.; Mao, J. Monitoring-Based Analysis of Wind-Induced Vibrations of Ultra-Long Stay Cables during an Exceptional Wind Event. J. Wind. Eng. Ind. Aerodyn. 2022, 221, 104883. [Google Scholar] [CrossRef]
- Amer, T.S.; Bek, M.A.; Abouhmr, M.K. On the Vibrational Analysis for the Motion of a Harmonically Damped Rigid Body Pendulum. Nonlinear Dyn. 2018, 91, 2485–2502. [Google Scholar] [CrossRef]
- Bek, M.A.; Amer, T.S.; Sirwah, M.A.; Awrejcewicz, J.; Arab, A.A. The Vibrational Motion of a Spring Pendulum in a Fluid Flow. Results Phys. 2020, 19, 103465. [Google Scholar] [CrossRef]
- Amer, T.S.; Galal, A.A.; Elnaggar, S. The Vibrational Motion of a Dynamical System Using Homotopy Perturbation Technique. Appl. Math. 2020, 11, 1081–1099. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Jiang, X.; Wu, L.; Qin, J.; Li, Y. Pair-Copula-Based Trivariate Joint Probability Model of Wind Speed, Wind Direction and Angle of Attack. J. Wind Eng. Ind. Aerodyn. 2022, 225, 105010. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, F.; Zhang, M.; Dai, Y.; Qin, J.; Zhang, J. Observations of Periodic Thermally-Developed Winds beside a Bridge Region in Mountain Terrain Based on Field Measurement. J. Wind Eng. Ind. Aerodyn. 2022, 225, 104996. [Google Scholar] [CrossRef]
- Diana, G.; Omarini, S. A Non-Linear Method to Compute the Buffeting Response of a Bridge Validation of the Model through Wind Tunnel Tests. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104163. [Google Scholar] [CrossRef]
- Wu, L.; Woody Ju, J.; Zhang, J.; Zhang, M.; Li, Y. Vibration Phase Difference Analysis of Long-Span Suspension Bridge during Flutter. Eng. Struct. 2023, 276, 115351. [Google Scholar] [CrossRef]
- Cui, C.; Ma, R.; Hu, X.; He, W. Vibration Analysis for Pendent Pedestrian Path of a Long-Span Extradosed Bridge. Sustainability 2019, 11, 4664. [Google Scholar] [CrossRef]
- Amman, O.H.; von Kármán, T.; Woodruff, G.B. The Failure of the Tacoma Narrows Bridge; Federal Works Agency: Washington, DC, USA, 1941. [Google Scholar]
- Chen, A.; He, X.; Xiang, H. Identification of 18 Flutter Derivatives of Bridge Decks. J. Wind Eng. Ind. Aerodyn. 2002, 90, 2007–2022. [Google Scholar] [CrossRef]
- Scanlan, R.H.; Tomko, J.J. Airfoil and Bridge Deck Flutter Derivatives. J. Eng. Mech. 1971, 97, 1717–1737. [Google Scholar] [CrossRef]
- Ma, T.; Zhao, L.; Shen, X.; Ge, Y. Case Study of Three-Dimensional Aeroelastic Effect on Critical Flutter Wind Speed of Long-Span Bridges. J. Wind Eng. Ind. Aerodyn. 2021, 212, 104614. [Google Scholar] [CrossRef]
- Sauder, H.S.; Sarkar, P.P. A 3-DOF Forced Vibration System for Time-Domain Aeroelastic Parameter Identification. Wind Struct. 2017, 24, 481–500. [Google Scholar] [CrossRef]
- Xu, F.; Wu, T.; Ying, X.; Kareem, A. Higher-Order Self-Excited Drag Forces on Bridge Decks. J. Eng. Mech. 2016, 142, 06015007. [Google Scholar] [CrossRef]
- Guo, J.; Tang, H.; Li, Y.; Wu, L.; Wang, Z. Optimization for Vertical Stabilizers on Flutter Stability of Streamlined Box Girders with Mountainous Environment. Adv. Struct. Eng. 2020, 23, 205–218. [Google Scholar] [CrossRef]
- Kusano, I.; Cid Montoya, M.; Baldomir, A.; Nieto, F.; Jurado, J.Á.; Hernández, S. Reliability Based Design Optimization for Bridge Girder Shape and Plate Thicknesses of Long-Span Suspension Bridges Considering Aeroelastic Constraint. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104176. [Google Scholar] [CrossRef]
- Zhou, Z.; Mao, W.; Ding, Q. Experimental and Numerical Studies on Flutter Stability of a Closed Box Girder Accounting for Ground Effects. J. Fluids Struct. 2019, 84, 1–17. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Zhang, Z.; Ying, X. Energy Budget Analysis and Engineering Modeling of Post-Flutter Limit Cycle Oscillation of a Bridge Deck. J. Wind. Eng. Ind. Aerodyn. 2019, 188, 410–420. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Yu, X.D.; Yang, G.; Spencer, B.F. Wind-Induced Self-Excited Loads on Bridges. J. Struct. Eng. 2005, 131, 1783–1793. [Google Scholar] [CrossRef]
- Siedziako, B.; Øiseth, O. Modeling of Self-Excited Forces during Multimode Flutter: An Experimental Study. Wind Struct. 2018, 27, 293–309. [Google Scholar] [CrossRef]
- Von Karman, T.; Sears, W.R. Airfoil Theory for Non-Uniform Motion. J. Aeronaut. Sci. 1938, 5, 379–390. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flup; Twentieth Annual Report of the National Advisory Committee for Aeronautics; NACA: Washington, DC, USA, 1935; pp. 413–434. [Google Scholar]
- Edwards, J.W.; Ashley, H.; Breakwell, J.V. Unsteady Aerodynamic Modeling for Arbitrary Motions. AIAA J. 1979, 17, 365–374. [Google Scholar] [CrossRef]
- Sun, M.; Wang, W. Method for Calculating the Unsteady Flow of an Elliptical Circulation-Control Airfoil. J. Aircr. 1989, 26, 907–913. [Google Scholar] [CrossRef]
- Stangfeld, C.; Rumsey, C.L.; Mueller-Vahl, H.; Greenblatt, D.; Nayeri, C.; Paschereit, C.O. Unsteady Thick Airfoil Aerodynamics: Experiments, Computation, and Theory. In Proceedings of the 45th AIAA Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Catlett, M.R.; Anderson, J.M.; Badrya, C.; Baeder, J.D. Unsteady Response of Airfoils Due to Small-Scale Pitching Motion with Considerations for Foil Thickness and Wake Motion. J. Fluids Struct. 2020, 94, 102889. [Google Scholar] [CrossRef]
- Chiu, T.W. A Two-Dimensional Second-Order Vortex Panel Method for the Flow in a Cross-Wind over a Train and Other Two-Dimensional Bluff Bodies. J. Wind Eng. Ind. Aerodyn. 1991, 37, 43–64. [Google Scholar] [CrossRef]
- Chiu, T.W. Prediction of the Aerodynamic Loads on a Railway Train in a Cross-Wind at Large Yaw Angles Using an Integrated Two- and Three-Dimensional Source/Vortex Panel Method. J. Wind Eng. Ind. Aerodyn. 1995, 57, 19–39. [Google Scholar] [CrossRef]
- Valentine, D.T.; Madhi, F. Unsteady Potential Flow Theory and Numerical Analysis of Forces on Cylinders Induced by Nearby Oscillating Disturbances. In Proceedings of the American Society of Mechanical Engineers Digital Collection, Honolulu, HA, USA, 31 May–5 June 2009; pp. 631–639. [Google Scholar]
- Henrici, P. Cauchy Integrals on Closed Curves. In Applied and Computational Complex Analysis, Volume 3: Discrete Fourier Analysis, Cauchy Integrals, Construction of Conformal Maps, Univalent Functions; John Wiley & Sons: Hoboken, NJ, USA, 1993; pp. 113–119. [Google Scholar]
- Wu, L.; Zhou, Z.; Zhang, J.; Zhang, M. A Numerical Method for Conformal Mapping of Closed Box Girder Bridges and Its Application. Sustainability 2023, 15, 6291. [Google Scholar] [CrossRef]
- Wu, L.; Ju, J.W.; Zhang, M.; Li, Y.; Qi, J. Aerostatic Pressure of Streamlined Box Girder Based on Conformal Mapping Method and Its Application. Wind Struct. 2022, 35, 243–253. [Google Scholar] [CrossRef]
- Segletes, S.B.; Walters, W.P. A Note on the Application of the Extended Bernoulli Equation. Int. J. Impact Eng. 2002, 27, 561–576. [Google Scholar] [CrossRef]
- Katz, V.J. The History of Stokes’ Theorem. Math. Mag. 1979, 52, 146–156. [Google Scholar] [CrossRef]
- Larsen, A. Aerodynamic Aspects of the Final Design of the 1624 m Suspension Bridge across the Great Belt. J. Wind Eng. Ind. Aerodyn. 1993, 48, 261–285. [Google Scholar] [CrossRef]
- Reinhold, T.A.; Brinch, M.; Damsgaard, A. Wind Tunnel Tests for the Great Belt Link. In Proceedings of the Aerodynamics of Large Bridges: Proceeding of the First International Symposium on Aerodynamics of Large Bridges; Taylor & Francis: Copenhagen, Denmark, 1992; pp. 255–267. [Google Scholar]
- Honore Walther, J. Discrete Vortex Method for Two-Dimensional Flow Past Bodies of Arbitrary Shape Undergoing Prescribed Rotary and Translational Motion; Technical University of Denmark: Copenhagen, Denmark, 1994. [Google Scholar]


| SBG | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | 8.79 | −0.57i | 6.45 | 0.45i | −0.07 | 0.16i | 0.16 | −0.09i | 0.09 | −0.04i |
| B2 | 8.86 | −0.70i | 6.30 | 0.59i | −0.01 | 0.16i | 0.18 | −0.12i | 0.06 | −0.02i |
| B3 | 8.93 | −0.82i | 6.16 | 0.72i | 0.07 | 0.13i | 0.19 | −0.14i | 0.03 | 0.01i |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Zhang, M.; Jiang, F.; Zhou, Z.; Li, Y. An Analytical Solution for Unsteady Aerodynamic Forces on Streamlined Box Girders with Coupled Vibration. Sustainability 2023, 15, 7312. https://doi.org/10.3390/su15097312
Wu L, Zhang M, Jiang F, Zhou Z, Li Y. An Analytical Solution for Unsteady Aerodynamic Forces on Streamlined Box Girders with Coupled Vibration. Sustainability. 2023; 15(9):7312. https://doi.org/10.3390/su15097312
Chicago/Turabian StyleWu, Lianhuo, Mingjin Zhang, Fanying Jiang, Zelin Zhou, and Yongle Li. 2023. "An Analytical Solution for Unsteady Aerodynamic Forces on Streamlined Box Girders with Coupled Vibration" Sustainability 15, no. 9: 7312. https://doi.org/10.3390/su15097312





