Research on Autonomous Vehicle Obstacle Avoidance Path Planning with Consideration of Social Ethics
Abstract
1. Introduction
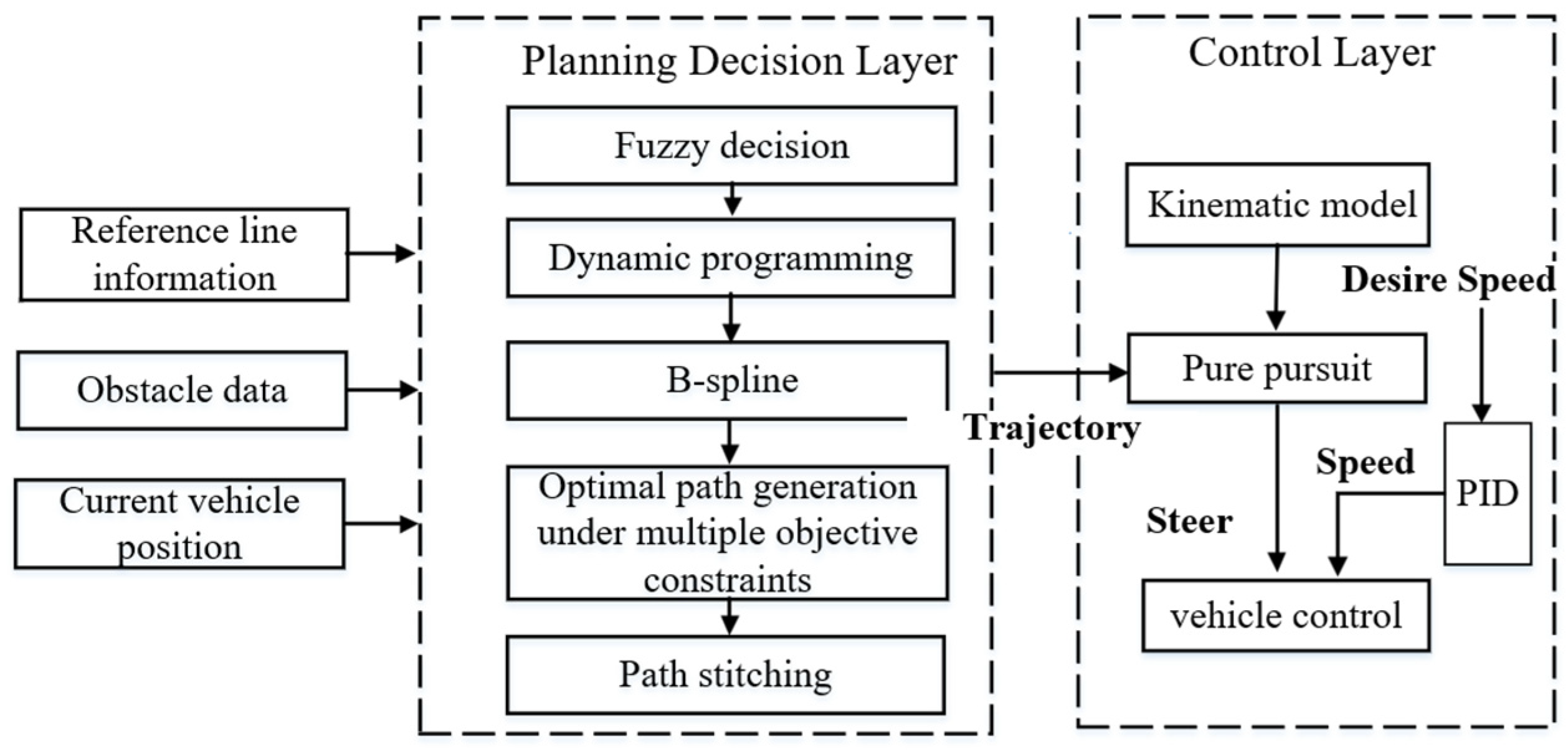
2. Algorithm Framework
- (1)
- The obstacle information as well as the reference line information and the vehicle’s current position information are sent down to the planning decision layer.
- (2)
- Based on the relative speed and obstacle distance used to formulate fuzzy rules, obtain the planning willingness to carry out the defuzzification and make dynamic planning decisions.
- (3)
- Based on the current position of the vehicle as the starting point to the state space horizontal and vertical sampling, the use of dynamic planning algorithms is implemented to obtain a collection of trajectories composed of different horizontal and vertical combinations of coordinate points.
- (4)
- Based on the trajectory combinations obtained in (3), different path curve clusters are obtained by fitting using B-spline curves.
- (5)
- Based on the curve clusters, calculate the obstacle cost, path cost, and mean curvature cost for the path points on the curves that meet the distance and then normalise them to obtain the path with the smallest cost as the optimal path output.
- (6)
- Splice the reference line path with the path obtained based on (5), input it into the downstream controller, and track it using the pure tracking algorithm.
2.1. Fuzzy Algorithm Decision
2.2. Dynamic Programming Algorithm
- (1)
- Take the current point of the vehicle as the starting point and set the number of layers and columns in terms of horizontal and vertical distances, i.e., determine the width and length of the state space sampling.
- (2)
- Search and solve the cost function of the first layer through the dynamic programming algorithm, and the surrogate value of each layer is stored in the current node, and the node of the previous layer serves as the parent node of the next layer when incrementing step by step, accumulating the cost values until the end of the cycle, and then finally obtaining the minimum value of the cost of the last layer and backtracking to the previous parent node in turn to obtain the longitudinal position of the discrete points of the trajectory of the obstacle avoidance, and finally obtaining each point by transverse displacement scattering. Carry out horizontal displacement scattering points, and finally obtain the coordinate information of each point.
- (3)
- Finally, the B-spline curve is fitted to ensure the smoothness of the trajectory, and a planned trajectory is finally output.
2.3. B-Spline Curves
2.4. Cost Function
- 1.
- Path length cost
- 2.
- Average curvature of the path cost
- 3.
- Obstacle type cost
- a.
- Calculate the matching points of obstacles on the path
- b.
- Lateral displacement of S from the obstacle
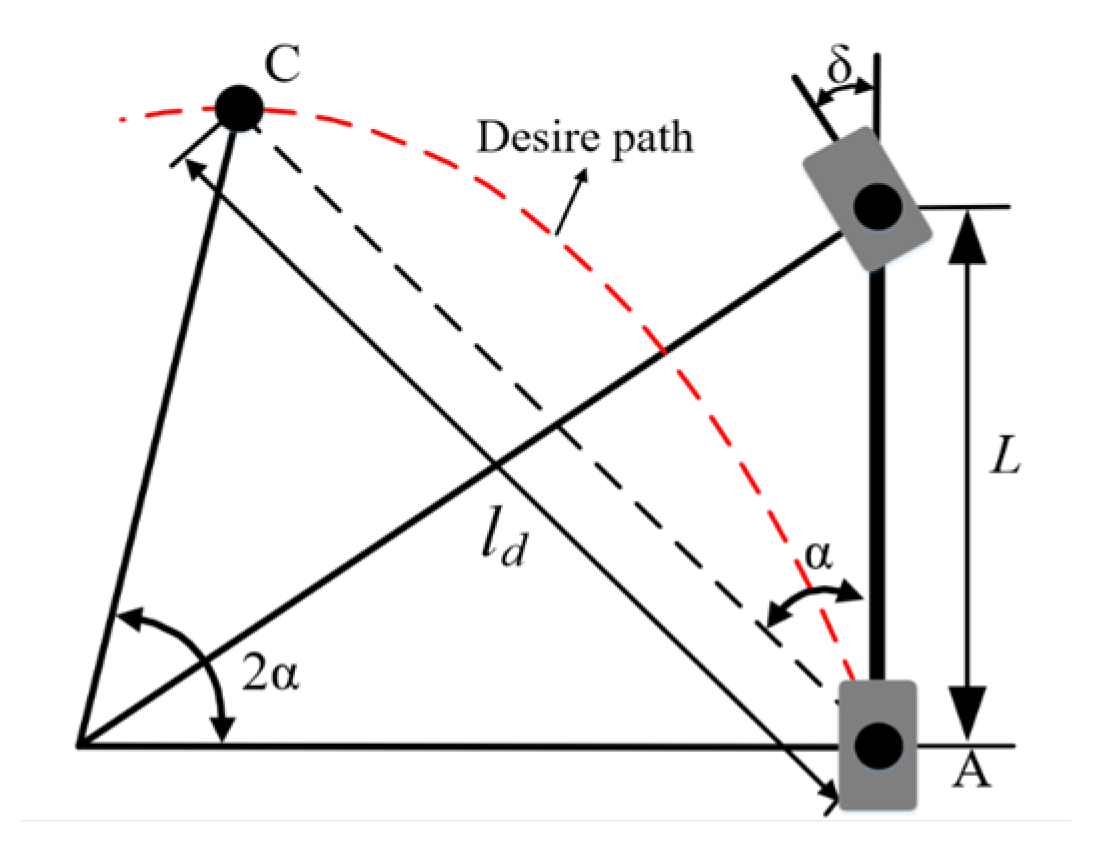
2.5. Pure Pursuit
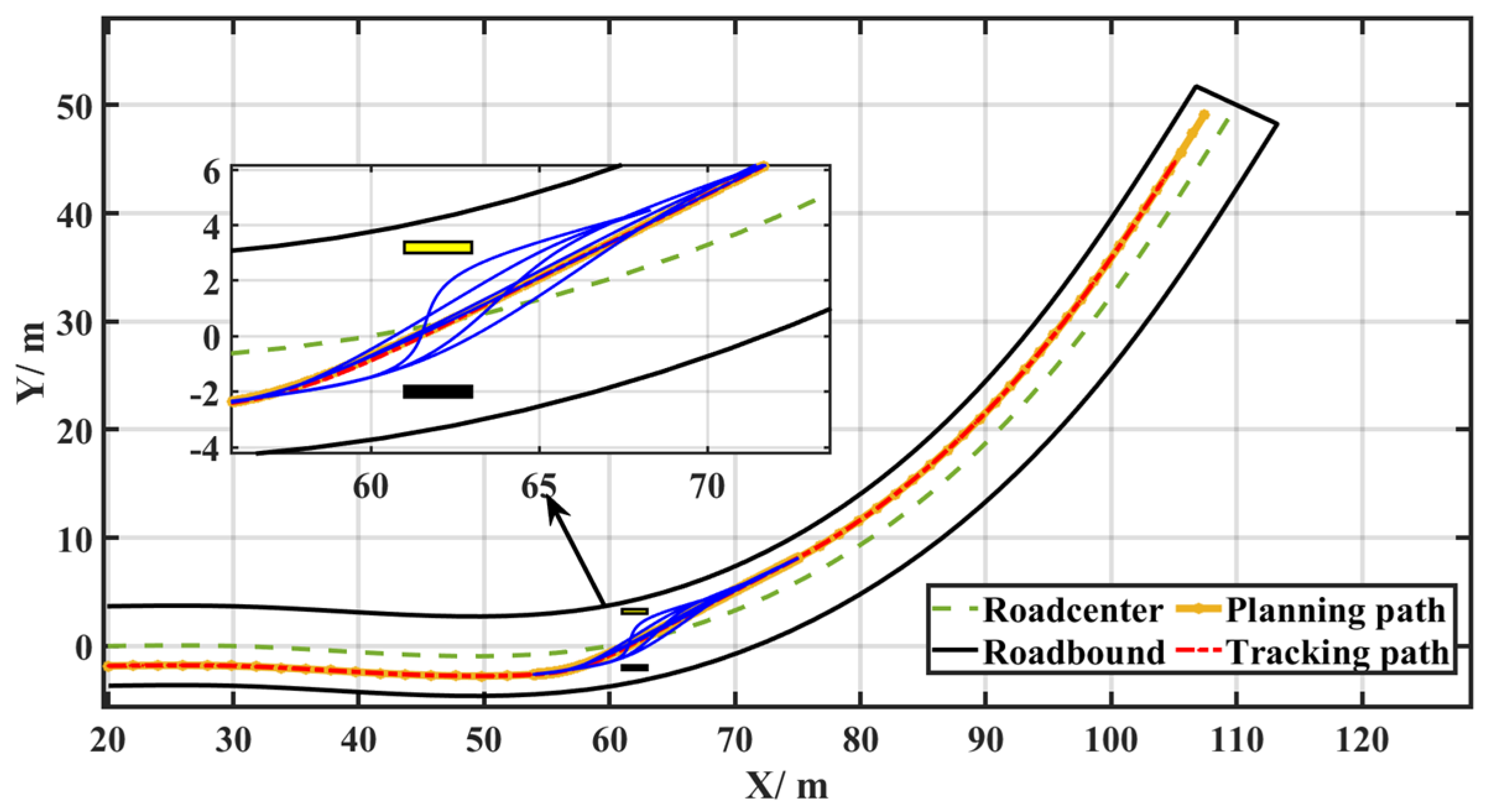
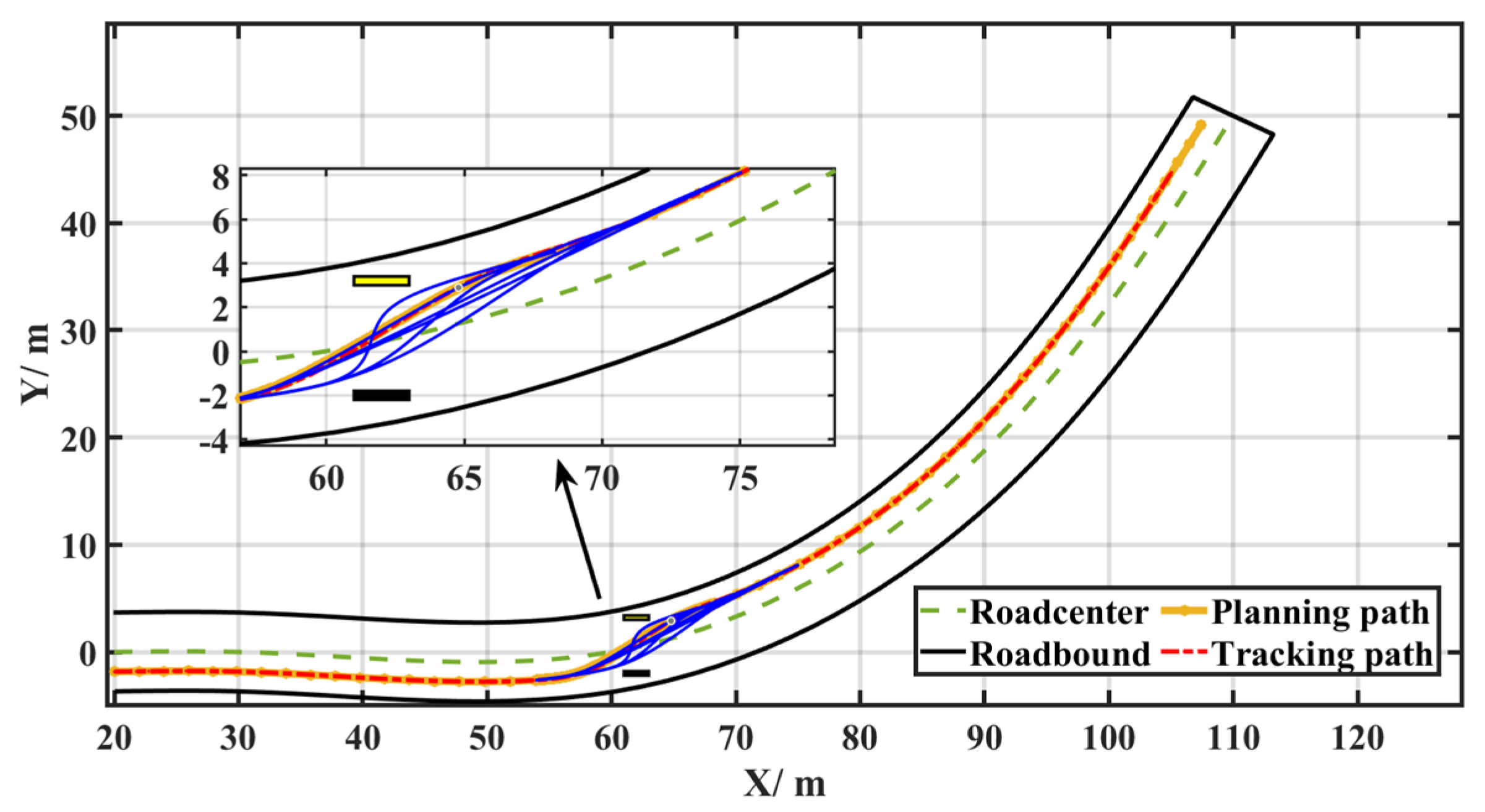
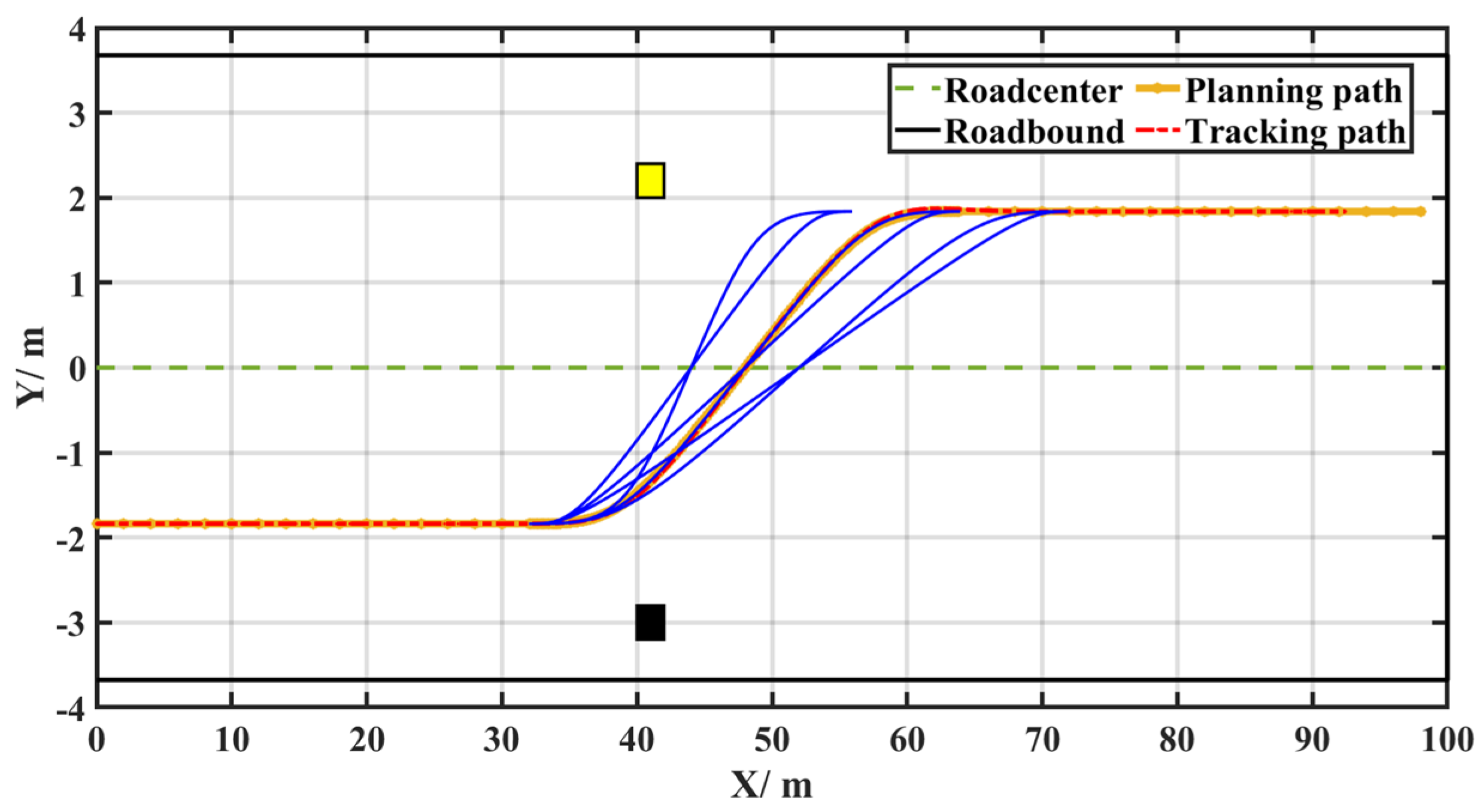
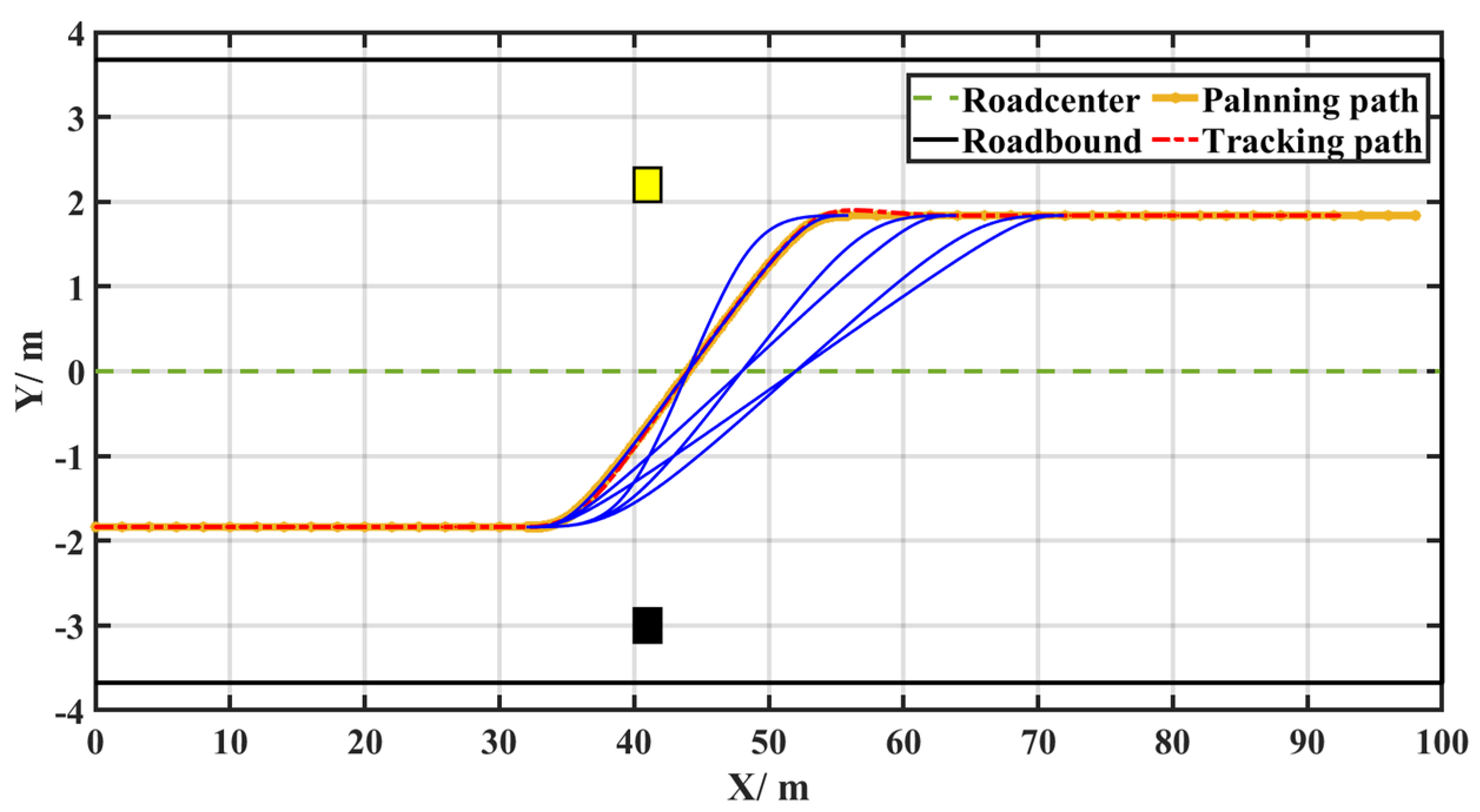
3. Simulation
- (1)
- Curve condition
- (2)
- Straight-line condition
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixao, T.M.; Mutz, F.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Shi, S. Research Status of Autonomous Vehicle Path Planning. In Proceedings of the SHS Web of Conferences, Virtual Event, 26 August 2022; EDP Sciences: Les Ulis, France, 2022; Volume 144, p. 02019. [Google Scholar]
- Robinson, J.; Smyth, J.; Woodman, R.; Donzella, V. Ethical considerations and moral implications of autonomous vehicles and unavoidable collisions. Theor. Issues Ergon. Sci. 2022, 23, 435–452. [Google Scholar] [CrossRef]
- Almaskati, D.; Kermanshachi, S.; Pamidimukkala, A. Investigating the impacts of autonomous vehicles on crash severity and traffic safety. Front. Built Environ. 2024, 10, 1383144. [Google Scholar] [CrossRef]
- Evans, K.; de Moura, N.; Chauvier, S.; Chatila, R.; Dogan, E. Ethical decision making in autonomous vehicles: The AV ethics project. Sci. Eng. Ethics 2020, 26, 3285–3312. [Google Scholar] [CrossRef] [PubMed]
- Resnik, D.B.; Andrews, S.L. A precautionary approach to autonomous vehicles. AI Ethics 2023, 4, 403–418. [Google Scholar] [CrossRef] [PubMed]
- Thomson, J.J. The trolley problem. Yale Law J. 1984, 94, 1395. [Google Scholar] [CrossRef]
- De Moura, N.; Chatila, R.; Evans, K.; Chauvier, S.; Dogan, E. Ethical decision making for autonomous vehicles. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2022; IEEE: New York, NY, USA, 2020; pp. 2006–2013. [Google Scholar]
- Wang, H.; Huang, Y.; Khajepour, A.; Cao, D.; Lv, C. Ethical decision-making platform in autonomous vehicles with lexicographic optimization-based model predictive controller. IEEE Trans. Veh. Technol. 2020, 69, 8164–8175. [Google Scholar] [CrossRef]
- Geisslinger, M.; Poszler, F.; Betz, J.; Lütge, C.; Lienkamp, M. Autonomous driving ethics: From trolley problem to ethics of risk. Philos. Technol. 2021, 34, 1033–1055. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, X.; Yang, L.; Huang, Z. Ethics dilemmas and autonomous vehicles: Ethics preference modeling and implementation of personal ethics setting for autonomous vehicles in dilemmas. IEEE Intell. Transp. Syst. Mag. 2022, 15, 177–189. [Google Scholar] [CrossRef]
- Geisslinger, M.; Poszler, F.; Lienkamp, M. An ethical trajectory planning algorithm for autonomous vehicles. Nat. Mach. Intell. 2023, 5, 137–144. [Google Scholar] [CrossRef]
- Pickering, J.E.; Ashman, P.; Gilbert, A.; Petrovic, D.; Warwick, K.; Burnham, K.J. Model-to-decision approach for autonomous vehicle convoy collision ethics. In Proceedings of the 2018 UKACC 12th International Conference on Control (CONTROL), Sheffield, UK, 5–7 September 2018; IEEE: New York, NY, USA, 2018; pp. 301–308. [Google Scholar]
- Geisslinger, M.; Trauth, R.; Kaljavesi, G.; Lienkamp, M. Maximum acceptable risk as criterion for decision-making in autonomous vehicle trajectory planning. IEEE Open J. Intell. Transp. Syst. 2023, 4, 570–579. [Google Scholar] [CrossRef]
- Faulhaber, A.K.; Dittmer, A.; Blind, F.; Wächter, M.A.; Timm, S.; Sütfeld, L.R.; Stephan, A.; Pipa, G.; König, P. Human decisions in moral dilemmas are largely described by utilitarianism: Virtual car driving study provides guidelines for autonomous driving vehicles. Sci. Eng. Ethics 2019, 25, 399–418. [Google Scholar] [CrossRef] [PubMed]
- Rhim, J.; Lee, J.H.; Chen, M.; Lim, A. A deeper look at autonomous vehicle ethics: An integrative ethical decision-making framework to explain moral pluralism. Front. Robot. AI 2021, 8, 632394. [Google Scholar] [CrossRef] [PubMed]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]


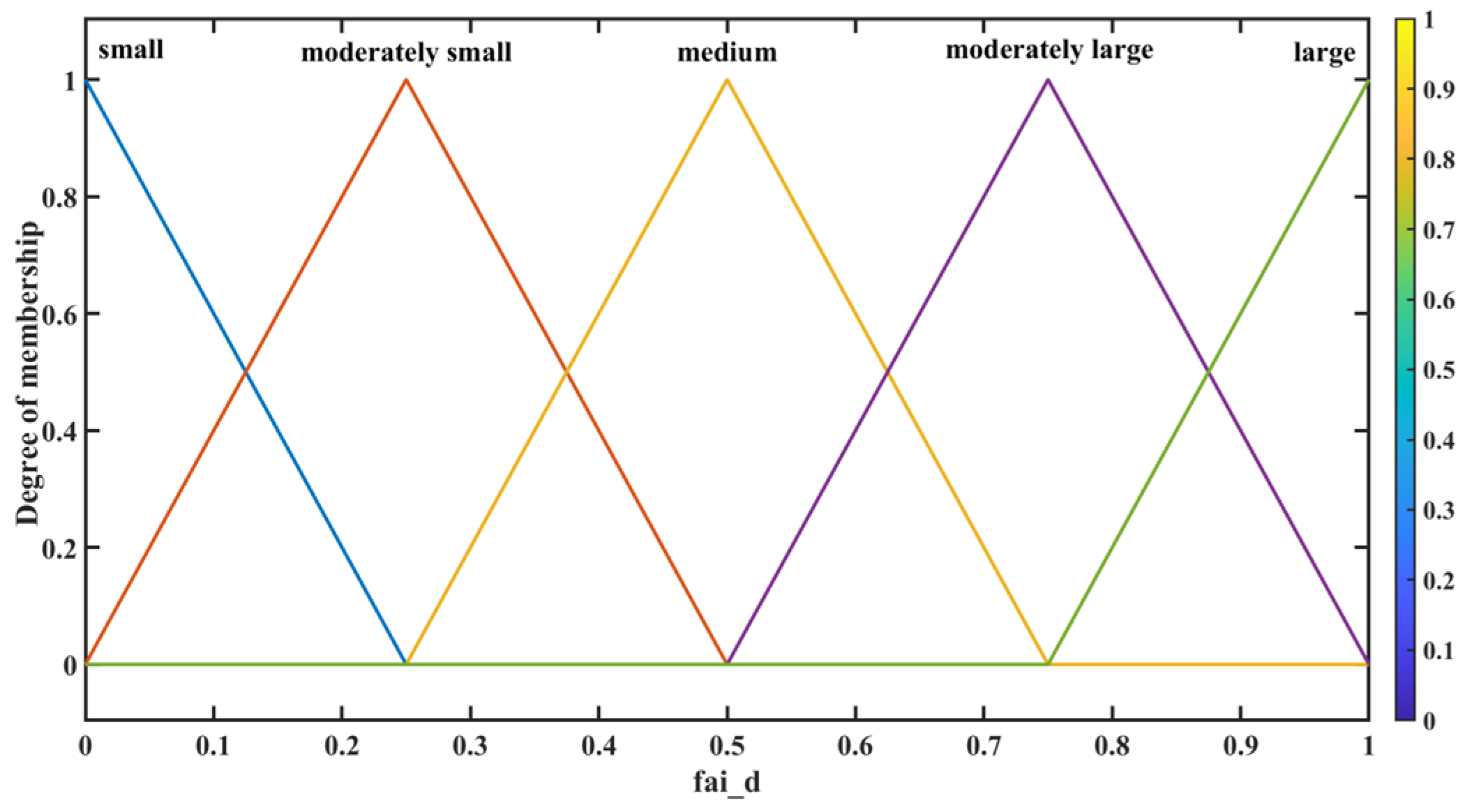







| φh | φv | |||||
|---|---|---|---|---|---|---|
| φd | small | moderately small | medium | moderately strong | strong | |
| small | moderately weak | moderately strong | moderately strong | strong | strong | |
| moderately small | moderately weak | moderately strong | moderately strong | strong | strong | |
| medium | weak | moderately weak | moderately strong | moderately strong | moderately strong | |
| moderately strong | weak | weak | moderately weak | moderately strong | moderately strong | |
| strong | weak | weak | weak | moderately weak | moderately strong | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Jing, H.; Zhong, G.; Wang, J.; Wang, T. Research on Autonomous Vehicle Obstacle Avoidance Path Planning with Consideration of Social Ethics. Sustainability 2024, 16, 4763. https://doi.org/10.3390/su16114763
Wang L, Jing H, Zhong G, Wang J, Wang T. Research on Autonomous Vehicle Obstacle Avoidance Path Planning with Consideration of Social Ethics. Sustainability. 2024; 16(11):4763. https://doi.org/10.3390/su16114763
Chicago/Turabian StyleWang, Lanwen, Hui Jing, Guoan Zhong, Jiachen Wang, and Tao Wang. 2024. "Research on Autonomous Vehicle Obstacle Avoidance Path Planning with Consideration of Social Ethics" Sustainability 16, no. 11: 4763. https://doi.org/10.3390/su16114763
APA StyleWang, L., Jing, H., Zhong, G., Wang, J., & Wang, T. (2024). Research on Autonomous Vehicle Obstacle Avoidance Path Planning with Consideration of Social Ethics. Sustainability, 16(11), 4763. https://doi.org/10.3390/su16114763







