Optimization Design of Indoor Environmental Ventilation in Buildings Based on Improved SVR-PSO Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Construction of Numerical Models for Airflow Organization and Aerosol Diffusion
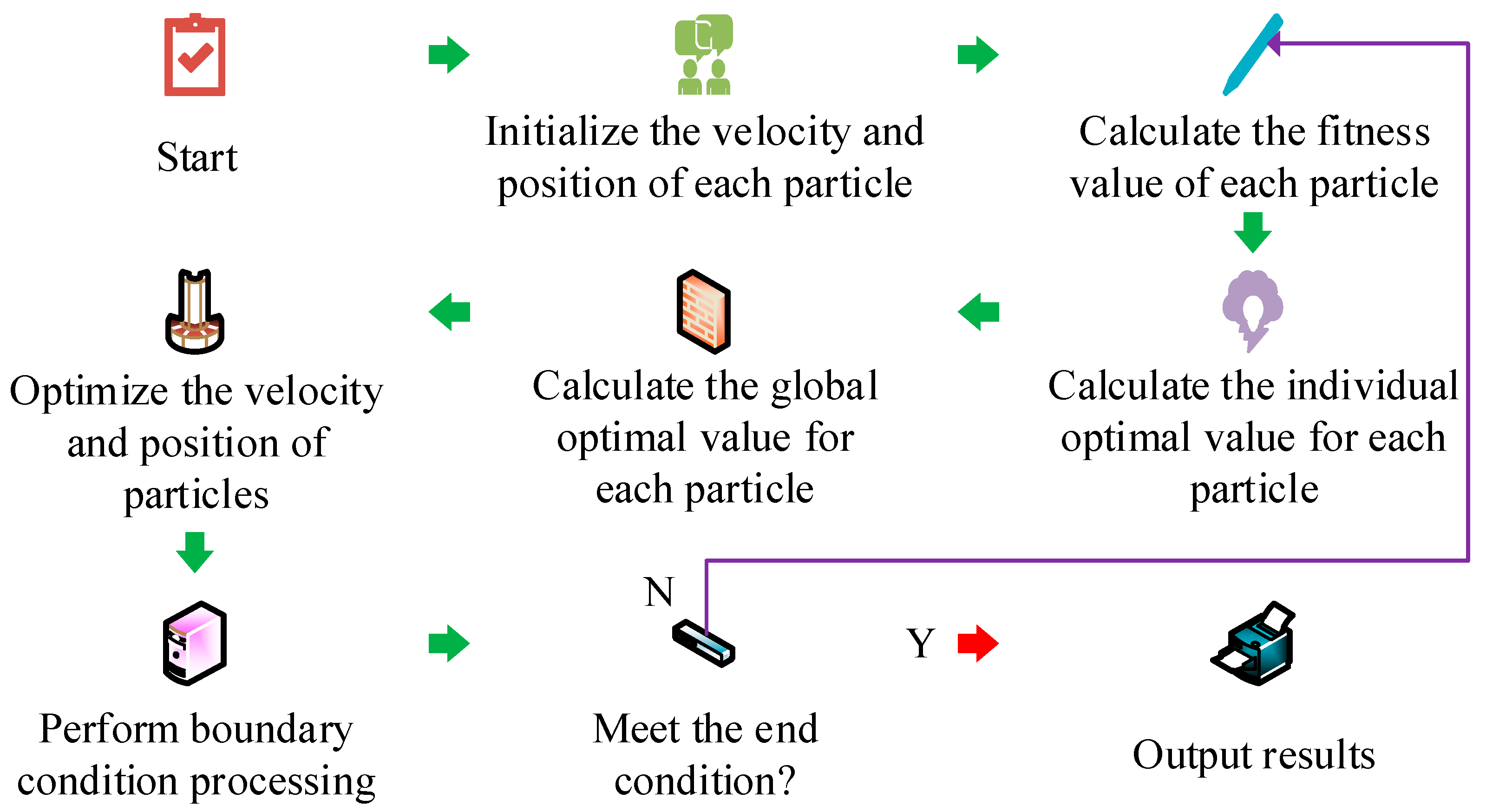
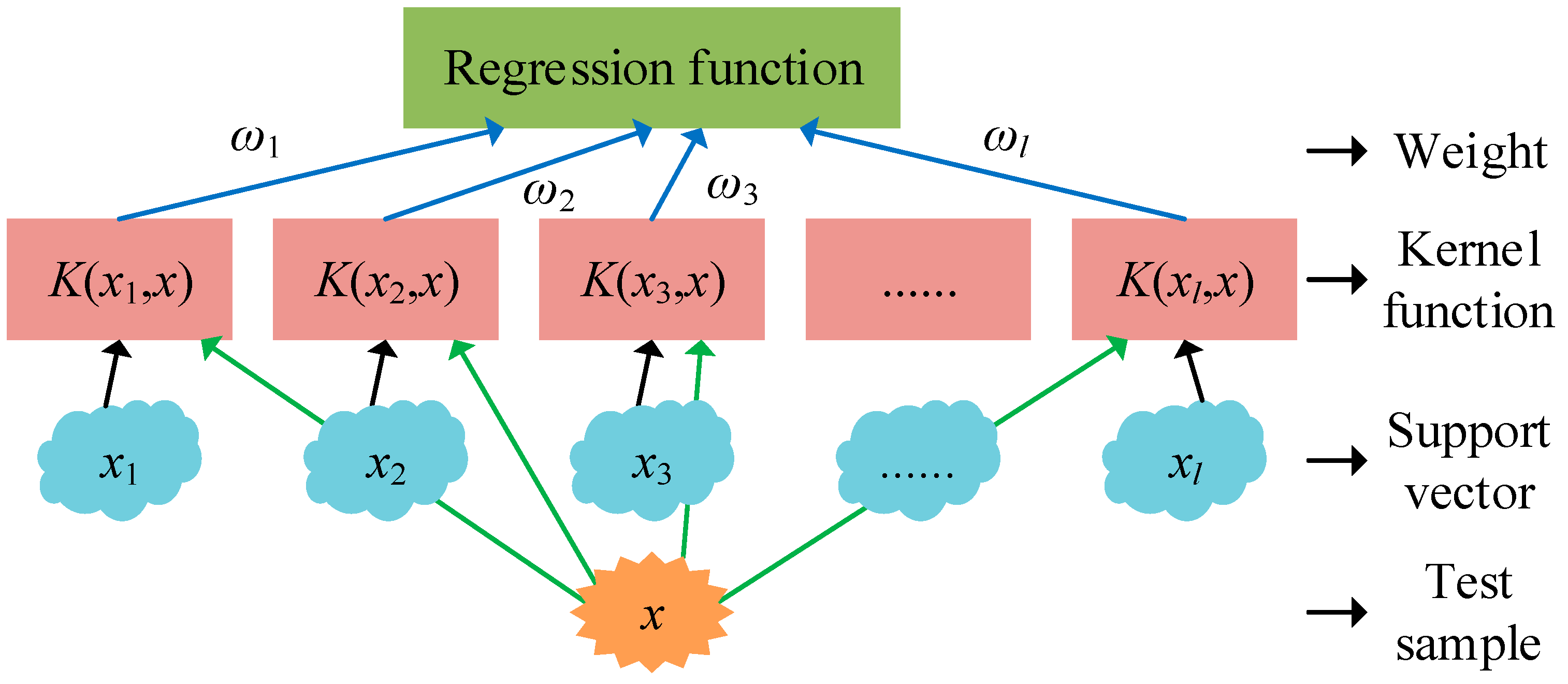
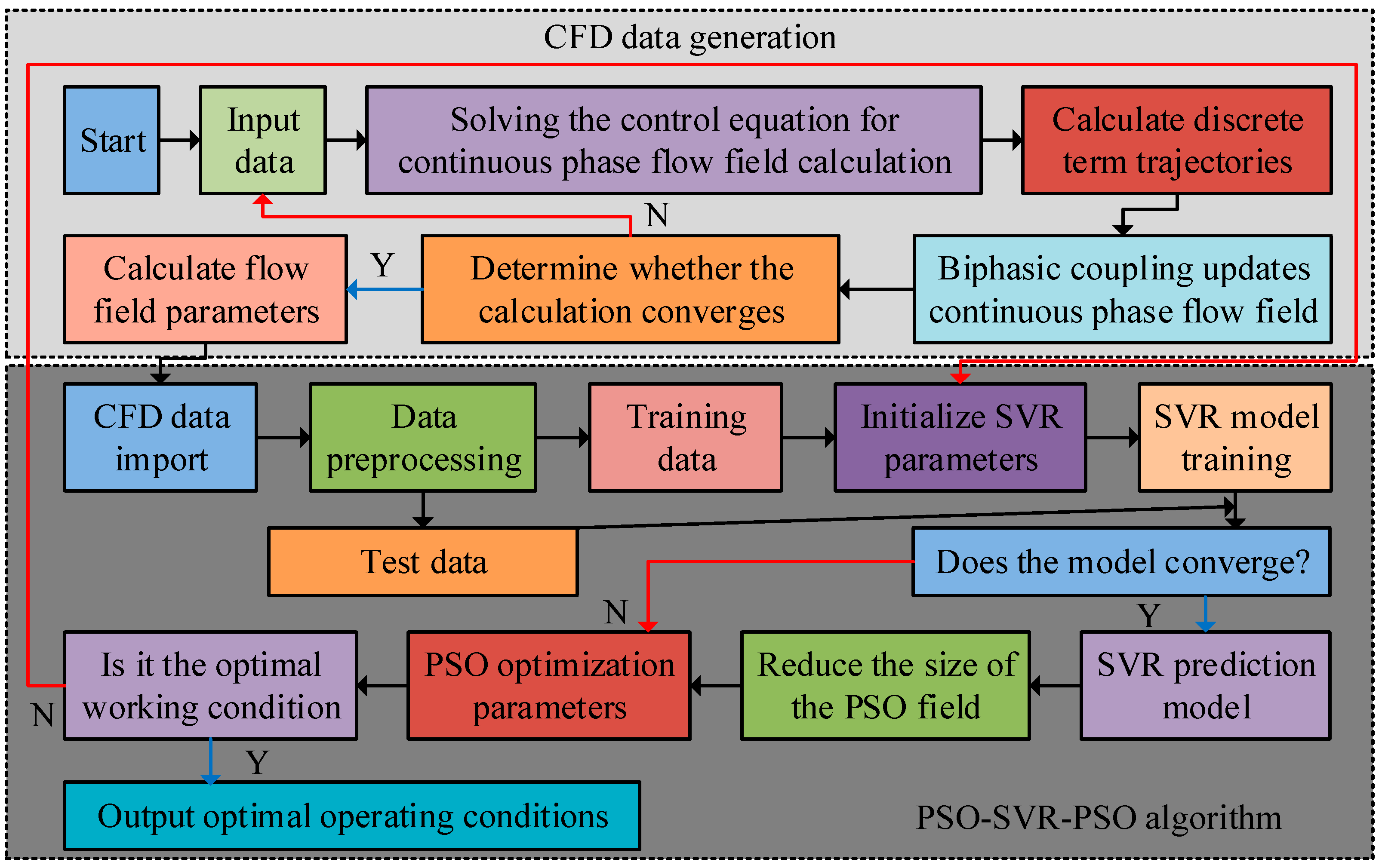
2.2. Design of Improved SVR-PSO Algorithm for Multi-Objective Optimization of Ventilation Methods
3. Results and Discussion
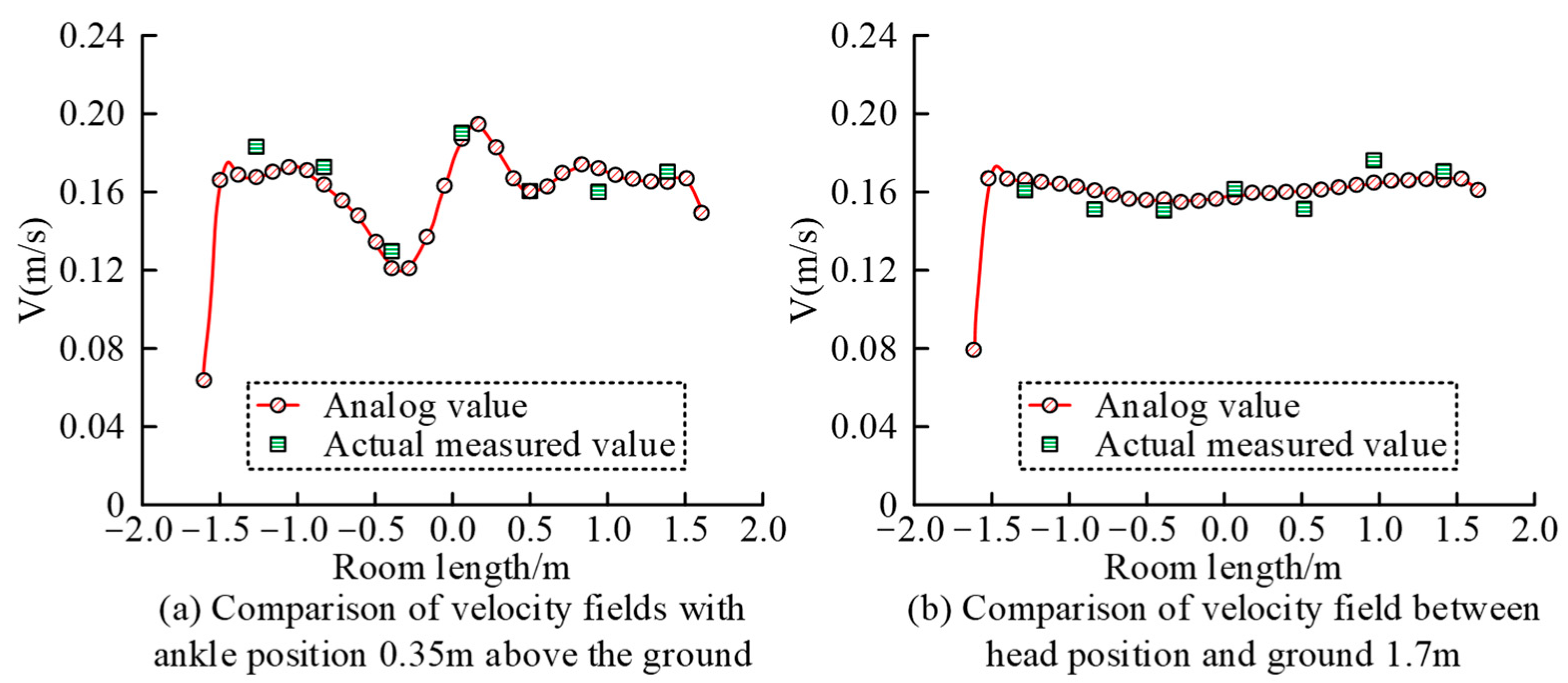
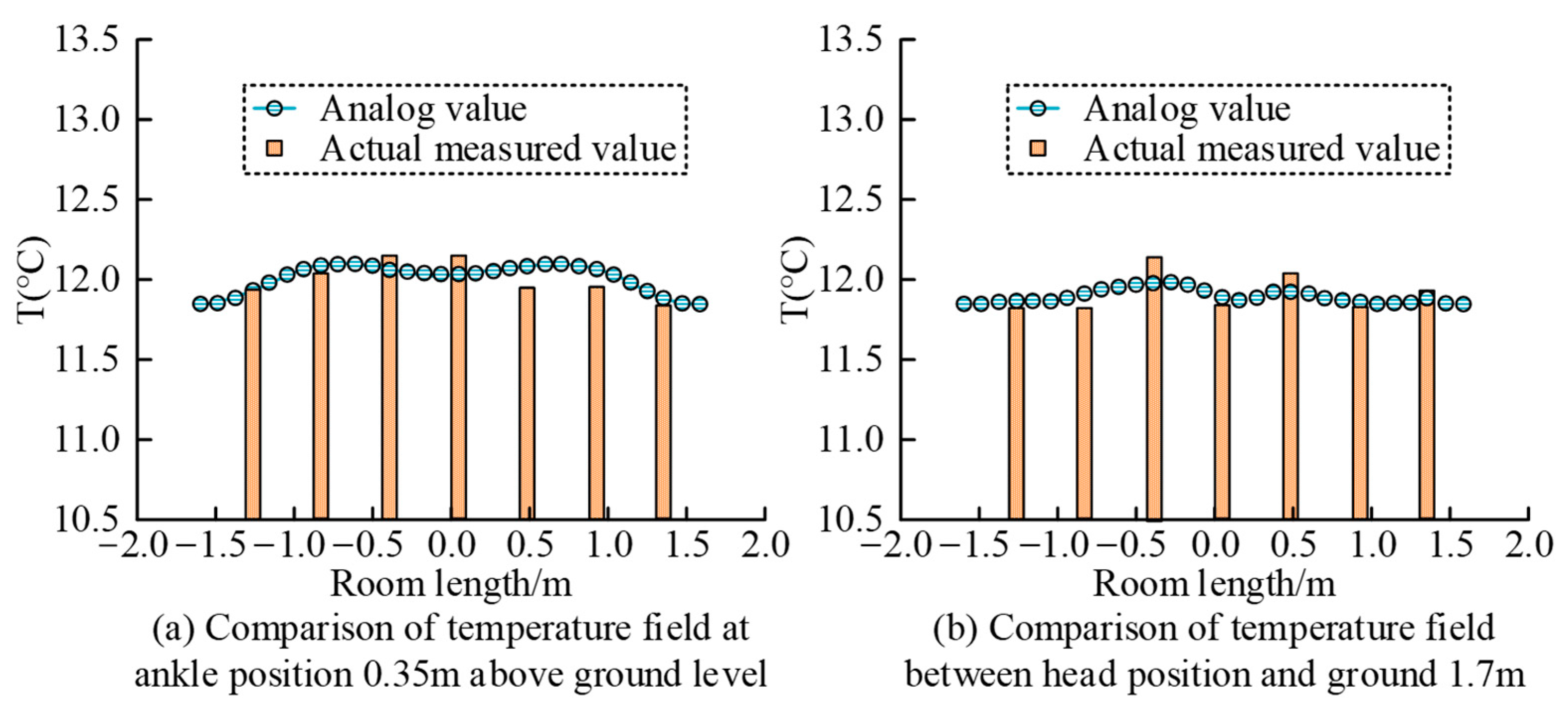
3.1. Validation of Numerical Models
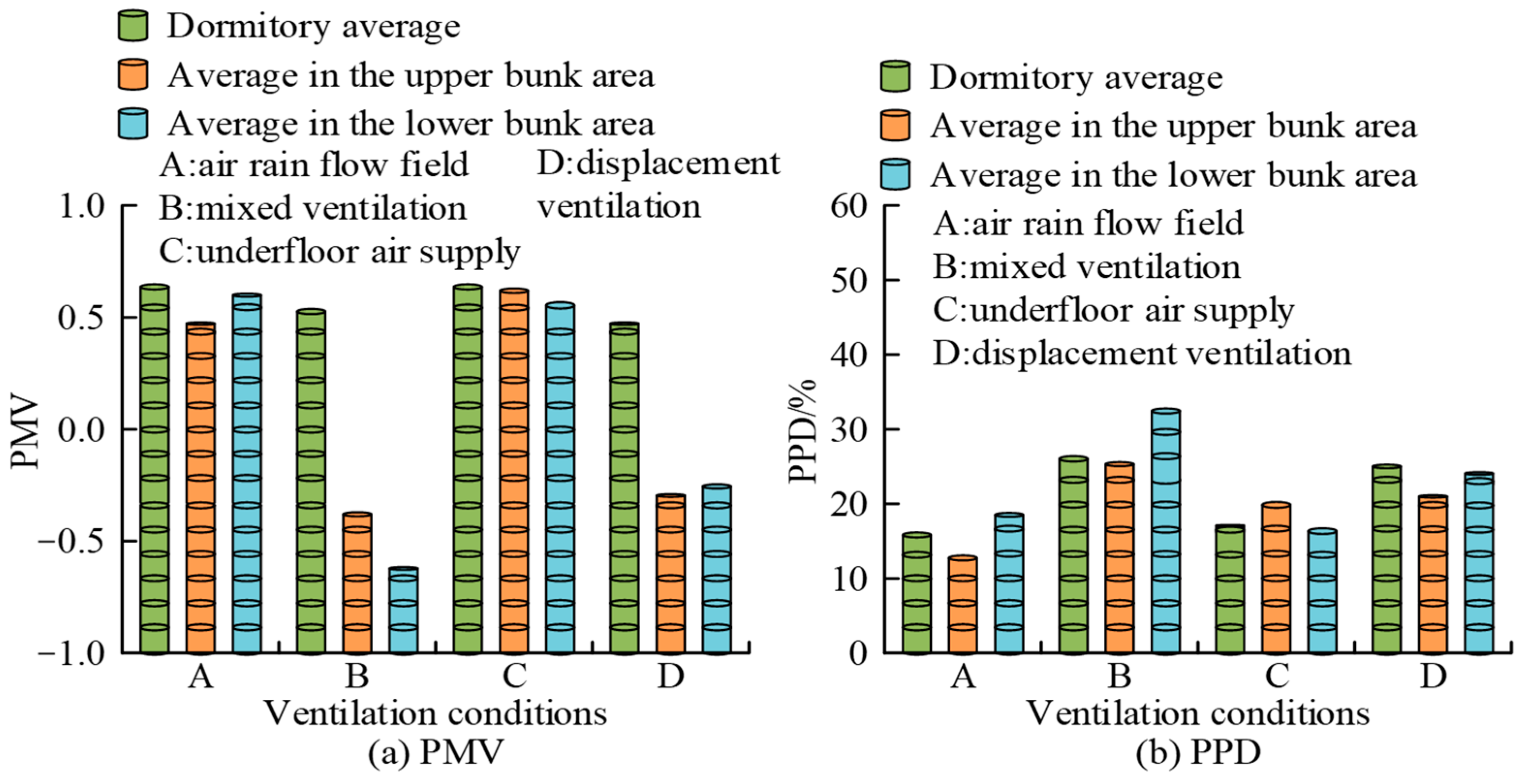
3.2. Simulation Results Analysis of Different Ventilation Methods
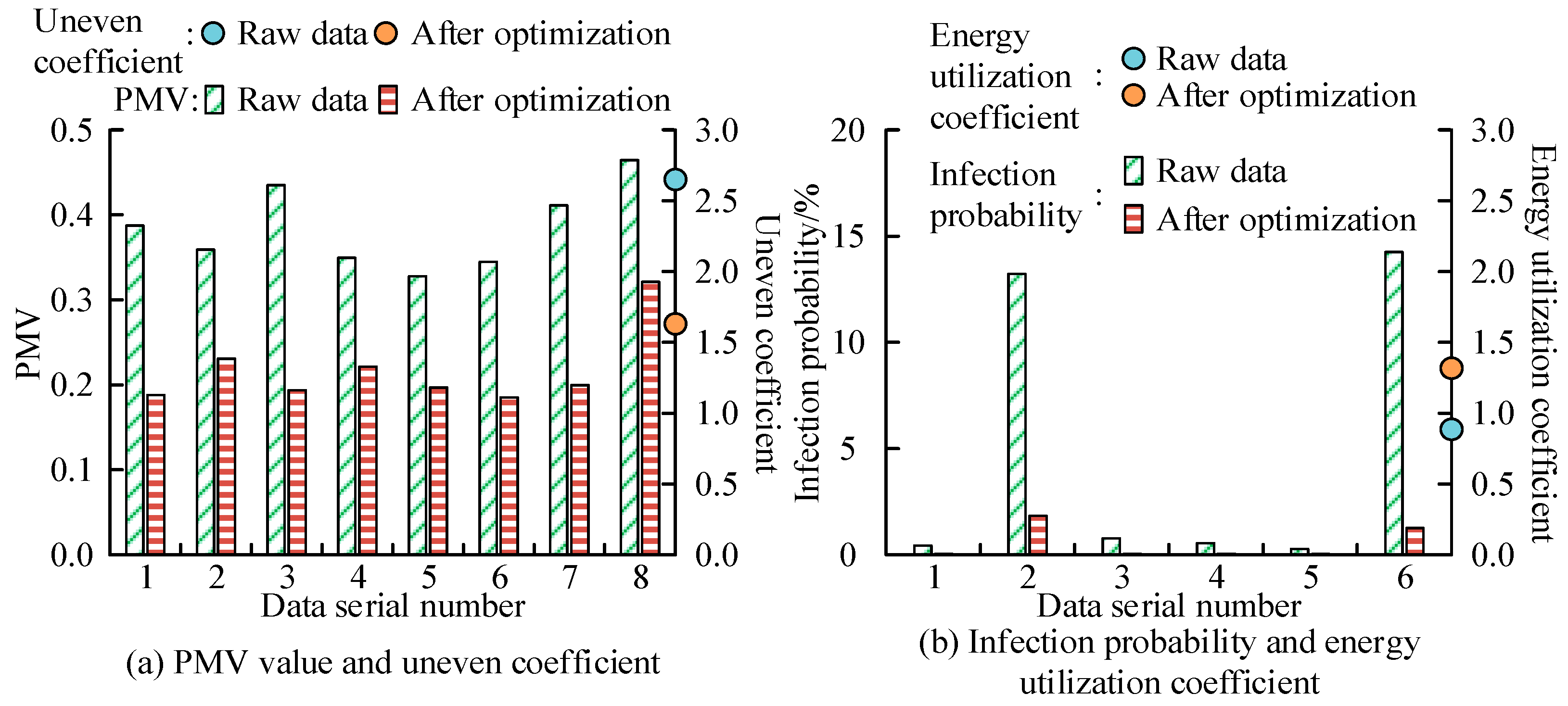
3.3. Analysis of Multi-Objective Optimization Results for the “Air Rain” Flow Field
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nazaroff, W.W. Indoor particle dynamics. Indoor Air 2004, 14, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Loth, E. Numerical approaches for motion of dispersed particles, droplets and bubbles. Prog. Energy Combust. Sci. 2000, 26, 161–223. [Google Scholar] [CrossRef]
- Dhahri, M.; Aouinet, H. Investigation of temperature distribution, air flow pattern and thermal comfort in natural ventilation of building using solar chimney. World J. Eng. 2020, 17, 78–86. [Google Scholar] [CrossRef]
- Xie, E.; Zhao, W.; Xu, Z.; Zhang, X.; Xu, W.; Wang, T. A numerical study on smoke back-layering length in V-shaped tunnels under natural ventilation. Fire Mater. 2022, 46, 130–143. [Google Scholar] [CrossRef]
- Degois, J.; Veillette, M.; Poulin, P.; Lévesque, B.; Duchaine, C. Indoor air quality assessment in dwellings with different ventilation strategies in Nunavik and impacts on bacterial and fungal microbiota. Indoor Air 2021, 31, 2213–2225. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Jia, M.; Bin, L.; Wang, L.; Zhong, D. Regulation and optimization of air quantity in a mine ventilation network with multiple fans. Arch. Min. Sci. 2022, 67, 179–193. [Google Scholar]
- Song, C.; Zhao, T.; Liu, Y.; Wang, D. Distribution characteristics of indoor oxygen concentration under natural ventilation in oxygen-enriched buildings at high altitudes. Build. Simul. 2021, 14, 1823–1841. [Google Scholar] [CrossRef]
- Jeong, S.G.; Wallace, L.; Rim, D. Contributions of Coagulation, Deposition, and Ventilation to the Removal of Airborne Nanoparticles in Indoor Environments. Environ. Sci. Technol. 2021, 55, 9730–9739. [Google Scholar] [CrossRef] [PubMed]
- Ghazvineh, S.; Salimi, M.; Dehghan, S.; Asemi-Rad, A.; Dehdar, K.; Salimi, A. Stimulating olfactory epithelium mitigates mechanical ventilation-induced hippocampal inflammation and apoptosis. Hippocampus 2023, 33, 880–885. [Google Scholar] [CrossRef]
- Lee, J.A.; Mcpeck, M.; Cuccia, A.D.; Smaldone, G.C. Real-Time Analysis of Dry-Side Nebulization with Heated Wire Humidification During Mechanical Ventilation. Respir. Care 2022, 67, 914–928. [Google Scholar] [CrossRef]
- Ting, C.H.; Tan, F.W.; Kuo, C.L. Investigations of structure strength and ventilation performance for agriproduct corrugated cartons under long-term transportation trip. Packag. Technol. Sci. 2022, 35, 821–832. [Google Scholar]
- Wang, S.; Xing, J.; Jiang, Z.; Dai, Y. A decentralized, model-free, global optimization method for energy saving in heating, ventilation and air conditioning systems. Build. Serv. Eng. Res. Technol. 2020, 41, 414–428. [Google Scholar] [CrossRef]
- Ju, F.L.; Liu, L.; Yu, X. An analytical study to evaluate the impact of distributed zone fans on the air flow rate in a mechanical ventilation system. Build. Serv. Eng. Res. Technol. 2020, 41, 507–516. [Google Scholar] [CrossRef]
- Singh, M.; Jradi, M.; Shaker, H.R. Monitoring and Evaluation of Building Ventilation System Fans Operation using Performance Curves. Energy Built Environ. 2020, 1, 307–318. [Google Scholar] [CrossRef]
- Groumpos, P.P. A Critical Historic Overview of Artificial Intelligence: Issues, Challenges, Opportunities, and Threats. Artif. Intell. Appl. 2023, 1, 197–213. [Google Scholar] [CrossRef]
- Olivetti, S.; Gil, M.A.; Sridharan, V.K.; Hein, A.M. Merging computational fluid dynamics and machine learning to reveal animal migration strategies. Methods Ecol. Evol. 2021, 12, 1186–1200. [Google Scholar] [CrossRef]
- Cao, Q.; Li, L.; You, H.; Liu, H. Computational study of dynamics of confined droplets under electric field: Effect of contact angle. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 1775–1796. [Google Scholar] [CrossRef]
- Biswas, T.; Dharmatti, S. Interior and H∞ feedback stabilization for sabra shell model of turbulence. Math. Methods Appl. Sci. 2023, 46, 1852–1883. [Google Scholar] [CrossRef]
- Kundu, J. Design, analysis, set-up fabrication, control, and a novel analytical approach of a levitation prototype for a symmetric shaped object. Asian J. Control 2023, 25, 537–550. [Google Scholar] [CrossRef]
- Liu, D.; Yao, G. Time-varying dynamic analysis of a plate entering the finite subsonic airflow field. Thin-Walled Struct. 2022, 180, 145–157. [Google Scholar] [CrossRef]
- Ajmera, K.; Tewari, T.K. SR-PSO: Server residual efficiency-aware particle swarm optimization for dynamic virtual machine scheduling. Extremes 2023, 26, 15459–15495. [Google Scholar] [CrossRef]
- Binjie, G.; Jie, C.; Feng, P.; Weili, X. Incremental learning for Lagrangian ε-twin support vector regression. Soft Comput. 2023, 27, 5357–5375. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, M.; Zhang, C.; Yin, S.; Jia, J.; Kim, C. Optimization Design of Indoor Environmental Ventilation in Buildings Based on Improved SVR-PSO Model. Sustainability 2024, 16, 5256. https://doi.org/10.3390/su16125256
Han M, Zhang C, Yin S, Jia J, Kim C. Optimization Design of Indoor Environmental Ventilation in Buildings Based on Improved SVR-PSO Model. Sustainability. 2024; 16(12):5256. https://doi.org/10.3390/su16125256
Chicago/Turabian StyleHan, Mengmeng, Chunxiao Zhang, Sihui Yin, Jingjing Jia, and Chulsoo Kim. 2024. "Optimization Design of Indoor Environmental Ventilation in Buildings Based on Improved SVR-PSO Model" Sustainability 16, no. 12: 5256. https://doi.org/10.3390/su16125256
APA StyleHan, M., Zhang, C., Yin, S., Jia, J., & Kim, C. (2024). Optimization Design of Indoor Environmental Ventilation in Buildings Based on Improved SVR-PSO Model. Sustainability, 16(12), 5256. https://doi.org/10.3390/su16125256






