Improving Plane Fitting Accuracy with Rigorous Error Models of Structured Light-Based RGB-D Sensors
Abstract
:1. Introduction
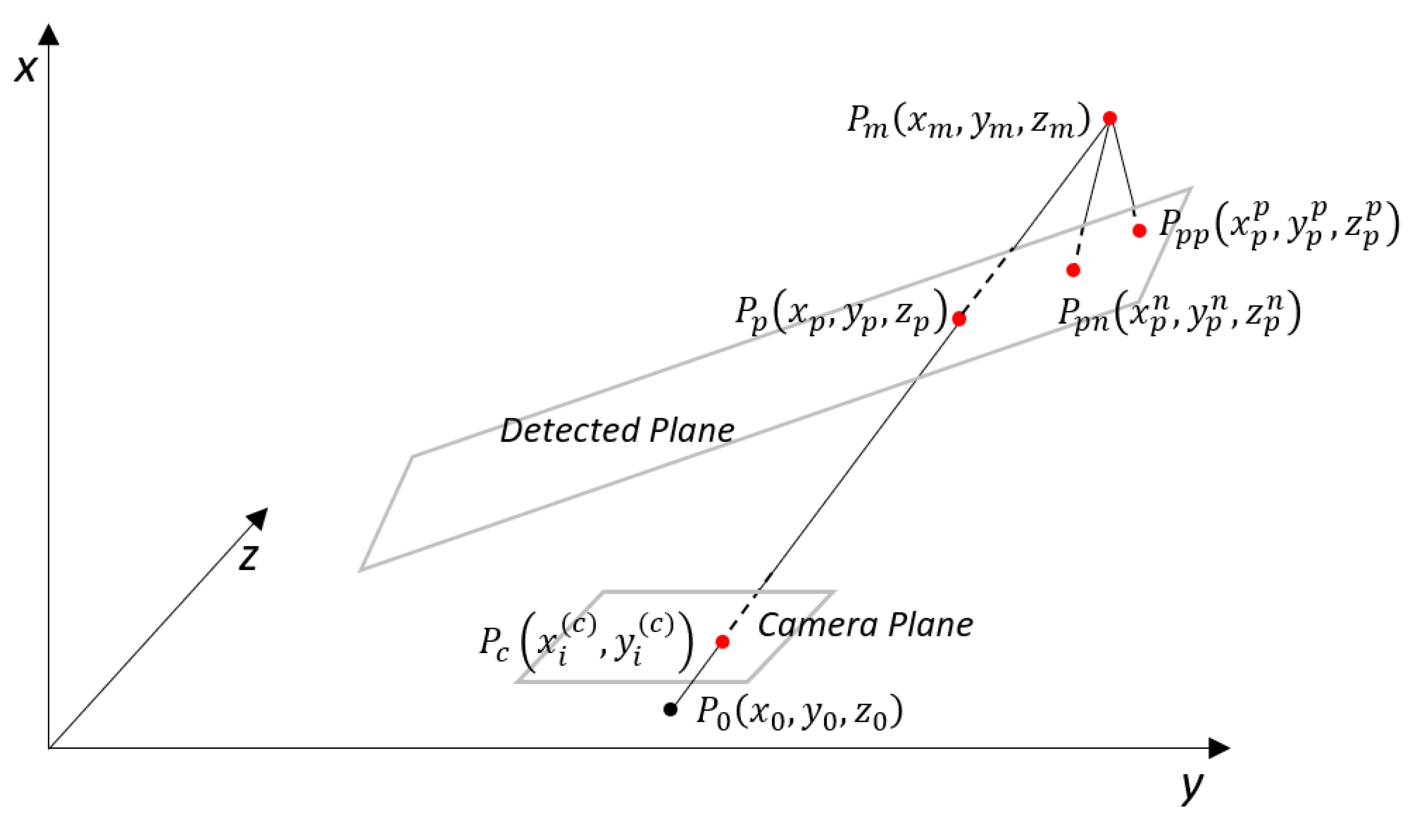
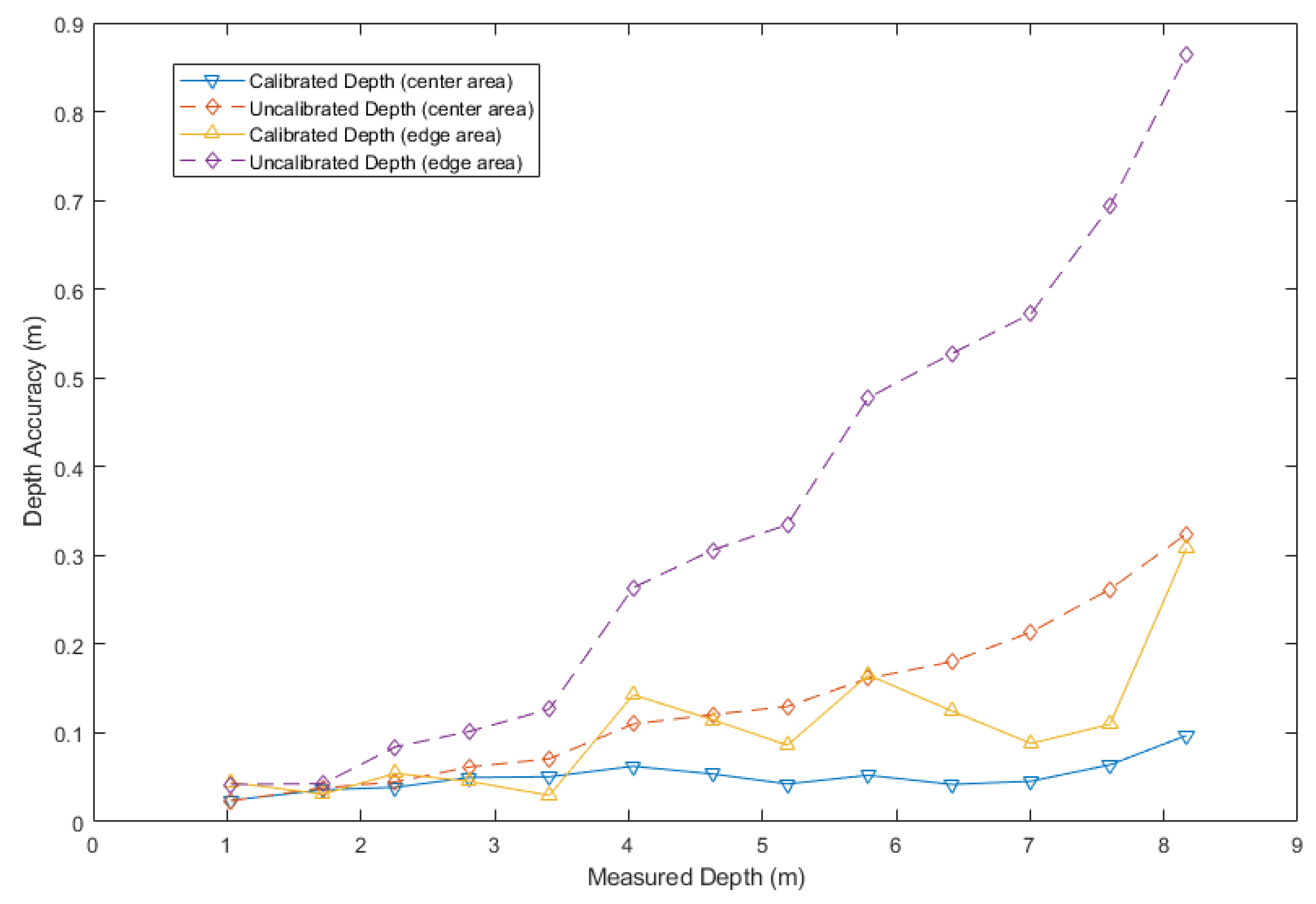
2. Error Distribution of SL Depth Sensors
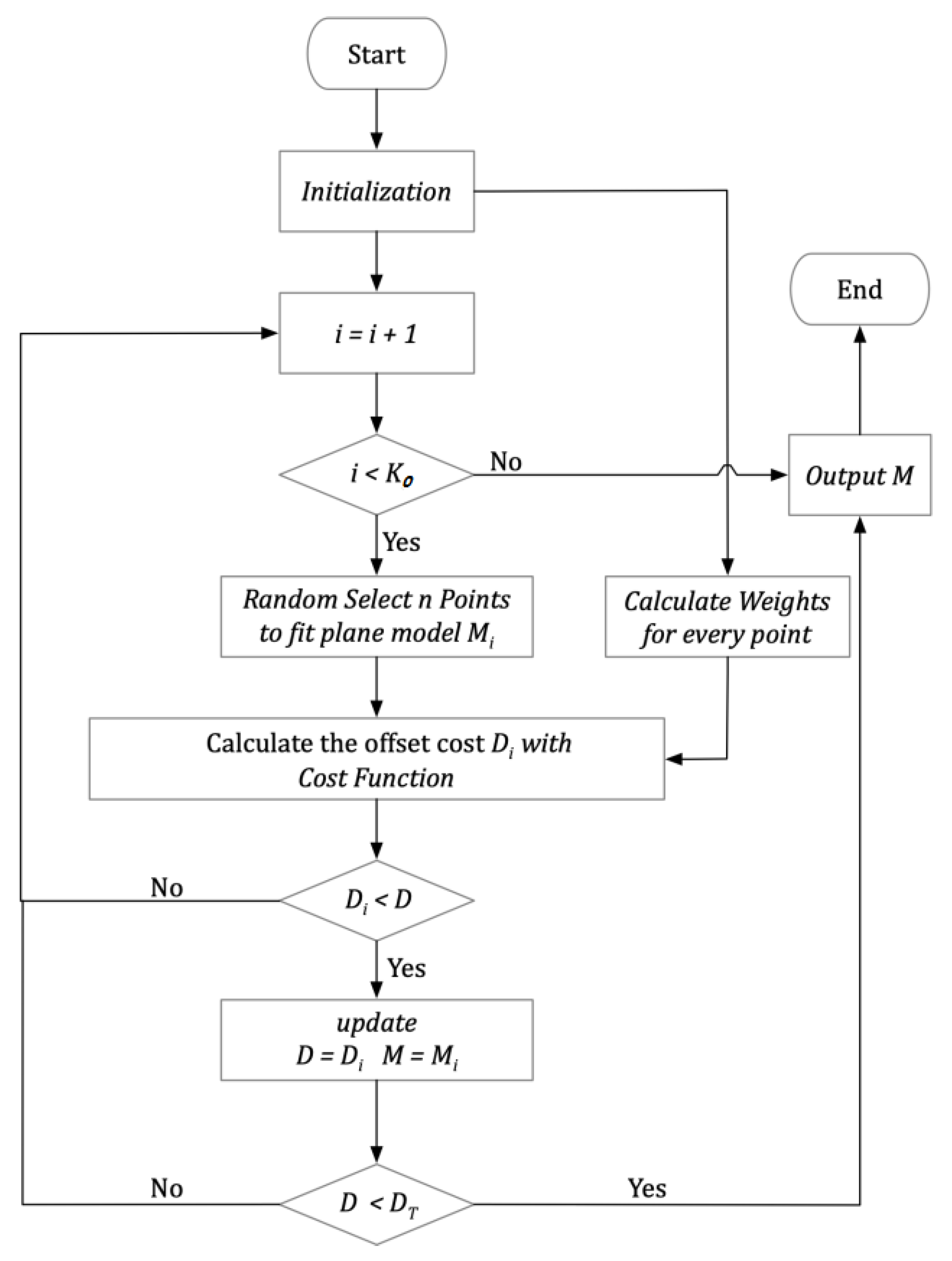
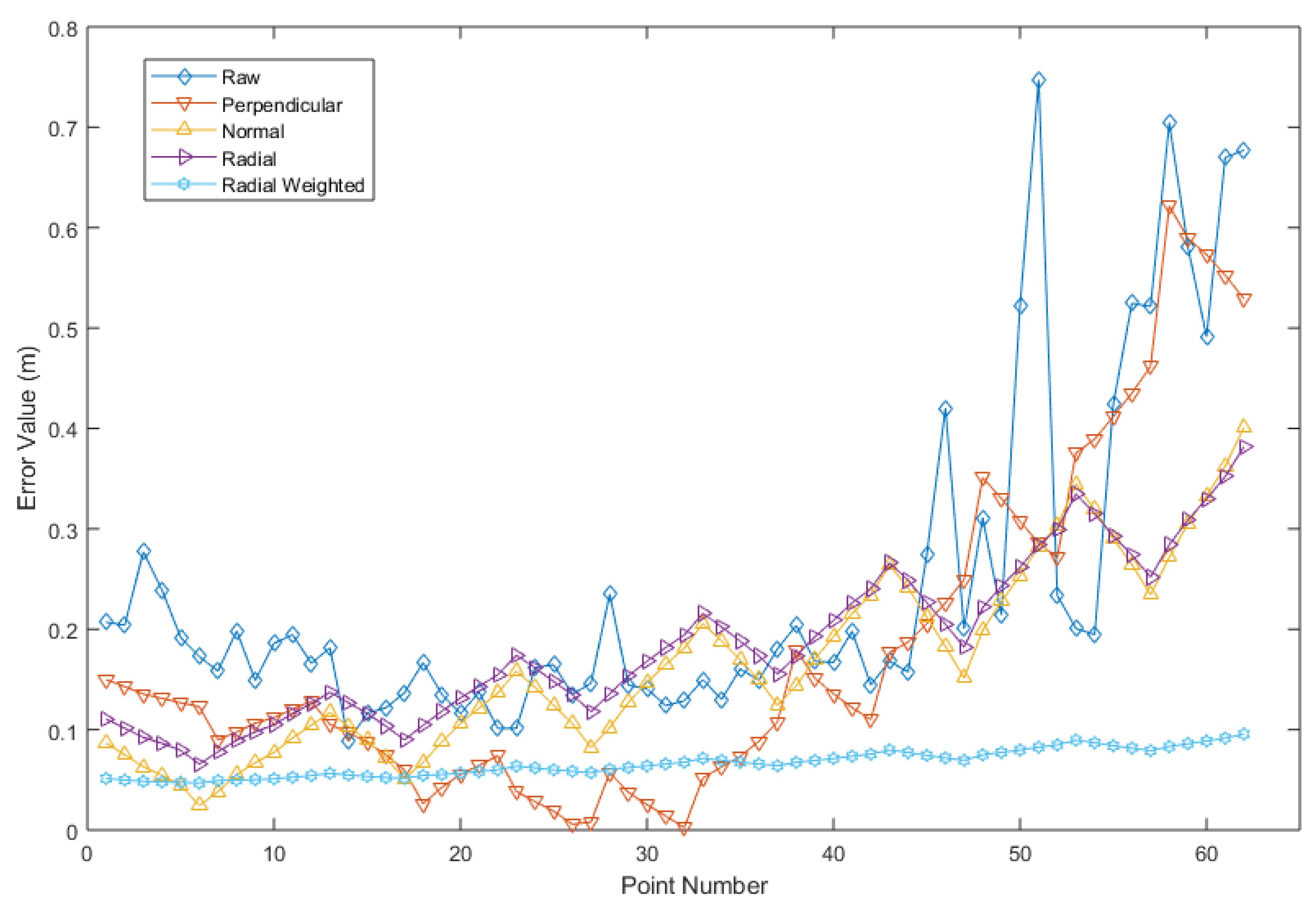
3. Modified RANSAC Algorithm
- Initialize the program with input point cloud and iteration limit ;
- Select points randomly from point cloud to generate the candidate plane model ;
- Calculate the mean offset between each point in point cloud and the candidate plane model based on a cost function;
- Update the best fitting plane model and the corresponding mean offset ;
- Repeat steps 1–4 until the iteration number is larger than the iteration limit or the value of is smaller than the threshold (in this paper, ).
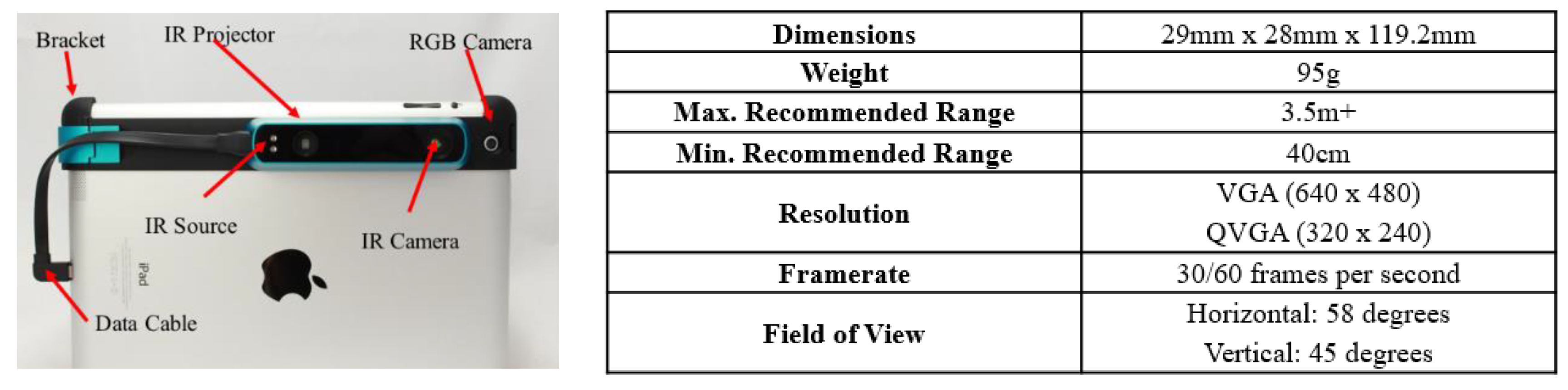
4. Experiments and Results
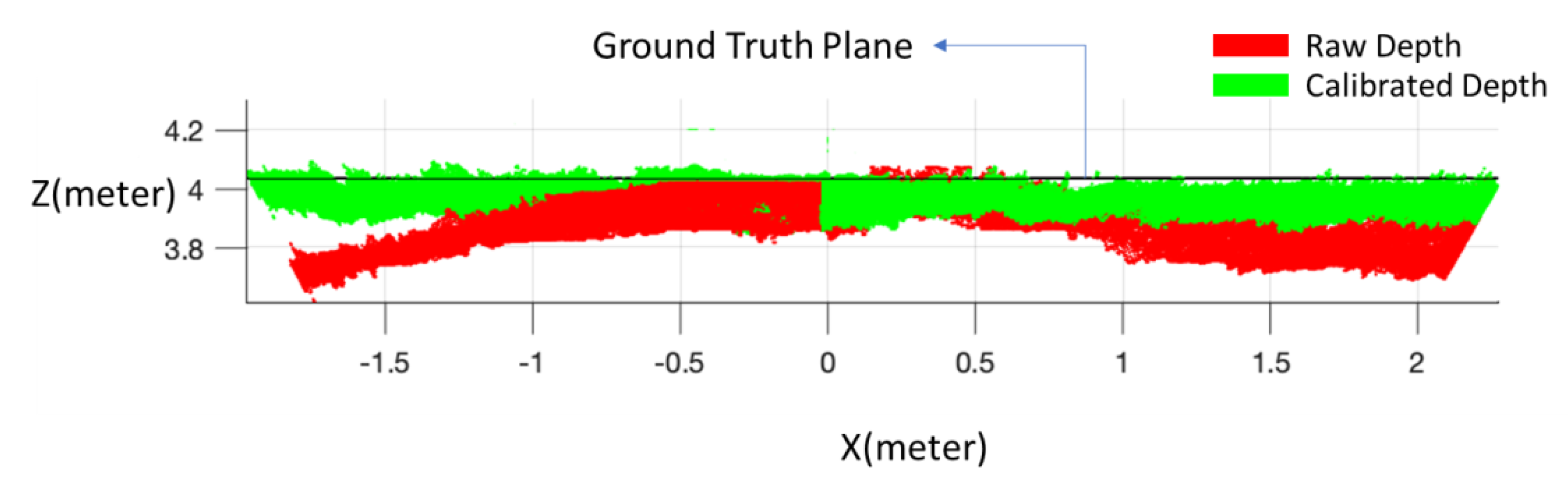
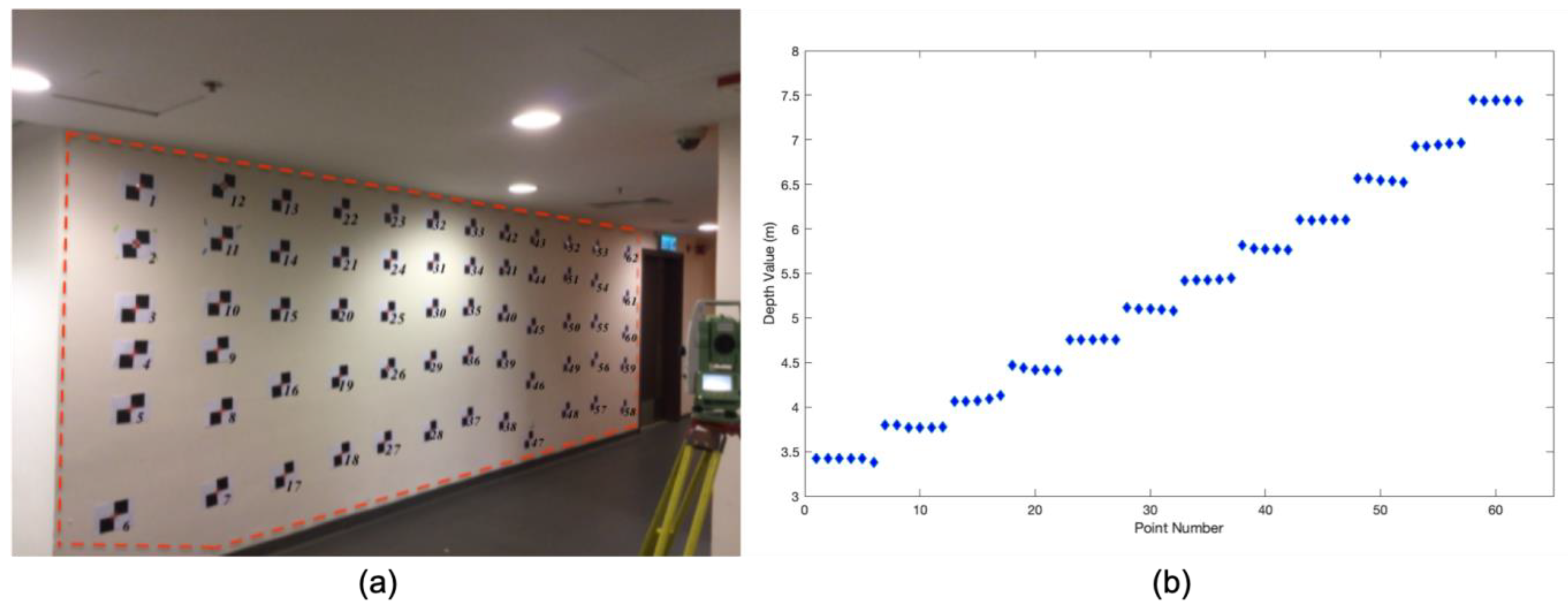
4.1. Experiment for Different Operating Ranges
4.2. Experiment for Large Depth Measurement Scales
4.3. Experiment with Kinect V2
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Dorninger, P.; Pfeifer, N. A comprehensive automated 3D approach for building extraction, reconstruction, and regularization from airborne laser scanning point clouds. Sensors 2008, 8, 7323–7343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, C.; Cho, Y.K.; Kim, C. Automatic BIM component extraction from point clouds of existing buildings for sustainability applications. Autom. Constr. 2015, 56, 1–13. [Google Scholar] [CrossRef]
- Patra, S.; Bhowmick, B.; Banerjee, S.; Kalra, P. High Resolution Point Cloud Generation from Kinect and HD Cameras using Graph Cut. VISAPP 2012, 12, 311–316. [Google Scholar]
- Seif, H.G.; Hu, X.J.E. Autonomous driving in the iCity-HD maps as a key challenge of the automotive industry. Engineering 2016, 2, 159–162. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Liang, M.; Urtasun, R. Hdnet: Exploiting hd maps for 3d object detection. In Proceedings of the Conference on Robot Learning, Osaka, Japan, 30 October–1 November 2019; pp. 146–155. [Google Scholar]
- Biswas, J.; Veloso, M. Depth camera based indoor mobile robot localization and navigation. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1697–1702. [Google Scholar]
- Whitty, M.; Cossell, S.; Dang, K.S.; Guivant, J.; Katupitiya, J. Autonomous navigation using a real-time 3d point cloud. In Proceedings of the Australasian Conference on Robotics and Automation, Brisbane, Australia, 1–3 December 2010; pp. 1–3. [Google Scholar]
- Wang, C.; Tanahashi, H.; Hirayu, H.; Niwa, Y.; Yamamoto, K. Comparison of local plane fitting methods for range data. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA; pp. 663–669. [Google Scholar]
- Kim, K.; Davis, L.S. Multi-Camera tracking and segmentation of occluded people on ground plane using search-Guided particle filtering. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 98–109. [Google Scholar]
- Trevor, A.J.; Gedikli, S.; Rusu, R.B.; Christensen, H.I. Efficient Organized Point Cloud Segmentation with Connected Components. In Proceedings of the 3rd Workshop on Semantic Perception Mapping and Exploration (SPME), Karlsruhe, Germany, 5 May 2013. [Google Scholar]
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings-Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef] [Green Version]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D mapping: Using Kinect-Style depth cameras for dense 3D modeling of indoor environments. Int. J. Robot. Res. 2012, 31, 647–663. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Shao, L.; Xu, D.; Shotton, J. Enhanced computer vision with microsoft kinect sensor: A review. IEEE Trans. Cybern. 2013, 43, 1318–1334. [Google Scholar]
- Hulik, R.; Spanel, M.; Smrz, P.; Materna, Z. Continuous plane detection in point-Cloud data based on 3D Hough Transform. J. Vis. Commun. Image Represent. 2014, 25, 86–97. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Q.; Chen, W.; Darwish, W.; Wu, B.; Hu, H.; Chen, M. Enhanced RGB-D mapping method for detailed 3D indoor and outdoor modeling. Sensors 2016, 16, 1589. [Google Scholar] [CrossRef] [Green Version]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference, Intelligent Robots and Systems (IROS), Algarve, Portuga, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Newcombe, R.A.; Izadi, S.; Hilliges, O.; Molyneaux, D.; Kim, D.; Davison, A.J.; Kohi, P.; Shotton, J.; Hodges, S.; Fitzgibbon, A. KinectFusion: Real-Time dense surface mapping and tracking. In Proceedings of the 2011 10th IEEE International Symposium, Mixed and Augmented Reality (ISMAR), Basel, Switzerland, 26–29 October 2011; pp. 127–136. [Google Scholar]
- Darwish, W.; Tang, S.; Li, W.; Chen, W. A new calibration method for commercial RGB-d sensors. Sensors 2017, 17, 1204. [Google Scholar] [CrossRef] [Green Version]
- Chai, Z.; Sun, Y.; Xiong, Z. A Novel Method for LiDAR Camera Calibration by Plane Fitting. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; pp. 286–291. [Google Scholar]
- Xu, L.; Au, O.C.; Sun, W.; Li, Y.; Li, J. Hybrid plane fitting for depth estimation. In Proceedings of the 2012 Asia-Pacific, Signal & Information Processing Association Annual Summit and Conference (APSIPA ASC), Hollywood, CA, USA, 3–6 December 2012; pp. 1–4. [Google Scholar]
- Habbecke, M.; Kobbelt, L. Iterative multi-View plane fitting. In Proceedings of the International Fall Workshop of Vision, Modeling, and Visualization, Aachen, Germany, 22–24 November 2006; pp. 73–80. [Google Scholar]
- Habbecke, M.; Kobbelt, L. A surface-Growing approach to multi-View stereo reconstruction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Xu, K.; Huang, H.; Shi, Y.; Li, H.; Long, P.; Caichen, J.; Sun, W.; Chen, B. Autoscanning for coupled scene reconstruction and proactive object analysis. ACM Trans. Graph. (TOG) 2015, 34, 177. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Hong, L.; Chen, G. Segment-Based stereo matching using graph cuts. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 74–81. [Google Scholar]
- Oniga, F.; Nedevschi, S. Processing dense stereo data using elevation maps: Road surface, traffic isle, and obstacle detection. IEEE Trans. Veh. Technol. 2010, 59, 1172–1182. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Borrmann, D.; Elseberg, J.; Lingemann, K.; Nüchter, A. The 3d hough transform for plane detection in point clouds: A review and a new accumulator design. 3D Res. 2011, 2, 3. [Google Scholar] [CrossRef]
- Bolles, R.C.; Fischler, M.A. A RANSAC-Based Approach to Model Fitting and Its Application to Finding Cylinders in Range Data. In Proceedings of the International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 637–643. [Google Scholar]
- Sande, C.V.D.; Soudarissanane, S.; Khoshelham, K. Assessment of relative accuracy of AHN-2 laser scanning data using planar features. Sensors 2010, 10, 8198–8214. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J. Matching with PROSAC-Progressive sample consensus. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 220–226. [Google Scholar]
- Torr, P.H.; Zisserman, A. MLESAC: A new robust estimator with application to estimating image geometry. Comput. Vis. Image Underst. 2000, 78, 138–156. [Google Scholar] [CrossRef] [Green Version]
- Holz, D.; Behnke, S. Approximate triangulation and region growing for efficient segmentation and smoothing of range images. Robot. Auton. Syst. 2014, 62, 1282–1293. [Google Scholar] [CrossRef]
- Fuersattel, P.; Placht, S.; Maier, A.; Riess, C. Geometric primitive refinement for structured light cameras. Mach. Vis. Appl. 2018, 29, 313–327. [Google Scholar] [CrossRef]
- Heikkila, J.; Silven, O. A four-Step camera calibration procedure with implicit image correction. In Proceedings of the Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, USA, 17–19 June 1997; p. 1106. [Google Scholar]
- Darwish, W.; Li, W.; Tang, S.; Wu, B.; Chen, W. A Robust Calibration Method for Consumer Grade RGB-D Sensors for Precise Indoor Reconstruction. IEEE Access 2019, 7, 8824–8833. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-Cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Li, L.; Yang, F.; Zhu, H.; Li, D.; Li, Y.; Tang, L. An improved RANSAC for 3D point cloud plane segmentation based on normal distribution transformation cells. Remote Sens. 2017, 9, 433. [Google Scholar] [CrossRef] [Green Version]
- Miyagawa, S.; Yoshizawa, S.; Yokota, H. Trimmed Median PCA for Robust Plane Fitting. In Proceedings of the 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 753–757. [Google Scholar]
- Occipital. Structure Sensor. Available online: https://structure.io/structure-sensor (accessed on 5 December 2019).







| P1 | P2 | K1 | K2 | K3 |
|---|---|---|---|---|
| 1.182 × 10−7 | −6.864 × 10−13 | 4.217 × 10−5 | 1.410 × 10−5 | −4.616 × 10−11 |
| Ranges | Distance Type | Δdr (cm) | ||
|---|---|---|---|---|
| Close (1.23 m) | LS | 1.5 ± 0.01 | 1.9 ± 0.02 | 2.1 ± 0.02 |
| Perpendicular | 2.3 ± 1.35 | 0.9 ± 0.65 | 1.6 ± 0.82 | |
| Normal | 2.2 ± 1.57 | 0.8 ± 0.67 | 1.5 ± 0.91 | |
| Radial | 1.8 ± 0.99 | 0.7 ± 0.54 | 1.3 ± 0.62 | |
| Radial Weighted | 0.9± 0.05 | 0.6± 0.16 | 0.8± 0.04 | |
| Middle (2.47 m) | LS | 2.9 ± 0.05 | 2.6 ± 0.13 | 2.9 ± 0.14 |
| Perpendicular | 2.7 ± 0.95 | 1.6 ± 1.14 | 3.7 ± 1.23 | |
| Normal | 2.6 ± 1.02 | 1.8 ± 1.09 | 3.6 ± 1.13 | |
| Radial | 2.4 ± 0.96 | 1.3 ± 1.07 | 3.2 ± 1.04 | |
| Radial Weighted | 1.1± 0.20 | 1.2± 0.04 | 2.7± 0.24 | |
| Far (4.31 m) | LS | 3.7 ± 0.21 | 13.3 ± 0.66 | 14.3 ± 0.70 |
| Perpendicular | 3.6 ± 1.69 | 8.9 ± 3.18 | 10.9 ± 4.09 | |
| Normal | 2.5 ± 1.39 | 7.4 ± 2.82 | 9.6 ± 2.93 | |
| Radial | 2.6 ± 1.35 | 6.5 ± 2.44 | 8.6 ± 2.62 | |
| Radial Weighted | 0.9± 0.46 | 5.8± 0.64 | 6.6± 0.69 |
| Δdr (cm) | |||
|---|---|---|---|
| LS | 3.3 ± 0.5 | 20.3 ± 0.7 | 27.4 ± 0.3 |
| Perpendicular | 3.7 ± 1.1 | 16.8 ± 3.8 | 25.7 ± 7.8 |
| Normal | 2.6 ± 1.0 | 12.4 ± 3.1 | 20.8 ± 5.6 |
| Radial | 2.2 ± 0.7 | 13.8 ± 1.6 | 23.0 ± 2.4 |
| Radial Weighted | 0.5± 0.2 | 4.8± 0.7 | 7.2± 2.2 |
| Δdr (cm) | |||
|---|---|---|---|
| LS | 4.8 ± 0.2 | 22.2 ± 0.3 | 29.6 ± 0.4 |
| Perpendicular | 2.7 ± 0.7 | 15.5 ± 2.2 | 25.4 ± 3.7 |
| Normal | 1.7 ± 1.1 | 12.1 ± 2.9 | 20.2 ± 3.0 |
| Radial | 1.5 ± 0.7 | 10.8 ± 2.0 | 15.6 ± 3.5 |
| Radial Weighted | 0.9 ± 0.4 | 7.1 ± 0.7 | 9.6 ± 0.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, W.; Darwish, W.; Tang, S.; Hu, Y.; Chen, W. Improving Plane Fitting Accuracy with Rigorous Error Models of Structured Light-Based RGB-D Sensors. Remote Sens. 2020, 12, 320. https://doi.org/10.3390/rs12020320
Li Y, Li W, Darwish W, Tang S, Hu Y, Chen W. Improving Plane Fitting Accuracy with Rigorous Error Models of Structured Light-Based RGB-D Sensors. Remote Sensing. 2020; 12(2):320. https://doi.org/10.3390/rs12020320
Chicago/Turabian StyleLi, Yaxin, Wenbin Li, Walid Darwish, Shengjun Tang, Yuling Hu, and Wu Chen. 2020. "Improving Plane Fitting Accuracy with Rigorous Error Models of Structured Light-Based RGB-D Sensors" Remote Sensing 12, no. 2: 320. https://doi.org/10.3390/rs12020320
APA StyleLi, Y., Li, W., Darwish, W., Tang, S., Hu, Y., & Chen, W. (2020). Improving Plane Fitting Accuracy with Rigorous Error Models of Structured Light-Based RGB-D Sensors. Remote Sensing, 12(2), 320. https://doi.org/10.3390/rs12020320





