Noise Floor and Signal-to-Noise Ratio of Radio Occultation Observations: A Cross-Mission Statistical Comparison
Abstract
:1. Introduction
2. Data and Methods
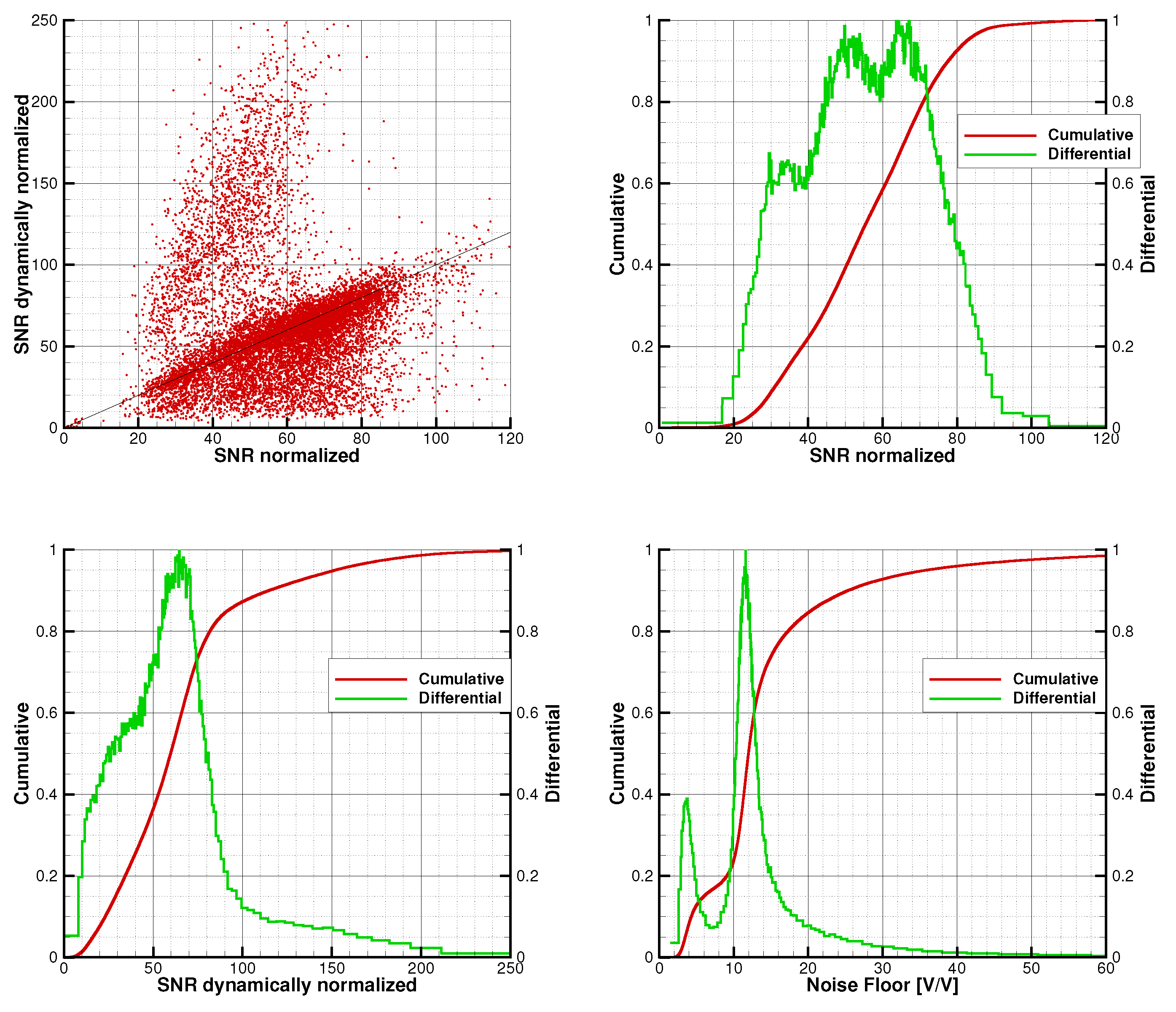
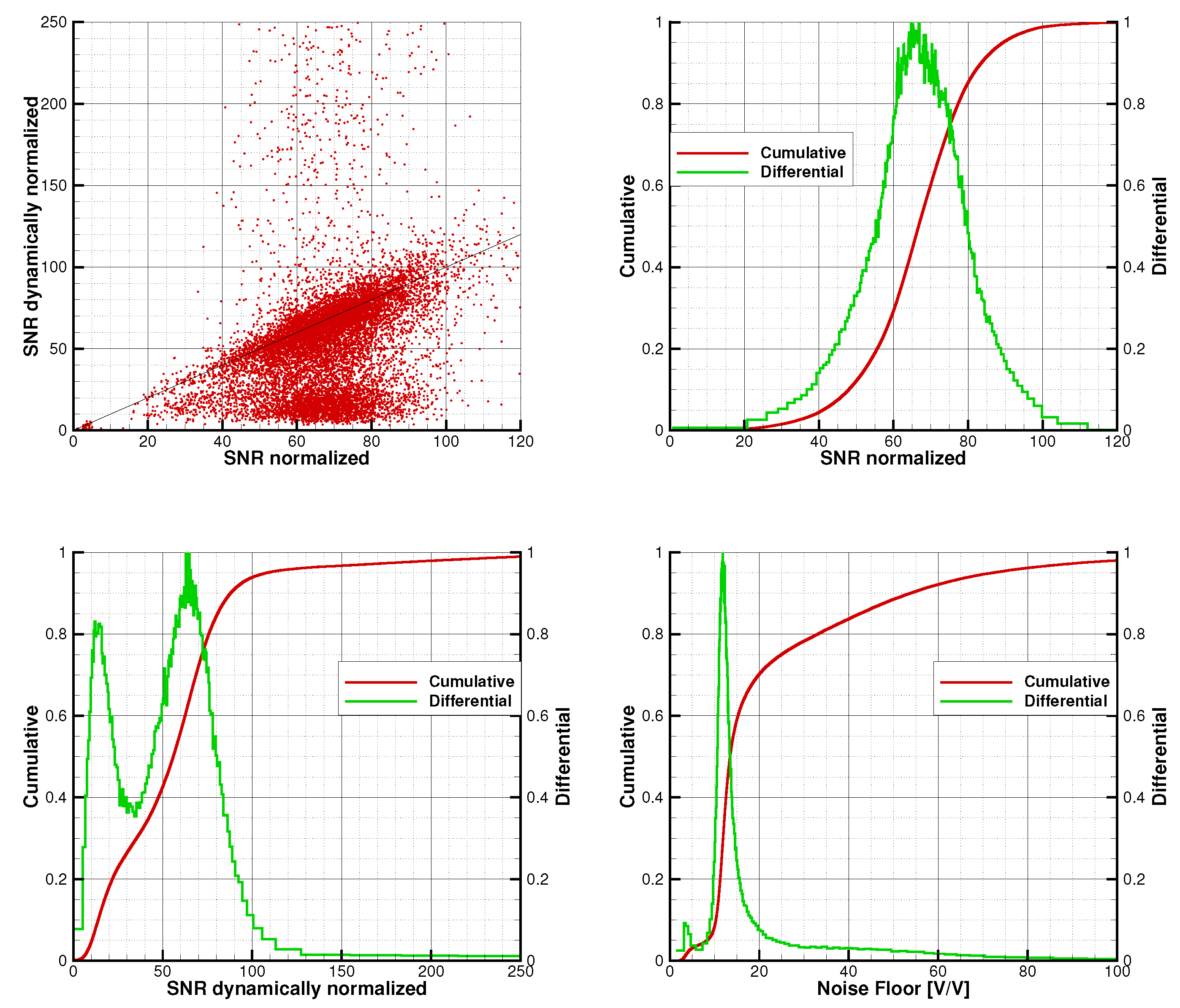
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDAAC | COSMIC Data Analysis and Archive Center |
| CICERO | Community Initiative for Cellular Earth Remote Observation |
| COSMIC | Constellation Observing System for Meteorology, Ionosphere, and Climate |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| GLONASS | Global Navigation Satellite System (Russian navigation system) |
| GNSS | Global Navigation Satellite System |
| GO | Geometrical Optics |
| GPS | Global Positioning System |
| METOP | Meteorological Operational Satellite |
| MSISE | Mass-Spectrometer-Incoherent-Scatter model Extended |
| NF | Noise Floor |
| PBL | Planetary Boundary Layer |
| Probability Distribution Function | |
| RMS | Root-Mean-Square |
| QC | Quality Control |
| QZSS | Quasi-Zenith Satellite System |
| RO | Radio Occultation |
| SNR | Signal-to-Noise Ratio |
| WO | Wave Optics |
References
- Sokolovskiy, S.; Schreiner, W.; Weiss, J.; Zeng, Z.; Hunt, D.; Braun, J. Initial Assessment of COSMIC-2 Data in the Lower Troposphere. In Proceedings of the Joint 6th ROM SAF Data User Workshop and 7th IROWG Workshop, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.G.; Xia-Serafino, W.; Lynch, E. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using In Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Lin, C.Y.; Lin, C.C.H.; Liu, J.Y.; Rajesh, P.K.; Matsuo, T.; Chou, M.Y.; Tsai, H.F.; Yeh, W.H. The Early Results and Validation of FORMOSAT-7/COSMIC-2 Space Weather Products: Global Ionospheric Specification and Ne-Aided Abel Electron Density Profile. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028028. [Google Scholar] [CrossRef]
- Bonnedal, M.; Christensen, J.; Carlström, A.; Berg, A. Metop-GRAS in-orbit instrument performance. GPS Solut. 2010, 14, 109–120. [Google Scholar] [CrossRef]
- Schreiner, W.; Sokolovskiy, S.; Hunt, D.; Rocken, C.; Kuo, Y.H. Analysis of GPS radio occultation data from the FORMOSAT-3/COSMIC and Metop/GRAS missions at CDAAC. Atmos. Meas. Tech. 2011, 4, 2255–2272. [Google Scholar] [CrossRef] [Green Version]
- Von Engeln, A.; Andres, Y.; Marquardt, C.; Sancho, F. GRAS radio occultation on-board of Metop. Adv. Space Res. 2011, 47, 336–347. [Google Scholar] [CrossRef]
- Hsieh, M.E.; Chen, Y.-C.; Hsiao, L.F.; Chang., L.-Y.; Huang, C.Y. Case Study of Impact of Assimilating MetOp GPS Radio Occultation Observation on Top of COSMIC Data on Typhoon Forecast. J. Aeronaut. Astrnaut. Aviat. 2018, 50, 375–390. [Google Scholar] [CrossRef]
- Rapp, M.; Dörnbrack, A.; Kaifler, B. An intercomparison of stratospheric gravity wave potential energy densities from METOP GPS radio occultation measurements and ECMWF model data. Atmos. Meas. Tech. 2018, 11, 1031–1048. [Google Scholar] [CrossRef] [Green Version]
- Irisov, V.; Duly, T.; Nguyen, V.; Masters, D.; Correig, O.N.; Tan, L.; Yuasa, T.; Ector, D. Recent radio occultation profile results obtained from Spire CubeSat GNSS-RO constellation. In Proceedings of the AGU Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Irisov, V.; Ector, D.; Duly, T.; Nguyen, V.; Nogues-Correig, O.; Tan, L.; Yuasa, T. Atmospheric Radio Occultation Observation from Spire CubeSat Nanosatellites. In Proceedings of the AMS Annual Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Gorbunov, M.; Koval, O.; Kirchengast, G. Kirkwood Distribution Function and its Application for the Analysis of Radio Occultation Observations. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, EUMETSAT ROM SAF, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Irisov, V.; Nguyen, V.; Duly, T.; Nogues-Correig, O.; Tan, L.; Yuasa, T.; Masters, D.; Sikarin, R.; Gorbunov, M.; Rocken, C. Radio Occultation Observations and Processing from Spire’s CubeSat Constellation. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, EUMETSAT ROM SAF, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Bowler, N.E. An assessment of GNSS radio occultationdata produced by Spire. Q. J. R. Meteorol. Soc. 2020, 146, 3772–3788. [Google Scholar] [CrossRef]
- Kursinski, E.R. Weather & Space Weather RO Data from PlanetiQ Commercial GNSS RO. In Proceedings of the Joint 6th ROM SAF Data User Workshop and 7th IROWG Workshop, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Chang, H.; Lee, J.; Wang, Y.; Breitsch, B.; Morton, Y.J. Preliminary Assessment of CICERO Radio Occultation Performance by Comparing with COSMIC I Data. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation, Online, 21–25 September 2020. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Schreiner, W.; Zeng, Z.; Hunt, D.; Lin, Y.C.; Kuo, Y.H. Observation, analysis, and modeling of deep radio occultation signals: Effects of tropospheric ducts and interfering signals. Radio Sci. 2014, 49, 954–970. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D. On the uncertainty of radio occultation inversions in the lower troposphere. J. Geophys. Res. 2010, 115, D22111. [Google Scholar] [CrossRef] [Green Version]
- Sokolovskiy, S.; Rocken, C.; Hunt, D.; Schreiner, W.; Johnson, J.; Masters, D.; Esterhuizen, S. GPS profiling of the lower troposphere from space: Inversion and demodulation of the open-loop radio occultation signals. Geophys. Res. Lett. 2006, 33, L14816. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Lauritsen, K.B. Analysis of wave fields by Fourier integral operators and its application for radio occultations. Radio Sci. 2004, 39, RS4010. [Google Scholar] [CrossRef]
- Jensen, A.S.; Lohmann, M.S.; Nielsen, A.S.; Benzon, H.H. Geometrical optics phase matching of radio occultation signals. Radio Sci. 2004, 39, RS3009. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.; Kirchengast, G.; Lauritsen, K.B. Generalized canonical transform method for radio occultation sounding with improved retrieval in the presence of horizontal gradients. Atmos. Meas. Tech. 2021, 14, 853–867. [Google Scholar] [CrossRef]
- Hedin, A.E. Extension of MSIS thermosphere model into the middle and lower atmosphere. J. Geophys. Res. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Modeling and inverting radio occultation signals in the moist troposphere. Radio Sci. 2001, 36, 441–458. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Sokolovskiy, S.V. Remote Sensing of Refractivity from Space for Global Observations of Atmospheric Parameters; Report 119; Max–Planck Institute for Meteorology: Hamburg, Germany, 1993; 58p. [Google Scholar]
- Scherllin-Pirscher, B.; Syndergaard, S.; Foelsche, U.; Lauritsen, K.B. Generation of a bending angle radio occultation climatology (BAROCLIM) and its use in radio occultation retrievals. Atmos. Meas. Tech. 2015, 8, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Shmakov, A.V. Statistically average atmospheric bending angle model based on COSMIC experimental data. Izv. Atmos. Oceanic Phys. 2016, 52, 622–628. [Google Scholar] [CrossRef]
- Beyerle, G.; Gorbunov, M.E.; Ao, C.O. Simulation studies of GPS radio occultation measurements. Radio Sci. 2003, 38, 1084. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Gurvich, A.S.; Shmakov, A.V. Back-propagation and radio-holographic methods for investigation of sporadic ionospheric E-layers from Microlab-1 data. Int. J. Remote Sens. 2002, 23, 675–685. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V.; Schreiner, W.; Rocken, C.; Hunt, D. Detection of high-altitude ionospheric irregularities with GPS/MET. Geophys. Res. Let. 2002, 29, 3-1–3-4. [Google Scholar] [CrossRef] [Green Version]
- Kuo, Y.H.; Wee, T.K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Inversion and Error Estimation of GPS Radio Occultation Data. J. Meteorolog. Soc. Jpn. 2004, 82, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Syndergaard, S. Modeling the impact of the Earth’s oblateness on the retrieval of temperature and pressure profiles from limb sounding. J. Atmos. Sol. Terr. Phys. 1998, 60, 171–180. [Google Scholar] [CrossRef]
- Xiaohua, X.; Zhenghang, L.; Jia, L. Correction on effect of Earth’s oblateness in inversion of GPS occultation data. Geo Spat. Inform. Sci. 2005, 8, 247–250. [Google Scholar] [CrossRef] [Green Version]








| G | R | E | J | |
|---|---|---|---|---|
| COSMIC | 11.1 | - | - | - |
| METOP-A | 11.6 | - | - | - |
| METOP-B | 12.0 | - | - | - |
| METOP-C | 11.8 | - | - | - |
| COSMIC-2 | 18.4 | 14.6 | - | - |
| Spire | 9.64 | 9.93 | 10.1 | 9.80 |
| G | R | E | J | |
|---|---|---|---|---|
| COSMIC | 685/883 | - | - | - |
| METOP-A | 642/957 | - | - | - |
| METOP-B | 741/961 | - | - | - |
| METOP-C | 788/1056 | - | - | - |
| COSMIC-2 | 1377/1917 | 1265/2095 | - | - |
| Spire | 305/460 | 318/591 | 218/330 | 263/379 |
| G | R | E | J | |
|---|---|---|---|---|
| COSMIC | 61.6/79.5 | - | - | - |
| METOP-A | 55.4/82.7 | - | - | - |
| METOP-B | 61.8/80.2 | - | - | - |
| METOP-C | 66.7/89.4 | - | - | - |
| COSMIC-2 | 74.7/104 | 86.8/143.8 | - | - |
| Spire | 31.6/47.8 | 32.0/59.5 | 21.6/32.6 | 26.9/38.7 |
| G | R | E | J | |
|---|---|---|---|---|
| COSMIC | 55.3/78.4 | - | - | - |
| METOP-A | 59.7/152 | - | - | - |
| METOP-B | 41.0/77.1 | - | - | - |
| METOP-C | 55.9/108 | - | - | - |
| COSMIC-2 | 63.9/102 | 72.7/140 | - | - |
| Spire | 29.4/46.2 | 31.0/57.9 | 21.5/32.8 | 25.7/39.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorbunov, M.; Irisov, V.; Rocken, C. Noise Floor and Signal-to-Noise Ratio of Radio Occultation Observations: A Cross-Mission Statistical Comparison. Remote Sens. 2022, 14, 691. https://doi.org/10.3390/rs14030691
Gorbunov M, Irisov V, Rocken C. Noise Floor and Signal-to-Noise Ratio of Radio Occultation Observations: A Cross-Mission Statistical Comparison. Remote Sensing. 2022; 14(3):691. https://doi.org/10.3390/rs14030691
Chicago/Turabian StyleGorbunov, Michael, Vladimir Irisov, and Christian Rocken. 2022. "Noise Floor and Signal-to-Noise Ratio of Radio Occultation Observations: A Cross-Mission Statistical Comparison" Remote Sensing 14, no. 3: 691. https://doi.org/10.3390/rs14030691
APA StyleGorbunov, M., Irisov, V., & Rocken, C. (2022). Noise Floor and Signal-to-Noise Ratio of Radio Occultation Observations: A Cross-Mission Statistical Comparison. Remote Sensing, 14(3), 691. https://doi.org/10.3390/rs14030691






