Exploring the Spatiotemporal Dynamics and Driving Factors of Net Ecosystem Productivity in China from 1982 to 2020
Abstract
:1. Introduction
2. Materials and Methods
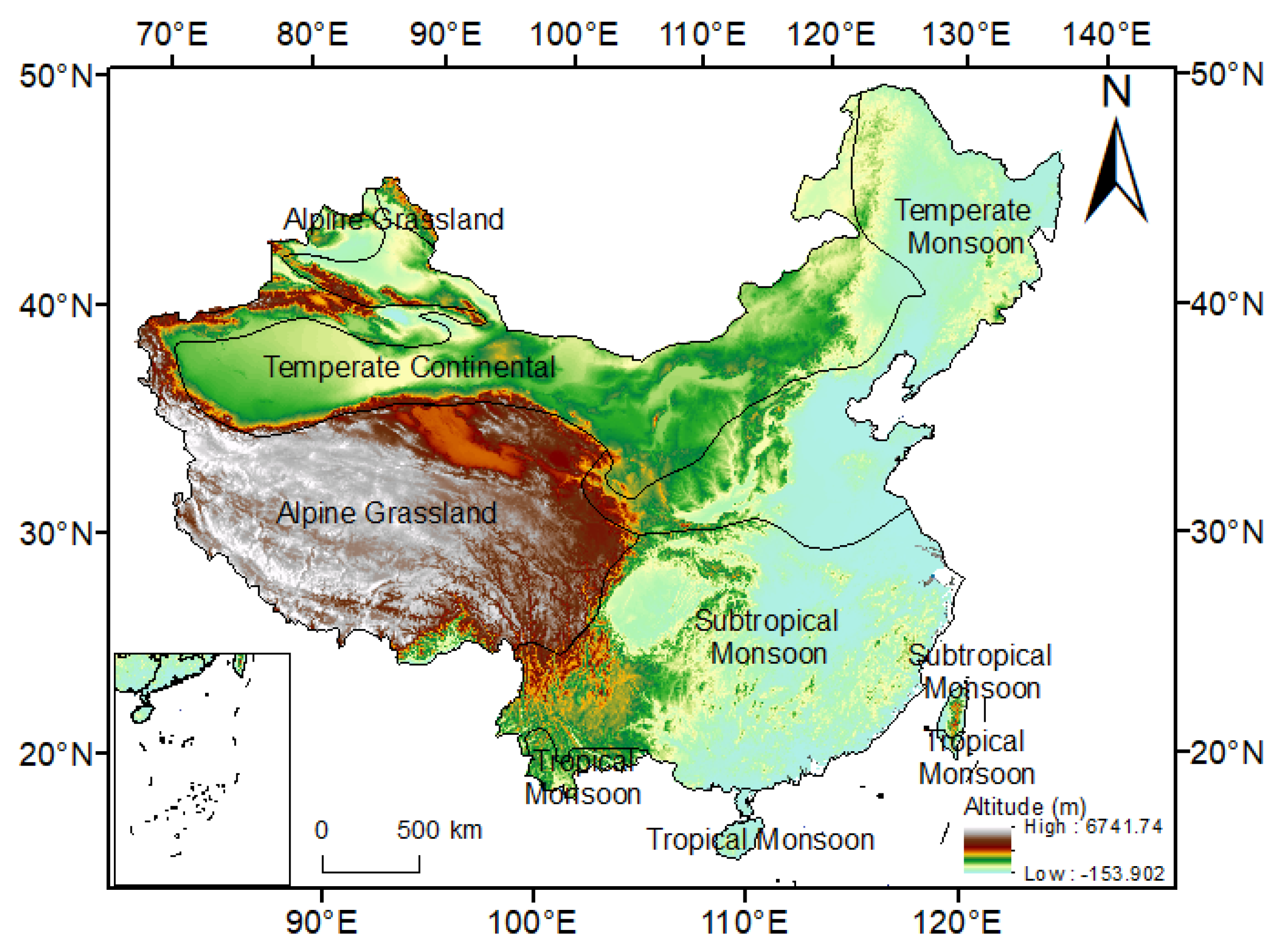
2.1. Study Area
2.2. Data Sources and Processing
2.2.1. NDVI Data
2.2.2. Meteorological Data
2.2.3. Land-Cover Data
2.2.4. DEM Data
2.2.5. FLUXNET Data
2.3. Research Methods
2.3.1. NPP Estimation
2.3.2. NEP Calculation
2.3.3. Spatiotemporal Variations
2.3.4. Geodetector Model
3. Results
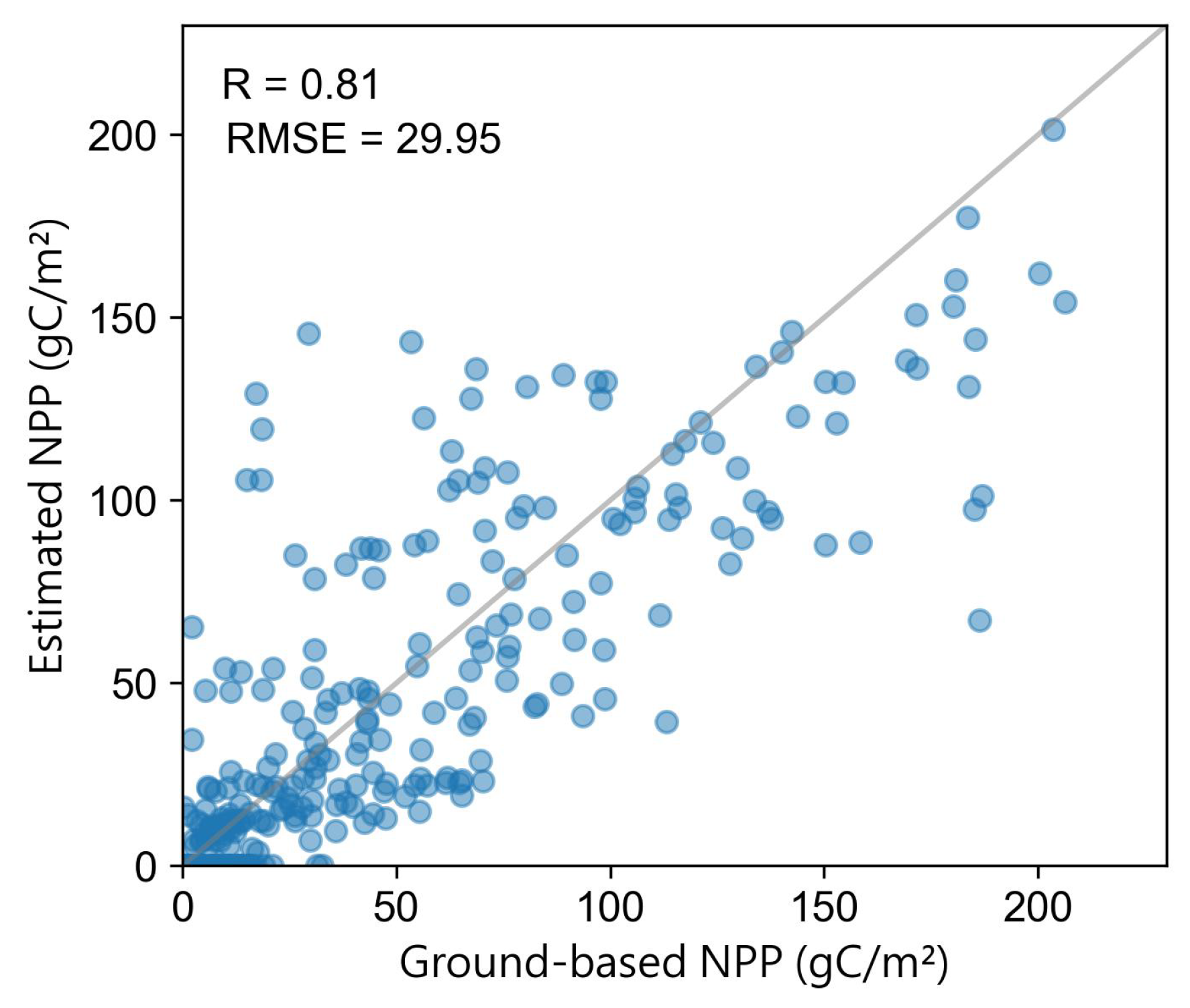
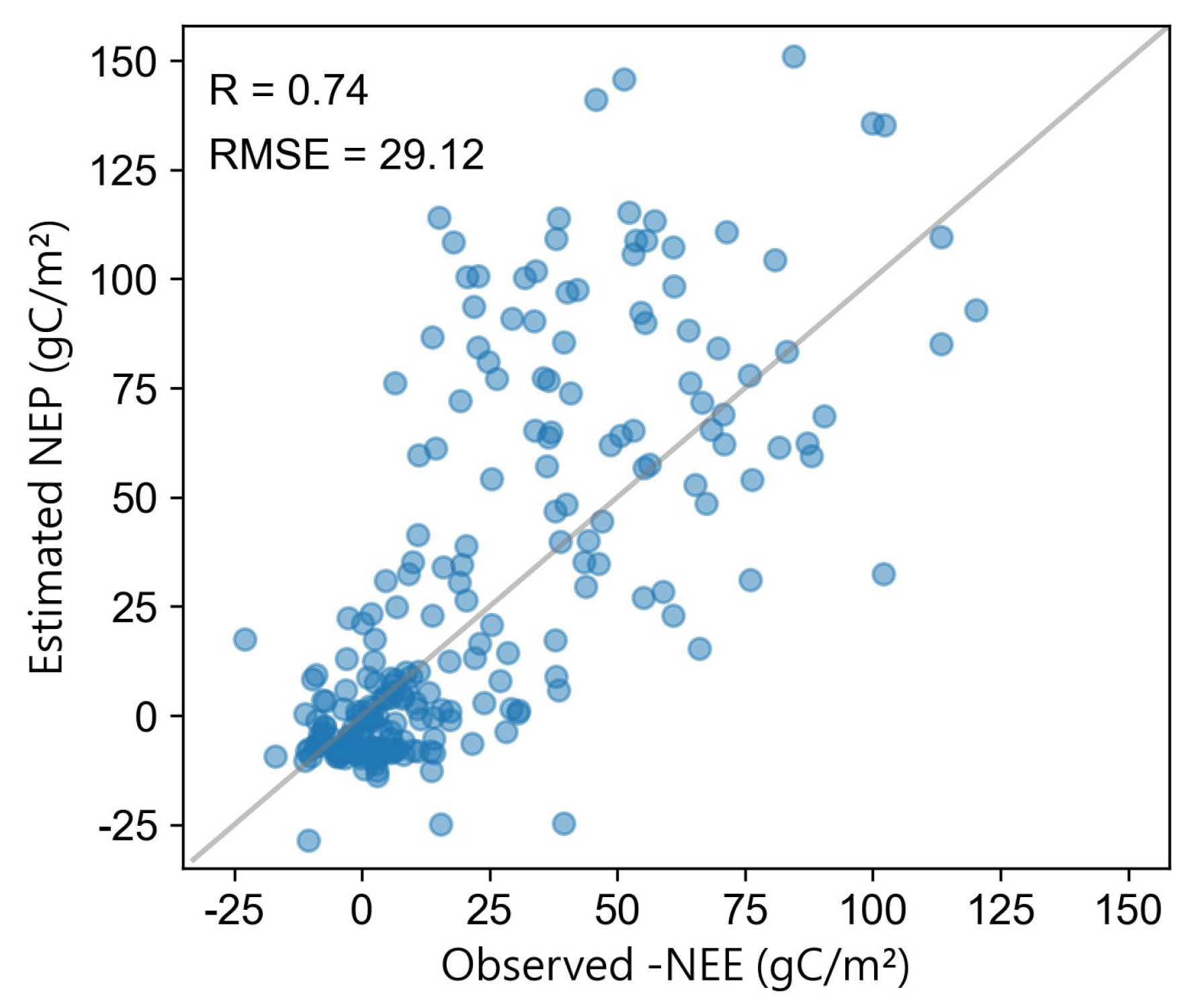
3.1. NPP and NEP Validation
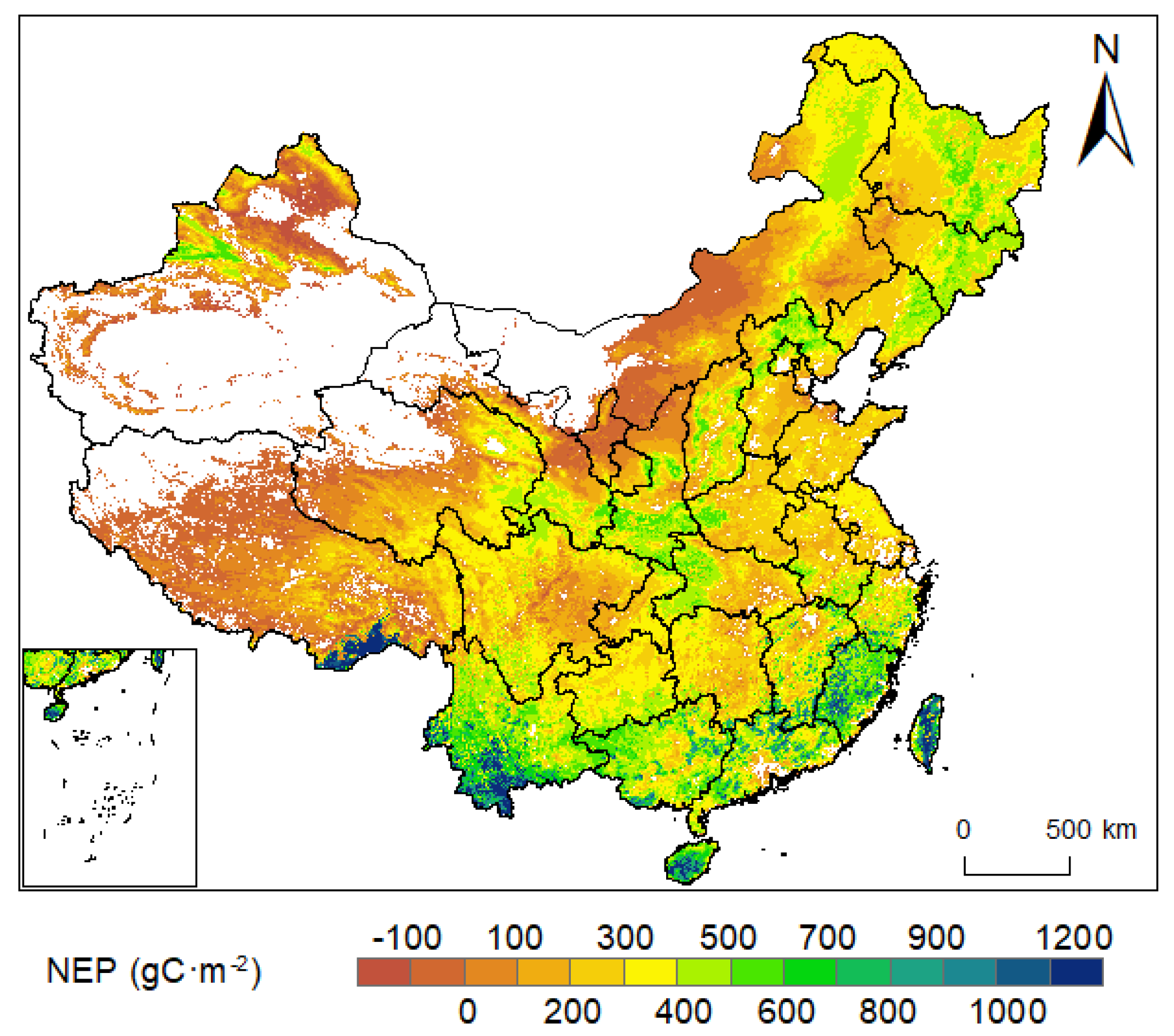
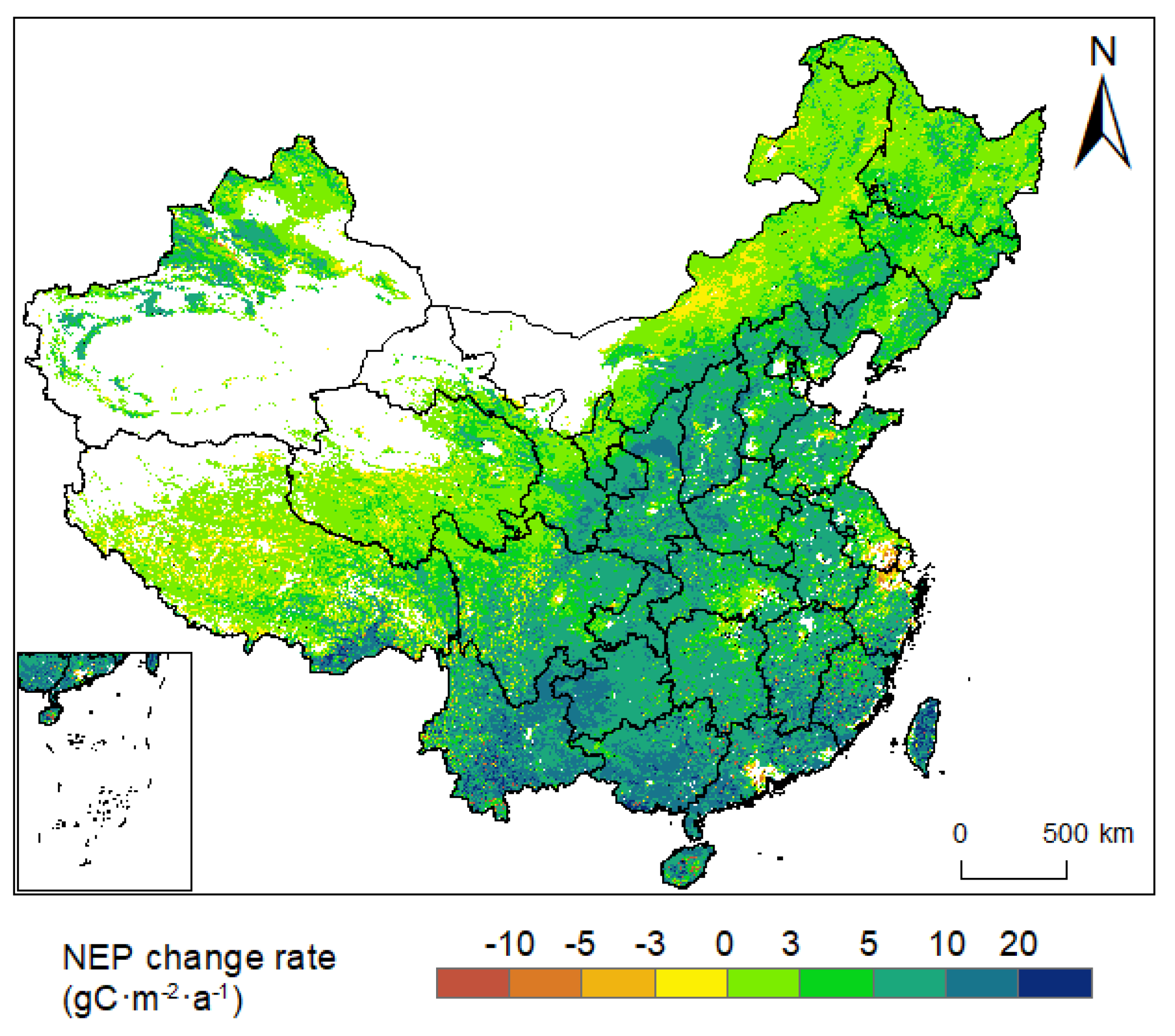
3.2. Spatial Distribution of NEP
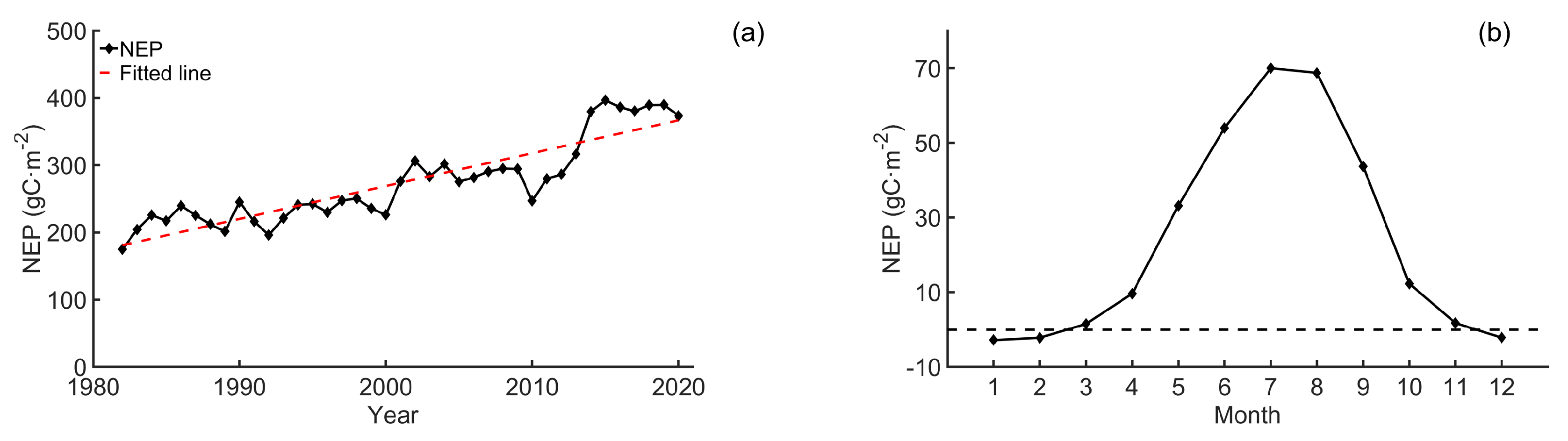
3.3. Spatiotemporal Variations in NEP
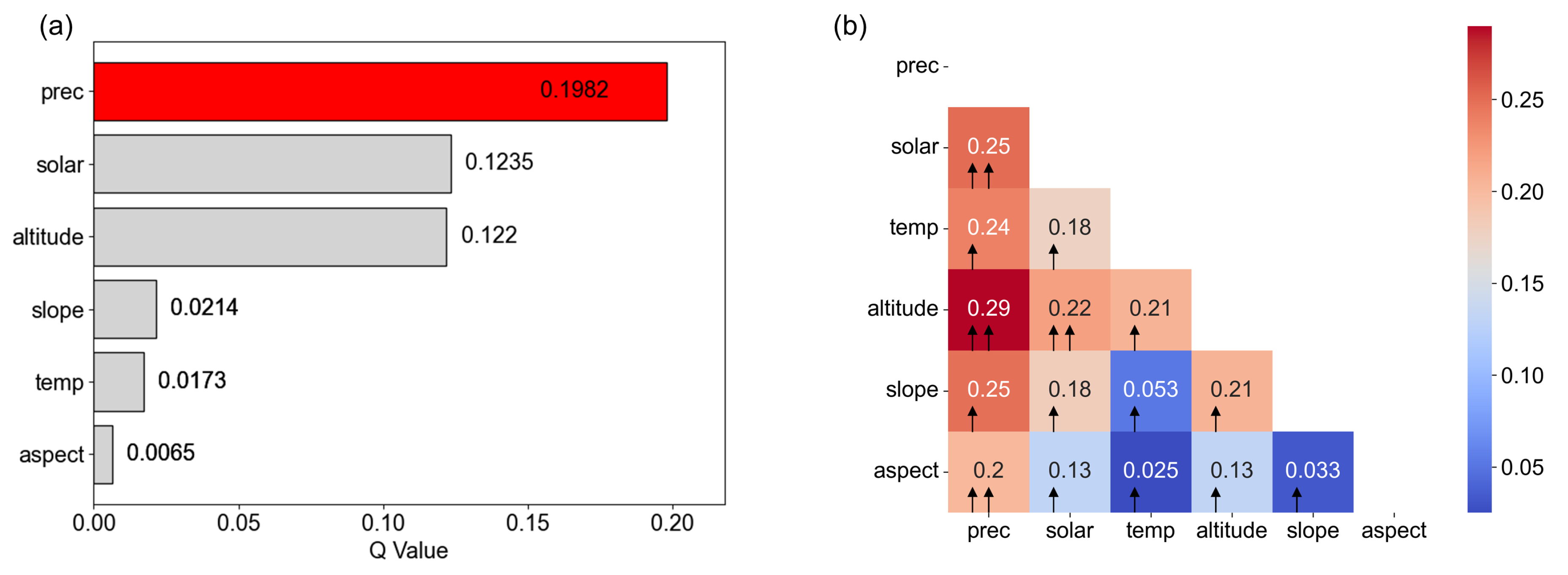
3.4. Driving Factors in NEP Variation
4. Discussion
5. Conclusions
- (1)
- The study revealed a distinct spatial distribution pattern of vegetation NEP in China. It was observed that NEP was generally lower in the northern regions and higher in the southern regions. Similarly, NEP was lower in the western areas than that in the eastern regions. The mean NEP of the study region over 39 years was 265.38 gC·m−2. The annual average carbon sequestration amounted to 1.89 PgC, indicating a large carbon sink.
- (2)
- During 1982–2020, the annual mean NEP of the Chinese vegetation region exhibited a general fluctuating upward trend. In terms of NEP seasonal change, the vegetation area in China was generally a carbon sink from March to November, and a carbon source from December to February. During the 39-year period, a significant proportion of vegetated regions in China showed an upward trend in NEP, and the overall average growth rate in China’s vegetation areas is 4.69 gC·m−2·a−1. This indicates an enhanced carbon sequestration capacity of these vegetated regions.
- (3)
- Precipitation, solar radiation, and altitude are the key driving forces on the temporal change in NEP among the climatic and topographic factors. The interactions between the driving factors showed significantly higher impacts on NEP change than the single factor. The interaction between precipitation rate and elevation has the strongest effect, with the q-statistic value of 0.29.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pathak, K.; Malhi, Y.; Sileshi, G.; Das, A.K.; Nath, A.J. Net ecosystem productivity and carbon dynamics of the traditionally managed Imperata grasslands of North East India. Sci. Total. Environ. 2018, 635, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Schimel, D.; Stephens, B.B.; Fisher, J.B. Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl. Acad. Sci. USA 2015, 112, 436–441. [Google Scholar] [CrossRef] [PubMed]
- Friend, A.D.; Lucht, W.; Rademacher, T.T.; Keribin, R.; Betts, R.; Cadule, P.; Ciais, P.; Clark, D.B.; Dankers, R.; Falloon, P.D.; et al. Carbon residence time dominates uncertainty in terrestrial vegetation responses to future climate and atmospheric CO2. Proc. Natl. Acad. Sci. USA 2014, 111, 3280–3285. [Google Scholar] [CrossRef] [PubMed]
- Bloom, A.A.; Exbrayat, J.F.; Van Der Velde, I.R.; Feng, L.; Williams, M. The decadal state of the terrestrial carbon cycle: Global retrievals of terrestrial carbon allocation, pools, and residence times. Proc. Natl. Acad. Sci. USA 2016, 113, 1285–1290. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hao, X.; Hao, H.; Fan, X.; Li, Y. Climate change decreased net ecosystem productivity in the arid region of central Asia. Remote Sens. 2021, 13, 4449. [Google Scholar] [CrossRef]
- Ge, W.; Deng, L.; Wang, F.; Han, J. Quantifying the contributions of human activities and climate change to vegetation net primary productivity dynamics in China from 2001 to 2016. Sci. Total. Environ. 2021, 773, 145648. [Google Scholar] [CrossRef] [PubMed]
- IGBP Terrestrial Carbon Working Group; Steffen, W.; Noble, I.; Canadell, J.; Apps, M.; Schulze, E.D.; Jarvis, P.G. The terrestrial carbon cycle: Implications for the Kyoto Protocol. Science 1998, 280, 1393–1394. [Google Scholar]
- Ruimy, A.; Saugier, B.; Dedieu, G. Methodology for the estimation of terrestrial net primary production from remotely sensed data. J. Geophys. Res. Atmos. 1994, 99, 5263–5283. [Google Scholar] [CrossRef]
- Guo, D.; Song, X.; Hu, R.; Zhu, X.; Jiang, Y.; Cai, S.; Zhang, Y.; Cui, X. Large-scale analysis of the spatiotemporal changes of Net Ecosystem Production in Hindu Kush Himalayan Region. Remote Sens. 2021, 13, 1180. [Google Scholar] [CrossRef]
- Liang, L.; Geng, D.; Yan, J.; Qiu, S.; Shi, Y.; Wang, S.; Wang, L.; Zhang, L.; Kang, J. Remote sensing estimation and spatiotemporal pattern analysis of terrestrial net ecosystem productivity in China. Remote Sens. 2022, 14, 1902. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, W.; Zhang, Y. The Change in Net Ecosystem Productivity and its Driving Mechanism in a Mountain Ecosystem of Arid Regions, Northwest China. Remote Sens. 2022, 14, 4046. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Y.; Sun, Y.; Xu, Y.; Xin, Y.; Mo, Y. Spatial and temporal variations of net ecosystem productivity in Xinjiang Autonomous Region, China based on remote sensing. Front. Plant Sci. 2023, 14, 1146388. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Fan, Q.; Qu, J.; Ding, X.; Niu, Z. Characteristics of carbon sources and sinks and their relationships with climate factors during the desertification reversal process in Yulin, China. Front. For. Glob. Chang. 2023, 6, 1288449. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Sun, R.; Kljun, N.; Zhang, L.; Wang, X.; Zhu, G. Spatial representativeness and uncertainty of eddy covariance carbon flux measurements for upscaling net ecosystem productivity to the grid scale. Agric. For. Meteorol. 2016, 230, 114–127. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, C.; Ma, X.; Zhang, X.; Yang, D.; Shao, Y. Spatiotemporal Variation Characteristics and Dynamic Persistence Analysis of Carbon Sources/Sinks in the Yellow River Basin. Remote Sens. 2023, 15, 323. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef]
- Huang, C.; Sun, C.; Nguyen, M.; Wu, Q.; He, C.; Yang, H.; Tu, P.; Hong, S. Spatio-temporal dynamics of terrestrial Net ecosystem productivity in the ASEAN from 2001 to 2020 based on remote sensing and improved CASA model. Ecol. Indic. 2023, 154, 110920. [Google Scholar] [CrossRef]
- Liu, M.; Bai, X.; Tan, Q.; Luo, G.; Zhao, C.; Wu, L.; Chen, F.; Li, C.; Yang, Y.; Ran, C.; et al. Climate change enhanced the positive contribution of human activities to net ecosystem productivity from 1983 to 2018. Front. Ecol. Evol. 2023, 10, 1101135. [Google Scholar] [CrossRef]
- Pei, Z.Y.; Ouyang, H.; Zhou, C.P.; Xu, X.L. Carbon Balance in an Alpine Steppe in the Qinghai-Tibet Plateau. J. Integr. Plant Biol. 2009, 51, 521–526. [Google Scholar] [CrossRef]
- Parton, W.; Morgan, J.; Smith, D.; Del Grosso, S.; Prihodko, L.; LeCain, D.; Kelly, R.; Lutz, S. Impact of precipitation dynamics on net ecosystem productivity. Glob. Chang. Biol. 2012, 18, 915–927. [Google Scholar] [CrossRef]
- Liang, W.; Yang, Y.; Fan, D.; Guan, H.; Zhang, T.; Long, D.; Zhou, Y.; Bai, D. Analysis of spatial and temporal patterns of net primary production and their climate controls in China from 1982 to 2010. Agric. For. Meteorol. 2015, 204, 22–36. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, F.; Zhang, L.; Zhao, J.; Zheng, H.; Zhang, F.; Wang, N.; Gu, J.; Zhao, Y.; Zhang, W. Changes and net ecosystem productivity of terrestrial ecosystems and their influencing factors in China from 2000 to 2019. Front. Plant Sci. 2023, 14, 1120064. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Tian, J.; He, J.; He, H.; Liu, G.; Zhang, Z.; Zhou, L. The spatial and temporal distribution of China’s forest carbon. Front. Ecol. Evol. 2023, 11, 1110594. [Google Scholar] [CrossRef]
- Gu, F.; Zhang, Y.; Huang, M.; Tao, B.; Liu, Z.; Hao, M.; Guo, R. Climate-driven uncertainties in modeling terrestrial ecosystem net primary productivity in China. Agric. For. Meteorol. 2017, 246, 123–132. [Google Scholar] [CrossRef]
- Yu, Z.; Ciais, P.; Piao, S.; Houghton, R.A.; Lu, C.; Tian, H.; Agathokleous, E.; Kattel, G.R.; Sitch, S.; Goll, D.; et al. Forest expansion dominates China’s land carbon sink since 1980. Nat. Commun. 2022, 13, 5374. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Shi, Y.; Sun, W.; Chang, J.; Zhu, J.; Chen, L.; Wang, X.; Guo, Y.; Zhang, H.; Yu, L.; et al. Terrestrial carbon sinks in China and around the world and their contribution to carbon neutrality. Sci. China Life Sci. 2022, 65, 861–895. [Google Scholar] [CrossRef] [PubMed]
- Kumar, L.; Mutanga, O. Google Earth Engine applications since inception: Usage, trends, and potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Tian, J.; Zhu, X.; Chen, J.; Wang, C.; Shen, M.; Yang, W.; Tan, X.; Xu, S.; Li, Z. Improving the accuracy of spring phenology detection by optimally smoothing satellite vegetation index time series based on local cloud frequency. ISPRS J. Photogramm. Remote Sens. 2021, 180, 29–44. [Google Scholar] [CrossRef]
- van Leeuwen, W.J.; Huete, A.R.; Laing, T.W. MODIS vegetation index compositing approach: A prototype with AVHRR data. Remote Sens. Environ. 1999, 69, 264–280. [Google Scholar] [CrossRef]
- Dai, X.; Yao, L.; Yuan, Z.; Sun, K. Characteristics of NDVI Temporal and Spatial Variation in the Source Area of the Yangtze River and Its Response to Hydrothermal Conditions. In Proceedings of the IOP Conference Series: Earth and Environmental Science, 2021; IOP Publishing: Bristol, UK, 2021; Volume 768, p. 012013. [Google Scholar]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Yu, T.; Sun, R.; Xiao, Z.; Zhang, Q.; Liu, G.; Cui, T.; Wang, J. Estimation of global vegetation productivity from global land surface satellite data. Remote Sens. 2018, 10, 327. [Google Scholar] [CrossRef]
- Cui, T.; Wang, Y.; Sun, R.; Qiao, C.; Fan, W.; Jiang, G.; Hao, L.; Zhang, L. Estimating vegetation primary production in the Heihe River Basin of China with multi-source and multi-scale data. PLoS ONE 2016, 11, e0153971. [Google Scholar] [CrossRef] [PubMed]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; He, H.; Yu, D.; Hu, H. Simulation of maximum light use efficiency for some typical vegetation types in China. Chin. Sci. Bull. 2006, 51, 457–463. [Google Scholar] [CrossRef]
- Yu, G.; Zheng, Z.; Wang, Q.; Fu, Y.; Zhuang, J.; Sun, X.; Wang, Y. Spatiotemporal pattern of soil respiration of terrestrial ecosystems in China: The development of a geostatistical model and its simulation. Environ. Sci. Technol. 2010, 44, 6074–6080. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Indag. Math. 1950, 12, 173. [Google Scholar]
- Jiang, W.; Yuan, L.; Wang, W.; Cao, R.; Zhang, Y.; Shen, W. Spatio-temporal analysis of vegetation variation in the Yellow River Basin. Ecol. Indic. 2015, 51, 117–126. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Ge, Y.; Xu, C. An optimal parameters-based geographical detector model enhances geographic characteristics of explanatory variables for spatial heterogeneity analysis: Cases with different types of spatial data. GISci. Remote Sens. 2020, 57, 593–610. [Google Scholar] [CrossRef]
- Ji, R.; Tan, K.; Wang, X.; Pan, C.; Xin, L. Spatiotemporal monitoring of a grassland ecosystem and its net primary production using Google Earth Engine: A case study of inner mongolia from 2000 to 2020. Remote Sens. 2021, 13, 4480. [Google Scholar] [CrossRef]
- Hui, D.; Yu, C.L.; Deng, Q.; Dzantor, E.K.; Zhou, S.; Dennis, S.; Sauve, R.; Johnson, T.L.; Fay, P.A.; Shen, W.; et al. Effects of precipitation changes on switchgrass photosynthesis, growth, and biomass: A mesocosm experiment. PLoS ONE 2018, 13, e0192555. [Google Scholar] [CrossRef] [PubMed]
- Castillioni, K.; Patten, M.A.; Souza, L. Precipitation effects on grassland plant performance are lessened by hay harvest. Sci. Rep. 2022, 12, 3282. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zeng, J.; Leng, S.; Fan, B.; Tang, J.; Jiang, C.; Huang, Y.; Zhang, Q.; Qu, Y.; Wang, W.; et al. The effects of air temperature and precipitation on the net primary productivity in China during the early 21st century. Front. Earth Sci. 2018, 12, 818–833. [Google Scholar] [CrossRef]
- Gang, C.; Zhou, W.; Chen, Y.; Wang, Z.; Sun, Z.; Li, J.; Qi, J.; Odeh, I. Quantitative assessment of the contributions of climate change and human activities on global grassland degradation. Environ. Earth Sci. 2014, 72, 4273–4282. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, X.; Wang, J.; He, H.; Wang, S.; Wang, M.; Piao, S.; Yan, H.; Ju, W.; Gu, F.; et al. Interannual variability of terrestrial net ecosystem productivity over China: Regional contributions and climate attribution. Environ. Res. Lett. 2019, 14, 014003. [Google Scholar] [CrossRef]
- Wang, H.; Yan, S.; Liang, Z.; Jiao, K.; Li, D.; Wei, F.; Li, S. Strength of association between vegetation greenness and its drivers across China between 1982 and 2015: Regional differences and temporal variations. Ecol. Indic. 2021, 128, 107831. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, Y.; Xu, J.; Wu, Z. Effects of climatic factors on the net primary productivity in the source region of Yangtze River, China. Sci. Rep. 2021, 11, 1376. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B.; Lu, M.; Zang, W.; Yu, T.; Chen, D. Quantitative distinction of the relative actions of climate change and human activities on vegetation evolution in the Yellow River Basin of China during 1981–2019. J. Arid Land 2023, 15, 91–108. [Google Scholar] [CrossRef]
- Nayak, R.K.; Patel, N.; Dadhwal, V. Estimation and analysis of terrestrial net primary productivity over India by remote-sensing-driven terrestrial biosphere model. Environ. Monit. Assess. 2010, 170, 195–213. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Liang, L.; Wang, Q.; Geng, D.; Wu, J.; Wang, S.; Chen, B. Estimation of European Terrestrial Ecosystem NEP Based on an Improved CASA Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 16, 1244–1255. [Google Scholar] [CrossRef]
- Shi, Z. Spatial-Temporal Simulation of Vegetation Carbon Sink and Its Influential Factors Based on CASA and GSMSR Model in Shaanxi Province. Master’s Thesis, Northwest A&F University, Shaanxi, China, 2015. [Google Scholar]
- Chapin, F.S.; Woodwell, G.M.; Randerson, J.T.; Rastetter, E.B.; Lovett, G.M.; Baldocchi, D.D.; Clark, D.A.; Harmon, M.E.; Schimel, D.S.; Valentini, R.; et al. Reconciling carbon-cycle concepts, terminology, and methods. Ecosystems 2006, 9, 1041–1050. [Google Scholar] [CrossRef]
- Reichle, D. The Global Carbon Cycle and Climate Change; Elsevier: Amsterdam, The Netherlands, 2019; Volume 1, p. 388. [Google Scholar]
- Yao, Y.; Li, Z.; Wang, T.; Chen, A.; Wang, X.; Du, M.; Jia, G.; Li, Y.; Li, H.; Luo, W.; et al. A new estimation of China’s net ecosystem productivity based on eddy covariance measurements and a model tree ensemble approach. Agric. For. Meteorol. 2018, 253, 84–93. [Google Scholar] [CrossRef]
- Wang, Q.; Zheng, H.; Zhu, X.; Yu, G. Primary estimation of Chinese terrestrial carbon sequestration during 2001–2010. Sci. Bull. 2015, 60, 577–590. [Google Scholar] [CrossRef]
- Zhu, X.J.; Yu, G.R.; He, H.L.; Wang, Q.F.; Chen, Z.; Gao, Y.N.; Zhang, Y.P.; Zhang, J.H.; Yan, J.H.; Wang, H.M.; et al. Geographical statistical assessments of carbon fluxes in terrestrial ecosystems of China: Results from upscaling network observations. Glob. Planet. Chang. 2014, 118, 52–61. [Google Scholar] [CrossRef]
- Chen, K.; Yang, C.; Bai, L.; Chen, Y.; Liu, R.; Chao, L. Effects of natural and human factors on vegetation normalized difference vegetation index based on geographical detectors in Inner Mongolia. Acta Ecol. Sin. 2021, 41, 4963–4975. [Google Scholar]
- Chen, Y.; Feng, X.; Tian, H.; Wu, X.; Gao, Z.; Feng, Y.; Piao, S.; Lv, N.; Pan, N.; Fu, B. Accelerated increase in vegetation carbon sequestration in China after 2010: A turning point resulting from climate and human interaction. Glob. Chang. Biol. 2021, 27, 5848–5864. [Google Scholar] [CrossRef]


| Site ID | Site Name | Period | Latitude | Longitude |
|---|---|---|---|---|
| CN-Cha | Changbaishan | 2003–2005 | 42.40N | 128.10E |
| CN-Cng | Changling | 2007–2010 | 44.59N | 123.51E |
| CN-Dan | Dangxiong | 2004–2005 | 30.50N | 91.07E |
| CN-Din | Dinghushan | 2003–2005 | 23.17N | 112.54E |
| CN-Du2 | Duolun_grassland | 2008 | 42.05N | 116.28E |
| CN-Du3 | Duolun Degraded Meadow | 2009 | 42.06N | 116.28E |
| CN-Ha2 | Haibei Shrubland | 2003–2005 | 37.61N | 101.33E |
| CN-HaM | Haibei Alpine Tibet site | 2002–2004 | 37.37N | 101.18E |
| CN-Qia | Qianyanzhou | 2003–2005 | 26.74N | 115.06E |
| CN-Sw2 | Siziwang Grazed | 2011 | 41.79N | 111.90E |
| Code | Land-Cover Type | NDVImax | NDVImin | SRmax | SRmin | SOCD (kg·m−2) | |
|---|---|---|---|---|---|---|---|
| 1 | ENF | 0.647 | 0.023 | 4.67 | 1.05 | 0.389 | 3.77 |
| 2 | EBF | 0.676 | 0.023 | 5.17 | 1.05 | 0.985 | 4.70 |
| 3 | DNF | 0.738 | 0.023 | 6.63 | 1.05 | 0.485 | 3.77 |
| 4 | DBF | 0.747 | 0.023 | 6.91 | 1.05 | 0.692 | 4.70 |
| 5 | MXF | 0.702 | 0.023 | 5.84 | 1.05 | 0.475 | 4.24 |
| 6 | Shrubland | 0.636 | 0.023 | 4.49 | 1.05 | 0.429 | 2.56 |
| 7 | Grassland | 0.634 | 0.023 | 4.46 | 1.05 | 0.542 | 1.82 |
| 8 | AL | 0.634 | 0.023 | 4.46 | 1.05 | 0.542 | 2.56 |
| 9 | Water | 0.634 | 0.023 | 4.46 | 1.05 | 0.542 | 0 |
| 10 | UBL | 0.634 | 0.023 | 4.46 | 1.05 | 0.542 | 0 |
| 11 | Bare Land | 0.634 | 0.023 | 4.46 | 1.05 | 0.542 | 0 |
| Relations of q-Value | Type of Interaction |
|---|---|
| Nonlinear weakened | |
| Single factor nonlinear weakened | |
| Bivariable enhanced | |
| Independent | |
| Nonlinear enhanced |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xu, Y.; Chen, T.; Zhang, F.; Zhu, S. Exploring the Spatiotemporal Dynamics and Driving Factors of Net Ecosystem Productivity in China from 1982 to 2020. Remote Sens. 2024, 16, 60. https://doi.org/10.3390/rs16010060
Chen Y, Xu Y, Chen T, Zhang F, Zhu S. Exploring the Spatiotemporal Dynamics and Driving Factors of Net Ecosystem Productivity in China from 1982 to 2020. Remote Sensing. 2024; 16(1):60. https://doi.org/10.3390/rs16010060
Chicago/Turabian StyleChen, Yang, Yongming Xu, Tianyu Chen, Fei Zhang, and Shanyou Zhu. 2024. "Exploring the Spatiotemporal Dynamics and Driving Factors of Net Ecosystem Productivity in China from 1982 to 2020" Remote Sensing 16, no. 1: 60. https://doi.org/10.3390/rs16010060
APA StyleChen, Y., Xu, Y., Chen, T., Zhang, F., & Zhu, S. (2024). Exploring the Spatiotemporal Dynamics and Driving Factors of Net Ecosystem Productivity in China from 1982 to 2020. Remote Sensing, 16(1), 60. https://doi.org/10.3390/rs16010060






