Neural Network-Based Estimation of Near-Surface Air Temperature in All-Weather Conditions Using FY-4A AGRI Data over China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Station Data
2.1.2. FY-4A/AGRI Data
2.1.3. GFS Data
2.1.4. ERA5-Land Data
2.1.5. Auxiliary Data
2.2. Methods
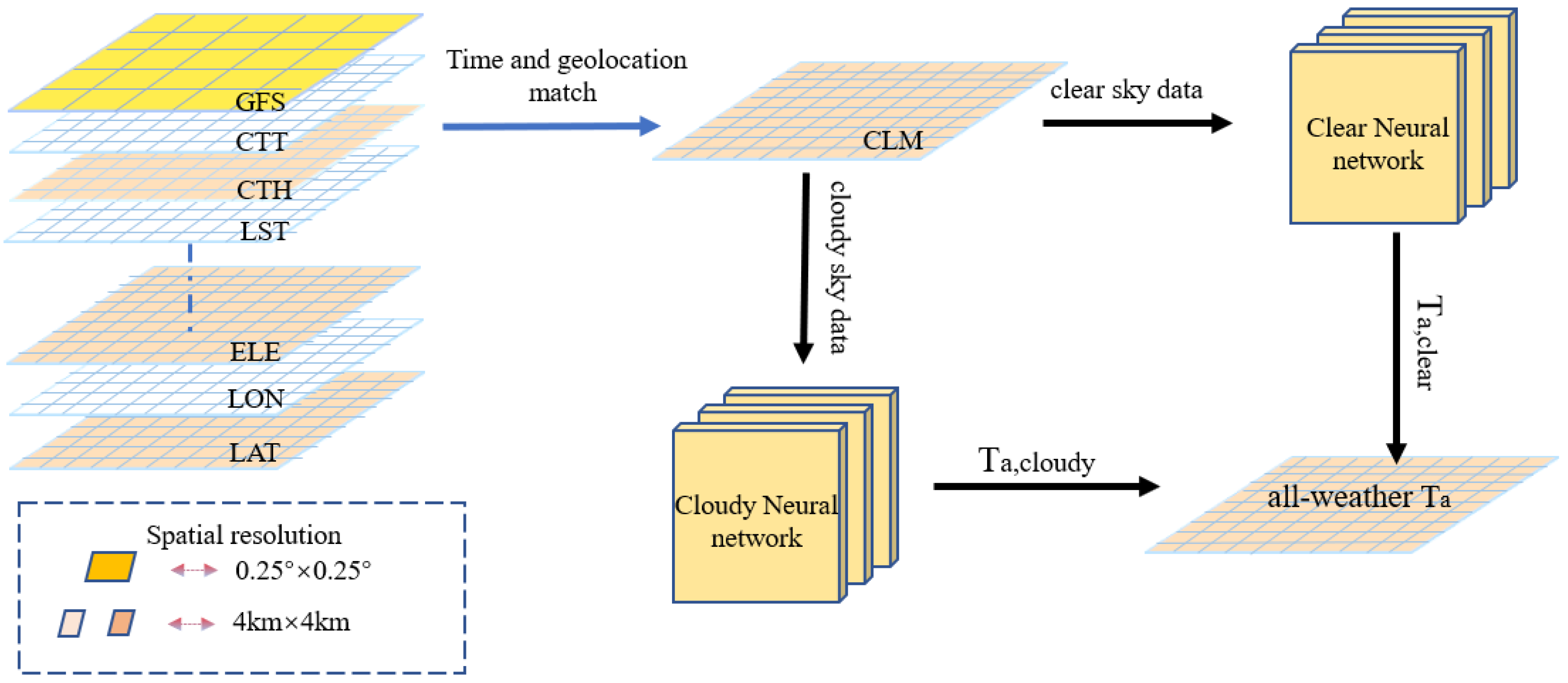
2.2.1. Ta,clear Estimation Model
2.2.2. Ta,cloudy Estimation Model
2.2.3. Data Processing
2.2.4. Neural Network Model
2.2.5. Statistical Metrics
3. Results
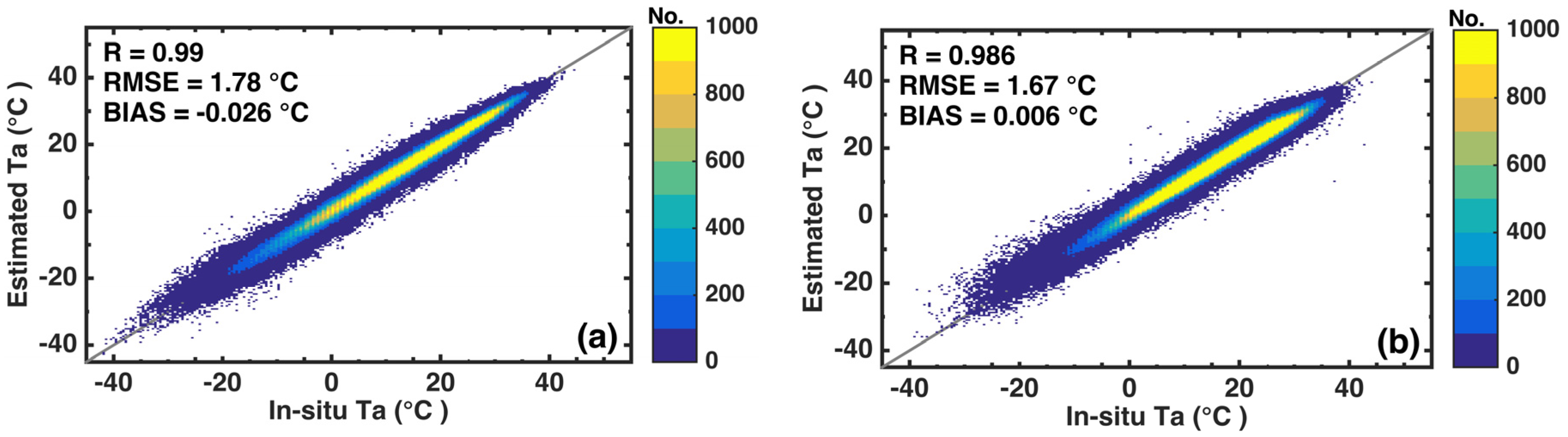
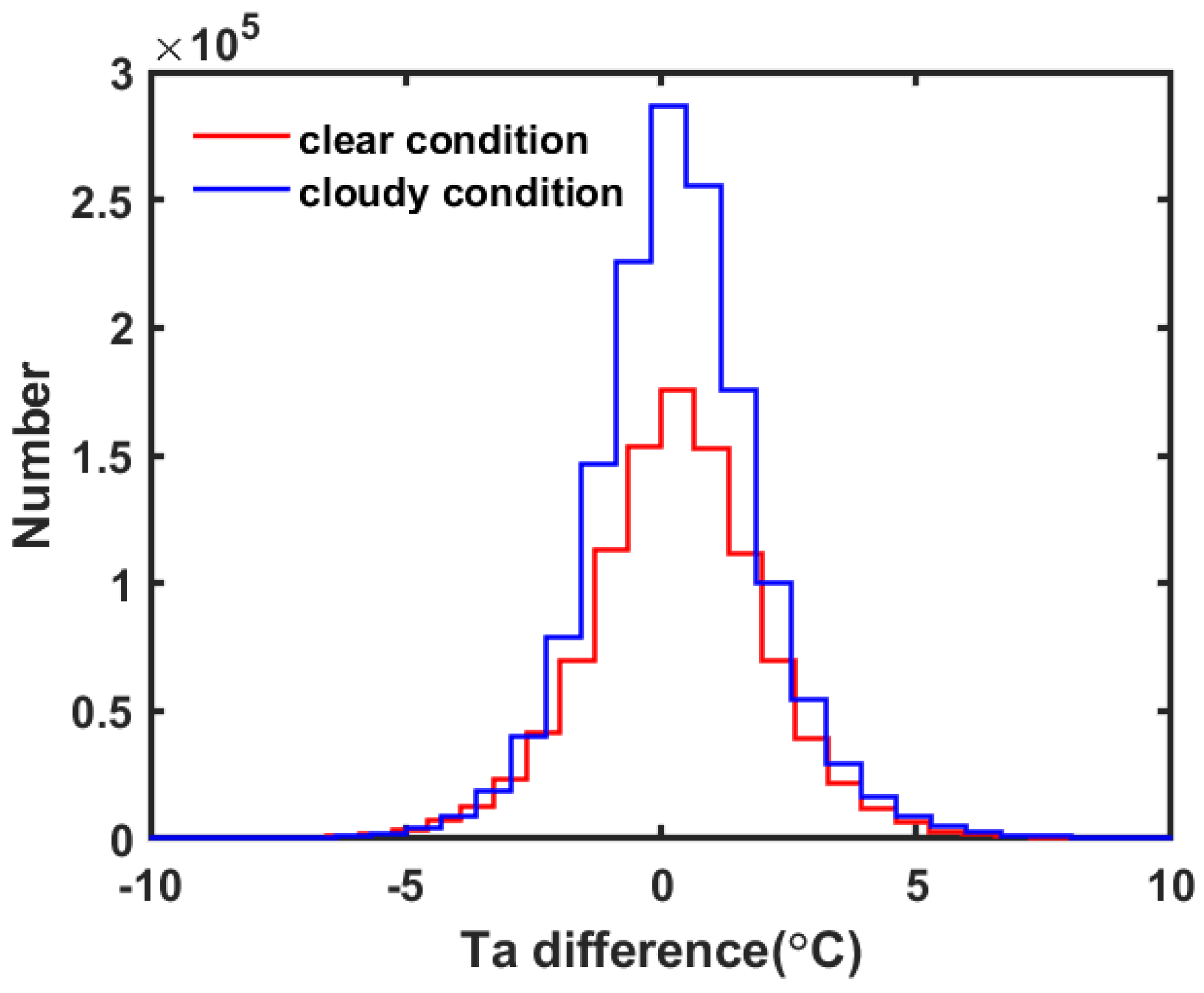
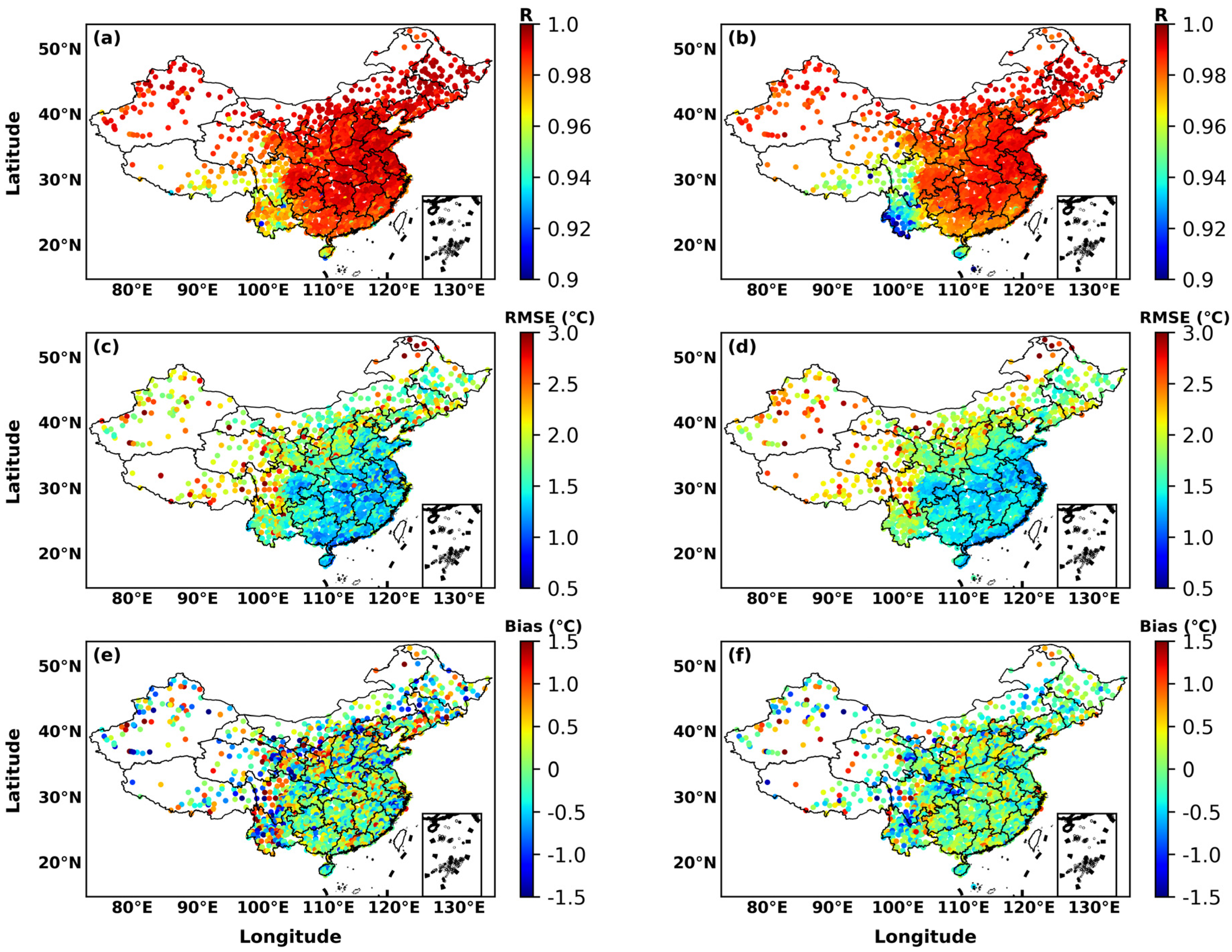
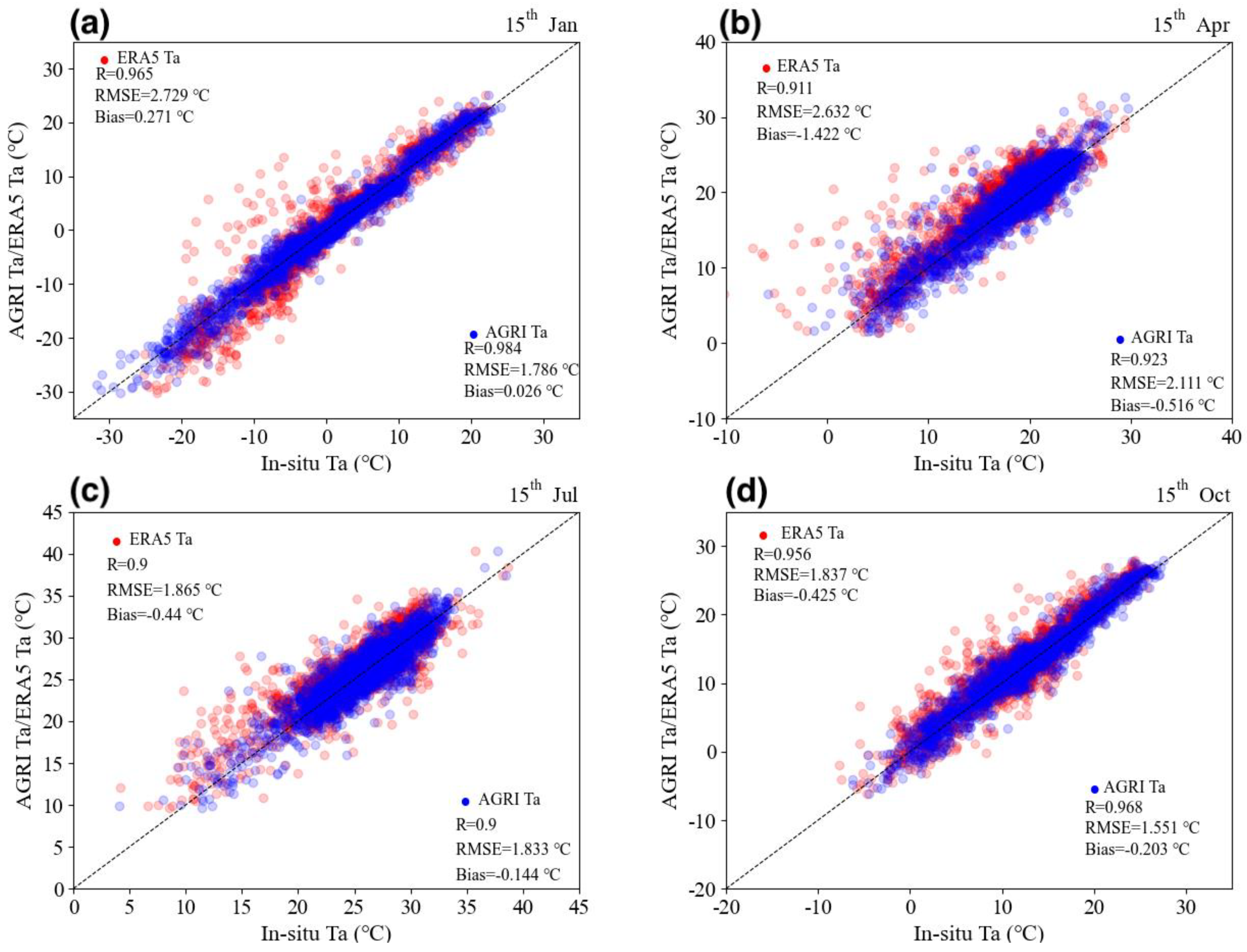
3.1. Overall Error Analysis
3.2. Spatial Distribution of Ta Error
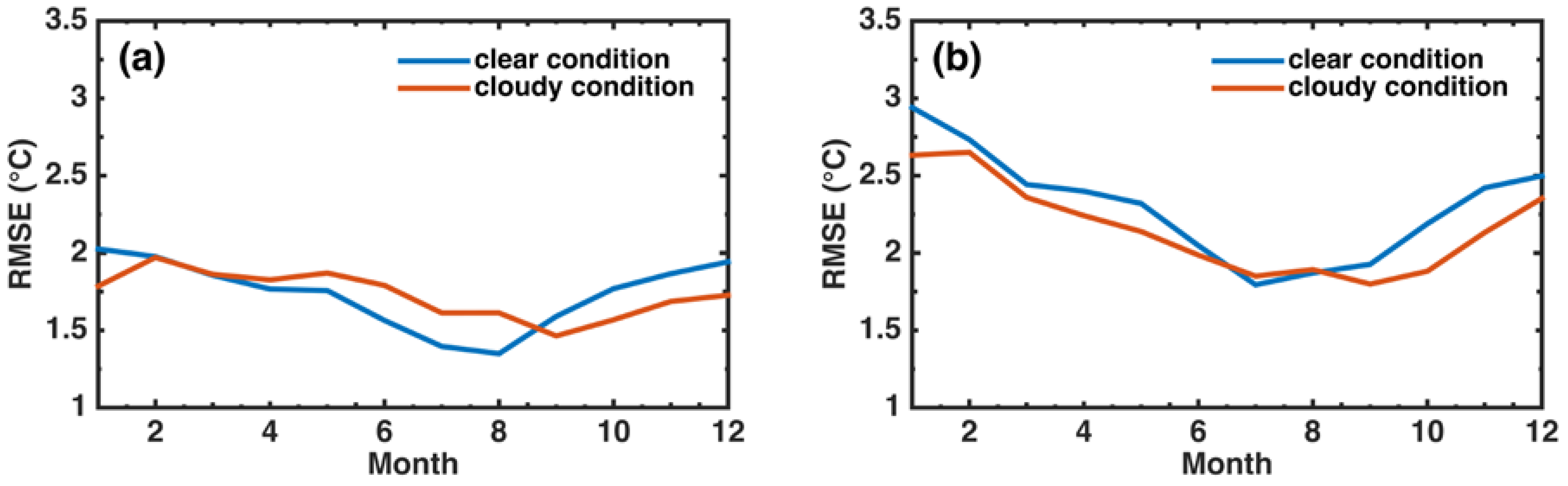
3.3. Seasonal Variation of Ta Estimation Error
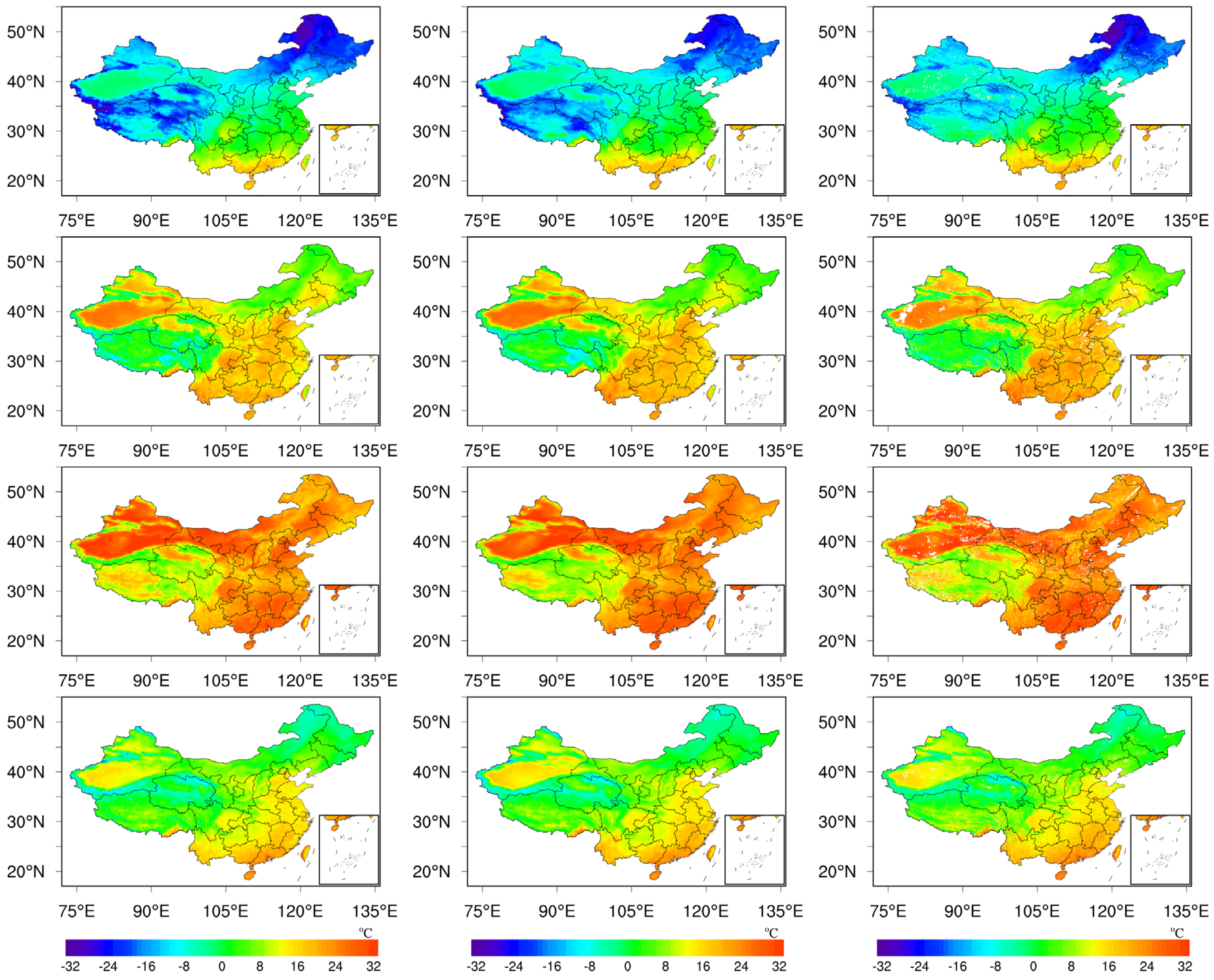
3.4. Comparisons with GFS/ERA5
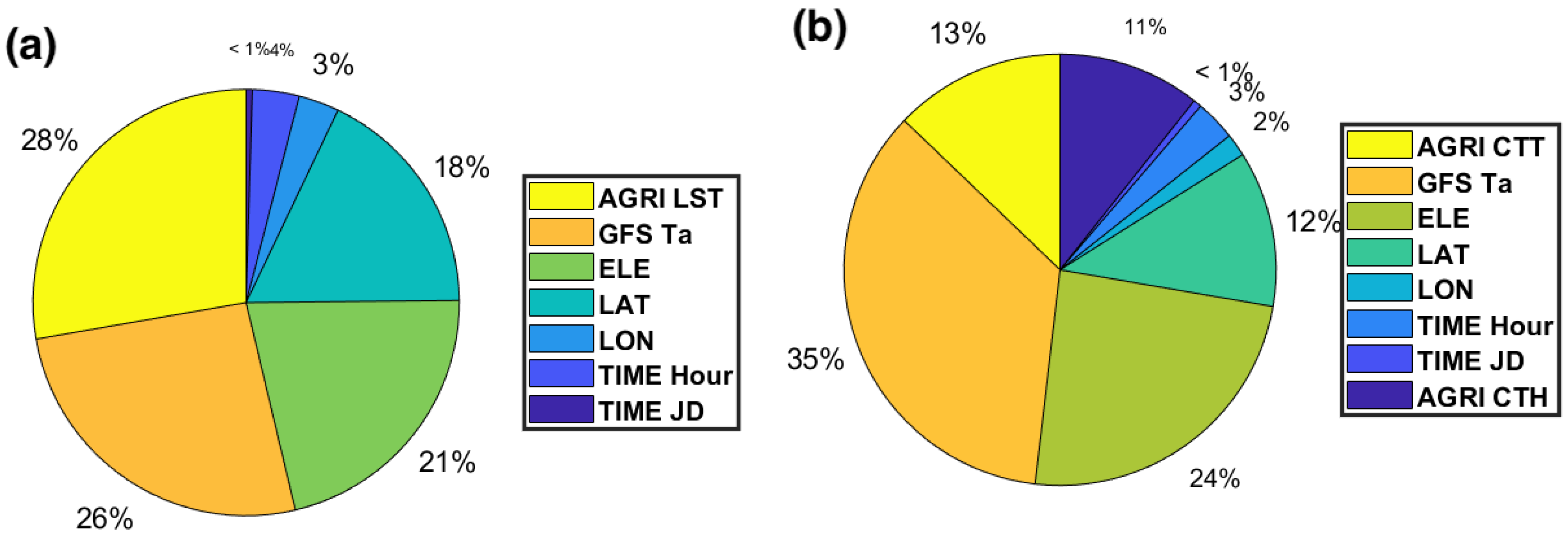
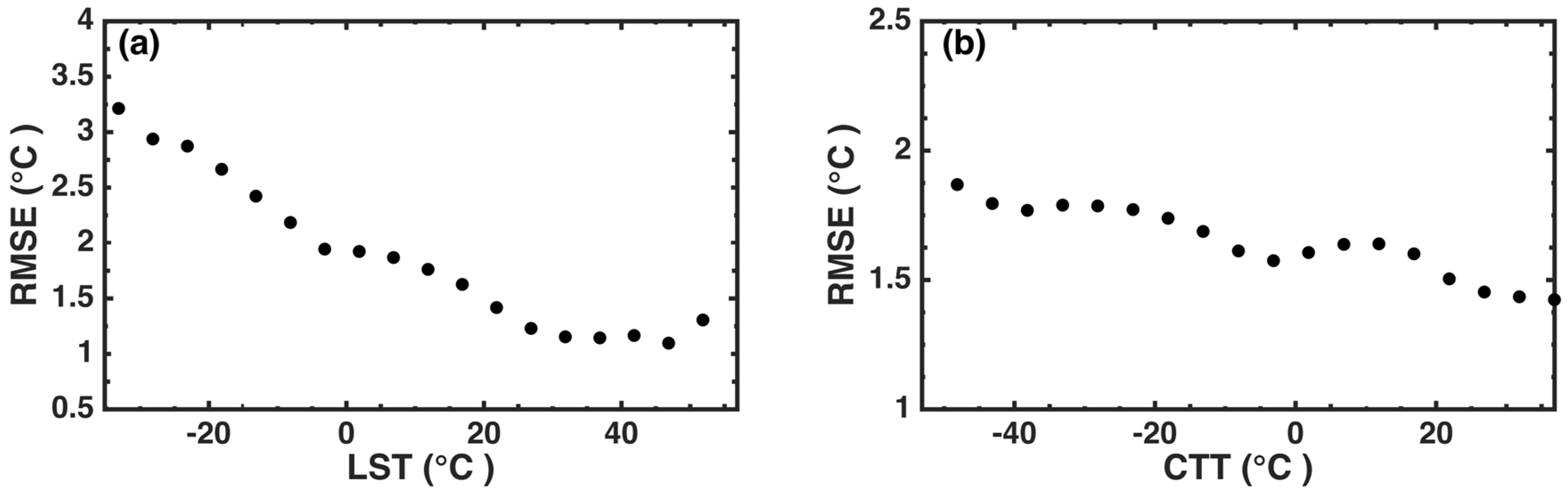
3.5. Model Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prince, S.D.; Goward, S.N. Global Primary Production: A Remote Sensing Approach. J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Cai, W.H.; Yang, J. Evaluation of MODIS Land Surface Temperature Data to Estimate Near-Surface Air Temperature in Northeast China. Remote Sens. 2017, 9, 410. [Google Scholar] [CrossRef]
- Santer, B.D.; Wigley, T.M.L.; Mears, C.; Wentz, F.J.; Klein, S.A.; Seidel, D.J.; Taylor, K.E.; Thorne, P.W.; Wehner, M.F.; Gleckler, P.J.; et al. Amplification of surface temperature trends and variability in the tropical atmosphere. Science 2005, 309, 1551–1556. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.P.; Moore, N.J.; Messina, J.P.; DeVisser, M.H.; Wu, J.P. Evaluation of estimating daily maximum and minimum air temperature with MODIS data in east Africa. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 128–140. [Google Scholar] [CrossRef]
- Good, E.J. An in situ-based analysis of the relationship between land surface “skin” and screen-level air temperatures. J. Geophys. Res. Atmos. 2016, 121, 8801–8819. [Google Scholar] [CrossRef]
- Błażejczyk, K.; Jendritzky, G.; Bröde, P.; Fiala, D.; Havenith, G.; Epstein, Y.; Psikuta, A.; Kampmann, B. An introduction to the universal thermal climate index (UTCI). Geogr. Pol. 2013, 86, 5–10. [Google Scholar] [CrossRef]
- Woolway, R.I.; Sharma, S.; Weyhenmeyer, G.A.; Debolskiy, A.; Golub, M.; Mercado-Bettín, D.; Perroud, M.; Stepanenko, V.; Tan, Z.L.; Grant, L.; et al. Phenological shifts in lake stratification under climate change. Nat. Commun. 2021, 12, 11. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Yang, K.; Tang, W.J.; Lu, H.; Qin, J.; Chen, Y.Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 11. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Gholamnia, M.; Alavipanah, S.K.; Darvishi Boloorani, A.; Hamzeh, S.; Kiavarz, M. Diurnal Air Temperature Modeling Based on the Land Surface Temperature. Remote Sens. 2017, 9, 915. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.C.; Huang, X.; Li, L.; Sun, J.; Wu, X.J.; Jiang, W.X. Developing a temporally accurate air temperature dataset for Mainland China. Sci. Total Environ. 2020, 706, 12. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Zhang, X.D.; Zhan, W.F.; Göttsche, F.M.; Liu, S.M.; Olesen, F.S.; Hu, W.X.; Dai, F.N. A Thermal Sampling Depth Correction Method for Land Surface Temperature Estimation From Satellite Passive Microwave Observation Over Barren Land. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4743–4756. [Google Scholar] [CrossRef]
- Ding, L.R.; Zhou, J.; Zhang, X.D.; Liu, S.M.; Cao, R.Y. Downscaling of surface air temperature over the Tibetan Plateau based on DEM. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 136–147. [Google Scholar] [CrossRef]
- Rao, Y.H.; Liang, S.L.; Wang, D.D.; Yu, Y.Y.; Song, Z.; Zhou, Y.; Shen, M.G.; Xu, B.Q. Estimating daily average surface air temperature using satellite land surface temperature and top-of-atmosphere radiation products over the Tibetan Plateau. Remote Sens. Environ. 2019, 234, 14. [Google Scholar] [CrossRef]
- Shen, H.F.; Jiang, Y.; Li, T.W.; Cheng, Q.; Zeng, C.; Zhang, L.P. Deep learning-based air temperature mapping by fusing remote sensing, station, simulation and socioeconomic data. Remote Sens. Environ. 2020, 240, 14. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.C.; Huang, X.; Cao, Q.; Peng, Y.Y. A method for improving the estimation of extreme air temperature by satellite. Sci. Total Environ. 2022, 837, 12. [Google Scholar] [CrossRef] [PubMed]
- Zou, J.; Lu, N.; Jiang, H.; Qin, J.; Yao, L.; Xin, Y.; Su, F.Z. Performance of air temperature from ERAS-Land reanalysis in coastal urban agglomeration of Southeast China. Sci. Total Environ. 2022, 828, 13. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; He, M.; Jiang, H.; Lu, N. Reconstruction of 60-year (1961–2020) surface air temperature on the Tibetan Plateau by fusing MODIS and ERA5 temperatures. Sci. Total Environ. 2022, 853, 13. [Google Scholar] [CrossRef]
- An, S.; Zhu, X.L.; Shen, M.G.; Wang, Y.F.; Cao, R.Y.; Chen, X.H.; Yang, W.; Chen, J.; Tang, Y.H. Mismatch in elevational shifts between satellite observed vegetation greenness and temperature isolines during 2000–2016 on the Tibetan Plateau. Glob. Chang. Biol. 2018, 24, 5411–5425. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.L.; Zhou, Q.; Zhang, S.L.; Deng, X.B. Estimation of Summer Air Temperature over China Using Himawari-8 AHI and Numerical Weather Prediction Data. Adv. Meteorol. 2019, 2019, 10. [Google Scholar] [CrossRef]
- Good, E. Daily minimum and maximum surface air temperatures from geostationary satellite data. J. Geophys. Res. Atmos. 2015, 120, 2306–2324. [Google Scholar] [CrossRef]
- Zaksek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS-J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
- Cresswell, M.P.; Morse, A.P.; Thomson, M.C.; Connor, S.J. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model. Int. J. Remote Sens. 1999, 20, 1125–1132. [Google Scholar] [CrossRef]
- Karimi, S.M.; Kisi, O.; Porrajabali, M.; Rouhani-Nia, F.; Shiri, J. Evaluation of the support vector machine, random forest and geo-statistical methodologies for predicting long-term air temperature. ISH J. Hydraul. Eng. 2018, 26, 376–386. [Google Scholar] [CrossRef]
- Mao, K.B.; Tang, H.J.; Wang, X.F.; Zhou, Q.B.; Wang, D.L. Near-surface air temperature estimation from ASTER data based on neural network algorithm. Int. J. Remote Sens. 2008, 29, 6021–6028. [Google Scholar] [CrossRef]
- Zhu, X.D.; Zhang, Q.; Xu, C.Y.; Sun, P.; Hu, P. Reconstruction of high spatial resolution surface air temperature data across China: A new geo-intelligent multisource data-based machine learning technique. Sci. Total Environ. 2019, 665, 300–313. [Google Scholar] [CrossRef] [PubMed]
- Czajkowski, K.P.; Goward, S.N.; Stadler, S.J.; Walz, A. Thermal Remote Sensing of Near Surface Environmental Variables: Application Over the Oklahoma Mesonet. Prof. Geogr. 2010, 52, 345–357. [Google Scholar] [CrossRef]
- Zhu, W.B.; Lü, A.F.; Jia, S.F. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Zhang, R.H.; Rong, Y.; Tian, J.; Su, H.B.; Li, Z.L.; Liu, S.H. A Remote Sensing Method for Estimating Surface Air Temperature and Surface Vapor Pressure on a Regional Scale. Remote Sens. 2015, 7, 6005–6025. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, Y.; Zhang, G.; Liang, C. Large-Scale Estimation of Hourly Surface Air Temperature Based on Observations from the FY-4A Geostationary Satellite. Remote Sens. 2023, 15, 1753. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Kimball, J.S.; Hong, S.Y. Retrievals of All-Weather Daily Air Temperature Using MODIS and AMSR-E Data. Remote Sens. 2014, 6, 8387–8404. [Google Scholar] [CrossRef]
- Meraner, A.; Ebel, P.; Zhu, X.X.; Schmitt, M. Cloud removal in Sentinel-2 imagery using a deep residual neural network and SAR-optical data fusion. ISPRS-J. Photogramm. Remote Sens. 2020, 166, 333–346. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Chen, Y.; Han, Q.; Deng, X.; Fan, J.; Duan, M.; Huang, Q. Estimation of high spatial resolution all-weather near-surface air temperature using FY-4A AGRI observations. Atmos. Res. 2023, 285, 106642. [Google Scholar] [CrossRef]
- Li, H.P.; Liu, H.L.; Duan, M.Z.; Deng, X.B.; Zhang, S.L. Estimation of Air Temperature under Cloudy Conditions Using Satellite-Based Cloud Products. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5. [Google Scholar] [CrossRef]
- Liu, S.H.; Su, H.B.; Tian, J.; Zhang, R.H.; Wang, W.Z.; Wu, Y.R. Evaluating Four Remote Sensing Methods for Estimating Surface Air Temperature on a Regional Scale. J. Appl. Meteorol. Climatol. 2017, 56, 803–814. [Google Scholar] [CrossRef]
- Wagner, W.; Naeimi, V.; Scipal, K.; de Jeu, R.; Martínez-Fernández, J. Soil moisture from operational meteorological satellites. Hydrogeol. J. 2007, 15, 121–131. [Google Scholar] [CrossRef]
- Zhihua, R.; Anyuan, X. Operational System Development on Three-step Quality Control of Observations from AWS. Meteorol. Mon. 2007, 33, 19–24. [Google Scholar]
- Zhang, P.; Zhu, L.; Tang, S.H.; Gao, L.; Chen, L.; Zheng, W.; Han, X.Z.; Chen, J.; Shao, J.L. General Comparison of FY-4A/AGRI with Other GEO/LEO Instruments and Its Potential and Challenges in Non-meteorological Applications. Front. Earth Sci. 2019, 6, 13. [Google Scholar] [CrossRef]
- Dong, L.; Xu, N.; Chen, L. Retrieval of FY-4A Land Surface Temperature for Operational Application. In Proceedings of the EGU General Assembly Conference Abstracts, Online, 4–8 May 2020. [Google Scholar]
- Ulivieri, C.; Cannizzaro, G. Land surface temperature retrievals from satellite measurements. Acta Astronaut. 1985, 12, 977–985. [Google Scholar] [CrossRef]
- Tan, Z.H.; Ma, S.; Zhao, X.B.; Yan, W.; Lu, W. Evaluation of Cloud Top Height Retrievals from China’s Next-Generation Geostationary Meteorological Satellite FY-4A. J. Meteorol. Res. 2019, 33, 553–562. [Google Scholar] [CrossRef]
- Liu, B.; Huo, J.; Lyu, D.R.; Wang, X. Assessment of FY-4A and Himawari-8 Cloud Top Height Retrieval through Comparison with Ground-Based Millimeter Radar at Sites in Tibet and Beijing. Adv. Atmos. Sci. 2021, 38, 1334–1350. [Google Scholar] [CrossRef]
- Cao, B.; Gruber, S.; Zheng, D.; Li, X. The ERA5-Land soil temperature bias in permafrost regions. Cryosphere 2020, 14, 2581–2595. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, H.L.; Deng, X.B.; Wang, H.; Zhang, S.L. Comparison of Machine-Learning Algorithms for Near-Surface Air-Temperature Estimation from FY-4A AGRI Data. Adv. Meteorol. 2020, 2020, 14. [Google Scholar] [CrossRef]
- Zhu, W.B.; Lu, A.F.; Jia, S.F.; Yan, J.B.; Mahmood, R. Retrievals of all-weather daytime air temperature from MODIS products. Remote Sens. Environ. 2017, 189, 152–163. [Google Scholar] [CrossRef]
- Du, M.X.; Zhang, M.J.; Wang, S.J.; Zhu, X.F.; Che, Y.J. Near-surface air temperature lapse rates in Xinjiang, northwestern China. Theor. Appl. Climatol. 2018, 131, 1221–1234. [Google Scholar] [CrossRef]
- Li, X.P.; Wang, L.; Chen, D.L.; Yang, K.; Xue, B.L.; Sun, L.T. Near-surface air temperature lapse rates in the mainland China during 1962–2011. J. Geophys. Res. Atmos. 2013, 118, 7505–7515. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Li, X.; Chen, D. Temporal and spatial changes in estimated near-surface air temperature lapse rates on Tibetan Plateau. Int. J. Climatol. 2018, 38, 2907–2921. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Shi, Y.; Jiang, Z.H.; Dong, L.P.; Shen, S.H. Statistical estimation of high-resolution surface air temperature from MODIS over the Yangtze River Delta, China. J. Meteorol. Res. 2017, 31, 448–454. [Google Scholar] [CrossRef]
- Li, X.M.; Zhou, Y.Y.; Asrar, G.R.; Zhu, Z.Y. Developing a 1 km resolution daily air temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 215, 74–84. [Google Scholar] [CrossRef]
- Oyler, J.W.; Ballantyne, A.; Jencso, K.; Sweet, M.; Running, S.W. Creating a topoclimatic daily air temperature dataset for the conterminous United States using homogenized station data and remotely sensed land skin temperature. Int. J. Climatol. 2015, 35, 2258–2279. [Google Scholar] [CrossRef]
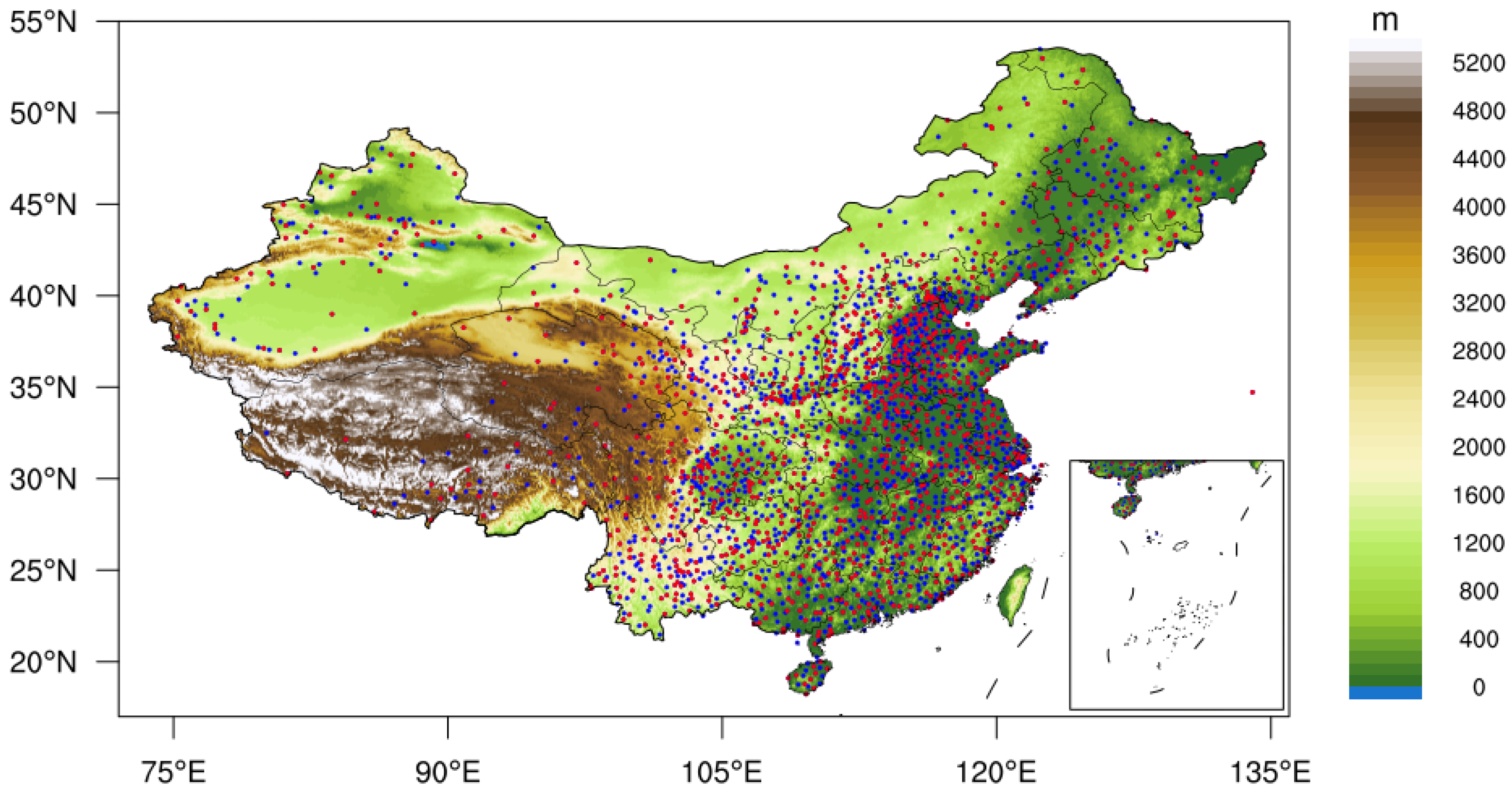

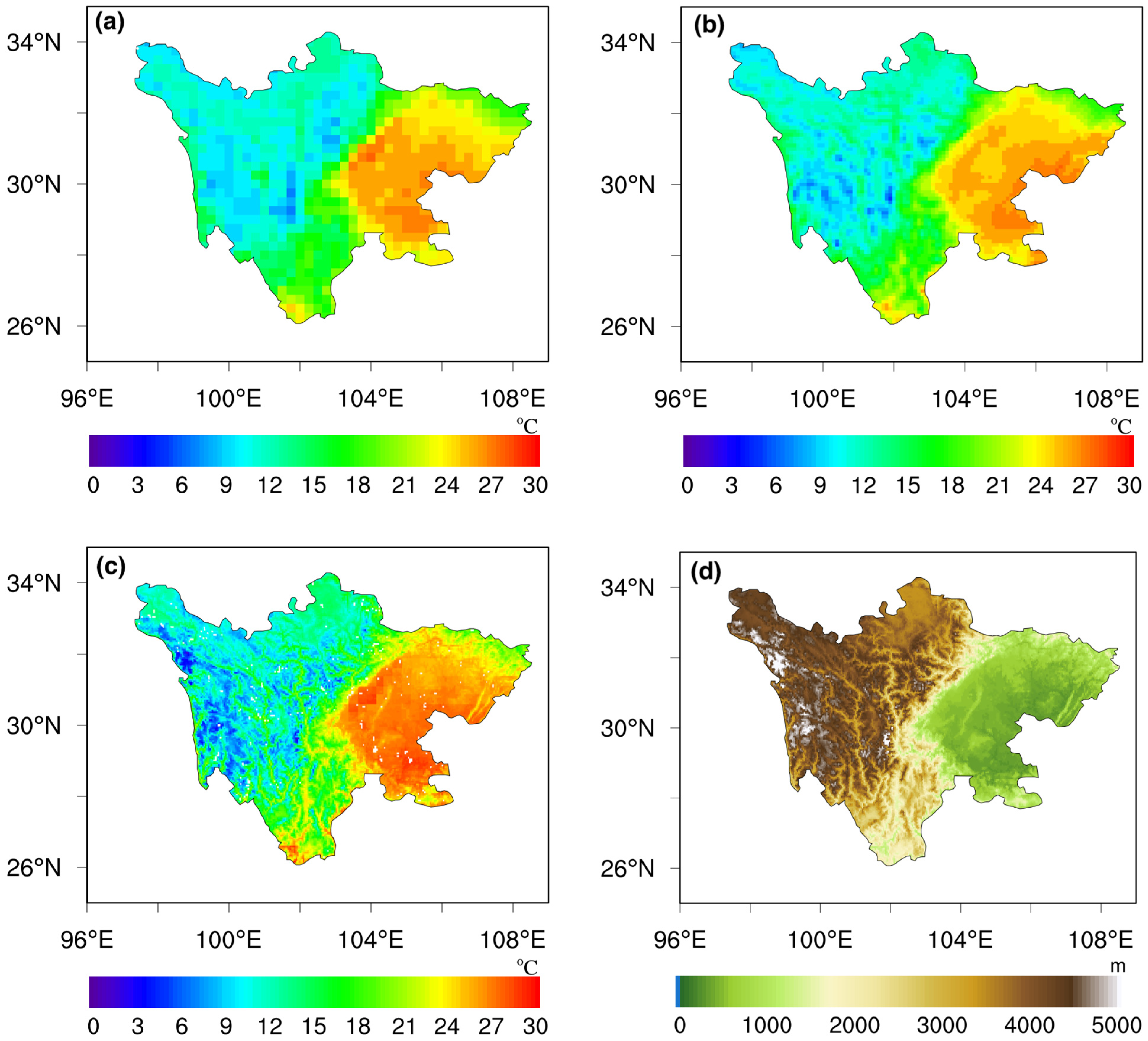

| Elevation (km) | Sites Number | Percent (%) |
|---|---|---|
| <0.0 | 1 | 0.04 |
| 0.0–1.0 | 1831 | 75.57 |
| 1.0–2.0 | 427 | 17.62 |
| 2.0–3.0 | 78 | 3.22 |
| 3.0–4.0 | 63 | 2.60 |
| 4.0–5.0 | 23 | 0.95 |
| Abbreviation | Units | Spatial Resolution | Temporal Resolution | Source |
|---|---|---|---|---|
| LST | K | 4 km | 15 min | NSMC |
| CTT | K | 4 km | 15 min | NSMC |
| CTH | m | 4 km | 15 min | NSMC |
| GFS Ta | K | 0.25° | 3 h | UCAR |
| elevation | m | 3 arc-s | - | NASA |
| NDVI | - | 250 m | 16 days | NASA |
| Latitude | - | 4 km | - | NSMC |
| Ta | °C | Site | 1 h | CMDC |
| Elevation (km) | Number | GFS | ERA5-Land | AGRI Ta | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R | RMSE (°C) | Bias (°C) | R | RMSE (°C) | Bias (°C) | R | RMSE (°C) | Bias (°C) | ||
| Clear sky | ||||||||||
| 0.0–1.0 | 730,560 | 0.98 | 2.38 | 0.40 | 0.99 | 2.12 | −0.29 | 0.99 | 1.62 | −0.03 |
| 1.0–2.0 | 207,110 | 0.97 | 3.17 | 0.81 | 0.97 | 2.68 | −0.01 | 0.99 | 2.02 | −0.01 |
| 2.0–3.0 | 32,973 | 0.96 | 2.94 | 0.39 | 0.96 | 3.04 | −0.57 | 0.98 | 2.17 | 0.17 |
| 3.0–4.0 | 33,997 | 0.94 | 3.42 | 0.18 | 0.92 | 4.36 | −1.67 | 0.97 | 2.38 | −0.12 |
| 4.0–5.0 | 11,866 | 0.94 | 3.43 | 0.37 | 0.95 | 3.55 | −1.77 | 0.97 | 2.44 | −0.06 |
| All | 1,016,506 | 0.98 | 2.62 | 0.47 | 0.98 | 2.39 | −0.31 | 0.99 | 1.81 | −0.02 |
| Cloudy sky | ||||||||||
| 0.0–1.0 | 1,131,100 | 0.98 | 1.88 | 0.14 | 0.99 | 1.86 | −0.21 | 0.99 | 1.54 | 0.01 |
| 1.0–2.0 | 237,650 | 0.97 | 2.41 | 0.36 | 0.98 | 2.38 | −0.37 | 0.98 | 1.97 | 0.04 |
| 2.0–3.0 | 39,787 | 0.97 | 2.22 | −0.09 | 0.95 | 3.49 | −0.82 | 0.97 | 2.01 | 0.11 |
| 3.0–4.0 | 35,615 | 0.95 | 2.84 | −0.54 | 0.92 | 4.47 | −2.79 | 0.97 | 2.28 | −0.17 |
| 4.0–5.0 | 10,913 | 0.95 | 3.09 | −0.22 | 0.95 | 3.71 | −2.08 | 0.96 | 2.62 | 0.24 |
| All | 1,455,065 | 0.98 | 2.01 | 0.15 | 0.98 | 2.15 | −0.32 | 0.98 | 1.72 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.-L.; Duan, M.-Z.; Zhou, X.-Q.; Zhang, S.-L.; Deng, X.-B.; Zhang, M.-L. Neural Network-Based Estimation of Near-Surface Air Temperature in All-Weather Conditions Using FY-4A AGRI Data over China. Remote Sens. 2024, 16, 3612. https://doi.org/10.3390/rs16193612
Liu H-L, Duan M-Z, Zhou X-Q, Zhang S-L, Deng X-B, Zhang M-L. Neural Network-Based Estimation of Near-Surface Air Temperature in All-Weather Conditions Using FY-4A AGRI Data over China. Remote Sensing. 2024; 16(19):3612. https://doi.org/10.3390/rs16193612
Chicago/Turabian StyleLiu, Hai-Lei, Min-Zheng Duan, Xiao-Qing Zhou, Sheng-Lan Zhang, Xiao-Bo Deng, and Mao-Lin Zhang. 2024. "Neural Network-Based Estimation of Near-Surface Air Temperature in All-Weather Conditions Using FY-4A AGRI Data over China" Remote Sensing 16, no. 19: 3612. https://doi.org/10.3390/rs16193612
APA StyleLiu, H.-L., Duan, M.-Z., Zhou, X.-Q., Zhang, S.-L., Deng, X.-B., & Zhang, M.-L. (2024). Neural Network-Based Estimation of Near-Surface Air Temperature in All-Weather Conditions Using FY-4A AGRI Data over China. Remote Sensing, 16(19), 3612. https://doi.org/10.3390/rs16193612






