Instantaneous Frequency Extraction for Nonstationary Signals via a Squeezing Operator with a Fixed-Point Iteration Method
Abstract
:1. Introduction
2. Foundational Background
2.1. The STFT and the Frequency Estimation Operator
2.2. Unbiased IF Estimation Based Fixed Point of FEO
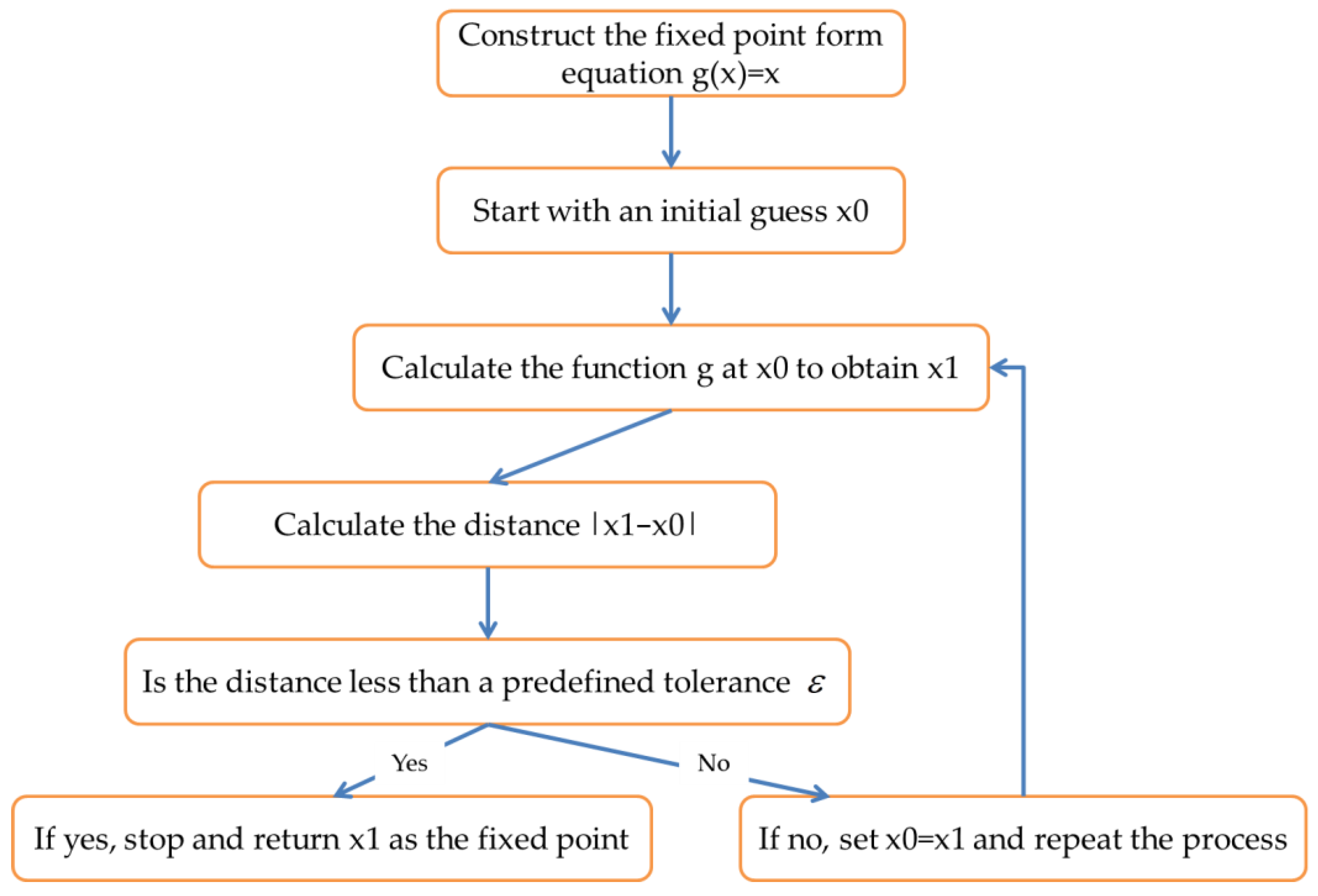
3. The Proposed Algorithm
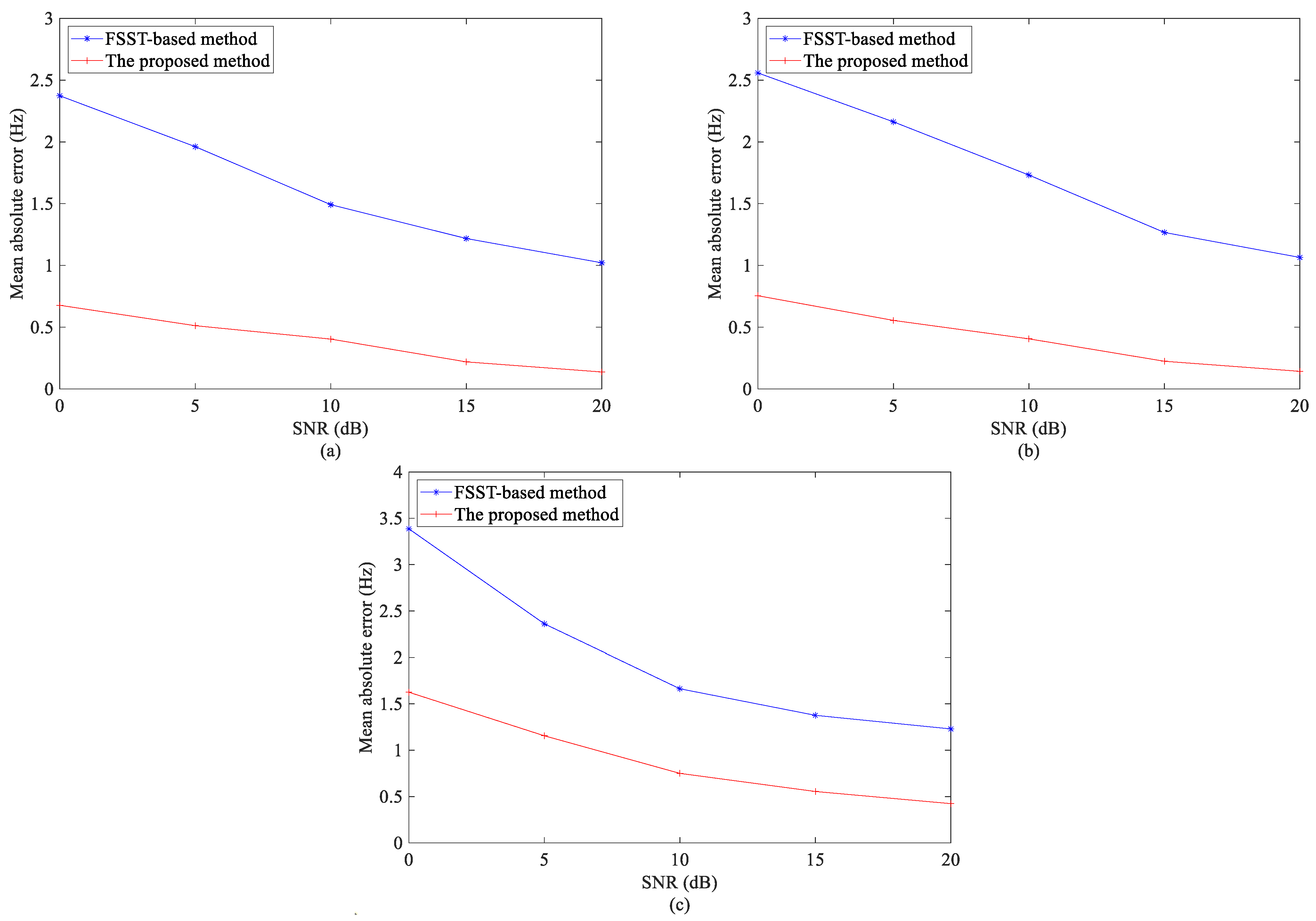
4. Experimental Results and Analysis
4.1. Single-Component Signal
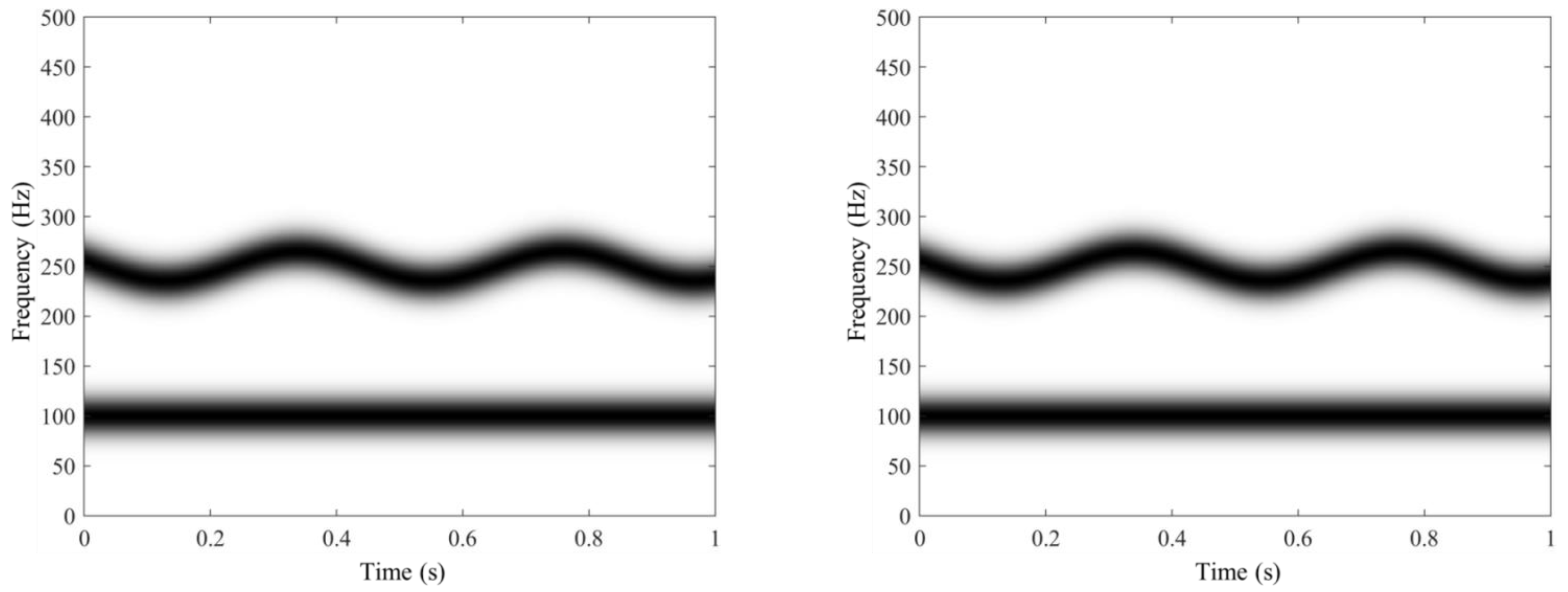
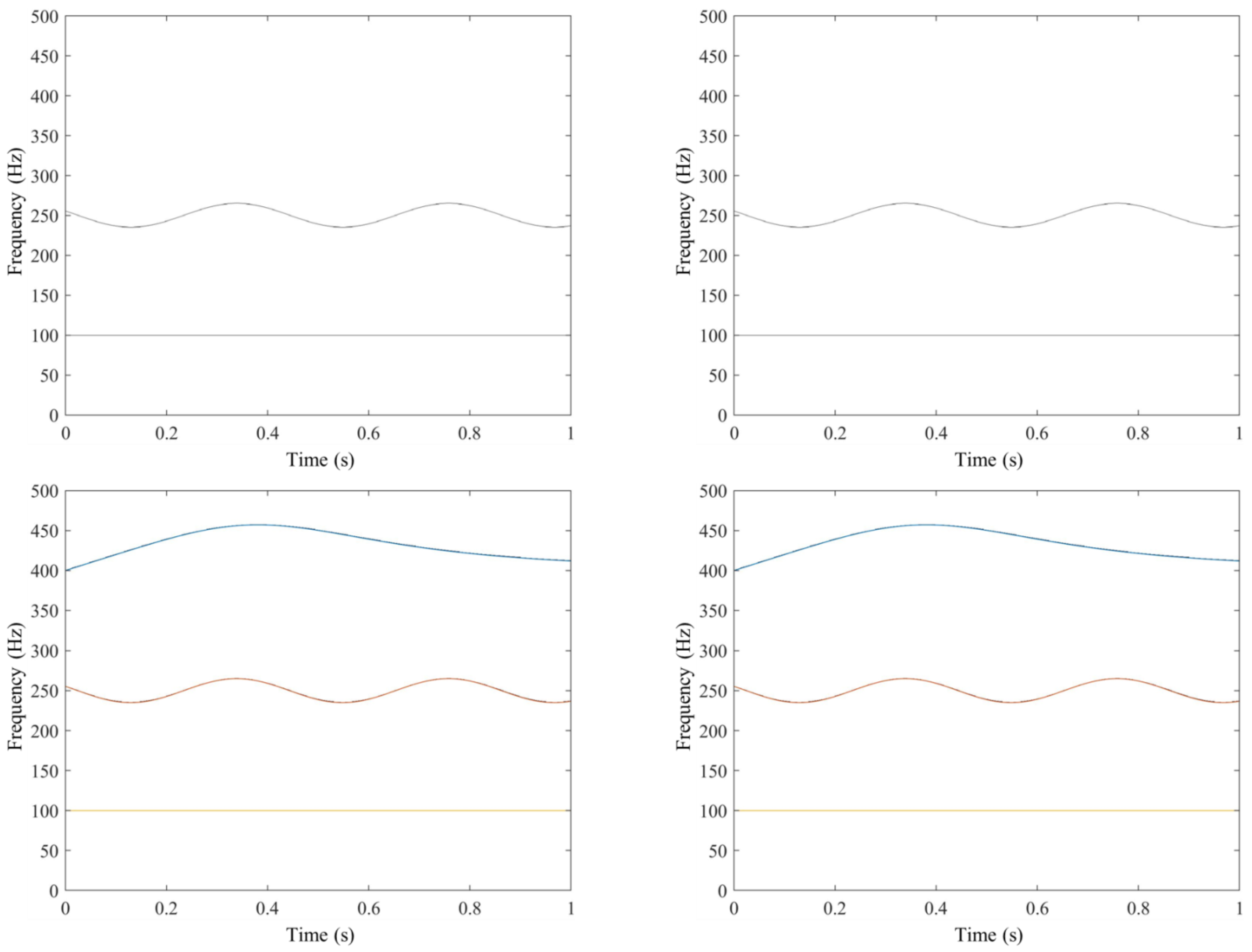
4.2. Multicomponent Signal
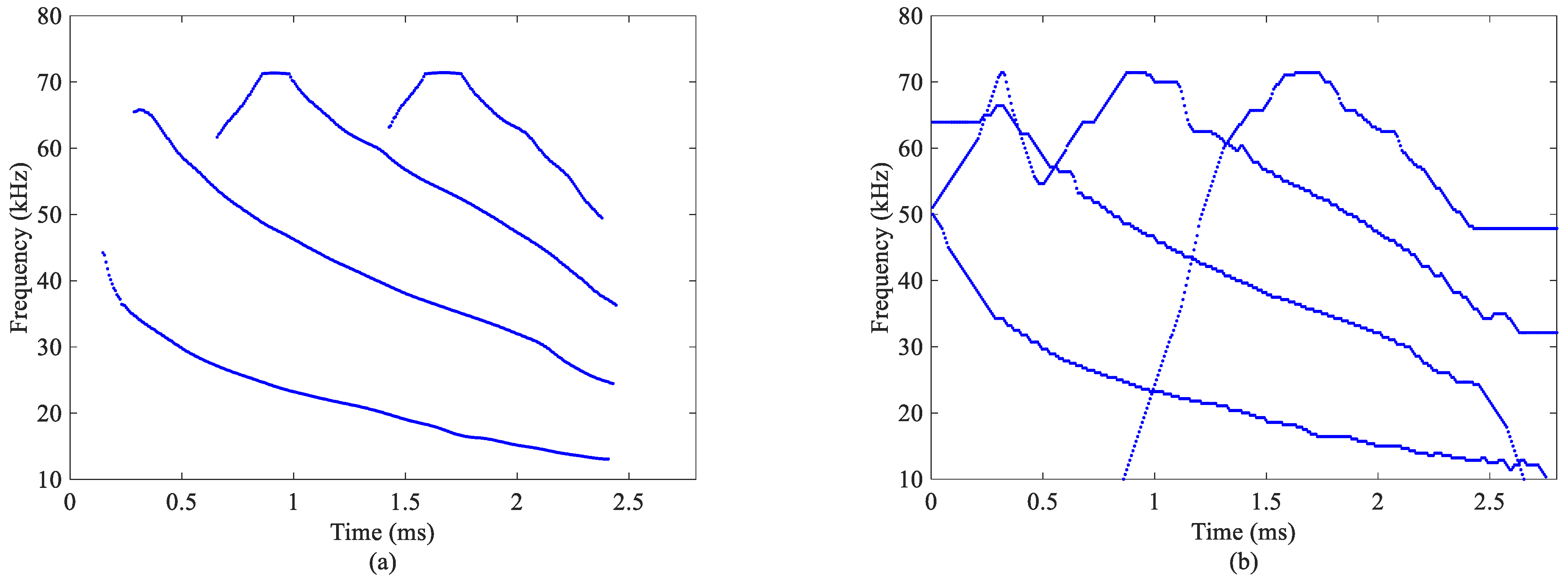
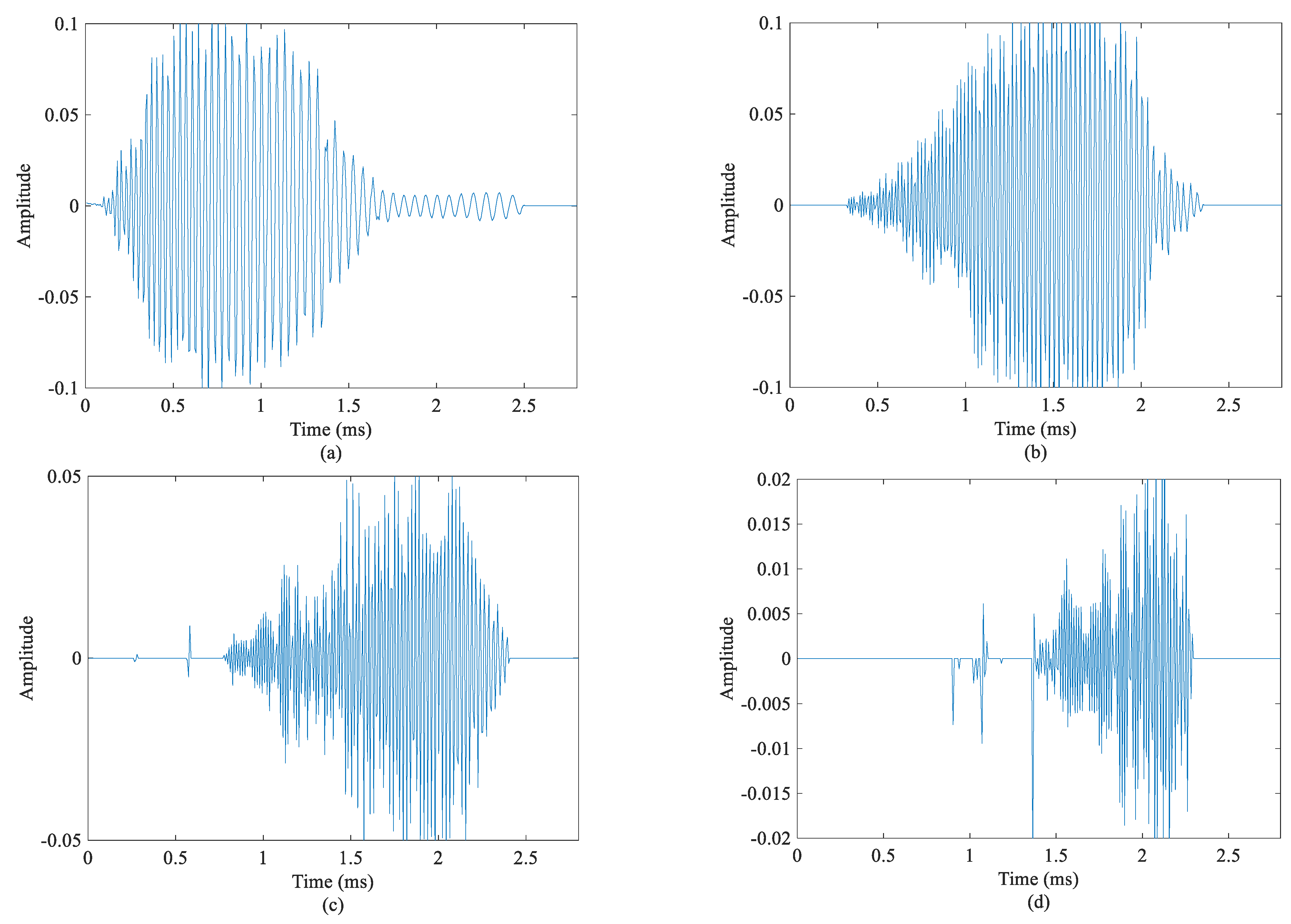
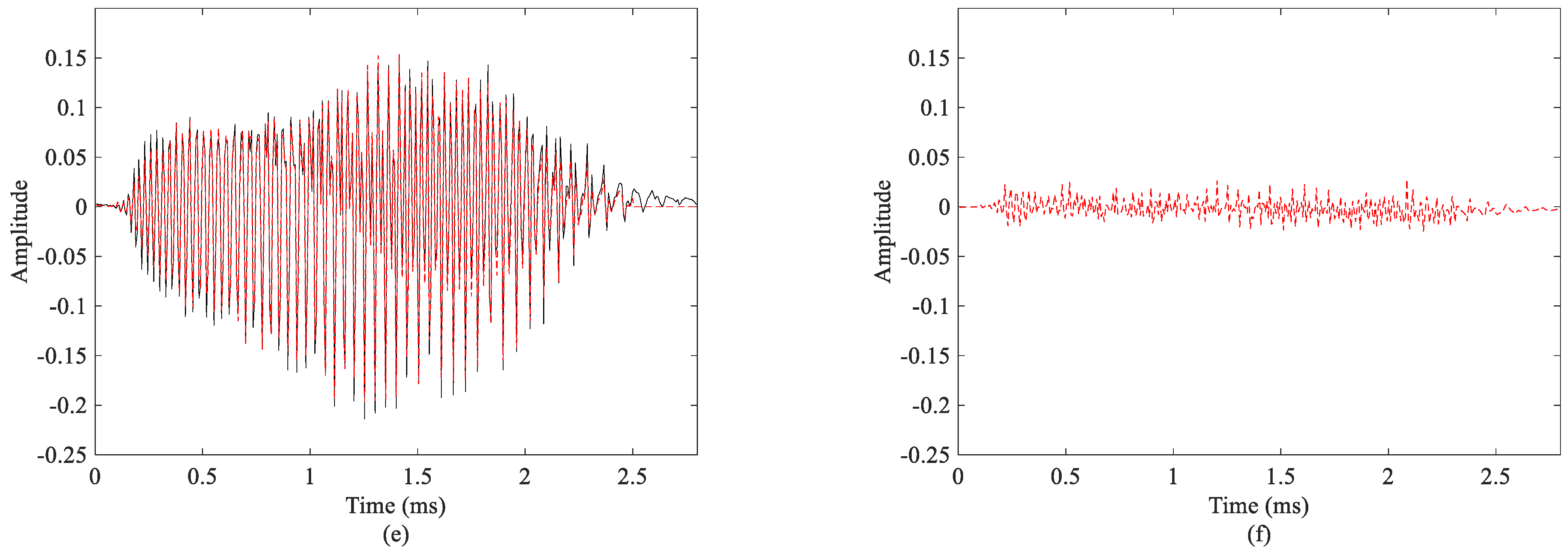
4.3. Bat Echolocation
4.4. Weak Component Detection
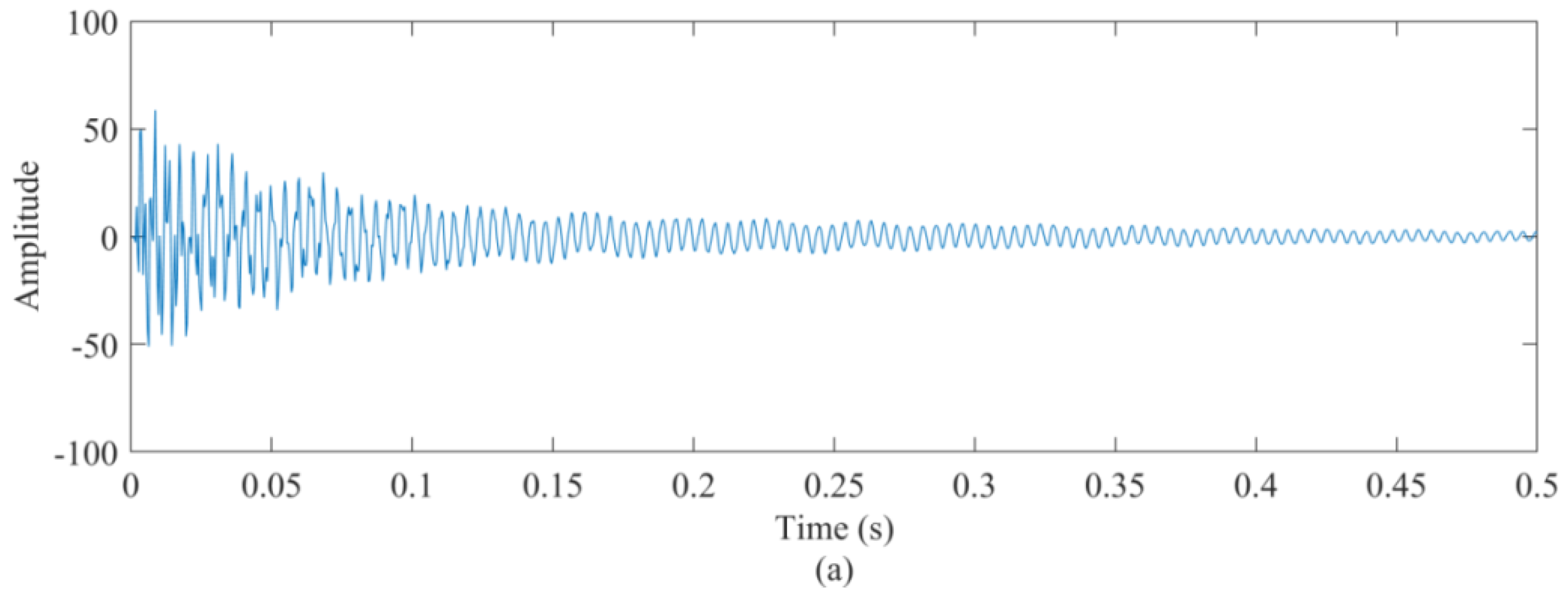
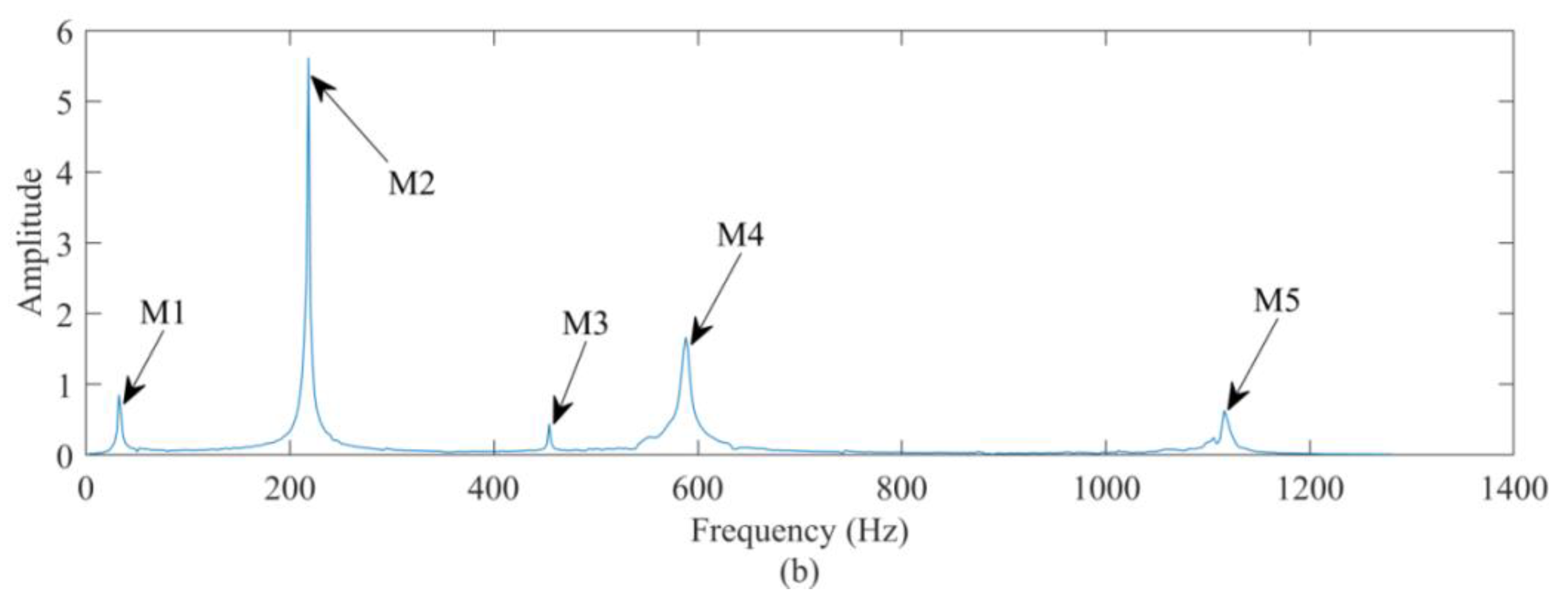
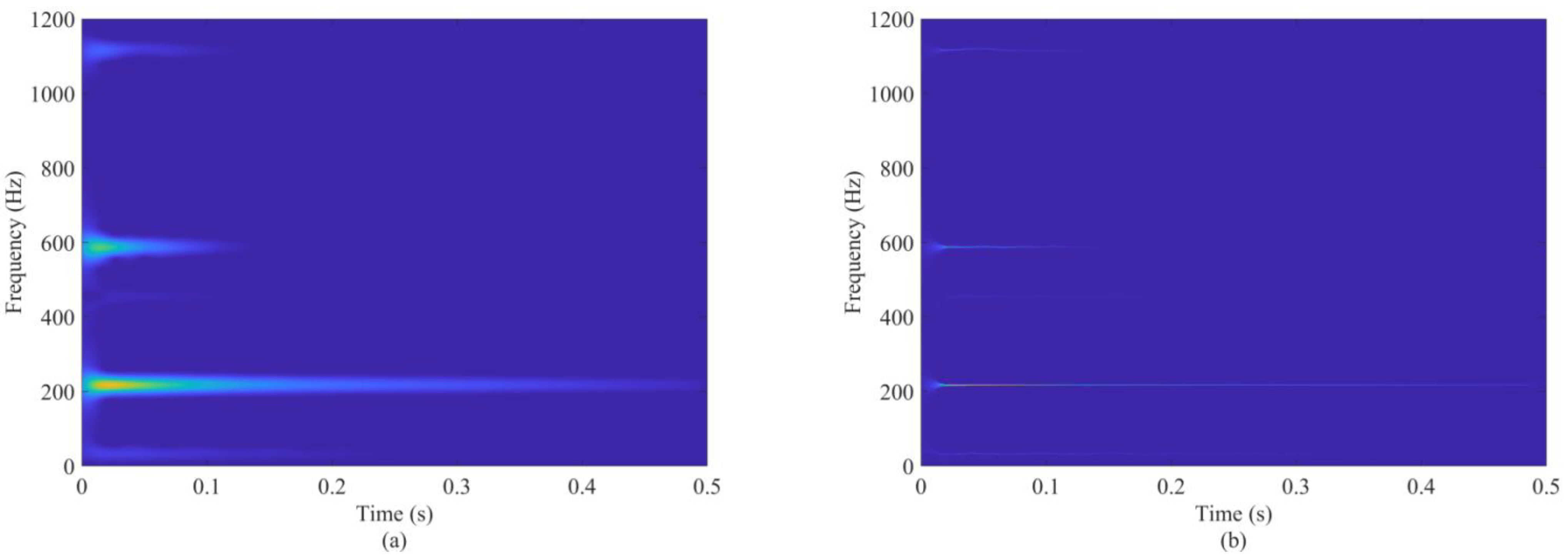
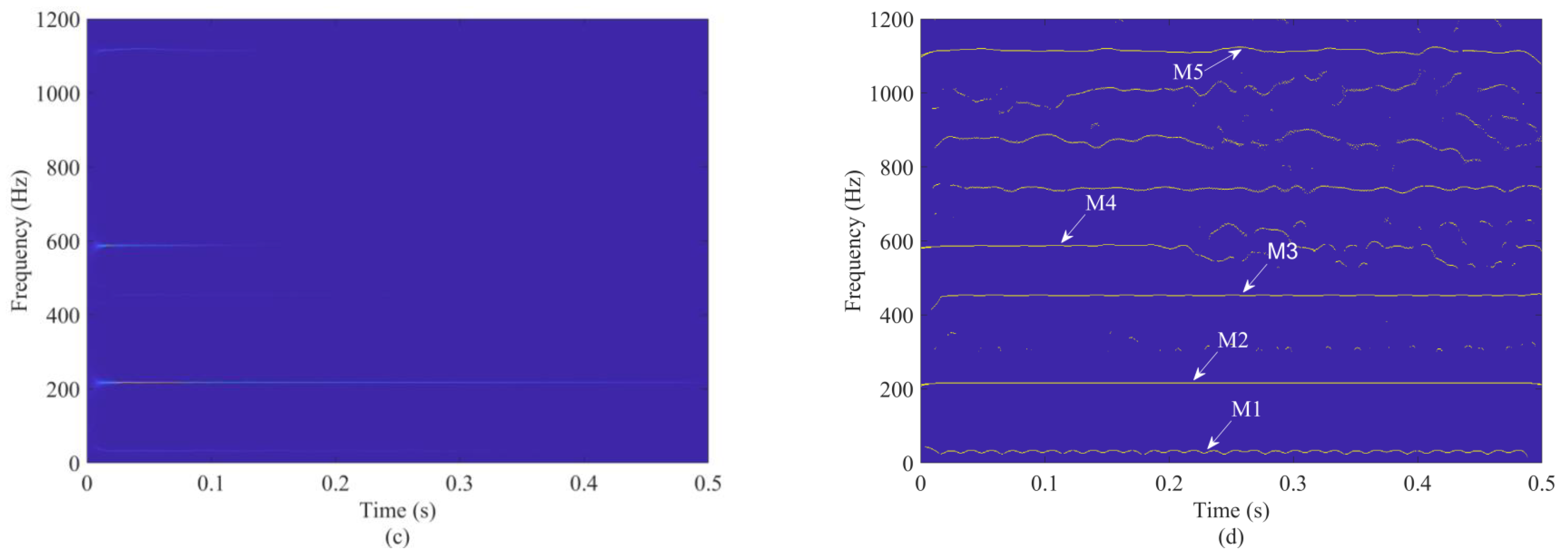
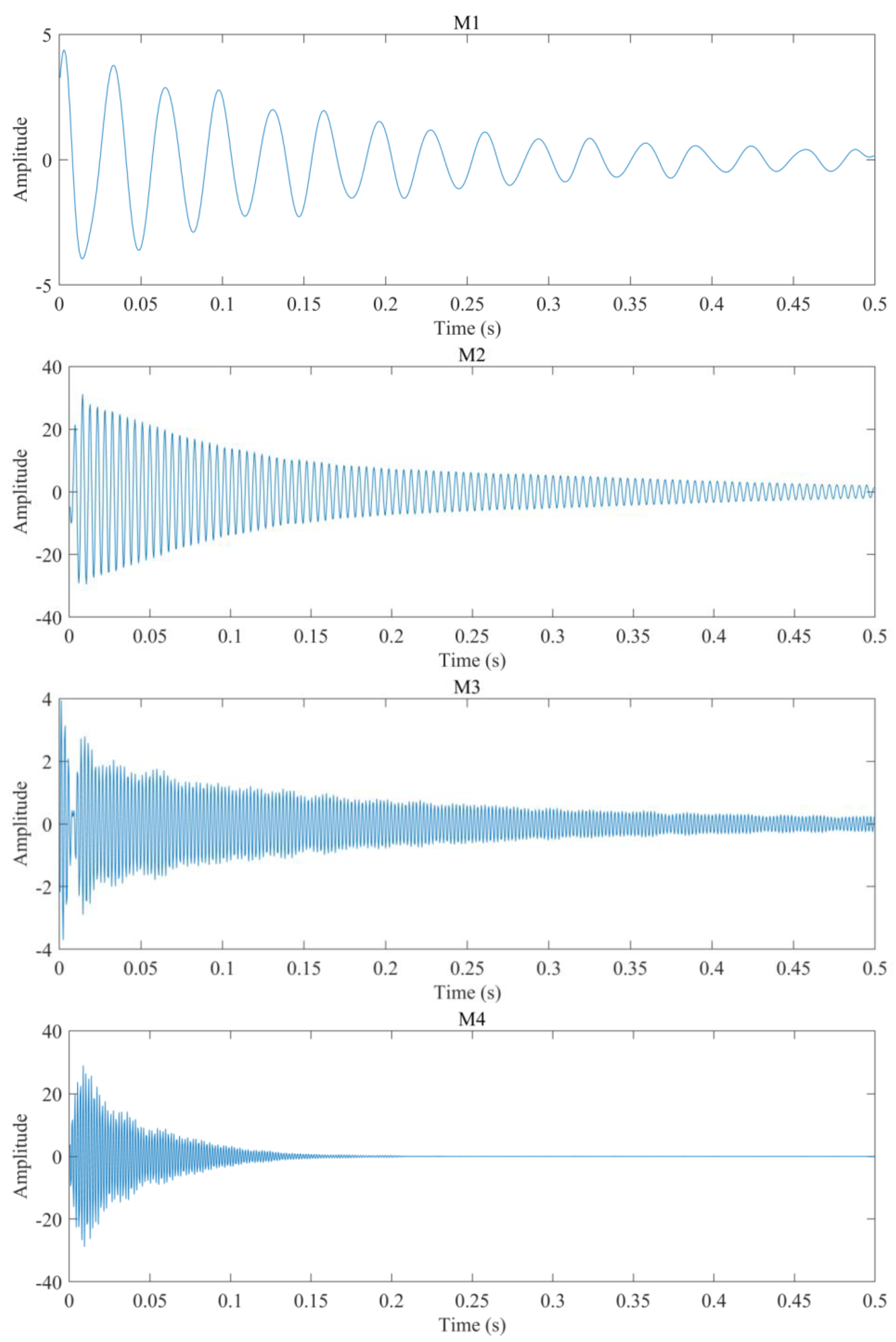
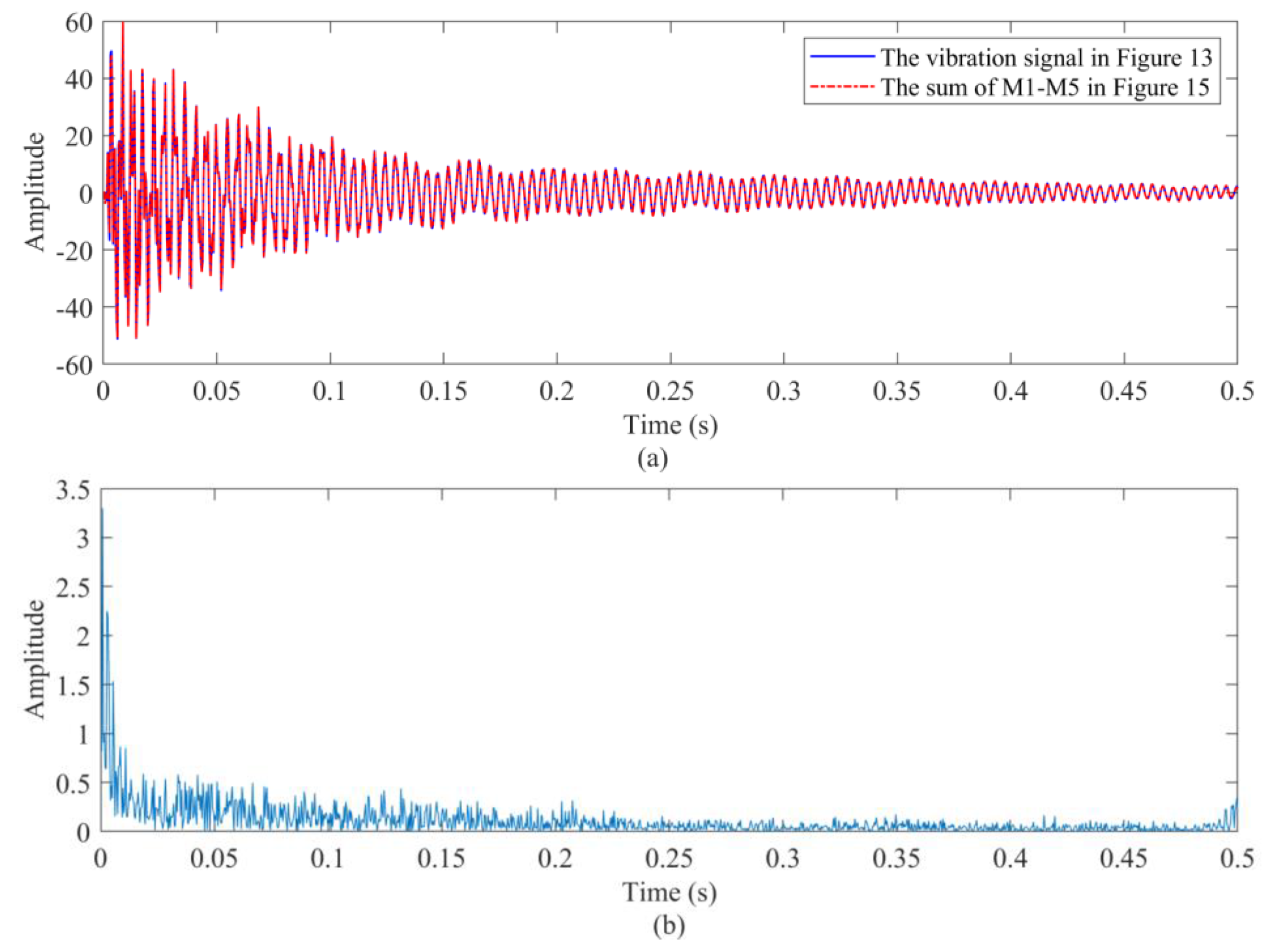
4.5. Vibration Signal
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals. IEEE Proc. 1992, 80, 510–538. [Google Scholar] [CrossRef]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal-Part 2: Algorithms and applications. IEEE Proc. 1992, 80, 540–568. [Google Scholar] [CrossRef]
- Borovkova, E.I.; Ponomarenko, V.I.; Karavaev, A.S.; Dubinkina, E.S.; Prokhorov, M.D. Method of Extracting the Instantaneous Phases and Frequencies of Respiration from the Signal of a Photoplethysmogram. Mathematics 2023, 11, 4903. [Google Scholar] [CrossRef]
- Guharaya, S.K.; Thakura, G.S.; Goodmana, F.J.; Rosena, S.L.; Houser, D. Analysis of non-stationary dynamics in the financial system. Econ. Lett. 2013, 121, 454–457. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Q.; Zhong, J.; Chen, Z.; Zhong, S. Parameterized Instantaneous Frequency Estimation Method for Vibration Signal with Nonlinear Frequency Modulation. Machines 2022, 10, 777. [Google Scholar] [CrossRef]
- Razzaq, H.S.; Hussain, Z.M. Instantaneous Frequency Estimation of FM Signals under Gaussian and Symmetric α-Stable Noise: Deep Learning versus Time–Frequency Analysis. Information 2023, 14, 18. [Google Scholar] [CrossRef]
- Cohen, L.; Lee, C. Instantaneous frequency and timefrequency distributions. Proc. IEEE Int. Symp. Circuits Syst. 1989, 2, 1231–1234. [Google Scholar]
- Stankovic, L.; Katkovnik, V. Algorithm for the instantaneous frequency estimation using time-frequency distributions with adaptive window width. IEEE Signal Process. Lett. 1998, 5, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Iatsenko, D.; McClintock, P.V.E.; Stefanovska, A. Extraction of instantaneous frequencies from ridges in time-frequency representations of signals. Signal Process. 2016, 125, 290–303. [Google Scholar] [CrossRef]
- Lovell, B.C.; Williamson, R.C. The statistical performance of some instantaneous frequency estimators. IEEE Trans. Signal Process. 1992, 40, 1708–1724. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.L.; Shi, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies. Rev. Geophys. 2008, 46. [Google Scholar] [CrossRef]
- Tary, J.B.; Herrera, R.H.; Han, J.J.; van der Baan, M. Spectral estimation–what is new? What is next? Rev. Geophys. 2014, 52, 723–749. [Google Scholar] [CrossRef]
- Gabor, D. Theory of communication. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory-Part II: Sampling theory and complex waves. Geophysics 1982, 47, 222–236. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Mansinha, L.; Lowe, R. Localization of the complex spectrum: The S transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Wignaer, E. On the quantum correction for the rmodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Ville, J. Theorie et applications de la notion de signal analytique. Cables Trans. 1948, 2A, 61–67. [Google Scholar]
- Swiercz, E.; Janczak, D.; Konopko, K. Estimation and Classification of NLFM Signals Based on the Time–Chirp Representation. Sensors 2022, 22, 8104. [Google Scholar] [CrossRef]
- Jurdana, V.; Vrankic, M.; Lopac, N.; Jadav, G.M. Method for Automatic Estimation of Instantaneous Frequency and Group Delay in Time–Frequency Distributions with Application in EEG Seizure Signals Analysis. Sensors 2023, 23, 4680. [Google Scholar] [CrossRef] [PubMed]
- Delprat, N.; Escudie, B.; Guillemain, P.; Kronland-Martinet, R.; Tchamitchian, P.; Torresani, B. Asymptotic wavelet and Gabor analysis: Extraction of instantaneous frequencies. IEEE Trans. Inf. Theory 1992, 38, 644–664. [Google Scholar] [CrossRef]
- Wu, H.T.; Chan, Y.H.; Lin, Y.T.; Yeh, Y.H. Using synchrosqueezing transform to discover breathing dynamics from ECG signals. Appl. Comput. Harmon. Anal. 2014, 36, 354–459. [Google Scholar] [CrossRef]
- Sandoval, S.; De Leon, P.L. Recasting the (Synchrosqueezed) Short-Time Fourier Transform as an Instantaneous Spectrum. Entropy 2022, 24, 518. [Google Scholar] [CrossRef] [PubMed]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-order synchrosqueezing transform or invertible reassignment? Towards ideal time-frequency representations. IEEE Trans. Signal Process. 2015, 63, 1335–1344. [Google Scholar] [CrossRef]
- Behera, R.; Meignen, S.; Oberlin, T. Theoretical analysis of the second-order synchrosqueezing transform. Appl. Comput. Harmon. Anal. 2018, 45, 379–404. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S. The second-order wavelet synchrosqueezing transform. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Han, B.; Zhou, Y.; Yu, G. Second-order synchroextracting wavelet transform for nonstationary signal analysis of rotating machinery. Signal Process. 2021, 186, 108123. [Google Scholar] [CrossRef]
- Yu, G.; Lin, T. Second-order transient-extracting transform for the analysis of impulsive-like signals. Mech. Syst. Signal Process. 2021, 147, 107069. [Google Scholar] [CrossRef]
- Pham, D.; Meignen, S. High-order synchrosqueezing transform for multicomponent signals analysis—With an application to gravitational-wave signal. IEEE Trans. Signal Process. 2017, 65, 3168–3178. [Google Scholar] [CrossRef]
- Lv, S.; Lv, Y.; Yuan, R.; Li, H. High-order synchroextracting transform for characterizing signals with strong AM-FM features and its application in mechanical fault diagnosis. Mech. Syst. Signal Process. 2022, 172, 108959. [Google Scholar] [CrossRef]
- Wang, S.; Chen, X.; Cai, G.; Chen, B.; Li, X.; He, Z. Matching demodulation transform and synchrosqueezing in time-frequency analysis. IEEE Trans. Signal Process. 2014, 62, 69–84. [Google Scholar] [CrossRef]
- Miao, Y.; Sun, H.; Qi, J. Synchro-Compensating Chirplet Transform. IEEE Signal Process. Lett. 2018, 25, 1413–1417. [Google Scholar] [CrossRef]
- Miao, Y.C.; Qasem, Z.A.H.; Li, Y.S. Adaptive directional ridge prediction tracker for instantaneous frequency estimation. Signal Process. 2023, 209, 109035. [Google Scholar] [CrossRef]
- Mandel, L. Interpretation of instantaneous frequency. Am. J. Phys. 1974, 42, 840–846. [Google Scholar] [CrossRef]
- Stanković, L.; Djurović, I.; Stanković, S.; Simeunović, M.; Djukanović, S.; Daković, M. Instantaneous frequency in time–frequency analysis: Enhanced concepts and performance of estimation algorithms. Digit. Signal Process. 2014, 35, 1–13. [Google Scholar] [CrossRef]
- Fitz, K.R.; Fulop, S.A. A unified theory of time-frequency reassignment. arXiv 2009, arXiv:0903.3080. [Google Scholar]
- Li, Z.; Gao, J.; Li, H.; Zhang, Z.; Liu, N.; Zhu, X. Synchroextracting transform: The theory analysis and comparisons with the synchrosqueezing transform. Signal Process. 2020, 166, 107243. [Google Scholar] [CrossRef]
- Auger, F.; Chassande-Mottin, E.; Flandrin, P. On phasemagnitude relationships in the short-time Fourier transform. IEEE Signal Process. Lett. 2012, 19, 267–270. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D.; Mclaughlin, S. On demodulation, ridge detection and synchrosqueezing for multicomponent signals. IEEE Trans. Signal Process. 2017, 65, 2093–2103. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. The Fourier-based synchrosqueezing transform. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 315–319. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gao, Z.; Sun, F.; Gao, J.; Zhang, W. Instantaneous Frequency Extraction for Nonstationary Signals via a Squeezing Operator with a Fixed-Point Iteration Method. Remote Sens. 2024, 16, 1412. https://doi.org/10.3390/rs16081412
Li Z, Gao Z, Sun F, Gao J, Zhang W. Instantaneous Frequency Extraction for Nonstationary Signals via a Squeezing Operator with a Fixed-Point Iteration Method. Remote Sensing. 2024; 16(8):1412. https://doi.org/10.3390/rs16081412
Chicago/Turabian StyleLi, Zhen, Zhaoqi Gao, Fengyuan Sun, Jinghuai Gao, and Wei Zhang. 2024. "Instantaneous Frequency Extraction for Nonstationary Signals via a Squeezing Operator with a Fixed-Point Iteration Method" Remote Sensing 16, no. 8: 1412. https://doi.org/10.3390/rs16081412
APA StyleLi, Z., Gao, Z., Sun, F., Gao, J., & Zhang, W. (2024). Instantaneous Frequency Extraction for Nonstationary Signals via a Squeezing Operator with a Fixed-Point Iteration Method. Remote Sensing, 16(8), 1412. https://doi.org/10.3390/rs16081412







