A Bayesian Approach for Forecasting the Probability of Large Earthquakes Using Thermal Anomalies from Satellite Observations
Abstract
:1. Introduction
2. Study Area and Data
2.1. Global Seismically Active Regions
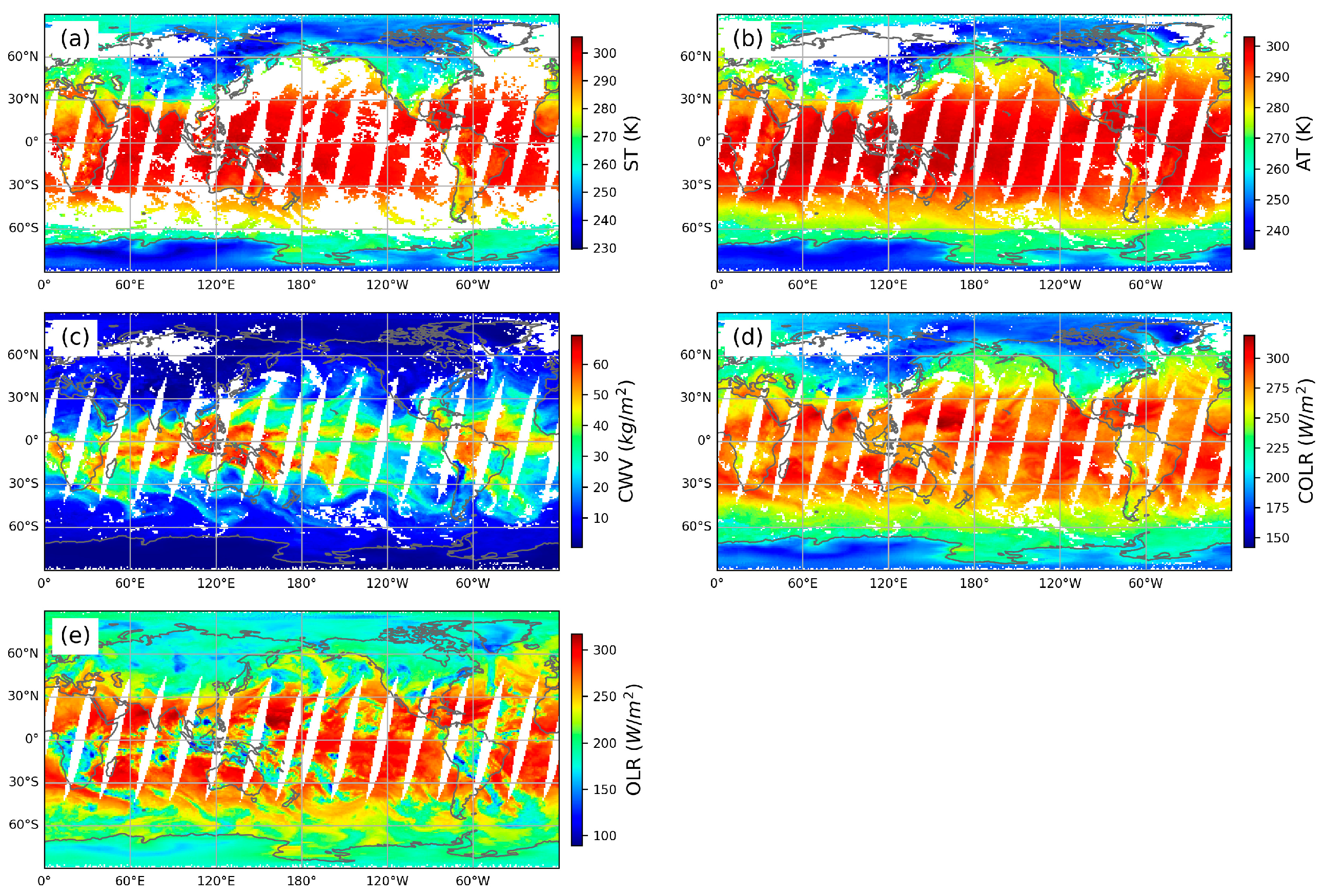
2.2. AIRS Dataset
3. Methods
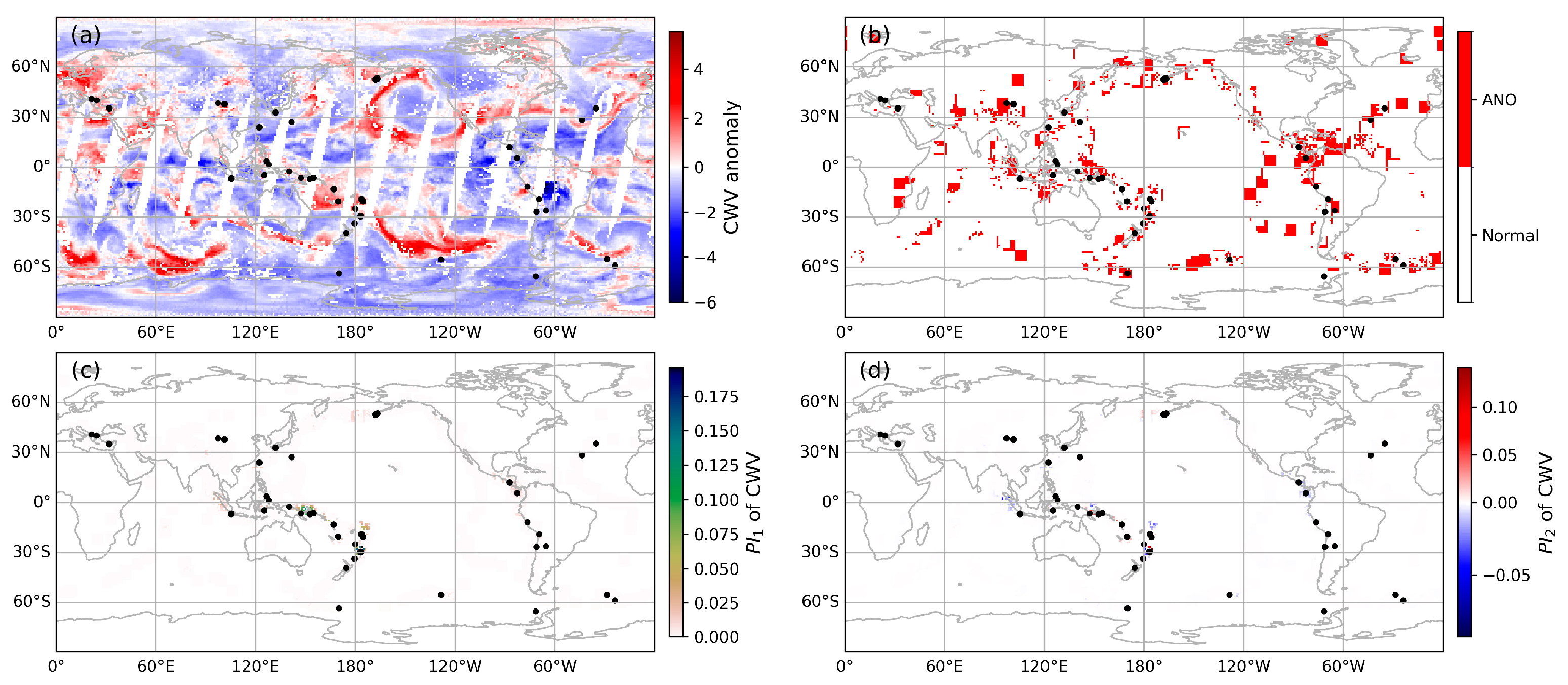
3.1. Pre-Seismic Anomaly Recognition
3.2. Earthquake Forecast Probability Based on Bayesian Theory
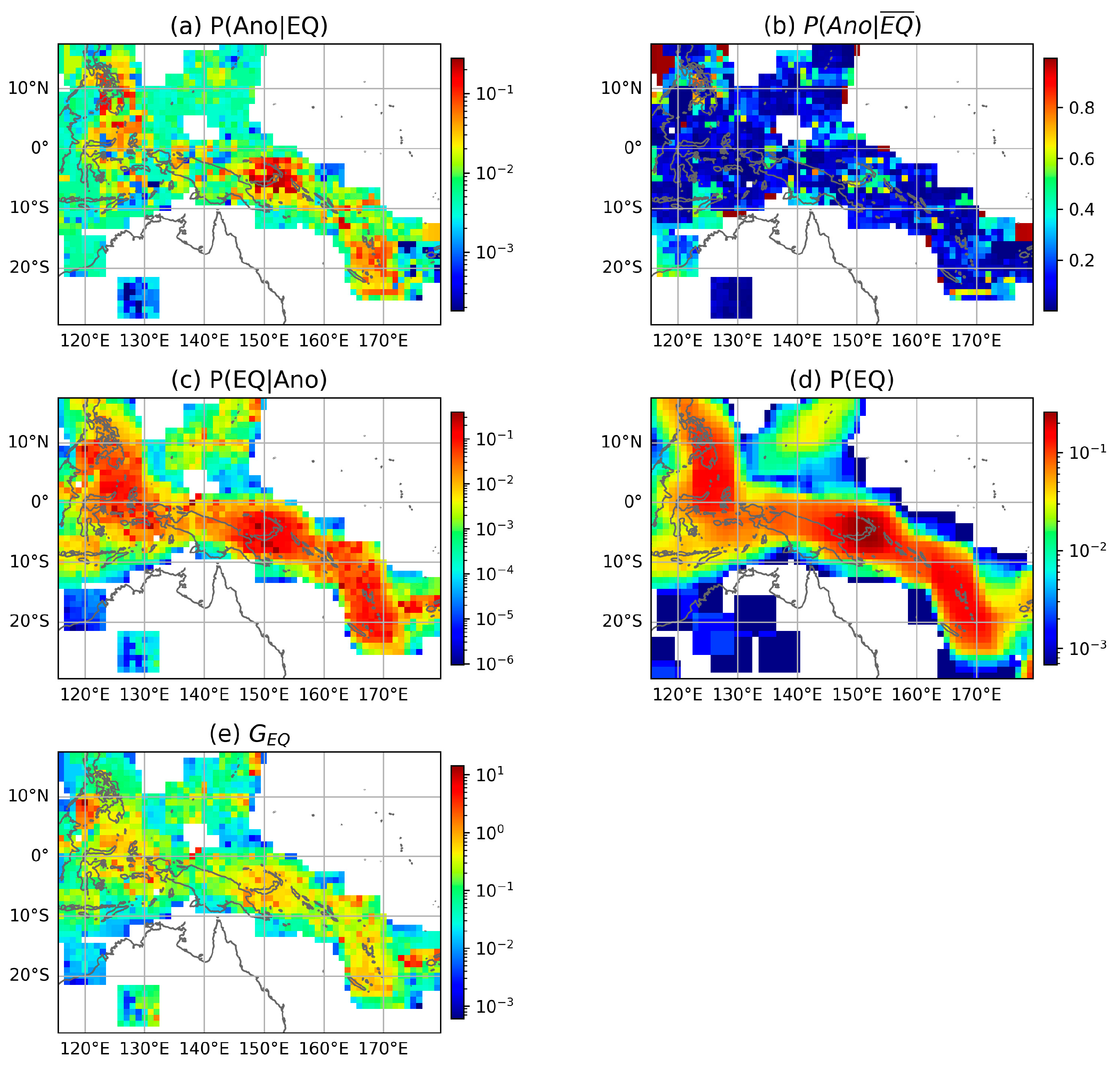
4. Results
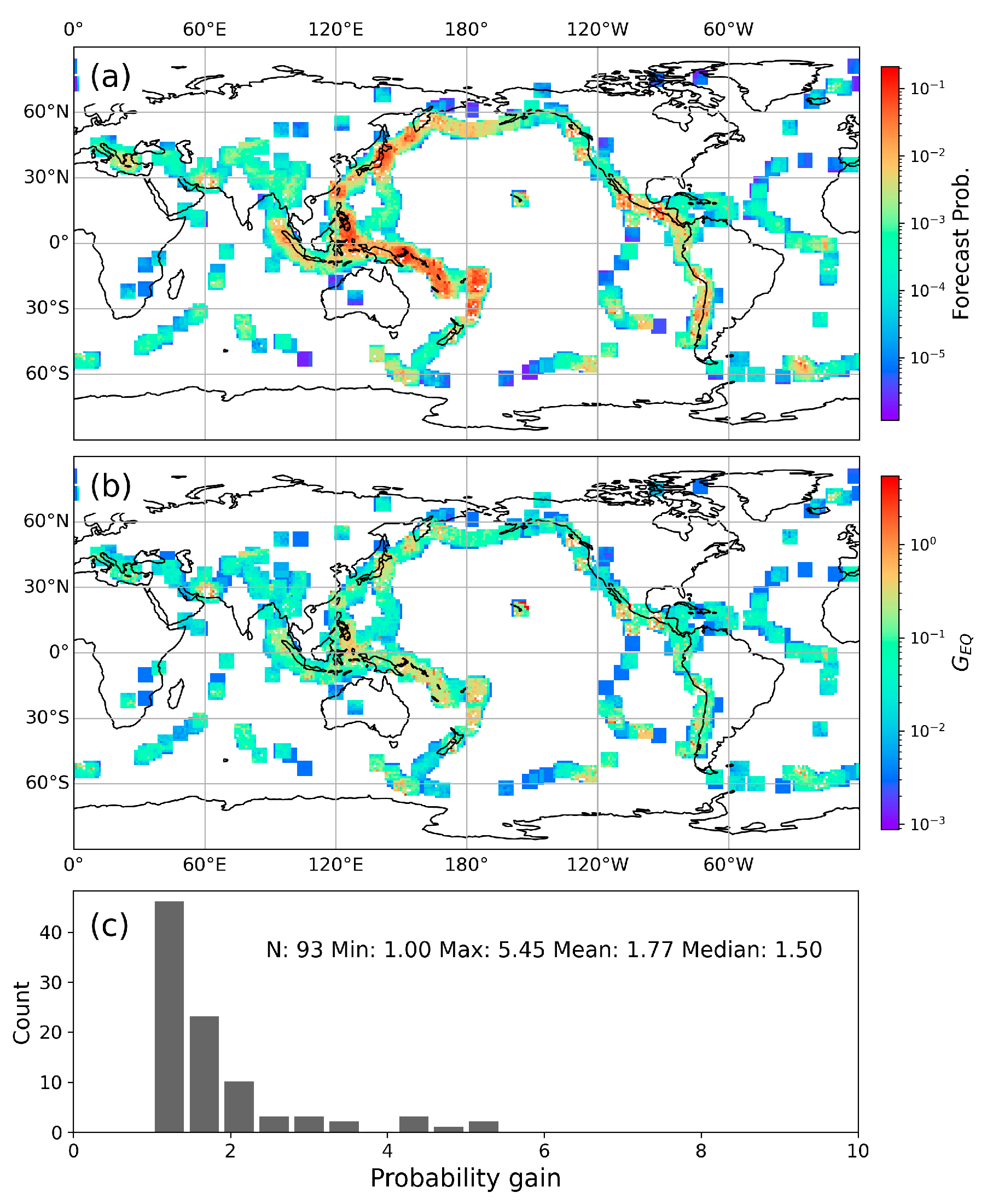
4.1. Global Probability of Earthquake Forecasting
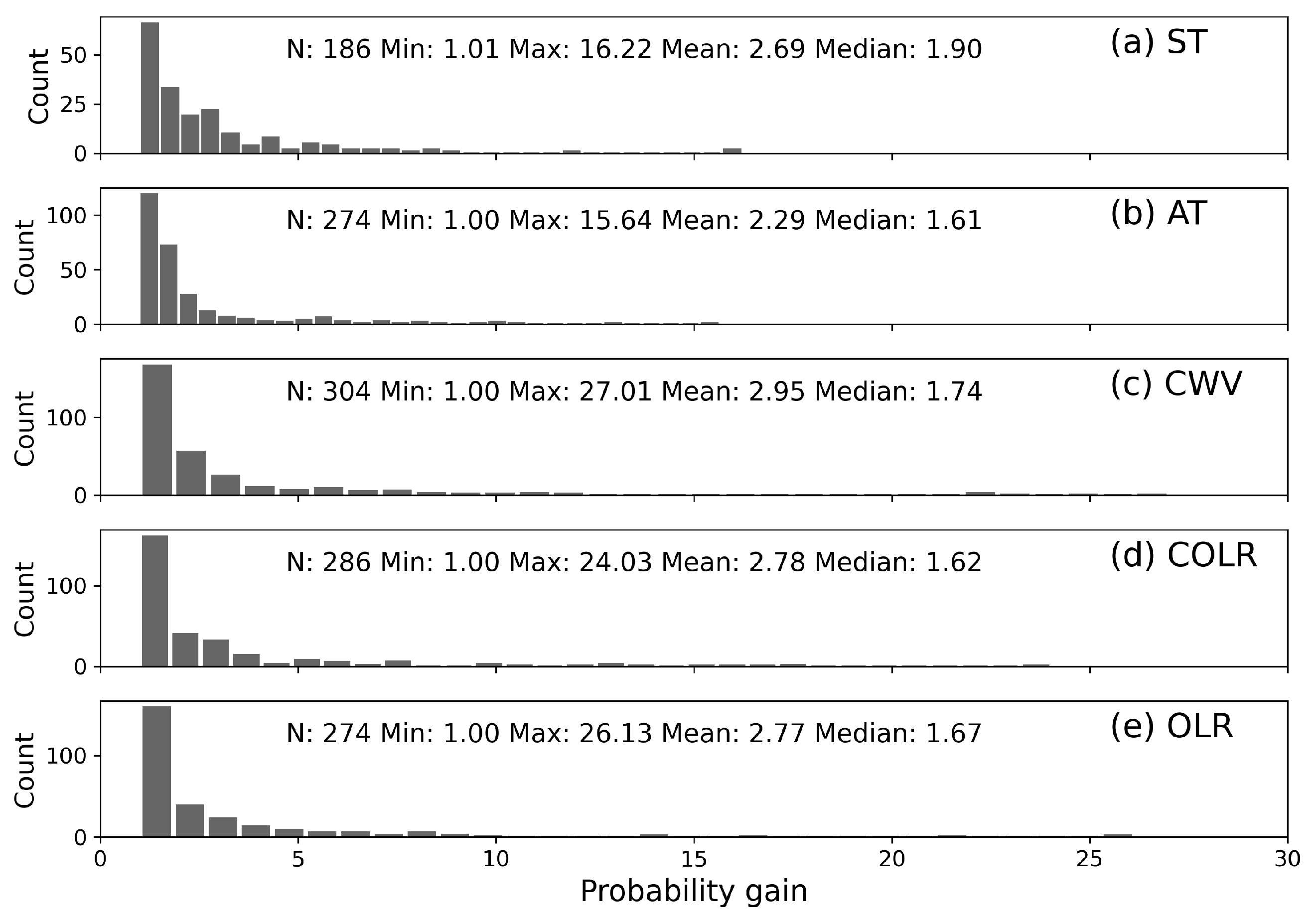
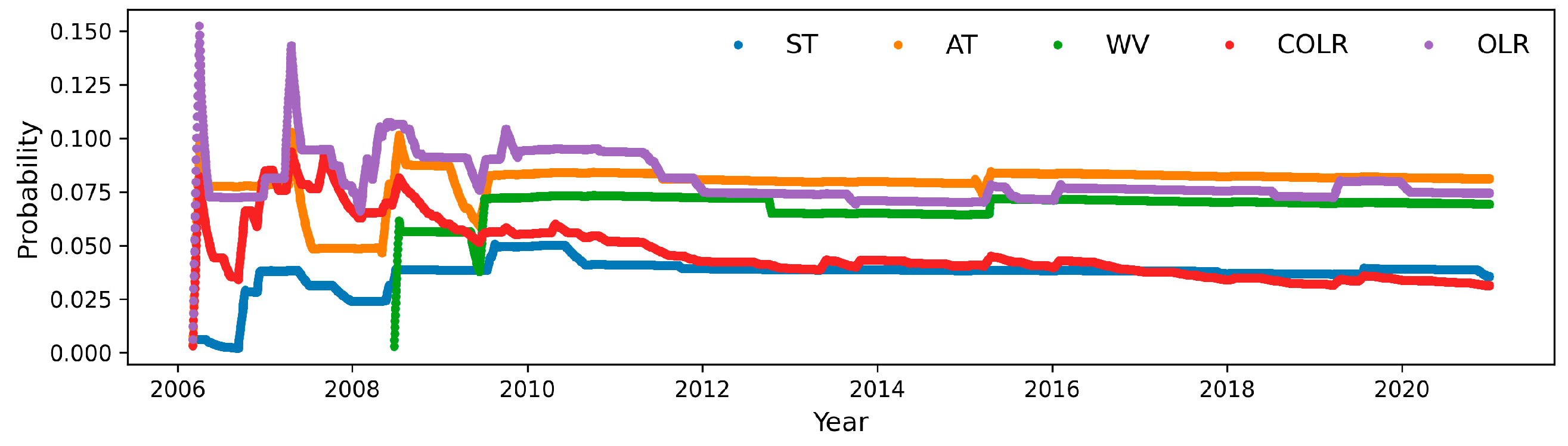
4.2. Probability Gains of Each Parameter
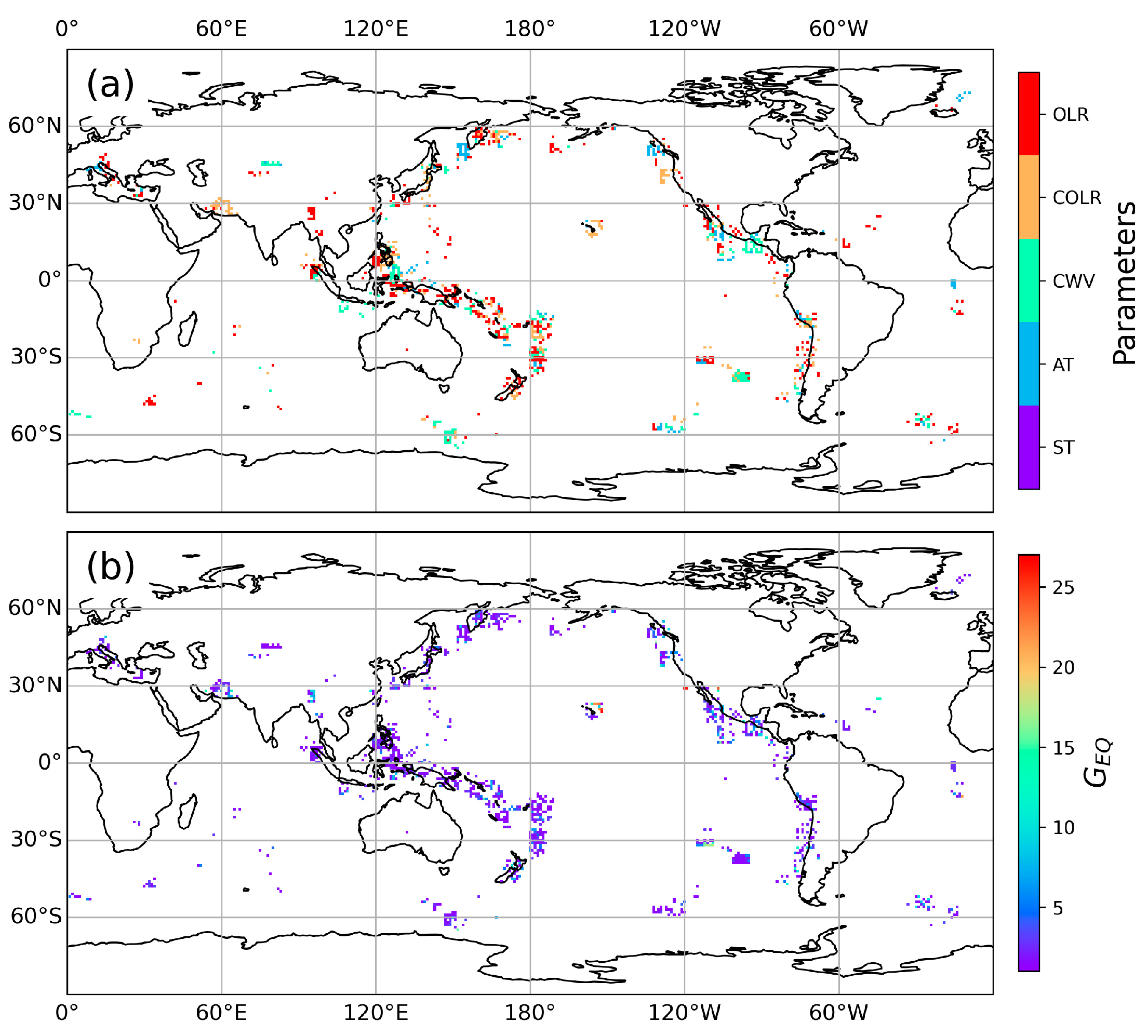
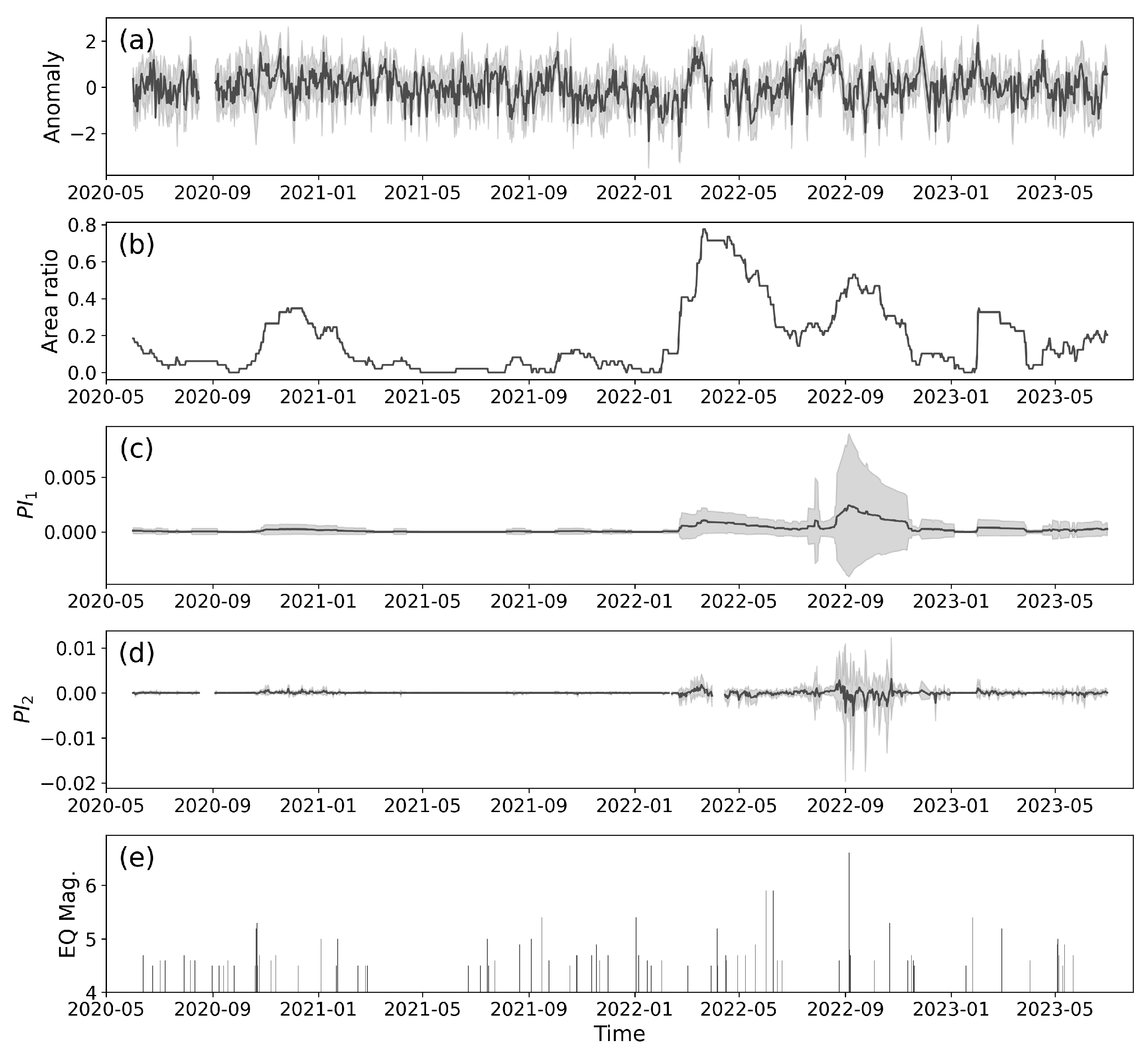
4.3. Time Scales for Obtaining the Stable Forecast Probability
4.4. Prospective Analysis of Earthquakes in 2021 and 2022
4.5. A Probabilistic Synthesis of Anomalies for Five Geophysical Parameters
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rundle, J.B.; Stein, S.; Donnellan, A.; Turcotte, D.L.; Klein, W.; Saylor, C. The complex dynamics of earthquake fault systems: New approaches to forecasting and nowcasting of earthquakes. Rep. Prog. Phys. 2021, 84, 076801. [Google Scholar] [CrossRef] [PubMed]
- Sykes, L.R. Intermediate- and long-term earthquake prediction. Proc. Natl. Acad. Sci. USA 1996, 93, 3732. [Google Scholar] [CrossRef] [PubMed]
- Falcone, G.; Spassiani, I.; Ashkenazy, Y.; Shapira, A.; Hofstetter, R.; Havlin, S.; Marzocchi, W. An Operational Earthquake Forecasting Experiment for Israel: Preliminary Results. Front. Earth Sci. 2021, 9, 729282. [Google Scholar] [CrossRef]
- Jiao, Z.-H.; Zhao, J.; Shan, X. Pre-seismic anomalies from optical satellite observations: A review. Nat. Hazards Earth Syst. Sci. 2018, 18, 1013–1036. [Google Scholar] [CrossRef]
- De Santis, A.; De Franceschi, G.; Spogli, L.; Perrone, L.; Alfonsi, L.; Qamili, E.; Cianchini, G.; Di Giovambattista, R.; Salvi, S.; Filippi, E.; et al. Geospace perturbations induced by the Earth: The state of the art and future trends. Phys. Chem. Earth Parts A/B/C 2015, 85–86, 17–33. [Google Scholar] [CrossRef]
- Satti, M.S.; Ehsan, M.; Abbas, A.; Shah, M.; de Oliveira-Júnior, J.F.; Naqvi, N.A. Atmospheric and ionospheric precursors associated with M ≥ 6.5 earthquakes from multiple satellites. J. Atmos. Sol.-Terr. Phys. 2022, 227, 105802. [Google Scholar] [CrossRef]
- Shah, M.; Ehsan, M.; Abbas, A.; Ahmed, A.; Jamjareegulgarn, P. Possible Thermal Anomalies Associated With Global Terrestrial Earthquakes During 2000–2019 Based on MODIS-LST. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Salh, H.; Muhammad, A.; Ghafar, M.M.; Külahcı, F. Potential utilization of air temperature, total electron content, and air relative humidity as possible earthquake precursors: A case study of Mexico M7.4 earthquake. J. Atmos. Sol.-Terr. Phys. 2022, 237, 105927. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Shen, X.; Campuzano, S.A.; Perrone, L.; Piscini, A.; Di Giovambattista, R.; Jin, S.; Ippolito, A.; Cianchini, G.; et al. Possible Lithosphere-Atmosphere-Ionosphere Coupling effects prior to the 2018 Mw = 7.5 Indonesia earthquake from seismic, atmospheric and ionospheric data. J. Asian Earth Sci. 2020, 188, 104097. [Google Scholar] [CrossRef]
- Console, R. Testing earthquake forecast hypotheses. Tectonophysics 2001, 338, 261–268. [Google Scholar] [CrossRef]
- Geller, R.J. Earthquake prediction: A critical review. Geophys. J. Int. 1997, 131, 425–450. [Google Scholar] [CrossRef]
- Chen, H.; Qin, S.; Xue, L.; Yang, B.; Zhang, K. Universal precursor seismicity pattern before locked-segment rupture and evolutionary rule for landmark earthquakes. Geosci. Front. 2022, 13, 101314. [Google Scholar] [CrossRef]
- Jordan, T.H.; Chen, Y.-T.; Gasparini, P.; Madariaga, R.; Main, I.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka, K.; Zschau, J. Operational earthquake forecasting: State of Knowledge and Guidelines for Utilization. Ann. Geophys. 2011, 54, 316–391. [Google Scholar]
- Jiao, Z.; Hao, Y.; Shan, X. A Spatially Self-Adaptive Multiparametric Anomaly Identification Scheme Based on Global Strong Earthquakes. Remote Sens. 2023, 15, 3803. [Google Scholar] [CrossRef]
- Fu, C.-C.; Lee, L.-C.; Ouzounov, D.; Jan, J.-C. Earth’s Outgoing Longwave Radiation Variability Prior to M ≥ 6.0 Earthquakes in the Taiwan Area During 2009–2019. Front. Earth Sci. 2020, 8, 364. [Google Scholar] [CrossRef]
- Pavlidou, E.; van der Meijde, M.; van der Werff, H.; Hecker, C. Time Series Analysis of Land Surface Temperatures in 20 Earthquake Cases Worldwide. Remote Sens. 2018, 11, 61. [Google Scholar] [CrossRef]
- Fidani, C. West Pacific Earthquake Forecasting Using NOAA Electron Bursts With Independent L-Shells and Ground-Based Magnetic Correlations. Front. Earth Sci. 2021, 9, 673105. [Google Scholar] [CrossRef]
- Shen, Z.-K.; Jackson, D.D.; Kagan, Y.Y. Implications of Geodetic Strain Rate for Future Earthquakes, with a Five-Year Forecast of M5 Earthquakes in Southern California. Seismol. Res. Lett. 2007, 78, 116–120. [Google Scholar] [CrossRef]
- Jackson, D.D.; Kagan, Y.Y. Testable Earthquake Forecasts for 1999. Seismol. Res. Lett. 1999, 70, 393–403. [Google Scholar] [CrossRef]
- Petersen, M.D.; Cao, T.; Campbell, K.W.; Frankel, A.D. Time-independent and Time-dependent Seismic Hazard Assessment for the State of California: Uniform California Earthquake Rupture Forecast Model 1.0. Seismol. Res. Lett. 2007, 78, 99–109. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; Zavala, J.L.C.; Urias, C.L.; Trejo Soto, M.E.; Aggarwal, S.P. A combined approach using b-value and ionospheric GPS-TEC for large earthquake precursor detection: A case study for the Colima earthquake of 7.7 Mw, Mexico. Acta Geod. Et Geophys. 2023, 58, 515–538. [Google Scholar] [CrossRef]
- Field, E.H.; Jordan, T.H.; Page, M.T.; Milner, K.R.; Shaw, B.E.; Dawson, T.E.; Biasi, G.P.; Parsons, T.; Hardebeck, J.L.; Michael, A.J.; et al. A Synoptic View of the Third Uniform California Earthquake Rupture Forecast (UCERF3). Seismol. Res. Lett. 2017, 88, 1259–1267. [Google Scholar] [CrossRef]
- Fidani, C.; Gherardi, F.; Facca, G.; Pierotti, L. Correlation between small earthquakes and CO2 anomalies in spring waters: A statistical experiment on the probability of seismic occurrence. Front. Earth Sci. 2023, 11, 1128949. [Google Scholar] [CrossRef]
- Wei, G.; Chen, K.; Meng, H. Bayesian Inversion of Finite-Fault Earthquake Slip Model Using Geodetic Data, Solving for Non-Planar Fault Geometry, Variable Slip, and Data Weighting. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025225. [Google Scholar] [CrossRef]
- Marzocchi, W.; Zechar, J.D.; Jordan, T.H. Bayesian Forecast Evaluation and Ensemble Earthquake Forecasting. Bull. Seismol. Soc. Am. 2012, 102, 2574–2584. [Google Scholar] [CrossRef]
- Darzi, A.; Halldorsson, B.; Hrafnkelsson, B.; Vogfjörð, K.S. Short-term Bayesian ETAS spatiotemporal forecasting of the Ölfus 2008 earthquake sequence in Iceland. Tectonophysics 2022, 839, 229522. [Google Scholar] [CrossRef]
- Dong, E.; Shcherbakov, R.; Goda, K. Testing the forecasting skills of aftershock models using a Bayesian framework. Front. Appl. Math. Stat. 2023, 9, 1126511. [Google Scholar] [CrossRef]
- Jaumé, S.C.; Sykes, L.R. Evolving Towards a Critical Point: A Review of Accelerating Seismic Moment/Energy Release Prior to Large and Great Earthquakes. In Seismicity Patterns, their Statistical Significance and Physical Meaning; Wyss, M., Shimazaki, K., Ito, A., Eds.; Birkhäuser: Basel, Switzerland, 1999; pp. 279–305. [Google Scholar]
- Jiao, Z.; Shan, X. Pre-Seismic Temporal Integrated Anomalies from Multiparametric Remote Sensing Data. Remote Sens. 2022, 14, 2343. [Google Scholar] [CrossRef]
- Jenkins, A.P.; Biggs, J.; Rust, A.C.; Rougier, J.C. Decadal Timescale Correlations Between Global Earthquake Activity and Volcanic Eruption Rates. Geophys. Res. Lett. 2021, 48, e2021GL093550. [Google Scholar] [CrossRef]
- Jiao, Z.-H.; Shan, X. Statistical framework for the evaluation of earthquake forecasting: A case study based on satellite surface temperature anomalies. J. Asian Earth Sci. 2021, 211, 104710. [Google Scholar] [CrossRef]
- Chahine, M.T.; Pagano, T.S.; Aumann, H.H.; Atlas, R.; Barnet, C.; Blaisdell, J.; Chen, L.; Divakarla, M.; Fetzer, E.J.; Goldberg, M.; et al. AIRS: Improving weather forecasting and providing new data on greenhouse gases. Bull. Am. Meteorol. Soc 2006, 87, 911–926. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Gerstenberger, M.C.; Wiemer, S.; Jackson, D.D.; Rhoades, D.A. Earthquake Likelihood Model Testing. Seismol. Res. Lett. 2007, 78, 17–29. [Google Scholar] [CrossRef]
- Zechar, J.D.; Jordan, T.H. Testing alarm-based earthquake predictions. Geophys. J. Int. 2008, 172, 715–724. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Ouzounov, D.P.; Karelin, A.V.; Davidenko, D.V. Physical bases of the generation of short-term earthquake precursors: A complex model of ionization-induced geophysical processes in the lithosphere-atmosphere-ionosphere-magnetosphere system. Geomagn. Aeron. 2015, 55, 521–538. [Google Scholar] [CrossRef]
- Katsumata, K.; Nakatani, M. Testing the seismic quiescence hypothesis through retrospective trials of alarm-based earthquake prediction in the Kurile–Japan subduction zone. Earth Planets Space 2021, 73, 100. [Google Scholar] [CrossRef]
- Wu, L.; Qi, Y.; Mao, W.; Lu, J.; Ding, Y.; Peng, B.; Xie, B. Scrutinizing and rooting the multiple anomalies of Nepal earthquake sequence in 2015 with the deviation–time–space criterion and homologous lithosphere–coversphere–atmosphere–ionosphere coupling physics. Nat. Hazards Earth Syst. Sci. 2023, 23, 231–249. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzola, C.; Hattori, K.; Pergola, N.; Tramutoli, V. Statistical Correlation Analysis between Thermal Infrared Anomalies Observed from MTSATs and Large Earthquakes Occurred in Japan (2005–2015). J. Geophys. Res. Solid Earth 2021, 126, e2020JB020108. [Google Scholar] [CrossRef]
- Molchanov, O.; Fedorov, E.; Schekotov, A.; Gordeev, E.; Chebrov, V.; Surkov, V.; Rozhnoi, A.; Andreevsky, S.; Iudin, D.; Yunga, S.; et al. Lithosphere-atmosphere-ionosphere coupling as governing mechanism for preseismic short-term events in atmosphere and ionosphere. Nat. Hazards Earth Syst. Sci 2004, 4, 757–767. [Google Scholar] [CrossRef]
- Garthwaite, P.H.; Mubwandarikwa, E. Selection of Weights for Weighted Model Averaging. Aust. N. Z. J. Stat. 2010, 52, 363–382. [Google Scholar] [CrossRef]
- Wang, K.; Rogers, G.C. Earthquake Preparedness Should Not Fluctuate on a Daily or Weekly Basis. Seismol. Res. Lett. 2014, 85, 569–571. [Google Scholar] [CrossRef]
- Jordan, T.H.; Jones, L.M. Operational Earthquake Forecasting: Some Thoughts on Why and How. Seismol. Res. Lett. 2010, 81, 571–574. [Google Scholar] [CrossRef]
- Tariq, M.A.; Shah, M.; Hernández-Pajares, M.; Iqbal, T. Pre-earthquake ionospheric anomalies before three major earthquakes by GPS-TEC and GIM-TEC data during 2015–2017. Adv. Space Res. 2019, 63, 2088–2099. [Google Scholar] [CrossRef]
- Shah, M.; Jin, S. Statistical characteristics of seismo-ionospheric GPS TEC disturbances prior to global Mw≥5.0 earthquakes (1998–2014). J. Geodyn. 2015, 92, 42–49. [Google Scholar] [CrossRef]
- Wang, T.; Griffin, J.D.; Brenna, M.; Fletcher, D.; Zeng, J.; Stirling, M.; Dillingham, P.W.; Kang, J. Earthquake forecasting from paleoseismic records. Nat Commun. 2024, 15, 1944. [Google Scholar] [CrossRef]
- Tramutoli, V.; Corrado, R.; Filizzola, C.; Genzano, N.; Lisi, M.; Pergola, N. From visual comparison to Robust Satellite Techniques: 30 years of thermal infrared satellite data analyses for the study of earthquake preparation phases. Boll. Geofis. Teor. Appl. 2015, 56, 167–202. [Google Scholar]
- Tramutoli, V.; Di Bello, G.; Pergola, N.; Piscitelli, S. Robust satellite techniques for remote sensing of seismically active areas. Ann. Geophys. 2001, 44, 295–312. [Google Scholar] [CrossRef]
- Genzano, N.; Filizzola, C.; Paciello, R.; Pergola, N.; Tramutoli, V. Robust Satellite Techniques (RST) for monitoring earthquake prone areas by satellite TIR observations: The case of 1999 Chi-Chi earthquake (Taiwan). J. Asian Earth Sci. 2015, 114, 289–298. [Google Scholar] [CrossRef]
- Genzano, N.; Aliano, C.; Corrado, R.; Filizzola, C.; Lisi, M.; Mazzeo, G.; Paciello, R.; Pergola, N.; Tramutoli, V. RST analysis of MSG-SEVIRI TIR radiances at the time of the Abruzzo 6 April 2009 earthquake. Nat. Hazards Earth Syst. Sci. 2009, 9, 2073–2084. [Google Scholar] [CrossRef]
- Chi, C.; Li, C.; Han, Y.; Yu, Z.; Li, X.; Zhang, D. Pre-earthquake anomaly extraction from borehole strain data based on machine learning. Sci. Rep. 2023, 13, 20095. [Google Scholar] [CrossRef]
- Cheng, C.; Hui, C.; Yang, J.; Shen, S. The relationship between heat flow and seismicity in global tectonically active zones. Open Geosci. 2020, 12, 1430–1439. [Google Scholar] [CrossRef]
- Saraf, A.K.; Rawat, V.; Choudhury, S.; Dasgupta, S.; Das, J. Advances in understanding of the mechanism for generation of earthquake thermal precursors detected by satellites. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 373–379. [Google Scholar] [CrossRef]
- Qiang, Z.; Xu, X.; Lin, C. Thermal infrared anomaly precursor of impending earthquakes. Chin. Sci. Bull. 1991, 36, 319–323. [Google Scholar] [CrossRef]
- Wu, L.; Cui, C.; Geng, N.; Wang, J. Remote sensing rock mechanics (RSRM) and associated experimental studies. Int. J. Rock Mech. Min. Sci. 2000, 37, 879–888. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.; Liu, Q.; Guo, Y.; Ren, Y.; Zhuo, Y.; Feng, J. A Potential Mechanism of the Satellite Thermal Infrared Seismic Anomaly Based on Change in Temperature Caused by Stress Variation: Theoretical, Experimental and Field Investigations. Remote Sens. 2022, 14, 5697. [Google Scholar] [CrossRef]
- Ma, J.; Sherman, S.I.; Guo, Y. Identification of meta-instable stress state based on experimental study of evolution of the temperature field during stick-slip instability on a 5° bending fault. Sci. China Earth Sci. 2012, 55, 869–881. [Google Scholar]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F.; Kulahci, I.G.; Cyr, G.; Ling, J.; Winnick, M.; Tregloan-Reed, J.; Freund, M.M. Air ionization at rock surfaces and pre-earthquake signals. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1824–1834. [Google Scholar] [CrossRef]
- Freund, F. Earthquake forewarning—A multidisciplinary challenge from the ground up to space. Acta Geophys. 2013, 61, 775–807. [Google Scholar] [CrossRef]
- Muto, F.; Kasahara, Y.; Hobara, Y.; Hayakawa, M.; Rozhnoi, A.; Solovieva, M.; Molchanov, O.A. Further study on the role of atmospheric gravity waves on the seismo-ionospheric perturbations as detected by subionospheric VLF/LF propagation. Nat. Hazards Earth Syst. Sci 2009, 9, 1111–1118. [Google Scholar] [CrossRef]
- Draz, M.U.; Shah, M.; Jamjareegulgarn, P.; Shahzad, R.; Hasan, A.M.; Ghamry, N.A. Deep Machine Learning Based Possible Atmospheric and Ionospheric Precursors of the 2021 Mw 7.1 Japan Earthquake. Remote Sens. 2023, 15, 1904. [Google Scholar] [CrossRef]

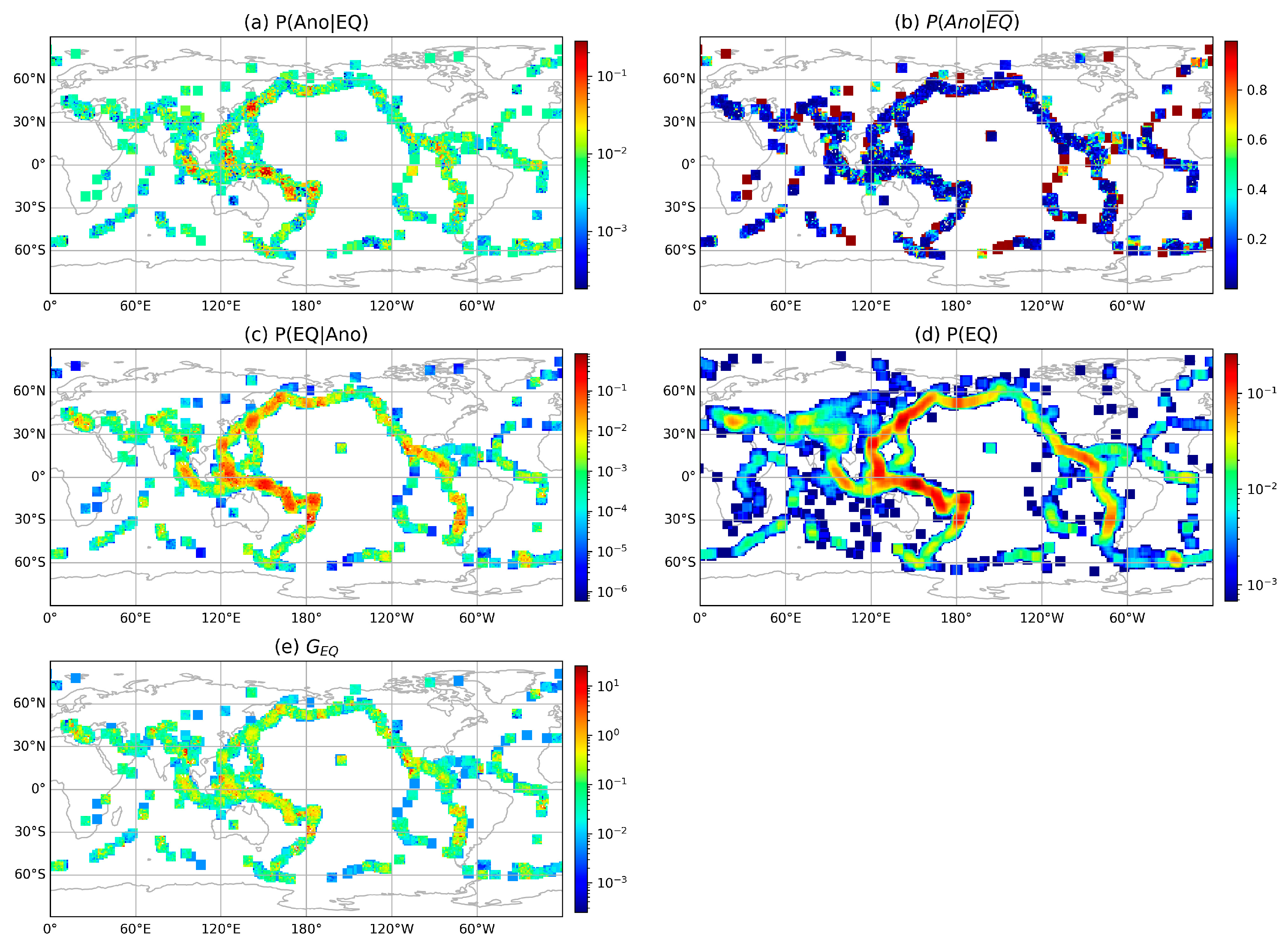
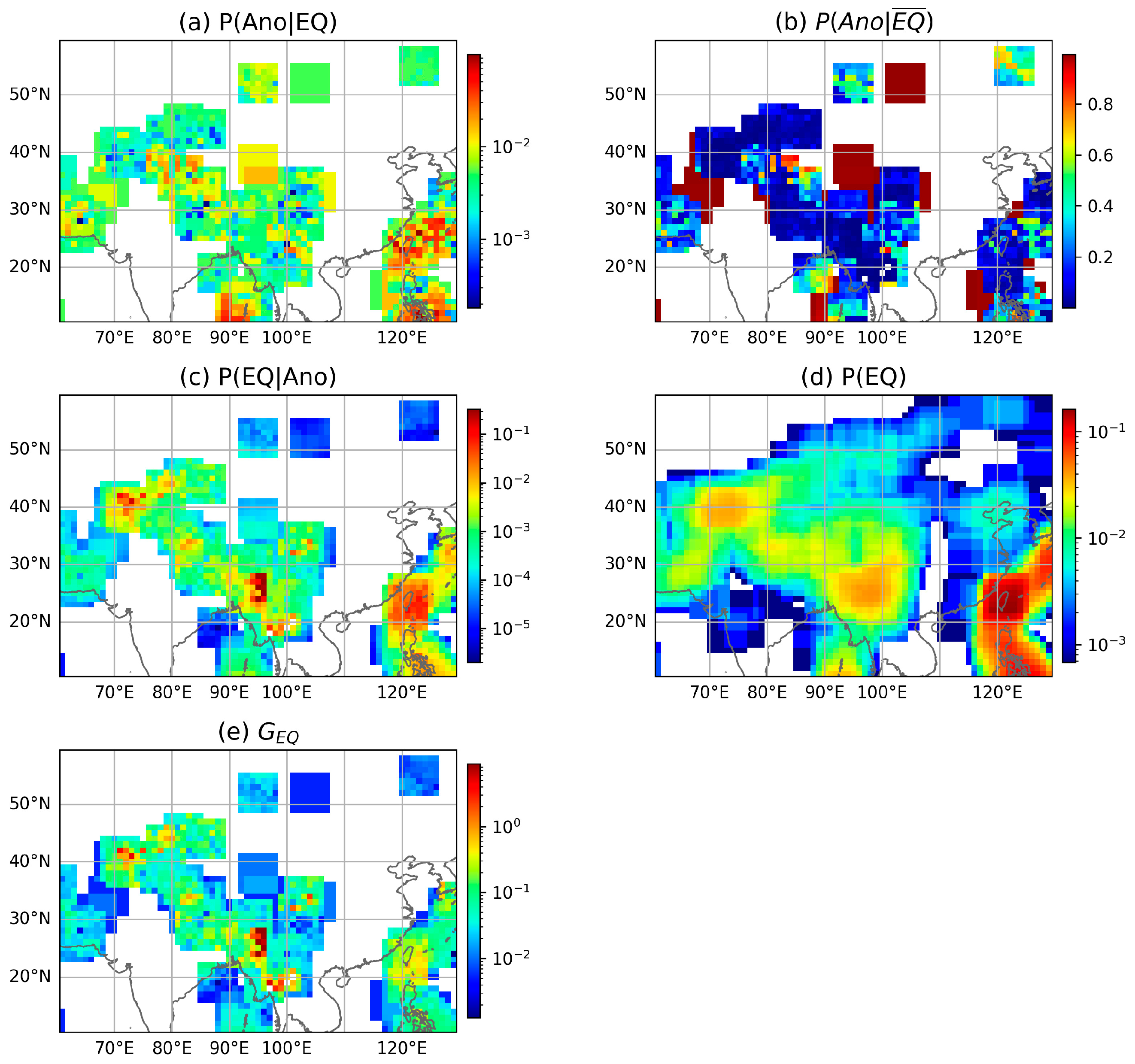
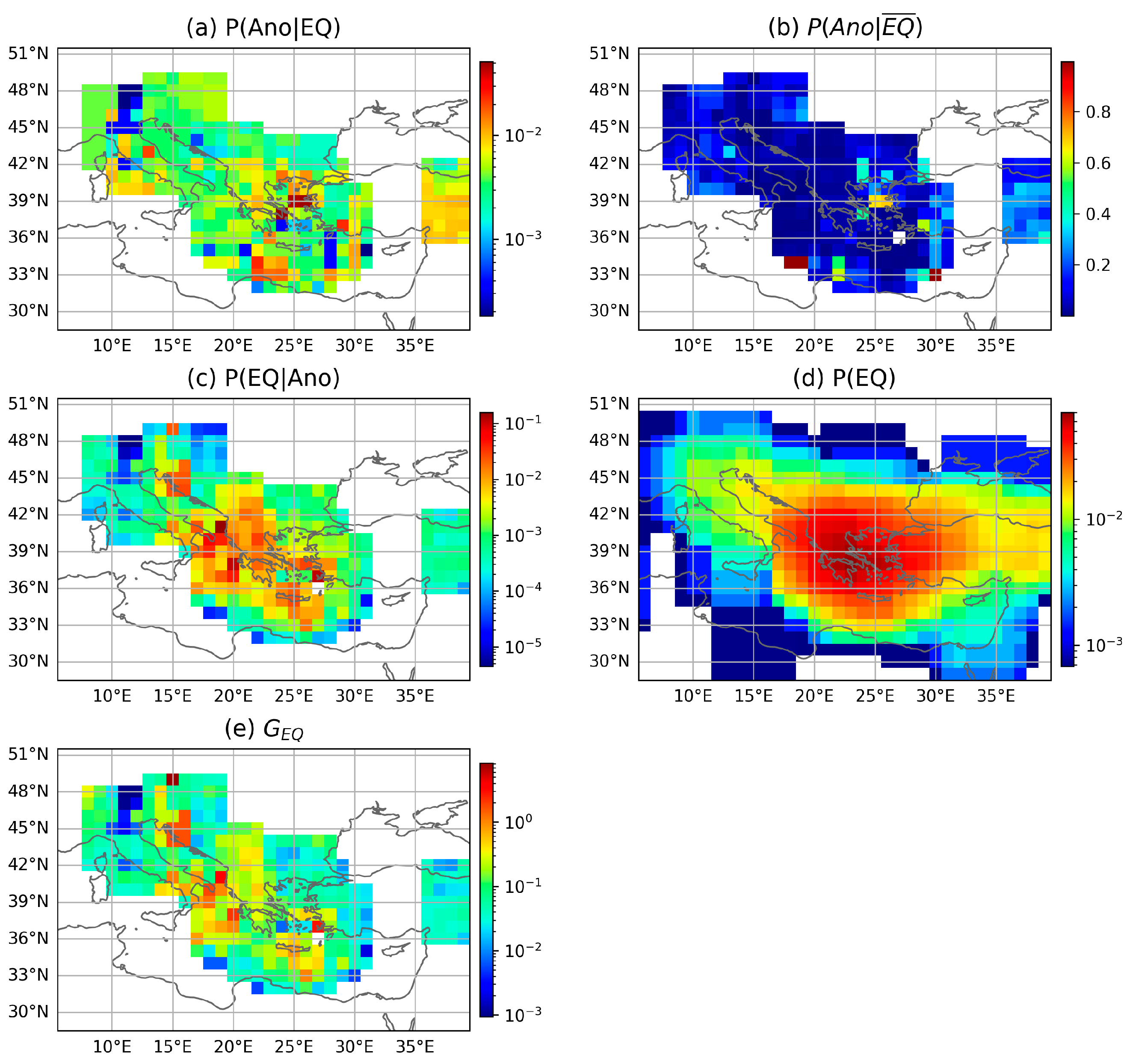
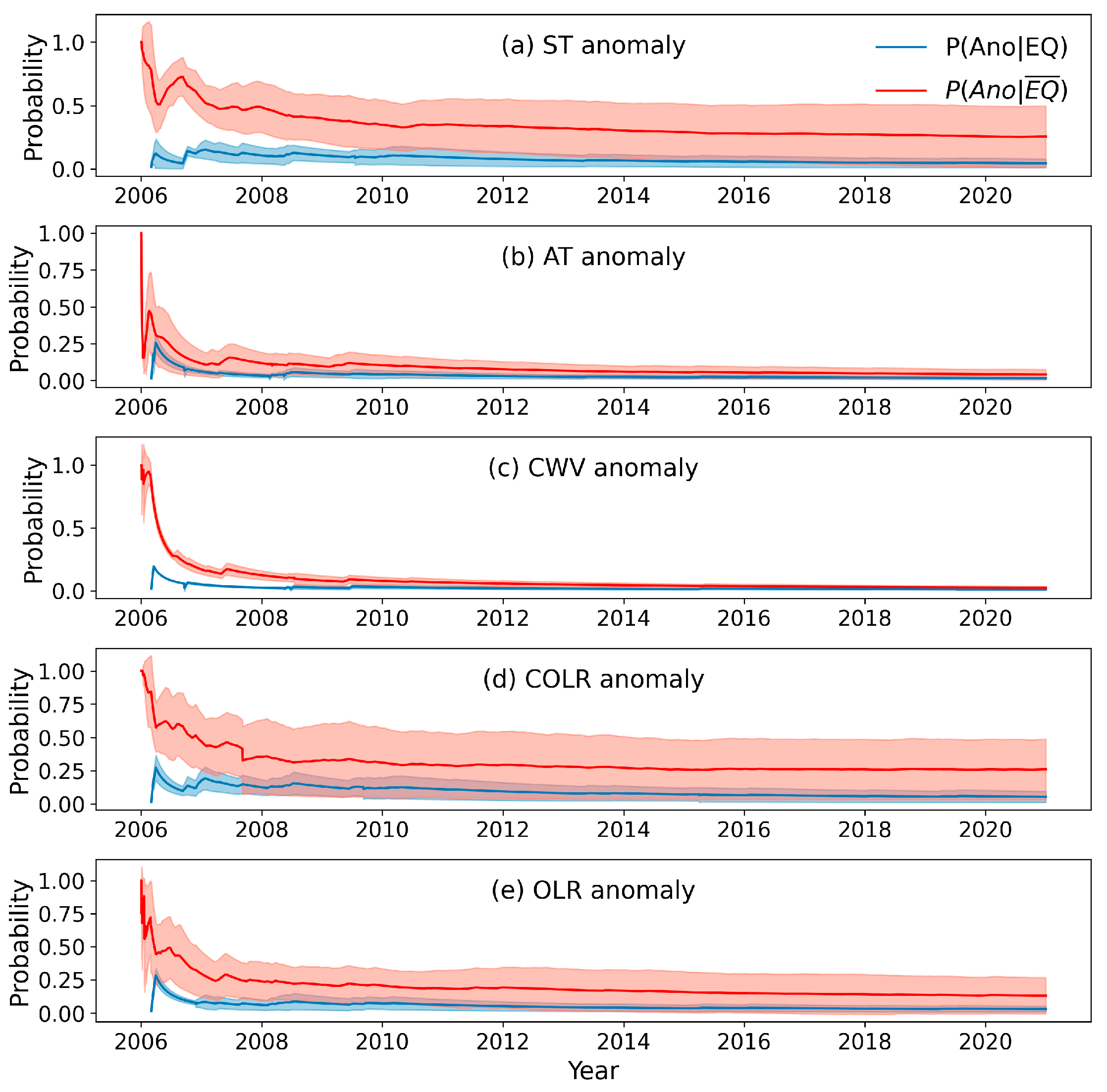
| ID | Time (UTC) | Latitude (°) | Longitude (°) | Depth (km) | Mag. |
|---|---|---|---|---|---|
| EQ01 | 19 Mar. 2021 06:11:27.113 | 31.9244 | 92.9147 | 8 | 5.7 |
| EQ02 | 28 Apr. 2021 02:21:26.221 | 26.7819 | 92.4586 | 34 | 6 |
| EQ03 | 21 May 2021 18:04:13.557 | 34.5884 | 98.2402 | 10 | 7.3 |
| EQ04 | 21 May 2021 13:48:37.268 | 25.7444 | 100.0155 | 9 | 6.1 |
| EQ05 | 10 Jul. 2021 02:14:43.154 | 38.9169 | 70.5539 | 12.84 | 5.7 |
| EQ06 | 25 Nov. 2021 23:45:41.780 | 22.8217 | 93.52 | 42.72 | 6.2 |
| EQ07 | 24 Dec. 2021 13:43:22.983 | 22.3639 | 101.6878 | 10 | 5.7 |
| EQ08 | 7 Jan. 2022 17:45:30.751 | 37.8152 | 101.2775 | 13 | 6.6 |
| EQ09 | 23 Jan. 2022 02:21:19.926 | 38.4613 | 97.3425 | 10 | 5.6 |
| EQ10 | 25 Mar. 2022 16:21:04.052 | 38.5196 | 97.2683 | 10 | 5.7 |
| EQ11 | 1 Jun. 2022 09:00:08.122 | 30.4155 | 102.9892 | 10 | 5.9 |
| EQ12 | 9 Jun. 2022 17:28:37.438 | 32.3747 | 101.9033 | 14.37 | 5.9 |
| EQ13 | 9 Jun. 2022 16:03:26.522 | 32.3152 | 101.8363 | 10.14 | 5.6 |
| EQ14 | 21 Jul. 2022 17:07:25.214 | 21.155 | 99.8813 | 5 | 5.9 |
| EQ15 | 5 Sep. 2022 04:52:19.634 | 29.6856 | 102.2278 | 12 | 6.6 |
| EQ16 | 8 Nov. 2022 20:27:23.418 | 29.2742 | 81.1486 | 18.082 | 5.7 |
| EQ17 | 28 Dec. 2022 17:16:36.243 | 41.8052 | 79.5408 | 10 | 5.6 |
| ID | ST | AT | CWV | COLR | OLR | Count |
|---|---|---|---|---|---|---|
| EQ01 | 1 | 1 | 0 | 1 | 1 | 4 |
| EQ02 | 0 | 1 | 0 | 1 | 0 | 2 |
| EQ03 | 0 | 1 | 1 | 1 | 1 | 4 |
| EQ04 | 0 | 0 | 1 | 0 | 1 | 2 |
| EQ05 | 1 | 0 | 1 | 1 | 1 | 4 |
| EQ06 | 0 | 1 | 0 | 0 | 0 | 1 |
| EQ07 | 0 | 0 | 1 | 0 | 0 | 1 |
| EQ08 | 0 | 1 | 1 | 0 | 0 | 2 |
| EQ09 | 0 | 0 | 1 | 0 | 0 | 1 |
| EQ10 | 0 | 0 | 1 | 0 | 0 | 1 |
| EQ11 | 1 | 1 | 0 | 1 | 1 | 4 |
| EQ12 | 1 | 1 | 0 | 1 | 1 | 4 |
| EQ13 | 1 | 1 | 0 | 0 | 0 | 2 |
| EQ14 | 1 | 1 | 0 | 0 | 0 | 2 |
| EQ15 | 1 | 1 | 0 | 1 | 0 | 3 |
| EQ16 | 0 | 0 | 1 | 1 | 0 | 2 |
| EQ17 | 0 | 1 | 1 | 0 | 0 | 2 |
| Count | 7 | 11 | 9 | 8 | 6 | 41 |
| ST | AT | CWV | COLR | OLR | |
|---|---|---|---|---|---|
| ST | 1.000 | 0.360 | 0.415 | 0.385 | 0.354 |
| AT | - | 1.000 | 0.326 | 0.369 | 0.372 |
| CWV | - | - | 1.000 | 0.387 | 0.349 |
| COLR | - | - | - | 1.000 | 0.363 |
| OLR | - | - | - | - | 1.000 |
| Weight | 0.196 | 0.204 | 0.200 | 0.197 | 0.203 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, Z.; Shan, X. A Bayesian Approach for Forecasting the Probability of Large Earthquakes Using Thermal Anomalies from Satellite Observations. Remote Sens. 2024, 16, 1542. https://doi.org/10.3390/rs16091542
Jiao Z, Shan X. A Bayesian Approach for Forecasting the Probability of Large Earthquakes Using Thermal Anomalies from Satellite Observations. Remote Sensing. 2024; 16(9):1542. https://doi.org/10.3390/rs16091542
Chicago/Turabian StyleJiao, Zhonghu, and Xinjian Shan. 2024. "A Bayesian Approach for Forecasting the Probability of Large Earthquakes Using Thermal Anomalies from Satellite Observations" Remote Sensing 16, no. 9: 1542. https://doi.org/10.3390/rs16091542
APA StyleJiao, Z., & Shan, X. (2024). A Bayesian Approach for Forecasting the Probability of Large Earthquakes Using Thermal Anomalies from Satellite Observations. Remote Sensing, 16(9), 1542. https://doi.org/10.3390/rs16091542








