Omnidirectional Manipulation of Microparticles on a Platform Subjected to Circular Motion Applying Dynamic Dry Friction Control
Abstract
:1. Introduction
2. Methodology
2.1. Mathematical Model
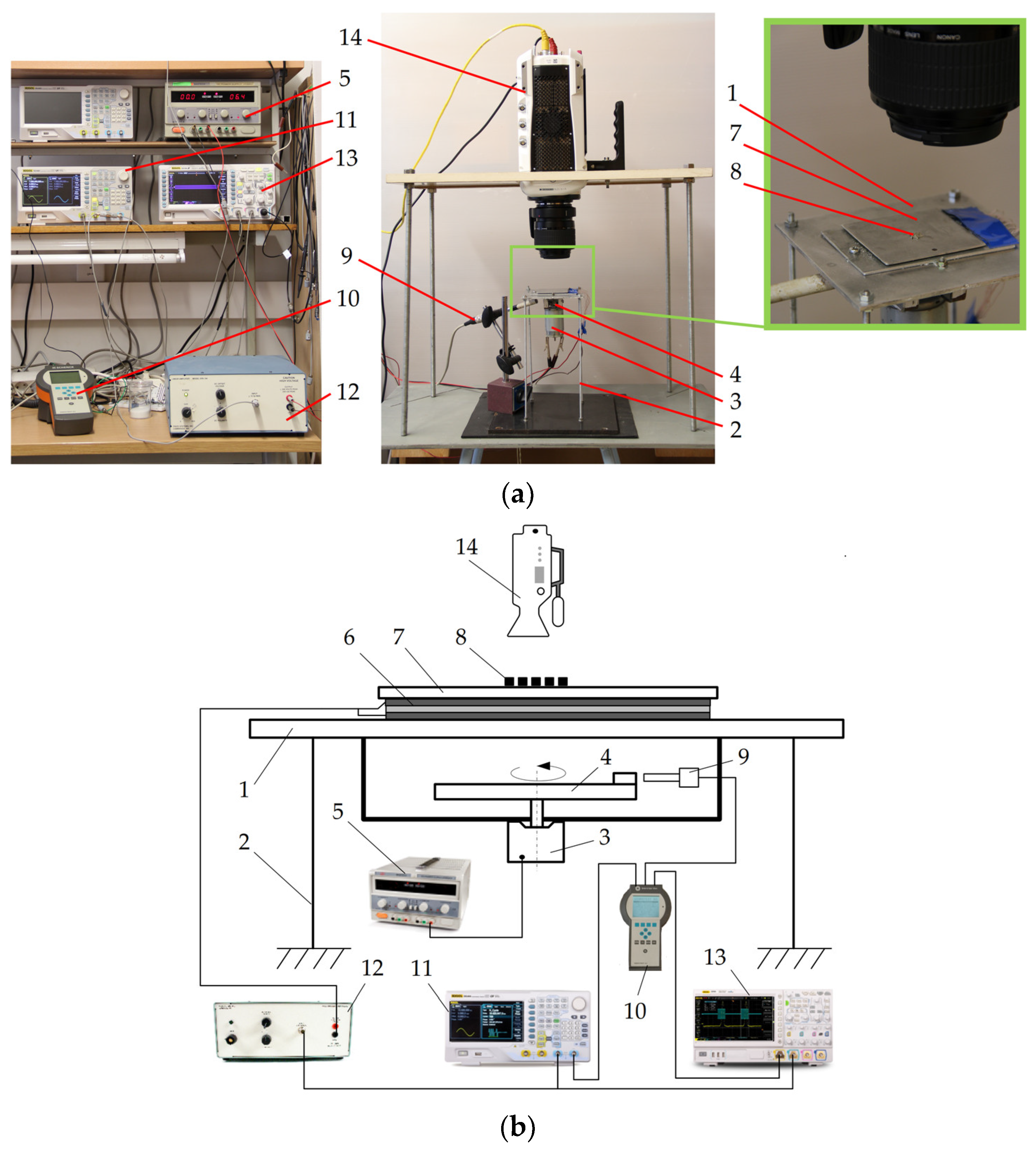
2.2. Methodology of Experimental Investigation
3. Results
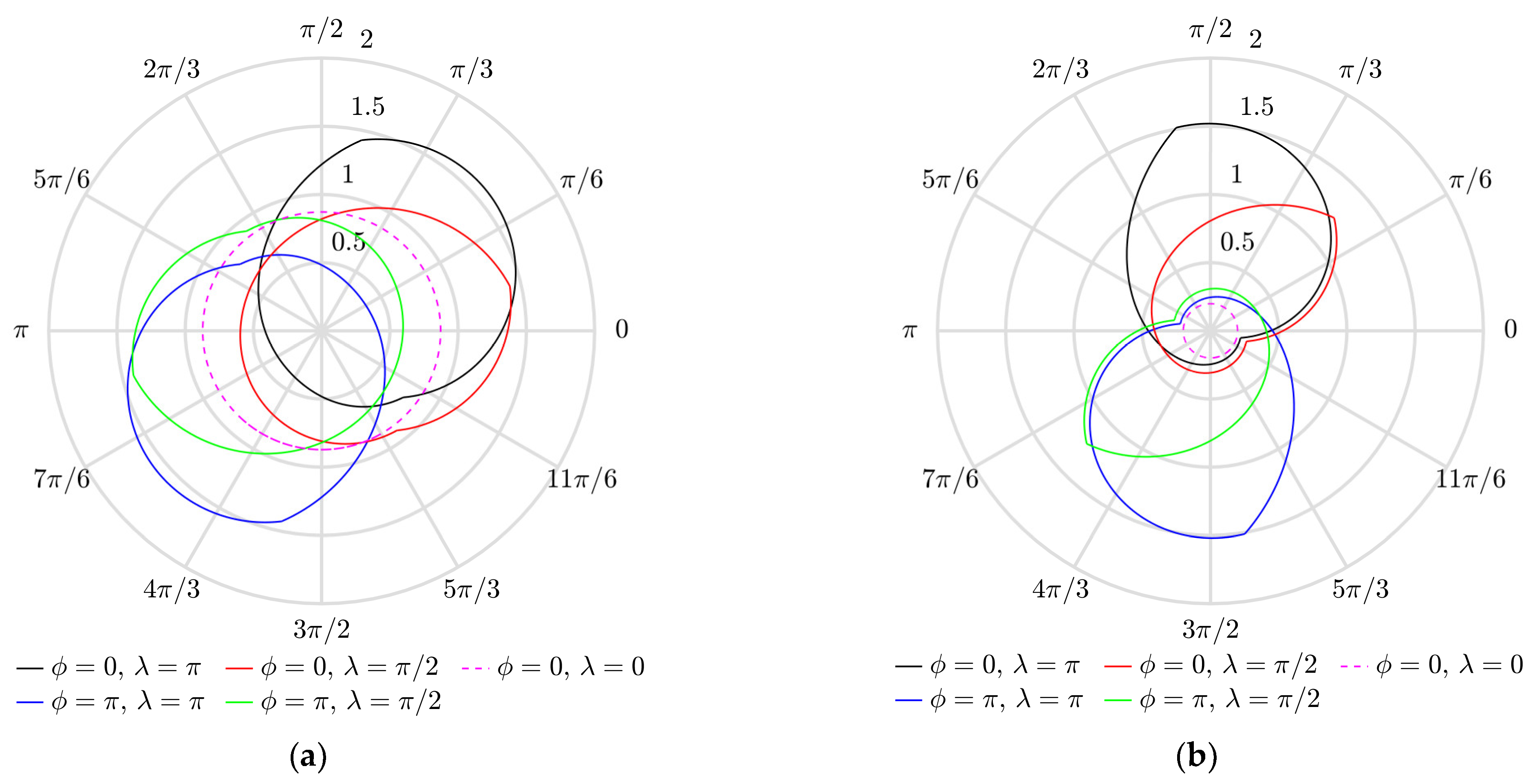
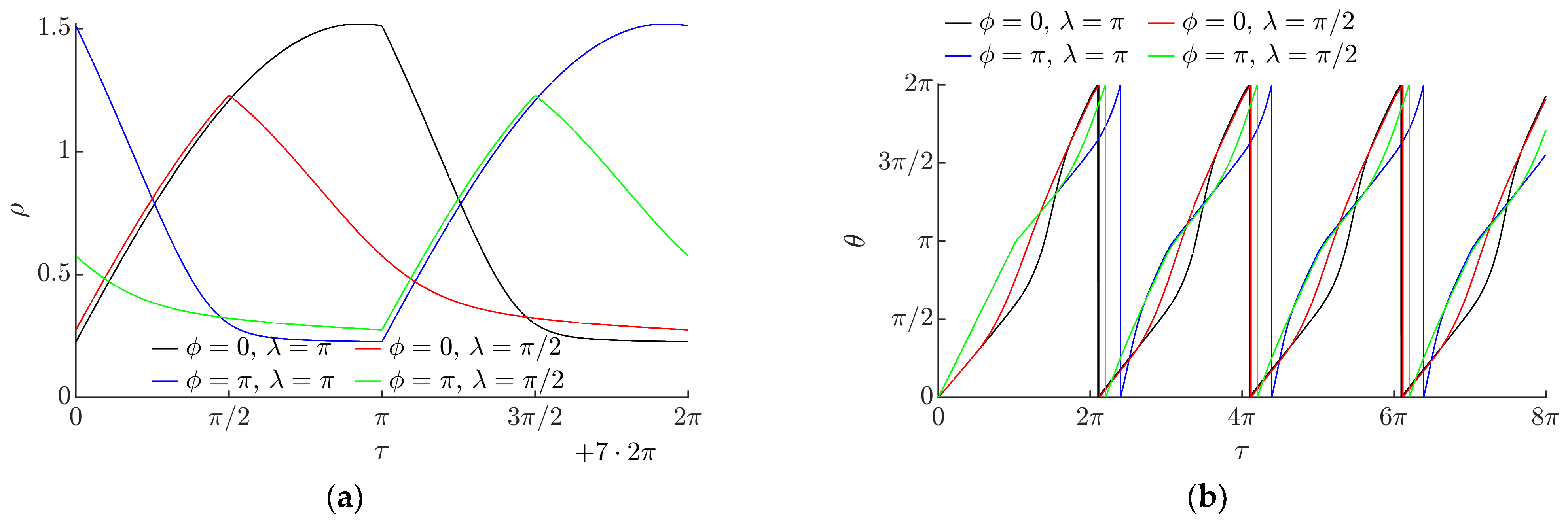
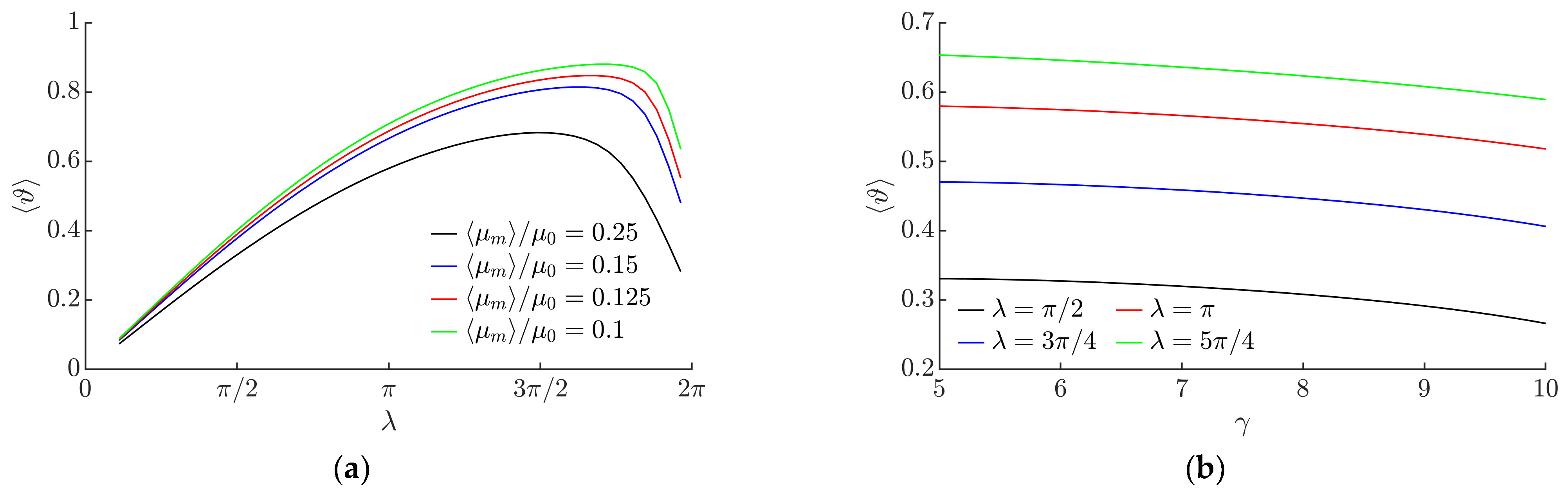
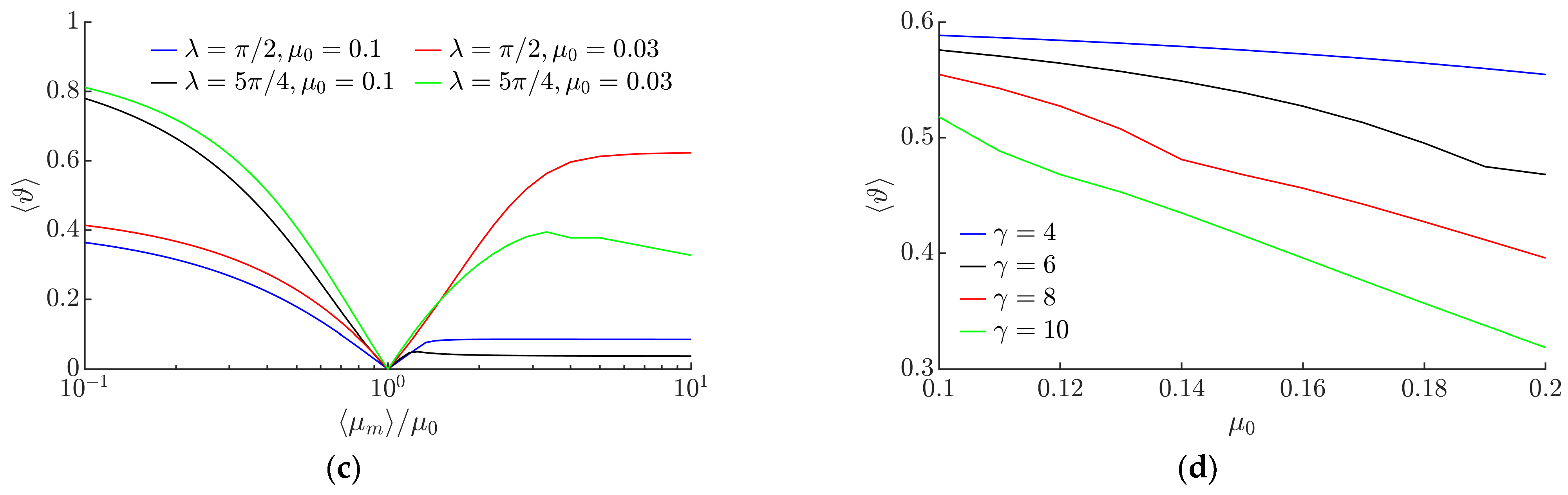
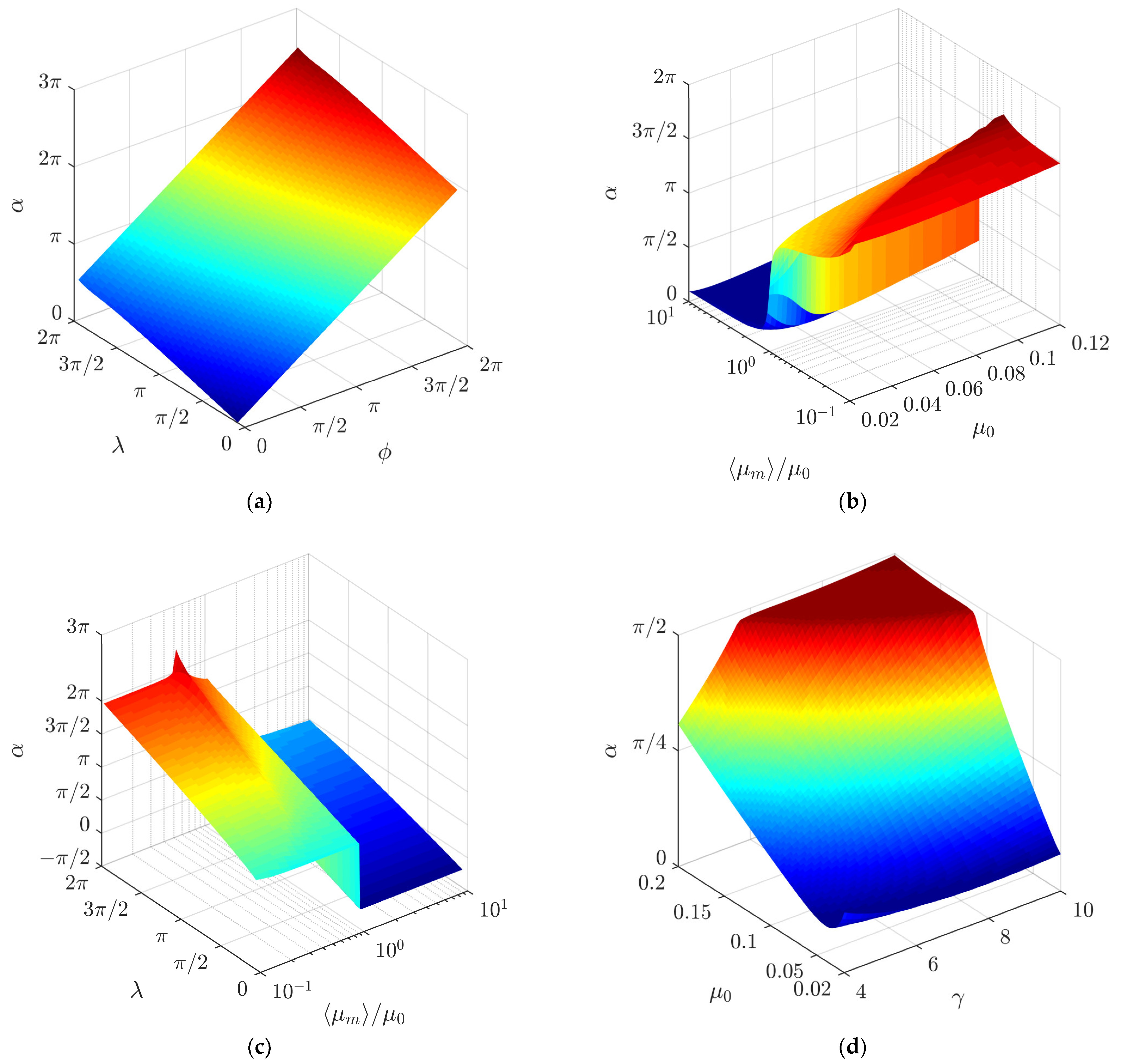
3.1. Modeling Results
3.2. Experimental Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Warnat, S.; King, H.; Wasay, A.; Sameoto, D.; Hubbard, T. Direct integration of MEMS, dielectric pumping and cell manipulation with reversibly bonded gecko adhesive microfluidics. J. Micromech. Microeng. 2016, 26, 097001. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Survey on recent designs of compliant micro-/nano-positioning stages. Actuators 2018, 7, 5. [Google Scholar] [CrossRef] [Green Version]
- Janusas, T.; Urbaite, S.; Palevicius, A.; Nasiri, S.; Janusas, G. Biologically Compatible Lead-Free Piezoelectric Composite for Acoustophoresis Based Particle Manipulation Techniques. Sensors 2021, 21, 483. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Ding, Y.; Long, H.; Guan, Y.; Lu, X.; Wang, Y.; Yang, L. Simulation of Optical Nano-Manipulation with Metallic Single and Dual Probe Irradiated by Polarized Near-Field Laser. Appl. Sci. 2022, 12, 815. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, T.; Zhang, Q.; Huang, J.; Hu, Q.; Li, Y.; Wang, C.; Zheng, H. 3D Acoustic Manipulation of Living Cells and Organisms Based on 2D Array. IEEE Trans. Biomed. Eng. 2022. [Google Scholar] [CrossRef]
- Chircov, C.; Grumezescu, A.M. Microelectromechanical Systems (MEMS) for Biomedical Applications. Micromachines 2022, 13, 164. [Google Scholar] [CrossRef]
- Rashid, N.F.A.; Deivasigamani, R.; Wee, M.F.; Hamzah, A.A.; Buyong, M.R. Integration of a Dielectrophoretic Tapered Aluminum Microelectrode Array with a Flow Focusing Technique. Sensors 2021, 21, 4957. [Google Scholar] [CrossRef]
- Ahmad, B.; Chambon, H.; Tissier, P.; Bolopion, A. Laser Actuated Microgripper Using Optimized Chevron-Shaped Actuator. Micromachines 2021, 12, 1487. [Google Scholar] [CrossRef]
- Fontana, G.; Ruggeri, S.; Legnani, G.; Fassi, I. Performance assessment of a modular device for micro-sphere singularization. Precis. Eng. 2021, 71, 29–35. [Google Scholar] [CrossRef]
- Potekhina, A.; Voicu, R.; Muller, R.; Al-Zandi, M.H.; Wang, C. Design and characterization of a polymer electrothermal microgripper with a polynomial flexure for efficient operation and studies of moisture effect on negative deflection. Microsyst. Technol. 2021, 27, 2723–2731. [Google Scholar] [CrossRef]
- Zore, A.; Čerin, R.; Munih, M. Impact of a Robot Manipulation on the Dimensional Measurements in an SPC-Based Robot Cell. Appl. Sci. 2021, 11, 6397. [Google Scholar] [CrossRef]
- Tiwari, B.; Billot, M.; Clévy, C.; Agnus, J.; Piat, E.; Lutz, P. A Two-Axis Piezoresistive Force Sensing Tool for Microgripping. Sensors 2021, 21, 6059. [Google Scholar] [CrossRef] [PubMed]
- Ragulskis, K.; Spruogis, B.; Bogdevičius, M.; Matuliauskas, A.; Mištinas, V.; Ragulskis, L. Mechanical systems of precise robots with vibrodrives, in which the direction of the exciting force coincides with the line of relative motion of the system. Mechanika 2021, 27, 408–414. [Google Scholar] [CrossRef]
- Fan, C.; Shirafuji, S.; Ota, J. Modal Planning for Cooperative Non-Prehensile Manipulation by Mobile Robots. Appl. Sci. 2019, 9, 462. [Google Scholar] [CrossRef] [Green Version]
- Feemster, M.; Piepmeier, J.A.; Biggs, H.; Yee, S.; ElBidweihy, H.; Firebaugh, S.L. Autonomous microrobotic manipulation using visual servo control. Micromachines 2020, 11, 132. [Google Scholar] [CrossRef] [Green Version]
- Rizwan, M.; Shiakolas, P.S. On the optimum synthesis of a microconveyor platform for micropart translocation using differential evolution. Inverse Probl. Sci. Eng. 2013, 21, 1335–1351. [Google Scholar] [CrossRef]
- Ablay, G. Model-Free Controller Designs for a Magnetic Micromanipulator. J. Dyn. Syst. Meas. Control 2021, 143, 031003. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Yan, P. Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner. Micromachines 2021, 12, 212. [Google Scholar] [CrossRef]
- Ferrara-Bello, A.; Vargas-Chable, P.; Vera-Dimas, G.; Vargas-Bernal, R.; Tecpoyotl-Torres, M. XYZ Micropositioning System Based on Compliance Mechanisms Fabricated by Additive Manufacturing. Actuators 2021, 10, 68. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, X.; Kojima, M.; Huang, Q.; Arai, T. Advances in Micromanipulation Actuated by Vibration-Induced Acoustic Waves and Streaming Flow. Appl. Sci. 2020, 10, 1260. [Google Scholar] [CrossRef] [Green Version]
- Röthlisberger, M.; Schuck, M.; Kulmer, L.; Kolar, J.W. Contactless Picking of Objects Using an Acoustic Gripper. Actuators 2021, 10, 70. [Google Scholar] [CrossRef]
- Wijaya, H.; Latifi, K.; Zhou, Q. Two-dimensional manipulation in mid-air using a single transducer acoustic levitator. Micromachines 2019, 10, 257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Wu, L.; Wang, Y. Study on Particle Manipulation in a Metal Internal Channel under Acoustic Levitation. Micromachines 2022, 13, 18. [Google Scholar] [CrossRef] [PubMed]
- Guex, A.G.; Di Marzio, N.; Eglin, D.; Alini, M.; Serra, T. The waves that make the pattern: A review on acoustic manipulation in biomedical research. Mater. Today Bio 2021, 10, 100110. [Google Scholar] [CrossRef]
- Akkoyun, F.; Gucluer, S.; Ozcelik, A. Potential of the acoustic micromanipulation technologies for biomedical research. Biomicrofluidics 2021, 15, 061301. [Google Scholar] [CrossRef]
- Li, J.; Shen, C.; Tony, J.H.; Cummer, S.A. Acoustic tweezer with complex boundary-free trapping and transport channel controlled by shadow waveguides. Sci. Adv. 2021, 7, eabi5502. [Google Scholar] [CrossRef]
- Devendran, C.; Collins, D.J.; Neild, A. The role of channel height and actuation method on particle manipulation in surface acoustic wave (SAW)-driven microfluidic devices. Microfluid. Nanofluidics 2022, 26, 9. [Google Scholar] [CrossRef]
- Reznik, D.; Canny, J.; Goldberg, K. Analysis of part motion on a longitudinally vibrating plate. In Proceedings of the 1997 IEEE/RSJ International Conference on Intelligent Robot and Systems, Grenoble, France, 11 September 1997; IEEE: Piscataway, NJ, USA, 1997; pp. 421–427. [Google Scholar] [CrossRef] [Green Version]
- Mayyas, M. Parallel Manipulation Based on Stick-Slip Motion of Vibrating Platform. Robotics 2020, 9, 86. [Google Scholar] [CrossRef]
- Mayyas, M. Modeling and analysis of vibratory feeder system based on robust stick–slip motion. J. Vib. Control 2021, 10775463211009633. [Google Scholar] [CrossRef]
- Klemiato, M.; Czubak, P. Control of the transport direction and velocity of the two-way reversible vibratory conveyor. Arch. Appl. Mech. 2019, 89, 1359–1373. [Google Scholar] [CrossRef] [Green Version]
- Buzzoni, M.; Battarra, M.; Mucchi, E.; Dalpiaz, G. Motion analysis of a linear vibratory feeder: Dynamic modeling and experimental verification. Mech. Mach. Theory 2017, 114, 98–110. [Google Scholar] [CrossRef]
- Gursky, V.; Krot, P.; Korendiy, V.; Zimroz, R. Dynamic Analysis of an Enhanced Multi-Frequency Inertial Exciter for Industrial Vibrating Machines. Machines 2022, 10, 130. [Google Scholar] [CrossRef]
- Frei, P.U.; Wiesendanger, M.; Büchi, R.; Ruf, L. Simultaneous planar transport of multiple objects on individual trajectories using friction forces. In Distributed Manipulation; Böhringer, K.F., Choset, H., Eds.; Springer: Boston, MA, USA, 2000; pp. 49–64. [Google Scholar] [CrossRef]
- Ihor, V. Vibratory conveying by harmonic longitudinal and polyharmonic normal vibrations of inclined conveying track. J. Vib. Acoust. 2022, 144, 011004. [Google Scholar] [CrossRef]
- Kharkongor, B.; Pohlong, S.S.; Mahato, M.C. Net transport in a periodically driven potential-free system. Physica A Stat. Mech. Appl. 2021, 562, 125341. [Google Scholar] [CrossRef]
- Palencia, J.L.D. Travelling Waves Approach in a Parabolic Coupled System for Modelling the Behaviour of Substances in a Fuel Tank. Appl. Sci. 2021, 11, 5846. [Google Scholar] [CrossRef]
- Cao, H.X.; Jung, D.; Lee, H.; Go, G.; Nan, M.; Choi, E.; Kim, C.; Park, J.; Kang, B. Micromotor Manipulation Using Ultrasonic Active Traveling Waves. Micromachines 2021, 12, 192. [Google Scholar] [CrossRef]
- Zouaghi, A.; Zouzou, N.; Dascalescu, L. Assessment of forces acting on fine particles on a traveling-wave electric field conveyor: Application to powder manipulation. Powder Technol. 2019, 343, 375–382. [Google Scholar] [CrossRef]
- Kumar, A.; DasGupta, A. Generation of circumferential harmonic travelling waves on thin circular plates. J. Sound Vib. 2020, 478, 115343. [Google Scholar] [CrossRef]
- Viswarupachari, C.; DasGupta, A.; Pratik Khastgir, S. Vibration induced directed transport of particles. J. Vib. Acoust. 2012, 134, 051005. [Google Scholar] [CrossRef]
- Mitani, A.; Matsuo, Y. Feeding of microparts along an asymmetric surface using horizontal and symmetric vibrations—Development of asymmetric surfaces using anisotropic etching process of single-crystal silicon. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Thailand, 7–11 December 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 795–800. [Google Scholar] [CrossRef]
- Le, P.H.; Dinh, T.X.; Mitani, A.; Hirai, S. A study on the motion of micro-parts on a saw-tooth surface by the PTV method. J. Dyn. Control Syst. 2012, 6, 73–80. [Google Scholar] [CrossRef] [Green Version]
- Le, P.H.; Mitani, A.; Xuan, T.; Hirai, S. Feed and align microparts on symmetrically vibrating saw-tooth surface. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5282–5286. [Google Scholar] [CrossRef]
- Kilikevičius, S.; Fedaravičius, A.; Daukantienė, V.; Liutkauskienė, K.; Paukštaitis, L. Manipulation of Miniature and Microminiature Bodies on a Harmonically Oscillating Platform by Controlling Dry Friction. Micromachines 2021, 12, 1087. [Google Scholar] [CrossRef] [PubMed]
- Kilikevičius, S.; Fedaravičius, A.; Daukantienė, V.; Liutkauskienė, K. Analysis on Conveying of Miniature and Microparts on a Platform Subjected to Sinusoidal Displacement Cycles with Controlled Dry Friction. Mechanika 2022, 28, 38–44. [Google Scholar] [CrossRef]
- Kilikevičius, S.; Fedaravičius, A. Vibrational Transportation on a Platform Subjected to Sinusoidal Displacement Cycles Employing Dry Friction Control. Sensors 2021, 21, 7280. [Google Scholar] [CrossRef] [PubMed]
- Benad, J.; Nakano, K.; Popov, V.L.; Popov, M. Active control of friction by transverse oscillations. Friction 2019, 7, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Kapelke, S.; Seemann, W. On the effect of longitudinal vibrations on dry friction: Modelling aspects and experimental investigations. Tribol. Lett. 2018, 66, 79. [Google Scholar] [CrossRef]
- Menga, N.; Bottiglione, F.; Carbone, G. Dynamically induced friction reduction in micro-structured interfaces. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Bakšys, B.; Ramanauskytė, K. Vibratory positioning and search of automatically assembled parts on a horizontally vibrating plane. J. Vibroeng. 2009, 11, 56–67. [Google Scholar]
- Kilikevičius, S.; Liutkauskienė, K.; Fedaravičius, A. Nonprehensile Manipulation of Parts on a Horizontal Circularly Oscillating Platform with Dynamic Dry Friction Control. Sensors 2021, 21, 5581. [Google Scholar] [CrossRef]
- Yu, D.; Dai, K.; Zhang, J.; Yang, B.; Zhang, H.; Ma, S. Failure Mechanism of Multilayer Ceramic Capacitors under Transient High Impact. Appl. Sci. 2020, 10, 8435. [Google Scholar] [CrossRef]
- Yau, Y.; Hwu, K.; Shieh, J. Applying FPGA Control with ADC-Free Sampling to Multi-Output Forward Converter. Electronics 2021, 10, 1010. [Google Scholar] [CrossRef]



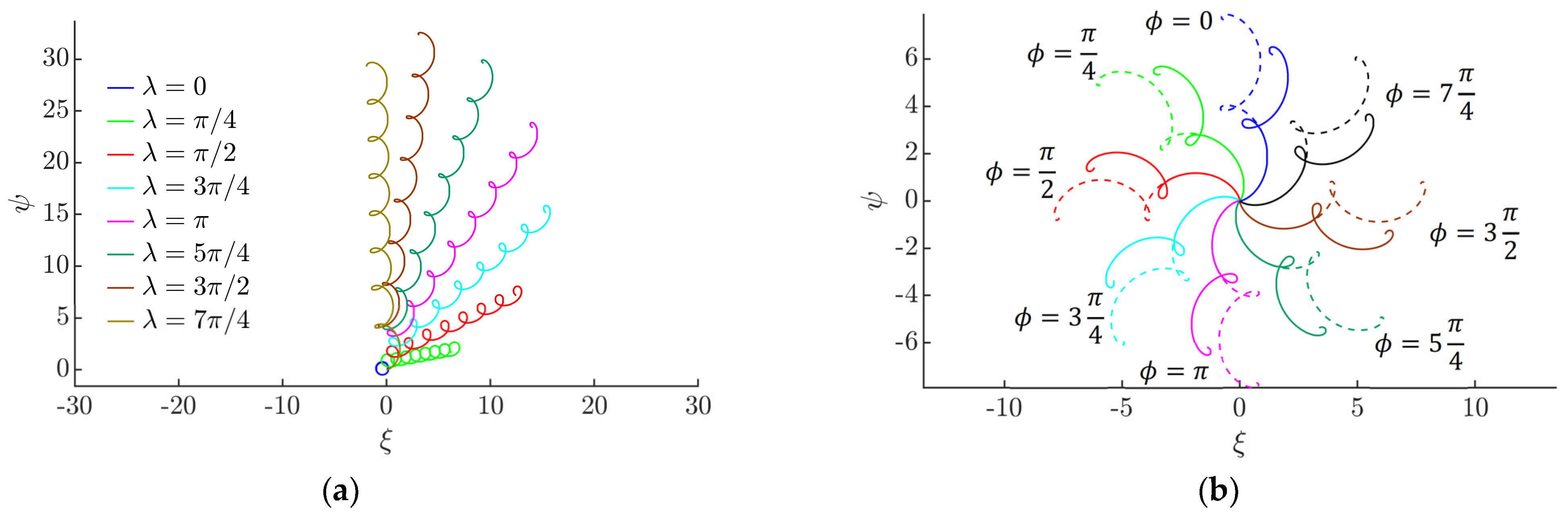



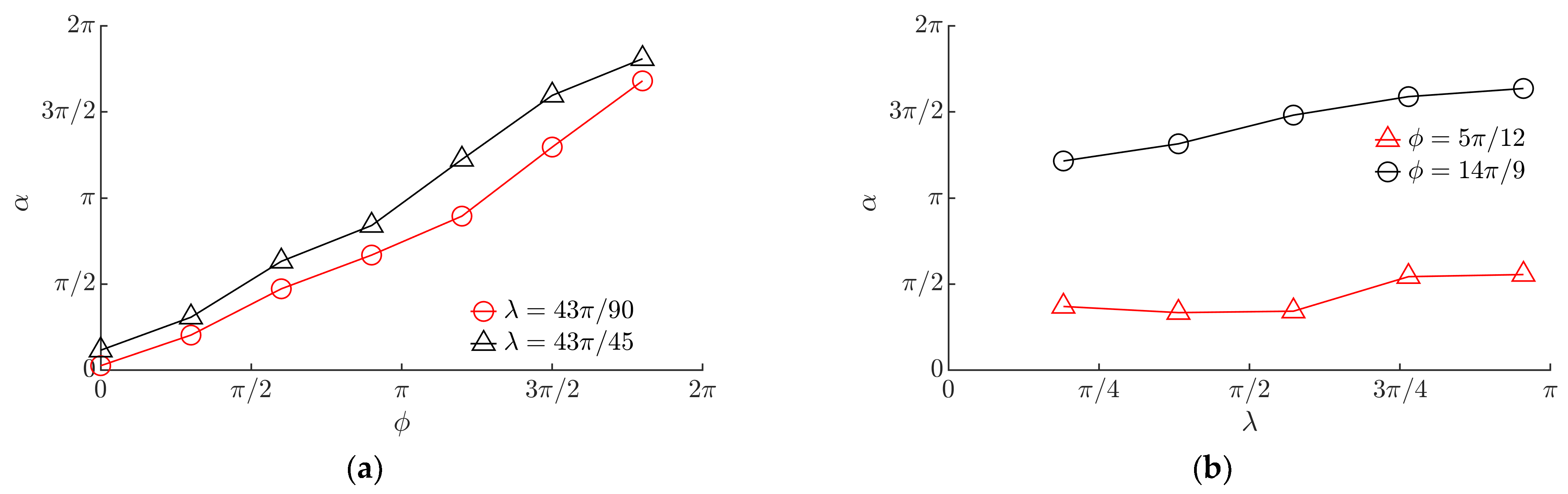

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilikevičius, S.; Liutkauskienė, K.; Uldinskas, E.; El Banna, R.; Fedaravičius, A. Omnidirectional Manipulation of Microparticles on a Platform Subjected to Circular Motion Applying Dynamic Dry Friction Control. Micromachines 2022, 13, 711. https://doi.org/10.3390/mi13050711
Kilikevičius S, Liutkauskienė K, Uldinskas E, El Banna R, Fedaravičius A. Omnidirectional Manipulation of Microparticles on a Platform Subjected to Circular Motion Applying Dynamic Dry Friction Control. Micromachines. 2022; 13(5):711. https://doi.org/10.3390/mi13050711
Chicago/Turabian StyleKilikevičius, Sigitas, Kristina Liutkauskienė, Ernestas Uldinskas, Ribal El Banna, and Algimantas Fedaravičius. 2022. "Omnidirectional Manipulation of Microparticles on a Platform Subjected to Circular Motion Applying Dynamic Dry Friction Control" Micromachines 13, no. 5: 711. https://doi.org/10.3390/mi13050711
APA StyleKilikevičius, S., Liutkauskienė, K., Uldinskas, E., El Banna, R., & Fedaravičius, A. (2022). Omnidirectional Manipulation of Microparticles on a Platform Subjected to Circular Motion Applying Dynamic Dry Friction Control. Micromachines, 13(5), 711. https://doi.org/10.3390/mi13050711






