Toward Higher Integration Density in Femtosecond-Laser-Written Programmable Photonic Circuits
Abstract
:1. Introduction
2. Fabrication Improvements
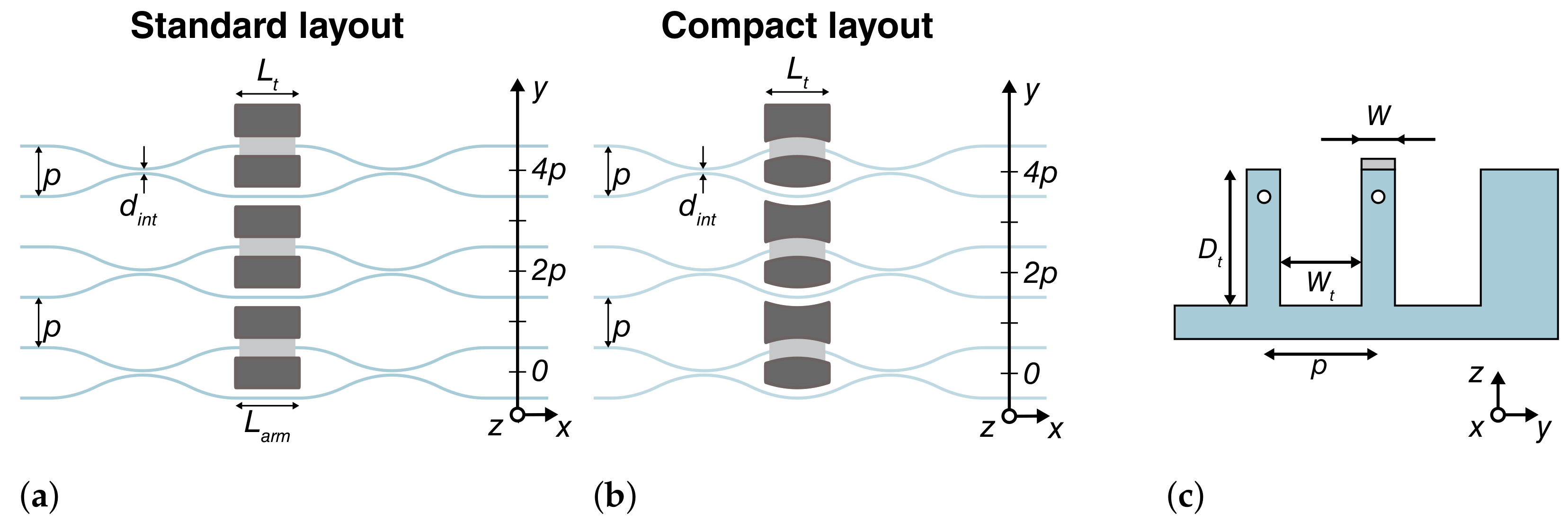
2.1. Compact Mach–Zehnder Interferometer Design
2.2. Two-Metal Photolithography Technique for Thermal Phase Shifters
3. Experimental Results
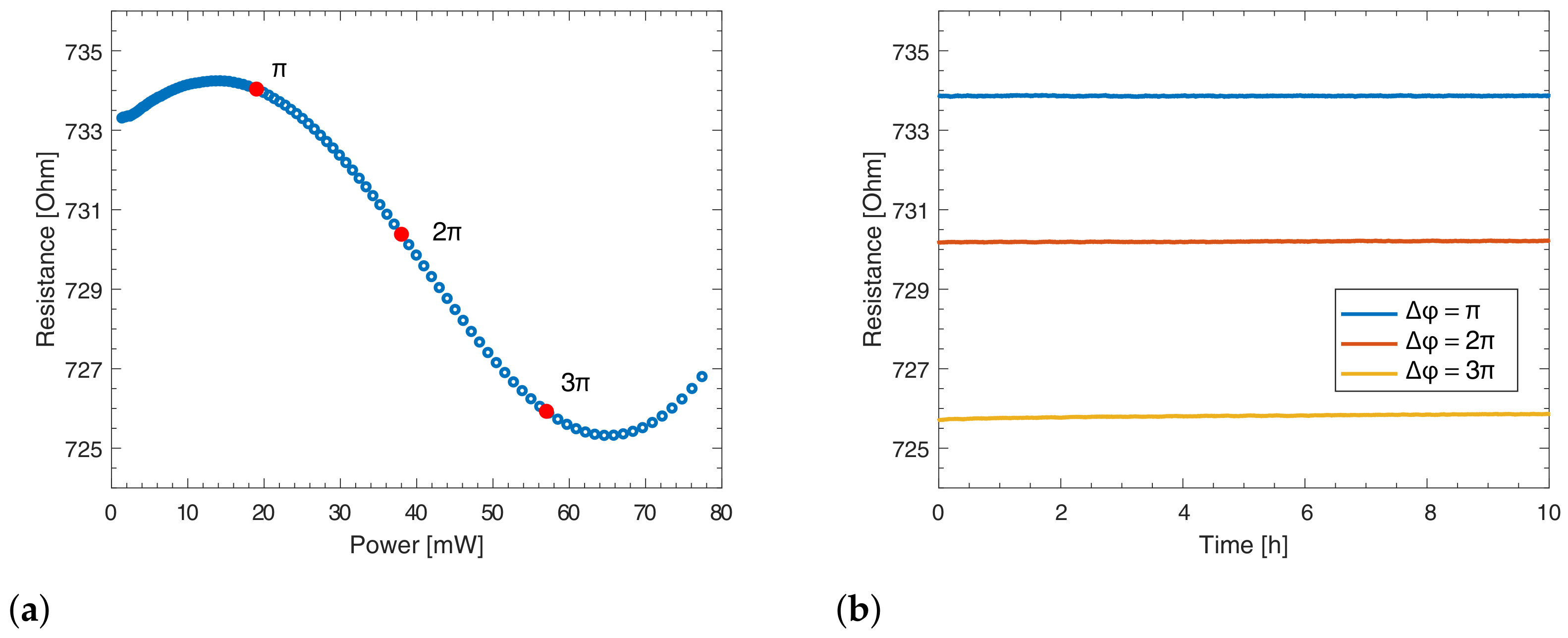
3.1. Electrical Measurements
3.2. Optical Measurements
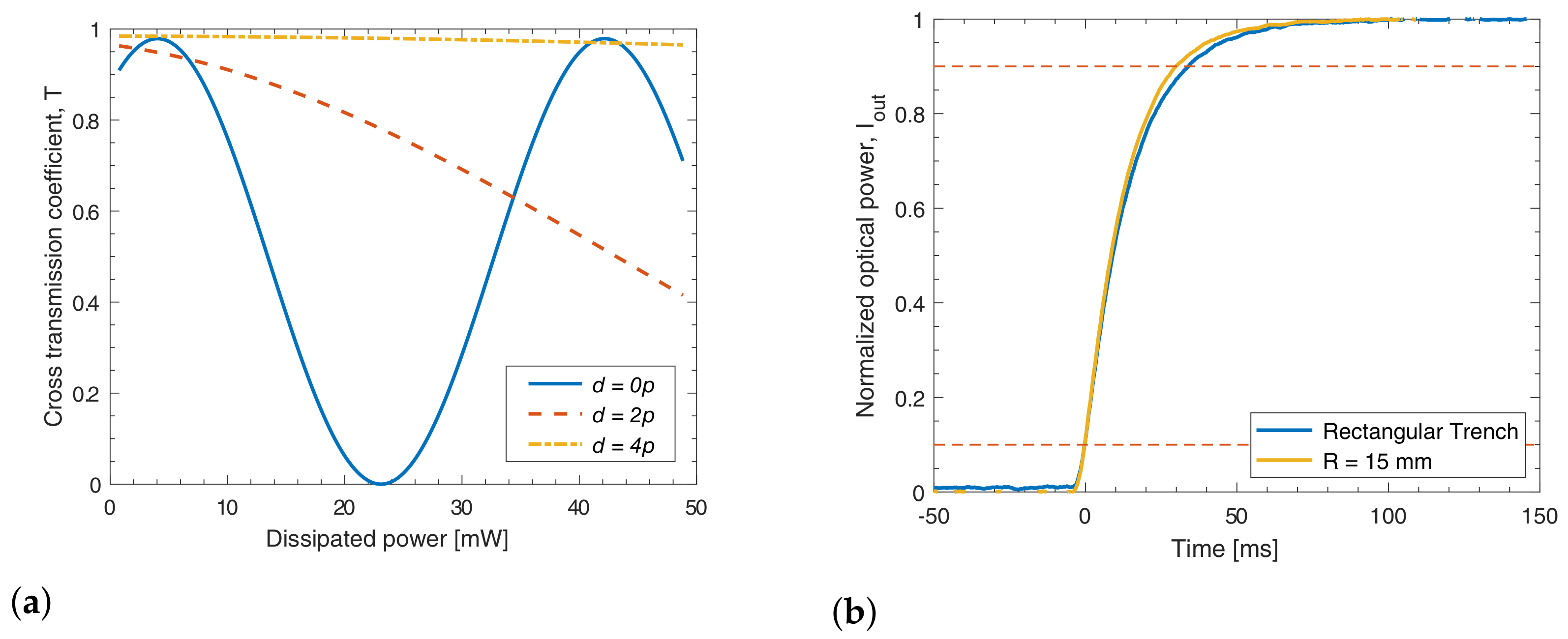
3.2.1. Dissipated Power
3.2.2. Thermal Crosstalk
3.2.3. Dynamic Response
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Bergholm, V.; Brádler, K.; Bromley, T.R.; Collins, M.J.; Dhand, I.; Fumagalli, A.; Gerrits, T.; Goussev, A.; Helt, L.G.; et al. Quantum circuits with many photons on a programmable nanophotonic chip. Nature 2021, 591, 54–60. [Google Scholar] [CrossRef]
- Pelucchi, E.; Fagas, G.; Aharonovich, I.; Englund, D.; Figueroa, E.; Gong, Q.; Hannes, H.; Liu, J.; Lu, C.Y.; Matsuda, N.; et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 2022, 4, 194–208. [Google Scholar] [CrossRef]
- Annoni, A.; Guglielmi, E.; Carminati, M.; Ferrari, G.; Sampietro, M.; Miller, D.A.; Melloni, A.; Morichetti, F. Unscrambling light—Automatically undoing strong mixing between modes. Light. Sci. Appl. 2017, 6, e17110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, D.A.B. Waves, modes, communications, and optics: A tutorial. Adv. Opt. Photonics 2019, 11, 679–825. [Google Scholar] [CrossRef] [Green Version]
- Bogaerts, W.; Pérez, D.; Capmany, J.; Miller, D.A.; Poon, J.; Englund, D.; Morichetti, F.; Melloni, A. Programmable photonic circuits. Nature 2020, 586, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Ruocco, A.; Ribeiro, A.; Vanacker, L.; Bogaerts, W. Demonstration of a 4 × 4-port universal linear circuit. Optica 2016, 3, 1348–1357. [Google Scholar] [CrossRef]
- Harris, N.C.; Carolan, J.; Bunandar, D.; Prabhu, M.; Hochberg, M.; Baehr-Jones, T.; Fanto, M.L.; Smith, A.M.; Tison, C.C.; Alsing, P.M.; et al. Linear programmable nanophotonic processors. Optica 2018, 5, 1623–1631. [Google Scholar] [CrossRef]
- Taballione, C.; van der Meer, R.; Snijders, H.J.; Hooijschuur, P.; Epping, J.P.; de Goede, M.; Kassenberg, B.; Venderbosch, P.; Toebes, C.; van den Vlekkert, H.; et al. A universal fully reconfigurable 12-mode quantum photonic processor. Mater. Quantum Technol. 2021, 1, 035002. [Google Scholar] [CrossRef]
- Taballione, C.; Anguita, M.C.; de Goede, M.; Venderbosch, P.; Kassenberg, B.; Snijders, H.; Kannan, N.; Smith, D.; Epping, J.P.; van der Meer, R.; et al. 20-Mode Universal Quantum Photonic Processor. arXiv 2022, arXiv:2203.01801. [Google Scholar] [CrossRef]
- Reck, M.; Zeilinger, A.; Bernstein, H.J.; Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 1994, 73, 58–61. [Google Scholar] [CrossRef]
- Clements, W.R.; Humphreys, P.C.; Metcalf, B.J.; Kolthammer, W.S.; Walsmley, I.A. Optimal design for universal multiport interferometers. Optica 2016, 3, 1460. [Google Scholar] [CrossRef]
- de Goede, M.; Snijders, H.; Venderbosch, P.; Kassenberg, B.; Kannan, N.; Smith, D.H.; Taballione, C.; Epping, J.P.; van den Vlekkert, H.; Renema, J.J. High Fidelity 12-Mode Quantum Photonic Processor Operating at InGaAs Quantum Dot Wavelength. arXiv 2022, arXiv:2204.05768. [Google Scholar]
- Carolan, J.; Harrold, C.; Sparrow, C.; Martín-López, E.; Russell, N.J.; Silverstone, J.W.; Shadbolt, P.J.; Matsuda, N.; Oguma, M.; Itoh, M.; et al. Universal linear optics. Science 2015, 349, 711–716. [Google Scholar] [CrossRef] [Green Version]
- Dyakonov, I.V.; Pogorelov, I.A.; Bobrov, I.B.; Kalinkin, A.A.; Straupe, S.S.; Kulik, S.P.; Dyakonov, P.V.; Evlashin, S.A. Reconfigurable Photonics on a Glass Chip. Phys. Rev. Appl. 2018, 10, 044048. [Google Scholar] [CrossRef] [Green Version]
- Pentangelo, C.; Ceccarelli, F.; Piacentini, S.; Albiero, R.; Urbinati, E.; Giano, N.D.; Atzeni, S.; Crespi, A.; Osellame, R. Universal photonic processors fabricated by femtosecond laser writing. In Integrated Optics: Devices, Materials, and Technologies XXVI; García-Blanco, S.M., Cheben, P., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2022; Volume 12004, pp. 63–67. [Google Scholar] [CrossRef]
- Corrielli, G.; Crespi, A.; Osellame, R. Femtosecond laser micromachining for integrated quantum photonics. Nanophotonics 2021, 10, 3789–3812. [Google Scholar] [CrossRef]
- Corrielli, G.; Atzeni, S.; Piacentini, S.; Pitsios, I.; Crespi, A.; Osellame, R. Symmetric polarization-insensitive directional couplers fabricated by femtosecond laser writing. Opt. Express 2018, 26, 15101–15109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crespi, A.; Osellame, R.; Ramponi, R.; Bentivegna, M.; Flamini, F.; Spagnolo, N.; Viggianiello, N.; Innocenti, L.; Mataloni, P.; Sciarrino, F. Suppression law of quantum states in a 3D photonic fast Fourier transform chip. Nat. Commun. 2016, 7, 10469. [Google Scholar] [CrossRef] [Green Version]
- Hoch, F.; Piacentini, S.; Giordani, T.; Tian, Z.N.; Iuliano, M.; Esposito, C.; Camillini, A.; Carvacho, G.; Ceccarelli, F.; Spagnolo, N.; et al. Reconfigurable continuously-coupled 3D photonic circuit for Boson Sampling experiments. NPJ Quantum Inf. 2022, 8, 55. [Google Scholar] [CrossRef]
- Flamini, F.; Magrini, L.; Rab, A.S.; Spagnolo, N.; D’Ambrosio, V.; Mataloni, P.; Sciarrino, F.; Zandrini, T.; Crespi, A.; Ramponi, R.; et al. Thermally reconfigurable quantum photonic circuits at telecom wavelength by femtosecond laser micromachining. Light. Sci. Appl. 2015, 4, e354. [Google Scholar] [CrossRef] [Green Version]
- Ceccarelli, F.; Atzeni, S.; Prencipe, A.; Farinaro, R.; Osellame, R. Thermal Phase Shifters for Femtosecond Laser Written Photonic Integrated Circuits. J. Light. Technol. 2019, 37, 4275–4281. [Google Scholar] [CrossRef]
- Ceccarelli, F.; Atzeni, S.; Pentangelo, C.; Pellegatta, F.; Crespi, A.; Osellame, R. Low Power Reconfigurability and Reduced Crosstalk in Integrated Photonic Circuits Fabricated by Femtosecond Laser Micromachining. Laser Photonics Rev. 2020, 14, 2000024. [Google Scholar] [CrossRef]
- Arriola, A.; Gross, S.; Jovanovic, N.; Charles, N.; Tuthill, P.G.; Olaizola, S.M.; Fuerbach, A.; Withford, M.J.; Liao, Y.; Song, J.; et al. Low bend loss waveguides enable compact, efficient 3D photonic chips. Opt. Express 2013, 21, 2978–2986. [Google Scholar] [CrossRef]
- Lee, T.; Sun, Q.; Beresna, M.; Brambilla, G. Low bend loss femtosecond laser written waveguides exploiting integrated microcrack. Sci. Rep. 2021, 11, 23770. [Google Scholar] [CrossRef]
- Li, Y.; Qu, S. Water-assisted femtosecond laser ablation for fabricating three-dimensional microfluidic chips. Curr. Appl. Phys. 2013, 13, 1292–1295. [Google Scholar] [CrossRef]
- Marcinkowski, M.J.; Lipsitt, H.A. Electrical Resistivity of Chromium in the Vicinity of the Néel Temperature. J. Appl. Phys. 1961, 32, 1238–1240. [Google Scholar] [CrossRef]
- Arajs, S.; Rao, K.V.; Åström, H.U.; de Young, T.F. Determination of Néel Temperatures of Binary Chromium Alloys from Electrical Resistivity Data. Phys. Scr. 1973, 8, 109–112. [Google Scholar] [CrossRef]
- Ohashi, M.; Ohashi, K.; Sawabu, M.; Miyagawa, M.; Kubota, T.; Takanashi, K. Unconventional drop in the electrical resistance of chromium metal thin films at low temperature. Phys. Lett. A 2016, 380, 3133–3137. [Google Scholar] [CrossRef] [Green Version]
- Rapp, O.; Benediktsson, G.; Åström, H.U.; Arajs, S.; Rao, K.V. Electrical resistivity of antiferromagnetic chromium near the Néel temperature. Phys. Rev. B 1978, 18, 3665–3673. [Google Scholar] [CrossRef]
- Pentangelo, C.; Atzeni, S.; Ceccarelli, F.; Osellame, R.; Crespi, A. Analytical modeling of the static and dynamic response of thermally actuated optical waveguide circuits. Phys. Rev. Res. 2021, 3, 023094. [Google Scholar] [CrossRef]
- Bell, B.A.; Walmsley, I.A. Further compactifying linear optical unitaries. APL Photonics 2021, 6, 070804. [Google Scholar] [CrossRef]

| Isolation Design | Cell Length (mm) | (mW) | (%) | (ms) | (ms) |
|---|---|---|---|---|---|
| Rectangular trenches, | 7.42 | 35.02 | 21.31 | 34.4 | 57.7 |
| Curved trench, | 7.64 | 38.23 | 20.17 | 29.9 | 52.5 |
| Curved trench, | 6.83 | 38.33 | 20.07 | 28.9 | 55.4 |
| Curved trench, | 5.92 | 38.10 | 18.64 | 29.8 | 50.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albiero, R.; Pentangelo, C.; Gardina, M.; Atzeni, S.; Ceccarelli, F.; Osellame, R. Toward Higher Integration Density in Femtosecond-Laser-Written Programmable Photonic Circuits. Micromachines 2022, 13, 1145. https://doi.org/10.3390/mi13071145
Albiero R, Pentangelo C, Gardina M, Atzeni S, Ceccarelli F, Osellame R. Toward Higher Integration Density in Femtosecond-Laser-Written Programmable Photonic Circuits. Micromachines. 2022; 13(7):1145. https://doi.org/10.3390/mi13071145
Chicago/Turabian StyleAlbiero, Riccardo, Ciro Pentangelo, Marco Gardina, Simone Atzeni, Francesco Ceccarelli, and Roberto Osellame. 2022. "Toward Higher Integration Density in Femtosecond-Laser-Written Programmable Photonic Circuits" Micromachines 13, no. 7: 1145. https://doi.org/10.3390/mi13071145
APA StyleAlbiero, R., Pentangelo, C., Gardina, M., Atzeni, S., Ceccarelli, F., & Osellame, R. (2022). Toward Higher Integration Density in Femtosecond-Laser-Written Programmable Photonic Circuits. Micromachines, 13(7), 1145. https://doi.org/10.3390/mi13071145








