Femtosecond Laser Percussion Drilling of Silicon Using Repetitive Single Pulse, MHz-, and GHz-Burst Regimes
Abstract
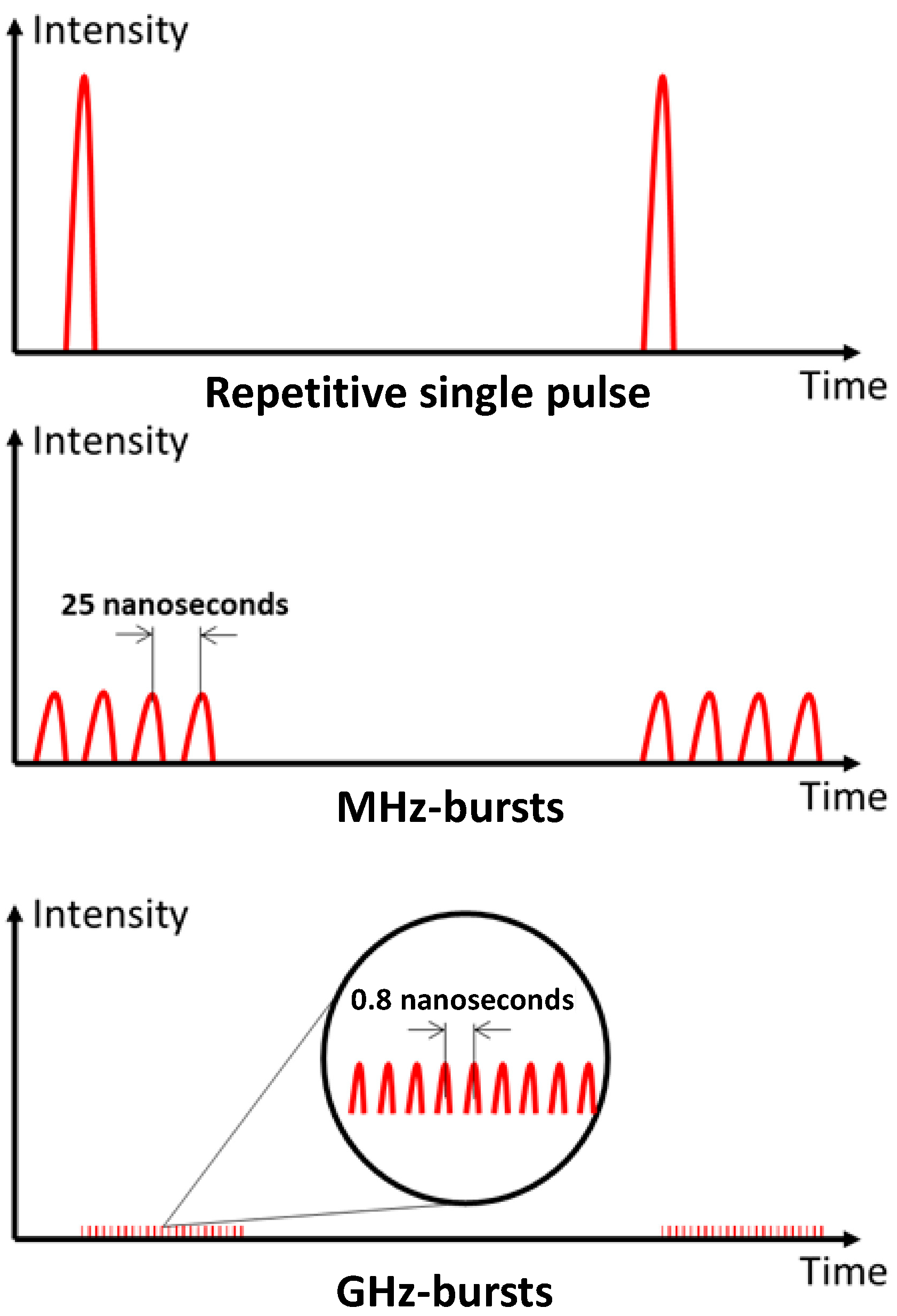
:1. Introduction
2. Materials and Methods
3. Results
3.1. Silicon Drilling with GHz-Bursts of Femtosecond Pulses
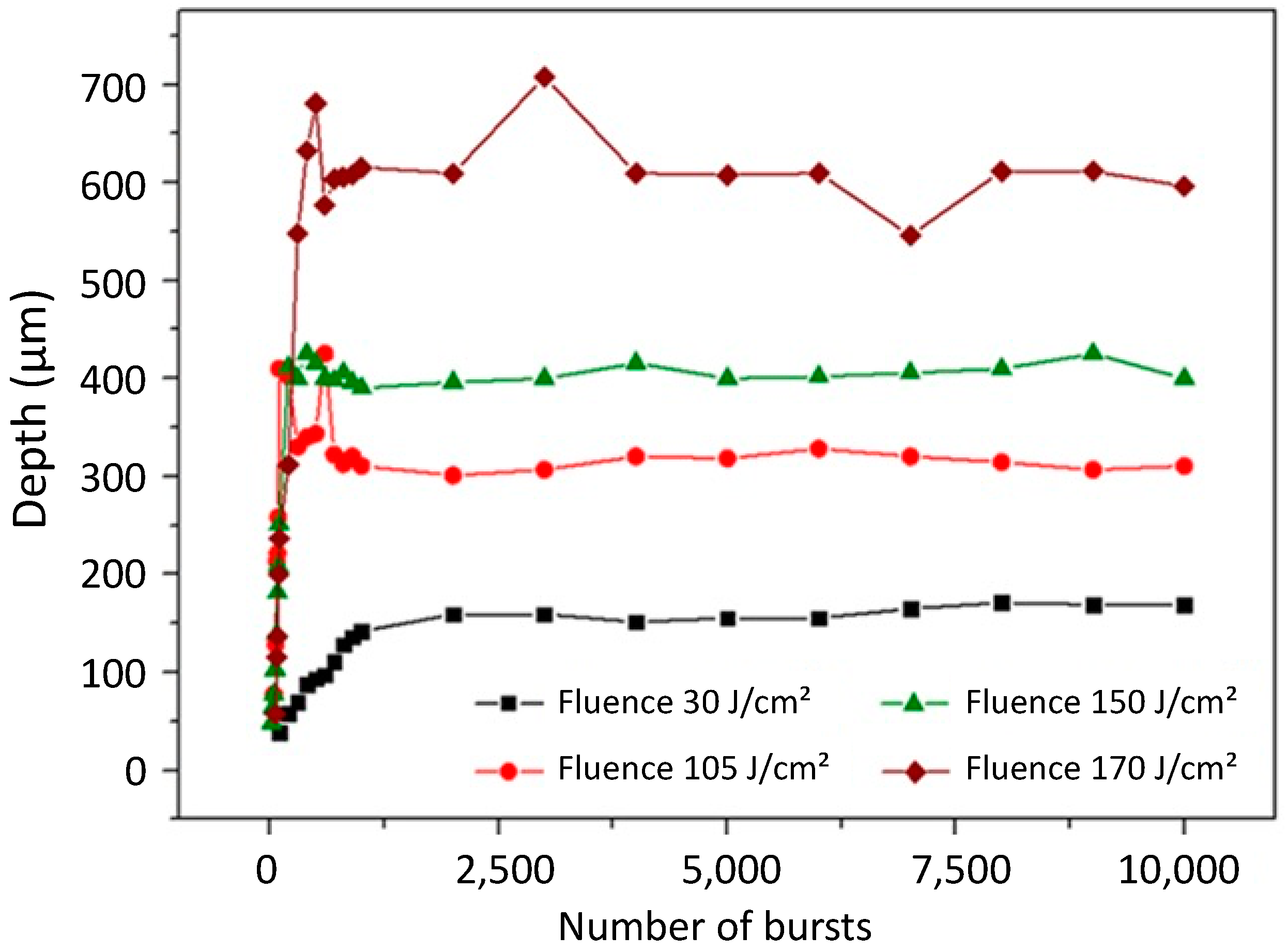
3.1.1. Burst Fluence
3.1.2. Burst Duration
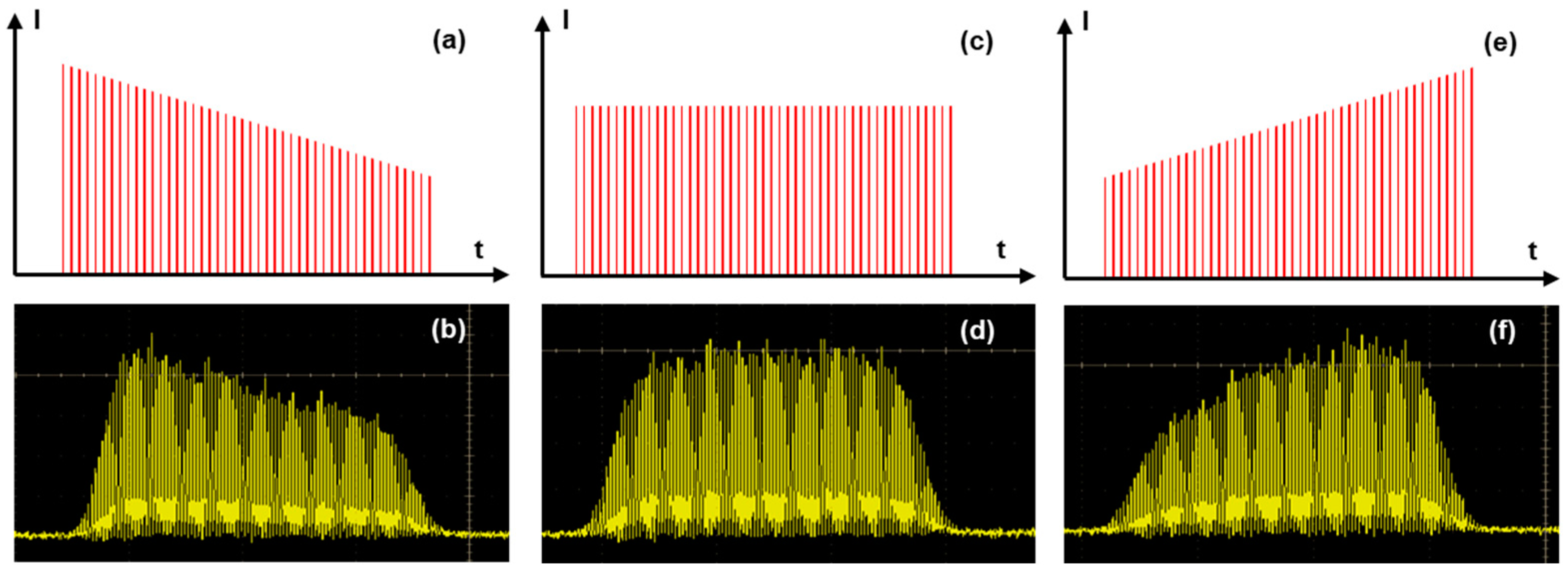
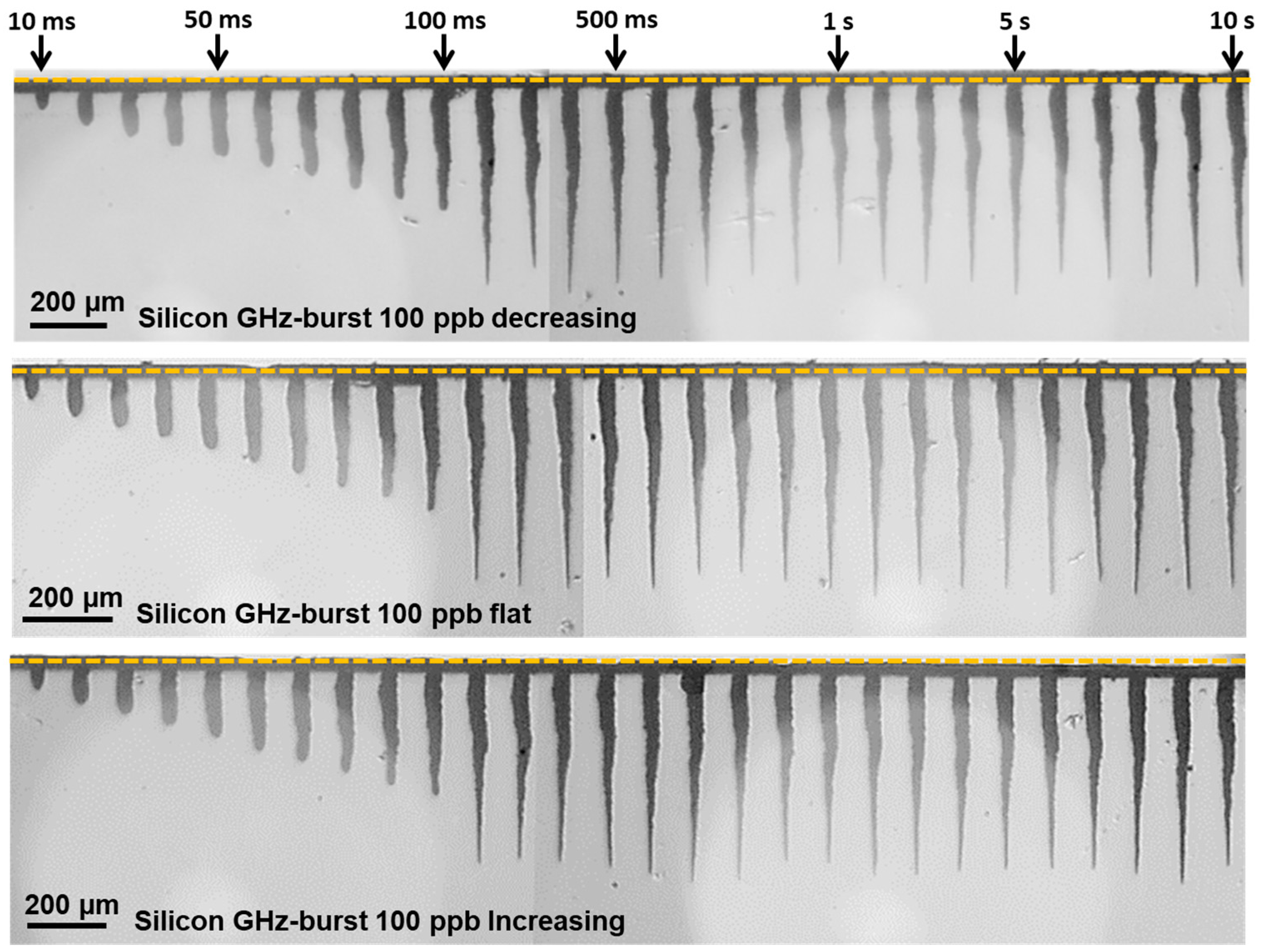
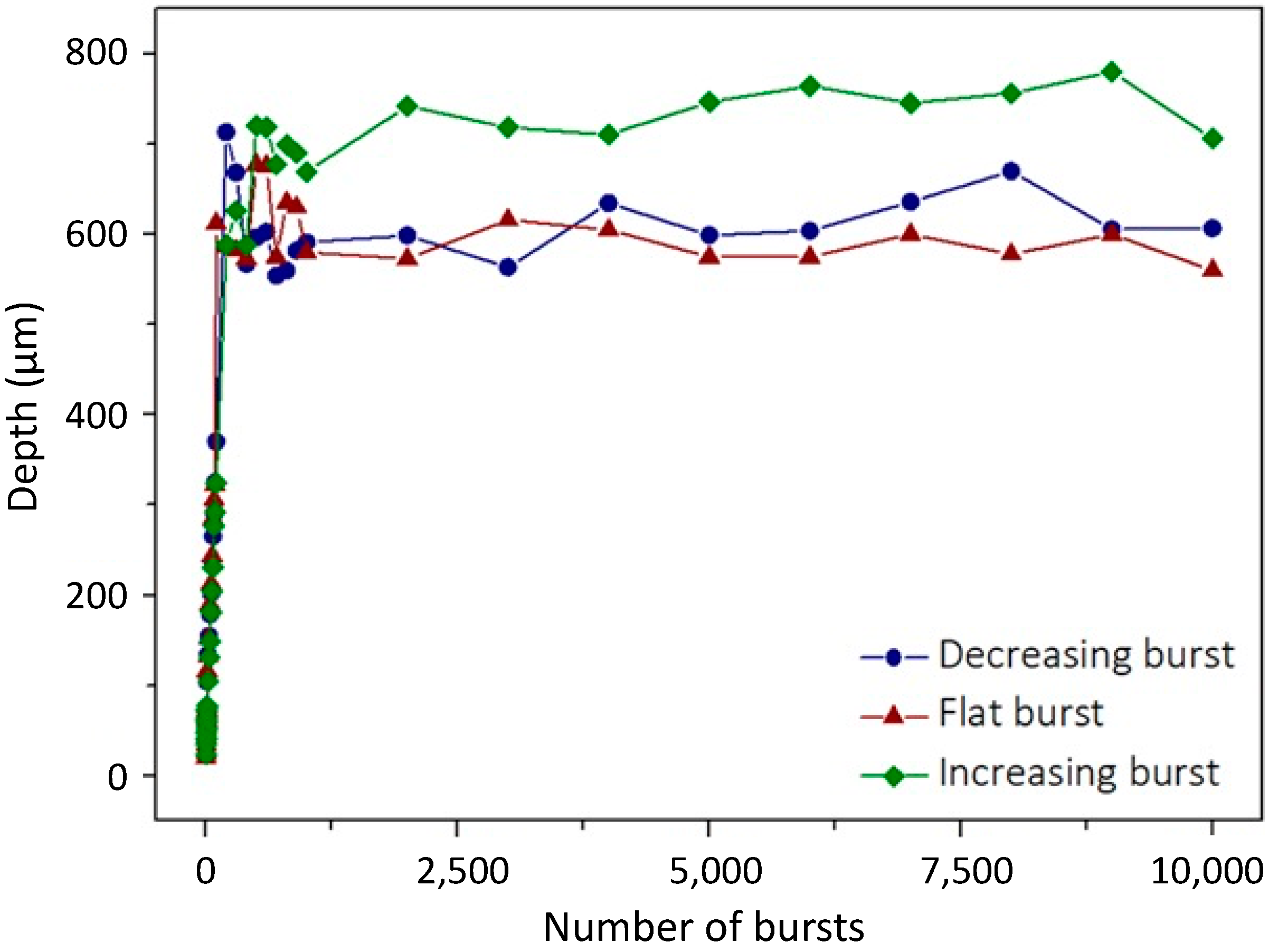
3.1.3. Burst Shape
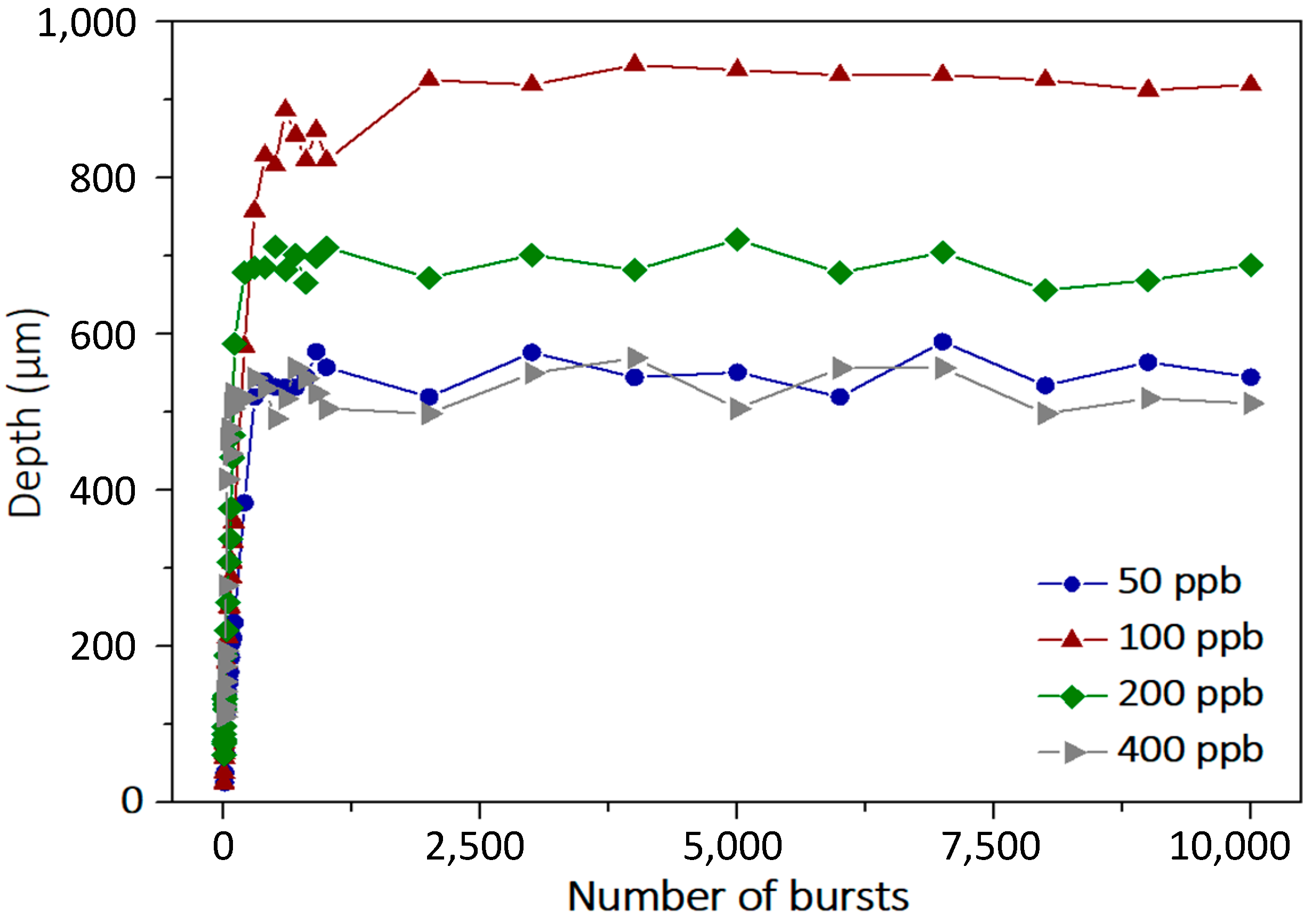
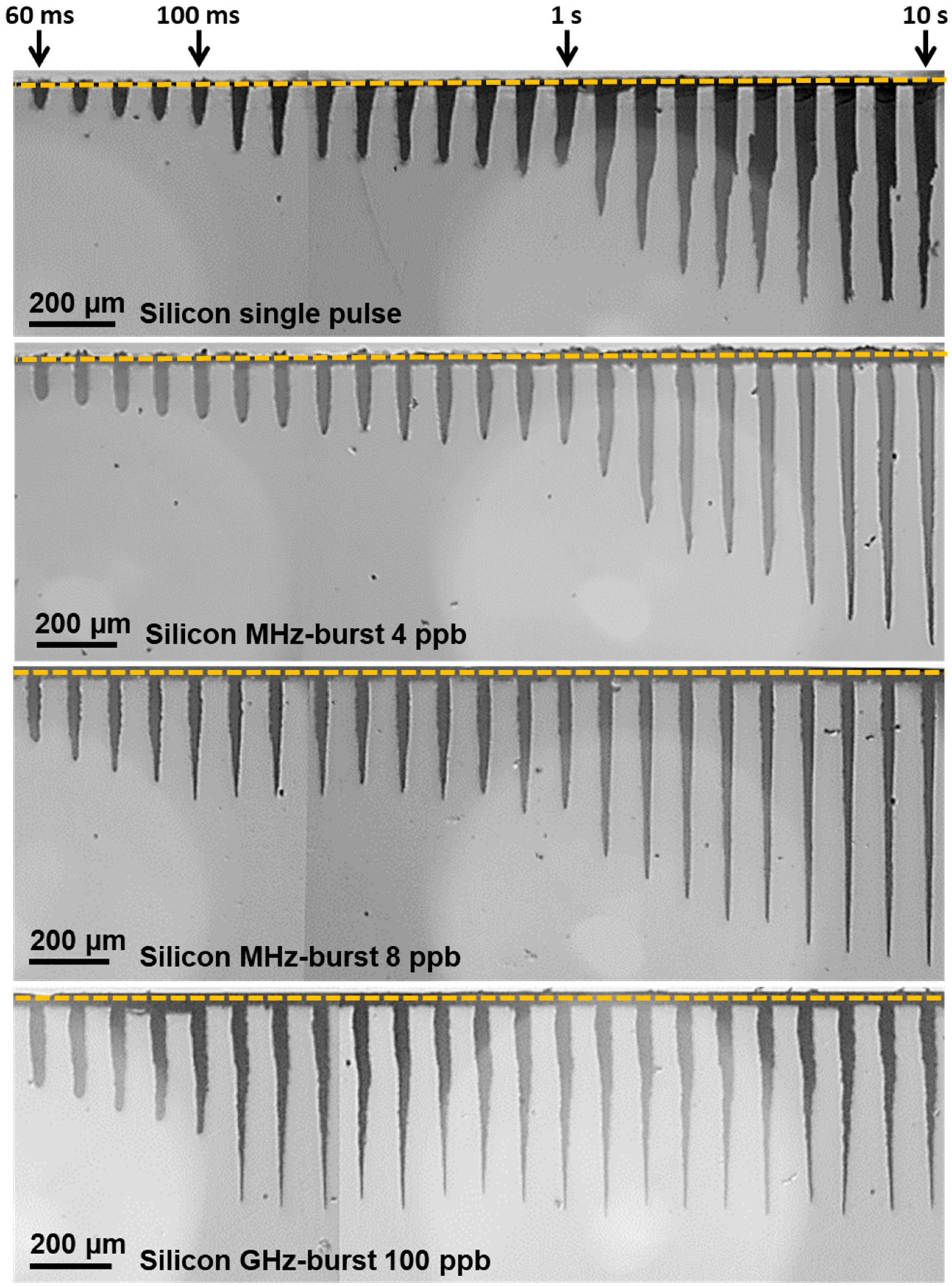
3.2. Comparison of Single Pulse, MHz-, and GHz-Burst Regimes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kerse, C.; Kalaycoglu, H.; Elahi, P.; Cetin, B.; Kesim, D.; Akçaalan, O.; Yavas, S.; Asik, M.; Oktem, B.; Hoogland, H.; et al. Ablation-cooled material removal with ultrafast bursts of pulses. Nature 2016, 537, 84–88. [Google Scholar] [CrossRef] [PubMed]
- Elahi, P.; Akçaalan, O.; Ertek, C.; Eken, K.; Ilday, F.O.; Kalaycoglu, H. High-power Yb-doped all-fiber laser delivering 300 fs pulses for high-speed ablation-cooled materiel removal. Opt. Lett. 2018, 43, 535–538. [Google Scholar] [CrossRef] [PubMed]
- Bonamis, G.; Mishchik, K.; Audouard, E.; Hönninger, C.; Mottay, E.; Lopez, J.; Manek-Hönninger, I. High efficiency femtosecond laser ablation with gigahetz level burst. J. Laser Appl. 2019, 31, 22205. [Google Scholar] [CrossRef]
- Mishchik, K.; Bonamis, G.; Qiao, J.; Lopez, J.; Audouard, E.; Mottay, E.; Hönninger, C.; Manek-Hönninger, I. High-efficiency femtosecond ablation of silicon with GHz repetition rate laser source. Opt. Lett. 2019, 44, 2193–2196. [Google Scholar] [CrossRef]
- Bonamis, G.; Audouard, E.; Hönninger, C.; Lopez, J.; Mishchik, K.; Mottay, E.; Manek-Hönninger, I. Systematic study of laser ablation with GHz bursts of femtosecond pulses. Opt. Expr. 2020, 28, 27702–27714. [Google Scholar] [CrossRef] [PubMed]
- Metzner, D.; Lickschat, P.; Engel, A.; Lampke, T.; Weißmantel, S. Ablation characteristics on silicon from ultrafast laser radiation containing single MHz and GHz burst pulses. Appl. Phys. A 2022, 128, 723. [Google Scholar] [CrossRef]
- Hirsiger, T.; Gafner, M.; Remund, S.M.; Chaja, M.W.; Urniezius, A.; Butkus, S.; Neuenschwander, B. Machining metals and silicon with GHz bursts: Surprising tremendous reduction of the specific removal rate for surface texturing applications. In Proceedings of the Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXV, San Francisco, CA, USA, 1–6 February 2020; Volume 11267. [Google Scholar]
- Žemaitis, A.; Gaidys, M.; Gečys, P.; Barkauskas, M.; Gedvilas, M. Femtosecond laser ablation by bibursts in the MHz and GHz pulse repetition rates. Opt. Expr. 2021, 29, 7641–7653. [Google Scholar] [CrossRef] [PubMed]
- Förster, D.J.; Jaeggi, B.; Michalowski, A.; Neuenschwander, B. Review on Experimental and Theoretical Investigations of Ultra-Short Pulsed Laser Ablation of Metals with Burst Pulses. Materials 2021, 14, 3331. [Google Scholar] [CrossRef]
- Sugioka, K. Will GHz burst mode create a new path to femtosecond laser processing? Int. J. Extreme Manuf. 2021, 3, 43001. [Google Scholar] [CrossRef]
- Metzner, D.; Lickschat, P.; Weißmantel, S. Optimization of the ablation process using ultrashort pulsed laser radiation in different burst modes. J. Laser Appl. 2021, 33, 12057. [Google Scholar] [CrossRef]
- Metzner, D.; Lickschat, P.; Kreisel, C.; Lampke, T.; Weißmantel, S. Study on laser ablation of glass using MHz-to-GHz burst pulses. Appl. Phys. A 2022, 128, 637. [Google Scholar] [CrossRef]
- Balage, P.; Lopez, J.; Bonamis, G.; Hönninger, C.; Manek-Hönninger, I. Crack-free high-aspect ratio holes in glasses by top–down percussion drilling with infrared femtosecond laser GHz-bursts. Int. J. Extrem. Manuf. 2023, 5, 15002. [Google Scholar] [CrossRef]
- Van Kerschaver, E.; Beaucarne, G. Back-contact solar cells: A review. Prog. Photovolt. 2006, 14, 107–123. [Google Scholar] [CrossRef]
- Halbwax, M.; Sarnet, T.; Delaporte, P.; Sentis, M.; Etienne, H.; Torregrosa, F.; Vervisch, V.; Perichaud, I.; Martinuzzi, S. Micro and nano-structuration of silicon by femtosecond laser: Application to silicon photovoltaic cells fabrication. Thin Solid Film. 2008, 516, 6791–6795. [Google Scholar] [CrossRef]
- Kononenko, T.V.; Sovyk, D.N.; Kononenko, V.V.; Konov, V.I. Optimization strategy for high-quality laser milling of silicon. Opt. Laser Technol. 2022, 150, 107921. [Google Scholar] [CrossRef]
- Migliore, L. Enhancing silicon cutting performance by shaping the focused beam. In Photon Processing in Microelectronics and Photonics VI; SPIE: Washington, DC, USA, 2007; Volume 6458. [Google Scholar]
- Haupt, O.; Schuetz, V.; Schoonderbeek, A.; Richter, L.; Kling, R. High Quality Laser Cleaving Process for Mono-and Polycrystalline Silicon. In Laser-Based Micro-and Nanopackaging and Assembly III; SPIE: Washington, DC, USA, 2009; Volume 7202. [Google Scholar]
- Chambonneau, M.; Blothe, M.; Li, Q.; Fedorov, V.Y.; Heuermann, T.; Gebhardt, M.; Gaida, C.; Tertelmann, S.; Sotier, F.; Limpert, J.; et al. Transverse Ultrafast Laser Inscription in Bulk Silicon. Phys. Rev. Res. 2021, 3, 43037. [Google Scholar] [CrossRef]
- Tokel, O.; Turnali, A.; Makey, G.; Elahi, P.; Çolakoğlu, T.; Ergeçen, E.; Yavuz, O.; Hübner, R.; Borra, M.Z.; Pavlov, I.; et al. In-chip microstructures and photonic devices fabricated by nonlinear laser lithography deep inside silicon. Nat. Photonics 2017, 11, 639–645. [Google Scholar] [CrossRef]
- Chambonneau, M.; Chanal, M.; Sanner, N.; Grojo, D. Writing waveguides inside monolithic crystalline silicon with nanosecond laser pulses. Opt. Lett. 2016, 41, 4875–4878. [Google Scholar] [CrossRef]
- Pavlov, I.; Tokel, O.; Pavlova, S.; Kadan, V.; Makey, G.; Turnali, A.; Yavuz, Ö.; Ilday, F.Ö. Femtosecond laser written waveguides deep inside silicon. Opt. Lett. 2017, 42, 3028–3031. [Google Scholar] [CrossRef]
- Wang, X.; Yu, X.; Berg, M.J.; Chen, P.; Lacroix, B.; Lei, S. Curved waveguides in silicon written by a shaped laser beam. Opt. Express 2021, 29, 14201–14207. [Google Scholar] [CrossRef] [PubMed]
- Chambonneau, M.; Richter, D.; Nolte, S.; Grojo, D. Inscribing diffraction gratings in bulk silicon with nanosecond laser pulses. Opt. Lett. 2018, 43, 6069–6072. [Google Scholar] [CrossRef]
- Sugimoto, K.; Matsuo, S. Inscribing diffraction grating inside silicon substrate using a subnanosecond laser in one photon absorption wavelength. Sci. Rep. 2020, 10, 21451. [Google Scholar] [CrossRef] [PubMed]
- Weng, W.; Deng, Q.; Yang, P.; Yin, K. Femtosesond laser-chemical hybrid processing for achieving substrate-independent superhydrophobic surfaces. J. Cent. South Univ. 2024, 31, 1–10. [Google Scholar] [CrossRef]
- Bhuyan, M.K.; Courvoisier, F.; Lacourt, P.A.; Jacquot, M.; Salut, R.; Furfaro, L.; Dudley, J.M. High aspect ratio nanochannel machining using single shot femtosecond Bessel beams. Appl. Phys. Lett. 2010, 97, 81102. [Google Scholar] [CrossRef]
- Chambonneau, M.; Wang, X.; Yu, X.; Li, Q.; Chaudanson, D.; Lei, S.; Grojo, D. Positive- and negativetone structuring of crystalline silicon by laser-assisted chemical etching. Opt. Lett. 2019, 44, 1619–1622. [Google Scholar] [CrossRef]
- Wang, A.; Sopeña, P.; Grojo, D. Burst mode enabled ultrafast laser inscription inside gallium arsenide. Int. J. Extrem. Manuf. 2022, 4, 45001. [Google Scholar] [CrossRef]
- Ohmura, E.; Fukuyo, F.; Fukumitsu, K.; Morita, H. Internal modified-layer formation mechanism into silicon with nanosecond laser. J. Achiev. Mater. Manuf. Eng. 2006, 17, 381–384. [Google Scholar]
- Verburg, P.C.; Römer, G.R.B.E.; Huis, A.J. Two-photon-induced internal modification of silicon by erbium-doped fiber laser. Opt. Express 2014, 22, 21958–21971. [Google Scholar] [CrossRef]
- Mitra, S.; Chanal, M.; Clady, R.; Mouskeftaras, A.; Grojo, D. Millijoule femtosecond micro-bessel beams for ultra-high aspect ratio machining. Appl. Opt. 2015, 54, 7358–7365. [Google Scholar] [CrossRef]
- Grojo, D.; Mouskeftaras, A.; Delaporte, P.; Lei, S. Limitations to laser machining of silicon using femtosecond micro-Bessel beams in the infrared. J. Appl. Phys. 2015, 117, 153105. [Google Scholar] [CrossRef]
- He, F.; Yu, J.; Tan, Y.; Chu, W.; Zhou, C.; Cheng, Y. Tailoring femtosecond 1.5-μm bessel beams for manufacturing high-aspect-ratio throughsilicon vias. Sci. Rep. 2017, 7, 40785. [Google Scholar] [CrossRef] [PubMed]
- Chambonneau, M.; Li, Q.; Fedorov, V.Y.; Blothe, M.; Schaarschmidt, K.; Lorenz, M.; Tzortzakis, S.; Nolte, S. Taming ultrafast laser filaments for optimized semiconductor–metal welding. Laser Photonics Rev. 2021, 15, 2000433. [Google Scholar] [CrossRef]
- Sopeña, P.; Wang, A.; Mouskeftaras, A.; Grojo, D. Transmission Laser Welding of Similar and Dissimilar Semiconductor Materials. Laser Photonics Rev. 2022, 16, 2200208. [Google Scholar] [CrossRef]
- Matsumoto, H.; Lin, Z.; Kleinert, J. Ultrafast laser ablation of copper with GHz bursts. In Laser Applications in Microelectronic and Optoelectronic Manufacturing (LAMOM) XXIII (International Society for Optics and Photonics, San Francisco, CA, 2018); SPIE: Washington, DC, USA, 2018; Volume 10519, p. 1051902. [Google Scholar]
- Neuenschwander, B.; Jaeggi, B.; Foerster, D.J.; Kramer, T.; Remund, S. Influence of the burst mode onto the specific removal rate for metals and semiconductors. J. Laser Appl. 2019, 31, 22203. [Google Scholar] [CrossRef]
- Matsumoto, H.; Lin, Z.; Schrauben, J.N.; Kleinert, J. Ultrafast laser ablation of silicon with ∼GHz bursts. J. Laser Appl. 2021, 33, 32010. [Google Scholar] [CrossRef]
- Lopez, J.; Niane, S.; Bonamis, G.; Balage, P.; Audouard, E.; Hönninger, C.; Mottay, E.; Manek-Hönninger, I. Percussion drilling in glasses and process dynamics with femtosecond laser GHz-bursts. Opt. Expr. 2022, 30, 12533. [Google Scholar] [CrossRef] [PubMed]
- Balage, P.; Bonamis, G.; Lafargue, M.; Guilberteau, T.; Delaigue, M.; Hönninger, C.; Qiao, J.; Lopez, J.; Manek-Hönninger, I. Advances in Femtosecond Laser GHz-Burst Drilling of Glasses: Influence of Burst Shape and Duration. Micromachines 2023, 14, 1158. [Google Scholar] [CrossRef]
- Balage, P.; Lafargue, M.; Guilberteau, T.; Bonamis, G.; Hönninger, C.; Lopez, J.; Manek-Hönninger, I. Comparative Study of Percussion Drilling in Glasses with a Femtosecond Laser in Single Pulse, MHz-Burst, and GHz-Burst Regimes and Optimization of the Hole Aspect Ratio. Micromachines 2023, 14, 1754. [Google Scholar] [CrossRef]
- Brusberg, L.; Queisser, M.; Gentsch, C.; Schröder, H.; Lang, K.D. Advances in CO2-laser drilling of glass substrates. Phys. Proc. 2012, 39, 548–555. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balage, P.; Lafargue, M.; Guilberteau, T.; Bonamis, G.; Hönninger, C.; Lopez, J.; Manek-Hönninger, I. Femtosecond Laser Percussion Drilling of Silicon Using Repetitive Single Pulse, MHz-, and GHz-Burst Regimes. Micromachines 2024, 15, 632. https://doi.org/10.3390/mi15050632
Balage P, Lafargue M, Guilberteau T, Bonamis G, Hönninger C, Lopez J, Manek-Hönninger I. Femtosecond Laser Percussion Drilling of Silicon Using Repetitive Single Pulse, MHz-, and GHz-Burst Regimes. Micromachines. 2024; 15(5):632. https://doi.org/10.3390/mi15050632
Chicago/Turabian StyleBalage, Pierre, Manon Lafargue, Théo Guilberteau, Guillaume Bonamis, Clemens Hönninger, John Lopez, and Inka Manek-Hönninger. 2024. "Femtosecond Laser Percussion Drilling of Silicon Using Repetitive Single Pulse, MHz-, and GHz-Burst Regimes" Micromachines 15, no. 5: 632. https://doi.org/10.3390/mi15050632
APA StyleBalage, P., Lafargue, M., Guilberteau, T., Bonamis, G., Hönninger, C., Lopez, J., & Manek-Hönninger, I. (2024). Femtosecond Laser Percussion Drilling of Silicon Using Repetitive Single Pulse, MHz-, and GHz-Burst Regimes. Micromachines, 15(5), 632. https://doi.org/10.3390/mi15050632




