Abstract
We study a duel game in which each player has incomplete knowledge of the game parameters. We present a simple, heuristically motivated and easily implemented algorithm by which, in the course of repeated plays, each player estimates the missing parameters and consequently learns his optimal strategy.
1. Introduction
We study a two-player zero-sum duel game in which certain game parameters are unknown, and we present an algorithm by which each player can estimate the opponent’s parameters and consequently learn his optimal strategy.
The duel game with which we are concerned has been presented in (), and a similar one was examined in (). The game is a variation of a duel game and, more generally, games of timing, as presented in (); (); ().
We call the two players and ; for , has a kill probability vector , with the component (for ) giving the probability that kills his opponent when he shoots at him from distance d. In our analysis, we make the following assumptions:
- The kill probabilities are given by a function, f:where is a parameter vector.
- Each knows the general form and his own parameter vector , but not that of his opponent.
- The duel will be repeated a large number of times.
Each ’s goal is to compute a strategy that optimizes his payoff, which (as will be seen in Section 2), depends on both and ; since does not know his opponents kill probability, he does not know either his own or his opponent’s payoff. In short, we have an incomplete information game.
Games of incomplete information are those in which each player has only partial information about the payoff parameters. Clearly, the players must utilize some form of learning, namely the use of information (i.e., data) collected from previous plays of a game to adjust their strategies through belief update, imitation, reinforcement etc.
The first work on learning in games was, arguably, the introduction of the fictitious play algorithm in (); (). In later years, several approaches to learning were proposed in the literature.
The Bayesian game approach introduced by () has led to intensive research on the subject of Bayesian games; for a recent review, see (). However, the main corpus of this literature is concerned with Bayesian reasoning for a single play of a game, rather than learning from repeated plays, and this point of view is not particularly relevant to our approach.
Another approach, which can be understood as a form of “intergenerational” learning, is that of evolutionary game theory, as presented in (); (); (), but this is not directly concerned with games of incomplete information and hence is also not very relevant to our approach. However, for some interesting remarks on the connection between learning and evolutionary game theory, see the book by ().
The main approach to learning in games is the one exemplified by ()’s seminal book The Theory Of Learning In Games. This has spawned a tremendous amount of research; a recent overview of the field appears in ().
Fudenberg and Levine’s approach is directly relevant to learning in the duel game, but we believe it is too general. In particular, we have not been able to find any works which address the specific case in which the functional form of payoff functions is known to the players and it is only required to estimate parameter values.
This is essentially a problem of parameter estimation, and there is another research corpus in which this problem is addressed explicitly: that of machine learning. Particularly relevant to our needs is the literature on multi-agent reinforcement learning, such as (); (). Reinforcement learning is a basic component of machine learning and, in the machine learning community, the connection between multi-agent problems and game theory has long been recognized (; ); recent and very extensive reviews can be found in (); ().
In particular, the issue of convergence of parameter estimation has been comprehensively studied (; ; ; ). An important conclusion of these and related works is the trade-off between exploration and exploitation. Quoting from (): “… understanding exploration remains an important endeavour as it allows agents to avoid suboptimal, or potentially unsafe areas of their state space … In addition, it is empirically known that the choice of exploration rate impacts the expected total reward”.
In short, extensive literature on learning and incomplete information games is available but, while some ingenious and highly technical approaches have been proposed, we believe that much simpler techniques suffice for our duel learning problem. This is mainly due to the fact that each player knows the general form of the kill probabilities and only needs to estimate his opponent’s parameter vector. Hence, in the current paper, we propose a simple, heuristically motivated, and easily implemented algorithm which allows each player to estimate his optimal strategy, using the information collected from repeated plays of the duel.
The paper is organized as follows. In Section 2 we present the rules of the game. In Section 3 we solve the game under the assumption of complete information. In Section 4 we present our algorithm for solving the game when the players have incomplete information. In Section 5 we evaluate the algorithm by numerical experiments. Finally, in Section 6 we summarize our results and present our conclusions.
2. Game Description
The duel with which we are concerned is a zero-sum game played between players and , under the following rules.
- It is played in discrete rounds (time steps) .
- In the first turn, the players are at distance D.
- (resp. ) plays on odd (resp. even) rounds.
- On his turn, each player has two choices: (i) he can shoot his opponent or (ii) he can move one step forward, reducing their distance by one.
- If shoots (with ), he has a kill probability of hitting (and killing) his opponent, where d is their current distance. If he misses, the opponent can walk right next to him and shoot him for a certain kill.
- Each player’s payoff is 1 if he kills the opponent and if he is killed. Note that a player who misses his shot has payoff , since the opponent will approach him at distance one and shoot at him with kill probability one.
For , we will denote by the position of at round t. The starting positions are and , with . The distance between the players at time t is
For , the kill probability is a decreasing function with . It is convenient to describe the kill probabilities as vectors:
This duel can be modeled as an extensive form game or tree game. The game tree is a directed graph with vertex set
where
- the vertex corresponds to a game state in which the players are at distance d, and
- the vertex is a terminal vertex, in which the “active” player has fired at his opponent.
The edges correspond to state transitions; it is easy to see that the edge set is
An example of the game tree, for , appears in Figure 1. The circular (resp. square) vertices are the ones in which (resp. ) is active, and the rhombic vertices are the terminal ones.
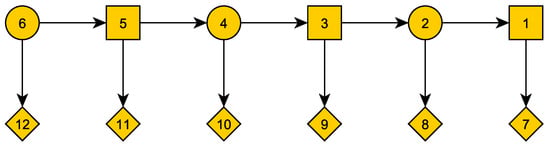
Figure 1.
Game tree example.
To complete the description of the game, we will define the expected payoff for the terminal vertices. Note that the terminal vertex is the child of the nonterminal vertex d in which:
- The distance of the players is d and, assuming to be the active player, his probability of hitting his opponent is .
- The active player is (resp. ) if d is even (resp. odd).
Keeping the above in mind, we see that the payoff (to ) of vertex is
Since this is a zero-sum game, the payoff to at vertex is . This completes the description of the duel.
3. Solution with Complete Information
It is easy to solve the above duel when each player knows D and both and . We construct the game tree as described in Section 2 and we solve it by backward induction. Since the method is standard, we simply give an example of its application. Suppose that
We take , , , . The kill probabilities are as seen in Table 1.

Table 1.
Kill probabilities.
The game tree with terminal payoffs is illustrated in Figure 2.
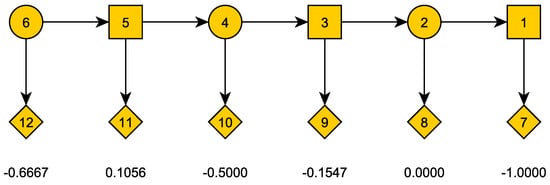
Figure 2.
Game tree example with values of terminal vertices.
By the standard backward induction procedure, we select the optimal action at each vertex and also compute the values of the nonterminal vertices. These are indicated in Figure 3 (optimal actions correspond to thick edges). We see that the game value is , attained by shooting when the players are at distance 3 (which happens in round 4).
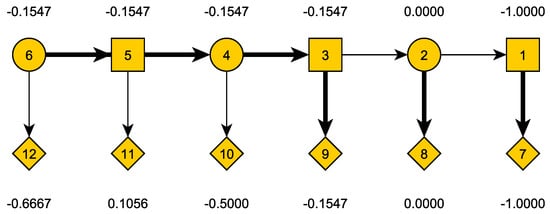
Figure 3.
Game tree example with values of all vertices.
We next present a proposition which characterizes each player’s optimal strategy in terms of a shooting threshold.1 In the following, we use the standard notation by which “” denotes the “other player”, i.e., and .2
Theorem 1.
We define for the shooting criterion vectors where
Then, the optimal strategy for is to shoot as soon as it is his turn and the distance of the players is less than or equal to the shooting threshold , where:
Proof.
Suppose the players are at distance d and the active player is .
- If will not shoot in the next round, when their distance will be , then must also not shoot in the current round, because he will have a higher kill probability in his next turn, when they will be at distance .
- If will shoot in the next round, when their distance will be , then should shoot if (his kill probability now) is higher than (’s miss probability in the next round). In other words, must shoot ifor, equivalently, if
Hence, we can reason as follows:
- At vertex 1, is active and his only choice is to shoot.
- At vertex 2, is active and he knows will certainly shoot in the next round. Hence, will shoot if he has an advantage, i.e., ifThis is equivalent to and will always be true.
- Hence, at vertex 3, is active and he knows that will certainly shoot in the next round (at vertex d). So, will shoot ifwhich is equivalent to . Also, if , then will know, when the game is at vertex 4, that will not shoot when at 3. So, will not shoot when at 4. But then, when at 5, knows that will not shoot when at 4. Continuing in this manner, we see that implies that firing will take place exactly at the vertex 2.
- On the other hand, if , then knows when at 4 that will shoot at the next round. So, when at 4, should shoot if . If, on the other hand, , then will not shoot when at 4 and will shoot when at 3.
- We continue in this manner for increasing values of d. Since both and are decreasing with d, there will exist a maximum value (it could equal D) in which some will be greater than one and will be active; then, must shoot as soon as the game reaches or passes vertex and he “has the action”.
This completes the proof. □
Returning to our previous example, we compute the vectors for and list them in the following Table 2.

Table 2.
Shooting criterion.
For the shooting criterion is last satisfied when the distance is ; this happens at round 4, in which is inactive, so he should shoot at round 5. However, for the shooting criterion is also last satisfied at distance and round 4, in which is active; so, he should shoot at round 4. This is the same result we obtained with backward induction.
4. Solution with Incomplete Information
As already mentioned, the implementation of either the backward induction or the shooting criterion requires complete information, i.e., knowledge by both players of all game parameters: D, , and .
In what follows, we will assume that the players’ kill probabilities have the functional form (where is a parameter vector):
Suppose now that both players know D and but, for , only knows his own parameter vector and is ignorant of the opponent’s . Hence, each knows , but not . Consequently, neither player knows his payoff function, which depends on both and .
In this case, obviously, the players cannot perform the computations of either backward induction or the shooting criterion. Instead, assuming that the players will engage in multiple duels, we propose the use of an heuristic “exploration-and-exploitation” approach in which each player initially adopts a random strategy and, using information collected from played games, he gradually builds and refines an estimate of his optimal strategy. Our approach is implemented by Algorithm 1, presented below in pseudocode.
| Algorithm 1 Learning the Optimal Duel Strategy. |
|
The following remarks explain the operation of the algorithm.
- In line 1, the algorithm takes as input: (i) the duel parameters D, , and ; (ii) two learning parameters ; and (iii) the number R of duels used in the learning process.
- Then, in lines 2–3, the true kill probability (for ) is computed by the function CompKillProb, which simply computesWe emphasize that these are the true kill probabilities.
- In line 4, randomly selected parameter vector estimates are generated.
- Then, the algorithm enters the loop of lines 5–15 (executed for R iterations), which constitutes the main learning process.
- (a)
- In lines 6–7 we compute new estimates of the kill probabilities , by function CompKillProb, based on the estimates of parameters :We emphasize that these are estimates of the kill probabilities, based on the parameter estimates .
- (b)
- In lines 8–9 we compute new estimates of the shooting thresholds , by function CompShootDist. For , this is achieved by computing the shooting criterion using the (known to ) and the (estimated by ) .
- (c)
- In line 10, (which will be used as a standard deviation parameter) is divided by the factor .
- (d)
- In line 11, the result of the duel is computed by the function PlayDuel. This is achieved as follows:
- For , selects a random shooting distance from the discrete normal distribution () with mean and standard deviation .
- With both selected, it is clear which player will shoot first; the outcome of the shot (hit or miss) is a Bernoulli random variable with success probability , where is the shooting player. Note that is the true kill probability.
The result is stored in a table X, which contains the data (shooting distance, shooting player, hit or miss) of every duel played up to the r-th iteration. - (e)
- In line 12, the entire game records X are used by EstKillProb to obtain empirical estimates of the kill probabilities . These estimates are as follows:where
- (f)
- In lines 13–14 the function EstPars uses a least squares algorithm to find (only for the who currently has the action) values which minimize the squared error
- (g)
- In line 16, the algorithm returns the final estimates of optimal shooting distances and parameters .
The core of the algorithm is the exploration-exploitation approach, which is implemented by the gradual reduction of in line 10. Since , we have .
Exploration is predominant in the initial iterations of the algorithm, when the relatively large value of implies that the players use essentially random shooting thresholds. In this phase, ’s shooting threshold and, consequently, his payoff, is suboptimal. However, since is also using various, randomly selected shooting thresholds, collects information about ’s kill probability at various distances. This information can be used to estimate ; the fact that the functional form of the kill probabilities is known results in a tractable parameter estimation problem.
As r increases, we gradually enter the exploitation phase. Namely, tends to zero, which means that each uses a shooting threshold that is, with high probability, very close to the one which is optimal with respect to , and his current estimate of , the opponent’s kill probability. Provided a sufficient amount of information was collected in the exploration phase, is sufficiently close to to ensure that the used shooting threshold is close to the optimal one. The key issue is to choose a learning rate that is “sufficiently slow” to ensure that the exploration phase is long enough to provide enough information for convergence of the parameter estimates to the true parameter values, but not “too slow”, because this will result in slow convergence. This is the exploration-exploitation dilemma, which has been extensively studied in the reinforcement learning literature. For several Q-learning algorithms it has been established that convergence to the optimal policy is guuaranteed, provided the learning rate is sufficiently slow (; ; ); in this manner, a balance is achieved between exploration, which collects data on long-term payoff, and exploitation, which maximizes near-term payoff. Similar conclusions have been established for multi-agent reinforcement learning (; ).
Since our approach is heuristic, the evaluation of an “appropriately slow” learning rate is performed by the numerical experiments in Section 5. Before proceeding, let us note that “methods with the best theoretical bounds are not necessarily those that perform best in practice” ().
5. Experiments
Since the motivation for our proposed algorithm is heuristic, in this section, we give an empirical evaluation of its performance. In the following numerical experiments, we will investigate the influence of both the duel parameters (D, , ) and the algorithm parameters (, , R).
5.1. Experiments Setup
In the following subsection, we present several experiment groups, all of which share the same structure. Each experiment group corresponds to a particular form of the kill probability functions. In each case, the kill probability parameters, along with the initial player distance D, are the game parameters. For each choice of game parameters we proceed as follows.
First, we select the learning parameters and the number of learning steps R. These, together with the game parameters, are the experiment parameters. Then, we select a number J of estimation experiments to run for each choice of experiment parameters. For each of the J experiments, we compute the following quantities:
- The relative error of the final kill probability parameter estimates. For a given parameter , this error is defined to be
- The relative error of the shooting threshold estimates. Letting be the estimate of the shooting threshold based on the true kill probability vector and kill probability vector estimate , this error is defined to be
- The relative error of the optimal payoff estimates. Letting be the estimate of the optimal payoff (computed from the estimated shooting thresholds ), this error is defined to beNote that , because the game is zero-sum.
5.2. Experiment Group A
In this group, the kill probability function has the form:
Let us look at the final results of a representative run of the learning algorithm. With , , , and , we run the learning algorithm with , , and for three different values . In Figure 4 we plot the logarithm (with base 10) of the relative payoff error (we have added to deal with the logarithm of zero error). The three curves plotted correspond to the values 1.001, 1.01, and 1.05. We see that, for all values, the algorithm achieves zero relative error; in other words, it learns the optimal strategy for both players. Furthermore, convergence is achieved by the 1500th iteration of the algorithm (1500th duel played), as seen by the achieved logarithm value (recall that we have added to the error, hence the true error is zero). Convergence is fastest for the largest value, i.e., , and slowest for the smallest value, .
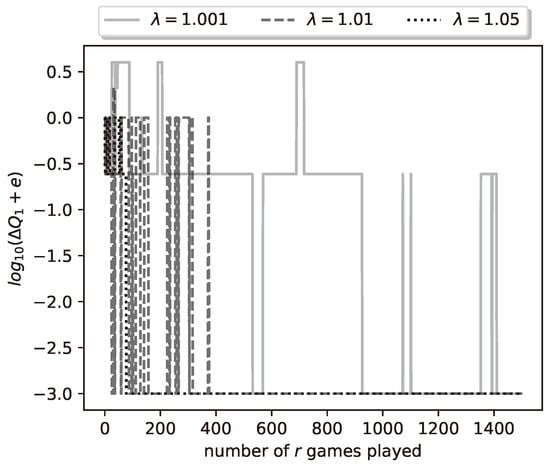
Figure 4.
Plot of logarithmic relative error of ’s payoff for a representative run of the learning process.
In Figure 5, we plot the logarithmic relative errors . These also, as expected, have converged to zero by the 1500th iteration.
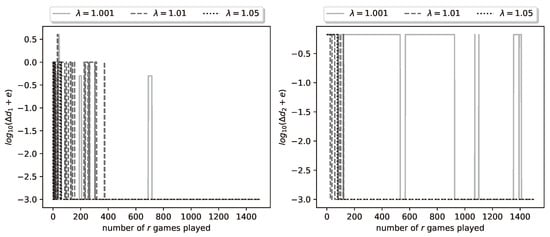
Figure 5.
Plot of logarithmic relative errors and for a representative run of the learning process.
The fact that the estimates of the optimal shooting thresholds and strategies achieve zero error does not imply that the same is true of the kill probability parameter estimates. In Figure 6 we plot the relative errors and .
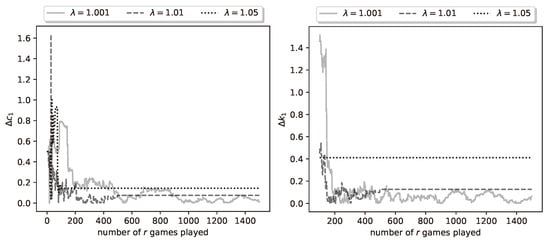
Figure 6.
Plot of relative parameter errors and for a representative run of the learning process.
It can be seen that these errors do not converge to zero; in fact, for , the errors converge to fixed nonzero values, which indicates that the algorithm obtains wrong estimates. However, the error is sufficiently small to still result in zero-error estimates of the shooting thresholds. The picture is similar for the errors and ; hence, their plots are omitted.
In the above, we have given results for a particular run of the learning algorithm. This was a successful run, in the sense that it obtained zero-error estimates of the optimal strategies (and shooting thresholds). However, since our algorithm is stochastic, it is not guaranteed that every run will result in zero-error estimates. To better evaluate the algorithm, we ran it times and averaged the obtained results. In particular, in Figure 7, we plot the average of ten curves of the type plotted in Figure 4. Note that now we plot the curve for plays of the duel.
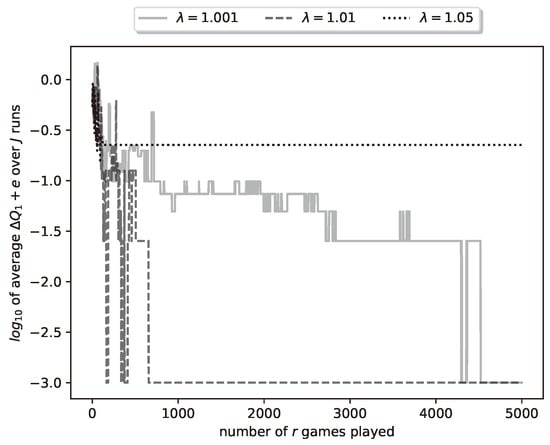
Figure 7.
Plot of (’s payoff) for a representative run of the learning process.
Several observations can be made regarding Figure 7.
- For the smallest value, namely, , the respective curve reaches at . This corresponds to zero average error, which means that, in some algorithm runs, it took more than 4500 iterations (duel plays) to reach zero error.
- For , all runs of the algorithm reached zero-error after runs.
- Finally, for , the average error never reached zero; in fact, 3 out of 10 runs converged to nonzero-error estimates, i.e., to non-optimal strategies.
The above observations corroborate the remarks at the end of Section 4 regarding reinforcement learning. Namely, a small learning rate (in our case small ) results in higher probability of converging to the true parameter values, but also in slower convergence. This can be explained as follows: a small results in higher values for a large proportion of duels played by the algorithm; i.e., in more extensive exploration, which however results in slower exploitation (convergence).
We concluded this group of experiments by running the learning algorithm for various combinations of game parameters; for each combination, we recorded the average error attained at the end of the algorithm (i.e., at ). The results are summarized in the following Table 3, Table 4 and Table 5.

Table 3.
Values of final average relative error for , and various values of , , . D is fixed at .

Table 4.
Round at which converged to zero for all sessions for , and various values of , , . D is fixed at . If did not converge for all sessions, we note for how many sessions it converged.

Table 5.
Fraction of learning sessions that converged to for different values of D and .
From Table 6 and Table 7, we see that for , almost all learning sessions conclude in zero , while increasing the value of results in more sessions concluding with non-zero error estimates. Furthermore, we observe that when the average converges to zero for multiple values of , the convergence is faster for bigger . These results highlight the trade off between exploration and exploitation discussed above.

Table 6.
Values of final average relative error for , and various values of , , . D is fixed at .

Table 7.
Round at which converged to zero for all sessions for , and various values of , , . D is fixed at . If did not converge for all sessions we note for how many sessions it converged.
Finally, in Table 8, we see how many learning sessions were run and how many converged to the zero error estimate for different values of D and .

Table 8.
Fraction of learning sessions that converged to for different values of D and .
5.3. Experiment Group B
In this group, the kill probability function is piecewise linear:
Let us look again at the final results of a representative run of the learning algorithm. With , , , , and , we run the learning algorithm with , , and for the values . In Figure 8 we plot the logarithm (with base 10) of the relative payoff error . We see similar results as in Group A, for all values, the algorithm achieves zero relative error. Convergence is achieved by the 300th iteration of the algorithm and it is fastest for , and slowest for . The plots of the errors , are omitted, since they are similar to the ones given in Figure 5.
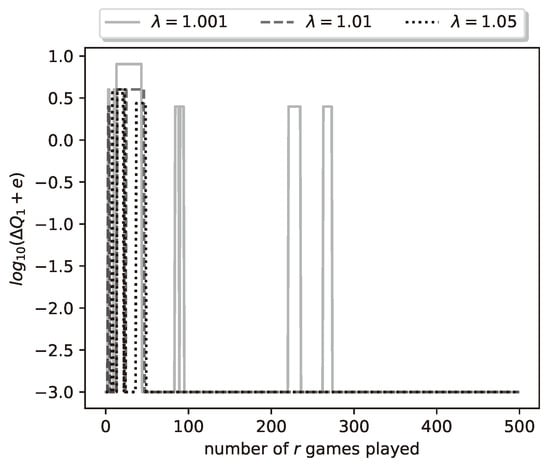
Figure 8.
Plot of logarithmic relative error of ’s payoff for a representative run of the learning process.
As in Group A, the fact that the estimates of the optimal shooting thresholds and strategies achieve zero error does not imply that the same is true for the kill probability parameter estimates. For example, in this particular run, the relative error converges to a nonzero value, i.e., the algorithm obtains a wrong estimate of . However, the error is sufficiently small to still result in a zero-error estimate of the shooting thresholds.
As in Group A, to better evaluate the algorithm, we ran it times and averaged the obtained results. In particular, in Figure 9, we plot the average of ten curves of the type plotted in Figure 4. Note that we now plot the curve for plays of the duel.
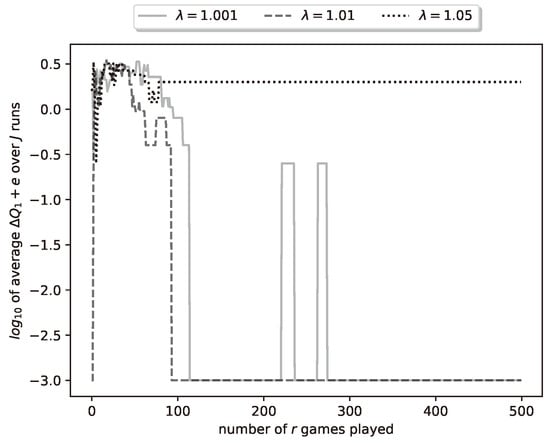
Figure 9.
Plot of (’s payoff) for a representative run of the learning process.
We again ran the learning algorithm for various combinations of game parameters and recorded the average error attained at the end of the algorithm (again at ) for each combination. The results are summarized in the following tables.
From Table 6 and Table 7, we observe that for most parameter combinations, all learning sessions concluded with a zero for the smaller values. However, for , the algorithm failed to converge and exhibited a high relative error. Notably, increasing from 1.001 to 1.01 generally accelerated convergence, although this is not guaranteed in every case. In one instance, a higher (specifically ) led to a slower average convergence of to zero, indicating the importance of initial random shooting choices. We also observed that the results for the highest were suboptimal, with the algorithm failing to converge in varying numbers of sessions, such as in 1 out of 10 or even 5 out of 10 cases. Notably, when convergence did occur, it happened relatively quickly, with sessions typically completing in under 1000 iterations. These findings also highlight the trade-off between exploration and exploitation, as discussed earlier.
Finally, in Table 8, we see how many learning sessions were run and how many converged to the zero-error estimate for different values of D and .
6. Discussion
We proposed an algorithm for estimating unknown game parameters and optimal strategies for a duel game through the course of repeated plays. We tested an algorithm for two models of the kill probability function and found that it converged for the majority of tests. Furthermore, we observed the established relationship between higher learning rates and reduced convergence quality, underscoring the trade-off between learning speed and stability in convergence. Future research could investigate additional models of the accuracy probability function, including scenarios where the two players employ distinct models, and work toward establishing theoretical bounds on the algorithm’s probabilistic convergence.
Author Contributions
All authors contributed equally to all parts of this work, namely conceptualization, methodology, software, validation, formal analysis, writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Notes
| 1 | This proposition is stated informally in (). |
| 2 | We use the same notation for several other quantities as will be seen in the sequel. |
References
- Alexander, J. M. (2023). Evolutionary game theory. Cambridge University Press. [Google Scholar]
- Alonso, E., D’Inverno, M., Kudenko, D., Luck, M., & Noble, J. (2001). Learning in multi-agent systems. The Knowledge Engineering Review, 16, 277–284. [Google Scholar] [CrossRef]
- Brown, G. W. (1949). Some notes on computation of games solutions (Rand Corporation Report). Rand Corporation. [Google Scholar]
- Cressman, R. (2003). Evolutionary dynamics and extensive form games. MIT Press. [Google Scholar]
- Fox, M., & Kimeldorf, G. S. (1969). Noisy duels. SIAM Journal on Applied Mathematics, 17, 353–361. [Google Scholar] [CrossRef]
- Fudenberg, D., & Levine, D. K. (1998). The theory of learning in games. MIT Press. [Google Scholar]
- Fudenberg, D., & Levine, D. K. (2016). Whither game theory? Towards a theory of learning in games. Journal of Economic Perspectives, 30, 151–170. [Google Scholar] [CrossRef]
- Garnaev, A. (2000). Games of Timing. In Search games and other applications of game theory (pp. 81–120). Springer. [Google Scholar]
- Gronauer, S., & Diepold, K. (2022). Multi-agent deep reinforcement learning: A survey. Artificial Intelligence Review, 55, 895–943. [Google Scholar] [CrossRef]
- Harsanyi, J. C. (1962). Bargaining in ignorance of the opponent’s utility function. Journal of Conflict Resolution, 6, 29–38. [Google Scholar] [CrossRef]
- Hussain, A., Belardinelli, F., & Paccagnan, D. (2023). The impact of exploration on convergence and performance of multi-agent Q-learning dynamics. In International conference on machine learning (Vol. 1). PMLR. [Google Scholar]
- Ishii, S., Yoshida, W., & Yoshimoto, J. (2002). Control of exploitation–exploration meta-parameter in reinforcement learning. Neural Networks, 15, 665–687. [Google Scholar] [CrossRef] [PubMed]
- Jain, G., Kumar, A., & Bhat, S. A. (2024). Recent developments of game theory and reinforcement learning approaches: A systematic review. IEEE Access, 12, 9999–10011. [Google Scholar] [CrossRef]
- Leonardos, S., Piliouras, G., & Spendlove, K. (2021). Exploration-exploitation in multi-agent competition: Convergence with bounded rationality. Advances in Neural Information Processing Systems, 34, 26318–26331. [Google Scholar]
- Martin, C., & Sandholm, T. (2021, February 8–9). Efficient exploration of zero-sum stochastic games [Conference session]. AAAI Workshop on Reinforcement Learning in Games, Virtual Workshop. [Google Scholar]
- Mertikopoulos, P., & Sandholm, W. H. (2016). Learning in games via reinforcement and regularization. Mathematics of Operations Research, 41, 1297–1324. [Google Scholar] [CrossRef]
- Nowe, A., Vrancx, P., & De Hauwere, Y.-M. (2012). Game theory and multi-agent reinforcement learning. In Reinforcement learning: State-of-the-art (pp. 441–470). Springer. [Google Scholar]
- Osband, I., & Van Roy, B. (2017). Why is posterior sampling better than optimism for reinforcement learning? In International conference on machine learning (pp. 2701–2710). PMLR. [Google Scholar]
- Polak, B. (2007). Backward induction: Reputation and duels. Open Yale Courses. Available online: https://oyc.yale.edu/economics/econ-159/lecture-16 (accessed on 19 January 2025).
- Prisner, E. (2014). Game theory through examples (Vol. 46). American Mathematical Society. [Google Scholar]
- Radzik, T. (1988). Games of timing related to distribution of resources. Journal of Optimization Theory and Applications, 58, 443–471. [Google Scholar] [CrossRef]
- Rezek, I., Leslie, D. S., Reece, S., Roberts, S. J., Rogers, A., Dash, R. K., & Jennings, N. R. (2008). On similarities between inference in game theory and machine learning. Journal of Artificial Intelligence Research, 33, 259–283. [Google Scholar] [CrossRef]
- Robinson, J. (1951). An iterative method of solving a game. Annals of Mathematics, 54, 296–301. [Google Scholar] [CrossRef]
- Roy, D. (2003). The discrete normal distribution. Communications in Statistics-Theory and Methods, 32, 1871–1883. [Google Scholar] [CrossRef]
- Singh, S., Jaakkola, T., Littman, M. L., & Szepesvari, C. (2000). Convergence results for single-step on-policy reinforcement learning algorithms. Machine Learning, 38, 287–308. [Google Scholar] [CrossRef]
- Tanimoto, J. (2015). Fundamentals of evolutionary game theory and its applications. Springer. [Google Scholar]
- Weibull, J. W. (1997). Evolutionary game theory. MIT Press. [Google Scholar]
- Yang, Y., & Wang, J. (2020). An overview of multi-agent reinforcement learning from game theoretical perspective. arXiv, arXiv:2011.00583. [Google Scholar]
- Zamir, S. (2020). Bayesian games: Games with incomplete information. Springer. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).