Topology Optimization of Metal and Carbon Fiber Reinforced Plastic (CFRP) Laminated Battery-Hanging Structure
Abstract
:1. Introduction
2. Methodology
2.1. Discrete Material Topology Optimization
2.2. Manufacturing Constraints
2.3. Filtering Technique
2.4. Design Sensitivity Analysis
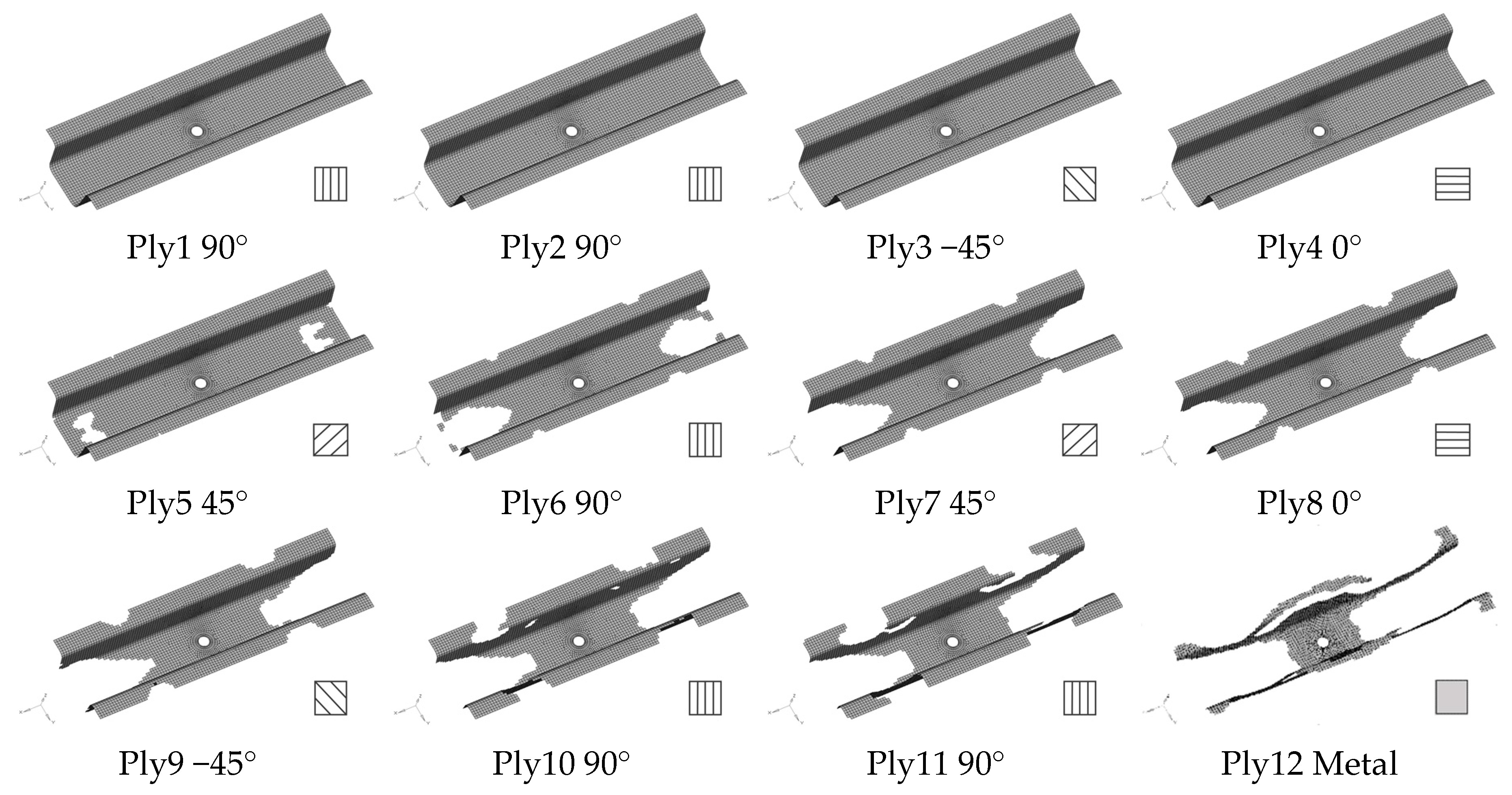
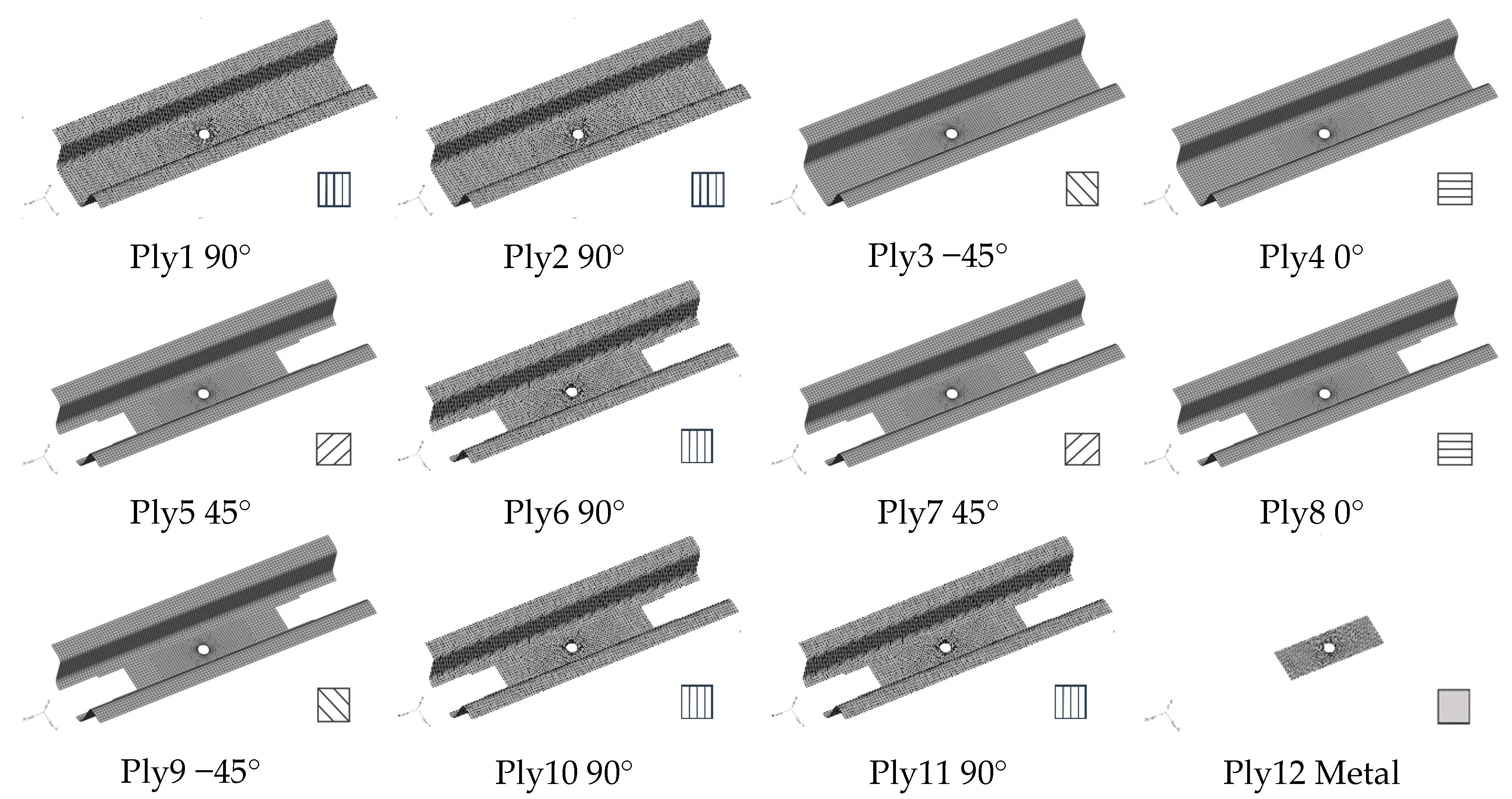
3. Optimization of a CFRP-Laminated Battery-Hanging Structure
3.1. Finite Element Model
3.2. Design Optimization of the Battery-Hanging Structure
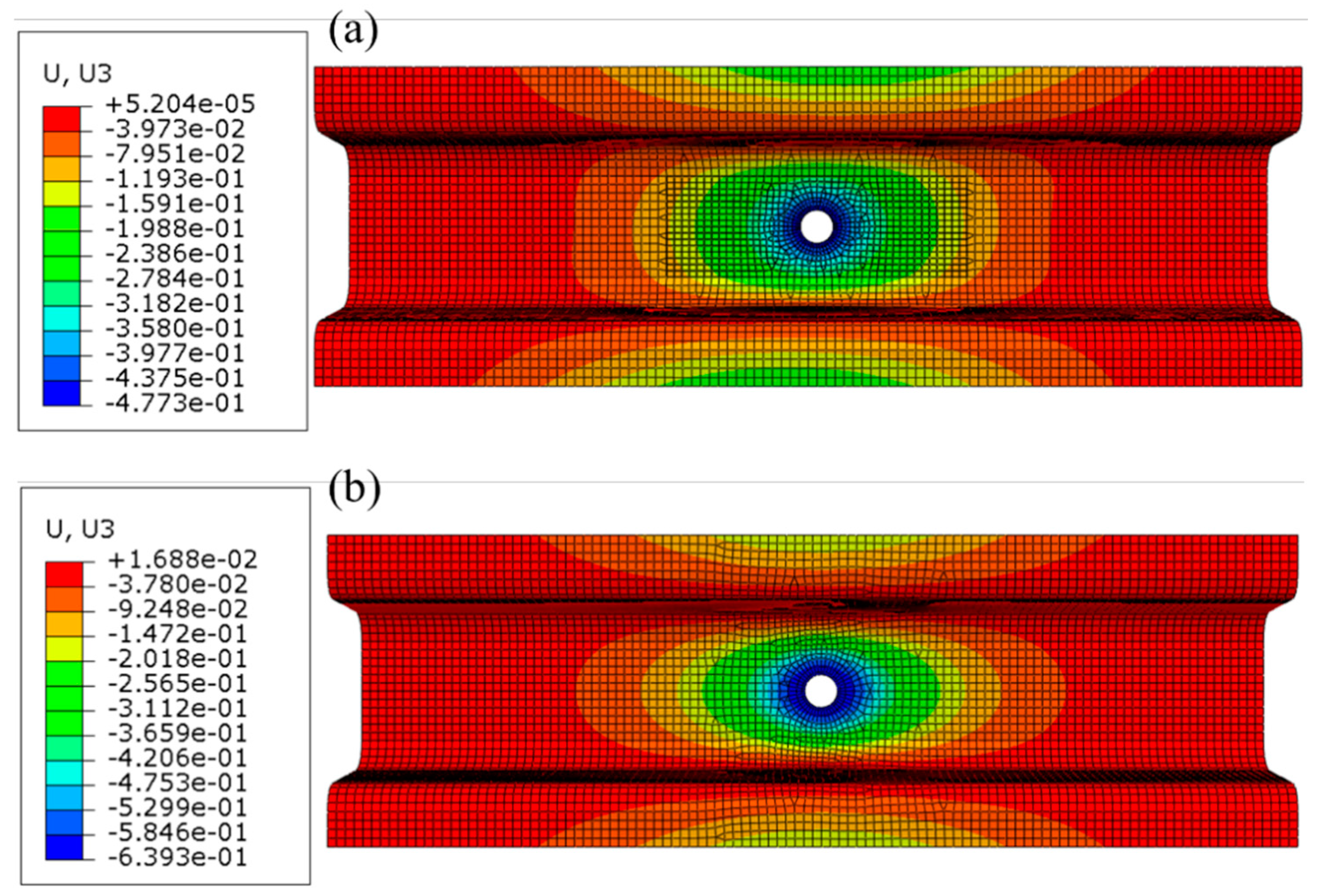
3.3. Comparison between Original Steel Structure and the Optimized Structure
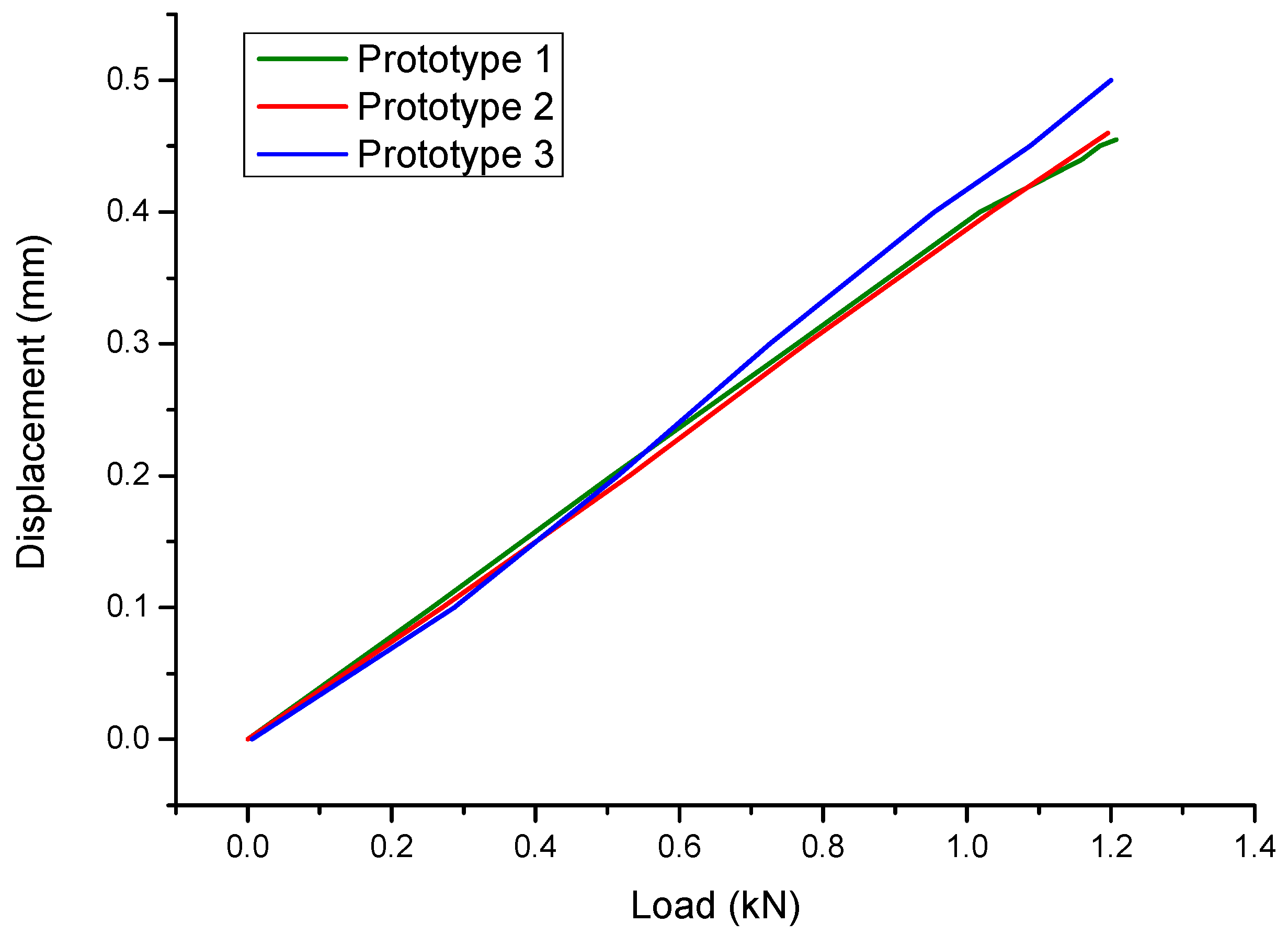
4. Prototype and Experimental Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luin, B.; Petelin, S.; Al-Mansour, F. Microsimulation of Electric Vehicle Energy Consumption. Energy 2019, 174, 24–32. [Google Scholar] [CrossRef]
- Fontaras, G.; Zacharof, N.-G.; Ciuffo, B. Fuel Consumption and Co2 Emissions from Passenger Cars in Europe–Laboratory Versus Real-World Emissions. Prog. Energy Combust. Sci. 2017, 60, 97–131. [Google Scholar] [CrossRef]
- Ha, N.S.; Lu, G. A Review of Recent Research on Bio-Inspired Structures and Materials for Energy Absorption Applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Wu, C.; Gao, Y.; Fang, J.; Lund, E.; Li, Q. Discrete Topology Optimization of Ply Orientation for a Carbon Fiber Reinforced Plastic (Cfrp) Laminate Vehicle Door. Mater. Des. 2017, 128, 9–19. [Google Scholar] [CrossRef]
- Wu, C.; Gao, Y.; Fang, J.; Lund, E.; Li, Q. Simultaneous Discrete Topology Optimization of Ply Orientation and Thickness for Carbon Fiber Reinforced Plastic-Laminated Structures. J. Mech. Des. 2019, 141, 044501. [Google Scholar] [CrossRef]
- Lee, J.-M.; Min, B.-J.; Park, J.; Kim, D.-H.; Kim, B.; Ko, D.-C. Design of Lightweight Cfrp Automotive Part as an Alternative for Steel Part by Thickness and Lay-up Optimization. Materials 2019, 12, 2309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.-C.; Park, D.-H.; Jung, H.-S.; Lee, S.H.; Jeong, W.Y.; Kim, K.-Y.; Lim, D.Y. Design for Carbon Fiber Lamination of Pmi Foam Cored Cfrp Sandwich Composite Applied to Automotive Rear Spoiler. Fibers Polym. 2020, 21, 156–161. [Google Scholar] [CrossRef]
- Salas, R.A.; Ramírez-Gil, F.J.; Montealegre-Rubio, W.; Silva, E.C.N.; Reddy, J.N. Optimized Dynamic Design of Laminated Piezocomposite Multi-Entry Actuators Considering Fiber Orientation. Comput. Methods Appl. Mech. Eng. 2018, 335, 223–254. [Google Scholar] [CrossRef]
- Le Riche, R.; Haftka, R.T. Optimization of Laminate Stacking Sequence for Buckling Load Maximization by Genetic Algorithm. AIAA J. 1993, 31, 951–956. [Google Scholar] [CrossRef]
- Le Riche, R.; Haftka, R.T. Improved Genetic Algorithm for Minimum Thickness Composite Laminate Design. Compos. Eng. 1995, 5, 143–161. [Google Scholar] [CrossRef]
- Nagendra, S.; Jestin, D.; Gürdal, Z.; Haftka, R.T.; Watson, L.T. Improved Genetic Algorithm for the Design of Stiffened Composite Panels. Comput. Struct. 1996, 58, 543–555. [Google Scholar] [CrossRef] [Green Version]
- Kogiso, N.; Watson, L.T.; Gürdal, Z.; Haftka, R.T. Genetic Algorithms with Local Improvement for Composite Laminate Design. Struct. Optim. 1994, 7, 207–218. [Google Scholar] [CrossRef] [Green Version]
- Irisarri, F.X.; Lasseigne, A.; Leroy, F.H.; Le Riche, R. Optimal Design of Laminated Composite Structures with Ply Drops Using Stacking Sequence Tables. Compos. Struct. 2014, 107, 559–569. [Google Scholar] [CrossRef]
- Ghiasi, H.; Pasini, D.; Lessard, L. Optimum Stacking Sequence Design of Composite Materials Part I: Constant Stiffness Design. Compos. Struct. 2009, 90, 1–11. [Google Scholar] [CrossRef]
- Ghiasi, H.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Optimum Stacking Sequence Design of Composite Materials Part II: Variable Stiffness Design. Compos. Struct. 2010, 93, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A Review on Optimization of Composite Structures Part I: Laminated Composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Albazzan, M.A.; Harik, R.; Tatting, B.F.; Gürdal, Z. Efficient Design Optimization of Nonconventional Laminated Composites Using Lamination Parameters: A State of the Art. Compos. Struct. 2019, 209, 362–374. [Google Scholar] [CrossRef]
- Bruyneel, M. Sfp—A New Parameterization Based on Shape Functions for Optimal Material Selection: Application to Conventional Composite Plies. Struct. Multidiscip. Optim. 2010, 43, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Gao, T.; Zhang, W.; Duysinx, P. A Bi-Value Coding Parameterization Scheme for the Discrete Optimal Orientation Design of the Composite Laminate. Int. J. Numer. Methods Eng. 2012, 91, 98–114. [Google Scholar] [CrossRef]
- Stegmann, J.; Lund, E. Discrete Material Optimization of General Composite Shell Structures. Int. J. Numer. Methods Eng. 2005, 62, 2009–2027. [Google Scholar] [CrossRef]
- Sørensen, S.N.; Sørensen, R.; Lund, E. Dmto–a Method for Discrete Material and Thickness Optimization of Laminated Composite Structures. Struct. Multidiscip. Optim. 2014, 50, 25–47. [Google Scholar] [CrossRef] [Green Version]
- Korayem, A.H.; Chen, S.J.; Zhang, Q.H.; Li, C.Y.; Zhao, X.L.; Duan, W.H. Failure of Cfrp-to-Steel Double Strap Joint Bonded Using Carbon Nanotubes Modified Epoxy Adhesive at Moderately Elevated Temperatures. Compos. Part B Eng. 2016, 94, 95–101. [Google Scholar] [CrossRef]
- Nguyen, T.-C.; Bai, Y.; Al-Mahaidi, R.; Zhao, X.-L. Time-Dependent Behaviour of Steel/Cfrp Double Strap Joints Subjected to Combined Thermal and Mechanical Loading. Compos. Struct. 2012, 94, 1826–1833. [Google Scholar] [CrossRef]
- Zhang, Z.; Shan, J.; Tan, X.; Zhang, J. Improvement of the Laser Joining of Cfrp and Aluminum Via Laser Pre-Treatment. Int. J. Adv. Manuf. Technol. 2016, 90, 3465–3472. [Google Scholar] [CrossRef]
- Zhang, K.; Shi, D.; Wang, W.; Wang, Q. Mechanical Characterization of Hybrid Lattice-to-Steel Joint with Pyramidal Cfrp Truss for Marine Application. Compos. Struct. 2017, 160, 1198–1204. [Google Scholar] [CrossRef]
- Sørensen, S.N.; Lund, E. Topology and Thickness Optimization of Laminated Composites Including Manufacturing Constraints. Struct. Multidiscip. Optim. 2013, 48, 249–265. [Google Scholar] [CrossRef]
- Stolpe, M.; Svanberg, K. An Alternative Interpolation Scheme for Minimum Compliance Topology Optimization. Struct. Multidiscip. Optim. 2001, 22, 116–124. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, Y.; Wu, C.; Fang, J.; Li, Q. Robust Topology Optimization for Multiple Fiber-Reinforced Plastic (Frp) Composites under Loading Uncertainties. Struct. Multidiscip. Optim. 2019, 59, 695–711. [Google Scholar] [CrossRef]
- Gersborg, A.R.; Andreasen, C.S. An Explicit Parameterization for Casting Constraints in Gradient Driven Topology Optimization. Struct. Multidiscip. Optim. 2011, 44, 875–881. [Google Scholar] [CrossRef]
- Sørensen, R.; Lund, E. Thickness Filters for Gradient Based Multi-Material and Thickness Optimization of Laminated Composite Structures. Struct. Multidiscip. Optim. 2015, 52, 227–250. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On Projection Methods, Convergence and Robust Formulations in Topology Optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical Instabilities in Topology Optimization: A Survey on Procedures Dealing with Checkerboards, Mesh-Dependencies and Local Minima. Struct. Multidiscip. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kulikov, G.; Plotnikova, S.V. Equivalent Single-Layer and Layerwise Shell Theories and Rigid-Body Motions—Part I: Foundations. Mech. Adv. Mater. Struct. 2005, 12, 275–283. [Google Scholar] [CrossRef]
- Kulikov, G.M.; Plotnikova, S.V. Equivalent Single-Layer and Layerwise Shell Theories and Rigid-Body Motions—Part II: Computational Aspects. Mech. Adv. Mater. Struct. 2005, 12, 331–340. [Google Scholar] [CrossRef]
- Zhang, J.; Ning, L.; Hao, Y.; Sang, T. Topology Optimization for Crashworthiness and Structural Design of a Battery Electric Vehicle. Int. J. Crashworthiness 2020, 1–10. [Google Scholar] [CrossRef]
- Svanberg, K. The Method of Moving Asymptotes—A New Method for Structural Optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Svanberg, K. The Method of Moving Asymptotes (MMA) with Some Extensions. In Optimization of Large Structural Systems; Springer: Dordrecht, The Netherlands, 1993; pp. 555–566. [Google Scholar]






| Symbol | Parameters for CFRP Material | Value |
|---|---|---|
| Ply thickness for CFRP | 0.2 mm | |
| Longitudinal Young’s modulus | 90 GPa | |
| Transverse Young’s modulus | 6.5 GPa | |
| Shear modulus | 3.5 GPa | |
| Density for CFRP | 1900 kg/m3 | |
| Longitudinal tensile strength | 1800 MPa | |
| Longitudinal compressive strength | 1100 MPa | |
| Transverse tensile strength | 30 MPa | |
| Transverse compressive strength | 144 MPa | |
| Shear strength | 60 MPa | |
| Poisson’s ratio | 0.3 |
| Symbol | Parameter for Metal Material | Value |
|---|---|---|
| Young’s modulus | 210 GPa | |
| Thickness | 1.2 mm | |
| Poisson’s ratio | 0.3 | |
| Density | 7900 kg/m3 |
| Protype 1 | Protype 2 | Protype 3 | Mean | FEA | Error | |
|---|---|---|---|---|---|---|
| Displacement (mm) | 0.44 | 0.45 | 0.49 | 0.460 | 0.477 | 3.70% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Xu, Y.; Gao, Y. Topology Optimization of Metal and Carbon Fiber Reinforced Plastic (CFRP) Laminated Battery-Hanging Structure. Polymers 2020, 12, 2495. https://doi.org/10.3390/polym12112495
Chen J, Xu Y, Gao Y. Topology Optimization of Metal and Carbon Fiber Reinforced Plastic (CFRP) Laminated Battery-Hanging Structure. Polymers. 2020; 12(11):2495. https://doi.org/10.3390/polym12112495
Chicago/Turabian StyleChen, Jiaju, Yanan Xu, and Yunkai Gao. 2020. "Topology Optimization of Metal and Carbon Fiber Reinforced Plastic (CFRP) Laminated Battery-Hanging Structure" Polymers 12, no. 11: 2495. https://doi.org/10.3390/polym12112495






