Flexural Creep Behavior of High-Density Polyethylene Lumber and Wood Plastic Composite Lumber Made from Thermally Modified Wood
Abstract
:1. Introduction
2. Experimental
2.1. Material
2.2. WPC and HDPE Sample Preparation
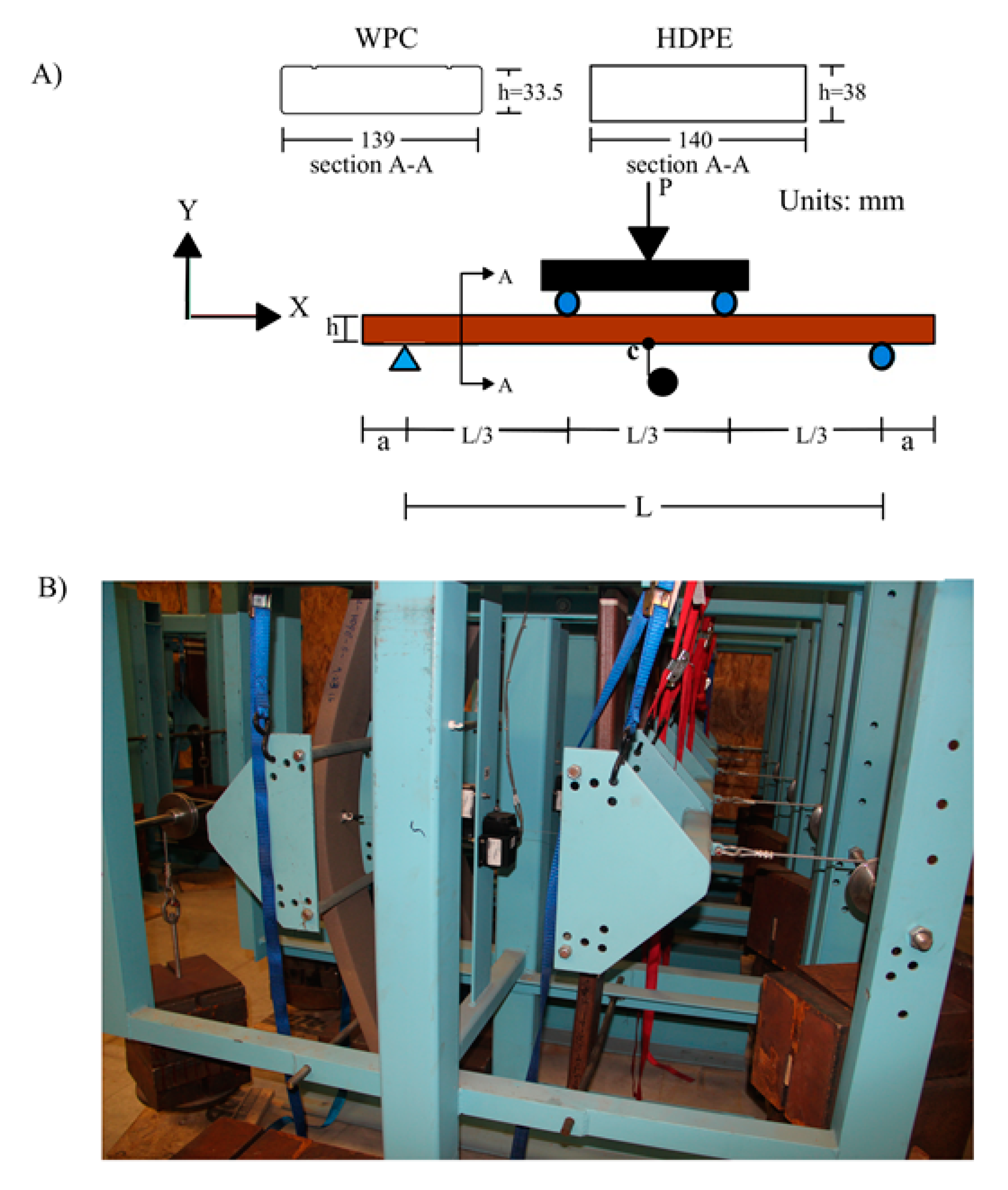
2.3. 180-Day Creep Experimental Setup
2.4. Quasi-Static Tests
3. Results and Discussion
3.1. Determination of the Creep Stress Levels
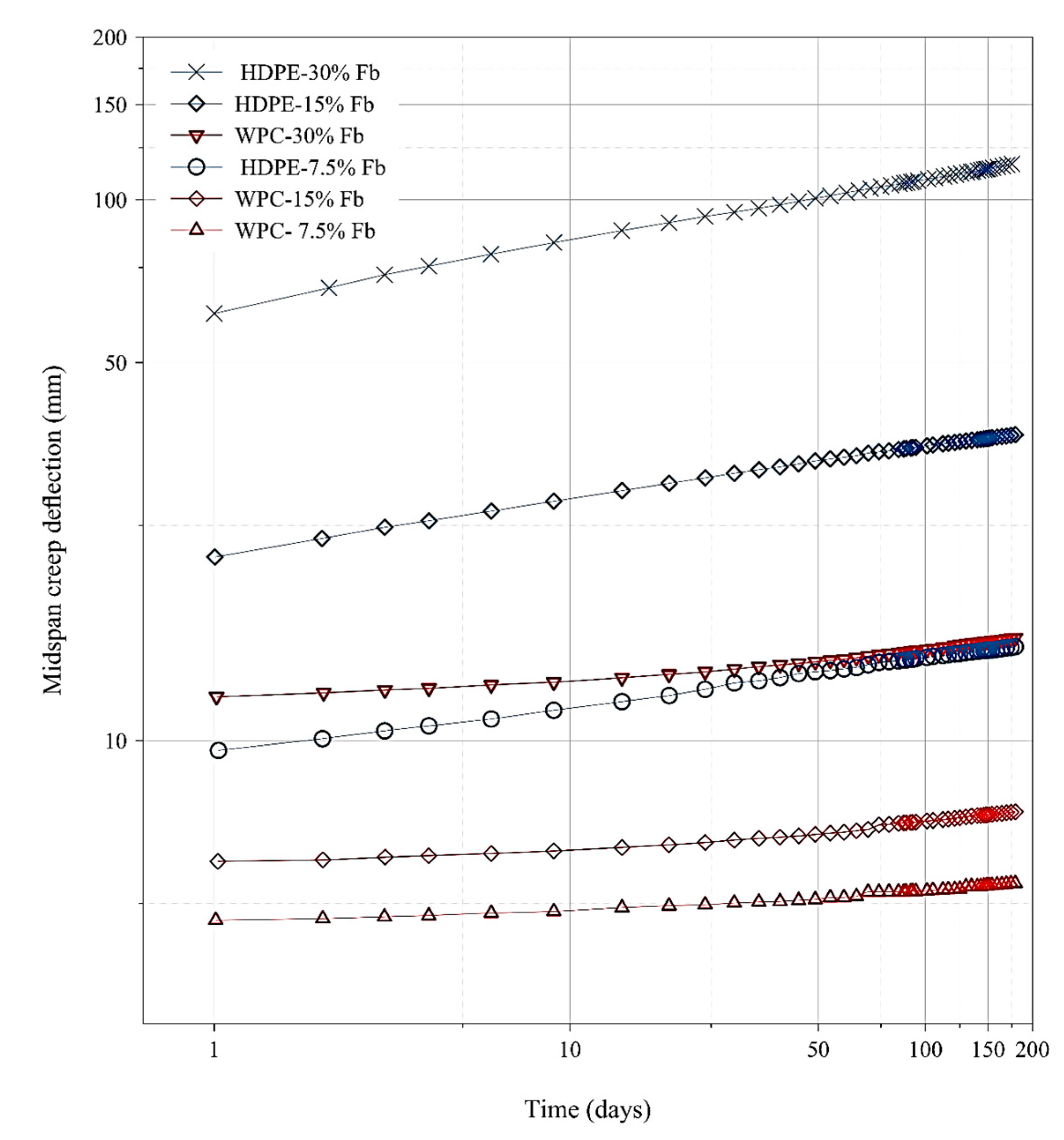
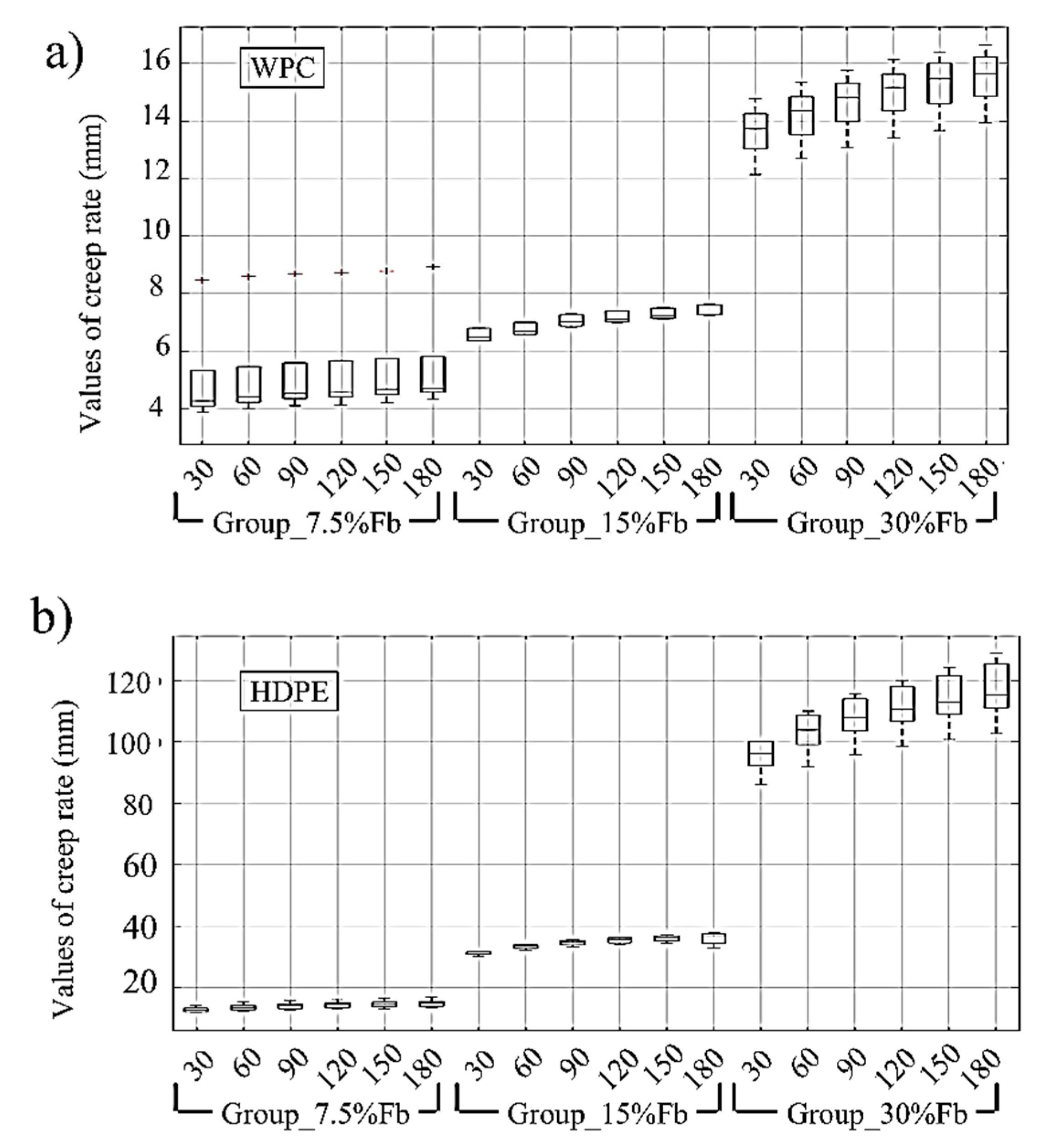
3.2. Experimental Comparison Between the Long-Term Creep of WPC and HDPE Lumber
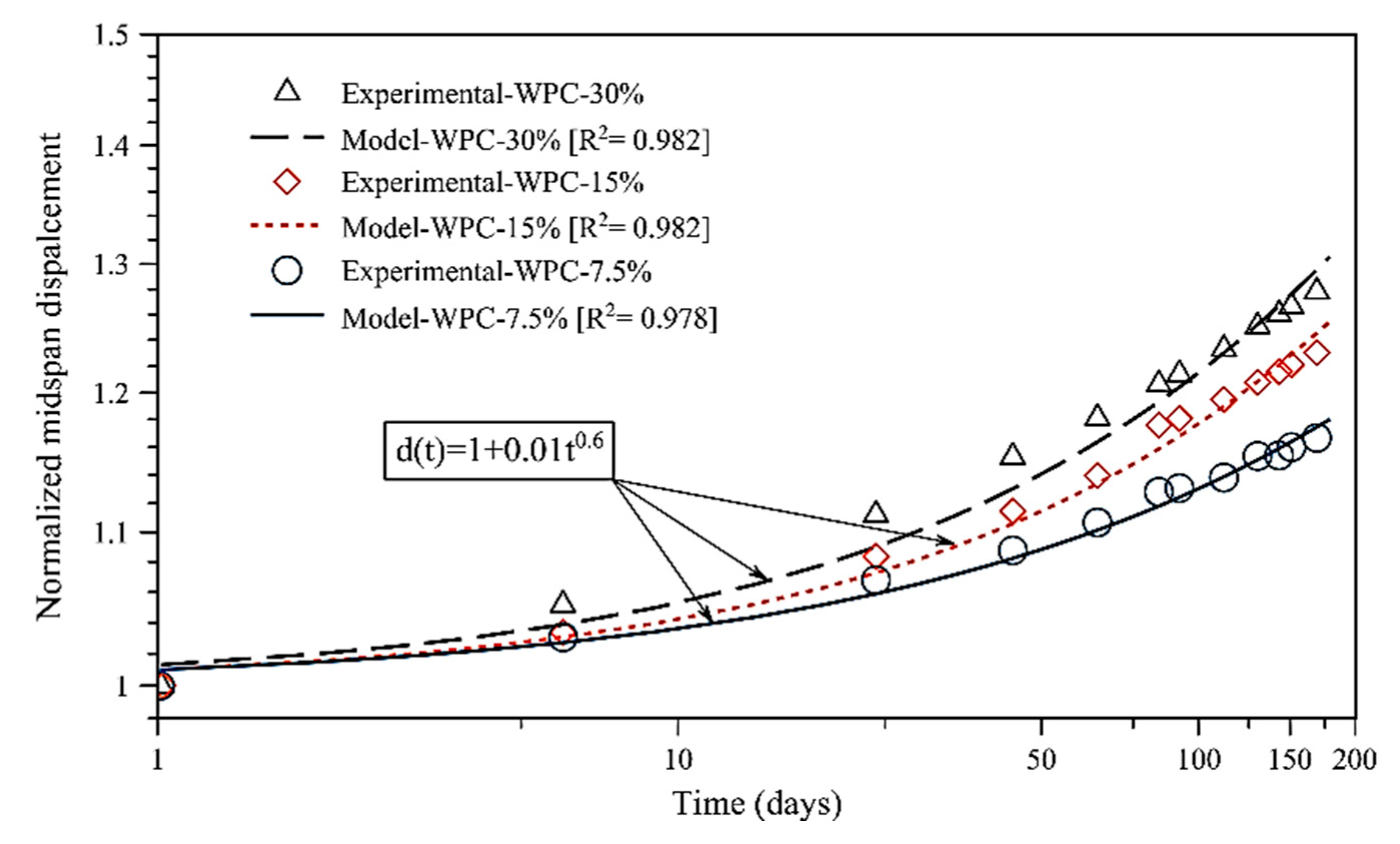
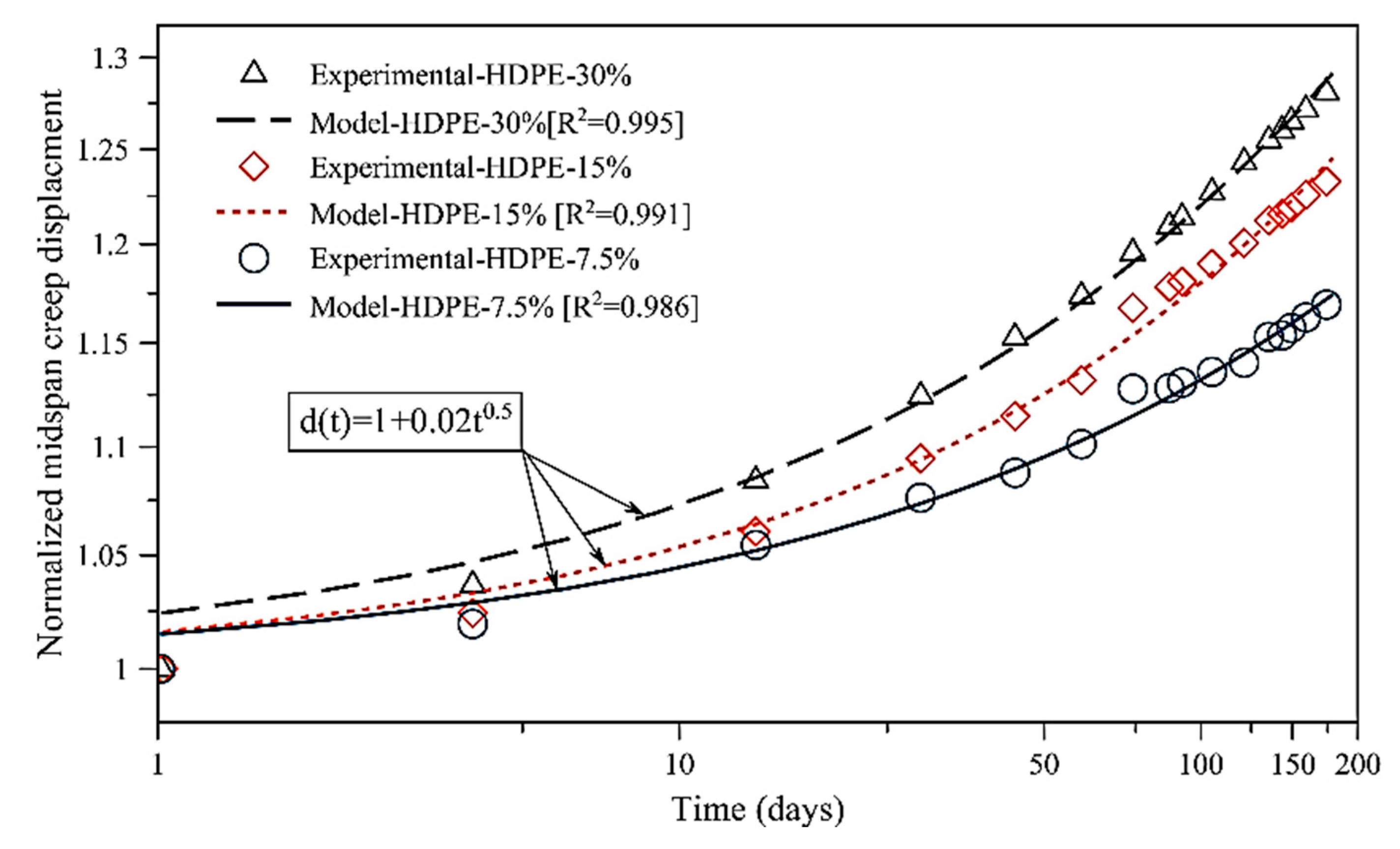
3.3. Time-Dependent Creep Modeling
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klyosov, A.A. Wood-Plastic Composites; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Slaughter, A.E. Design and fatigue of a structural wood-plastic composite. Master of Science thesis, Washington State University, Pullman, WA, USA, 2004. [Google Scholar]
- Daniel, A.-V. Structural Performance of Wood Plastic Composite Sheet Piling. J. Mater. Civil Eng. 2010, 12, 1235–1243. [Google Scholar]
- Gardner, D.; Han, Y. Towards Structural Wood-Plastic Composites: Technical Innovations. In Proceedings of the 6th Meeting of the Nordic-Baltic Network in Wood Material Science and Engineering (WSE), Tallinn, Estonia, 21–22 October 2010. [Google Scholar]
- Haiar, K.J. Performance and Design of Prototype Wood-Plastic Composite Sections; Washington State University: Pullman, WA, USA, 2000. [Google Scholar]
- Hamel, S.E. Modeling the Time-Dependent Flexural Response of Wood-Plastic Composite Materials. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, January 2011. [Google Scholar]
- Dura, M.J. Behavior of Hybrid Wood Plastic Composite-Fiber Reinforced Polymer Structural Members for Use in Sustained Loading Applications. Master’s Thesis, The University of Maine, Orono, ME, USA, May 2005. [Google Scholar]
- Melissa, K. Structural Design of Hollow Extruded WPC Sheet Piling. Master’s Thesis, January 2006. Available online: http://digitalcommons.library.umaine.edu/etd/117 (accessed on 12 December 2018).
- Bright, K.D.; Smith, P.M. Perceptions of New and Established Waterfront Materials by US Marine Decision Makers. Wood Fiber Sci. 2007, 34, 186–204. [Google Scholar]
- Tamrakar, S.; Lopez-Anido, R.A. Water Absorption of Wood Polypropylene Composite Sheet Piles and Its Influence on Mechanical Properties. Constr. Build. Mater. 2011, 25, 3977–3988. [Google Scholar] [CrossRef]
- Alrubaie, M.A.; Lopez-Anido, R.A.; Gardner, D.J.; Tajvidi, M.; Han, Y. Experimental investigation of the hygrothermal creep strain of wood–plastic composite lumber made from thermally modified wood. J. Thermoplast. Compos. Mater. 2019. [Google Scholar] [CrossRef]
- Alrubaie, M.A.; Lopez-Anido, R.A.; Gardner, D.J.; Tajvidi, M.; Han, Y. Modeling the hygrothermal creep behavior of wood plastic composite (WPC) lumber made from thermally modified wood. J. Thermoplast. Compos. Mater. 2019. [Google Scholar] [CrossRef]
- InnovaSea Systems, Inc. A4700 BRIDLE SYSTEM IN GRID MOORING CELL. 2016 [cited September 2017]. Available online: www.innovasea.com (accessed on 17 September 2017).
- Vandenbroucke, K.; Metzlaff, M. Abiotic stress tolerant crops: Genes, pathways and bottlenecks. In Sustainable Food Production; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–17. [Google Scholar]
- InnovaSea Systems, Inc. Report on Structural Damage to A4800 AquaPod; InnovaSea Systems, Inc.: Orono, ME, USA, 2015. [Google Scholar]
- Gardner, D.J. Development of Structural Wood Plastic Composite Timber for Innovative Marine Application. In Research Reinvestment Funds (RRF) Seed Grant Program; The University of Maine: Orono, ME, USA, 2015; p. 23. [Google Scholar]
- Commerce, D.O. Water Temperature Table of All Coastal Regions. Available online: https://www.nodc.noaa.gov/dsdt/cwtg/all.html (accessed on 23 June 2018).
- Gibson, R.F. Principles of Composite Material Mechanics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using AbaqusTM; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Tamrakar Sandeep, R.A.L.-A.; Kiziltas, A.; Gardner, D.J. Time and temperature dependent response of a wood–polypropylene composite. Compos. Part A 2011, 42, 834–842. [Google Scholar] [CrossRef]
- Pooler, D.J. The Temperature Dependent Non-Linear Response of a Wood Plastic Composite; Washington State University: Pullman, WA, USA, 2001. [Google Scholar]
- ASTM International. Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastic Lumber and Related Products, D6109-13; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Hamel, S.E.; Hermanson, J.C.; Cramer, S.M. Predicting the flexure response of wood-plastic composites from uni-axial and shear data using a finite-element model. J. Mater. Civ. Eng. 2014, 26, 04014098. [Google Scholar] [CrossRef]
- Abaqus/CAE. Computer Software; SIMULIA Inc.: Providence, RI, USA, 2017. [Google Scholar]
- ASTM International. Standard Specification for Evaluation of Duration of Load and Creep Effects of Wood and Wood-Based Products, D6815-09 (Reapproved 2015); ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar]
- Alrubaie, M.A. Investigating the Time-dependent and the Mechanical Behavior of Wood Plastic Composite Lumber Made from Thermally Modified Wood in the Use of Marine Aquacultural Structures. Ph.D. Thesis, The University of Maine, Orono, ME, USA, 8 April 2019. [Google Scholar]
- Alrubaie, M.A.A.; Gardner, D.J.; Lopez-Anido, R.A. Structural Performance of HDPE and WPC Lumber Components Used in Aquacultural Geodesic Spherical Cages. Polymers 2020, 12, 26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Page, S.H. Aquapod Systems aquaculture Aquapod systems for Sustainable Ocean Aquaculture Aquaculture. In Sustainable Food Production; Springer: Berlin/Heidelberg, Germany, 2013; pp. 223–235. [Google Scholar]
- King, D.; Hamel, S. The Tensile Creep Response of a Wood-Plastic Composite in Cold Regions. In Proceedings of the 10th International Symposium on Cold Regions Development, Anchorage, AK, USA, 2–5 June 2013; pp. 771–778. [Google Scholar]
- Chassagne, P.; Saïd, E.B.; Jullien, J.F.; Galimard, P. Three dimensional creep model for wood under variable humidity-numerical analyses at different material scales. Mech. Time-Depend. Mater. 2005, 9, 1–21. [Google Scholar] [CrossRef]
- Hamel, S.E.; Hermanson, J.C.; Cramer, S.M. Mechanical and time-dependent behavior of wood–plastic composites subjected to tension and compression. J. Thermoplast. Compos. Mater. 2013, 26, 968–987. [Google Scholar] [CrossRef]
- Chang, F.-C. Creep Behaviour of Wood-Plastic Composites; University of British Columbia: Vancouver, BC, Canada, 2011. [Google Scholar]
- Tangent Technologies, L. Polyforce Sturctural Recycled Plastic Lumber. 2015 [cited November 2018]. Mechanical propertied of the HDPE Polyforce Lumber. Available online: http://tangentusa.com/wp-content/uploads/2016/01/PolyForce_DataSheet_01_20_16.pdf (accessed on 12 December 2018).
- ASTM International. Standard Test Methods for Compressive and Flexural Creep and Creep-Rupture of Plastic Lumber and Shapes, D6112-13; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]


| Material | Name of the Group | Applied Stress Level | E (GPa) | Mean Fb (MPa) | Applied Flexural Creep Stress Level (MPa) |
|---|---|---|---|---|---|
| WPC | group 7.5% Fb | 7% Fb | 4.34 ± 0.26 | 41.2 ± 4.53 | 3.0 ± 0.08 |
| group 15% Fb | 14% Fb | 5.9 ± 0.04 | |||
| group 30% Fb | 29% Fb | 11.8 ± 0.09 | |||
| HDPE | group 7.5% Fb | 8% Fb | 0.93 ± 0.03 | 14.1 ± 0.70 | 1.1 ± 0.05 |
| group 15% Fb | 16% Fb | 2.2 ± 0.04 | |||
| group 30% Fb | 31% Fb | 4.4 ± 0.09 |
| Material % of Fb | D0 (mm) | ε0 (%) |
|---|---|---|
| WPC-7.5% | 2.96 | 0.1 |
| WPC-15% | 5.8 | 0.2 |
| WPC-30% | 11.3 | 0.3 |
| HDPE-7.5% | 5.5 | 0.2 |
| HDPE-15% | 8.74 | 0.3 |
| HDPE-30% | 18.71 | 0.6 |
| Creep Rate and FD | Material-% of Fb | |||||
|---|---|---|---|---|---|---|
| WPC-7.5% | WPC-15% | WPC-30% | HDPE-7.5% | HDPE-15% | HDPE-30% | |
| D30-D0 | 0.54 | 0.99 | 2.35 | 7.31 | 15.57 | 72.54 |
| D60-D30 | 0.13 | 0.21 | 0.57 | 0.77 | 1.72 | 7.80 |
| D90-D60 | 0.12 | 0.28 | 0.45 | 0.51 | 1.04 | 4.62 |
| D120-D90 | 0.05 | 0.12 | 0.35 | 0.36 | 0.65 | 3.45 |
| D150-D120 | 0.08 | 0.12 | 0.29 | 0.25 | 0.5 | 2.87 |
| D180-D150 | 0.06 | 0.09 | 0.23 | 0.22 | 0.62 | 2.47 |
| FD180 | 1.22 | 1.33 | 1.28 | 2.71 | 3.88 | 5.11 |
| Material Name-% of Fb | Outer Fiber Strain at Failure % | Mid-Span Displacement at Failure (mm) | Predicted Mid-Span Creep Displacement in 10 Years (mm) |
|---|---|---|---|
| WPC-7.5% | 1.040 | 46 | 6 |
| WPC-15% | 11 | ||
| WPC-30% | 22 | ||
| HDPE-7.5% | 3.004 | 120 | 21 |
| HDPE-15% | 50 | ||
| HDPE-30% | 165 |
| Material Type | Model Parameters | |
|---|---|---|
| d1 | m | |
| WPC | 0.011 | 0.596 |
| HDPE | 0.018 | 0.494 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrubaie, M.A.A.; Lopez-Anido, R.A.; Gardner, D.J. Flexural Creep Behavior of High-Density Polyethylene Lumber and Wood Plastic Composite Lumber Made from Thermally Modified Wood. Polymers 2020, 12, 262. https://doi.org/10.3390/polym12020262
Alrubaie MAA, Lopez-Anido RA, Gardner DJ. Flexural Creep Behavior of High-Density Polyethylene Lumber and Wood Plastic Composite Lumber Made from Thermally Modified Wood. Polymers. 2020; 12(2):262. https://doi.org/10.3390/polym12020262
Chicago/Turabian StyleAlrubaie, Murtada Abass A., Roberto A. Lopez-Anido, and Douglas J. Gardner. 2020. "Flexural Creep Behavior of High-Density Polyethylene Lumber and Wood Plastic Composite Lumber Made from Thermally Modified Wood" Polymers 12, no. 2: 262. https://doi.org/10.3390/polym12020262
APA StyleAlrubaie, M. A. A., Lopez-Anido, R. A., & Gardner, D. J. (2020). Flexural Creep Behavior of High-Density Polyethylene Lumber and Wood Plastic Composite Lumber Made from Thermally Modified Wood. Polymers, 12(2), 262. https://doi.org/10.3390/polym12020262