Material-Dependent Effect of Common Printing Parameters on Residual Stress and Warpage Deformation in 3D Printing: A Comprehensive Finite Element Analysis Study
Abstract
:1. Introduction
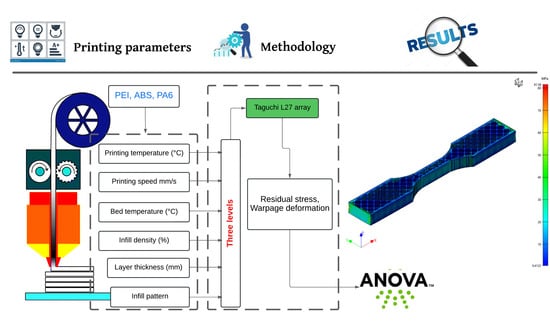
2. Numerical Process
2.1. Materials Selection and Used Samples
2.2. Printing Parameter Selection
- Printing temperature: This refers to the temperature of the 3D printer’s extruder nozzle, which melts the filament as it is deposited layer by layer to create the 3D-printed object. The temperature affects the viscosity of the filament, which in turn affects the flow rate and the bonding between layers.
- Printing speed: This parameter refers to the rate at which the printer head moves along the X–Y plane. Printing speed has an impact on the cooling time of each layer, which affects the strength of the bonds between layers.
- Bed temperature: This parameter refers to the temperature of the 3D printer’s build platform, which can be heated to promote a better adhesion between the printed object and the build surface. The temperature also affects the rate of the cooling of the bottom layer.
- Infill density: This refers to the amount of material that is used to fill the internal space of the 3D-printed object. Increasing the infill density can improve the strength and rigidity of the printed object, but it also increases the time and cost required to print the object.
- Layer thickness: This parameter refers to the height of each layer of the 3D-printed object. A thinner layer height produces a smoother surface finish, while a thicker layer height can reduce printing time.
- Infill pattern: This parameter refers to the shape and structure of the infill material within the printed object. Different infill patterns have different strengths and can affect the structural integrity of the 3D-printed object.
2.3. Taguchi Fractional Factorial Design
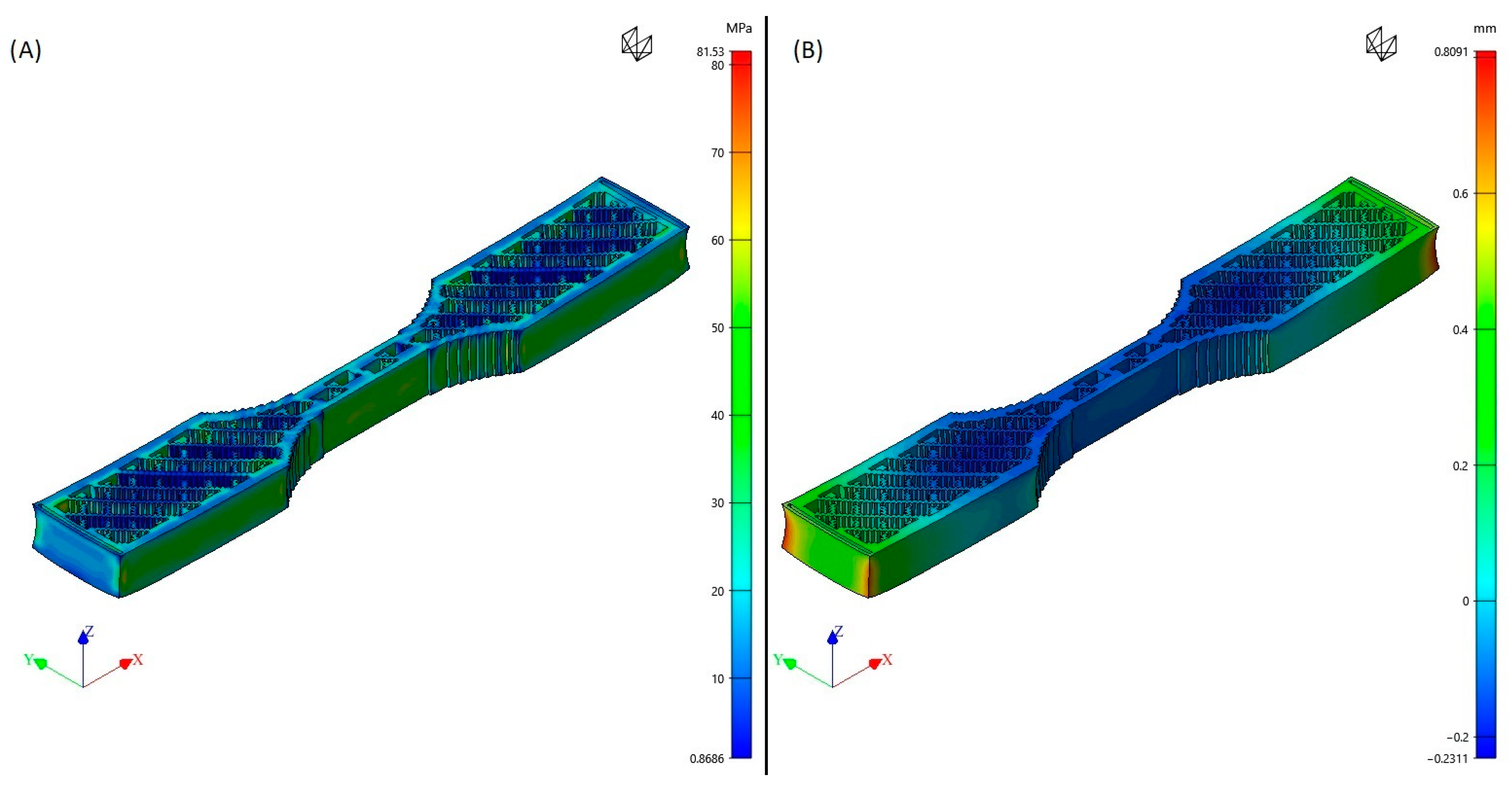
2.4. Simulation Procedure
3. Numerical Results and Statistical Analysis
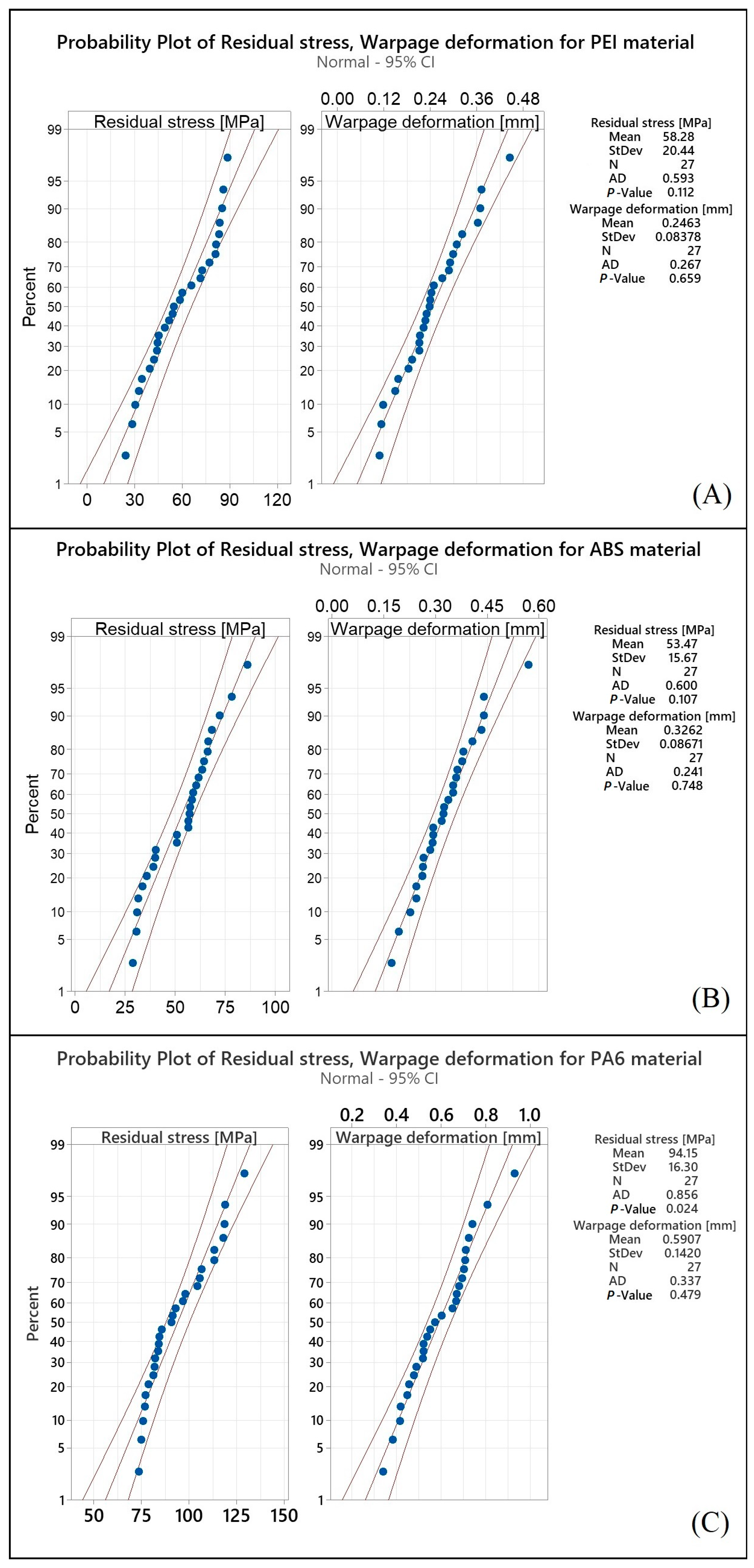
Probability Plots and ANOVA
4. Discussion
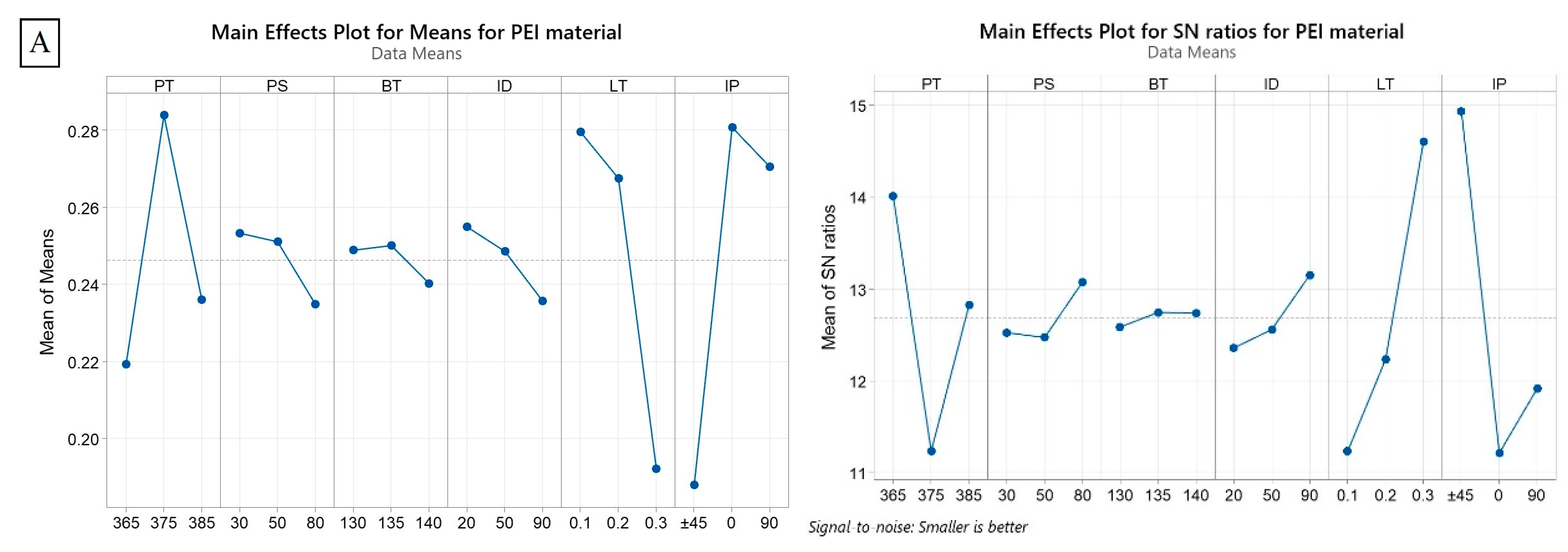
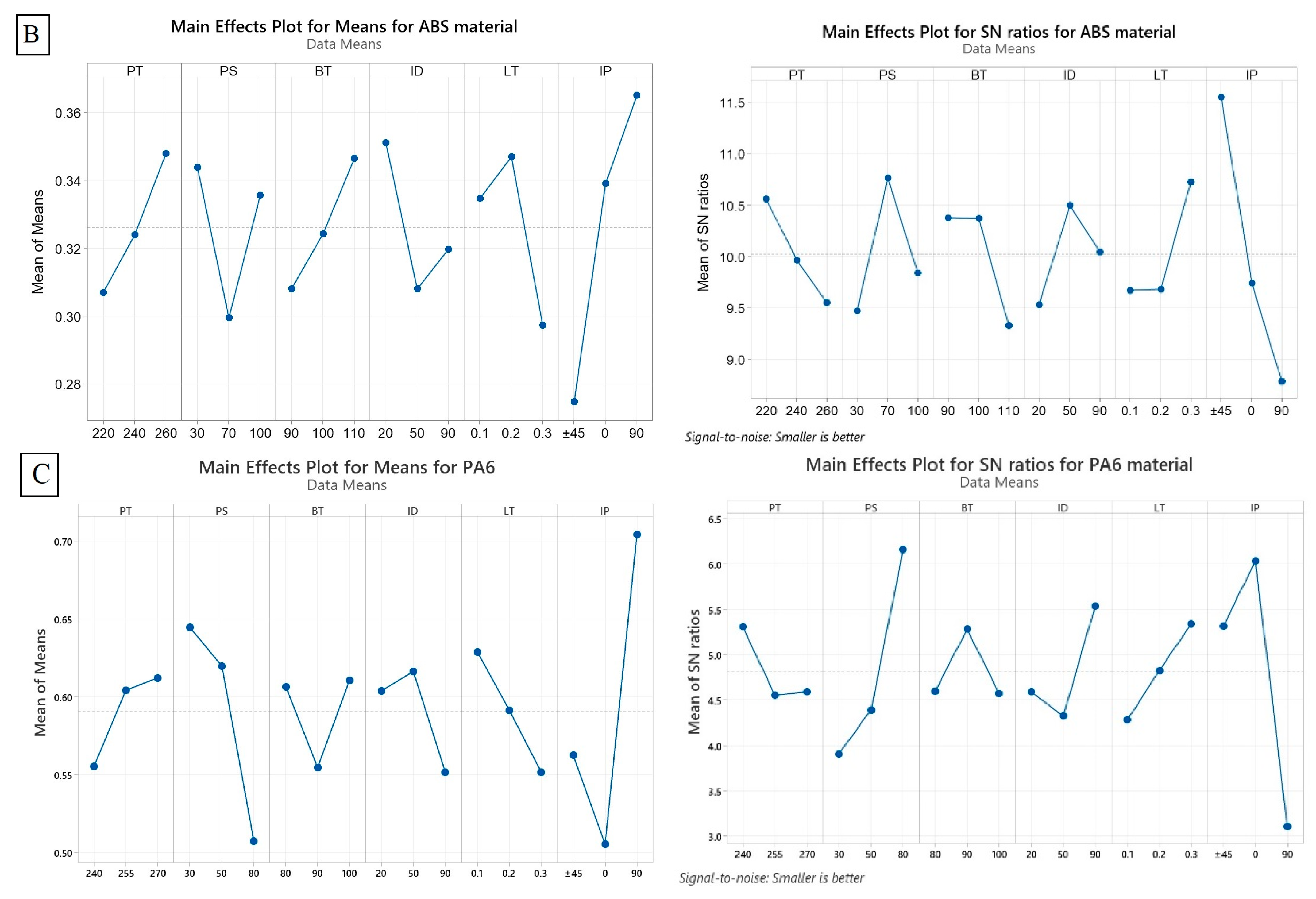
4.1. ANOVA and Mean Effect Plot (MEP) for Residual Stress
4.2. ANOVA and Mean Effect Plot (MEP) for Warpage Deformation
5. Conclusions
- The importance of each parameter in relation to residual stress varies depending on the material being printed. This indicates that all investigated parameters are material-dependent to some extent.
- Layer thickness is a consistently important parameter affecting the residual stress value for all three materials, suggesting that it is relatively less sensitive to material differences.
- Infill density demonstrates the varying levels of importance among materials influencing the residual stress. PA6 shows the highest contribution (30.73%), followed by PEI (15.25%) and ABS (4.64%). This implies that infill density is more sensitive to material differences.
- Printing temperature significantly contributes to reducing residual stress in PA6 (33.81%), while it does not significantly impact PEI and ABS. This suggests that printing temperature is more material-dependent.
- The infill pattern parameter demonstrates the highest contribution to reducing warpage deformation across all three materials, namely PEI, ABS, and PA6. This observation highlights its significance in minimizing warpage, irrespective of material variations.
- In terms of printing temperature, it exerts a relatively low impact on warpage deformation for PA6 (2.74%) while having a moderate effect on ABS (3.3%) and high PEI (13.4%).
- Printing speed exhibits a minor influence on mitigating warpage deformation for PEI (0.77%) and ABS (5.69%), but it significantly affects PA6 with a substantial impact of 21.19%.
- Bed temperature has a minimal effect on warpage deformation for PEI (0.06%), a relatively higher impact for ABS (4.69%), and a medium influence on PA6 (2.45%).
- Infill density demonstrates a limited influence on warpage deformation for PEI (1.18%), while it exerts a considerable effect on PA6 (6.18%). For ABS, its impact falls within the moderate range (3%).
- Layer thickness plays a crucial role in warpage deformation, yielding a substantial impact for PEI (20.73%) and a moderate effect for ABS (4.74%) and PA6 (4.29%).
- The limited research available on the material-specific effects of PEI in 3D printing calls for future investigations to explore its unique characteristics, such as thermal and mechanical properties, and their impact on residual stress and warpage deformation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Run | PT (°C) | PS (mm/s) | BT (°C) | ID (%) | LT (mm) | IP (°) | Residual Stress (MPa) | Warpage Deformation (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 365 | 30 | 130 | 20 | 0.1 | 0 | 83.53 | 0.37 |
| 2 | 365 | 30 | 130 | 20 | 0.2 | ±45 | 34.72 | 0.12 |
| 3 | 365 | 30 | 130 | 20 | 0.3 | 90 | 30.57 | 0.22 |
| 4 | 365 | 50 | 135 | 50 | 0.1 | 0 | 81.12 | 0.36 |
| 5 | 365 | 50 | 135 | 50 | 0.2 | ±45 | 33.00 | 0.11 |
| 6 | 365 | 50 | 135 | 50 | 0.3 | 90 | 28.50 | 0.21 |
| 7 | 365 | 80 | 140 | 90 | 0.1 | 0 | 88.67 | 0.25 |
| 8 | 365 | 80 | 140 | 90 | 0.2 | ±45 | 54.11 | 0.21 |
| 9 | 365 | 80 | 140 | 90 | 0.3 | 90 | 58.49 | 0.11 |
| 10 | 375 | 30 | 135 | 90 | 0.1 | ±45 | 85.95 | 0.21 |
| 11 | 375 | 30 | 135 | 90 | 0.2 | 90 | 65.89 | 0.45 |
| 12 | 375 | 30 | 135 | 90 | 0.3 | 0 | 54.90 | 0.19 |
| 13 | 375 | 50 | 140 | 20 | 0.1 | ±45 | 81.58 | 0.31 |
| 14 | 375 | 50 | 140 | 20 | 0.2 | 90 | 39.69 | 0.29 |
| 15 | 375 | 50 | 140 | 20 | 0.3 | 0 | 44.68 | 0.27 |
| 16 | 375 | 80 | 130 | 50 | 0.1 | ±45 | 77.34 | 0.23 |
| 17 | 375 | 80 | 130 | 50 | 0.2 | 90 | 44.10 | 0.37 |
| 18 | 375 | 80 | 130 | 50 | 0.3 | 0 | 42.41 | 0.23 |
| 19 | 385 | 30 | 140 | 50 | 0.1 | 90 | 85.20 | 0.24 |
| 20 | 385 | 30 | 140 | 50 | 0.2 | 0 | 60.16 | 0.29 |
| 21 | 385 | 30 | 140 | 50 | 0.3 | ±45 | 45.31 | 0.18 |
| 22 | 385 | 50 | 130 | 90 | 0.1 | 90 | 83.48 | 0.30 |
| 23 | 385 | 50 | 130 | 90 | 0.2 | 0 | 72.74 | 0.24 |
| 24 | 385 | 50 | 130 | 90 | 0.3 | ±45 | 49.35 | 0.16 |
| 25 | 385 | 80 | 135 | 20 | 0.1 | 90 | 71.72 | 0.24 |
| 26 | 385 | 80 | 135 | 20 | 0.2 | 0 | 51.93 | 0.32 |
| 27 | 385 | 80 | 135 | 20 | 0.3 | ±45 | 24.39 | 0.15 |
| Run | PT (°C) | PS (mm/s) | BT (°C) | ID (%) | LT (mm) | IP (°) | Residual Stress (MPa) | Warpage Deformation (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 220 | 30 | 90 | 20 | 0.1 | 0 | 50.87 | 0.41 |
| 2 | 220 | 30 | 90 | 20 | 0.2 | ±45 | 57.39 | 0.23 |
| 3 | 220 | 30 | 90 | 20 | 0.3 | 90 | 31.54 | 0.36 |
| 4 | 220 | 70 | 100 | 50 | 0.1 | 0 | 78.04 | 0.24 |
| 5 | 220 | 70 | 100 | 50 | 0.2 | ±45 | 56.40 | 0.17 |
| 6 | 220 | 70 | 100 | 50 | 0.3 | 90 | 30.55 | 0.36 |
| 7 | 220 | 100 | 110 | 90 | 0.1 | 0 | 50.91 | 0.28 |
| 8 | 220 | 100 | 110 | 90 | 0.2 | ±45 | 72.24 | 0.32 |
| 9 | 220 | 100 | 110 | 90 | 0.3 | 90 | 33.59 | 0.38 |
| 10 | 240 | 30 | 100 | 90 | 0.1 | ±45 | 63.32 | 0.26 |
| 11 | 240 | 30 | 100 | 90 | 0.2 | 90 | 66.09 | 0.44 |
| 12 | 240 | 30 | 100 | 90 | 0.3 | 0 | 40.18 | 0.29 |
| 13 | 240 | 70 | 110 | 20 | 0.1 | ±45 | 56.53 | 0.44 |
| 14 | 240 | 70 | 110 | 20 | 0.2 | 90 | 60.51 | 0.32 |
| 15 | 240 | 70 | 110 | 20 | 0.3 | 0 | 35.75 | 0.26 |
| 16 | 240 | 100 | 90 | 50 | 0.1 | ±45 | 61.51 | 0.29 |
| 17 | 240 | 100 | 90 | 50 | 0.2 | 90 | 58.87 | 0.34 |
| 18 | 240 | 100 | 90 | 50 | 0.3 | 0 | 31.11 | 0.26 |
| 19 | 260 | 30 | 110 | 50 | 0.1 | 90 | 64.27 | 0.35 |
| 20 | 260 | 30 | 110 | 50 | 0.2 | 0 | 68.12 | 0.43 |
| 21 | 260 | 30 | 110 | 50 | 0.3 | ±45 | 40.14 | 0.32 |
| 22 | 260 | 70 | 90 | 90 | 0.1 | 90 | 66.35 | 0.35 |
| 23 | 260 | 70 | 90 | 90 | 0.2 | 0 | 86.09 | 0.29 |
| 24 | 260 | 70 | 90 | 90 | 0.3 | ±45 | 39.15 | 0.24 |
| 25 | 260 | 100 | 100 | 20 | 0.1 | 90 | 57.05 | 0.38 |
| 26 | 260 | 100 | 100 | 20 | 0.2 | 0 | 58.30 | 0.57 |
| 27 | 260 | 100 | 100 | 20 | 0.3 | ±45 | 28.84 | 0.19 |
| Run | PT (°C) | PS (mm/s) | BT (°C) | ID (%) | LT (mm) | IP (°) | Residual Stress (MPa) | Warpage Deformation (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 240 | 30 | 80 | 20 | 0.1 | 0 | 77.43 | 0.54 |
| 2 | 240 | 30 | 80 | 20 | 0.2 | ±45 | 76.17 | 0.71 |
| 3 | 240 | 30 | 80 | 20 | 0.3 | 90 | 84.20 | 0.67 |
| 4 | 240 | 50 | 90 | 50 | 0.1 | 0 | 76.94 | 0.52 |
| 5 | 240 | 50 | 90 | 50 | 0.2 | ±45 | 82.38 | 0.55 |
| 6 | 240 | 50 | 90 | 50 | 0.3 | 90 | 73.70 | 0.65 |
| 7 | 240 | 80 | 100 | 90 | 0.1 | 0 | 96.94 | 0.42 |
| 8 | 240 | 80 | 100 | 90 | 0.2 | ±45 | 90.93 | 0.34 |
| 9 | 240 | 80 | 100 | 90 | 0.3 | 90 | 75.10 | 0.60 |
| 10 | 255 | 30 | 90 | 90 | 0.1 | ±45 | 119.00 | 0.49 |
| 11 | 255 | 30 | 90 | 90 | 0.2 | 90 | 104.60 | 0.74 |
| 12 | 255 | 30 | 90 | 90 | 0.3 | 0 | 106.70 | 0.52 |
| 13 | 255 | 50 | 100 | 20 | 0.1 | ±45 | 81.53 | 0.81 |
| 14 | 255 | 50 | 100 | 20 | 0.2 | 90 | 83.83 | 0.67 |
| 15 | 255 | 50 | 100 | 20 | 0.3 | 0 | 91.57 | 0.52 |
| 16 | 255 | 80 | 80 | 50 | 0.1 | ±45 | 93.24 | 0.57 |
| 17 | 255 | 80 | 80 | 50 | 0.2 | 90 | 129.20 | 0.70 |
| 18 | 255 | 80 | 80 | 50 | 0.3 | 0 | 78.97 | 0.42 |
| 19 | 270 | 30 | 100 | 50 | 0.1 | 90 | 105.60 | 0.70 |
| 20 | 270 | 30 | 100 | 50 | 0.2 | 0 | 98.26 | 0.71 |
| 21 | 270 | 30 | 100 | 50 | 0.3 | ±45 | 113.30 | 0.72 |
| 22 | 270 | 50 | 80 | 90 | 0.1 | 90 | 113.40 | 0.93 |
| 23 | 270 | 50 | 80 | 90 | 0.2 | 0 | 118.60 | 0.45 |
| 24 | 270 | 50 | 80 | 90 | 0.3 | ±45 | 118.00 | 0.48 |
| 25 | 270 | 80 | 90 | 20 | 0.1 | 90 | 85.95 | 0.68 |
| 26 | 270 | 80 | 90 | 20 | 0.2 | 0 | 82.04 | 0.46 |
| 27 | 270 | 80 | 90 | 20 | 0.3 | ±45 | 84.60 | 0.38 |
References
- Dasgupta, A.; Dutta, P. A Comprehensive Review on 3D Printing Technology: Current Applications and Challenges. Jordan J. Mech. Ind. Eng. 2022, 16, 529–542. [Google Scholar]
- Pervaiz, S.; Qureshi, T.A.; Kashwani, G.; Kannan, S. 3D Printing of Fiber-Reinforced Plastic Composites Using Fused Deposition Modeling: A Status Review. Materials 2021, 14, 4520. [Google Scholar] [CrossRef] [PubMed]
- Tümer, E.H.; Erbil, H.Y. Extrusion-Based 3D Printing Applications of PLA Composites: A Review. Coatings 2021, 11, 390. [Google Scholar] [CrossRef]
- Gregory, D.A.; Fricker, A.T.R.; Mitrev, P.; Ray, M.; Asare, E.; Sim, D.; Larpnimitchai, S.; Zhang, Z.; Ma, J.; Tetali, S.S.V.; et al. Additive Manufacturing of Polyhydroxyalkanoate-Based Blends Using Fused Deposition Modelling for the Development of Biomedical Devices. J. Funct. Biomater. 2023, 14, 40. [Google Scholar] [CrossRef]
- Bagi, I.; Béda, P.B. Modelling of a Specific Bone Replacement Material. Mater. Sci. Forum 2003, 414–415, 353–358. [Google Scholar] [CrossRef]
- El-Sayegh, S.; Romdhane, L.; Manjikian, S. A Critical Review of 3D Printing in Construction: Benefits, Challenges, and Risks. Arch. Civ. Mech. Eng. 2020, 20, 34. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Parada, L.; Mayuet, P.; Gámez, A. Custom Design of Packaging through Advanced Technologies: A Case Study Applied to Apples. Materials 2019, 12, 467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ISO ASTM 52900-21; Additive Manufacturing—General Principles—Fundamentals and Vocabulary. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- Rubies, E.; Palacín, J. Design and FDM/FFF Implementation of a Compact Omnidirectional Wheel for a Mobile Robot and Assessment of ABS and PLA Printing Materials. Robotics 2020, 9, 43. [Google Scholar] [CrossRef]
- Jafferson, J.M.; Chatterjee, D. A Review on Polymeric Materials in Additive Manufacturing. Mater. Today Proc. 2021, 46, 1349–1365. [Google Scholar] [CrossRef]
- Borsodi, E.; Takács, Á. Generative Design: An Overview and Its Relationship to Artificial Intelligence. Des. Mach. Struct. 2022, 12, 54–60. [Google Scholar] [CrossRef]
- Hameed, A.Z.; Aravind Raj, S.; Kandasamy, J.; Shahzad, M.A.; Baghdadi, M.A. 3D Printing Parameter Optimization Using Taguchi Approach to Examine Acrylonitrile Styrene Acrylate (ASA) Mechanical Properties. Polymers 2022, 14, 3256. [Google Scholar] [CrossRef]
- Gao, G.; Xu, F.; Xu, J. Parametric Optimization of FDM Process for Improving Mechanical Strengths Using Taguchi Method and Response Surface Method: A Comparative Investigation. Machines 2022, 10, 750. [Google Scholar] [CrossRef]
- Yankin, A.; Serik, G.; Danenova, S.; Alipov, Y.; Temirgali, A.; Talamona, D.; Perveen, A. Optimization of Fatigue Performance of FDM ABS and Nylon Printed Parts. Micromachines 2023, 14, 304. [Google Scholar] [CrossRef] [PubMed]
- Alzyod, H.; Ficzere, P. The Influence of the Layer Orientation on Ultimate Tensile Strength of 3D Printed Poly-Lactic Acid. Jordan J. Mech. Ind. Eng. 2022, 16, 361–367. [Google Scholar]
- Kousiatza, C.; Chatzidai, N.; Karalekas, D. Temperature Mapping of 3D Printed Polymer Plates: Experimental and Numerical Study. Sensors 2017, 17, 456. [Google Scholar] [CrossRef] [Green Version]
- Thumsorn, S.; Prasong, W.; Ishigami, A.; Kurose, T.; Kobayashi, Y.; Ito, H. Influence of Ambient Temperature and Crystalline Structure on Fracture Toughness and Production of Thermoplastic by Enclosure FDM 3D Printer. J. Manuf. Mater. Process. 2023, 7, 44. [Google Scholar] [CrossRef]
- Yang, C.-J.; Huang, W.-K.; Lin, K.-P. Three-Dimensional Printing Quality Inspection Based on Transfer Learning with Convolutional Neural Networks. Sensors 2023, 23, 491. [Google Scholar] [CrossRef]
- Turek, P. The Influence of the Layer Thickness Change on the Accuracy of the Zygomatic Bone Geometry Manufactured Using the FDM Technology. In Proceedings of the 1st International Electronic Conference on Machines and Applications, Online, 15–30 September 2022; MDPI: Basel, Switzerland, 2022; p. 26. [Google Scholar]
- Song, D.; Chung Baek, A.M.; Koo, J.; Busogi, M.; Kim, N. Forecasting Warping Deformation Using Multivariate Thermal Time Series and K-Nearest Neighbors in Fused Deposition Modeling. Appl. Sci. 2020, 10, 8951. [Google Scholar] [CrossRef]
- Ekinci, B.; Ehrmann, A. Influence of Printing Parameters on the Dimensional Accuracy of Concave/Convex Objects in FDM Printing. In Proceedings of the 3rd International Electronic Conference on Applied Sciences, Online, 1–15 December 2022; MDPI: Basel, Switzerland, 2022; p. 40. [Google Scholar]
- Karalekas, D.; Rapti, D. Investigation of the Processing Dependence of SL Solidification Residual Stresses. Rapid Prototyp. J. 2002, 8, 243–247. [Google Scholar] [CrossRef]
- Karalekas, D.; Aggelopoulos, A. Study of Shrinkage Strains in a Stereolithography Cured Acrylic Photopolymer Resin. J. Mater. Process. Technol. 2003, 136, 146–150. [Google Scholar] [CrossRef]
- Kechagias, J.; Chaidas, D.; Vidakis, N.; Salonitis, K.; Vaxevanidis, N.M. Key Parameters Controlling Surface Quality and Dimensional Accuracy: A Critical Review of FFF Process. Mater. Manuf. Process. 2022, 37, 963–984. [Google Scholar] [CrossRef]
- Kantaros, A.; Karalekas, D. Fiber Bragg Grating Based Investigation of Residual Strains in ABS Parts Fabricated by Fused Deposition Modeling Process. Mater. Des. 2013, 50, 44–50. [Google Scholar] [CrossRef]
- Pourali, M.; Peterson, A.M. Thermal Modeling of Material Extrusion Additive Manufacturing. In Polymer-Based Additive Manufacturing: Recent Developments; ACS Publications: Washington, DC, USA, 2019; pp. 115–130. ISBN 1947-5918. [Google Scholar]
- Casavola, C.; Cazzato, A.; Moramarco, V.; Pappalettera, G. Residual Stress Measurement in Fused Deposition Modelling Parts. Polym. Test. 2017, 58, 249–255. [Google Scholar] [CrossRef]
- Croccolo, D.; de Agostinis, M.; Olmi, G. Experimental Characterization and Analytical Modelling of the Mechanical Behaviour of Fused Deposition Processed Parts Made of ABS-M30. Comput. Mater. Sci. 2013, 79, 506–518. [Google Scholar] [CrossRef]
- Domingo-Espin, M.; Puigoriol-Forcada, J.M.; Garcia-Granada, A.-A.; Llumà, J.; Borros, S.; Reyes, G. Mechanical Property Characterization and Simulation of Fused Deposition Modeling Polycarbonate Parts. Mater. Des. 2015, 83, 670–677. [Google Scholar] [CrossRef]
- Zhou, Y.; Nyberg, T.; Xiong, G.; Liu, D. Temperature Analysis in the Fused Deposition Modeling Process. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 678–682. [Google Scholar]
- Costa, S.F.; Duarte, F.M.; Covas, J.A. Thermal Conditions Affecting Heat Transfer in FDM/FFE: A Contribution towards the Numerical Modelling of the Process. Virtual Phys. Prototyp. 2015, 10, 35–46. [Google Scholar] [CrossRef] [Green Version]
- Cattenone, A.; Morganti, S.; Alaimo, G.; Auricchio, F. Finite Element Analysis of Additive Manufacturing Based on Fused Deposition Modeling: Distortions Prediction and Comparison With Experimental Data. J. Manuf. Sci. Eng. 2019, 141, 011010. [Google Scholar] [CrossRef]
- Ferreira, R.T.L.; Quelho de Macedo, R. Residual Thermal Stress in Fused Deposition Modelling. In Proceedings of the 24th ABCM International Congress of Mechanicl Engineering, Curitiba, Brazil, 3–8 December 2017; ABCM: Cambridge, UK, 2017. [Google Scholar]
- Xia, H.; Lu, J.; Dabiri, S.; Tryggvason, G. Fully Resolved Numerical Simulations of Fused Deposition Modeling. Part I: Fluid Flow. Rapid Prototyp. J. 2018, 24, 463–476. [Google Scholar] [CrossRef]
- Zhang, Y.; Kevin Chou, Y. 3D FEA Simulations of Fused Deposition Modeling Process. In Proceedings of the International Manufacturing Science and Engineering Conference, Ypsilanti, MI, USA, 8–11 October 2006; American Society of Mechanical Engineers: New York, NY, USA, 2008; pp. 1121–1128. [Google Scholar] [CrossRef]
- Bertevas, E.; Férec, J.; Khoo, B.C.; Ausias, G.; Phan-Thien, N. Smoothed Particle Hydrodynamics (SPH) Modeling of Fiber Orientation in a 3D Printing Process. Phys. Fluids 2018, 30, 103103. [Google Scholar] [CrossRef]
- Alzyod, H.; Ficzere, P. Optimizing Fused Filament Fabrication Process Parameters for Quality Enhancement of PA12 Parts Using Numerical Modeling and Taguchi Method. Heliyon 2023, 9, e14445. [Google Scholar] [CrossRef]
- Syrlybayev, D.; Zharylkassyn, B.; Seisekulova, A.; Perveen, A.; Talamona, D. Optimization of the Warpage of Fused Deposition Modeling Parts Using Finite Element Method. Polymers 2021, 13, 3849. [Google Scholar] [CrossRef]
- Gao, R.; Xie, J.; Yang, J.; Zhuo, C.; Fu, J.; Zhao, P. Research on the Fused Deposition Modeling of Polyether Ether Ketone. Polymers 2021, 13, 2344. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.-C.; Wu, Y.-R.; Li, M.-H.; Wu, H.-W. Minimizing Warpage of ABS Prototypes Built with Low-Cost Fused Deposition Modeling Machine Using Developed Closed-Chamber and Optimal Process Parameters. Int. J. Adv. Manuf. Technol. 2019, 101, 593–602. [Google Scholar] [CrossRef]
- Hexagon AB. MSC Software Corporation MX User’s Guide; Hexagon AB: Stockholm, Sweden, 2021; p. 268. [Google Scholar]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2014. [CrossRef]
- Ding, S.; Zou, B.; Wang, P.; Ding, H. Effects of Nozzle Temperature and Building Orientation on Mechanical Properties and Microstructure of PEEK and PEI Printed by 3D-FDM. Polym. Test. 2019, 78, 105948. [Google Scholar] [CrossRef]
- Gómez-Gras, G.; Pérez, M.A.; Fábregas-Moreno, J.; Reyes-Pozo, G. Experimental Study on the Accuracy and Surface Quality of Printed versus Machined Holes in PEI Ultem 9085 FDM Specimens. Rapid Prototyp. J. 2021, 27, 1–12. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y.; Liang, Z.; Liu, Y. The Influence of Fused Deposition Modeling Parameters on the Properties of PA6/PA66 Composite Specimens by the Taguchi Method and Analysis of Variance. 3D Print. Addit. Manuf. 2023. [Google Scholar] [CrossRef]
- Dey, A.; Yodo, N. A Systematic Survey of FDM Process Parameter Optimization and Their Influence on Part Characteristics. J. Manuf. Mater. Process. 2019, 3, 64. [Google Scholar] [CrossRef] [Green Version]
- Popescu, D.; Zapciu, A.; Amza, C.; Baciu, F.; Marinescu, R. FDM Process Parameters Influence over the Mechanical Properties of Polymer Specimens: A Review. Polym. Test. 2018, 69, 157–166. [Google Scholar] [CrossRef]
- Bachchhav, B.D.; Hendre, K.N. Wear Performance of Asbestos-Free Brake Pad Materials. Jordan J. Mech. Ind. Eng. 2022, 16, 459–469. [Google Scholar]
- Ribeiro, J.; Lopes, H.; Queijo, L.; Figueiredo, D. Optimization of Cutting Parameters to Minimize the Surface Roughness in the End Milling Process Using the Taguchi Method. Period. Polytech. Mech. Eng. 2017, 61, 30–35. [Google Scholar] [CrossRef]
- Qazi, M.I.; Akhtar, R.; Abas, M.; Khalid, Q.S.; Babar, A.R.; Pruncu, C.I. An Integrated Approach of GRA Coupled with Principal Component Analysis for Multi-Optimization of Shielded Metal Arc Welding (SMAW) Process. Materials 2020, 13, 3457. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, K.C.P.; Li, Q.; Luo, W.; Guo, J. Impacts of Sample Size on Calculation of Pavement Texture Indicators with 1 mm 3D Surface Data. Period. Polytech. Transp. Eng. 2017, 46, 42. [Google Scholar] [CrossRef] [Green Version]
- Vishwas, M.; Basavaraj, C.K.; Vinyas, M. Experimental Investigation Using Taguchi Method to Optimize Process Parameters of Fused Deposition Modeling for ABS and Nylon Materials. Mater. Today Proc. 2018, 5, 7106–7114. [Google Scholar] [CrossRef]
- Daly, M.; Tarfaoui, M.; Chihi, M.; Bouraoui, C. FDM Technology and the Effect of Printing Parameters on the Tensile Strength of ABS Parts. Int. J. Adv. Manuf. Technol. 2023, 126, 5307–5323. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, A.S.; Sun, J.; Quan, Z.; Gu, B.; Sun, B.; Cotton, C.; Heider, D.; Chou, T.-W. Characterization of Residual Stress and Deformation in Additively Manufactured ABS Polymer and Composite Specimens. Compos. Sci. Technol. 2017, 150, 102–110. [Google Scholar] [CrossRef]
- Feroz Ali, L.; Raghul, R.; Yogesh Muthu Ram, M.; Harshavardhan Reddy, V.; Shakil Kanna, N. Evaluation of the Polyamide’s Mechanical Properties for Varying Infill Percentage in FDM Process. Mater. Today Proc. 2022, 68, 2509–2514. [Google Scholar] [CrossRef]
- Kaplun, B.W.; Zhou, R.; Jones, K.W.; Dunn, M.L.; Yakacki, C.M. Influence of Orientation on Mechanical Properties for High-Performance Fused Filament Fabricated Ultem 9085 and Electro-Statically Dissipative Polyetherketoneketone. Addit. Manuf. 2020, 36, 101527. [Google Scholar] [CrossRef]
- Yogeshwaran, K.; Das, S. Mechanical Properties of Fused Deposition Modelling Processed Parts: A Review. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Yadav, A.; Rohru, P.; Babbar, A.; Kumar, R.; Ranjan, N.; Chohan, J.S.; Kumar, R.; Gupta, M. Fused Filament Fabrication: A State-of-the-Art Review of the Technology, Materials, Properties and Defects. Int. J. Interact. Des. Manuf. 2022, 1–23. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, M.; Guo, Z.; Sang, L.; Hou, W. Investigation of Processing Parameters on Tensile Performance for FDM-Printed Carbon Fiber Reinforced Polyamide 6 Composites. Compos. Commun. 2020, 22, 100478. [Google Scholar] [CrossRef]
- Wu, W.; Geng, P.; Li, G.; Zhao, D.; Zhang, H.; Zhao, J. Influence of Layer Thickness and Raster Angle on the Mechanical Properties of 3D-Printed PEEK and a Comparative Mechanical Study between PEEK and ABS. Materials 2015, 8, 5834–5846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costa, A.A.; Martinho, P.G.; Barreiros, F.M. Comparison between the Mechanical Recycling Behaviour of Amorphous and Semicrystalline Polymers: A Case Study. Recycling 2023, 8, 12. [Google Scholar] [CrossRef]

| Properties | Material | ||
|---|---|---|---|
| PEI | ABS | PA6 | |
| Filament diameter (mm) | 1.75 | 1.75 | 1.75 |
| Density (g/cm3) | 1.34 | 1.04 | 1.14 |
| Poisson ratio | 0.35 | 0.36 | 0.37 |
| Printing temperature (°C) | 365–385 | 220–260 | 240–270 |
| Bed temperature (°C) | 130–140 | 90–110 | 80–100 |
| Printing speed (mm/s) | 30–80 | 30–100 | 30–80 |
| Strength (MPa) | 54 | 43 | 80 |
| Elasticity modulus (MPa) | 2050 | 1750 | 3300 |
| Parameter | Units | Material | Levels | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| Printing temperature (PT) | (°C) | PEI/ABS/PA6 | 365/220/240 | 375/240/255 | 385/260/270 |
| Printing speed (PS) | (mm/s) | PEI/ABS/PA6 | 30 | 50/70/50 | 80/100/80 |
| Bed temperature (BT) | (°C) | PEI/ABS/PA6 | 130/90/80 | 135/100/90 | 140/110/100 |
| Infill density (ID) | (%) | Low (20) | Medium (50) | High (90) | |
| Layer thickness (LT) | (mm) | 0.2 | 0.3 | 0.4 | |
| Infill pattern (IP) | 0° | ±45° | 90° | ||
| Material | Source | DF | Seq SS | Adj SS | Adj MS | F | P | % Contribution |
|---|---|---|---|---|---|---|---|---|
| PEI | PT | 2.00 | 8.29 | 8.29 | 4.14 | 2.43 | 0.12 | 2.88 |
| PS | 2.00 | 2.10 | 2.10 | 1.05 | 0.62 | 0.55 | 0.73 | |
| BT | 2.00 | 9.28 | 9.28 | 4.64 | 2.72 | 0.10 | 3.23 | |
| ID | 2.00 | 43.85 | 43.85 | 21.93 | 12.85 | 0.00 | 15.25 | |
| LT | 2.00 | 180.99 | 180.99 | 90.50 | 53.03 | 0.00 | 62.94 | |
| IP | 2.00 | 19.15 | 19.15 | 9.57 | 5.61 | 0.02 | 6.66 | |
| Error | 14.00 | 23.89 | 23.89 | 1.71 | 8.31 | |||
| Total | 26.00 | 287.54 | 100.00 | |||||
| ABS | PT | 2.00 | 3.42 | 3.42 | 1.71 | 1.69 | 0.22 | 1.75 |
| PS | 2.00 | 4.54 | 4.54 | 2.27 | 2.24 | 0.14 | 2.32 | |
| BT | 2.00 | 0.18 | 0.18 | 0.09 | 0.09 | 0.92 | 0.09 | |
| ID | 2.00 | 9.09 | 9.09 | 4.54 | 4.49 | 0.03 | 4.64 | |
| LT | 2.00 | 163.24 | 163.24 | 81.62 | 80.62 | 0.00 | 83.40 | |
| IP | 2.00 | 1.10 | 1.10 | 0.55 | 0.54 | 0.59 | 0.56 | |
| Error | 14.00 | 14.17 | 14.17 | 1.01 | 7.24 | |||
| Total | 26.00 | 195.73 | 100.00 | |||||
| PA6 | PT | 2.00 | 18.79 | 18.79 | 9.40 | 9.37 | 0.00 | 33.81 |
| PS | 2.00 | 2.33 | 2.33 | 1.16 | 1.16 | 0.34 | 4.19 | |
| BT | 2.00 | 2.12 | 2.12 | 1.06 | 1.06 | 0.37 | 3.82 | |
| ID | 2.00 | 17.08 | 17.08 | 8.54 | 8.51 | 0.00 | 30.73 | |
| LT | 2.00 | 0.76 | 0.76 | 0.38 | 0.38 | 0.69 | 1.37 | |
| IP | 2.00 | 0.46 | 0.46 | 0.23 | 0.23 | 0.80 | 0.82 | |
| Error | 14.00 | 14.04 | 14.04 | 1.00 | 25.26 | |||
| Total | 26.00 | 55.58 | 100.00 |
| Material | Source | DF | Seq SS | Adj SS | Adj MS | F | P | % Contribution |
|---|---|---|---|---|---|---|---|---|
| PEI | PT | 2 | 34.67 | 34.67 | 17.34 | 2.55 | 0.11 | 13.40 |
| PS | 2 | 1.99 | 1.99 | 0.99 | 0.15 | 0.87 | 0.77 | |
| BT | 2 | 0.14 | 0.14 | 0.07 | 0.01 | 0.99 | 0.06 | |
| ID | 2 | 3.05 | 3.05 | 1.52 | 0.22 | 0.80 | 1.18 | |
| LT | 2 | 53.65 | 53.65 | 26.83 | 3.94 | 0.04 | 20.73 | |
| IP | 2 | 69.99 | 69.99 | 35.00 | 5.14 | 0.02 | 27.05 | |
| Error | 14 | 95.28 | 95.28 | 6.81 | 36.82 | |||
| Total | 26 | 258.78 | 100.00 | |||||
| ABS | PT | 2.00 | 4.62 | 4.62 | 2.31 | 0.43 | 0.66 | 3.30 |
| PS | 2.00 | 7.96 | 7.96 | 3.98 | 0.75 | 0.49 | 5.69 | |
| BT | 2.00 | 6.56 | 6.56 | 3.28 | 0.62 | 0.55 | 4.69 | |
| ID | 2.00 | 4.20 | 4.20 | 2.10 | 0.39 | 0.68 | 3.00 | |
| LT | 2.00 | 6.63 | 6.63 | 3.32 | 0.62 | 0.55 | 4.74 | |
| IP | 2.00 | 35.40 | 35.40 | 17.70 | 3.32 | 0.07 | 25.30 | |
| Error | 14.00 | 74.54 | 74.54 | 5.32 | 53.28 | |||
| Total | 26.00 | 139.91 | 100.00 | |||||
| PA6 | PT | 2.00 | 3.26 | 3.26 | 1.63 | 0.69 | 0.52 | 2.74 |
| PS | 2.00 | 25.16 | 25.16 | 12.58 | 5.34 | 0.02 | 21.19 | |
| BT | 2.00 | 2.91 | 2.91 | 1.46 | 0.62 | 0.55 | 2.45 | |
| ID | 2.00 | 7.33 | 7.33 | 3.67 | 1.56 | 0.25 | 6.18 | |
| LT | 2.00 | 5.09 | 5.09 | 2.54 | 1.08 | 0.37 | 4.29 | |
| IP | 2.00 | 42.00 | 42.00 | 21.00 | 8.92 | 0.00 | 35.38 | |
| Error | 14.00 | 32.97 | 32.97 | 2.36 | 27.77 | |||
| Total | 26.00 | 118.72 | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzyod, H.; Ficzere, P. Material-Dependent Effect of Common Printing Parameters on Residual Stress and Warpage Deformation in 3D Printing: A Comprehensive Finite Element Analysis Study. Polymers 2023, 15, 2893. https://doi.org/10.3390/polym15132893
Alzyod H, Ficzere P. Material-Dependent Effect of Common Printing Parameters on Residual Stress and Warpage Deformation in 3D Printing: A Comprehensive Finite Element Analysis Study. Polymers. 2023; 15(13):2893. https://doi.org/10.3390/polym15132893
Chicago/Turabian StyleAlzyod, Hussein, and Peter Ficzere. 2023. "Material-Dependent Effect of Common Printing Parameters on Residual Stress and Warpage Deformation in 3D Printing: A Comprehensive Finite Element Analysis Study" Polymers 15, no. 13: 2893. https://doi.org/10.3390/polym15132893