Experimental and Simulation Study on Failure of Thermoplastic Carbon Fiber Composite Laminates under Low-Velocity Impact
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Materials
- (1)
- The matrix phase is composed of Elium®188 thermoplastic resin, sourced from Arkema in France, combined with a benzoyl peroxide (BPO) initiator in a mass ratio of 100:2.
- (2)
- The fiber phase is constituted by a ProFinishTM carbon fiber bidirectional woven fabric, with an areal density of 200 g/m2.
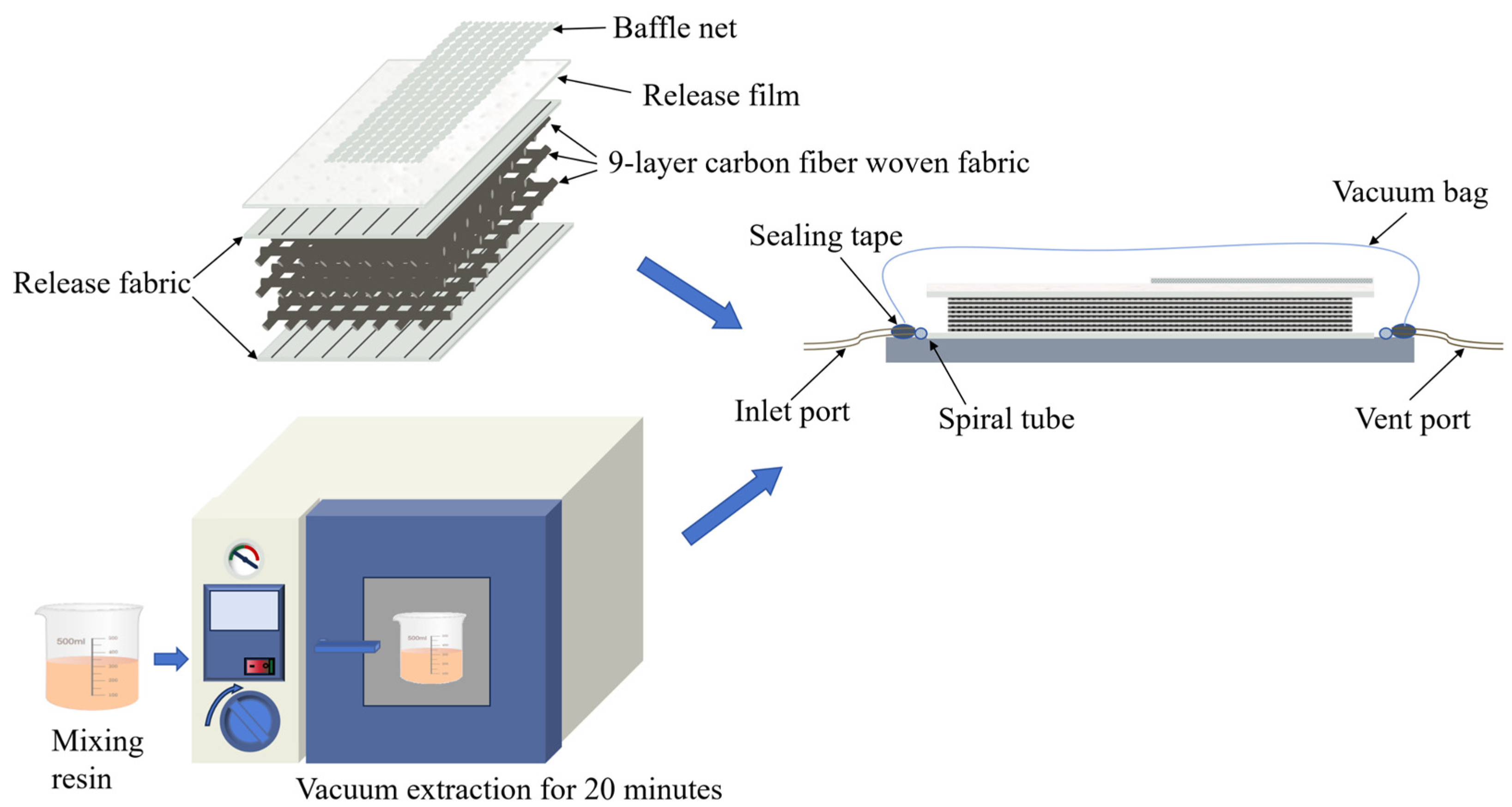
2.2. Preparation
2.3. Testing
3. Numerical Model
3.1. Finite Element Model
3.1.1. Assembly
3.1.2. Meshing
3.1.3. Contact Settings and Material Properties
3.2. Damage Modeling
3.2.1. Failure Criteria
3.2.2. Damage Evolution Model
4. Results and Discussion
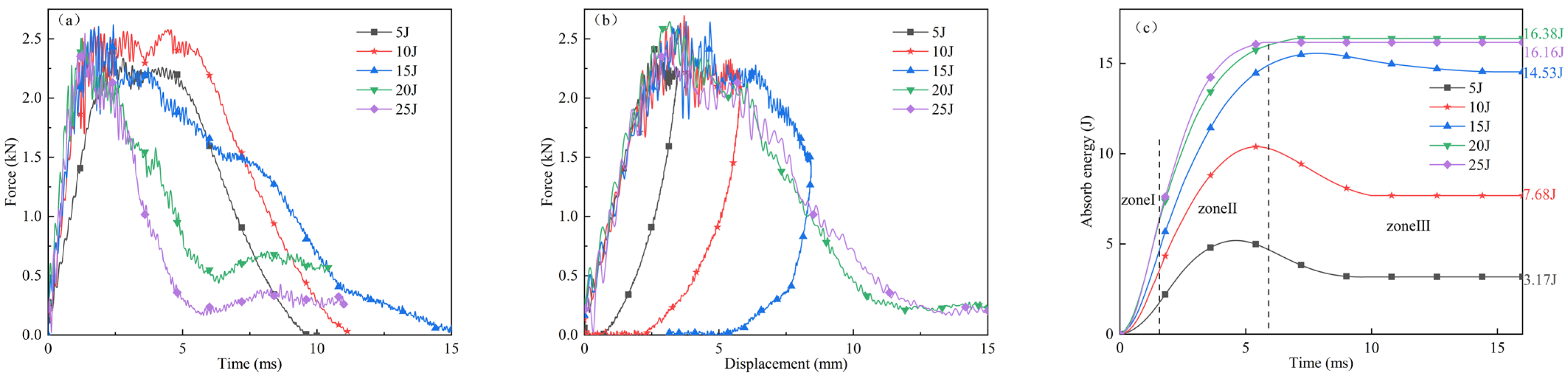
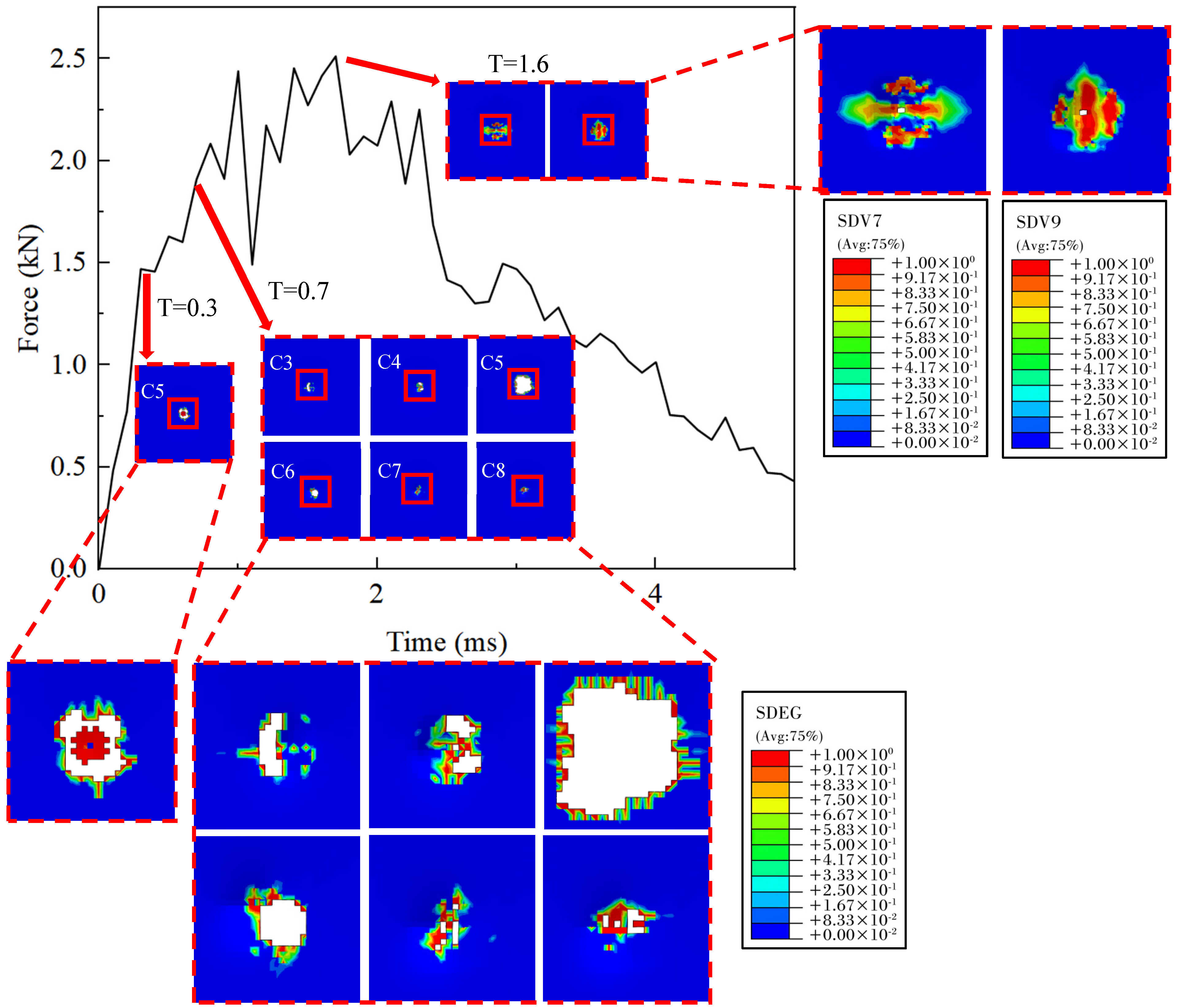
4.1. Experimental Results
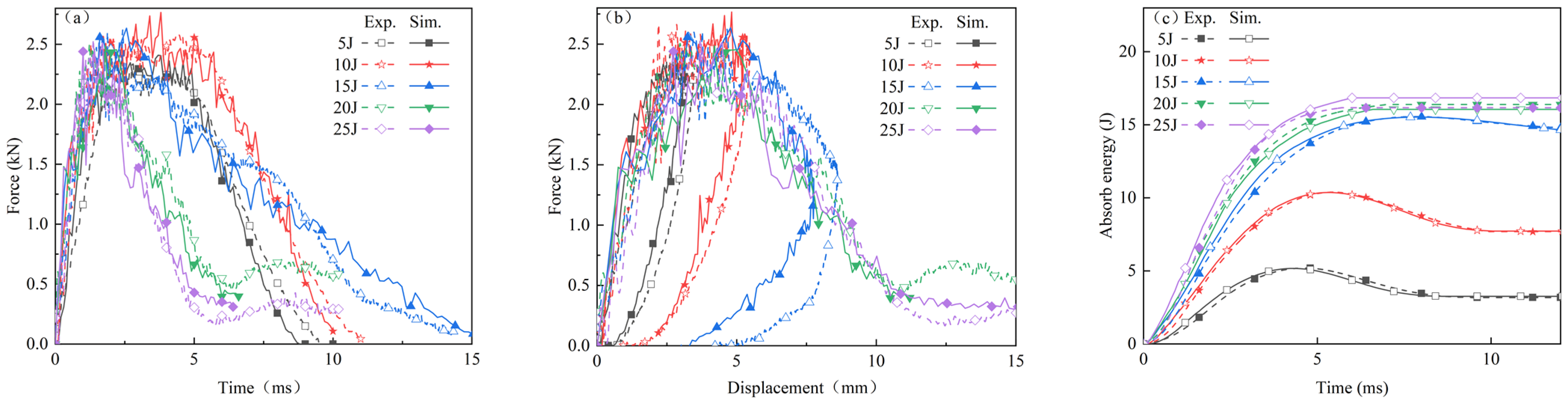
4.2. Finite Element Simulation Validation
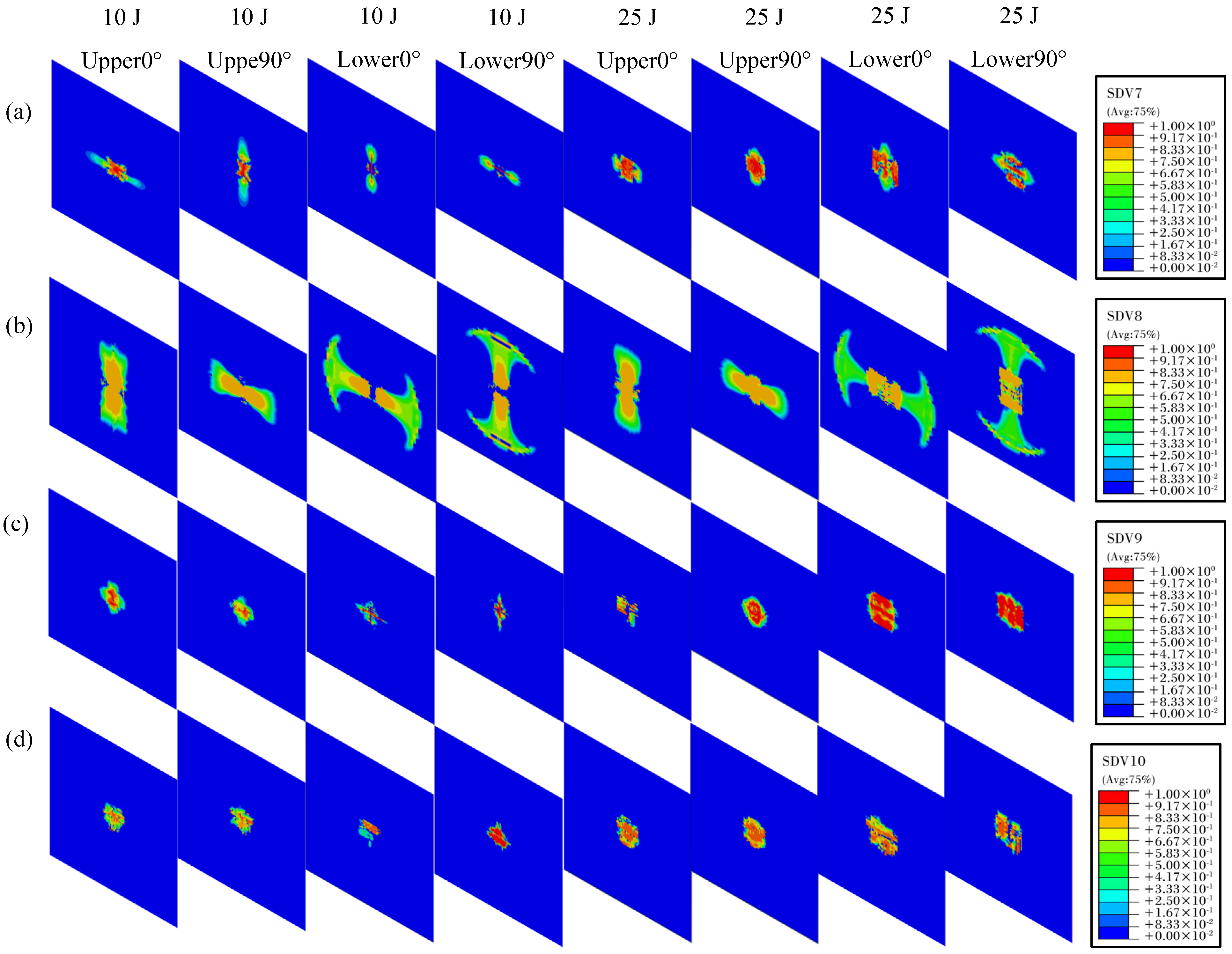
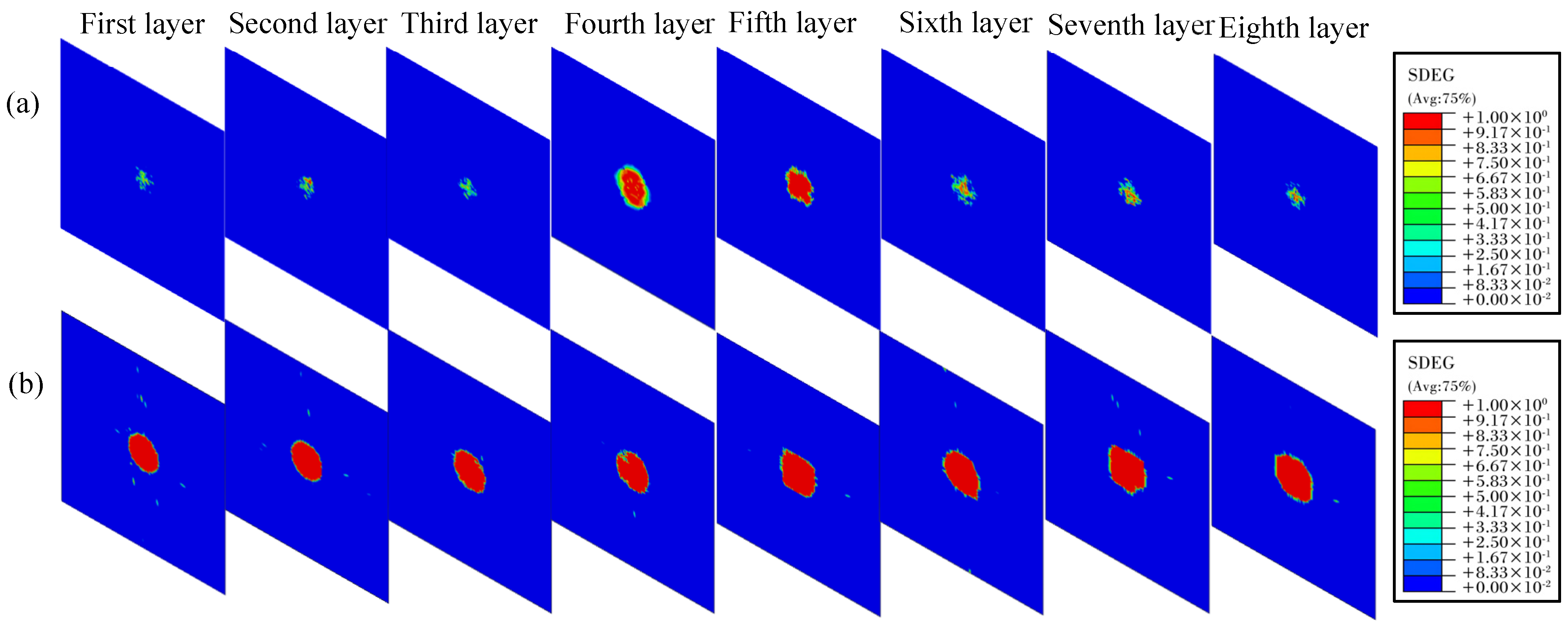
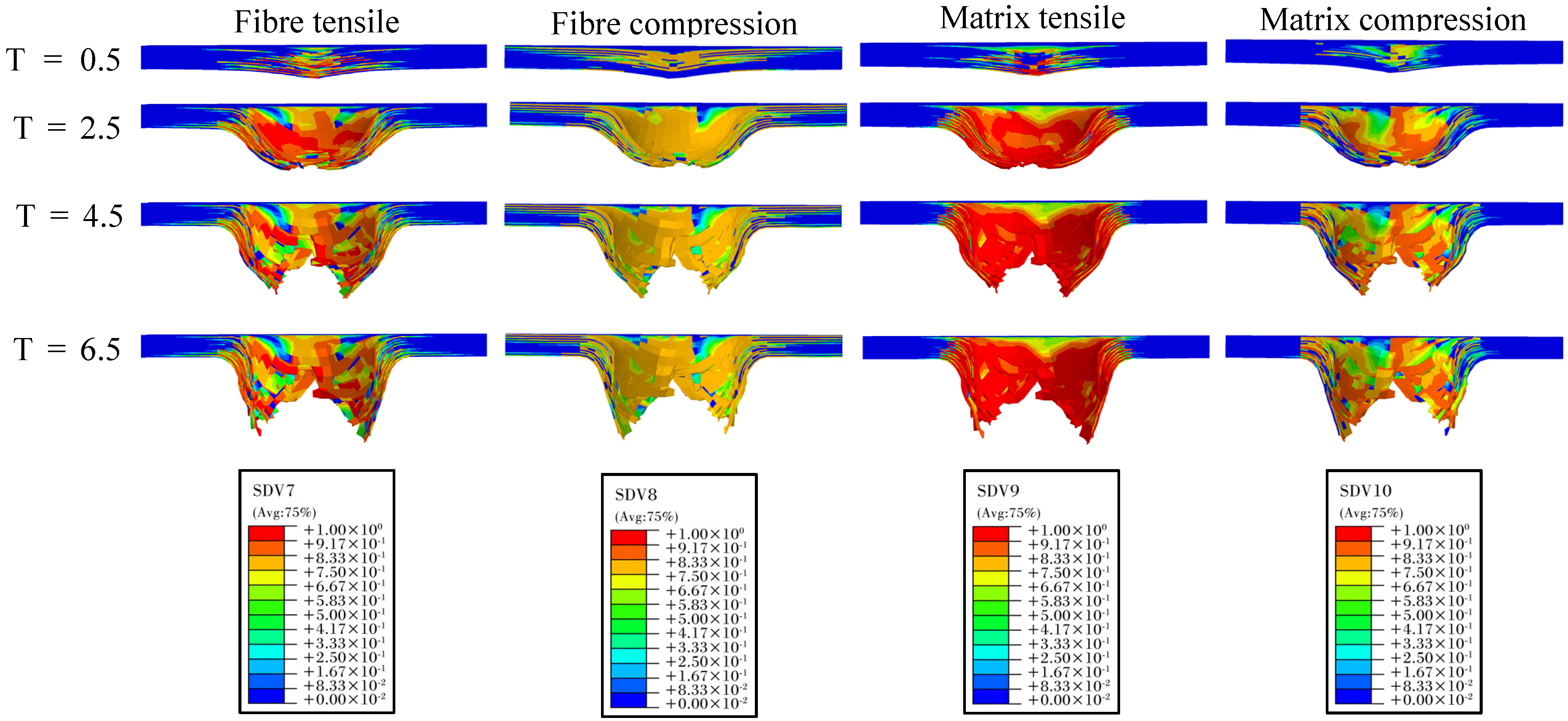
4.3. Impact Damage Analysis
5. Conclusions
- (1)
- This study has successfully developed a progressive damage model for thermoplastic carbon fiber-reinforced composite laminates under low-velocity impact. The model adeptly simulates the mechanical response and damage characteristics of laminates constructed from woven fabrics across a spectrum of impact energies. It is capable of accurately capturing non-penetration damage behavior and can also replicate the entire process of localized damage, delamination, and failure, culminating in final penetration, under low-velocity impact conditions. The predicted peak error and absorbed energy error are maintained within a 5% margin, and the trends of the mechanical response curves closely mirror the experimental results. The damage patterns predicted by the simulation align with the findings from XCT scans, thereby further substantiating the model’s reliability.
- (2)
- The impact damage in laminates predominantly stems from delamination and intralayer tensile failure. When the impact energy surpasses the load-bearing threshold, initial compression damage is localized on the impact side, whereas tensile damage manifests on the non-impact side. As the impact continues, tensile damage expands rapidly, and fiber fracture ensues layer by layer once the tensile limit is exceeded in the bottom layer, accompanied by extensive delamination and layer spalling.
- (3)
- The extent of interlaminar delamination damage expands in tandem with the escalation of impact energy, with the middle layer experiencing the most extensive damage area. Delamination is notably more pronounced on the bottom surface than on the top surface, and the distribution of delamination damage across the layers is roughly symmetrical around the neutral layer. This phenomenon can be attributed to the combined effect of friction and shear stress. Initial damage typically presents as internal delamination, which may remain invisible on the surface yet substantially diminishes the structure’s compressive strength and service life. Consequently, enhancing the interlaminar bonding performance can markedly augment the overall load-bearing capacity of the laminate.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Y.; Zhang, Z.; Wang, S.; Pan, B.; Sun, M.; Zhang, G.; Chai, H.; Wu, H.; Jiang, S. Effect of embedded periodic fiber placement gap defects on the microstructure and bistable behavior of thermoplastic composite laminates. Polym. Compos. 2023, 44, 9008–9025. [Google Scholar] [CrossRef]
- Liao, Z.; Qiu, C.; Yang, J.; Yang, J.; Yang, L. Accelerating the Layup Sequences Design of Composite Laminates via Theory-Guided Machine Learning Models. Polymers 2022, 14, 3229. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Huang, L.; Dai, Y. Dynamic Response and Damage Accumulation of Laminated Composites under Repeated Low-Velocity Impacts. Materials 2023, 16, 778. [Google Scholar] [CrossRef] [PubMed]
- Cantwell, W.J.; Morton, J. The impact resistance of composite materials—A review. Composites 1991, 22, 347–362. [Google Scholar] [CrossRef]
- Davies, G.A.O.; Zhang, X. Impact damage prediction in carbon composite structures. Int. J. Impact Eng. 1995, 16, 149–170. [Google Scholar] [CrossRef]
- Reyes, G.; Sharma, U. Modeling and damage repair of woven thermoplastic composite laminates subjected to low velocity impact. Compos. Part A Appl. Sci. Manuf. 2010, 41, 226–237. [Google Scholar] [CrossRef]
- Abrate, S. Impact on laminated composite materials. Appl. Mech. Rev. 1998, 51, 733–761. [Google Scholar] [CrossRef]
- Wang, X.; He, J.; Guo, W.; Zhou, Y.; Zhu, Y. Three-dimensional damage quantification of low velocity impact damage in thin composite plates using phased-array ultrasound. Ultrasonics 2021, 110, 106264. [Google Scholar] [CrossRef] [PubMed]
- Qiang, X.; Wang, T.; Xue, H.; Ding, J.; Deng, C. Study on Low-Velocity Impact and Residual Compressive Mechanical Properties of Carbon Fiber–Epoxy Resin Composites. Materials 2024, 17, 3766. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, P.; Wang, S. Numerical investigation on the repeated low-velocity impact behavior of composite laminates. Compos. Part B Eng. 2020, 185, 107771. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Chen, X. Damage assessment of braided composite tube subjected to repeated transverse impact. Thin-Walled Struct. 2020, 156, 107004. [Google Scholar] [CrossRef]
- Geiringer, H. Review: R. Hill, The Mathematical Theory of Plasticity. Bull. Am. Math. Soc. 1952, 58, 507–512. [Google Scholar] [CrossRef]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, P.; Wang, S. Finite element analysis of a modified progressive damage model for composite laminates under low-velocity impact. Compos. Struct. 2019, 225, 111113. [Google Scholar] [CrossRef]
- Camanho, P.P.; Maimí, P.; Dávila, C.G. Prediction of size effects in notched laminates using continuum damage mechanics. Compos. Sci. Technol. 2007, 67, 2715–2727. [Google Scholar] [CrossRef]
- Shi, Y.; Soutis, C. Modelling low velocity impact induced damage in composite laminates. Mech. Adv. Mater. Mod. Process. 2017, 3, 14. [Google Scholar] [CrossRef]
- Hoang, M.N.; Wang, M.A. A novel mode-dependent and probabilistic semi-discrete damage model for progressive failure analysis of composite laminates—Part I: Meshing strategy and mixed-mode law. Compos. Part C Open Access 2020, 3, 100073. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, B.; Wang, S. Finite element analysis on impact response and damage mechanism of composite laminates under single and repeated low-velocity impact. Aerosp. Sci. Technol. 2022, 129, 105831. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Wu, X. Three-dimensional progressive damage modeling of low-speed impact on composite laminates. Compos. Struct. 2023, 289, 115485. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A Finite Element Calculation of Stress Intensity Factors by a Modified Crack Closure Integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G. Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials; NASA Technical Memorandum; No. NAS 1.15: 211737; NASA: Washington, DC, USA, 2002.
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Fan, C.; Jar, P.Y.B.; Cheng, J.J.R. Cohesive zone with continuum damage properties for simulation of delamination development in fibre composites and failure of adhesive joints. Eng. Fract. Mech. 2008, 75, 3866–3880. [Google Scholar] [CrossRef]
- Feng, Z.; Li, X.; Zhang, Y.; Wang, J. Development of a hybrid XFEM-CZM model for damage prediction in composite laminates under complex loading conditions. Compos. Struct. 2019, 210, 324–332. [Google Scholar] [CrossRef]
- Xu, W.; Liu, P.; Zhang, H. Enhancing damage prediction accuracy in composite materials using machine learning techniques. Mater. Des. 2020, 192, 108731. [Google Scholar] [CrossRef]
- Zhao, W. Numerical Simulation of Low-Velocity Impact of Carbon Fiber Reinforced Thermoplastic Composites. Doctoral Dissertation, Shandong University, Jinan, China, 2024. [Google Scholar]
- Yang, L.; Liao, Z.; Qiu, C.; Hong, Z.; Yang, J. Experimental study on the impact resistance and damage tolerance of thermoplastic FMLs. Thin-Walled Struct. 2024, 196, 111435. [Google Scholar] [CrossRef]
- Kazemi, M.; Shanmugam, L.; Dadashi, A.; Shakouri, M.; Lu, D.; Du, Z.; Hu, Y.; Wang, J.; Zhang, W.; Yang, L.; et al. Investigating the roles of fiber, resin, and stacking sequence on the low-velocity impact response of novel hybrid thermoplastic composites. Compos. Part B Eng. 2021, 207, 108554. [Google Scholar] [CrossRef]
- Shi, Y.; Swait, T.; Soutis, C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012, 94, 2902–2913. [Google Scholar] [CrossRef]
- Ebadi-Rajoli, J.; Akhavan-Safar, A.; Hosseini-Toudeshky, H.; da Silva, L. Progressive damage modelling of composite materials subjected to mixed mode cyclic loading using cohesive zone model. Mech. Mater. 2020, 143, 103322. [Google Scholar] [CrossRef]
- Confalonieri, F.; Perego, U. Simulation of fracture and delamination in layered shells due to blade cutting. J. Serbian Soc. Comput. Mech. 2017, 11, 139–151. [Google Scholar] [CrossRef]
- Cui, W.; Wisnom, M.R.; Jones, M.I. A Comparison of Fracture Criteria to Predict Delamination of Unidirectional Glass/Epoxy Specimens. J. Compos. Mater. 1992, 26, 2720–2741. [Google Scholar] [CrossRef]
- Zwingmann, B.; Liu, Y.; Schlaich, M.; Janetzko, S. Progressive damage simulation in 3D four-directional braided composites considering the jamming-action-induced yarn deformation. Compos. Struct. 2017, 178, 330–340. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Karnati, S.R.; Shivakumar, K. Limited Input Benzeggagh and Kenane delamination failure criterion for mixed-mode loaded fiber reinforced composite laminates. Int. J. Fract. 2020, 222, 221–230. [Google Scholar] [CrossRef]
- Zhang, C.; Duodu, A.E.; Gu, J. Finite element modeling of damage development in cross-ply composite laminates subjected to low velocity impact. Compos. Struct. 2017, 173, 219–227. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. Simulating low-velocity impact induced delamination in composites by a quasi-static load model with surface-based cohesive contact. Compos. Struct. 2015, 125, 51–57. [Google Scholar] [CrossRef]





| Parameter | Numerical Value | Parameter | Numerical Value |
|---|---|---|---|
| 57.3 | 15 | ||
| 3 | 50 | ||
| 3 | 60 | ||
| 0.32 | 60 | ||
| 0.32 | |||
| 0.49 | |||
| 5.1 | 62.3 | ||
| 4.08 | 92.3 | ||
| 650 | 0.28 | ||
| 240 | 0.79 |
| Energy | 5 J | 10 J | 15 J | 20 J | 25 J |
| Experiment | 2.39 kN | 2.67 kN | 2.62 kN | 2.50 kN | 2.54 kN |
| Simulation | 2.41 kN | 2.76 kN | 2.64 kN | 2.49 kN | 2.51 kN |
| Error | 0.84% | 3.37% | 0.76% | 0.40% | 1.18% |
| Energy | 5 J | 10 J | 15 J | 20 J | 25 J |
| Experiment | 3.17 J | 7.68 J | 14.53 J | 16.38 J | 16.16 J |
| Simulation | 3.26 J | 7.73 J | 14.17 J | 16.06 J | 16.84 J |
| Error | 2.84% | 0.65% | 2.48% | 1.95% | 4.21% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Huang, X.; Liao, Z.; Wei, Z.; Zou, J. Experimental and Simulation Study on Failure of Thermoplastic Carbon Fiber Composite Laminates under Low-Velocity Impact. Polymers 2024, 16, 2581. https://doi.org/10.3390/polym16182581
Yang L, Huang X, Liao Z, Wei Z, Zou J. Experimental and Simulation Study on Failure of Thermoplastic Carbon Fiber Composite Laminates under Low-Velocity Impact. Polymers. 2024; 16(18):2581. https://doi.org/10.3390/polym16182581
Chicago/Turabian StyleYang, Lei, Xiaolin Huang, Zhenhao Liao, Zongyou Wei, and Jianchao Zou. 2024. "Experimental and Simulation Study on Failure of Thermoplastic Carbon Fiber Composite Laminates under Low-Velocity Impact" Polymers 16, no. 18: 2581. https://doi.org/10.3390/polym16182581
APA StyleYang, L., Huang, X., Liao, Z., Wei, Z., & Zou, J. (2024). Experimental and Simulation Study on Failure of Thermoplastic Carbon Fiber Composite Laminates under Low-Velocity Impact. Polymers, 16(18), 2581. https://doi.org/10.3390/polym16182581








