Research on Passivation Simulation of Plasticizer N-Butylnitroxyethylnitramine (BuNENA) in Hydroxy-Terminated Polyether (HTPE) Propellants
Abstract
:1. Introduction
2. Experiment Setup
2.1. Materials
2.2. Substitute Material Preparation
2.3. Passivation Experiment
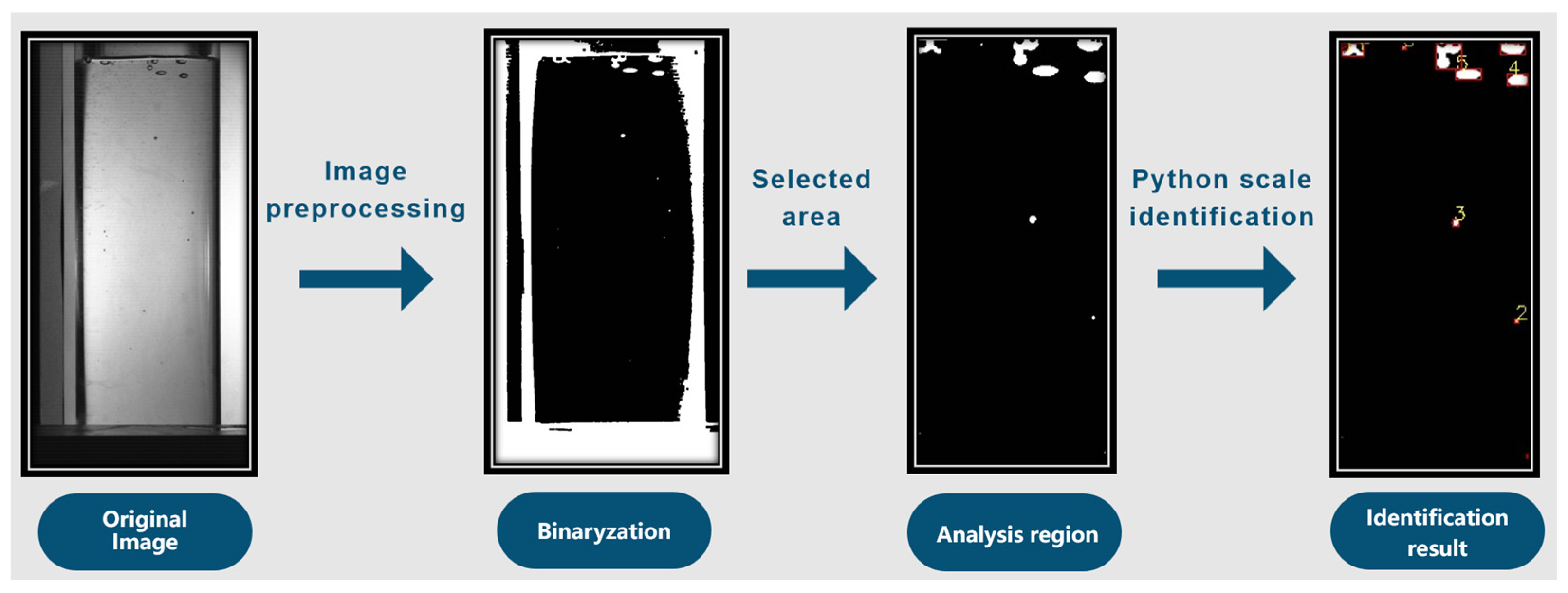
2.4. Determination of Moisture Content and Video Recognition Test
3. Theoretical Models
3.1. Buoyancy Force
3.2. Drag Force
3.3. Boiling Condition and Bubble Growth
3.4. Fluid Model
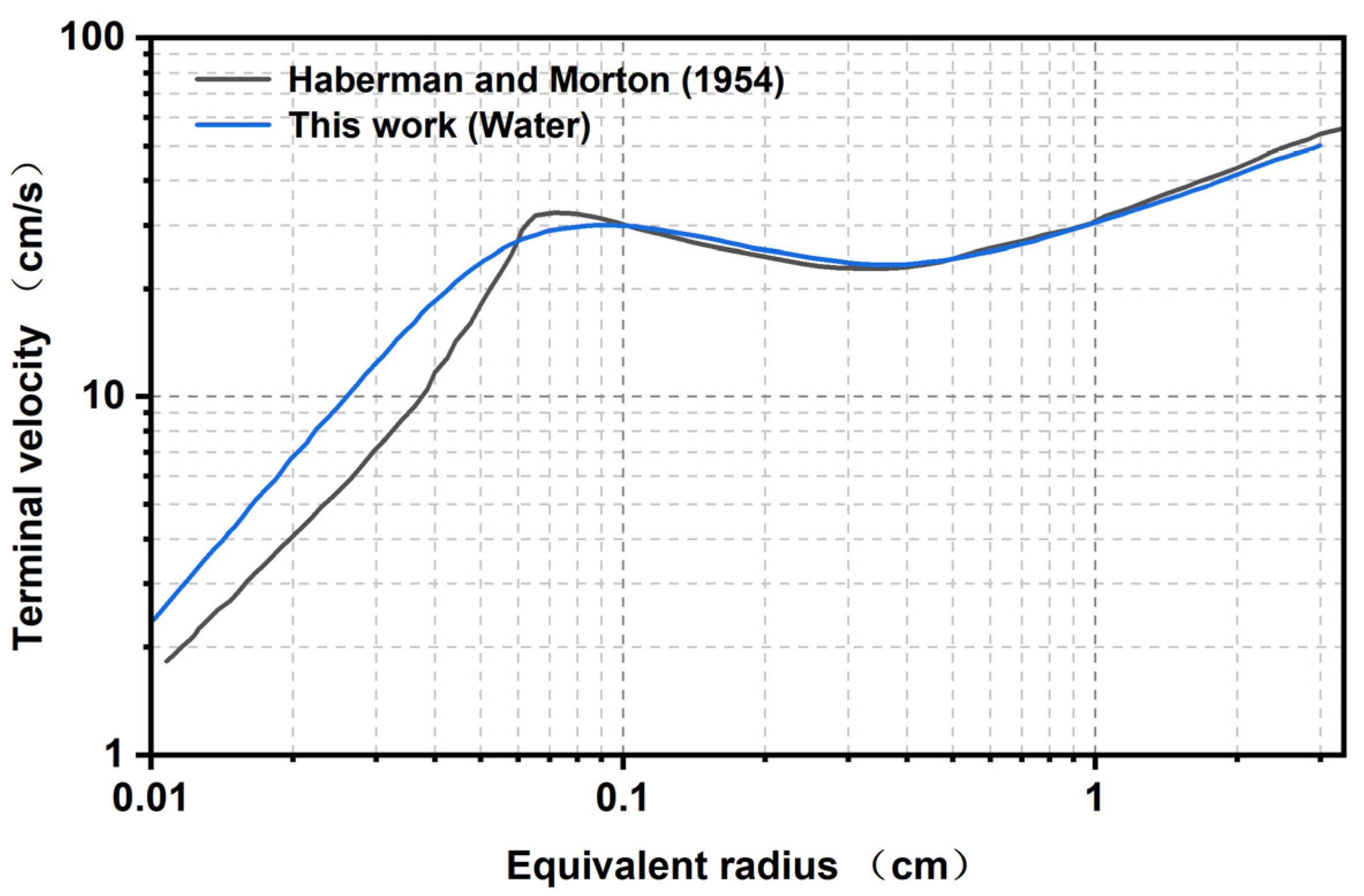
3.5. Model Verification
4. Results and Discussion
4.1. Experimental Results of Video Recognition
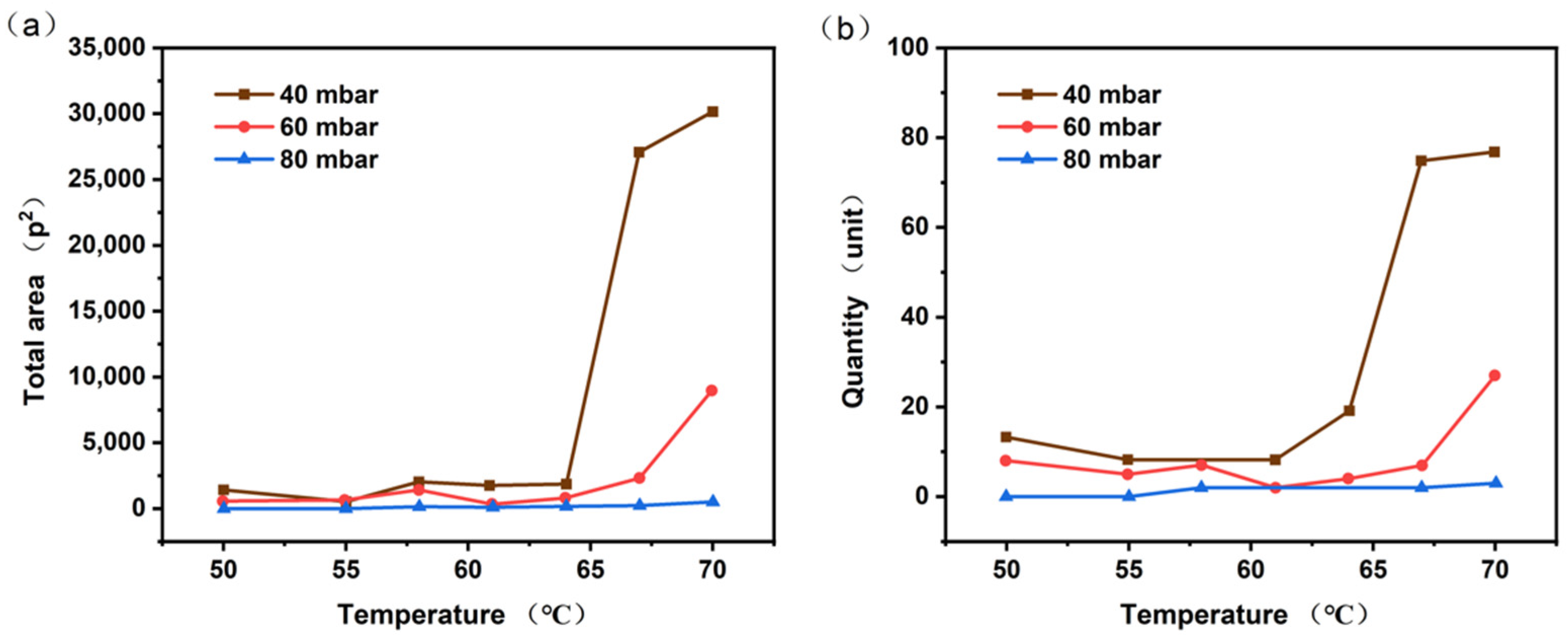
4.1.1. Bubble Size and Parameters
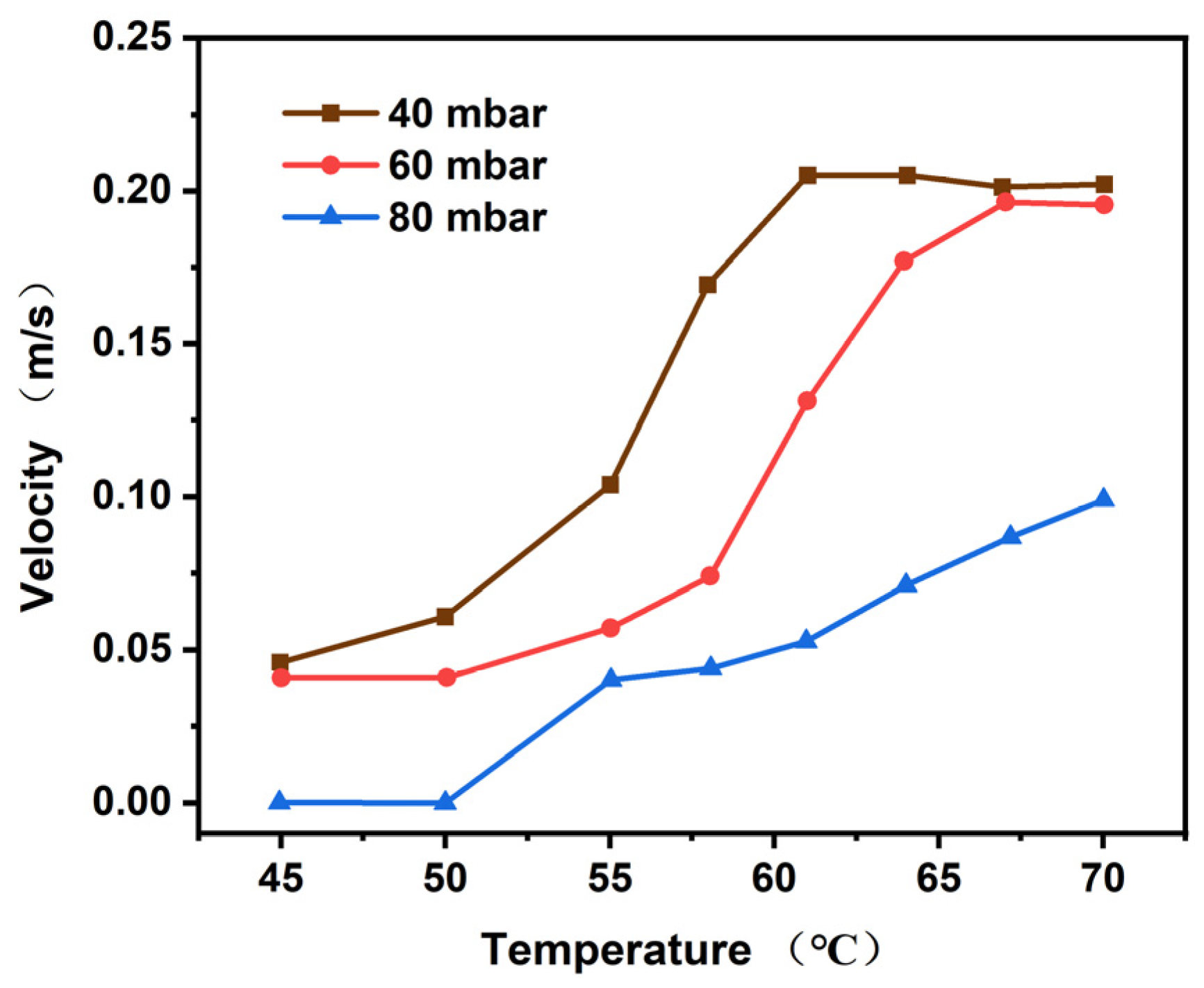
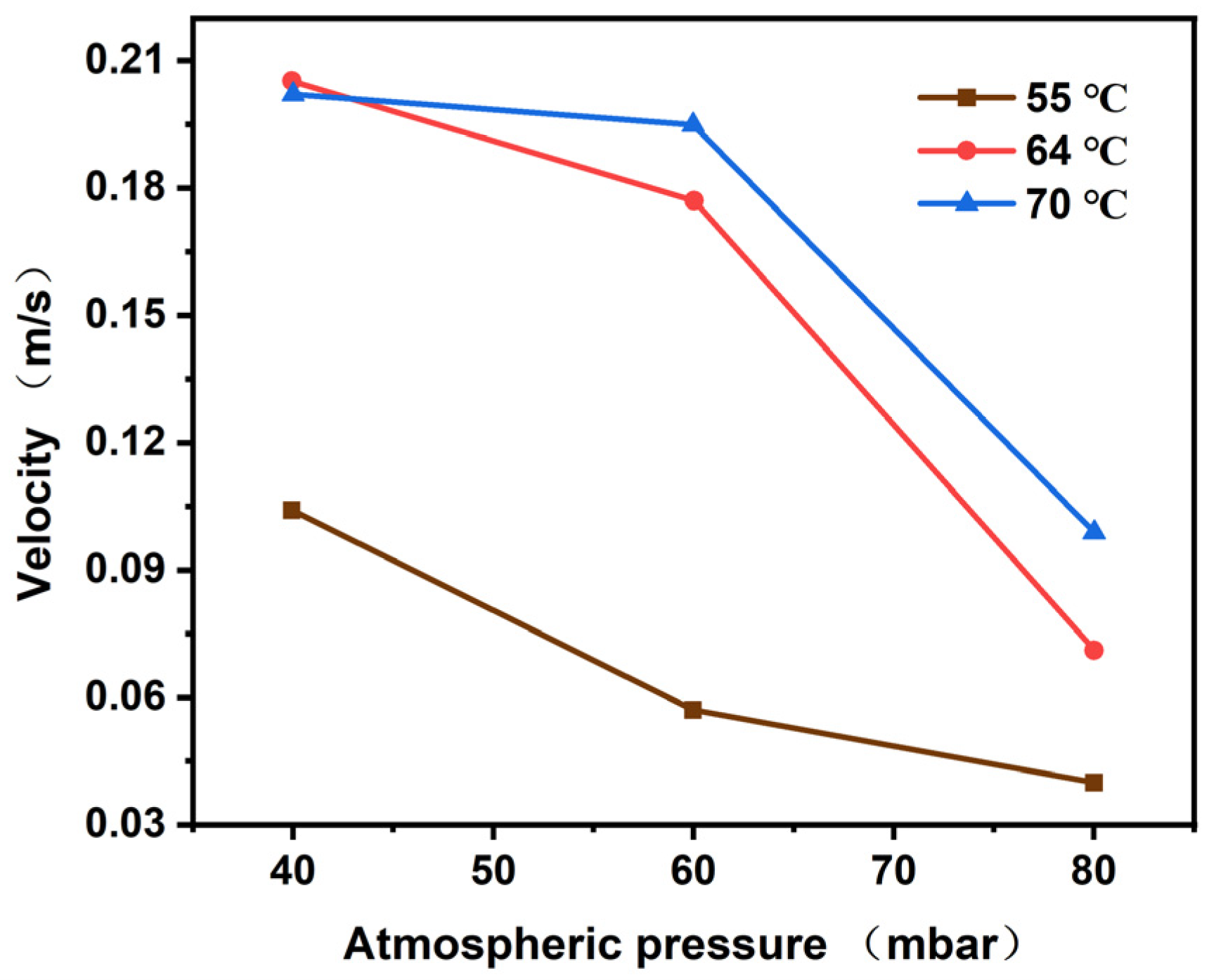
4.1.2. Bubble Velocity Analysis
4.1.3. Moisture Content Analysis
4.2. Simulation Result
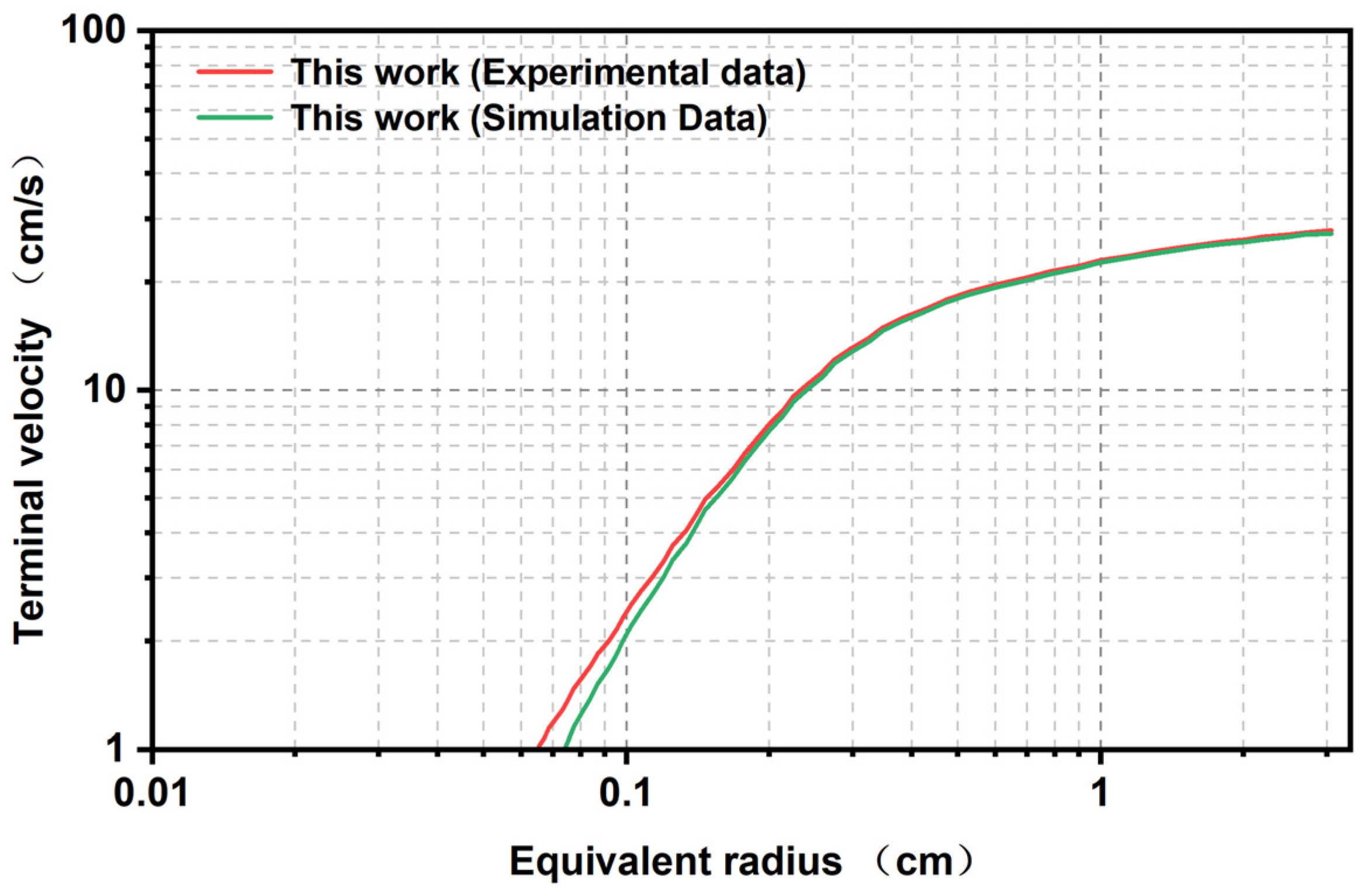
4.3. Comparison of Experimental Results and Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Damse, R.S.; Omprakash, B.; Tope, B.G.; Chakraborthy, T.K.; Singh, A. Study of Nn-butyl-N-(2-nitroxyethyl) nitramine in RDX based gun propellant. J. Hazard. Mater. 2009, 167, 1222–1225. [Google Scholar] [CrossRef] [PubMed]
- Kumari, D.; Balakshe, R.; Banerjee, S.; Singh, H. Energetic plasticizers for gun & rocket propellants. Rev. J. Chem. 2012, 2, 240–262. [Google Scholar] [CrossRef]
- Qi, X.F.; Zhang, X.H.; Guo, X.; Zhang, W.; Chen, Z.; Zhang, J.P. Experiments and simulation on plastication of NENA on NC. Guti Huojian Jishu/J. Solid Rocket. Technol. 2013, 36, 269–273. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Hou, J.; Zhan, L.W.; Li, B.D. Synthesis of BuNENA in a continuous flow microreactor. J. Flow Chem. 2023, 13, 449–456. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, Z.; Xu, B.; Zhu, Y.; Wang, X.; Yang, J.; Chen, Q.; Ma, Y.; Chen, F.; Liao, X. Influence of different energetic plasticizers on the performance of NC-RDX nitramine gun propellants. J. Sci. Adv. Mater. Devices 2024, 9, 100650. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, Z.; Xu, B.; Chen, F.; Wei, X.; Long, Y.; Liao, X. Thermal decomposition kinetics and storage life prediction of nitramine propellants with different energetic plasticizers based on model-fitting method. Case Stud. Therm. Eng. 2024, 61, 105014. [Google Scholar] [CrossRef]
- Khanlari, T.; Bayat, Y.; Bayat, M.; Sheibani, N. Synthesis, characterization, and curing of propylene oxide and glycidyl nitrate random copolymer (GN-ran-PO) and investigation of its compatibility with different energetic plasticizers. J. Mol. Struct. 2021, 1231, 130008. [Google Scholar] [CrossRef]
- Qi, X.; Li, H.; Zhao, Y.; Yan, N. Comparison of the structural and physical properties of nitrocellulose plasticized by N-butyl-N-(2-nitroxy-ethyl) nitramine and nitroglycerin: Computational simulation and experimental studies. J. Hazard. Mater. 2019, 362, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Ding, L.; Chang, H.; Zhu, Y.L.; Wang, G.Y. Study on thermal hazard of plasticizers BuNENA and NG. Guti Huojian Jishu/J. Solid Rocket. Technol. 2020, 43, 756–762. [Google Scholar] [CrossRef]
- Rao, K.P.; Sikder, A.K.; Kulkarni, M.A.; Bhalerao, M.M.; Gandhe, B.R. Studies on n-Butyl Nitroxyethylnitramine (n-BuNENA): Synthesis, Characterization and Propellant Evaluations. Propellants Explos. Pyrotech. Int. J. Deal. Sci. Technol. Asp. Energetic Mater. 2004, 29, 93–98. [Google Scholar] [CrossRef]
- Landsem, E.; Jensen, T.L.; Hansen, F.K.; Unneberg, E.; Kristensen, T.E. Neutral Polymeric Bonding Agents (NPBA) and Their Use in Smokeless Composite Rocket Propellants Based on HMX-GAP-BuNENA. Propellants Explos. Pyrotech. 2012, 37, 581–591. [Google Scholar] [CrossRef]
- Wang, Y.; Rong, H.; Zhang, X.; Chen, Y.; Luo, W.; Liu, Y.; Tian, Y. Influences of Bu-NENA and BDNPA/F Plasticizers on the Properties of Binder for High-Energy NEPE Propellants. Propellants Explos. Pyrotech. 2021, 46, 950–961. [Google Scholar] [CrossRef]
- Wang, Y.L.; Chen, Y.; Liu, Y.F. Decomposition Kinetics and Cook-Off Numerical Simulation of Insensitive Energetic Plasticizer Plasticized Propellants. Key Eng. Mater. 2022, 905, 263–268. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Saha, S.; Patel, J.; Bhagat, S.; Kumar, A.; Pawar, R.B.; Sudhir, S.S.; Chowdhury, A.; Namboothiri, I.N.; Kumbhakarna, N. Tetrazole-grafted-hydroxyl terminated polybutadiene: A novel energetic binder for solid rocket propulsion. Eur. Polym. J. 2024, 217, 113330. [Google Scholar] [CrossRef]
- Li, J.Q.; Fan, X.Z.; Tang, Q.F.; Li, J.Z.; Wang, G.Q.; Ren, X.N.; Mei, Z.T. Slow cook-off behavior and thermal decomposition characteristics of HTPE propellants. Guti Huojian Jishu/J. Solid Rocket. Technol. 2019, 42, 597–603. [Google Scholar] [CrossRef]
- Chen, K.K.; Sang, C.; Wen, X.M.; Pang, S.P.; Luo, Y.J. Effect of Plasticizer on Mechanical and Thermal Properties of In Situ-Prepared Block Hydroxyl-Terminated Polyether Applied in Propellants. Polym. Sci. Ser. A 2021, 63, 238–251. [Google Scholar] [CrossRef]
- Abdullah, M.; Gholamian, F.; Zarei, A.R. Noncrystalline binder based composite propellant. Int. Sch. Res. Not. 2013, 2013, 679710. [Google Scholar] [CrossRef]
- Shim, H.M.; Kim, S.J.; Park, Y.C.; Min, B.S. Quantum Mechanical Investigation on Decomposition Pathways of BuNENA. Propellants Explos. Pyrotech. 2022, 47, e202100194. [Google Scholar] [CrossRef]
- Feng, Y.; Sun, L.; Mo, Z.; Du, M.; Zhu, C.; Yang, W.; Xu, X. An evaluation of predictive correlations for the terminal rising velocity of a single bubble in quiescent clean liquid. Int. J. Multiph. Flow 2024, 173, 104736. [Google Scholar] [CrossRef]
- Gupta, A.; Roy, S. Euler–Euler simulation of bubbly flow in a rectangular bubble column: Experimental validation with Radioactive Particle Tracking. Chem. Eng. J. 2013, 225, 818–836. [Google Scholar] [CrossRef]
- Laborde-Boutet, C.; Larachi, F.; Dromard, N.; Delsart, O.; Schweich, D. CFD simulation of bubble column flows: Investigations on turbulence models in RANS approach. Chem. Eng. Sci. 2009, 64, 4399–4413. [Google Scholar] [CrossRef]
- Pourtousi, M.; Sahu, J.N.; Ganesan, P. Effect of interfacial forces and turbulence models on predicting flow pattern inside the bubble column. Chem. Eng. Process. Process Intensif. 2014, 75, 38–47. [Google Scholar] [CrossRef]
- Masood, R.M.A.; Delgado, A. Numerical investigation of the interphase forces and turbulence closure in 3D square bubble columns. Chem. Eng. Sci. 2014, 108, 154–168. [Google Scholar] [CrossRef]
- Xiao, Q.; Yang, N.; Li, J. Stability-constrained multi-fluid CFD models for gas–liquid flow in bubble columns. Chem. Eng. Sci. 2013, 100, 279–292. [Google Scholar] [CrossRef]
- Tabib, M.V.; Roy, S.A.; Joshi, J.B. CFD simulation of bubble column—An analysis of interphase forces and turbulence models. Chem. Eng. J. 2008, 139, 589–614. [Google Scholar] [CrossRef]
- Jin, D.; Xiong, J.; Cheng, X. Investigation on interphase force modeling for vertical and inclined upward adiabatic bubbly flow. Nucl. Eng. Des. 2019, 350, 43–57. [Google Scholar] [CrossRef]
- Jiang, X.; Yang, N.; Yang, B. Computational fluid dynamics simulation of hydrodynamics in the riser of an external loop airlift reactor. Particuology 2016, 27, 95–101. [Google Scholar] [CrossRef]
- Tas-Koehler, S.; Liao, Y.; Hampel, U. A critical analysis of drag force modelling for disperse gas-liquid flow in a pipe with an obstacle. Chem. Eng. Sci. 2021, 246, 117007. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhao, C.; Bo, H. Analyses and modified models for bubble shape and drag coefficient covering a wide range of working conditions. Int. J. Multiph. Flow 2020, 127, 103265. [Google Scholar] [CrossRef]
- Hashemi, A.R.; de Parga-Regalado, A.M.A.; Ryzhakov, P.B. Data-Driven Analysis of Droplet Morphology in Inkjet Systems: Toward Generating Stable Single-Drop Regimes. arXiv 2025, arXiv:2501.13801. [Google Scholar] [CrossRef]
- Prakash, M.; Cleary, P.W.; Pyo, S.H.; Woolard, F. A new approach to boiling simulation using a discrete particle based method. Comput. Graph. 2015, 53, 118–126. [Google Scholar] [CrossRef]
- Miller, S. Methods for computing the boiling temperature of water at varying pressures. Bull. Am. Meteorol. Soc. 2017, 98, 1485–1491. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Karayiannis, T.G. Pool boiling review: Part I–Fundamentals of boiling and relation to surface design. Therm. Sci. Eng. Prog. 2021, 25, 101024. [Google Scholar] [CrossRef]
- Plesset, M.S.; Zwick, S.A. The growth of vapor bubbles in superheated liquids. J. Appl. Phys. 1954, 25, 493–500. [Google Scholar] [CrossRef]
- Moreno, E.; Larese, A.; Cervera, M. Modelling of Bingham and Herschel–Bulkley flows with mixed P1/P1 finite elements stabilized with orthogonal subgrid scale. J. Non-Newton. Fluid Mech. 2016, 228, 1–16. [Google Scholar] [CrossRef]
- Cotela Dalmau, J.; Oñate Ibáñez de Navarra, E.; Rossi, R. Applications of Turbulence Modeling in CIVIL Engineering; International Centre for Numerical Methods in Engineering (CIMNE): Barcelona, Spain, 2016; Available online: http://hdl.handle.net/2117/189085 (accessed on 21 April 2025).
- Hu, H.; Lu, Y.; Guo, L.; Chen, X.; Wang, Q.; Wang, J.; Li, Q. Effects of system pressure on nucleate boiling: Insights from molecular dynamics. J. Mol. Liq. 2024, 402, 124745. [Google Scholar] [CrossRef]
- Ren, S.; Zhou, W. Pre-CHF boiling heat transfer performance on tube bundles with or without enhanced surfaces—A review. Ann. Nucl. Energy 2020, 139, 107278. [Google Scholar] [CrossRef]
- Kalani, A.; Kandlikar, S.G. Enhanced pool boiling with ethanol at subatmospheric pressures for electronics cooling. J. Heat Transf. 2013, 135, 111002. [Google Scholar] [CrossRef]
- Surtaev, A.; Serdyukov, V.; Malakhov, I. Effect of subatmospheric pressures on heat transfer, vapor bubbles and dry spots evolution during water boiling. Exp. Therm. Fluid Sci. 2020, 112, 109974. [Google Scholar] [CrossRef]
- Sakashita, H. Bubble growth rates and nucleation site densities in saturated pool boiling of water at high pressures. J. Nucl. Sci. Technol. 2011, 48, 734–743. [Google Scholar] [CrossRef]
- Schäfer, R.; Merten, C.; Eigenberger, G. Bubble size distributions in a bubble column reactor under industrial conditions. Exp. Therm. Fluid Sci. 2002, 26, 595–604. [Google Scholar] [CrossRef]
- Gong, M.; Wu, Y.; Ding, L.; Cheng, K.; Wu, J. Visualization study on nucleate pool boiling of ethane, isobutane and their binary mixtures. Exp. Therm. Fluid Sci. 2013, 51, 164–173. [Google Scholar] [CrossRef]
- Hutter, C.; Kenning, D.B.R.; Sefiane, K.; Karayiannis, T.G.; Lin, H.; Cummins, G.; Walton, A.J. Experimental pool boiling investigations of FC-72 on silicon with artificial cavities and integrated temperature microsensors. Exp. Therm. Fluid Sci. 2010, 34, 422–433. [Google Scholar] [CrossRef]
- Kim, J.; Huh, C.; Kim, M.H. On the growth behavior of bubbles during saturated nucleate pool boiling at sub-atmospheric pressure. Int. J. Heat Mass Transf. 2007, 50, 3695–3699. [Google Scholar] [CrossRef]
- Ghazivini, M.; Hafez, M.; Ratanpara, A.; Kim, M. A review on correlations of bubble growth mechanisms and bubble dynamics parameters in nucleate boiling. J. Therm. Anal. Calorim. 2022, 147, 6035–6071. [Google Scholar] [CrossRef]
- Al-Zaidi, A.H.; Mahmoud, M.M.; Ivanov, A.; Karayiannis, T.G. Bubble nucleation site density, generation frequency and departure diameter in flow boiling of HFE-7100. Int. J. Heat Mass Transf. 2025, 242, 126830. [Google Scholar] [CrossRef]
- Hamzekhani, S.; Falahieh, M.M.; Akbari, A. Bubble departure diameter in nucleate pool boiling at saturation: Pure liquids and binary mixtures. Int. J. Refrig. 2014, 46, 50–58. [Google Scholar] [CrossRef]
- Haberman, W.L.; Morton, R.K. An Experimental Investigation of the Drag and Shape of Air Bubbles Rising in Various Liquids; David W. Taylor Model Basin: Washington, DC, USA, 1953. [Google Scholar] [CrossRef]






| Materials | Viscosity (20 °C)/cP | Viscosity (50 °C)/cP | Density (20 °C) g/mL |
|---|---|---|---|
| HTPE | 142.4 | 88 | / |
| 220 mL Glycerin + 160 mL BuNENA | 148.8 | 81.6 | 1.17 |
| Temperature/°C | 45 | 50 | 55 | 58 | 61 | 64 | 67 | 70 | 75 |
|---|---|---|---|---|---|---|---|---|---|
| Vacuum degree/mbar (Internal pressure/Pa) | 40/60/80/100 4000/6000/8000/10,000 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Rossi, R.; Deng, R.; Wu, Y.; Liu, H.; Hao, L.; Fu, X. Research on Passivation Simulation of Plasticizer N-Butylnitroxyethylnitramine (BuNENA) in Hydroxy-Terminated Polyether (HTPE) Propellants. Polymers 2025, 17, 1147. https://doi.org/10.3390/polym17091147
Guo Z, Rossi R, Deng R, Wu Y, Liu H, Hao L, Fu X. Research on Passivation Simulation of Plasticizer N-Butylnitroxyethylnitramine (BuNENA) in Hydroxy-Terminated Polyether (HTPE) Propellants. Polymers. 2025; 17(9):1147. https://doi.org/10.3390/polym17091147
Chicago/Turabian StyleGuo, Zhiming, Riccardo Rossi, Rui Deng, Yuheng Wu, Hanwen Liu, Lin Hao, and Xiaolong Fu. 2025. "Research on Passivation Simulation of Plasticizer N-Butylnitroxyethylnitramine (BuNENA) in Hydroxy-Terminated Polyether (HTPE) Propellants" Polymers 17, no. 9: 1147. https://doi.org/10.3390/polym17091147
APA StyleGuo, Z., Rossi, R., Deng, R., Wu, Y., Liu, H., Hao, L., & Fu, X. (2025). Research on Passivation Simulation of Plasticizer N-Butylnitroxyethylnitramine (BuNENA) in Hydroxy-Terminated Polyether (HTPE) Propellants. Polymers, 17(9), 1147. https://doi.org/10.3390/polym17091147







