Mathematical Models of Leaf Area Index and Yield for Grapevines Grown in the Turpan Area, Xinjiang, China
Abstract
:1. Introduction
2. Materials and Methods
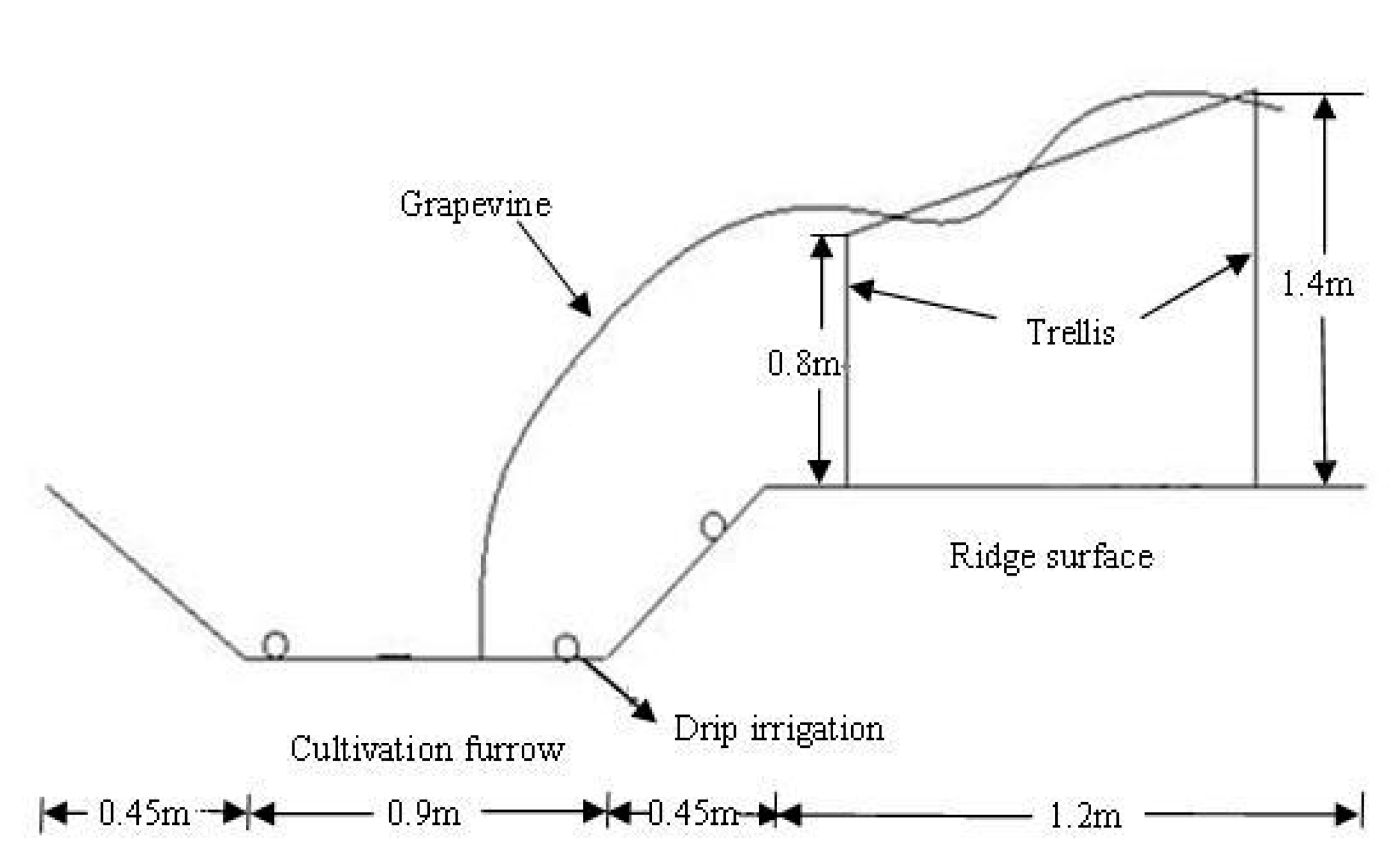
2.1. Experimental Fields
2.2. Experimental Design
2.3. GDD Calculations
2.4. Leaf Area Index Growth Models
2.5. Statistical Analysis
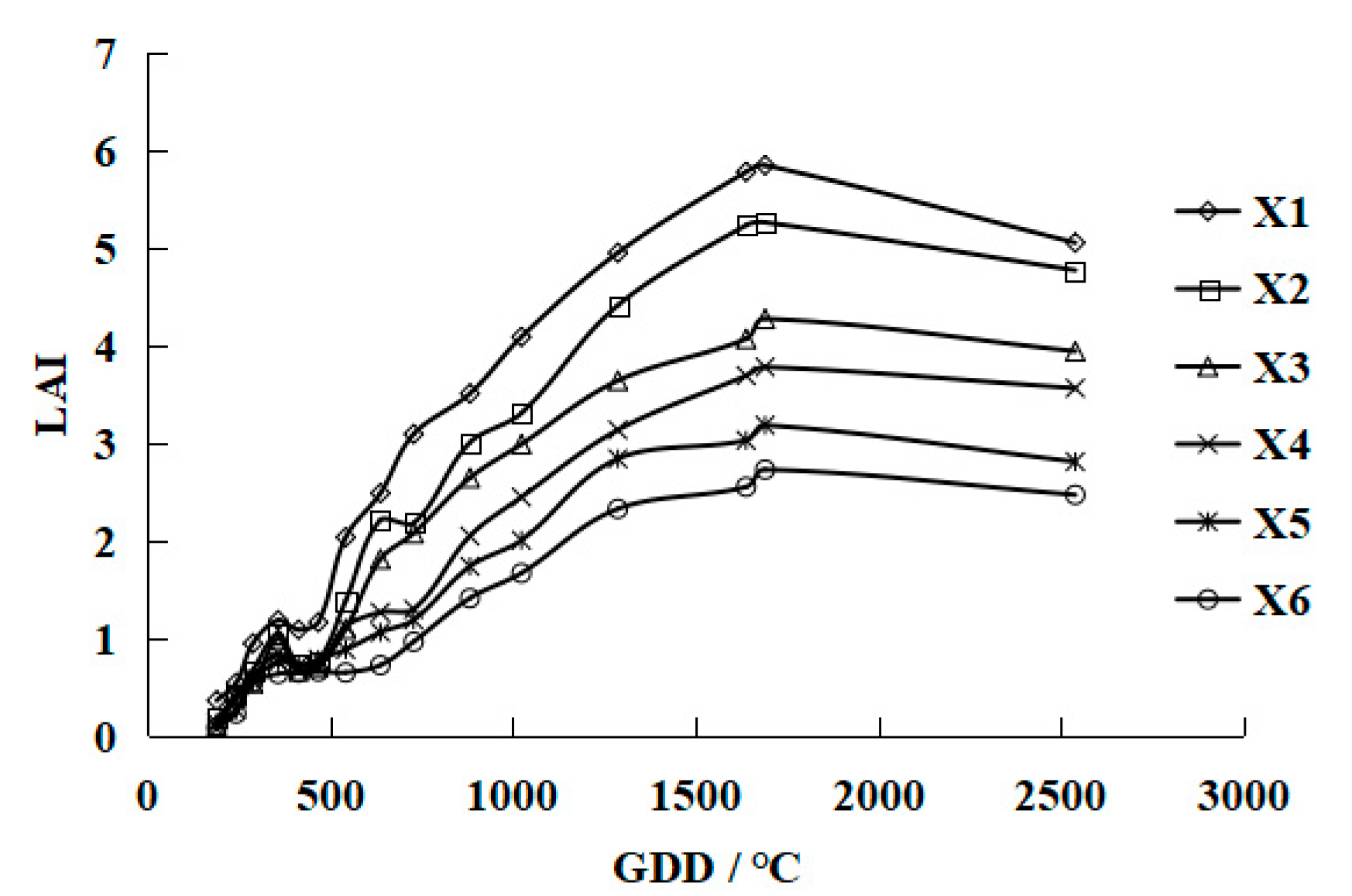
3. Results and Discussion
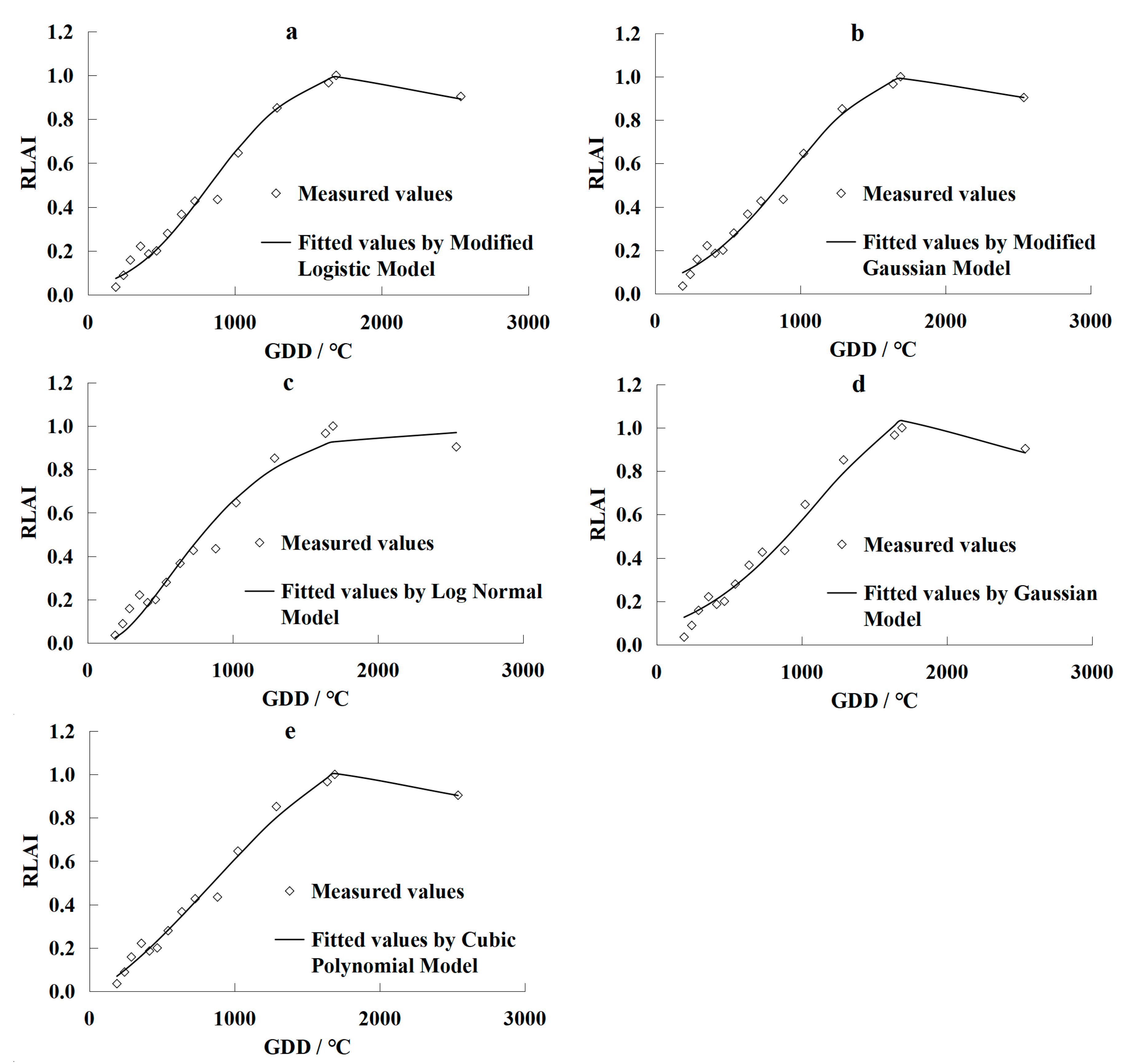
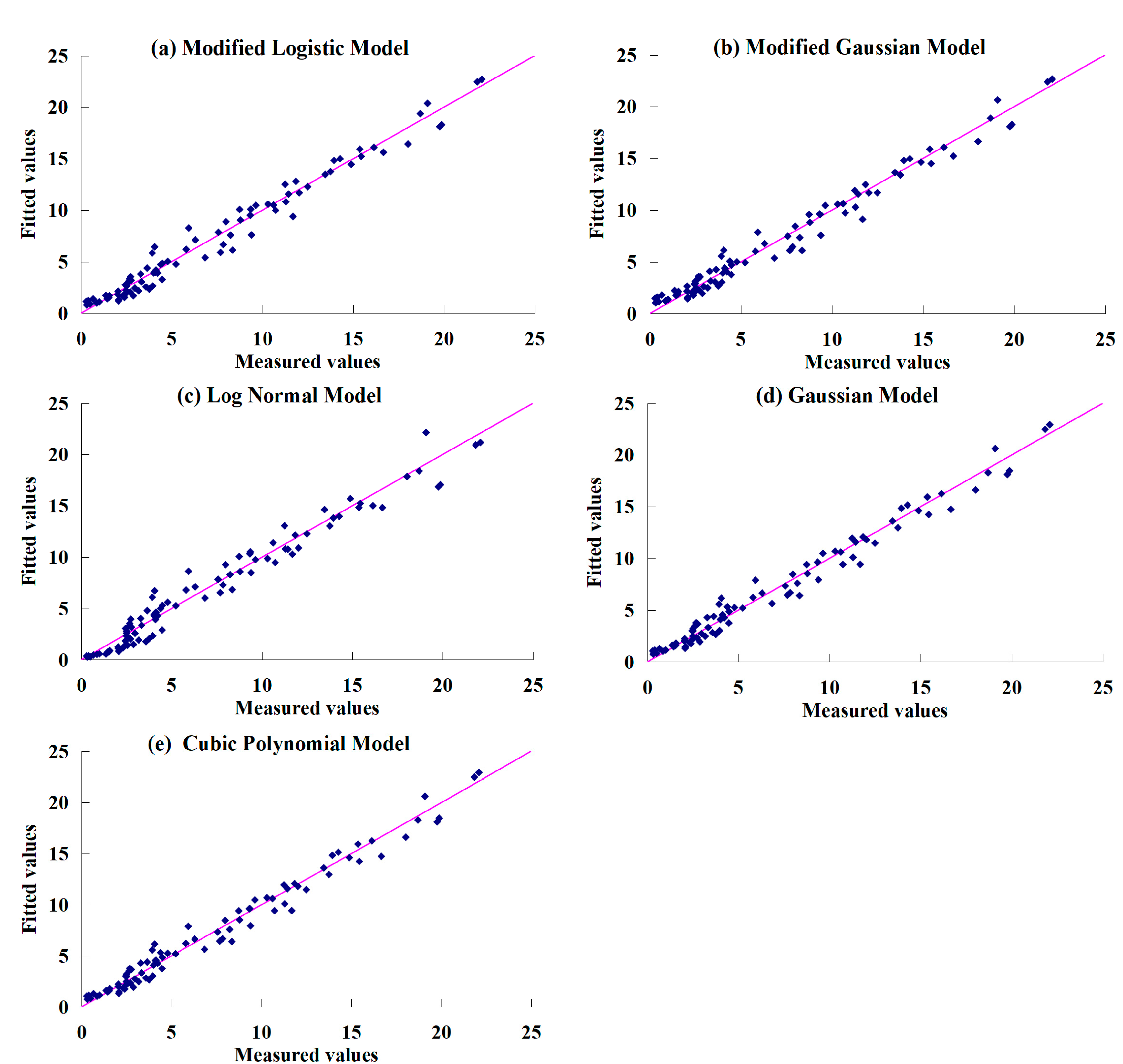
3.1. Leaf Area Index Simulation Models
3.2. The Relationship between Water Consumption and LAI
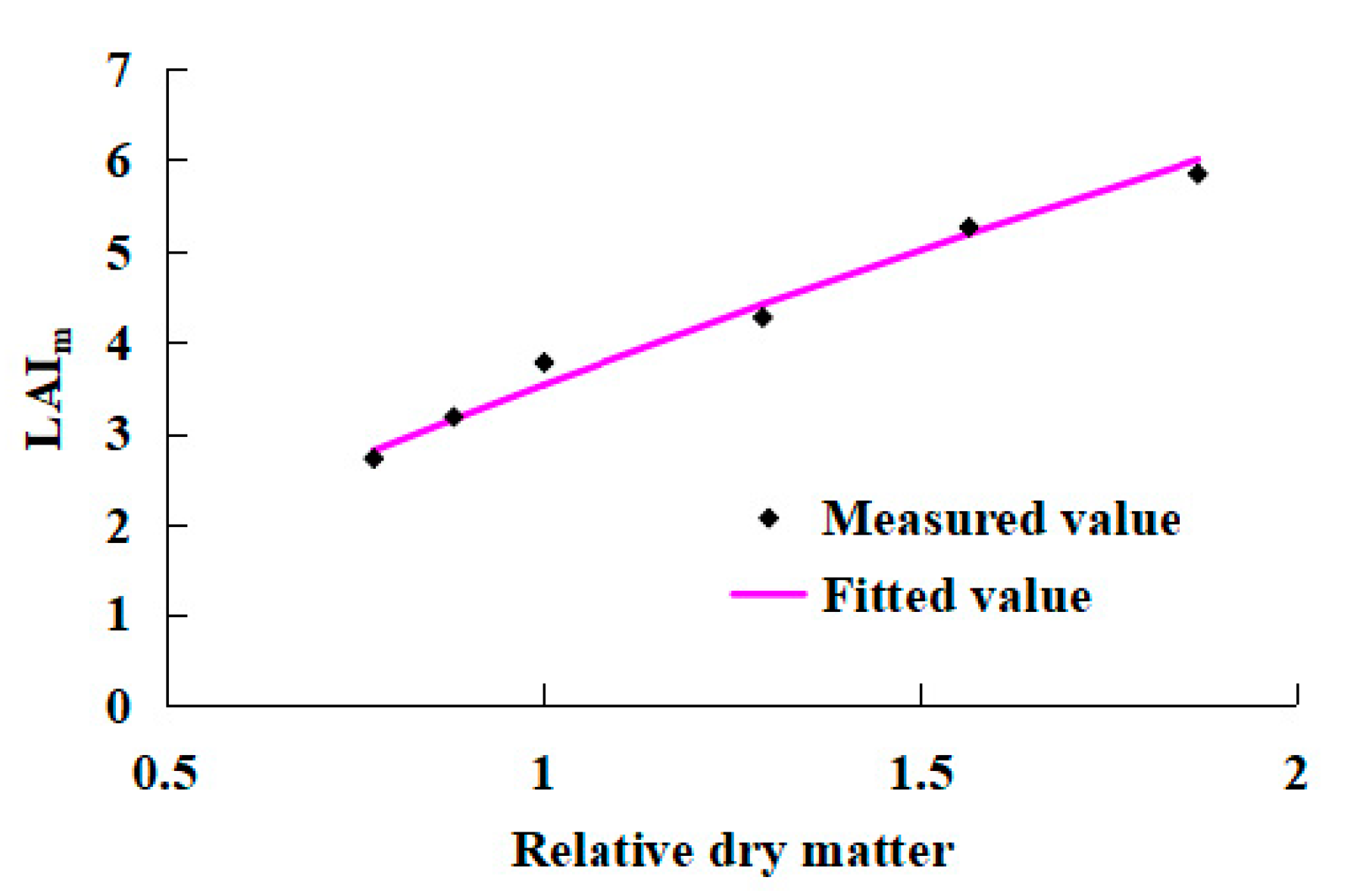
3.3. Relationship between LAI and Dry Mass
3.4. Mathematical Model of Yields
4. Conclusions
- (1)
- Normalizing the measured LAI values makes it possible to disregard the impacts of irrigation quotas on the changes in grapevine LAI. The Linthe universal models were developed by the modified logistic model, the modified Gaussian model, the log-normal model, the Gaussian model, and the cubic polynomial model. Results using these models showed that they accurately fitted the measured data of LAI over the grapevines growing season in Turpan. However, the Gaussian and log-normal models yielded less accurate results than the other three models;
- (2)
- Universal LAI models were developed to describe the relationship between the peak LAI value and water consumption. The models can be used to fit the dynamic changes of LAI over the growing season for different drip irrigation regimes. To ensure the yields of grapevine during the growth period, the water consumption must be at least 132.46 mm in the Turpan area;
- (3)
- When the water consumption was in the range of 637.5 mm—11,215 mm, the biomass increased linearly, and the harvest index for the grapes was a quadratic polynomial function of the peak leaf area index. According to the relationships between yield, dry matter and harvest index, a mathematical yield model was proposed that relies on a single parameter: the peak leaf area index. Such descriptions of the relationship between yields and the harvest index can provide important information on improving water use efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Wit, C.T. Photosynthesis of leaf canopies. Agric. Res. Rep. 1965, 663, 413358. [Google Scholar]
- Boote, K.J.; Jones, J.W.; Hoogenboom, G. Simulation of crop growth: CROPGRO model. In Agricultural Systems Modeling and Simulation; Peart, R.M., Curry, R.B., Eds.; Marcel Dekker, Inc.: New York, NY, USA, 1998; pp. 651–692. [Google Scholar]
- Sinclair, T.R. Water and nitrogen limitation in soybean grain production I. Model development. Field Crops Res. 1986, 15, 125–141. [Google Scholar] [CrossRef]
- Boogard, H.L.; van Diepen, C.A.; Rutter, R.P.; Cabrera, J.M.C.A.; van Laar, H.H. User’s Guide for the WOFOST 7.1 Crop Growth Simulation Model and WOFOST Control Center 1.5; Technical Document 52; DLO Winand Staring Centre: Wageningen, The Netherlands, 1995. [Google Scholar]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model STICS. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Liben, F.M.; Wortmann, C.S.; Yang, H.; Lindquist, J.L.; Tadesse, T.; Wegary, D. Crop model and weather data generation evaluation for conservation agriculture in Ethiopia. Field Crop Res. 2018, 228, 122–134. [Google Scholar] [CrossRef]
- Manivasagam, V.S.; Rozenstein, O. Practices for upscaling crop simulation models from field scale to large regions. Comput. Electron. Agric. 2020, 175, 105554. [Google Scholar] [CrossRef]
- Demarez, V.; Duthoit, S.; Baret, F. Estimation of leaf area and clumping indexes of crops with hemispherical photographs. Agric. For. Meteorol. 2008, 148, 644–655. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Sanchez-Molina, J.A.; Li, M.; Berenguel, M.; Yang, X.T.; Bienvenido, J.F. Leaf area index estimation for a greenhouse transpiration model using external climate conditions based on genetics algorithms, back-propagation neural networks and nonlinear autoregressive exogenous models. Agric. Water Manag. 2017, 183, 107–115. [Google Scholar] [CrossRef]
- Behera, S.K.; Srivastava, P.; Pathre, U.V.; Tuli, R. An indirect method of estimating leaf area index in Jatropha curcas L. using LAI-2000 Plant Canopy An7alyzer. Agric. For. Meteorol. 2010, 150, 307–311. [Google Scholar] [CrossRef]
- Thimonier, A.; Sedivy, I.; Schleppi, P. Estimating leaf area index in different types of mature forest stands in Switzerland: A comparison of methods. Eur. J. For. Res. 2010, 129, 543–562. [Google Scholar] [CrossRef]
- Hasegawa, K.; Matsuyama, H.; Tsuzuki, H.; Sweda, T. Improving the estimation of leaf area index by using remotely sensed NDVI with BRDF signatures. Remote Sens. Environ. 2010, 114, 514–519. [Google Scholar] [CrossRef]
- Chianucci, F.; Cutini, A.; Corona, P.; Puletti, N. Estimation of leaf area index in understory deciduous trees using digital photography. Agric. For. Meteorol. 2014, 198, 259–264. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, M.I.; Hiura, T. Modeling leaf area index from litter collection and tree data in a deciduous broadleaf forest. Agric. For. Meteorol. 2011, 151, 1016–1022. [Google Scholar] [CrossRef]
- Lotka, A.J. Elements of Physical Biology; Williams & Wilkins: Baltimore, MD, USA, 1925. [Google Scholar]
- Liu, J.H.; Yan, Y.; Ali, A.; Yu, M.F.; Xu, Q.J.; Shi, P.J.; Chen, L. Simulation of crop growth, time to maturity and yield by an improved sigmoidal model. Sci. Rep. 2018, 8, 7030. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, X.; Zhang, X.; Wang, J.; Yang, Z. Winter wheat leaf area index inversion by the genetic algorithms neural network model based on SAR data. Int. J. Digit. Earth 2022, 15, 362–380. [Google Scholar] [CrossRef]
- Ma, C.Y.; Liu, M.X.; Ding, F.; Li, C.; Cui, Y.; Chen, W.; Wang, Y. Wheat growth monitoring and yield estimation based on remote sensing data assimilation into the SAFY crop growth model. Sci. Rep. 2022, 12, 5473. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Gao, F.; Anderson, M.C.; Kustas, W.P.; Alsina, M.M.; Sanchez, L.; Sams, B.; McKee, L.; Dulaney, W.; White, W.A.; et al. Daily Mapping of 30 m LAI and NDVI for grape yield prediction in california vineyards. Remote Sens. 2017, 9, 317. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.F.; Liu, J.G.; Shang, J.L.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Doring, J.; Stoll, M.; Kauer, R.; Frisch, M.; Tittmann, S. Indirect estimation of leaf area index in VSP-Trained grapevines using plant area index. Am. J. Enol. Vitic. 2014, 65, 153–158. [Google Scholar] [CrossRef]
- Wang, S.S. A generalized logistic model of single populations growth. J. Biomath. 1990, 5, 21–25. [Google Scholar]
- Wang, X.; Wang, Q.; Fan, J.; Su, L.; Shen, X. Logistic model analysis of winter wheat growth on China’s Loess Plateau. Can. J. Plant Sci. 2014, 94, 1471–1479. [Google Scholar]
- Liu, Y.; Su, L.; Wang, Q.; Zhang, J.; Shan, Y.; Deng, M. Comprehensive and quantitative analysis of growth characteristics of winter wheat in China based on growing degree days. Adv. Agron. 2020, 159, 237–273. [Google Scholar]
- Wang, K.; Su, L.J.; Wang, Q.J. Cotton growth model under drip irrigation with film mulching: A case study of Xinjiang, China. Agron. J. 2021, 113, 2417–2436. [Google Scholar] [CrossRef]
- Setiyono, T.D.; Weiss, A.; Specht, J.E.; Cassman, K.G.; Dobermann, A. Leaf area index simulation in soybean grown under near-optimal conditions. Field Crops Res. 2008, 108, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Fujikawa, H.; Kai, A.; Morozumi, S. A new logistic model for Escherichia coli growth at constant and dynamic temperatures. Food Microbiol. 2004, 21, 501–509. [Google Scholar] [CrossRef]
- Anandhi, A. Growing degree days-ecosystem indicator for changing diurnal temperatures and their impact on corn growth stages in Kansas. Ecol. Indic. 2016, 61, 149–158. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.J.; Lin, S.D.; Su, L.J. Quantitative Analysis of response of potato main growth index to growing degree days. Trans. Chin. Soc. Agric. Mach. 2020, 51, 306–316. [Google Scholar]
- Su, L.J.; Liu, Y.H.; Wang, Q.J. Rice growth model in China based on growing degree days. Trans. Chin. Soc. Agric. Eng. 2020, 36, 162–174. [Google Scholar]
- Liu, F.; Liu, Y.; Su, L.; Tao, W.; Wang, Q.; Deng, M. Integrated growth model of typical crops in China with regional parameters. Water 2022, 14, 1139. [Google Scholar] [CrossRef]
- Overman, A.R.; Wilkinson, S.R.; Wilson, D.M. An extended logistic model of forage grass response to applied nitrogen. Agron. J. 1994, 86, 617–620. [Google Scholar] [CrossRef]
- Overman, A.R. Rational basis for the logistic model for forage grass. J. Plant Nutr. 1995, 18, 995–1012. [Google Scholar] [CrossRef]
- Overman, A.R.; Evers, G.W.; Wilkinson, S.R. Coupling of dry matter and nutrient accumulation in forage grass. J. Plant Nutr. 1995, 18, 2629–2642. [Google Scholar] [CrossRef]
- Overman, A.R.; Martin, F.G.; Wilkinson, S.R. A logistic equation for yield response of forage grass to nitrogen. Commun. Soil Sci. Plant Anal. 1990, 21, 595–609. [Google Scholar] [CrossRef]
- Overman, A.R.; Wilkinson, S.R. Extended logistic model of forage grass response to applied nitrogen, phosphorus, and potassium. Trans. Am. Soc. Agric. Eng. 1995, 38, 103–108. [Google Scholar] [CrossRef]
- Yang, L.L.; Wang, Y.M.; Kang, M.Z.; Dong, Q.X. Simulation of Tomato Fruit Individual Growth Rule Based on Revised Logistic Model. Trans. Chin. Soc. Agric. Mach. 2008, 39, 81–84. [Google Scholar]
- Munitz, S.; Schwart, A.; Netzer, Y. Water consumption, crop coefficient and leaf area relations of a Vitis vinifera cv. ‘Cabernet Sauvignon’ vineyard. Agric. Water Manag. 2019, 219, 86–94. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L.; Bai, Y.L.; Lu, Y.L.; Ni, L.; Wang, Y.H.; Xu, M.Z. Quantitative Relationship Between Effective Accumulated Temperature and Plant Height & Leaf Area Index of Summer Maize Under Different Nitrogen, Phosphorus and Potassium Levels. Sci. Agric. Sin. 2021, 54, 4761–4777. [Google Scholar]
- Wang, R.J.; Li, S.Q.; Wang, Q.J.; Zheng, J.Y.; Fan, J.; Li, S.X. Evaluation of simulation models of spring-maize leaf area and biomass in semiarid agro-ecosystems. Chin. J. Eco-Agric. 2008, 16, 139–144. [Google Scholar] [CrossRef]
- Su, L.; Wang, Q.; Wang, C.; Shan, Y. Simulation models of leaf area index and yield for cotton grown with different soil conditioners. PLoS ONE 2015, 10, e0141835. [Google Scholar] [CrossRef]
- Lin, Z.H.; Xiang, Y.Q.; Mo, X.G.; Li, J.; Wang, L. Normalized leaf area index model for summer maize. Chin. J. Eco-Agric. 2003, 11, 69–72. [Google Scholar]
- Li, X.L.; Zhao, M.; Li, C.F.; Ge, J.Z.; Hou, H.P. Dynamic characteristics of leaf area index in maize and its model establishment based on accumulated temperature. ACTA Agron. Sin. 2011, 37, 321–330. [Google Scholar] [CrossRef]
- Wang, S.F.; Duan, A.W.; Xu, J.X. Dynamic changes and simulation model of plant height and leaf area index of winter wheat. J. Irrig. Drain. 2010, 29, 97–100. [Google Scholar]
- Li, W.F.; Meng, Y.L.; Zhao, X.H.; Chen, B.L.; Xu, N.Y.; Zhou, Z.G. Modeling of cotton boll maturation period and cottonseed biomass accumulation. Chin. J. Appl. Ecol. 2009, 20, 879–886. [Google Scholar]
- Wang, Q.J.; Wang, K.; Su, L.J.; Zhang, J.H.; Wei, K. Effect of irrigation amount, nitrogen application rate and planting density on cotton leaf area index and yield. Trans. CSAM 2021, 52, 300–312. [Google Scholar]
- McMaster, G.S.; Wilhelm, W.W. Growing degree-days: One equation, two interpretations. Agric. For. Meteorol. 1997, 87, 291–300. [Google Scholar] [CrossRef] [Green Version]
- Steduto, P.; Hsiao, T.C.; Fereres, E. On the conservative behavior of biomass water productivity. Irrig. Sci. 2007, 25, 189–207. [Google Scholar] [CrossRef] [Green Version]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop-The FAO Crop Model to simulate yield response to water: I. concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef] [Green Version]





| Irrigation Treatment | Irrigation Frequency | Irrigation Quota for Each Application (mm) | Irrigation Quota (mm) | Drip Irrigation Tape Parameters | ||
|---|---|---|---|---|---|---|
| Critical Watering Time | Non-Critical Watering Time | Drip Flow (L/h) | Dripper Spacing (cm) | |||
| X1 | 4.5 | 4.5 | 52.5 | 1215 | 2.7 | 40 |
| X2 | 4.5 | 9 | 52.5 | 1005 | ||
| X3 | 4.5 | 13.5 | 52.5 | 900 | ||
| X4 | 9 | 9 | 52.5 | 847.5 | ||
| X5 | 9 | 13.5 | 52.5 | 690 | ||
| X6 | 13.5 | 13.5 | 52.5 | 637.5 | ||
| Time/Days | GDD/°C | RLAI | Mean RLAI | Standard Deviation | |||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | ||||
| 97 | 190 | 0.0619 | 0.0336 | 0.0250 | 0.0204 | 0.0416 | 0.0313 | 0.0356 | 0.0148 |
| 101 | 243 | 0.0927 | 0.0790 | 0.0954 | 0.1011 | 0.0835 | 0.0836 | 0.0892 | 0.0085 |
| 104 | 289 | 0.1619 | 0.1283 | 0.1263 | 0.1613 | 0.1734 | 0.2010 | 0.1587 | 0.0283 |
| 109 | 358 | 0.2025 | 0.1991 | 0.2328 | 0.2225 | 0.2397 | 0.2327 | 0.2215 | 0.0170 |
| 113 | 414 | 0.1860 | 0.1391 | 0.1551 | 0.1756 | 0.2258 | 0.2370 | 0.1864 | 0.0386 |
| 117 | 468 | 0.1988 | 0.1654 | 0.1659 | 0.1848 | 0.2467 | 0.2416 | 0.2006 | 0.0361 |
| 123 | 543 | 0.3480 | 0.2633 | 0.2561 | 0.2961 | 0.2776 | 0.2377 | 0.2798 | 0.0388 |
| 129 | 638 | 0.4253 | 0.4203 | 0.4237 | 0.3348 | 0.3331 | 0.2652 | 0.3671 | 0.0663 |
| 135 | 729 | 0.5289 | 0.4142 | 0.4857 | 0.4061 | 0.3732 | 0.3534 | 0.4269 | 0.0674 |
| 144 | 883 | 0.5094 | 0.4706 | 0.4946 | 0.4156 | 0.3377 | 0.3811 | 0.4348 | 0.0680 |
| 152 | 1024 | 0.6992 | 0.6283 | 0.6994 | 0.6122 | 0.6297 | 0.6112 | 0.6467 | 0.0415 |
| 165 | 1288 | 0.8467 | 0.8383 | 0.8518 | 0.8294 | 0.8921 | 0.8525 | 0.8518 | 0.0216 |
| 182 | 1639 | 0.9885 | 0.9943 | 0.9519 | 0.9766 | 0.9513 | 0.9351 | 0.9663 | 0.0236 |
| 185 | 1691 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0 |
| 217 | 2540 | 0.8644 | 0.9067 | 0.9223 | 0.9427 | 0.8826 | 0.9053 | 0.9040 | 0.0278 |
| Model | Expression | Re/% | R2 | RMSE | Parameter Number |
|---|---|---|---|---|---|
| Modified Logistic Model | 7.45 | 0.9837 | 0.0414 | 4 | |
| Modified Gaussian Model | 6.49 | 0.9877 | 0.0361 | 4 | |
| Log-Normal Model | 8.16 | 0.9805 | 0.0454 | 3 | |
| Cubic Polynomial Model | 6.37 | 0.9881 | 0.0354 | 4 | |
| Gaussian Model | 10.60 | 0.9671 | 0.0589 | 3 |
| Measured LAIm Value | Predicted LAIm Value | |||||
|---|---|---|---|---|---|---|
| Modified Logistic Model | Modified Gaussian Model | Log Normal Model | Cubic Polynomial Model | Gaussian Model | ||
| X1 | 5.84 | 5.81 | 5.67 | 5.42 | 5.87 | 6.04 |
| X2 | 5.26 | 5.23 | 5.11 | 4.88 | 5.28 | 5.43 |
| X3 | 4.27 | 4.25 | 4.15 | 3.96 | 4.29 | 4.41 |
| X4 | 3.78 | 3.75 | 3.67 | 3.50 | 3.79 | 3.90 |
| X5 | 3.18 | 3.16 | 3.09 | 2.95 | 3.19 | 3.29 |
| X6 | 2.73 | 2.71 | 2.65 | 2.53 | 2.74 | 2.82 |
| Re/% | 0.59 | 2.91 | 7.29 | 0.43 | 3.29 | |
| RMSE | 0.0255 | 0.1258 | 0.3149 | 0.0184 | 0.1421 | |
| R2 | 0.9995 | 0.9868 | 0.9175 | 0.9997 | 0.9832 | |
| Measured Yield Value | Predicted Yield Value | |||||
|---|---|---|---|---|---|---|
| Modified Logistic Model | Modified Gaussian Model | Log Normal Model | Cubic Polynomial Model | Gaussian Model | ||
| X1 | 61.7 | 60.65 | 61.48 | 62.83 | 60.26 | 59.09 |
| X2 | 63.3 | 63.64 | 64.07 | 64.67 | 63.43 | 62.76 |
| X3 | 63.2 | 64.81 | 64.61 | 64.06 | 64.87 | 65.00 |
| X4 | 61.7 | 63.19 | 62.73 | 61.71 | 63.38 | 63.84 |
| X5 | 58.8 | 59.00 | 58.30 | 56.86 | 59.30 | 60.09 |
| X6 | 55.3 | 54.06 | 53.25 | 51.63 | 54.41 | 55.36 |
| Re/% | 1.85 | 1.92 | 3.09 | 1.99 | 2.74 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Tao, W.; Sun, Y.; Shan, Y.; Wang, Q. Mathematical Models of Leaf Area Index and Yield for Grapevines Grown in the Turpan Area, Xinjiang, China. Agronomy 2022, 12, 988. https://doi.org/10.3390/agronomy12050988
Su L, Tao W, Sun Y, Shan Y, Wang Q. Mathematical Models of Leaf Area Index and Yield for Grapevines Grown in the Turpan Area, Xinjiang, China. Agronomy. 2022; 12(5):988. https://doi.org/10.3390/agronomy12050988
Chicago/Turabian StyleSu, Lijun, Wanghai Tao, Yan Sun, Yuyang Shan, and Quanjiu Wang. 2022. "Mathematical Models of Leaf Area Index and Yield for Grapevines Grown in the Turpan Area, Xinjiang, China" Agronomy 12, no. 5: 988. https://doi.org/10.3390/agronomy12050988
APA StyleSu, L., Tao, W., Sun, Y., Shan, Y., & Wang, Q. (2022). Mathematical Models of Leaf Area Index and Yield for Grapevines Grown in the Turpan Area, Xinjiang, China. Agronomy, 12(5), 988. https://doi.org/10.3390/agronomy12050988







