Screening of Wheat Genotypes for Water Stress Tolerance Using Soil–Water Relationships and Multivariate Statistical Approaches
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Materials
2.2. Experimental Site and Growth Conditions
2.3. Experimental Design and Treatment Details
2.4. Measurements
2.4.1. Water Relations
2.4.2. Photosynthetic Pigment Estimation
2.4.3. Growth and Yield Parameters
2.4.4. Drought Tolerance Indices
2.4.5. Analysis of Variance
| No. | Drought Tolerance Indices | Formula Equations | References |
|---|---|---|---|
| 1 | Tolerance index (TOL) | TOL =Yp − Ys | [17] |
| 2 | Mean productivity (MP) | MP = (Yp + Ys)/2 | [17] |
| 3 | Geometrical mean productivity (GMP) | [18] | |
| 4 | Harmonic mean (HM) | HM = [2 × (Yp × Ys)]/(Yp + Ys) | [62] |
| 5 | Golden Mean (GM) | GM = (Yp + Ys)/(Yp − Ys) | [63] |
| 6 | Yield stability index (YSI) | YSI = Ys/Yp | [16] |
| 7 | Sensitivity drought index (SDI) | SDI = (Yp − Ys)/Yp | [64] |
| 8 | Drought susceptibility index (DSI) | [65] | |
| 9 | Stress tolerance index (STI) | [18] | |
| 10 | Drought resistance index (DI) | [25] |
2.4.6. Additive Main Effects and Multiplicative Interaction (AMMI)
2.4.7. Multi-Trait Genotype–Ideotype Distance Index (MGIDI)
3. Results
3.1. Analysis of Variance
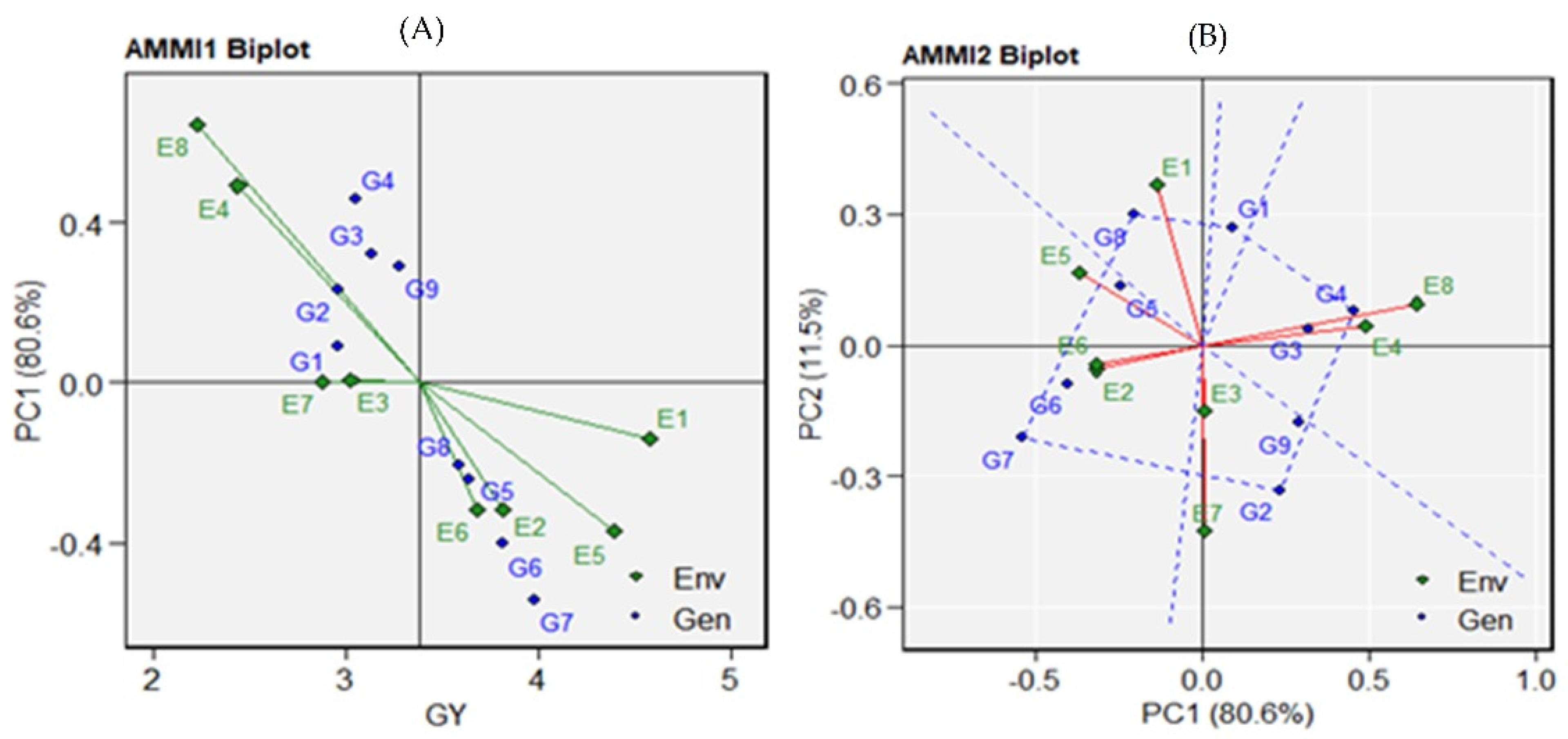
3.2. AMMI Analysis for Grain Yield
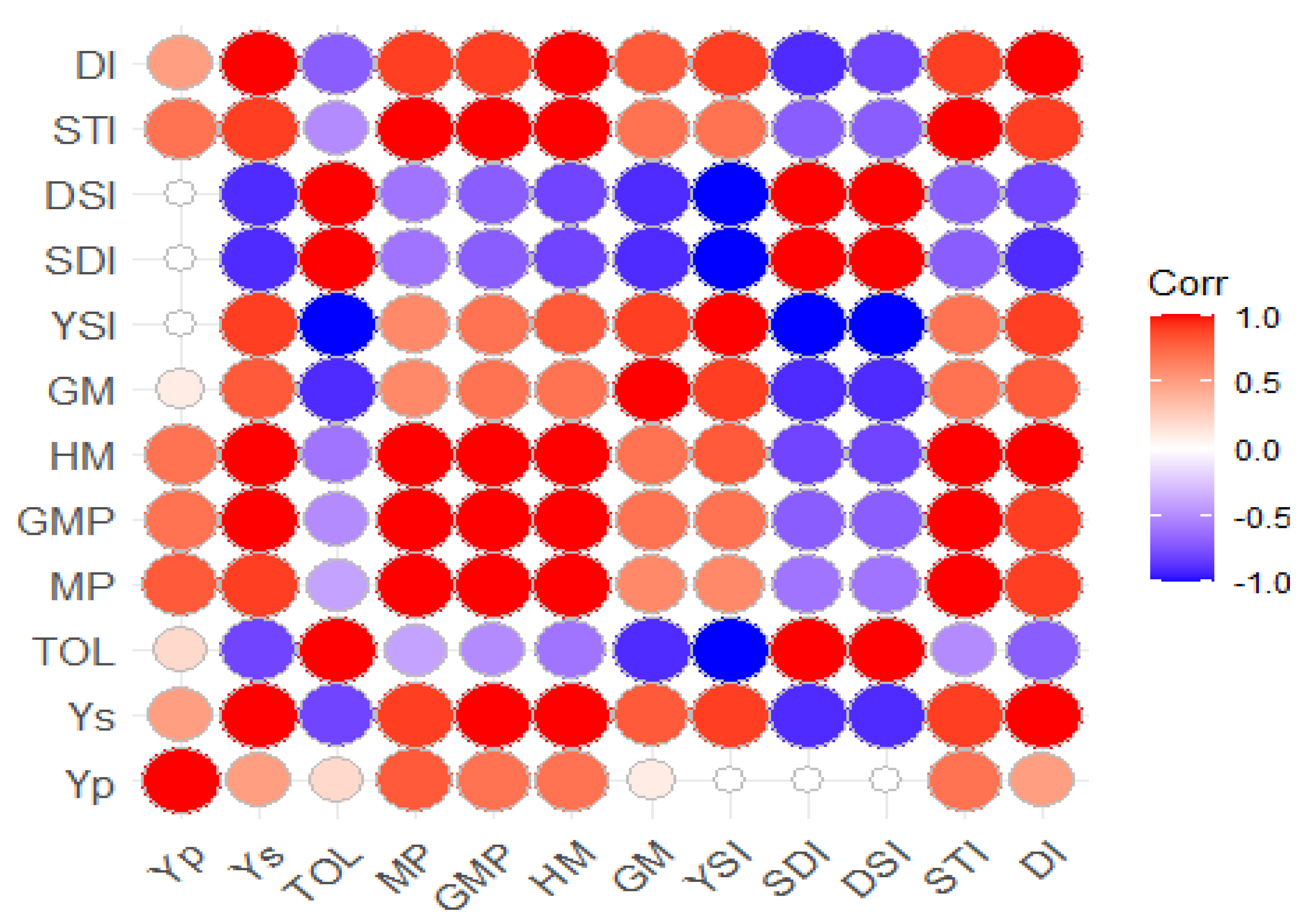
3.3. Correlation Analysis for Drought Indices
3.4. Analysis of Variance for Genotypes under Six Cases Using GMP and STI Values
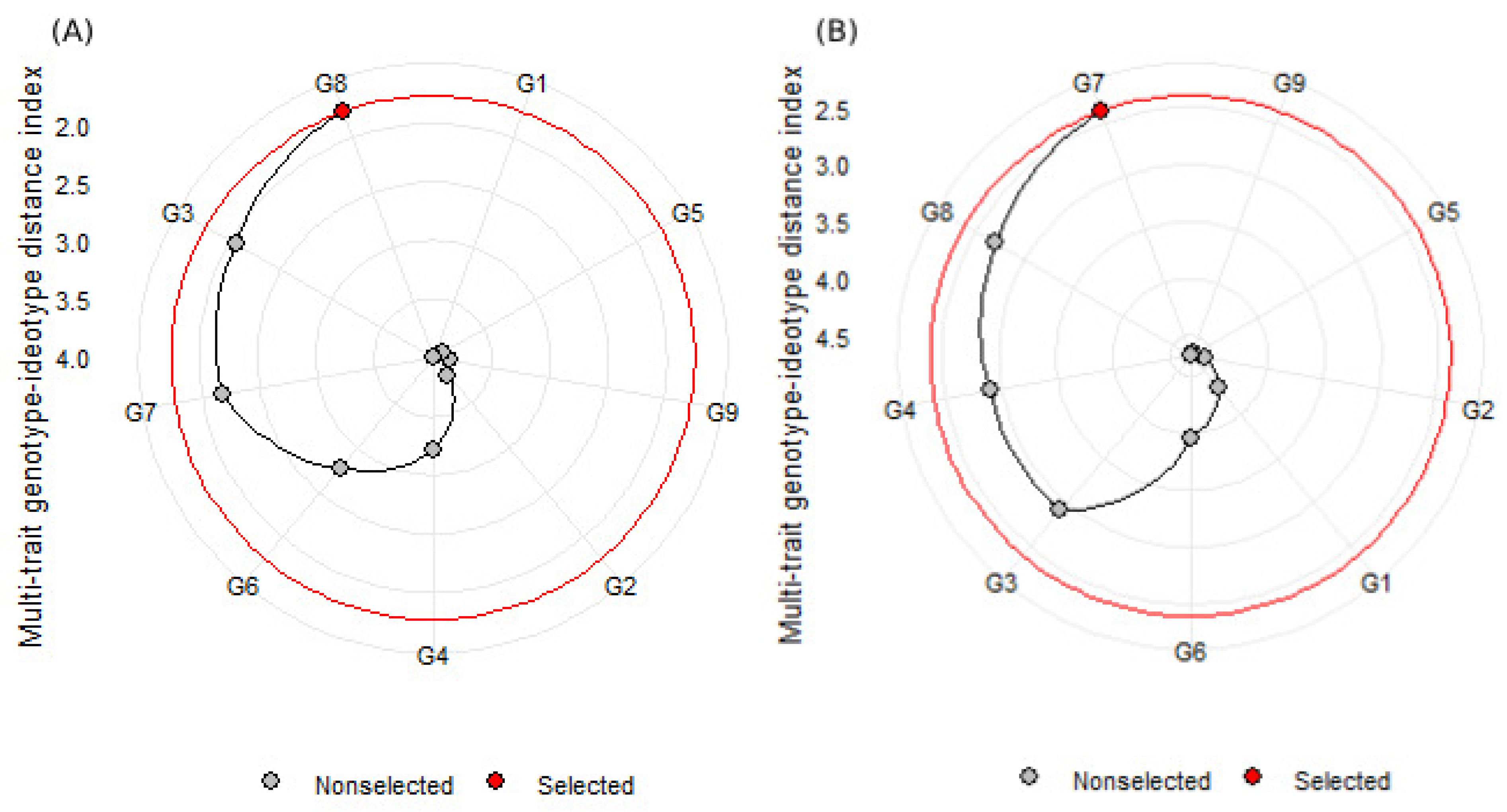
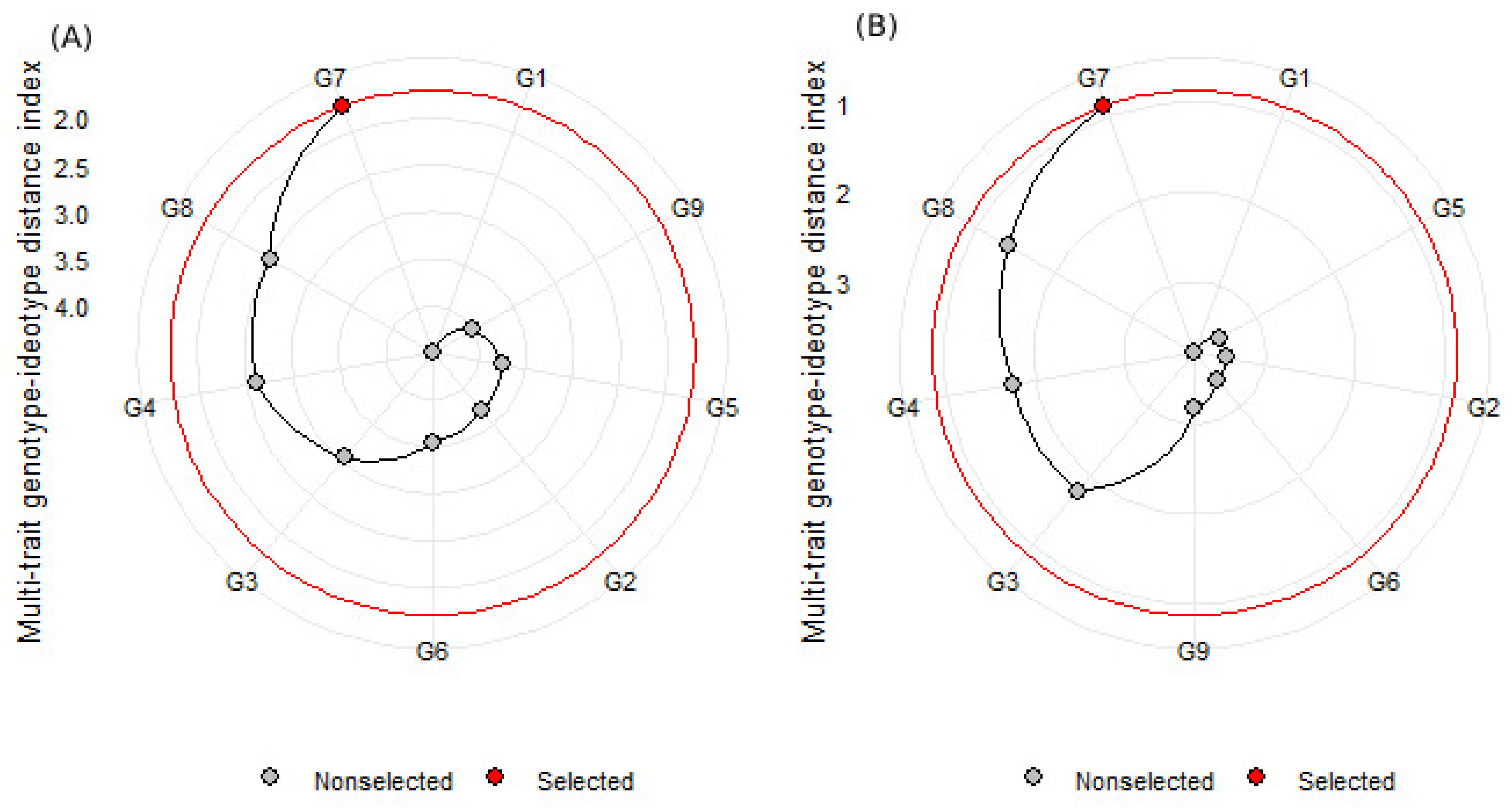
3.5. Genotype Selection Is Based on Multiple Traits Using MGIDI
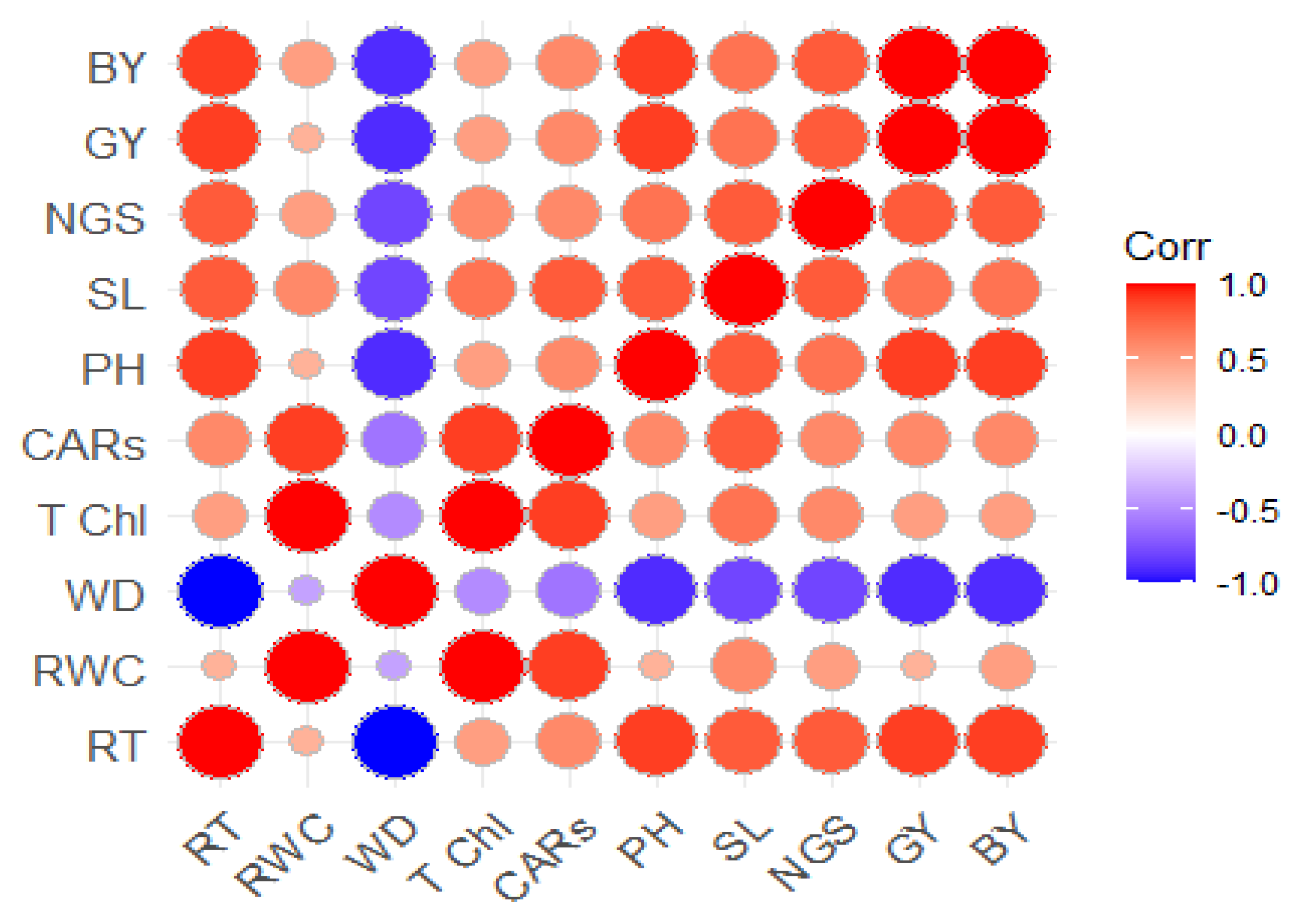
3.5.1. Phenotypic Correlation among Traits
3.5.2. Multi-Trait Genotype–Ideotype Distance Index (MGIDI)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Curtis, B.; Rajaram, S.; Macpherson, H. Bread Wheat: Improvement and Production; FAO Plant Production and Protection Series (FAO) No. 30; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2002. [Google Scholar]
- Ghanem, K.Z.; Hasham, M.M.; El-Sheshtawy, A.A.; El-Serafy, R.S.; Sheta, M.H. Biochar stimulated actual evapotranspiration and wheat productivity under water deficit conditions in sandy soil based on non-weighing lysimeter. Plants 2022, 11, 3346. [Google Scholar] [CrossRef] [PubMed]
- Mansour, H.A.; El Sayed, M.S.; Lightfoot, D.A. Molecular studies for drought tolerance in some Egyptian wheat genotypes under different irrigation systems. Open Agric. 2020, 5, 280–290. [Google Scholar] [CrossRef]
- Ghonaim, M.M.; Mohamed, H.I.; Omran, A.A. Evaluation of wheat (Triticum aestivum L.) salt stress tolerance using physiological parameters and retrotransposon-based markers. Genet. Resour. Crop Evol. 2021, 68, 227–242. [Google Scholar] [CrossRef]
- Abdel Halim, A.; Ghalab, E.; Elmaghraby, M. Effects of deficit irrigation regimes and potassium fertilization levels on the drought tolerance and water productivity of three wheat cultivars. J. Soil Sci. Agric. Eng. 2017, 8, 171–182. [Google Scholar] [CrossRef]
- Atteya, A.K.; El-Serafy, R.S.; El-Zabalawy, K.M.; Elhakem, A.; Genaidy, E.A. Exogenously supplemented proline and phenylalanine improve growth, productivity, and oil composition of salted moringa by up-regulating osmoprotectants and stimulating antioxidant machinery. Plants 2022, 11, 1553. [Google Scholar] [CrossRef] [PubMed]
- Saint Pierre, C.; Crossa, J.L.; Bonnett, D.; Yamaguchi-Shinozaki, K.; Reynolds, M.P. Phenotyping transgenic wheat for drought resistance. J. Exp. Bot. 2012, 63, 1799–1808. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Hasegawa, T.; Yin, X.; Zhu, Y.; Boote, K.; Adam, M.; Bregaglio, S.; Buis, S.; Confalonieri, R.; Fumoto, T.; et al. Uncertainties in predicting rice yield by current crop models under a wide range of climatic conditions. Glob. Chang. Biol. 2015, 21, 1328–1341. [Google Scholar] [CrossRef]
- Attia, M.A.E.-H.; Abou El-Enin, M.M.; Tahoun, A.M.A.; Abdelghany, F.I.M.; Serafy, R.S.E. Productivity of some barley cultivars as affected by supplemental irrigation under rainfed conditions. Aust. J. Crop Sci. 2022, 16, 665–675. [Google Scholar] [CrossRef]
- Rosmaina, R.; Ridho, A.; Zulfahmi, Z. Response of morpho-physiological traits to drought stress and screening of curly pepper (Capsicum annuum) genotypes for drought tolerance. Biodiversitas J. Biol. Divers. 2022, 23, 5469–5480. [Google Scholar] [CrossRef]
- Alonso-Blanco, C.; Aarts, M.G.M.; Bentsink, L.; Keurentjes, J.J.B.; Reymond, M.; Vreugdenhil, D.; Koornneef, M. What has natural variation taught us about plant development, physiology, and adaptation? Plant Cell 2009, 21, 1877–1896. [Google Scholar] [CrossRef]
- Sarkar, R.K.; Mahata, K.R.; Singh, D.P. Differential responses of antioxidant system and photosynthetic characteristics in four rice cultivars differing in sensitivity to sodium chloride stress. Acta Physiol. Plant. 2013, 35, 2915–2926. [Google Scholar] [CrossRef]
- Anower, M.R.; Boe, A.; Auger, D.; Mott, I.W.; Peel, M.D.; Xu, L.; Kanchupati, P.; Wu, Y. Comparative drought response in eleven diverse alfalfa accessions. J. Agron. Crop Sci. 2015, 203, 1–13. [Google Scholar] [CrossRef]
- Abenavoli, M.R.; Leone, M.; Sunseri, F.; Bacchi, M.; Sorgonà, A. Root phenotyping for drought tolerance in bean landraces from Calabria (Italy). J. Agron. Crop Sci. 2015, 202, 1–12. [Google Scholar] [CrossRef]
- Ali, M.B.; El-Sadek, A.N. Evaluation of drought tolerance indices for wheat (Triticum aestivum L.) under irrigated and rainfed conditions. Commun. Biometry Crop Sci. 2016, 11, 77–89. [Google Scholar]
- Bouslama, M.; Schapaugh, W.T. Stress Tolerance in Soybeans. I. Evaluation of three screening techniques for heat and drought tolerance. Crop Sci. 1984, 24, 933–937. [Google Scholar] [CrossRef]
- Rosielle, A.A.; Hamblin, J. Theoretical aspects of selection for yield in stress and non–stress environment. Crop Sci. 1981, 21, 943–946. [Google Scholar] [CrossRef]
- Fernandez, G.C. Effective selection criteria for assessing plant stress tolerance. In Proceedings of the International Symposium on Adaptation of Vegetables and Other Food Crops in Temperature and Water Stress, Shanhua, Taiwan, 13–16 August 1992; pp. 257–270. [Google Scholar]
- Sofi, P.A.; Rehman, K.; Ara, A.; Gull, M. Stress tolerance indices based on yield, phenology and biomass partitioning: A Review. Agric. Rev. 2018, 39, 292–299. [Google Scholar] [CrossRef]
- Bennani, S.; Birouk, A.; Jlibene, M.; Sanchez-Garcia, M.; Nsarellah, N.; Gaboun, F.; Tadesse, W. Drought-Tolerance QTLs associated with grain yield and related traits in spring bread wheat. Plants 2022, 11, 986. [Google Scholar] [CrossRef]
- Golabadi, M.; Arzani, A.; Mirmohammadi Maibody, S. Identification of microsatellite markers associated with grain protein content in durum wheat grown under drought stress at terminal growth stages. Cereal Res. Commun. 2012, 40, 215–224. [Google Scholar] [CrossRef]
- Talebi, R.; Fayaz, F.; Naji, A.M. Effective selection criteria for assessing drought stress tolerance in durum wheat (Triticum durum Desf.). Gen. Appl. Plant Physiol. 2009, 35, 64–74. [Google Scholar]
- Mohammadi, A.; Bihamta, M.; Soloki, R.; Roodaki, H.R. The study of qualitative and quantitative traits of navy bean and their relation with yield in suitable and limited irrigation conditions. J. Agric. Sci. 2008, 1, 231–243. [Google Scholar]
- Gholinezhad, E.; Darvishzadeh, R.; Bernousi, I. Evaluation of drought tolerance indices for selection of confectionery sunflower (Helianthus anuus L.) landraces under various environmental conditions. Not. Bot. Horti Agrobot. 2014, 42, 187–201. [Google Scholar] [CrossRef]
- Lan, J. Comparison of evaluating methods for agronomic drought resistance in crops. Acta Agric. Boreali-Occident. Sin. 1998, 7, 85–87. [Google Scholar]
- Nouraein, M.; Mohammadi, S.A.; Aharizad, S.; Moghaddam, M.; Sadeghzadeh, B. Evaluation of drought tolerance indices in wheat recombinant inbred line population. Ann. Biol. Res. 2013, 4, 113–122. [Google Scholar]
- Grzesiak, S.; Hordyńska, N.; Szczyrek, P.; Grzesiak, M.T.; Noga, A.; Szechyńska-Hebda, M. Variation among wheat (Triticum easativum L.) genotypes in response to the drought stress: I—Selection approaches. J. Plant Interact. 2019, 14, 30–44. [Google Scholar] [CrossRef]
- Mohammadi, R. Efficiency of yield-based drought tolerance indices to identify tolerant genotypes in durum wheat. Euphytica 2016, 211, 71–89. [Google Scholar] [CrossRef]
- Nogueira, A.P.O.; Sediyama, T.; Sousa, L.B.; Hamawaki, O.T.; Cruz, C.D.; Pereira, D.G.; Matsuo, E. Análise de trilha e correlações entre caracteres em soja cultivada em duas épocas de semeadura. J. Biosci. 2012, 28, 877–888. [Google Scholar]
- Singh, C.; Gupta, A.; Gupta, V.; Kumar, P.; Sendhil, R.; Tyagi, B.S.; Singh, G.; Chatrath, R.; Singh, G.P. Genotype x environment interaction analysis of multi-environment wheat trials in India using AMMI and GGE biplot models. Crop Breed. Appl. Biotechnol. 2019, 19, 309–318. [Google Scholar] [CrossRef]
- Gupta, V.; Kumar, M.; Singh, V.; Chaudhary, L.; Yashveer, S.; Sheoran, R.; Dalal, M.S.; Nain, A.; Lamba, K.; Gangadharaiah, N.; et al. Genotype by environment interaction analysis for grain yield of wheat (Triticum aestivum (L.) em.Thell) genotypes. Agriculture 2022, 12, 1002. [Google Scholar] [CrossRef]
- Wahlsten, D. Insensitivity of the analysis of variance to heredity-environment interaction. Behav. Brain Sci. 1990, 13, 109–120. [Google Scholar] [CrossRef]
- Bhartiya, A.; Aditya, J.P.; Kumari, V.; Kishore, N.; Purwar, J.P.; Kant, L.; Pattanayak, A. Stability analysis of soybean [Glycine Max (L.) Merrill] genotypes under multi-environments rainfed condition of North Western Himalayan Hills. Indian J. Genet. Plant Breed. 2018, 78, 342–347. [Google Scholar] [CrossRef]
- Regmi, D.; Poudel, M.R.; Bishwas, K.C.; Poudel, P.B. Yield stability of different elite wheat lines under drought and irrigated environments using AMMI and GGE biplots. Int. J. Appl. Sci. Biotechnol. 2021, 9, 98–106. [Google Scholar] [CrossRef]
- Oladosu, Y.; Rafii, M.Y.; Abdullah, N.; Magaji, U.; Miah, G.; Hussin, G.; Ramli, A. Genotype × environment interaction and stability analyses of yield and yield components of established and mutant rice genotypes tested in multiple locations in Malaysia. Acta Agric. Scand. Sect. B Soil Plant Sci. 2017, 67, 590–606. [Google Scholar] [CrossRef]
- Olivoto, T.; Nardino, M. MGIDI: Toward an effective multivariate selection in biological experiments. Bioinformatics 2021, 37, 1383–1389. [Google Scholar] [CrossRef]
- Prunier, J.G.; Colyn, M.; Legendre, X.; Nimon, K.F.; Flamand, M.C. Multicollinearity in spatial genetics: Separating the wheat from the chaff using commonality analyses. Mol. Ecol. 2015, 24, 263–283. [Google Scholar] [CrossRef] [PubMed]
- Olivoto, T.; Lúcio, A.D.C.; da Silva, J.A.G.; Marchioro, V.S.; de Souza, V.Q.; Jost, E. Mean performance and stability in multi-environment trials i: Combining features of AMMI and BLUP techniques. Agron. J. 2019, 111, 2949–2960. [Google Scholar] [CrossRef]
- Rocha, J.R.d.A.S.d.C.; Machado, J.C.; Carneiro, P.C.S. Multitrait index based on factor analysis and ideotype-design: Proposal and application on elephant grass breeding for bioenergy. GCB Bioenergy 2017, 10, 52–60. [Google Scholar] [CrossRef]
- Zuffo, A.M.; Steiner, F.; Aguilera, J.G.; Teodoro, P.E.; Teodoro, L.P.R.; Busch, A. Multi-trait stability index: A tool for simultaneous selection of soya bean genotypes in drought and saline stress. J. Agron. Crop Sci. 2020, 206, 815–822. [Google Scholar] [CrossRef]
- Szareski, V.J.; Carvalho, I.R.; Kehl, K.; Levien, A.M.; Nardino, M.; Demari, G.H.; Lautenchleger, F.; de Souza, V.Q.; Pedó, T.; Aumonde, T.Z. Univariate, multivariate techniques and mixed models applied to the adaptability and stability of wheat in the rio grande do sul state. Genet. Mol. Res. 2017, 16, 16039735. [Google Scholar] [CrossRef]
- Bizari, E.H.; Unêda-Trevisoli, S.H.; Val, B.H.P.; Pereira, E.d.M.; Mauro, A.O. Selection indices for agronomic traits in segregating populations of soybean. Rev. Ciênc. Agron. 2017, 48, 110–117. [Google Scholar] [CrossRef]
- Olivoto, T.; Nardino, M.; Meira, D.; Meier, C.; Follmann, D.N.; de Souza, V.Q.; Konflanz, V.A.; Baretta, D. Multi-trait selection for mean performance and stability in maize. Agron. J. 2021, 113, 3968–3974. [Google Scholar] [CrossRef]
- Bahgat, A.R.; Dahab, A.A.; Elhakem, A.; Gururani, M.A.; El-Serafy, R.S. Integrated action of rhizobacteria with aloe vera and moringa leaf extracts improves defense mechanisms in Hibiscus sabdariffa L. cultivated in saline soil. Plants 2023, 12, 3684. [Google Scholar] [CrossRef]
- Youssef, S.M.; El-Serafy, R.S.; Ghanem, K.Z.; Elhakem, A.; Abdel Aal, A.A. Foliar spray or soil drench: Microalgae application impacts on soil microbiology, morpho-physiological and biochemical responses, oil and fatty acid profiles of chia plants under alkaline stress. Biology 2022, 11, 1844. [Google Scholar] [CrossRef] [PubMed]
- El-Serafy, R.S.; El-Sheshtawy, A.N.A.; Dahab, A.A. Fruit peel soil supplementation induces physiological and biochemical tolerance in Schefflera arboricola L. grown under heat conditions. J. Soil Sci. Plant Nutr. 2023, 23, 1046–1059. [Google Scholar] [CrossRef]
- Gururani, M.A.; Atteya, A.K.; Elhakem, A.; El-Sheshtawy, A.N.A.; El-Serafy, R.S. Essential oils prolonged the cut carnation longevity by limiting the xylem blockage and enhancing the physiological and biochemical levels. PLoS ONE 2023, 3, e0281717. [Google Scholar] [CrossRef] [PubMed]
- Khalilzadeh, R.; Sharifi, R.S.; Jalilian, J. Antioxidant status and physiological responses of wheat (Triticum aestivum L.) to cycocel application and bio fertilizers under water limitation condition. J. Plant Interact. 2016, 11, 130–137. [Google Scholar] [CrossRef]
- Ahmad, A.; Aslam, Z.; Javed, T.; Hussain, S.; Raza, A.; Shabbir, R.; Mora-Poblete, F.; Saeed, T.; Zulfiqar, F.; Ali, M.M.; et al. Screening of wheat (Triticum aestivum L.) genotypes for drought tolerance through agronomic and physiological response. Agronomy 2022, 12, 287. [Google Scholar] [CrossRef]
- Shokat, S.; Sehgal, D.; Vikram, P.; Liu, F.; Singh, S. Molecular markers associated with agro-physiological traits under terminal drought conditions in bread wheat. Int. J. Mol. Sci. 2020, 21, 3156. [Google Scholar] [CrossRef]
- Bapela, T.; Shimelis, H.; Tsilo, T.J.; Mathew, I. Genetic Improvement of Wheat for Drought Tolerance: Progress, Challenges and Opportunities. Plants 2022, 11, 1331. [Google Scholar] [CrossRef]
- Sallam, A.; Alqudah, A.M.; Dawood, M.F.A.; Baenziger, P.S.; Börner, A. Drought Stress Tolerance in Wheat and Barley: Advances in Physiology, Breeding and Genetics Research. Int. J. Mol. Sci. 2019, 20, 3137. [Google Scholar] [CrossRef]
- Randhawa, H.S.; Asif, M.; Pozniak, C.; Clarke, J.M.; Graf, R.J.; Fox, S.L.; Humphreys, D.J.; Knox, R.E.; DePauw, R.M.; Singh, A.K.; et al. Application of molecular markers to wheat breeding in Canada. Plant Breed. 2013, 132, 458–471. [Google Scholar] [CrossRef]
- Page, A.L.; Miller, R.H.; Keeney, D.R. Methods of Soil Analysis. Part 2. Chemical and Microbiological Properties, 2nd ed.; American Society of Agronomy, Inc.: Madison, WI, USA, 1982. [Google Scholar]
- Klute, A. Methods of Soil Analysis. Part 1. Physical and Mineralogical Methods, 2nd ed.; American Society of Agronomy, Inc.: Madison, WI, USA, 1986. [Google Scholar]
- Steel, R.G.D.; Torrie, J.H. Principles and Procedures of Statistics: A Biometrical Approach; McGraw-Hill Science, Engineering &Mathematics: New York, NY, USA, 2000. [Google Scholar]
- Weatherley, P.E. Studies in the water relations of the cotton plant. 1. The field measurement of water deficits in leaves. New Phytol. 1950, 49, 81–97. [Google Scholar] [CrossRef]
- Barrs, H.D. Determination of water deficit in plant tissues. In Water Deficit and Plant Growth; Kozlowski, T.T., Ed.; Academic Press: New York, NY, USA, 1968; Volume 1, pp. 235–368. [Google Scholar]
- Dere, Ş.; GÜNEŞ, T.; Sivaci, R. Spectrophotometric determination of chlorophyll-a, b and total carotenoid contents of some algae species using different solvents. Turk. J. Bot. 1998, 22, 13–18. [Google Scholar]
- Shapiro, S.S.; WILK, M.B. An Analysis of variance test for normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Snedecor, G.W. Statistical Methods: Applied to Experiments in Agriculture and Biology; The Iowa State College Press: Ames, IA, USA, 1956. [Google Scholar]
- Dadbakhsh, A.; Yazdansepas, A.; Ahmadizadeh, M. Study drought stress on yield of wheat (Triticum aestivum L.) genotypes by drought tolerance indices. Adv. Environ. Biol. 2011, 5, 1804–1810. [Google Scholar]
- Moradi, H.; Akbari, G.A.; Khorasani, S.K.; Ramshini, H.A. Evaluation of drought tolerance in corn (Zea mays L.) New Hybrids with Using Stress Tolerance Indices. Eur. J. Sustain. Dev. 2012, 1, 543. [Google Scholar] [CrossRef]
- Farshadfar, E.; Javadinia, J. Evaluation of chickpea (Cicer arietinum L.) genotypes for drought tolerance. Seed Plant Improv. J. 2011, 27, 517–537. [Google Scholar]
- Fischer, R.A.; Maurer, R. Drought resistance in spring wheat cultivars. I. Grain yield responses. Aust. J. Agric. Res. 1978, 29, 897. [Google Scholar] [CrossRef]
- Zobel, R.W.; Wright, M.J.; Gauch, H.G. Statistical Analysis of a Yield Trial. Agron. J. 1988, 80, 388–393. [Google Scholar] [CrossRef]
- Kaiser, H.F. The Varimax Criterion for Analytic Rotation in Factor Analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Olivoto, T.; Lúcio, A.D. Metan: An R Package for multi–environment trial analysis. Methods Ecol. Evol. 2020, 11, 783–789. [Google Scholar] [CrossRef]
- Hashem, M.; Sandhu, K.S.; Ismail, S.M.; Börner, A.; Sallam, A. Validation and marker-assisted selection of DArT-genomic regions associated with wheat yield-related traits under normal and drought conditions. Front. Genet. 2023, 14, 1195566. [Google Scholar] [CrossRef] [PubMed]
- Akpınar, B.A.; Lucas, S.J.; Budak, H. Genomics approaches for crop improvement against abiotic stress. Sci. World J. 2013, 361921. [Google Scholar] [CrossRef] [PubMed]
- Tanin, M.J.; Saini, D.K.; Sandhu, K.S.; Pal, N.; Gudi, S.; Chaudhary, J.; Sharma, A. Consensus genomic regions associated with multiple abiotic stress tolerance in wheat and implications for wheat breeding. Sci. Rep. 2022, 12, 13680. [Google Scholar] [CrossRef] [PubMed]
- Sayed, K.A.K.; Ali, M.B.; Ibrahim, K.A.M.; Kheiralla, K.A.; EL-Hifny, M.Z. Response of flowering traits to water stress in yellow maize (Zea mays L.) using line × tester analysis. Egypt. J. Agron. 2022, 44, 131–161. [Google Scholar] [CrossRef]
- Kutlu, N.; Terzi, R.; Tekeli, C.; Senel, G.; Battal, P.; Kadioglu, A. Changes in anatomical structure and levels of endogenous phytohormones during leaf rolling in Ctenanthe setosa under drought stress. Turk. J. Biol. 2009, 33, 115–122. [Google Scholar] [CrossRef]
- Lambers, H.; Chapin, F.S.; Pons, T.L. Plant Physiological Ecology; Springer: New York, NY, USA, 2008. [Google Scholar]
- Sharma, A.; Wang, J.; Xu, D.; Tao, S.; Chong, S.; Yan, D.; Li, Z.; Yuan, H.; Zheng, B. Melatonin regulates the functional components of photosynthesis, antioxidant system, gene expression, and metabolic pathways to induce drought resistance in grafted Carya cathayensis plants. Sci. Total Environ. 2020, 713, 136675. [Google Scholar] [CrossRef] [PubMed]
- Potopová, V.; Boroneant, C.; Boincean, B.; Soukup, J. Impact of agricultural drought on main crop yields in the Republic of Moldova. Int. J. Climatol. 2016, 36, 2063–2082. [Google Scholar] [CrossRef]
- Alghabari, F.; Ihsan, M.Z.; Hussain, S.; Aishia, G.; Daur, I. Effect of Rht alleles on wheat grain yield and quality under high temperature and drought stress during booting and anthesis. Environ. Sci. Pollut. Res. 2015, 22, 15506–15515. [Google Scholar] [CrossRef]
- El-Mogy, M.M.; Atia, M.A.M.; Dhawi, F.; Fouad, A.S.; Bendary, E.S.A.; Khojah, E.; Samra, B.N.; Abdelgawad, K.F.; Ibrahim, M.F.M.; Abdeldaym, E.A. Towards better grafting: SCoT and CDDP analyses for prediction of the tomato rootstocks performance under drought stress. Agronomy 2022, 12, 153. [Google Scholar] [CrossRef]
- Emam, M.A.; Abd EL-Mageed, A.M.; Niedbała, G.; Sabrey, S.A.; Fouad, A.S.; Kapiel, T.; Piekutowska, M.; Mahmoud, S.A. Genetic characterization and agronomic evaluation of drought tolerance in ten egyptian wheat (Triticum aestivum L.) cultivars. Agronomy 2022, 12, 1217. [Google Scholar] [CrossRef]
- Hessini, K.; Issaoui, K.; Ferchichi, S.; Saif, T.; Abdelly, C.; Siddique, K.H.M.; Cruz, C. Interactive effects of salinity and nitrogen forms on plant growth, photosynthesis and osmotic adjustment in maize. Plant Physiol. Biochem. 2019, 139, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Sukumaran, S.; Claverie, E.; Sansaloni, C.; Dreisigacker, S.; Reynolds, M. Genetic dissection of heat and drought stress QTLs in phenology-controlled synthetic-derived recombinant inbred lines in spring wheat. Mol. Breed. 2019, 39, 1–18. [Google Scholar] [CrossRef]
- Khayatnezhad, M.; Hasanuzzaman, M.; Gholamin, R. Assessment of yield and yield components and drought tolerance at end-of season drought condition on corn hybrids (Zea mays L.). Aust. J. Crop Sci. 2011, 5, 1493–1500. [Google Scholar]
- Khakwani, A.A.; Dennett, M.D.; Munir, M.; Abid, M. Growth and yield response of wheat varieties to water stress at booting and anthesis stages of development. Pak. J. Bot. 2012, 44, 879–886. [Google Scholar]
- Maqbool, M.M.; Ali, A.; Haq, T.; Majeed, M.N.; Lee, D.J. Response of spring wheat (Triticum aestivum L.) to induced water stress at critical growth stages. Sarhad J. Agric. 2015, 31, 53–58. [Google Scholar]
- Al-Ghzawi, A.L.A.; Al-Ajlouni, Z.I.; Sane, K.O.; Bsoul, E.Y.; Musallam, I.; Khalaf, Y.B.; Al-Hajaj, N.; Al-Tawaha, A.R.; Aldwairi, Y.; Al-Saqqar, H. Yield stability and adaptation of four spring barley (Hordeum vulgare L.) cultivars under rainfed conditions. Res. Crop. 2019, 20, 10–18. [Google Scholar]
- Semcheddine, N.; Hafsi, M. Effect of Supplementary irrigation on agronomical and physiological traits in durum wheat (Triticum durum Desf.) genotypes. J. Agric. Sci. 2014, 6, 184. [Google Scholar] [CrossRef][Green Version]
- Ullah, H.; Santiago-Arenas, R.; Ferdous, Z.; Attia, A.; Datta, A. Improving water use efficiency, nitrogen use efficiency, and radiation use efficiency in field crops under drought stress: A Review. Adv. Agron. 2019, 156, 109–157. [Google Scholar]
- Kirigwi, F.M.; van Ginkel, M.; Trethowan, R.; Sears, R.G.; Rajaram, S.; Paulsen, G.M. Evaluation of selection strategies for wheat adaptation across water regimes. Euphytica 2004, 135, 361–371. [Google Scholar] [CrossRef]
- Esmail, R.M.; Eldessouky, S.E.; Sherin, A.M.; El-Demardash, I.S. Evaluation of new bread wheat lines (Triticum aestivum, L.) under normal and water stress conditions. Int. J. Chemtech Res. 2016, 9, 89–99. [Google Scholar]
- Ghasemi, A.; Zahediasl, S. Normality tests for statistical analysis: A guide for non-statisticians. Int. J. Endocrinol. Metab. 2012, 10, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Panda, R.K.; Behera, S.K.; Kashyap, P.S. Effective management of irrigation water for wheat under stressed conditions. Agric. Water Manag. 2003, 63, 37–56. [Google Scholar] [CrossRef]
- Abd El-Megeed, F.H.; Mohiy, M. Improving productivity of some bread wheat cultivars under water deficit stress using endophytic Bacillus sp. NGB-WhE3. Egypt. J. Bot. 2022, 62, 275–290. [Google Scholar] [CrossRef]
- Gomes, F.G. Curso de Estatística Experimental; FEALQ: Piracicaba, Brazil, 2009; 451p. [Google Scholar]
- Farshadfar, E.; Elyasi, P. Screening quantitative indicators of drought tolerance in bread wheat (Triticum aestivum L.) landraces. Eur. J. Exp. Biol. 2012, 2, 577–584. [Google Scholar]
- Anwaar, H.A.; Perveen, R.; Mansha, M.Z.; Abid, M.; Sarwar, Z.M.; Aatif, H.M.; Umar, U.U.D.; Sajid, M.; Aslam, H.M.U.; Alam, M.M.; et al. Assessment of grain yield indices in response to drought stress in wheat (Triticum aestivum L.). Saudi J. Biol. Sci. 2020, 27, 1818–1823. [Google Scholar] [CrossRef]
- Abdelghany, A.H.; Hanaa, M.; Abouzied, M.; Badran, S. Evaluation of some Egyptian wheat cultivars under water stress condition in the north western coast of Egypt. J. Agric. Environ. Sci. 2016, 15, 63–84. [Google Scholar]
- Abd El-Aty, M.; Gad, K.; Hefny, Y.; Shehata, M. Performance of some wheat (Triticum aestivum L.) genotypes and their drought tolerance indices under normal and water stress. Egypt. J. Soil Sci. 2024, 64, 19–30. [Google Scholar] [CrossRef]
- Benakanahalli, N.K.; Sridhara, S.; Ramesh, N.; Olivoto, T.; Sreekantappa, G.; Tamam, N.; Abdelbacki, A.M.M.; Elansary, H.O.; Abdelmohsen, S.A.M. A Framework for identification of stable genotypes basedon MTSI and MGDII indexes: An example in guar (Cymopsis tetragonoloba L.). Agronomy 2021, 11, 1221. [Google Scholar] [CrossRef]
- Olivoto, T.; de Souza, V.Q.; Nardino, M.; Carvalho, I.R.; Ferrari, M.; de Pelegrin, A.J.; Szareski, V.J.; Schmidt, D. Multicollinearity in path analysis: A simple method to reduce its effects. Agron. J. 2017, 109, 131–142. [Google Scholar] [CrossRef]
- Azrai, M.; Aqil, M.; Efendi, R.; Andayani, N.N.; Makkulawu, A.T.; Iriany, R.N.; Suarni; Yasin, M.; Suwardi; Zainuddin, B.; et al. A Comparative study on single and multiple trait selections of equatorial grown maize hybrids. Front. Sustain. Food Syst. 2023, 7, 1185102. [Google Scholar]
- Gauch, H.G. A Simple protocol for AMMI analysis of yield trials. Crop Sci. 2013, 53, 1860–1869. [Google Scholar] [CrossRef]
- Anuada, A.M.; Cruz, P.C.S.; De Guzman, L.E.P.; Sanchez, P.B. Grain yield variability and stability of corn varieties in rainfed areas in the philippines. J. Crop Sci. Biotechnol. 2021, 25, 133–147. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Rafii, M.Y.; Ramlee, S.I.; Jusoh, M.; Al Mamun, M. AMMI and GGE biplot analysis for yield Performance and Stability Assessment of Selected Bambara Groundnut (Vigna subterranea L. Verdc.) Genotypes under the multi-environmental trails (METs). Sci. Rep. 2021, 11, 22791. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.B.; El-Sadek, A.N.; Sayed, M.A.; Hassaan, M.A. AMMI biplot analysis of genotype× environment interaction in wheat in Egypt. Egypt. J. Plant Breed. 2015, 19, 1889–1901. [Google Scholar] [CrossRef]
- Pour-Aboughadareh, A.; Khalili, M.; Poczai, P.; Olivoto, T. Stability Indices to deciphering the genotype-by-environment interaction (GEI) Effect: An applicable review for use in plant breeding programs. Plants 2022, 11, 414. [Google Scholar] [CrossRef]
- de Oliveira, T.R.A.; de Carvalho, H.W.L.; Oliveira, G.H.F.; Costa, E.F.N.; Gravina, G.d.A.; dos Santos, R.D.; Carvalho Filho, J.L.S. Hybrid Maize Selection through GGE biplot analysis. Bragantia 2019, 78, 166–174. [Google Scholar] [CrossRef]


| Month | Temperature (°C) | Wind Speed (m s−1) | Relative Humidity (%) | Average Precipitation (mm day−1) | Surface Pressure (kPa) | ||
|---|---|---|---|---|---|---|---|
| Max | Min | Max | Min | ||||
| 2020/2021 | |||||||
| November | 24.64 | 13.66 | 5.15 | 1.87 | 63.38 | 0.36 | 100.10 |
| December | 22.57 | 10.47 | 5.08 | 1.97 | 60.63 | 0.02 | 100.14 |
| January | 21.52 | 8.33 | 5.82 | 2.34 | 59.04 | 0.07 | 100.26 |
| February | 21.78 | 8.29 | 5.26 | 2.05 | 61.52 | 0.72 | 100.26 |
| March | 23.27 | 9.20 | 6.11 | 2.09 | 62.38 | 3.36 | 100.06 |
| April | 29.43 | 11.71 | 6.54 | 2.63 | 50.20 | 0.13 | 99.98 |
| May | 36.84 | 17.90 | 6.72 | 2.40 | 36.64 | 0.00 | 99.64 |
| 2021/2022 | |||||||
| November | 27.71 | 15.14 | 4.81 | 1.96 | 61.68 | 0.67 | 100.02 |
| December | 19.37 | 8.96 | 5.84 | 2.17 | 68.45 | 0.34 | 100.19 |
| January | 16.76 | 5.40 | 5.51 | 2.14 | 67.08 | 1.08 | 100.30 |
| February | 19.48 | 6.57 | 5.67 | 2.20 | 66.60 | 0.39 | 100.22 |
| March | 21.82 | 7.46 | 6.87 | 2.36 | 54.20 | 0.06 | 100.21 |
| April | 32.22 | 14.14 | 6.82 | 2.73 | 38.93 | 0.02 | 99.61 |
| May | 33.80 | 16.94 | 7.21 | 2.63 | 39.17 | 0.04 | 99.74 |
| Property | 2020/2021 | 2021/2022 | Property | 2020/2021 | 2021/2022 |
|---|---|---|---|---|---|
| Particle size distribution: | Available water (AW, %) | 9.51 | 9.43 | ||
| Coarse sand (%) | 5.20 | 5.47 | Bulk density (Mg m−3) | 1.51 | 1.53 |
| Fine sand (%) | 76.56 | 76.54 | Total porosity (%) | 43.02 | 42.26 |
| Silt (%) | 4.81 | 5.31 | pH (1:2.5 soil water suspension) | 8.21 | 8.11 |
| Clay (%) | 13.43 | 12.68 | ECe (soil paste extract, dS m−1) | 1.65 | 1.69 |
| Textural class | Sandy loam | Sandy loam | Organic carbon (g kg−1) | 3.23 | 3.26 |
| Field capacity (, %) | 15.05 | 14.89 | Organic matter (g kg−1) | 5.56 | 5.61 |
| Permanent wilting point (%) | 5.54 | 5.46 | CaCO3 content (g kg−1) | 16.55 | 17.00 |
| Soluble cations: | Soluble anions: | ||||
| Ca2+ (mmolc L−1) | 8.24 | 8.59 | CO32− (mmolc L−1) | 0.00 | 0.00 |
| Mg 2+ (mmolc L−1) | 5.23 | 5.39 | HCO3− (mmolc L−1) | 8.56 | 9.33 |
| Na+ (mmolc L−1) | 1.72 | 1.69 | Cl− (mmolc L−1) | 6.23 | 6.45 |
| K+ (mmolc L−1) | 1.26 | 1.27 | SO42− (mmolc L−1) | 1.66 | 1.16 |
| Available macro- and micro-nutrients: | |||||
| N (mg kg−1) | 29.36 | 31.67 | Mn (mg kg−1) | 1.91 | 1.86 |
| P (mg kg−1) | 6.44 | 6.74 | Zn (mg kg−1) | 0.88 | 0.91 |
| K (mg kg−1) | 122.65 | 125.23 | Cu (mg kg−1) | 1.11 | 1.15 |
| Fe (mg kg−1) | 2.78 | 2.69 | |||
| Traits | Mean Square | C.V% | ||||
|---|---|---|---|---|---|---|
| Environments (E) | Rep. within Environment R(E) | Genotypes (G) | E × G | Error | ||
| df | 7 | 16 | 8 | 56 | 128 | |
| RT | 960.91 ** | 6.71 | 137.79 ** | 7.05 ** | 1.85 | 1.80 |
| RWC | 775.69 ** | 12.39 | 394.91 ** | 130.02 ** | 13.19 | 5.46 |
| WD | 960.91 ** | 6.71 | 137.79 ** | 7.05 ** | 1.85 | 5.51 |
| T Chl | 0.422 ** | 0.002 | 0.398 ** | 0.008 ** | 0.001 | 3.13 |
| CARs | 0.1123 ** | 0.0006 | 0.0671 ** | 0.0016 ** | 0.0005 | 4.99 |
| PH | 3140.80 ** | 2.74 | 302.53 ** | 31.90 ** | 2.58 | 1.85 |
| SL | 40.578 ** | 0.542 | 6.436 ** | 0.554 ** | 0.250 | 4.67 |
| NGS | 1032.07 ** | 2.89 | 212.80 ** | 10.22 ** | 5.36 | 4.41 |
| GY | 20.698 ** | 0.059 | 3.573 ** | 0.069 ** | 0.023 | 4.53 |
| BY | 163.120 ** | 0.282 | 22.823 ** | 0.598 ** | 0.173 | 3.55 |
| Source | df | SS | MS | F-Value | p-Value | TSS (%) | E × G (%) |
|---|---|---|---|---|---|---|---|
| E | 7 | 144.88 | 20.698 | 352.4 | 0.000 | 79.93 | |
| Rep. (E) | 16 | 0.939 | 0.058 | 2.51 | 0.002 | 0.52 | |
| G | 8 | 28.583 | 3.573 | 152.4 | 0.000 | 15.77 | |
| E × G | 56 | 3.840 | 0.068 | 2.93 | 0.000 | 2.12 | |
| Residuals | 128 | 3.00 | 0.023 | 1.66 | |||
| Total | 215 | 181.24 | |||||
| IPC1 | 14 | 3.095 | 0.221 | 9.43 | 0.000 | 80.60 | |
| IPC2 | 12 | 0.441 | 0.036 | 1.57 | 0.108 | 11.50 | |
| IPC3 | 10 | 0.244 | 0.024 | 1.04 | 0.414 | 6.35 | |
| IPC4 | 8 | 0.045 | 0.006 | 0.24 | 0.982 | 1.18 | |
| IPC5 | 6 | 0.011 | 0.002 | 0.08 | 0.998 | 0.36 | |
| IPC6 | 4 | 0.003 | 0.001 | 0.03 | 0.998 | 0.01 | |
| IPC7 | 2 | 0.002 | 0.001 | 0.03 | 0.970 | 0.00 |
| Index | Genotype | C1 | C2 | C3 | C4 | C5 | C6 |
|---|---|---|---|---|---|---|---|
| GMP | G1 | 3.79 c (7) | 3.32 cd (8) | 3.00 c (8) | 3.57 c (7) | 3.00e (9) | 2.70 d (9) |
| G2 | 3.66 c (9) | 3.23 d (9) | 2.91 c (9) | 3.53 c (8) | 3.10 e (8) | 2.72 d (8) | |
| G3 | 3.87 c (6) | 3.45 cd (6) | 3.18 c (6) | 3.67 c (6) | 3.20 e (6) | 2.96 cd (6) | |
| G4 | 3.76 c (8) | 3.39 cd (7) | 3.16 c (7) | 3.52 c (9) | 3.17 e (7) | 2.93 cd (7) | |
| G5 | 4.51 b (3) | 4.00 b (3) | 3.56 ab (3) | 4.38 b (3) | 3.85 bc (3) | 3.36 ab (3) | |
| G6 | 4.70 ab (2) | 4.15 ab (2) | 3.68 a (2) | 4.61 ab (2) | 4.05 b (2) | 3.43 a (2) | |
| G7 | 4.90 a (1) | 4.40 a (1) | 3.79 a (1) | 4.76 a (1) | 4.30 a (1) | 3.55 a (1) | |
| G8 | 4.45 b (4) | 3.95 b (4) | 3.52 ab (4) | 4.33 b (4) | 3.76 c (4) | 3.35 ab (4) | |
| G9 | 3.96 c (5) | 3.62 c (5) | 3.27 bc (5) | 3.80 c (5) | 3.52 d (5) | 3.12 bc (5) | |
| STI | G1 | 0.68 c (7) | 0.52 cd (8) | 0.43 c (8) | 0.66 c (7) | 0.47 e (9) | 0.37 d (9) |
| G2 | 0.64 c (9) | 0.50 d (9) | 0.40 c (9) | 0.65 c (8) | 0.50 e (8) | 0.38 d (8) | |
| G3 | 0.71 c (6) | 0.57 cd (6) | 0.48 c (6) | 0.70 c (6) | 0.53 e (6) | 0.45 cd (6) | |
| G4 | 0.67 c (8) | 0.55 cd (7) | 0.47 c (7) | 0.64 c (9) | 0.52 e (7) | 0.44 cd (7) | |
| G5 | 0.97 b (3) | 0.76 b (3) | 0.60 ab (3) | 1.00 b (3) | 0.77 bc (3) | 0.59 ab (3) | |
| G6 | 1.05 ab (2) | 0.82 b (2) | 0.65 a (2) | 1.10 ab (2) | 0.85 b (2) | 0.61 a (2) | |
| G7 | 1.14 a (1) | 0.92 a (1) | 0.68 a (1) | 1.18 a (1) | 0.96 a (1) | 0.65 a (1) | |
| G8 | 0.94 b (4) | 0.75 b (4) | 0.59 ab (4) | 0.97 b (4) | 0.73 c (4) | 0.58 ab (4) | |
| G9 | 0.75 c (5) | 0.62 c (5) | 0.51 bc (5) | 0.75 c (5) | 0.64 d (5) | 0.51 bc (5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheta, M.H.; Hasham, M.M.A.; Ghanem, K.Z.; Bayomy, H.M.; El-Sheshtawy, A.-N.A.; El-Serafy, R.S.; Naif, E. Screening of Wheat Genotypes for Water Stress Tolerance Using Soil–Water Relationships and Multivariate Statistical Approaches. Agronomy 2024, 14, 1029. https://doi.org/10.3390/agronomy14051029
Sheta MH, Hasham MMA, Ghanem KZ, Bayomy HM, El-Sheshtawy A-NA, El-Serafy RS, Naif E. Screening of Wheat Genotypes for Water Stress Tolerance Using Soil–Water Relationships and Multivariate Statistical Approaches. Agronomy. 2024; 14(5):1029. https://doi.org/10.3390/agronomy14051029
Chicago/Turabian StyleSheta, Mohamed H., Mostafa M. A. Hasham, Kholoud Z. Ghanem, Hala M. Bayomy, Abdel-Nasser A. El-Sheshtawy, Rasha S. El-Serafy, and Eman Naif. 2024. "Screening of Wheat Genotypes for Water Stress Tolerance Using Soil–Water Relationships and Multivariate Statistical Approaches" Agronomy 14, no. 5: 1029. https://doi.org/10.3390/agronomy14051029
APA StyleSheta, M. H., Hasham, M. M. A., Ghanem, K. Z., Bayomy, H. M., El-Sheshtawy, A.-N. A., El-Serafy, R. S., & Naif, E. (2024). Screening of Wheat Genotypes for Water Stress Tolerance Using Soil–Water Relationships and Multivariate Statistical Approaches. Agronomy, 14(5), 1029. https://doi.org/10.3390/agronomy14051029






