Estimation of Winter Wheat Chlorophyll Content Based on Wavelet Transform and the Optimal Spectral Index
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Experimental Area and Experimental Design
2.2. Data Acquisition
2.2.1. Remote Sensing Data Acquisition of Winter Wheat Canopy
2.2.2. Winter Wheat Chlorophyll Content Acquisition
2.3. Hyperspectral Data Preprocessing
2.3.1. SG Smoothing Processing
2.3.2. Continuous Wavelet Transform
2.4. Selection and Construction of Spectral Index
2.5. Model Construction
2.5.1. RF
2.5.2. SVM
2.5.3. GA-BP
2.6. Model Accuracy Validation
- (1)
- Evaluation indicators
- (2)
- Significance analysis
3. Results
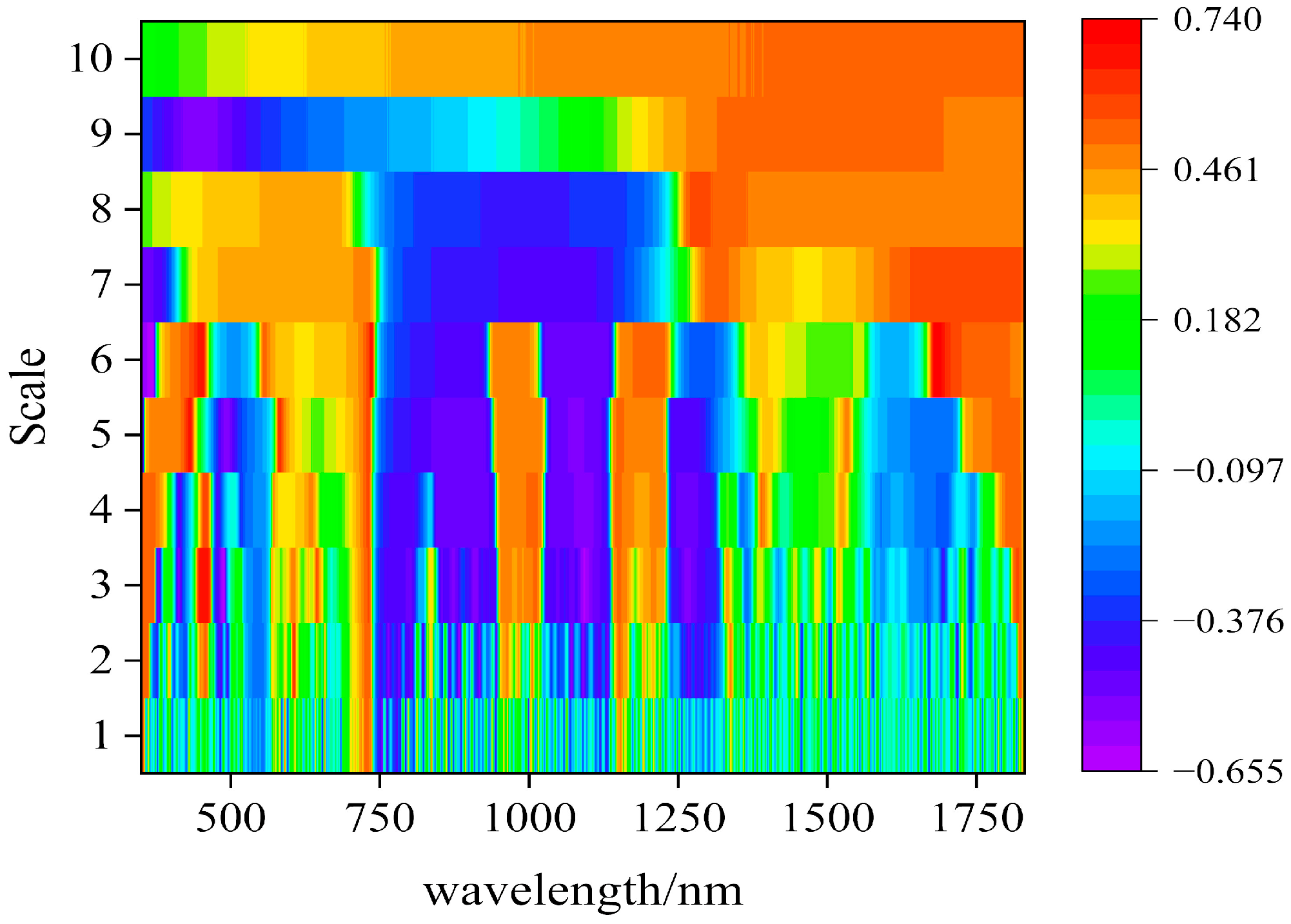
3.1. Correlation Analysis of Raw Hyperspectral Reflectance, Wavelet Transformed Hyperspectral Reflectance, and Chlorophyll Content
3.2. Construction of Spectral Indices and Extraction of Optimal Spectral Index Band Combinations
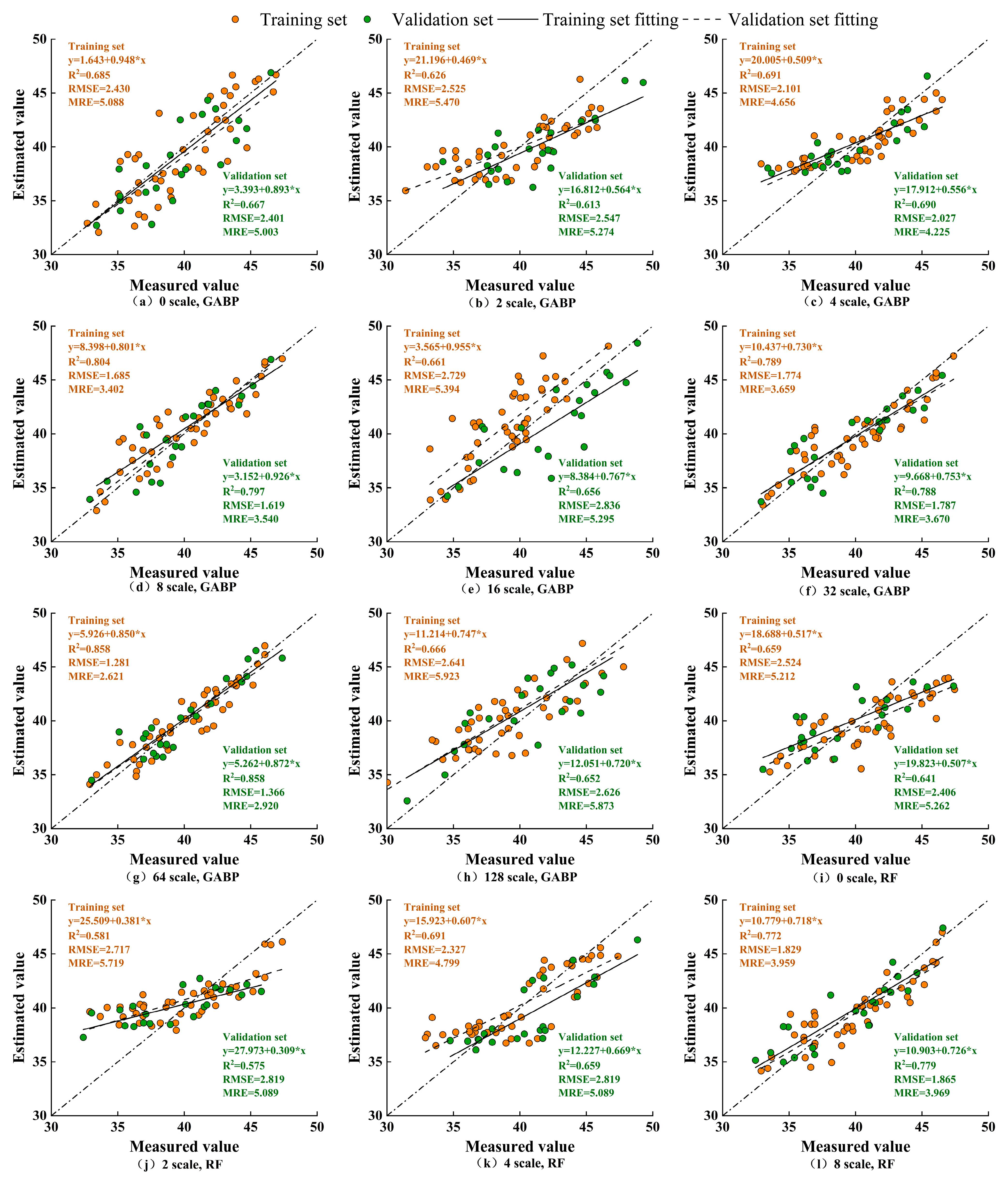
3.3. Winter Wheat Chlorophyll Content Prediction Model Construction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, Y.; Chen, B.; Liu, W.; Xue, X.; Liu, T.; Zhu, L.; Xing, H. Winter Wheat Mapping in Shandong Province of China with Multi-Temporal Sentinel-2Images. Appl. Sci. 2024, 14, 3940. [Google Scholar] [CrossRef]
- Wang, F.; He, Z.; Sayre, K.; Li, S.; Si, J.; Feng, B.; Kong, L. Wheat cropping systems and technologies in China. Field Crop. Red. 2009, 111, 181–188. [Google Scholar] [CrossRef]
- Coventry, D.R.; Gupta, R.K.; Yadav, A.; Poswal, R.S.; Chhokar, R.S.; Sharma, R.K.; Yadav, V.K.; Gill, S.C.; Kumar, A.; Mehta, A.; et al. Wheat quality and productivity as affected by varieties and sowing time in Haryana, India. Field Crop. Res. 2011, 123, 214–225. [Google Scholar] [CrossRef]
- Tang, Z.; Lu, J.; Xiang, Y.; Shi, H.; Sun, T.; Zhang, W.; Wang, H.; Zhang, X.; Li, Z.; Zhang, F. Farmland mulching and optimized irrigation increase water productivity and seed yield by regulating functional parameters of soybean (Glycine max L.) leaves. Agric. Water Manag. 2024, 298, 108875. [Google Scholar] [CrossRef]
- de Souza, R.; Peña-Fleitas, M.T.; Thompson, R.B.; Gallardo, M.; Grasso, R.; Padilla, F.M. The Use of Chlorophyll Meters to Assess Crop N Status and Derivation of Sufficiency Values for Sweet Pepper. Sensors 2019, 19, 2949. [Google Scholar] [CrossRef]
- Xavier, W.D.; Castoldi, G.; Cavalcante, T.J.; Rodrigues, C.R.; Trindade, P.R.; Luiz, I.A.; Damin, V. Portable Chlorophyll Meter for Indirect Evaluation of Photosynthetic Pigments and Nitrogen Content in Sweet Sorghum. Sugar Tech. 2021, 23, 560–570. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, X.; Xiang, Y.; Liang, J.; Guo, J.; Li, W.; Lu, J.; Du, R.; Li, Z.; Zhang, F. Application of hyperspectral technology for leaf function monitoring and nitrogen nutrient diagnosis in soybean (Glycine max L.) production systems on the Loess Plateau of China. Eur. J. Agron. 2024, 154, 127098. [Google Scholar] [CrossRef]
- Zhang, J.; Han, W.; Huang, L.; Zhang, Z.; Ma, Y.; Hu, Y. Leaf chlorophyll content estimation of winter wheat based on visible and near-infrared sensors. Sensors. 2016, 16, 437. [Google Scholar] [CrossRef]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D.C. A comparison of two techniques for nondestructive measurement of chlorophyll content in grapevine leaves. Agron. J. 2008, 100, 779–782. [Google Scholar] [CrossRef]
- Fountas, S.; Wulfsohn, D.; Blackmore, B.; Jacobsen, H.; Pedersen, S. A model of decision-making and information flows for information-intensive agriculture. Agr Syst. 2006, 87, 192–210. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, W.; Xiang, Y.; Liu, X.; Wang, X.; Shi, H.; Li, Z.; Zhang, F. Monitoring of Soil Moisture Content of Winter Oilseed Rape (Brassica napus L.) Based on Hyperspectral and Machine Learning Models. J. Soil Sci. Plant Nutr. 2024, 24, 1250–1260. [Google Scholar] [CrossRef]
- Tang, Z.; Xiang, Y.; Zhang, W.; Wang, X.; Zhang, F.; Chen, J. Research on potato (Solanum tuberosum L.) nitrogen nutrition diagnosis based on hyperspectral data. Agron. J. 2024, 116, 531–541. [Google Scholar] [CrossRef]
- Sampson, P.H.; Zarco-Tejada, P.J.; Mohammed, G.H.; Miller, J.R.; Noland, T.L. Hyperspectral remote sensing of forest condition: Estimating chlorophyll content in tolerant hardwoods. Forest Sci. 2003, 49, 381–391. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Yoder, B.J.; Pettigrew-Crosby, R.E. Predicting nitrogen and chlorophyll content and concentrations from reflectance spectra (400–2500 nm) at leaf and canopy scales. Remote Sens. Environ. 1995, 53, 199–211. [Google Scholar] [CrossRef]
- Saberioon, M.; Amin, M.; Anuar, A.; Gholizadeh, A.; Wayayok, A.; Khairunniza-Bejo, S. Assessment of rice leaf chlorophyll content using visible bands at different growth stages at both the leaf and canopy scale. Int. J. Appl. Earth Obs. 2014, 32, 35–45. [Google Scholar] [CrossRef]
- Yang, F.; Fan, Y.M.; Li, J.L.; Qian, Y.R.; Wang, Y.; Zhang, J. Hyperspectral data estimated rice and wheat leaf area index and chlorophyll density. Trans. Chin. Soc. Agric. Eng. 2010, 26, 237–243, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Briggs, F.H.; Bell, J.F.; Kesteven, M.J. Removing radio interference from contaminated astronomical spectra using an independent reference signal and closure relations. J. Korean Astron. Soc. 2000, 120, 3351. [Google Scholar] [CrossRef]
- Nie, P.; Guo, Y.; Lou, B.; Yang, C.; Cao, L.; Pan, W. Tool wear monitoring based on scSE-ResNet-50-TSCNN model integrating machine vision and force signals. Meas. Sci. Technol. 2024, 35, 086117. [Google Scholar] [CrossRef]
- Liu, D.D.; Nie, R.J.; Xu, X.B. Nitrogen estimation model for summer maize based on continuous wavelet transform and RF algorithm. Barley Cereal Sci. 2019, 36, 42–46, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ. 2010, 115, 659–670. [Google Scholar] [CrossRef]
- Bauer, M.E. Spectral inputs to crop identification and condition assessment. Proc. IEEE 1985, 73, 1071–1085. [Google Scholar] [CrossRef]
- Xu, M.; Liu, R.; Chen, J.M.; Liu, Y.; Shang, R.; Ju, W.; Wu, C.; Huang, W. Retrieving leaf chlorophyll content using a matrix-based vegetation index combination approach. Remote Sens. Environ. 2019, 224, 60–73. [Google Scholar] [CrossRef]
- Tang, Z.; Guo, J.; Xiang, Y.; Lu, X.; Wang, Q.; Wang, H.; Cheng, M.; Wang, H.; Wang, X.; An, J.; et al. Estimation of leaf area index and above-ground biomass of winter wheat based on optimal spectral index. Agronomy 2022, 12, 1729. [Google Scholar] [CrossRef]
- Higdon, D. A process-convolution approach to modelling temperatures in the North Atlantic Ocean. Envioron. Ecol. Stat. 1998, 5, 173–190. [Google Scholar] [CrossRef]
- Lawton, W. Applications of complex valued wavelet transforms to subband decomposition. IEEE Trans. Signal Process. 1993, 41, 3566–3568. [Google Scholar] [CrossRef]
- Heil, C.E.; Walnut, D.F. Continuous and discrete wavelet transforms. Siam Rev. 1989, 31, 628–666. [Google Scholar] [CrossRef]
- Rivera, J.P.; Verrelst, J.; Delegido, J.; Veroustraete, F.; Moreno, J. On the Semi-Automatic Retrieval of Biophysical Parameters Based on Spectral Index Optimization. Remote Sens. 2014, 6, 4927–4951. [Google Scholar] [CrossRef]
- Tran, T.V.; Reef, R.; Zhu, X. A review of spectral indices for mangrove remote sensing. Remote Sens. 2022, 14, 4868. [Google Scholar] [CrossRef]
- Liu, C.; Hu, Z.; Islam, A.T.; Kong, R.; Yu, L.; Wang, Y.; Chen, S.; Zhang, X. Hyperspectral characteristics and inversion model estimation of winter wheat under different elevated CO2 concentrations. Int J. Remote Sens. 2021, 42, 1035–1053. [Google Scholar] [CrossRef]
- Xu, G.; Liu, M.; Jiang, Z.; Söffker, D.; Shen, W. Bearing Fault Diagnosis Method Based on Deep Convolutional Neural Network and Random Forest Ensemble Learning. Sensors 2019, 19, 1088. [Google Scholar] [CrossRef]
- Shi, K.; Qiao, Y.; Zhao, W.; Wang, Q.; Liu, M.; Lu, Z. An improved random forest model of short-term wind-power forecasting to enhance accuracy, efficiency, and robustness. Wind Energy 2018, 21, 1383–1394. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Zeng, W.; Jia, J.; Zheng, Z.; Xie, C.; Guo, L. A comparison study: Support vector machines for binary classification in machine learning. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011; IEEE: Piscataway, NJ, USA, 2011; Volume 3, pp. 1621–1625. [Google Scholar] [CrossRef]
- Unger, R.; Moult, J. Genetic algorithms for protein folding simulations. J. Mol. Biol. 1993, 231, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.L.; Rosenthal, R.; Rubin, D.B. Comparing correlated correlation coefficients. Phychol Bull. 1992, 111, 172. [Google Scholar] [CrossRef]
- Ahmad, U.; Nasirahmadi, A.; Hensel, O.; Marino, S. Technology and Data Fusion Methods to Enhance Site-Specific Crop Monitoring. Agronomy 2022, 12, 555. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Berger, K.; Machwitz, M.; Kycko, M.; Kefauver, S.C.; Van Wittenberghe, S.; Gerhards, M.; Verrelst, J.; Atzberger, C.; van der Tol, C.; Damm, A.; et al. Multi-sensor spectral synergies for crop stress detection and monitoring in the optical domain: A review. Remote Sens. Environ. 2022, 280, 113198. [Google Scholar] [CrossRef]
- Shu, M.; Zuo, J.; Shen, M.; Yin, P.; Wang, M.; Yang, X.; Tang, J.; Li, B.; Ma, Y. Improving the estimation accuracy of SPAD values for maize leaves by removing UAV hyperspectral image backgrounds. Int. J. Remote Sens. 2021, 42, 5862–5881. [Google Scholar] [CrossRef]
- Li, C.H.; Shi, J.J.; Ma, C.Y.; Cui, Y.Q. Estimation of winter wheat chlorophyll content based on wavelet transform and fractional differential. Trans. Chin. Soc. Agric. Mach. 2021, 52, 172–182, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Wang, T.; Gao, M.; Cao, C.; You, J.; Zhang, X.; Shen, L. Winter wheat chlorophyll content retrieval based on machine learning using in situ hyperspectral data. Comput. Electron. Agric. 2022, 193, 106728. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Shi, B.; Fan, K.; Li, Z.; Chang, Q. Estimation of winter wheat canopy chlorophyll content based on canopy spectral transformation and machine learning method. Agronomy 2023, 13, 783. [Google Scholar] [CrossRef]
- Shi, M.; Jing, X.; Shi, X.L. Inversion of winter wheat chlorophyll content based on hyperspectral and GA-BP neural network model. Jiangsu J. Agric. Sci. 2022, 50, 56–62, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Fu, Z.; Jiang, J.; Gao, Y.; Krienke, B.; Wang, M.; Zhong, K.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; et al. Wheat Growth Monitoring and Yield Estimation based on Multi-Rotor Unmanned Aerial Vehicle. Remote Sens. 2020, 12, 508. [Google Scholar] [CrossRef]
- Sehra, S.; Flores, D.; Montañez, G.D. Undecidability of underfitting in learning algorithms. In Proceedings of the 2021 2nd International Conference on Computing and Data Science (CDS), Stanford, CA, USA, 28–29 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 591–594. [Google Scholar] [CrossRef]
- Lan, B.; Zhou, X.; Yang, N.; Sun, S. Spectral radius is a better metric than weighted NODF to detect network nestedness: Linking species coexistence to network structure using a plant–larval sawfly bipartite. Food Webs 2023, 36, e00303. [Google Scholar] [CrossRef]
- Zhu, Z.; Song, J.; He, S.; Liu, J.J.R.; Lam, H.-K. Event-Triggered Disturbance Rejection Control for Brain-Actuated Mobile Robot: An SSA-Optimized Sliding Mode Approach. IEEE-AMSE Trans. Mechatron. 2024, 1–12. [Google Scholar] [CrossRef]
- Reda, R.; Saffaj, T.; Ilham, B.; Saidi, O.; Issam, K.; Brahim, L.; El Hadrami, E.M. A comparative study between a new method and other machine learning algorithms for soil organic carbon and total nitrogen prediction using near infrared spectroscopy. Chemom. Intell. Lab. Syst. 2019, 195, 103873. [Google Scholar] [CrossRef]


| Select Index | Computing Formula | Literature Number |
|---|---|---|
| Ratio vegetation index (RI) | [30] | |
| Triangular vegetation index (TVI) | [30] | |
| Modified red edge simple ratio (mSR) | [30] | |
| Modified normalized difference index (mNDI) | [30] | |
| Difference index (DI) | [30] | |
| Soil-adjusted vegetation index (SAVI) | [30] | |
| Normalized difference vegetation index (NDVI) | [30] |
| Transformation Scale | Spectral Index | Correlation Coefficient | Optimal Spectral Index Combination |
|---|---|---|---|
| 0 | RI | 0.740 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.865 | ||
| SAVI | 0.829 | ||
| NDVI | 0.731 | ||
| TVI | 0.134 | ||
| mSR | 0.368 | ||
| mNDI | 0.736 | ||
| 2 | RI | 0.745 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.686 | ||
| SAVI | 0.684 | ||
| NDVI | 0.719 | ||
| TVI | 0.587 | ||
| mSR | 0.490 | ||
| mNDI | 0.718 | ||
| 4 | RI | 0.775 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.765 | ||
| SAVI | 0.779 | ||
| NDVI | 0.738 | ||
| TVI | 0.587 | ||
| mSR | 0.458 | ||
| mNDI | 0.713 | ||
| 8 | RI | 0.805 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.817 | ||
| SAVI | 0.815 | ||
| NDVI | 0.774 | ||
| TVI | 0.543 | ||
| mSR | 0.299 | ||
| mNDI | 0.794 | ||
| 16 | RI | 0.744 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.816 | ||
| SAVI | 0.841 | ||
| NDVI | 0.752 | ||
| TVI | 0.448 | ||
| mSR | 0.745 | ||
| mNDI | 0.793 | ||
| 32 | RI | 0.764 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.814 | ||
| SAVI | 0.845 | ||
| NDVI | 0.756 | ||
| TVI | 0.761 | ||
| mSR | 0.564 | ||
| mNDI | 0.759 | ||
| 64 | RI | 0.750 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.816 | ||
| SAVI | 0.842 | ||
| NDVI | 0.749 | ||
| TVI | 0.668 | ||
| mSR | 0.690 | ||
| mNDI | 0.749 | ||
| 128 | RI | 0.715 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.741 | ||
| SAVI | 0.755 | ||
| NDVI | 0.724 | ||
| TVI | 0.437 | ||
| mSR | 0.243 | ||
| mNDI | 0.703 | ||
| 256 | RI | 0.716 | RI, DI, SAVI, NDVI, mNDI |
| DI | 0.563 | ||
| SAVI | 0.731 | ||
| NDVI | 0.760 | ||
| TVI | 0.400 | ||
| mSR | 0.022 | ||
| mNDI | 0.744 | ||
| 512 | RI | 0.758 | RI, SAVI, NDVI, mSR, mNDI |
| DI | 0.571 | ||
| SAVI | 0.699 | ||
| NDVI | 0.759 | ||
| TVI | 0.124 | ||
| mSR | 0.674 | ||
| mNDI | 0.675 | ||
| 1024 | RI | 0.659 | RI, SAVI, NDVI, mSR, mNDI |
| DI | 0.607 | ||
| SAVI | 0.655 | ||
| NDVI | 0.658 | ||
| TVI | 0.526 | ||
| mSR | 0.690 | ||
| mNDI | 0.692 |
| Transformation Scale | Evaluation Indicators | GA-BP | RF | SVM | |||
|---|---|---|---|---|---|---|---|
| Training Set | Validation Set | Training Set | Validation Set | Training Set | Validation Set | ||
| 0 | R2 | 0.686 | 0.667 | 0.659 | 0.641 | 0.635 | 0.626 |
| RMSE | 2.430 | 2.401 | 2.524 | 2.406 | 2.841 | 2.685 | |
| MRE/% | 5.088 | 5.003 | 5.212 | 5.262 | 5.892 | 5.955 | |
| 2 | R2 | 0.626 | 0.613 | 0.581 | 0.575 | 0.564 | 0.556 |
| RMSE | 2.525 | 2.547 | 2.717 | 2.819 | 2.803 | 2.828 | |
| MRE/% | 5.470 | 5.274 | 5.719 | 6.089 | 5.887 | 6.273 | |
| 4 | R2 | 0.691 | 0.690 | 0.671 | 0.659 | 0.654 | 0.562 |
| RMSE | 2.101 | 2.028 | 2.327 | 2.381 | 2.532 | 2.583 | |
| MRE/% | 4.656 | 4.226 | 4.799 | 4.672 | 5.871 | 5.814 | |
| 8 | R2 | 0.804 | 0.798 | 0.773 | 0.779 | 0.738 | 0.736 |
| RMSE | 1.685 | 1.620 | 1.829 | 1.865 | 2.392 | 2.222 | |
| MRE/% | 3.402 | 3.540 | 3.959 | 3.969 | 5.039 | 5.038 | |
| 16 | R2 | 0.661 | 0.656 | 0.630 | 0.621 | 0.619 | 0.610 |
| RMSE | 2.729 | 2.836 | 2.789 | 2.837 | 3.257 | 3.363 | |
| MRE/% | 5.394 | 5.295 | 5.620 | 5.872 | 5.979 | 6.146 | |
| 32 | R2 | 0.789 | 0.788 | 0.765 | 0.758 | 0.731 | 0.733 |
| RMSE | 1.775 | 1.788 | 1.848 | 1.866 | 2.441 | 2.771 | |
| MRE/% | 3.659 | 3.670 | 3.689 | 4.169 | 5.321 | 5.276 | |
| 64 | R2 | 0.858 | 0.859 | 0.803 | 0.809 | 0.777 | 0.779 |
| RMSE | 1.281 | 1.366 | 1.563 | 1.663 | 1.808 | 1.978 | |
| MRE/% | 2.621 | 2.920 | 3.145 | 3.534 | 3.665 | 4.038 | |
| 128 | R2 | 0.665 | 0.652 | 0.621 | 0.619 | 0.613 | 0.609 |
| RMSE | 2.641 | 2.626 | 2.909 | 2.982 | 3.562 | 3.393 | |
| MRE/% | 5.923 | 5.873 | 6.155 | 6.212 | 6.853 | 7.271 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, Z.; Xiang, Y.; Tang, Z.; Huang, X.; Shi, H.; Sun, T.; Yang, W.; Cui, S.; Chen, G.; et al. Estimation of Winter Wheat Chlorophyll Content Based on Wavelet Transform and the Optimal Spectral Index. Agronomy 2024, 14, 1309. https://doi.org/10.3390/agronomy14061309
Liu X, Li Z, Xiang Y, Tang Z, Huang X, Shi H, Sun T, Yang W, Cui S, Chen G, et al. Estimation of Winter Wheat Chlorophyll Content Based on Wavelet Transform and the Optimal Spectral Index. Agronomy. 2024; 14(6):1309. https://doi.org/10.3390/agronomy14061309
Chicago/Turabian StyleLiu, Xiaochi, Zhijun Li, Youzhen Xiang, Zijun Tang, Xiangyang Huang, Hongzhao Shi, Tao Sun, Wanli Yang, Shihao Cui, Guofu Chen, and et al. 2024. "Estimation of Winter Wheat Chlorophyll Content Based on Wavelet Transform and the Optimal Spectral Index" Agronomy 14, no. 6: 1309. https://doi.org/10.3390/agronomy14061309






