Reanalysis Product-Based Nonstationary Frequency Analysis for Estimating Extreme Design Rainfall
Abstract
:1. Introduction
2. Study Site and Data
2.1. Study Site and Local Gauge Data
2.2. Reanalysis Products
3. Methodology
3.1. Bias Correction
3.2. Detecting Nonstationarity: Long-Term Trend Test
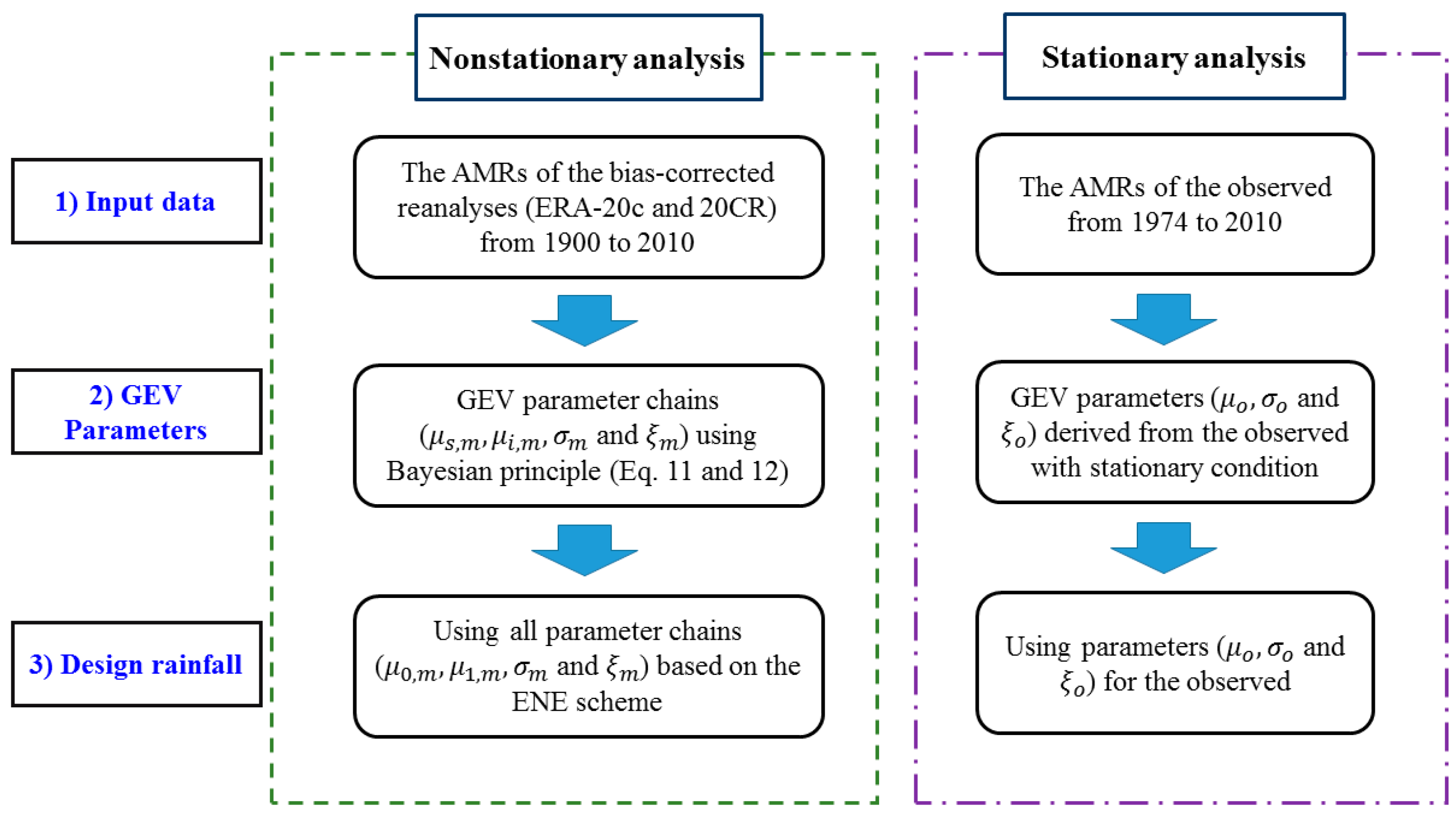
3.3. Rainfall Frequency Analysis with Nonstationary Condition
4. Results
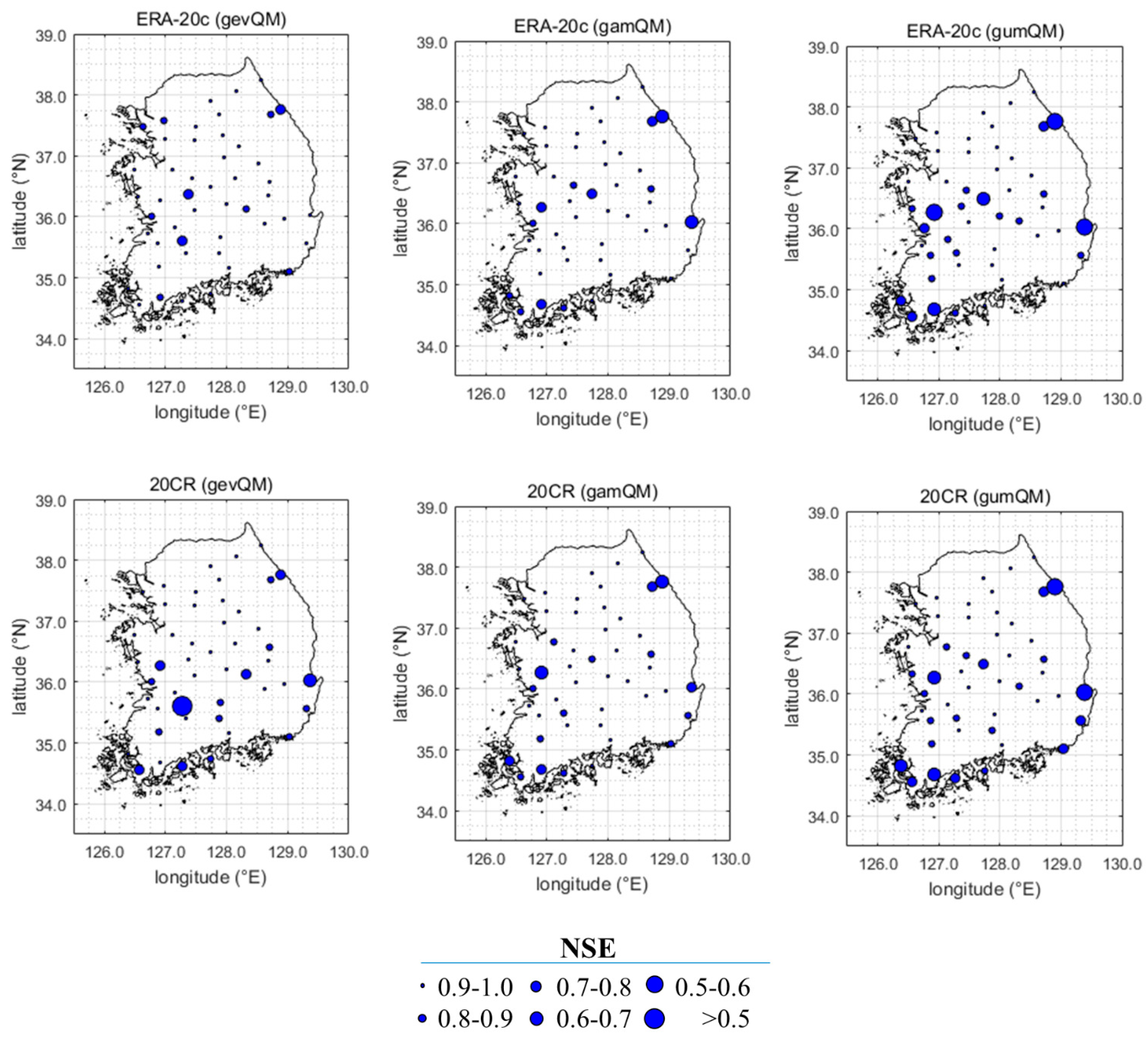
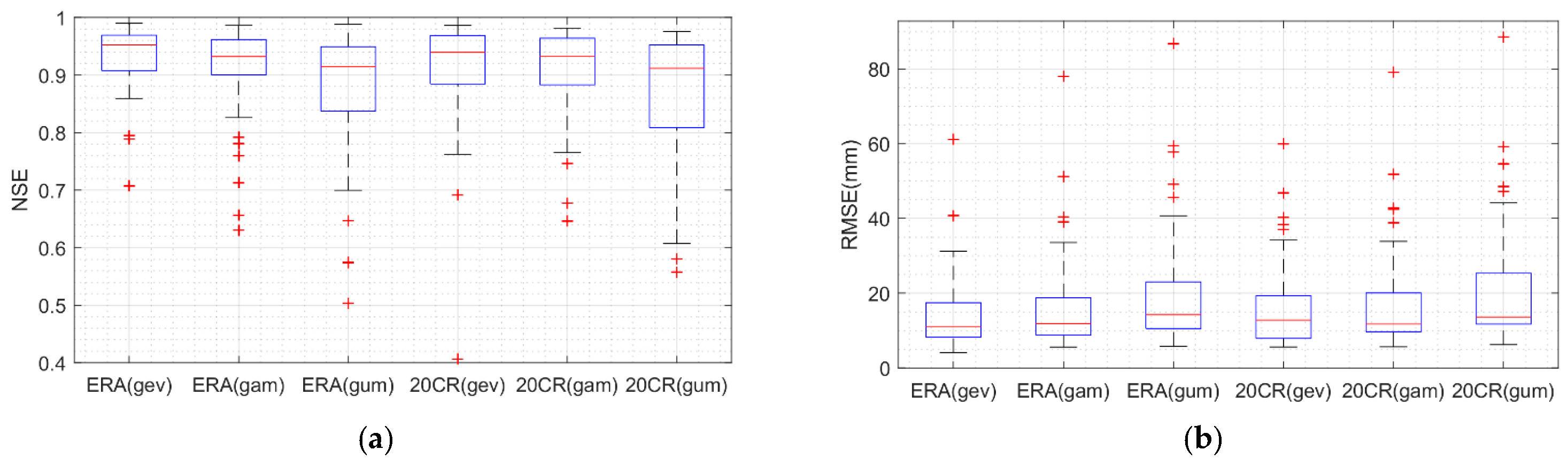
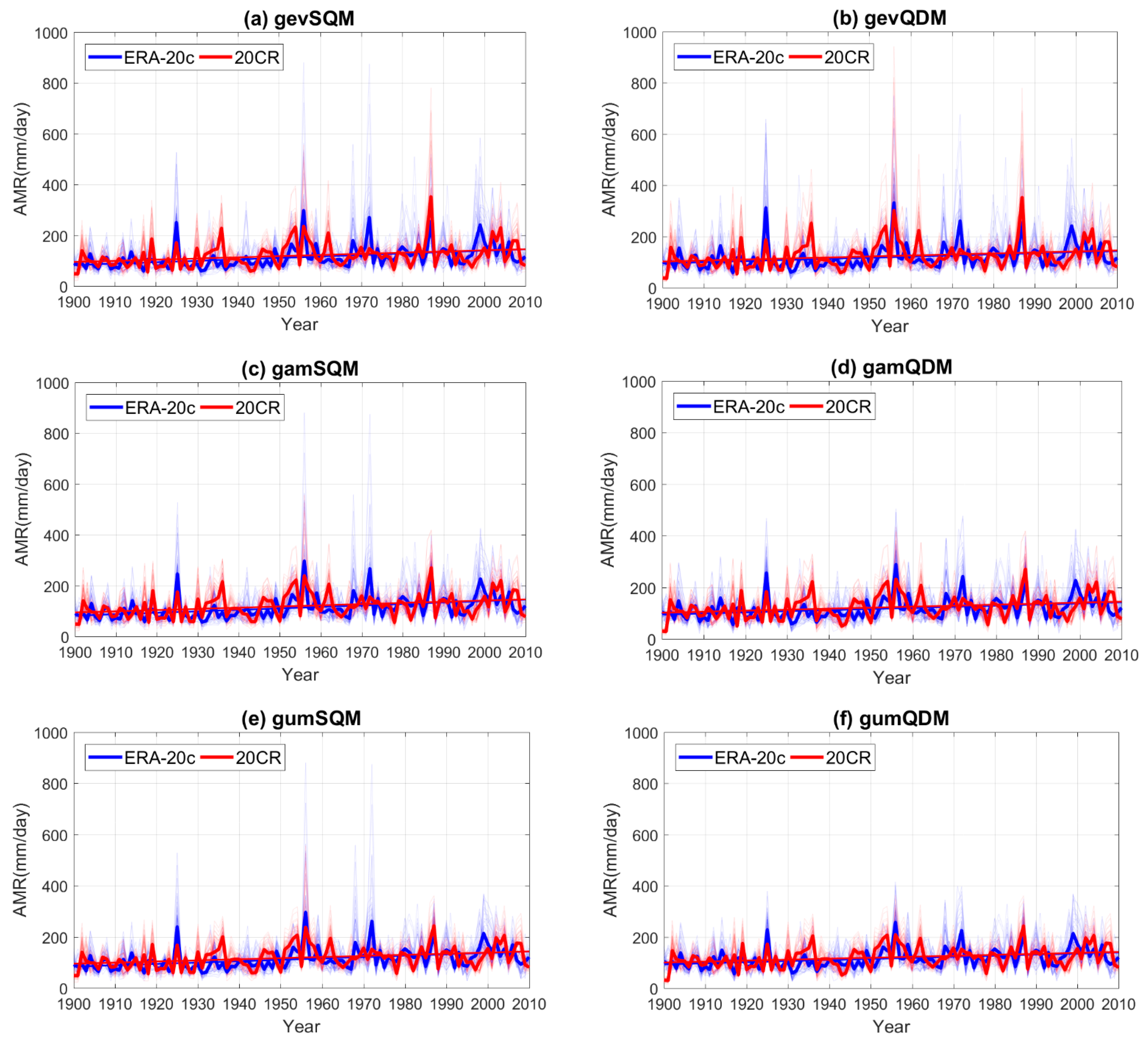
4.1. Bias Correction
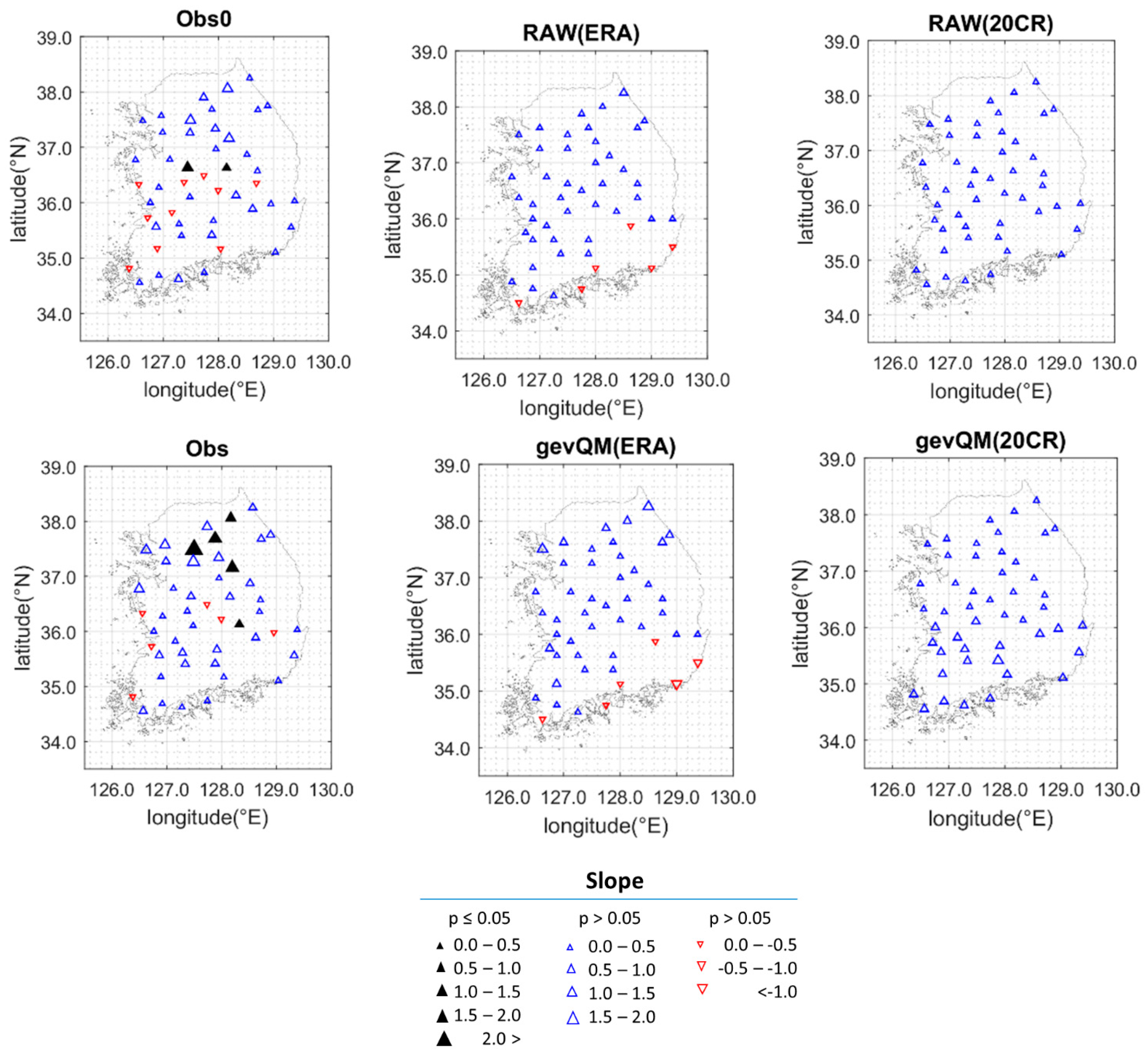
4.2. Long-Term Trend
4.3. Design Rainfalls with Nonstationary Condition
5. Discussion
6. Summary and Conclusions
- The applied QM approaches (gevQM, gamQM and gumQM) significantly improved the AMRs of ERA-20c and 20CR for the reference period. Among three QM schemes, gevQM performed the best in terms of RMSE and NSE.
- For long-term trend, no significant trend for the AMRs of the observed and the reanalyses can be found during the observational period. However, the century-long AMRs of the bias corrected ERA-20c and 20CR indicated the increasing trends. This result implies that the AMRs might have time-dependent characteristics and the trend in the long-term reanalysis datasets could be beneficial in estimating the future extreme design rainfall over South Korea with nonstationary frequency analysis.
- The design rainfalls estimated under nonstationary condition were influenced in estimating the future risk of extreme precipitation and the strength of the impact depends on the target return period and location. More specifically, the nonstationary design rainfalls in some parts of South Korea exceeded the classic design rainfalls by the observed. This result implies that the nonstationarity in the AMRs that the short-term observation often fails to detect could deteriorate the confidence of a project based on the observed data for the future risk in South Korea.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, L.; Aghakouchak, A. Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Evans, J.; Johnson, F.; Sharma, A. A comparison of methods for estimating climate change impact on design rainfall using a high-resolution RCM. J. Hydrol. 2017, 547, 413–427. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Climate Change 2014–Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: London, UK, 2014. [Google Scholar]
- De Luca, D.L.; Galasso, L. Stationary and non-stationary frameworks for extreme rainfall time series in southern Italy. Water 2018, 10, 1477. [Google Scholar] [CrossRef] [Green Version]
- Coles, S.; Pericchi, L.R.; Sisson, S. A fully probabilistic approach to extreme rainfall modeling. J. Hydrol. 2003, 273, 35–50. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
- Huard, D.; Mailhot, A.; Duchesne, S. Bayesian estimation of intensity-duration-frequency curves and of the return period associated to a given rainfall event. Stoch. Environ. Res. Risk Assess. 2010, 24, 337–347. [Google Scholar] [CrossRef]
- Tung, Y.K.; Wong, C.L. Assessment of design rainfall uncertainty for hydrologic engineering applications in Hong Kong. Stoch. Environ. Res. Risk Assess. 2014, 28, 583–592. [Google Scholar] [CrossRef]
- Van de Vyver, H. Bayesian estimation of rainfall intensity-duration-frequency relationships. J. Hydrol. 2015, 529, 1451–1463. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef] [Green Version]
- Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationarity case. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Zhang, Q.; Körnich, H.; Holmgren, K. How well do reanalyses represent the southern African precipitation? Clim. Dyn. 2013, 40, 951–962. [Google Scholar] [CrossRef]
- Hersbach, H.; Peubey, C.; Simmons, A.; Berrisford, P.; Poli, P.; Dee, D. ERA-20CM: A twentieth-century atmospheric model ensemble. Q. J. R. Meteorol. Soc. 2015, 141, 2350–2375. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Herold, N.; Dittus, A.J. Temperature and precipitation extremes in century-long gridded observations, reanalyses, and atmospheric model simulations. J. Geophys. Res. Atmos. 2016, 121, 11174–11189. [Google Scholar] [CrossRef] [Green Version]
- Gao, L.; Bernhardt, M.; Schulz, K.; Chen, X.W.; Chen, Y.; Liu, M.B. A First Evaluation of ERA-20CM over China. Mon. Weather Rev. 2016, 144, 45–57. [Google Scholar] [CrossRef]
- Poli, P.; Hersbach, H.; Dee, D.P.; Berrisford, P.; Simmons, A.J.; Vitart, F.; Laloyaux, P.; Tan, D.G.H.; Peubey, C.; Thépaut, J.-N. ERA-20C: An Atmospheric Reanalysis of the Twentieth Century. J. Clim. 2016, 29, 4083–4097. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P. The twentieth century reanalysis project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
- Kim, D.-I.; Han, D. Comparative study on long term climate data sources over South Korea. J. Water Clim. Chang. 2018, (in press). [Google Scholar] [CrossRef] [Green Version]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Mao, G.; Vogl, S.; Laux, P.; Wagner, S.; Kunstmann, H. Stochastic bias correction of dynamically downscaled precipitation fields for Germany through Copula-based integration of gridded observation data. Hydrol. Earth Syst. Sci. 2015, 19, 1787–1806. [Google Scholar] [CrossRef] [Green Version]
- Maraun, D. Bias Correcting Climate Change Simulations—A Critical Review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Nyunt, C.T.; Koike, T.; Yamamoto, A. Statistical bias correction for climate change impact on the basin scale precipitation in Sri Lanka, Philippines, Japan and Tunisia. Hydrol. Earth Syst. Sci. 2016. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef] [Green Version]
- Maraun, D.; Widmann, M. Statistical Downscaling and Bias Correction for Climate Research; Cambridge University Press: London, UK, 2018; pp. 170–200. [Google Scholar]
- Chang, H.; Kwon, W.-T. Spatial variations of summer precipitation trends in South Korea, 1973–2005. Environ. Res. Lett. 2007, 2, 45012. [Google Scholar] [CrossRef] [Green Version]
- Choi, G.; Collins, D.; Ren, G.; Trewin, B.; Baldi, M.; Fukuda, Y.; Afzaal, M.; Pianmana, T.; Gomboluudev, P.; Huong, P.T.T. Changes in means and extreme events of temperature and precipitation in the Asia-Pacific Network region, 1955–2007. Int. J. Climatol. 2009, 29, 1906–1925. [Google Scholar] [CrossRef]
- Jung, I.W.; Bae, D.H.; Kim, G. Recent trends of mean and extreme precipitation in Korea. Int. J. Climatol. 2011, 31, 359–370. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Miao, C.; Su, L.; Sun, Q.; Duan, Q. A nonstationary bias-correction technique to remove bias in GCM simulations. J. Geophys. Res. 2016, 121, 5718–5735. [Google Scholar] [CrossRef]
- Eum, H.I.; Cannon, A.J. Intercomparison of projected changes in climate extremes for South Korea: Application of trend preserving statistical downscaling methods to the CMIP5 ensemble. Int. J. Climatol. 2017, 37, 3381–3397. [Google Scholar] [CrossRef]
- Nahar, J.; Johnson, F.; Sharma, A. Assessing the extent of non-stationary biases in GCMs. J. Hydrol. 2017, 549, 148–162. [Google Scholar] [CrossRef] [Green Version]
- Nadarajah, S.; Choi, D. Maximum daily rainfall in South Korea. J. Earth Syst. Sci. 2007, 116, 311–320. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Burn, D.H. Non-stationary pooled flood frequency analysis. J. Hydrol. 2003, 276, 210–223. [Google Scholar] [CrossRef]
- El Adlouni, S.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobée, B. Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour. Res. 2007, 43, 1–13. [Google Scholar] [CrossRef]
- Leclerc, M.; Ouarda, T.B.M.J. Non-stationary regional flood frequency analysis at ungauged sites. J. Hydrol. 2007, 343, 254–265. [Google Scholar] [CrossRef]
- Cannon, A.J. A flexible nonlinear modelling framework for nonstationary generalized extreme value analysis in hydroclimatology. Hydrol. Process. 2010, 24, 673–685. [Google Scholar] [CrossRef]
- Panagoulia, D.; Economou, P.; Caroni, C. Stationary and nonstationary generalized extreme value modelling of extreme precipitation over a mountainous area under climate change. Environmetrics 2014, 25, 29–43. [Google Scholar] [CrossRef]
- Son, C.; Lee, T.; Kwon, H.H. Integrating nonstationary behaviors of typhoon and non-typhoon extreme rainfall events in East Asia. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Du, T.; Xiong, L.; Xu, C.Y.; Gippel, C.J.; Guo, S.; Liu, P. Return period and risk analysis of nonstationary low-flow series under climate change. J. Hydrol. 2015, 527, 234–250. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef] [Green Version]
- Read, L.K.; Vogel, R.M. Reliability, return periods, and risk under nonstationarity. Water Resour. Res. 2015, 51, 6381–6398. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Frequency of Recurrent Extremes under Nonstationarity. J. Hydrol. Eng. 2016, 21, 1–9. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J.; Vogel, R.M. Techniques for assessing water infrastructure for nonstationary extreme events: A review. Hydrol. Sci. J. 2018, 63, 325–352. [Google Scholar] [CrossRef]
- Berntell, E.; Zhang, Q.; Chafik, L.; Körnich, H. Representation of Multidecadal Sahel Rainfall Variability in 20th Century Reanalyses. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Diro, G.T.; Grimes, D.I.F.; Black, E.; O’Neill, A.; Pardo-Iguzquiza, E. Evaluation of reanalysis rainfall estimates over Ethiopia. Int. J. Climatol. 2009, 29, 67–78. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall spatial estimations: A review from spatial interpolation to multi-source data merging. Water 2019, 11, 579. [Google Scholar] [CrossRef] [Green Version]
- Hua, W.; Zhou, L.; Nicholson, S.E.; Chen, H.; Qin, M. Assessing reanalysis data for understanding rainfall climatology and variability over Central Equatorial Africa. Clim. Dyn. 2019, 53, 651–669. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.B.; Bray, M.; Han, D. An improved bias correction scheme based on comparative precipitation characteristics. Hydrol. Process. 2015, 29, 2258–2266. [Google Scholar] [CrossRef] [Green Version]
- Rabiei, E.; Haberlandt, U. Applying bias correction for merging rain gauge and radar data. J. Hydrol. 2015, 522, 544–557. [Google Scholar] [CrossRef]
- Kim, K.B.; Kwon, H.H.; Han, D. Bias correction methods for regional climate model simulations considering the distributional parametric uncertainty underlying the observations. J. Hydrol. 2015, 530, 568–579. [Google Scholar] [CrossRef] [Green Version]
- Volosciuk, C.; Maraun, D.; Vrac, M.; Widmann, M. A combined statistical bias correction and stochastic downscaling method for precipitation. Hydrol. Earth Syst. Sci. 2017, 21, 1693–1719. [Google Scholar] [CrossRef] [Green Version]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation. Hydrol. Sci. J. 2004, 49, 575–590. [Google Scholar] [CrossRef] [Green Version]
- Wilson, P.S.; Toumi, R. A fundamental probability distribution for heavy rainfall. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant quantile matching. J. Geophys. Res. Atmos. 2010, 115, 1–20. [Google Scholar] [CrossRef]
- Bürger, G.; Sobie, S.R.; Cannon, A.J.; Werner, A.T.; Murdock, T.Q. Downscaling extremes: An intercomparison of multiple methods for future climate. J. Clim. 2013, 26, 3429–3449. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. I, II, III. Proc. K. Ned. Akad. Wet. 1950, 53, 386–392, 521–525, 1397–1412. [Google Scholar]
- Sayemuzzaman, M.; Jha, M.K. Seasonal and annual precipitation time series trend analysis in North Carolina, United States. Atmos. Res. 2014, 137, 183–194. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend analysis in reference evapotranspiration using Mann-Kendall and Spearman’s Rho tests in arid regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Ouarda, T.B.M.J.; El-Adlouni, S. Bayesian nonstationary frequency analysis of hydrological variables. J. Am. Water Resour. Assoc. 2011, 47, 496–505. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Quantifying the Uncertainty of Design Floods under Nonstationary Conditions. J. Hydrol. Eng. 2014, 19, 1438–1446. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Chen, J.; Robertson, F.R.; Adler, R.F. Evaluation of global precipitation in reanalyses. J. Appl. Meteorol. Climatol. 2008, 47, 2279–2299. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, T.; Frauenfeld, O.W.; Ye, B.; Yang, D.; Qin, D. Evaluation of precipitation from the ERA-40, NCEP-1, and NCEP-2 Reanalyses and CMAP-1, CMAP-2, and GPCP-2 with ground-based measurements in China. J. Geophys. Res. Atmos. 2009, 114, 1–20. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, F. Evaluation of NCEP–CFSR, NCEP–NCAR, ERA-Interim, and ERA-40 reanalysis datasets against independent sounding observations over the Tibetan Plateau. J. Clim. 2013, 26, 206–214. [Google Scholar] [CrossRef] [Green Version]
- Brands, S.; Gutiérrez, J.M.; Herrera, S.; Cofiño, A.S. On the use of reanalysis data for downscaling. J. Clim. 2012, 25, 2517–2526. [Google Scholar] [CrossRef] [Green Version]
- Krueger, O.; Schenk, F.; Feser, F.; Weisse, R. Inconsistencies between long-term trends in storminess derived from the 20CR reanalysis and observations. J. Clim. 2013, 26, 868–874. [Google Scholar] [CrossRef] [Green Version]
- Poli, P.; Hersbach, H.; Tan, D.; Dee, D.; Thépaut, J.-N.; Simmons, A.; Peubey, C.; Laloyaux, P.; Komori, T.; Berrisford, P.; et al. The data assimilation system and initial performance evaluation of the ECMWF pilot reanalysis of the 20th-century assimilating surface observations only (ERA-20C). ERA Rep. Ser. 2013, 14, 59. [Google Scholar]
- Befort, D.J.; Wild, S.; Kruschke, T.; Ulbrich, U.; Leckebusch, G.C. Different long-term trends of extra-tropical cyclones and windstorms in ERA-20C and NOAA-20CR reanalyses. Atmos. Sci. Lett. 2016, 17, 586–595. [Google Scholar] [CrossRef] [Green Version]
- Wilks, D.S. Interannual variability and extreme-value characteristics of several stochastic daily precipitation models. Agric. For. Meteorol. 1999, 93, 153–169. [Google Scholar] [CrossRef]
- Vrac, M.; Naveau, P. Stochastic downscaling of precipitation: From dry events to heavy rainfalls. Water Resour. Res. 2007, 43, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Hundecha, Y.; Pahlow, M.; Schumann, A. Modeling of daily precipitation at multiple locations using a mixture of distributions to characterize the extremes. Water Resour. Res. 2009, 45, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Gutjahr, O.; Heinemann, G. Comparing precipitation bias correction methods for high-resolution regional climate simulations using COSMO-CLM. Theor. Appl. Climatol. 2013, 114, 511–529. [Google Scholar] [CrossRef]
- Smith, A.; Freer, J.; Bates, P.; Sampson, C. Comparing ensemble projections of flooding against flood estimation by continuous simulation. J. Hydrol. 2014, 511, 205–219. [Google Scholar] [CrossRef] [Green Version]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2013–2014. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, D.; Hisdal, H. Hydrological Projections for Floods in Norway under a Future Climate; Norwegian Water Resources and Energy Directorate: Oslo, Norway, 2011; p. 47.
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T.R. Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef] [Green Version]
- Flood Risk Assessments: Climate Change Allowances. 2017. Available online: https://www.gov.uk/guidance/flood-risk-assessments-climate-change-allowances (accessed on 31 January 2020).
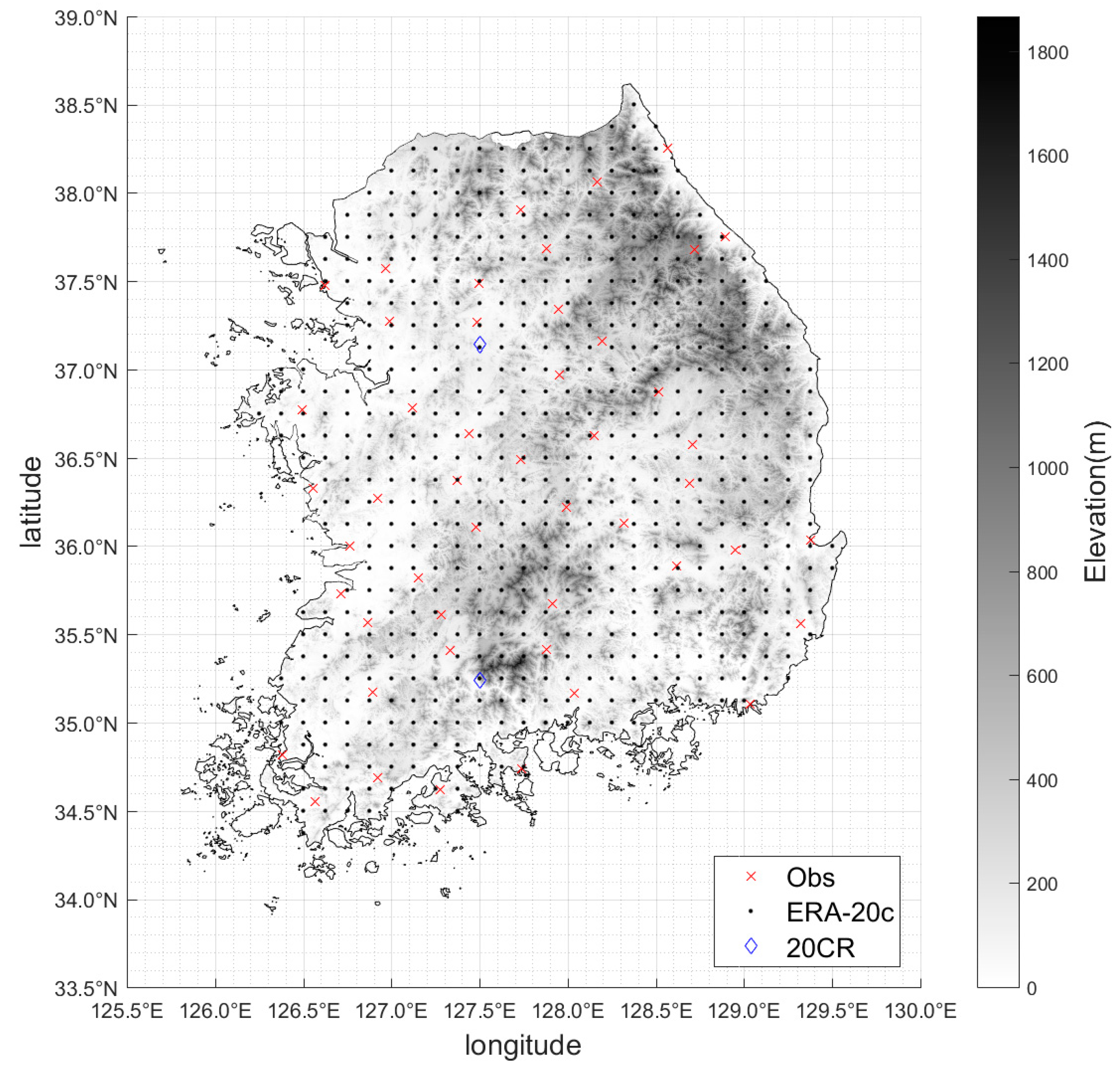





| Station No. | Name | Latitude (°N) | Longitude (°E) | Elevation (m. asl) |
|---|---|---|---|---|
| St. 1 | Sokcho | 38.2508 | 128.5644 | 19.5 |
| St. 2 | Daegwallyeong | 37.6769 | 128.7181 | 774.0 |
| St. 3 | Chuncheon | 37.9025 | 127.7356 | 79.1 |
| St. 4 | Gangneung | 37.7514 | 128.8908 | 27.4 |
| St. 5 | Seoul | 37.5714 | 126.9656 | 11.1 |
| St. 6 | Incheon | 37.4775 | 126.6247 | 69.6 |
| St. 7 | Wonju | 37.3375 | 127.9464 | 150.0 |
| St. 8 | Suwon | 37.2700 | 126.9875 | 38.3 |
| St. 9 | Chungju | 36.9700 | 127.9525 | 116.5 |
| St. 10 | Seosan | 36.7736 | 126.4958 | 30.3 |
| St. 11 | Cheongju | 36.6361 | 127.4428 | 58.6 |
| St. 12 | Daejeon | 36.3689 | 127.3742 | 70.3 |
| St. 13 | Chupungyeong | 36.2197 | 127.9944 | 246.1 |
| St. 14 | Andong | 36.5728 | 128.7072 | 141.5 |
| St. 15 | Pohang | 36.0325 | 129.3794 | 3.7 |
| St. 16 | Gunsan | 36.0019 | 126.7631 | 24.6 |
| St. 17 | Daegu | 35.8850 | 128.6189 | 65.5 |
| St. 18 | Jeonju | 35.8214 | 127.1547 | 54.8 |
| St. 19 | Ulsan | 35.5600 | 129.3200 | 36.0 |
| St. 20 | Gwangju | 35.1728 | 126.8914 | 73.8 |
| St. 21 | Busan | 35.1044 | 129.0319 | 71.0 |
| St. 22 | Mokpo | 34.8167 | 126.3811 | 39.4 |
| St. 23 | Yeosu | 34.7392 | 127.7406 | 66.0 |
| St. 24 | Jinju | 35.1636 | 128.0400 | 31.6 |
| St. 25 | Yangpyeong | 37.4886 | 127.4944 | 49.4 |
| St. 26 | Icheon | 37.2639 | 127.4842 | 79.4 |
| St. 27 | Inje | 38.0600 | 128.1669 | 201.6 |
| St. 28 | Hongcheon | 37.6833 | 127.8803 | 142.3 |
| St. 29 | Jecheon | 37.1592 | 128.1942 | 265.0 |
| St. 30 | Boeun | 36.4875 | 127.7339 | 176.4 |
| St. 31 | Cheonan | 36.7794 | 127.1211 | 24.0 |
| St. 32 | Boryeong | 36.3269 | 126.5572 | 16.9 |
| St. 33 | Buyeo | 36.2722 | 126.9206 | 12.7 |
| St. 34 | Geumsan | 36.1056 | 127.4817 | 171.7 |
| St. 35 | Buan | 35.7294 | 126.7164 | 13.4 |
| St. 36 | Imsil | 35.6122 | 127.2853 | 249.3 |
| St. 37 | Jeongeup | 35.5631 | 126.8658 | 46.0 |
| St. 38 | Namwon | 35.4053 | 127.3328 | 91.7 |
| St. 39 | Jangheung | 34.6886 | 126.9194 | 46.4 |
| St. 40 | Haenam | 34.5533 | 126.5689 | 14.4 |
| St. 41 | Goheung | 34.6181 | 127.2756 | 54.5 |
| St. 42 | Yeongju | 36.8717 | 128.5167 | 212.2 |
| St. 43 | Mungyeong | 36.6272 | 128.1486 | 172.0 |
| St. 44 | Uiseong | 36.3558 | 128.6883 | 83.2 |
| St. 45 | Gumi | 36.1306 | 128.3206 | 50.3 |
| St. 46 | Yeongcheon | 35.9772 | 128.9514 | 95.0 |
| St. 47 | Geochang | 35.6711 | 127.9108 | 222.4 |
| St. 48 | Sancheong | 35.4128 | 127.8789 | 0.8 |
| Method | ERA-20c | 20CR | ||
|---|---|---|---|---|
| RMSE (mm) | NSE | RMSE (mm) | NSE | |
| RAW | 79.81 | −0.579 | 95.40 | −1.256 |
| gevQM | 17.56 | 0.924 | 20.63 | 0.894 |
| gamQM | 22.34 | 0.876 | 22.46 | 0.875 |
| gumQM | 26.08 | 0.831 | 26.86 | 0.821 |
| Method | ERA-20c | 20CR | ||
|---|---|---|---|---|
| RMSE (mm) | NSE | RMSE (mm) | NSE | |
| gevQM | 14.30 | 0.933 | 16.69 | 0.905 |
| gamQM | 17.29 | 0.909 | 17.48 | 0.907 |
| gumQM | 20.31 | 0.871 | 21.09 | 0.864 |
| Method | ERA-20c | 20CR | ||
|---|---|---|---|---|
| z | b | z | b | |
| gevSQM | 5.51 | 0.50 | 3.43 | 0.38 |
| gevQDM | 4.21 | 0.40 | 2.67 | 0.34 |
| gamSQM | 5.56 | 0.55 | 3.53 | 0.45 |
| gamQDM | 4.06 | 0.41 | 2.71 | 0.37 |
| gumSQM | 5.50 | 0.52 | 3.59 | 0.42 |
| gumQDM | 4.30 | 0.40 | 2.91 | 0.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-I.; Han, D.; Lee, T. Reanalysis Product-Based Nonstationary Frequency Analysis for Estimating Extreme Design Rainfall. Atmosphere 2021, 12, 191. https://doi.org/10.3390/atmos12020191
Kim D-I, Han D, Lee T. Reanalysis Product-Based Nonstationary Frequency Analysis for Estimating Extreme Design Rainfall. Atmosphere. 2021; 12(2):191. https://doi.org/10.3390/atmos12020191
Chicago/Turabian StyleKim, Dong-IK, Dawei Han, and Taesam Lee. 2021. "Reanalysis Product-Based Nonstationary Frequency Analysis for Estimating Extreme Design Rainfall" Atmosphere 12, no. 2: 191. https://doi.org/10.3390/atmos12020191
APA StyleKim, D.-I., Han, D., & Lee, T. (2021). Reanalysis Product-Based Nonstationary Frequency Analysis for Estimating Extreme Design Rainfall. Atmosphere, 12(2), 191. https://doi.org/10.3390/atmos12020191







