The On-Line Integrated Mesoscale Chemistry Model BOLCHEM
Abstract
1. Introduction
2. Model Description
2.1. Boundary Layer and Vertical Diffusion
2.2. Convection and Precipitation
2.3. Gas Chemistry
2.4. Aerosol Dynamics
2.5. Radiation
2.6. Surface Fluxes
2.6.1. Anthropogenic Emissions
2.6.2. Soil and Vegetation Model: Moisture and Heat
2.6.3. Biogenic Gas Emissions
2.6.4. Sea Salt
2.6.5. Forest Fire Emissions
2.6.6. Dry Deposition
2.7. Numerical Core
2.8. Model Configuration and Previous Applications
3. Model Evaluation
3.1. Model Setup
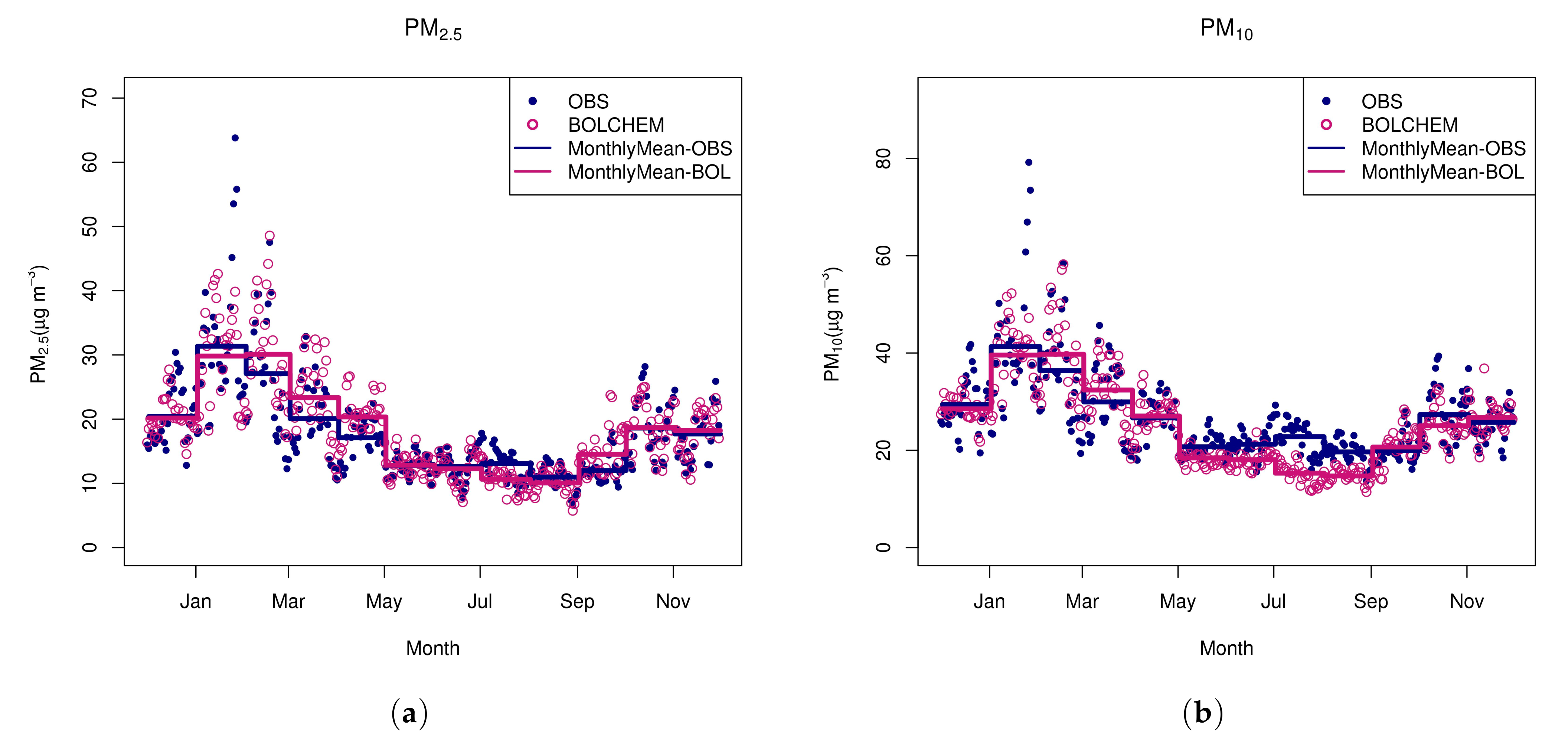
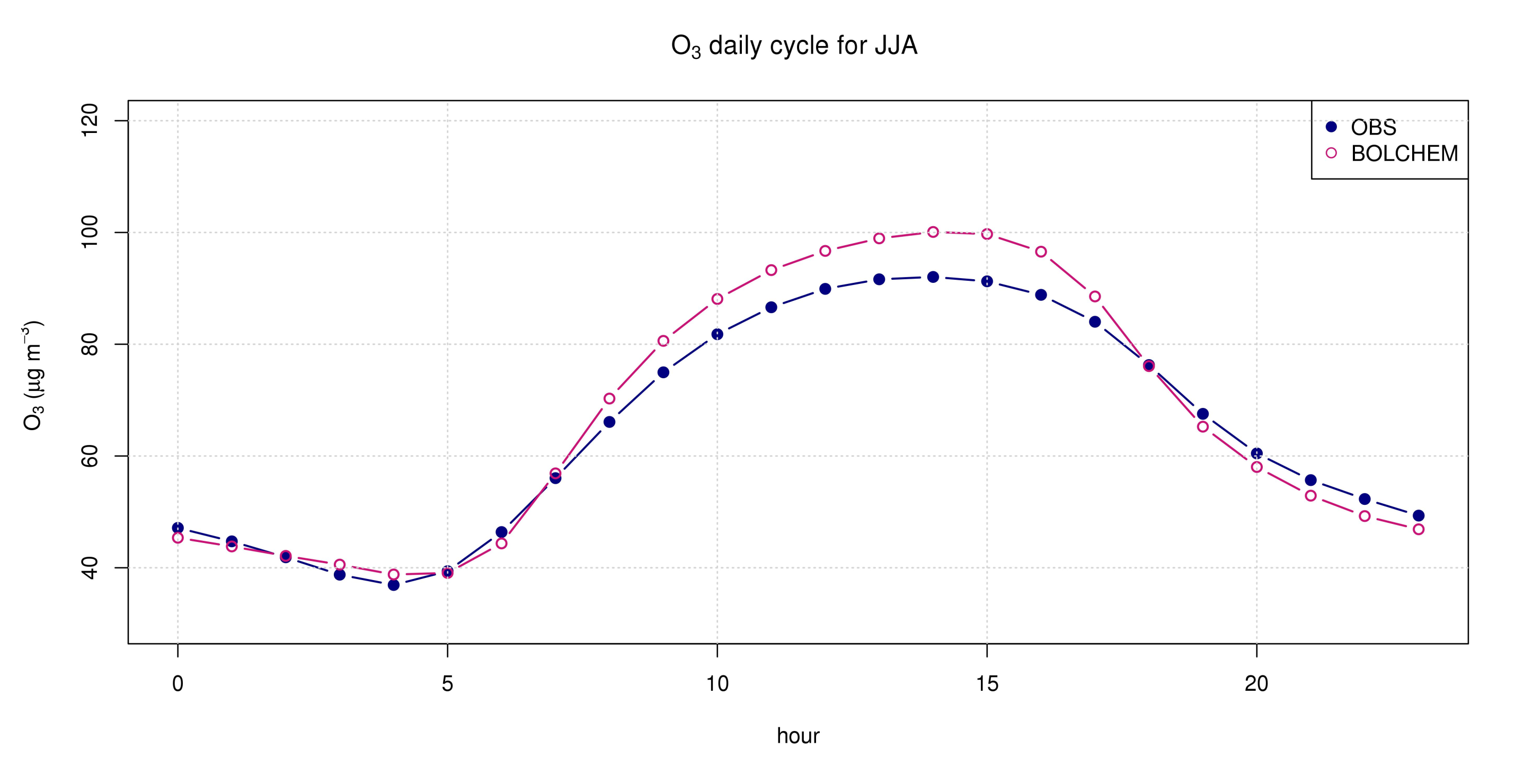
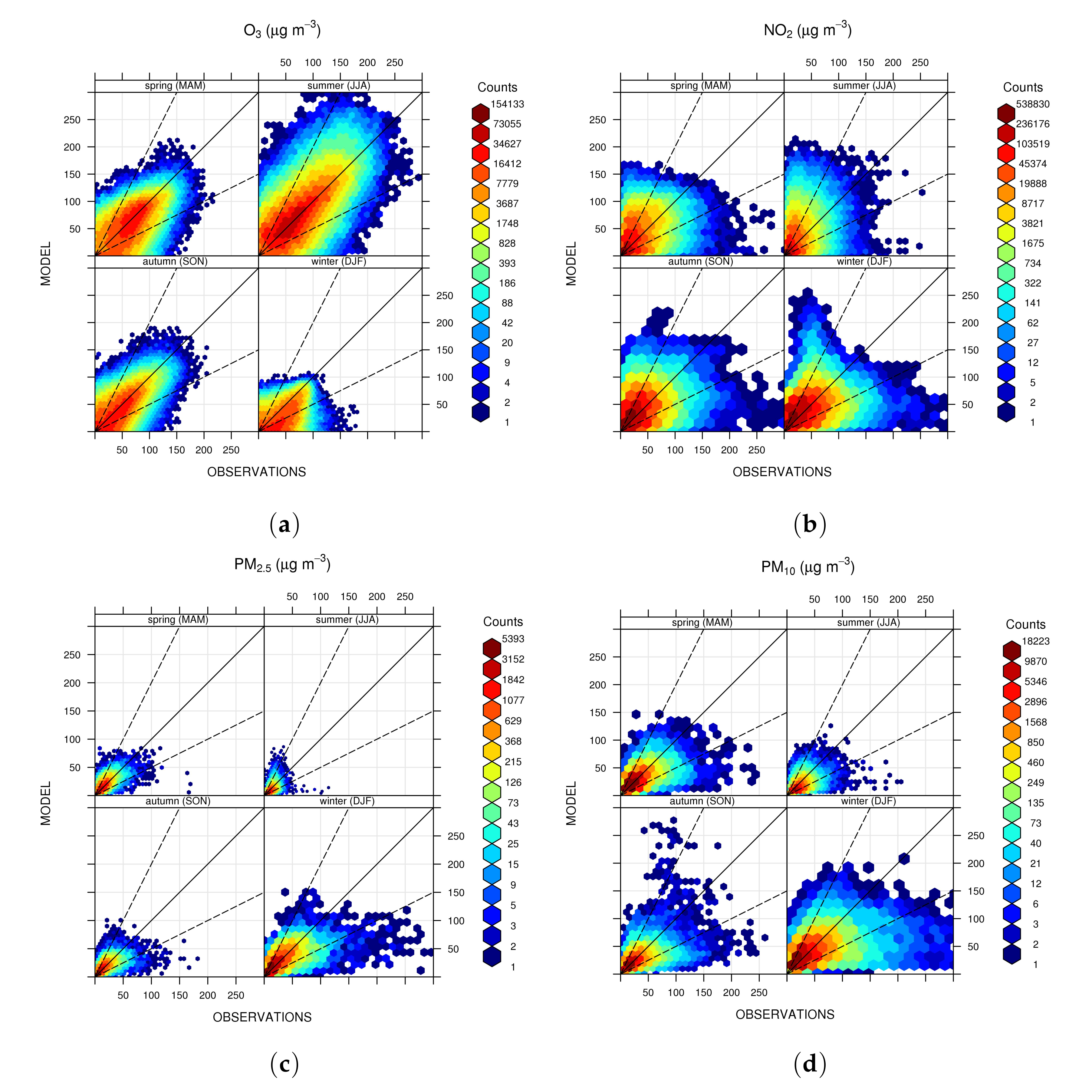
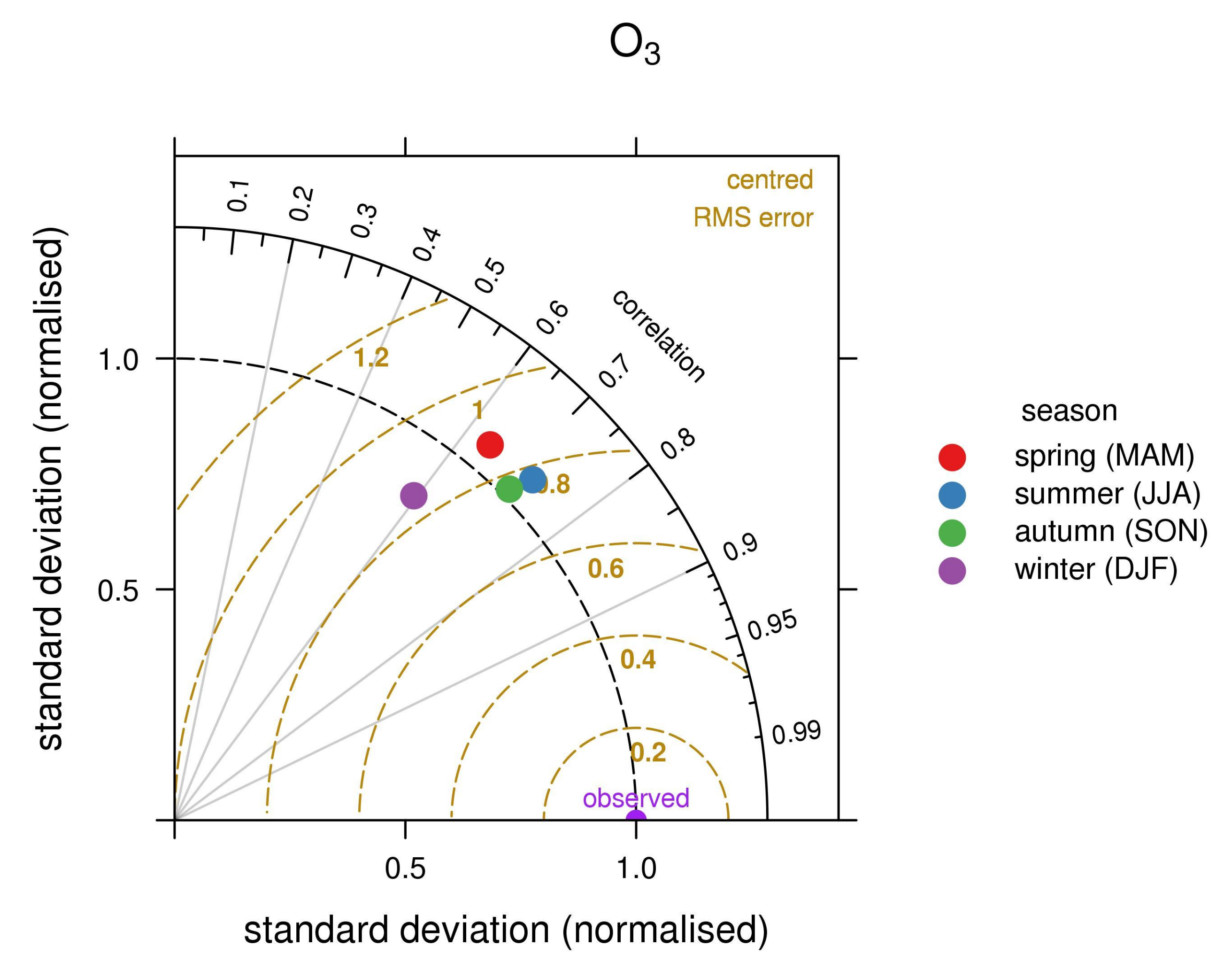
3.2. Model Results
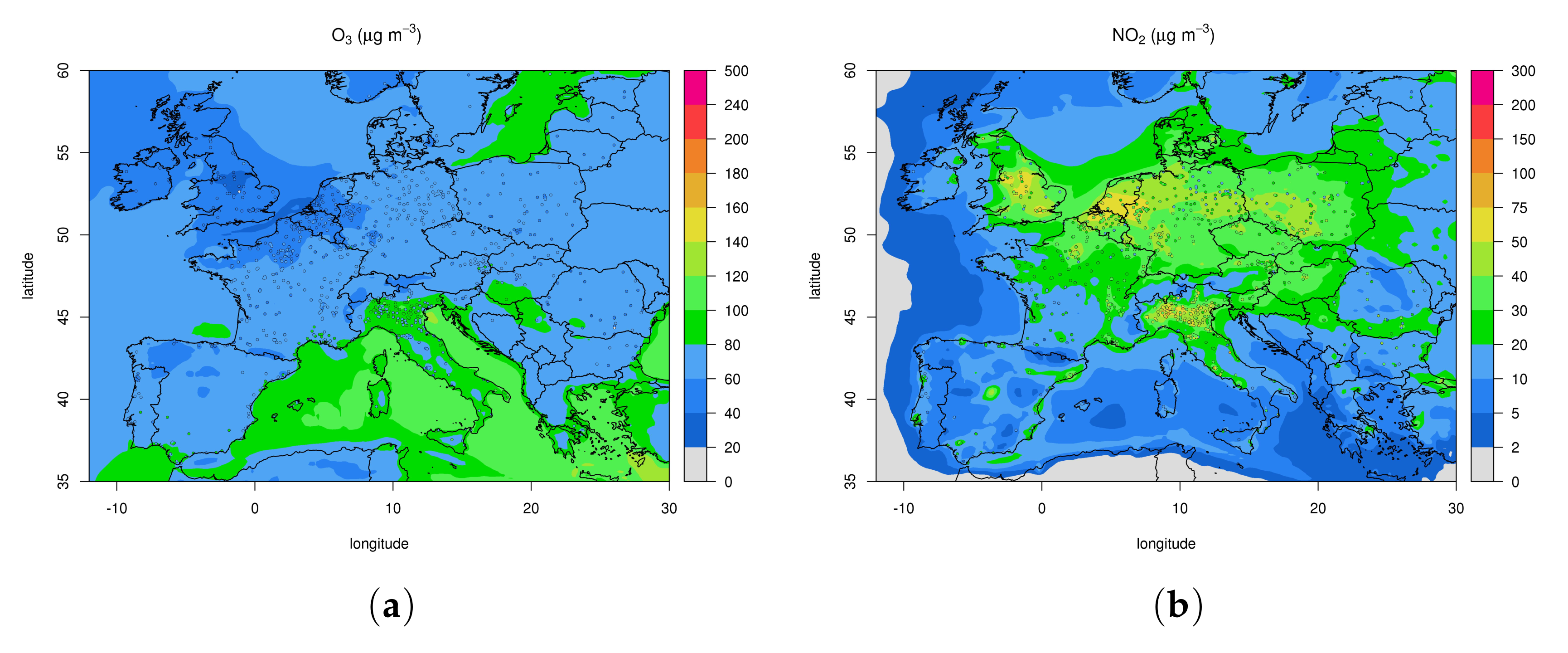
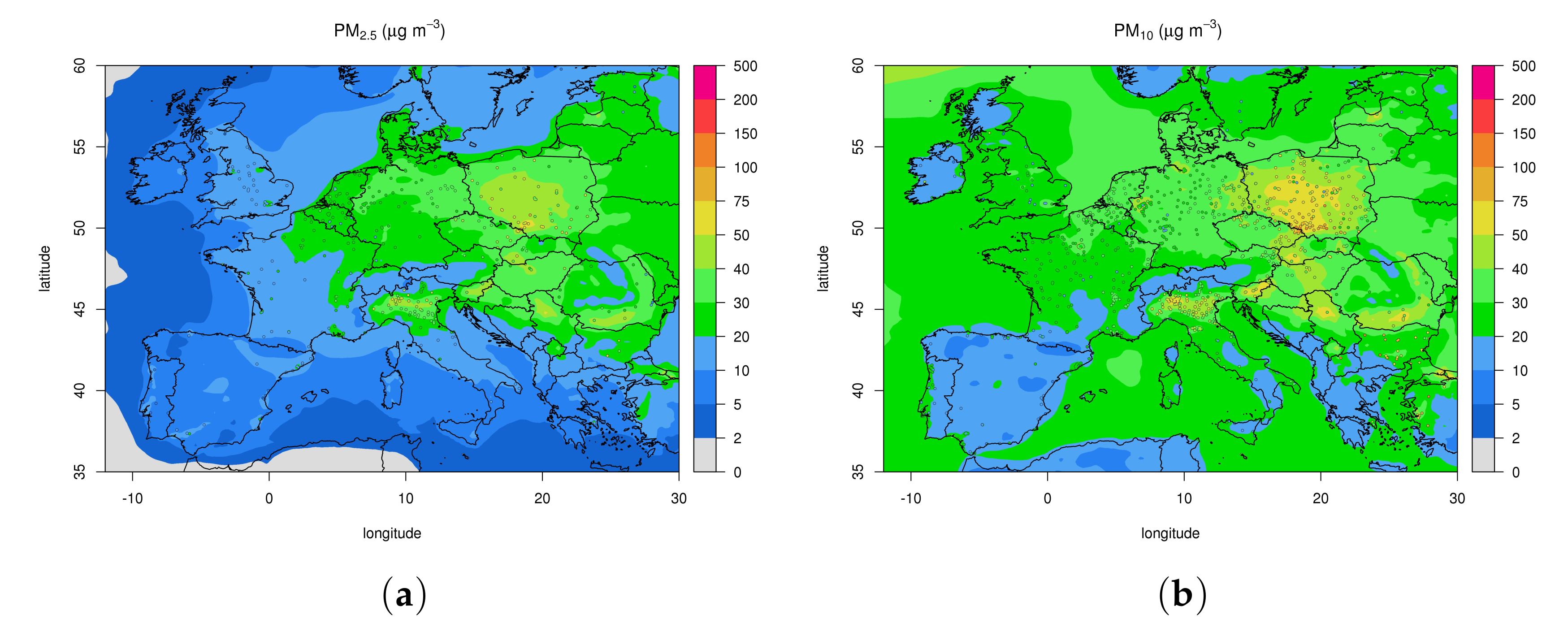
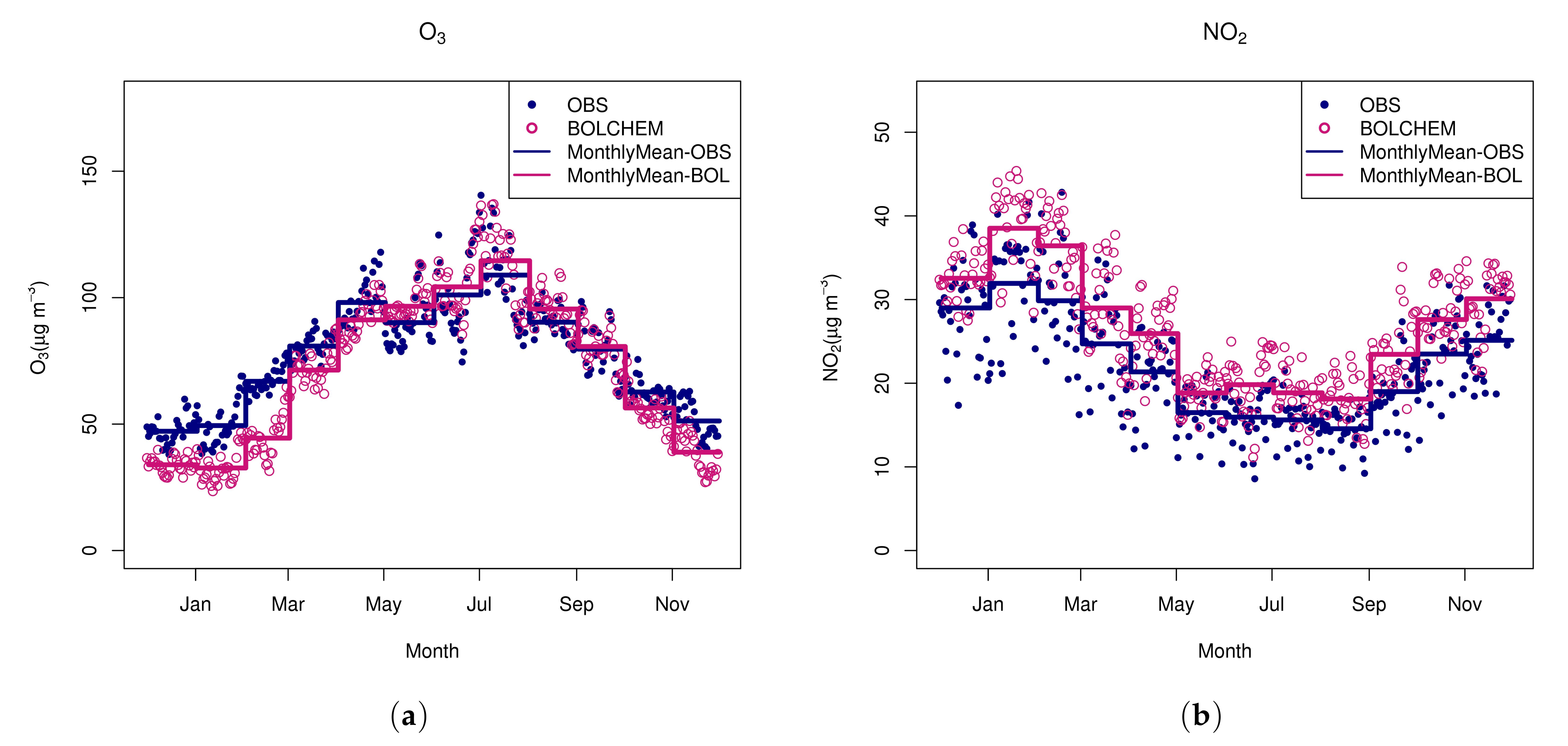
3.2.1. European Domain
3.2.2. Italian Domain
4. Conclusions
- estimation of emission potential and foliar biomass density referring to the vegetation dataset used in BOLCHEM, that is UMD Global Land Cover Classification (GLCC);
- implementation of a pre-processor system to allow the integration of the mineral dust flux simulated by the model DREAMABOL [83] model into BOLCHEM boundary condition;
- upgrade of the gas-phase chemical mechanism and aerosol module;
- a major challenge to complete BOLCHEM aerosol feedback description would be to study the effect of aerosol components that are currently not included in the radiation module, such as ammonium and nitrates.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Baklanov, A.; Schlünzen, K.; Suppan, P.; Baldasano, J.; Brunner, D.; Aksoyoglu, S.; Carmichael, G.; Douros, J.; Flemming, J.; Forkel, R.; et al. Online coupled regional meteorology chemistry models in Europe: Current status and prospects. Atmos. Chem. Phys. 2014, 14, 317–398. [Google Scholar] [CrossRef]
- Grell, G.; Peckham, S.; Schmitz, R.; McKeen, S.; Frost, G.; Skamarock, W.; Eder, B. Fully coupled “online” chemistry within the WRF model. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Vogel, B.; Vogel, H.; Bäumer, D.; Bangert, M.; Lundgren, K.; Rinke, R.; Stanelle, T. The comprehensive model system COSMO-ART—Radiative impact of aerosol on the state of the atmosphere on the regional scale. Atmos. Chem. Phys. 2009, 9, 8661–8680. [Google Scholar] [CrossRef]
- Baklanov, A.; Korsholm, U.; Nuterman, R.; Mahura, A.; Nielsen, K.; Sass, B.; Rasmussen, A.; Zakey, A.; Kaas, E.; Kurganskiy, A.; et al. Enviro-HIRLAM online integrated meteorology-chemistry modelling system: Strategy, methodology, developments and applications (v7.2). Geosci. Model Dev. 2017, 10, 2971–2999. [Google Scholar] [CrossRef]
- Savage, N.H.; Agnew, P.; Davis, L.S.; Ordóñez, C.; Thorpe, R.; Johnson, C.E.; O’Connor, F.M.; Dalvi, M. Air quality modelling using the Met Office Unified Model (AQUM OS24-26): Model description and initial evaluation. Geosci. Model Dev. 2013, 6, 353–372. [Google Scholar] [CrossRef]
- Morgenstern, O.; Braesicke, P.; O’Connor, F.; Bushell, A.; Johnson, C.; Osprey, S.; Pyle, J. Evaluation of the new UKCA climate-composition model—Part 2: The Troposphere. Geosci. Model Dev. 2014, 7, 41–91. [Google Scholar]
- Baklanov, A.; Baldasano, J.; Bouchet, V.; Brunner, D.; Ekman, A.; Galmarini, S.; Carmichael, G.; Grell, G.; Flemming, J.; Forkel, R.; et al. Coupled Chemistry-Meteorology/Climate Modelling (CCMM): Status and Relevance for Numerical Weather Prediction, Atmospheric Pollution and Climate Research; GAW Report No. 226, WWRP 2016-1, WCRP Report No. 9/2016; World Meteorological Organization (WMO): Geneva, Switzerland, 2016. [Google Scholar]
- Im, U.; Bianconi, R.; Solazzo, E.; Kioutsioukis, I.; Badia, A.; Balzarini, A.; Baró, R.; Bellasio, R.; Brunner, D.; Chemel, C.; et al. Evaluation of operational on-line-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2, Part I: Ozone. Atmos. Environ. 2015, 115, 404–420. [Google Scholar] [CrossRef]
- Im, U.; Bianconi, R.; Solazzo, E.; Kioutsioukis, I.A.B.; Balzarini, A.; Baró, R.; Bellasio, R.; Brunner, D.; Chemel, C.; Curci, G.; et al. Evaluation of operational on-line-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2, Part II: Particulate Matter. Atmos. Environ. 2015, 115, 421–441. [Google Scholar] [CrossRef]
- Baklanov, A.; Fay, B.; Kaminski, J. Overview of Existing Integrated (Off-Line and On-Line) Mesoscale Systems in Europe; COST Action 728, Working Group 2, Deliverable 2.1 Report; COST: Brussels, Belgium, 2007. [Google Scholar]
- Hollingsworth, A.; Engelen, R.; Textor, C.; Benedetti, A.; Boucher, O.; Chevallier, F.; Dethof, A.; Elbern, H.; Eskes, H.; Flemming, J.; et al. Toward a monitoring and forecasting system for atmospheric composition: The GEMS Project. Bull. Am. Meteorol. Soc. 2008, 89, 1147–1164. [Google Scholar] [CrossRef]
- Huijnen, V.H.J.; Eskes, H.J.; Poupkou, A.; Elbern, H.; Boersma, K.; Foret, G.M.; Sofiev, M.; Valdebenito, A.; Flemming, J.; Stein, O.; et al. Comparison of OMI NO2 tropospheric columns with an ensemble of global and European regional air quality models. Atmos. Chem. Phys. 2010, 10, 3273–3296. [Google Scholar] [CrossRef]
- Zyryanov, D.; Foret, G.; Eremenko, M.; Beekmann, M.; Cammas, J.; D’Isidoro, M.; Elbern, H.; Flemming, J.; Friese, E.; Kioutsioutkis, I.; et al. 3-D evaluation of tropospheric ozone simulations by an ensemble of regional Chemistry Transport Model. Atmos. Chem. Phys. 2012, 12, 3219–3240. [Google Scholar] [CrossRef]
- Mircea, M.; D’Isidoro, M.; Maurizi, A.; Vitali, L.; Monforti, F.; Zanini, G.; Tampieri, F. A comprehensive performance evaluation of the air quality model BOLCHEM to reproduce the ozone concentrations over Italy. Atmos. Environ. 2008, 42, 1169–1185. [Google Scholar] [CrossRef]
- Colette, A.; Granier, C.; Hodnebrog, O.; Jakobs, H.; Maurizi, A.; Nyiri, A.; Bessagnet, B.; D’Angiola, A.; D’Isidoro, M.; Gauss, M.; et al. Air quality trends in Europe over the past decade: A first multi- model assessment. Atmos. Chem. Phys. 2011, 11, 11657–11678. [Google Scholar] [CrossRef]
- Colette, A.; Granier, C.; Hodnebrog, O.; Jakobs, H.; Maurizi, A.; Nyiri, A.; Rao, S.; Amann, M.; Bessagnet, B.; D’Angiola, A.; et al. Future air quality in Europe: A multi-model assessment of projected exposure to ozone. Atmos. Chem. Phys. 2012, 12, 10613–10630. [Google Scholar] [CrossRef]
- Maurizi, A.; Russo, F.; D’Isidoro, M.; Tampieri, F. Nudging technique for scale bridging in air quality/climate atmospheric composition modelling. Atmos. Chem. Phys. 2012, 12, 3677–3685. [Google Scholar] [CrossRef]
- Cesari, R.; D’Isidoro, M.; Maurizi, A.; Mircea, M.; Monti, F.; Pizzigalli, C. Modelling dispersion of smoke from wildfires in a Mediterranean area. Int. J. Environ. Pollut. 2014, 55, 219–229. [Google Scholar] [CrossRef]
- Buccolieri, R.; Cesari, R.; Dinoi, A.; Maurizi, A.; Tampieri, F.; Di Sabatino, S. Impact of ship emissions on local air quality in a Mediterranean city’s harbour after the European sulphur directive. Int. J. Environ. Pollut. 2016, 59, 30–42. [Google Scholar] [CrossRef]
- Cesari, R.; Buccolieri, R.; Maurizi, A.; Landi, T.; Di Sabatino, S. Influence of Ship Emissions on Ozone Concentration in a Mediterranean Area: A modelling approach. In Air Pollution Modeling and its Application XXV, Springer Proceedings in Complexity; Springer: Cham, Switzerland, 2018; pp. 317–321. [Google Scholar]
- Buzzi, A.; D’Isidoro, M.; Davolio, S. A case-study of an orographic cyclone south of the Alps during the MAP SOP. Q. J. R. Meteorol. Soc. 2003, 129, 1795–1818. [Google Scholar] [CrossRef]
- Carter, W.P. A detailed mechanism for the gas-phase atmospheric reactions of organic compounds. Atmos. Environ. Part A Gen. Top. 1990, 24, 481–518. [Google Scholar] [CrossRef]
- Binkowski, F.S.; Shankar, U. The regional particulate matter model: 1. Model description and preliminary results. J. Geophys. Res. Atmos. 1995, 100, 26191–26209. [Google Scholar] [CrossRef]
- Binkowski, F.S.; Roselle, S.J. Models-3 Community Multiscale Air Quality (CMAQ) model aerosol component 1. Model description. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Osnovnye zakonomernosti turbulentnogo pere- meshivanija v prizemnom sloe atmosfery (Basic Laws of Turbulent Mixing in the Atmo- sphere Near the Ground). Tr. Geofiz. Inst. SSSR 1954, 24, 163–187. [Google Scholar]
- Fleagle, R.; Businger, J. An Introduction to Atmospheric Physics, 2nd ed.; International Geophysics; Elsevier: Amsterdam, The Netherlands, 1980; Volume 25. [Google Scholar]
- Beljaars, A.; Holtslag, A. Flux parameterization over land surfaces for atmospheric models. J. Appl. Meteorol. 1991, 30, 327–341. [Google Scholar] [CrossRef]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Large, W.; Pond, S. Open Ocean Momentum Flux Measurements in Moderate to Strong Winds. J. Phys. Oceanogr. 1981, 11, 324–336. [Google Scholar] [CrossRef]
- Cuxart, J.; Holtslag, A.; Beare, R.; Bazile, E.; Beljaars, A.; Cheng, A.; Conangla, L.; Ek, M.; Freedman, F.; Hamdi, R.; et al. Single-column model intercomparison for a stably stratified atmospheric boundary layer. Bound. Layer Meteorol. 2006, 118, 273–303. [Google Scholar] [CrossRef]
- Zampieri, M.; Malguzzi, P.; Buzzi, A. Sensitivity of quantitative precipitation forecasts to boundary layer parameterization: A flash flood case study in the Western Mediterranean. Nat. Hazards Earth Syst. Sci. 2005, 5, 603–612. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of Orography-Induced Turbulence in a Mesobeta-Scale Model. Mon. Weather Rev. 1989, 117, 1872–1890. [Google Scholar] [CrossRef]
- Blackadar, A. The vertical distribution of wind and turbulence exchange in a neutral atmosphere. J. Geophys. Res. 1962, 62, 3095–3102. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. Convective parameterization for mesoscale models: The Kain-Fritsch Scheme. In The Representation of Cumulus Convection in Numerical Models; Springer: Cham, Switzerland, 1993; pp. 165–170. [Google Scholar]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Wang, W.; Seaman, N.L. A comparison study of convective parameterization schemes in a mesoscale model. Mon. Weather Rev. 1997, 125, 252–278. [Google Scholar] [CrossRef]
- Ferretti, R.; Low-Nam, S.; Rotunno, R. Numerical simulations of the Piedmont flood of 4–6 November 1994. Tellus A Dyn. Meteorol. Oceanogr. 2000, 52, 162–180. [Google Scholar] [CrossRef]
- Simpson, D.; Benedictow, A.; Berge, H.; Bergström, R.; Emberson, L.D.; Fagerli, H.; Flechard, C.R.; Hayman, G.D.; Gauss, M.; Jonson, J.E.; et al. The EMEP MSC-W chemical transport model–technical description. Atmos. Chem. Phys. 2012, 12, 7825–7865. [Google Scholar] [CrossRef]
- Kumar, N.; Lurmann, F.; Carter, W. Development of the Flexible Chemical Mechanism Version of the Urban Airshed Model; Tech. Rep. STI-94470-1508-FR; UC Riverside: Riverside, CA, USA, 1995; pp. 1777–1789. [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; Wiley Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Sillman, S. The relation between ozone, NOx and hydrocarbons in urban and polluted rural environment. Atmos. Environ. 1999, 33, 1821–1845. [Google Scholar] [CrossRef]
- Carter, W.P. Development of a database for chemical mechanism assignments for volatile organic emissions. J. Air Waste Manag. Assoc. 2015, 65, 1171–1184. [Google Scholar] [CrossRef]
- Silibello, C.; Calori, G.; Brusasca, G.; Giudici, A.; Angelino, E.; Fossati, G.; Peroni, E.; Buganza, E. Modelling of PM10 concentrations over Milano urban area using two aerosol modules. Environ. Model. Softw. 2008, 23, 333–343. [Google Scholar] [CrossRef]
- Nenes, A.; Pandis, S.N.; Pilinis, C. ISORROPIA: A new thermodynamic equilibrium model for multiphase multicomponent inorganic aerosols. Aquat. Geochem. 1998, 4, 123–152. [Google Scholar] [CrossRef]
- Schell, B.; Ackermann, I.J.; Hass, H.; Binkowski, F.S.; Ebel, A. Modeling the formation of secondary organic aerosol within a comprehensive air quality model system. J. Geophys. Res. Atmos. 2001, 106, 28275–28293. [Google Scholar] [CrossRef]
- Whitby, K.T. The physical characteristics of sulfur aerosols. In Sulfur in the Atmosphere; Elsevier: Amsterdam, The Netherlands, 1978; pp. 135–159. [Google Scholar]
- Pankow, J.F. An absorption model of gas/particle partitioning of organic compounds in the atmosphere. Atmos. Environ. 1994, 28, 185–188. [Google Scholar] [CrossRef]
- Odum, J.R.; Hoffmann, T.; Bowman, F.; Collins, D.; Flagan, R.C.; Seinfeld, J.H. Gas/particle partitioning and secondary organic aerosol yields. Environ. Sci. Technol. 1996, 30, 2580–2585. [Google Scholar] [CrossRef]
- Ritter, B.; Geleyn, J. A Comprehensive Radiation Scheme for Numerical Weather Prediction Models with Potential Applications in Climate Simulations. Mon. Weather Rev. 1992, 120, 303–325. [Google Scholar] [CrossRef]
- Morcrette, J. Radiation and cloud radiative properties in the European Centre for Medium Range Weather Forecasts forecasting system. J. Geophys. Res. 1991, 96, 9121–9132. [Google Scholar] [CrossRef]
- Morcrette, J.; Barker, H.; Cole, J.; Iacono, M.; Pincus, R. Impact of a new radiation package, McRad, in the ECMWF Integrated Forecasting System. Mon. Weather Rev. 2008, 136, 4773–4798. [Google Scholar] [CrossRef]
- Mlawer, E.; Taubman, S.; Brown, P.; Iacono, M.; Clough, S. Radiative Transfer for Inhomogeneous Atmospheres: RRTM, a Validated Correlated-k Model for the Longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Tegen, I.; Hollrig, P.; Chin, M.; Fung, I.; Jacob, D.; Penner, J. Contribution of different aerosol species to the global aerosol extinction optical thickness: Estimates from model results. J. Geophys. Res. 1997, 102, 23895–23915. [Google Scholar] [CrossRef]
- Madronich, S.; Flocke, S. The Role of Solar Radiation in Atmospheric Chemistry. In Environmental Photochemistry. The Handbook of Environmental Chemistry (Reactions and Processes); Springer: Berlin/Heidelberg, Germany, 1999; Volume 2/2L. [Google Scholar]
- Crawford, J.; Shetter, R.; Lefer, B.; Cantrell, C.; Junkermann, W.; Madronich, S.; Calvert, J. Cloud impacts on UV spectral actinic flux observed during the International Photolysis Frequency Measurement and Model Intercomparison (IPMMI). J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Kuenen, J.; Visschedijk, A.; Jozwicka, M.; Denier Van Der Gon, H. TNO-MACC_II emission inventory; a multi-year (2003–2009) consistent high-resolution European emission inventory for air quality modelling. Atmos. Chem. Phys. 2014, 14, 10963–10976. [Google Scholar] [CrossRef]
- Monforti, F.A.P. Thoscane: A tool to detail corinair emission inventories. Environ. Model. Softw. 2005, 20, 505–508. [Google Scholar] [CrossRef]
- Hansen, M.C.; Defries, R.S.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. Int. J. Remote Sens. 2000, 21, 1331–1364. [Google Scholar] [CrossRef]
- Guenther, A.; Hewitt, C.; Erickson, D.; Fall, R.; Geron, C.; Graedel, T.; Harley, P.; Klinger, L.; Lerdau, M.; McKay, W.; et al. A global model of natural volatile organic compound emissions. J. Geophys. Res. Atmos. 1995, 100, 8873–8892. [Google Scholar] [CrossRef]
- Simpson, D.; Wilfried, W.; Börjesson, G.; Cinderby, S.; Ferreiro, A.; Guenther, A.; Nicholas Hewitt, C.; Janson, R.; Khalil, M.A.K.; Owen, S.; et al. Inventorying emissions from nature in Europe. J. Geophys. Res. Atmos. 1999, 104, 8113–8152. [Google Scholar] [CrossRef]
- Symeonidis, P.; Poupkou, A.; Gkantou, A.; Melas, D.; Yay, O.D.; Pouspourika, E.; Balis, D. Development of a computational system for estimating biogenic NMVOCs emissions based on GIS technology. Atmos. Environ. 2008, 42, 1777–1789. [Google Scholar] [CrossRef]
- Guenther, A.B.; Zimmerman, P.R.; Harley, P.C.; Monson, R.K.; Fall, R. Isoprene and Monoterpene Emission Rate Variability: Model Evaluations and Sensitivity Analyses. J. Geophys. Res. Atmos. 1993, 98, 12609–12617. [Google Scholar] [CrossRef]
- Zhang, K.M.; Knipping, E.M.; Wexler, A.; Bhave, P.V.; Tonnesen, G.S. Size distribution of sea-salt emissions as a function of relative humidity. Atmos. Environ. 2005, 39, 3373–3379. [Google Scholar] [CrossRef]
- Tang, I.N.; Tridico, A.C.; Fung, K.H. Thermodynamic and optical properties of sea salt aerosols. J. Geophys. Res. 1997, 102, 269–275. [Google Scholar] [CrossRef]
- Monahan, E.; Spiel, D.; Davidson, K. A model of marine aerosol generation via whitecaps and wave disruption. In Oceanic Whitecaps; Springer: Cham, Switzerland, 1986; pp. 167–174. [Google Scholar]
- Gong, S.L. A parameterization of sea-salt aerosol source function for sub- and super-micron particles. Glob. Biogeochem. Cycles 2003, 17, 1097. [Google Scholar] [CrossRef]
- Pizzigalli, C. Modelling wildfires in the Mediterranean area during summer 2007. Nuovo Cimento 2012, 35C, 137–146. [Google Scholar]
- Seiler, W.; Crutzen, P.J. Estimates of gross and net fluxes of carbon between the biosphere and the atmosphere from biomas burning. Clim. Chang. 1980, 2, 207–247. [Google Scholar] [CrossRef]
- Wesely, M.L. Parameterisation of surface resistances to gaseous dry deposition in regional-scale numerical models. Atmos. Environ. 1989, 23, 1293–1304. [Google Scholar] [CrossRef]
- Anav, A.; Menut, L.; Khvorostyanov, D.; Viovy, N. A comparison of two canopy conductance parameterizations to quantify the interactions between surface ozone and vegetation over Europe. J. Geophys. Res. 2012, 117, G03027. [Google Scholar] [CrossRef]
- Emberson, L.D.; Ashmore, M.R.; Cambridge, H.M.; Tuovinen, J.P.; Simpson, D. Modelling stomatal flux across Europe. Environ. Pollut. 2000, 109, 403–413. [Google Scholar] [CrossRef]
- Lorenz, E. Energy and Numerical Weather Prediction. Tellus 1960, 12, 157–167. [Google Scholar] [CrossRef]
- Arakawa, A.; Lamb, V. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model. Methods Comput. Phys. Adv. Res. Appl. 1977, 17, 173–265. [Google Scholar]
- Leheman, R. On the choice of relaxation coefficients for Davies’ lateral boundary scheme for regional weather prediction models. Meteorol. Atmos. Phys. 1993, 52, 1–14. [Google Scholar] [CrossRef]
- Billet, S.; Toro, E.F. On WAF-type schemes for multidimensional hyperbolic conservation laws. J. Comput. Phys. 1997, 130, 1–24. [Google Scholar] [CrossRef]
- Godunov, S. A difference method for numerical calculation of discontinuous solutions of the equations of hydrodynamics. Math. Sb. (N. S.) 1993, 47, 271–306. [Google Scholar]
- Hubbard, M.; Nikiforakis, N. A three-dimensional, adaptive, Godunov-type model for global atmospheric flows. Mon. Weather Rev. 2003, 131, 1848–1864. [Google Scholar] [CrossRef]
- Davies, H.C. A lateral boundary formulation for multi-level prediction models. Q. J. R. Meteorol. Soc. 1976, 102, 405–418. [Google Scholar]
- Aidaoui, L.; Maurizi, A.; Azzi, A. Modelled NO2 tropospheric columns at different resolutions versus OMI satellite data: Analysis of a 1-year BOLCHEM simulation over Europe. Air Qual. Atmos. Health 2015, 8, 163–174. [Google Scholar] [CrossRef]
- Marécal, V.; Peuch, V.H.; Andersson, C.; Andersson, S.; Arteta, J.; Beekmann, M.; Benedictow, A.; Bergström, R.; Bessagnet, B.; Cansado, A.; et al. A regional air quality forecasting system over Europe: The MACC-II daily ensemble production. Geosci. Model Dev. 2015, 8, 2777–2813. [Google Scholar] [CrossRef]
- Poupkou, A.; Giannaros, T.; Markakis, K.; Kioutsioukis, I.; Curci, G.; Melas, D.; Zerefos, C. A model for European Biogenic Volatile Organic Compound emissions: Software development and first validation. Environ. Model. Softw. 2010, 25, 1845–1856. [Google Scholar] [CrossRef]
- Cesari, R.; Landi, T.; Maurizi, A. The coupled chemistry-meteorology model BOLCHEM: An application to air pollution in the Po Valley (Italy) hot spot. Int. J. Environ. Pollut. 2019, 65, 1–24. [Google Scholar] [CrossRef]
- Binietoglou, I.; Basart, S.; Alados-Arboledas, L.; Amiridis, V.; Argyrouli, A.; Baars, H.; Baldasano, J.; Balis, D.; Belegante, L.; Bravo-Aranda, J.; et al. A methodology for investigating dust model performance using synergistic EARLINET/AERONET dust concentration retrievals. Atmos. Meas. Tech. 2015, 8, 3577–3600. [Google Scholar] [CrossRef]

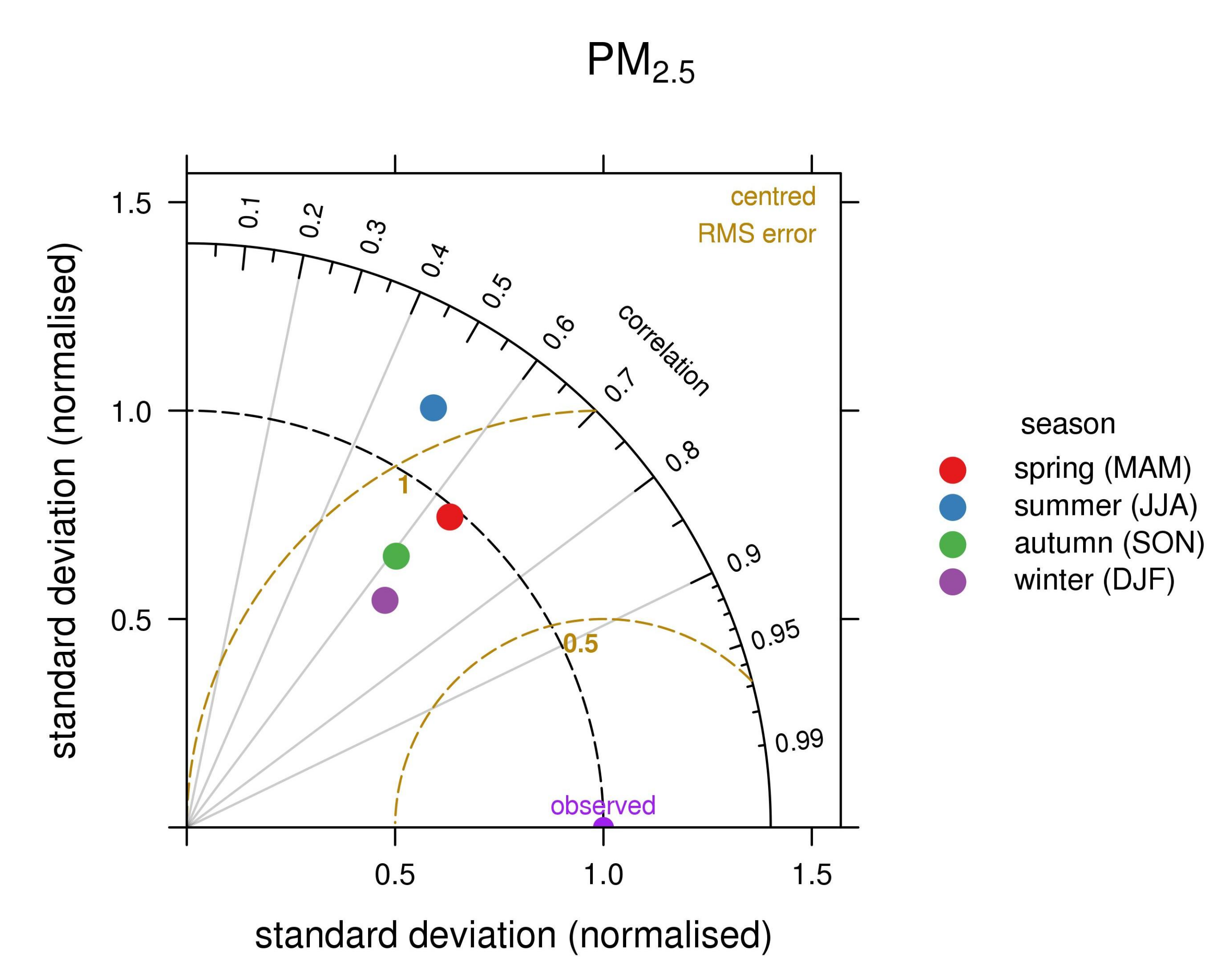
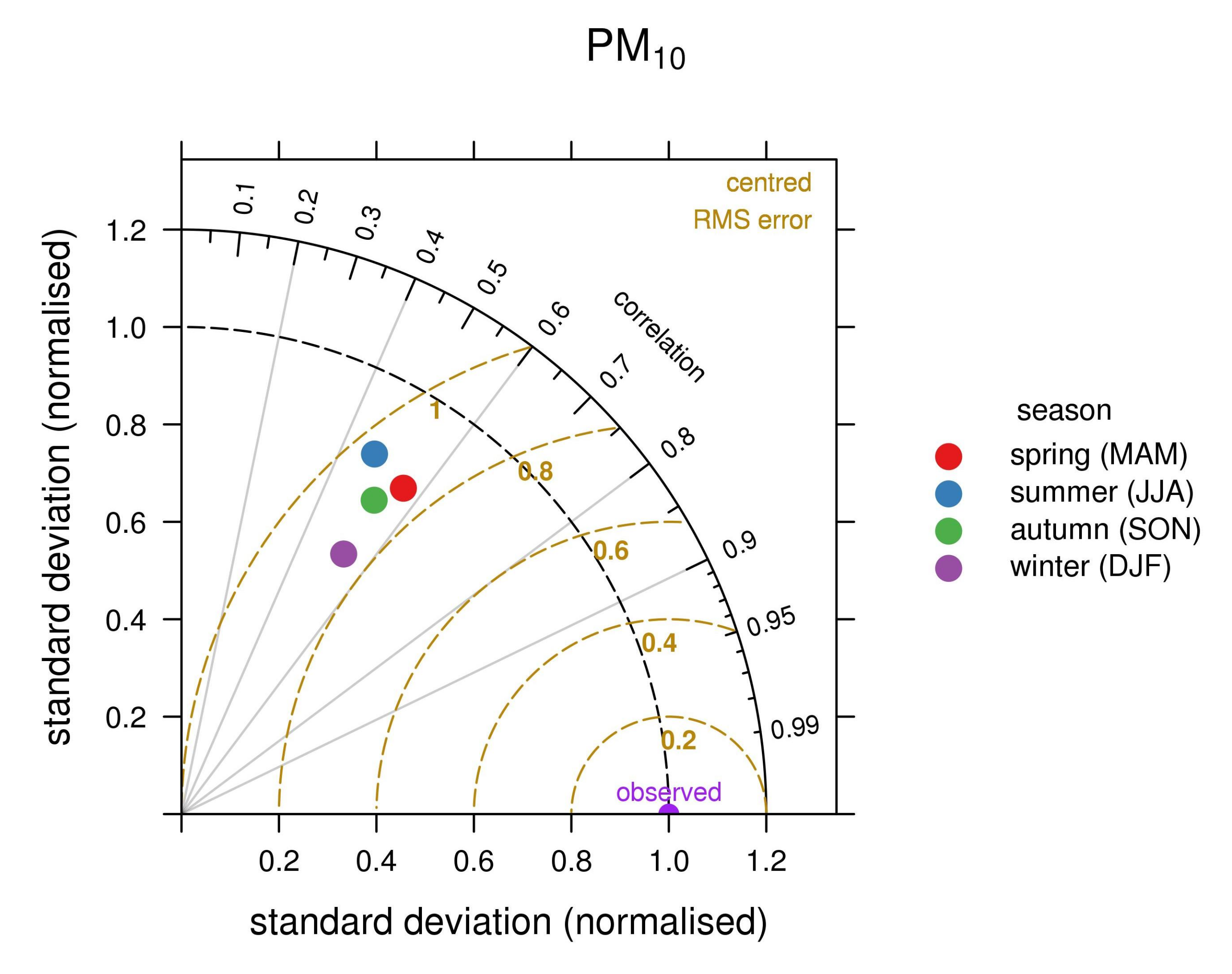
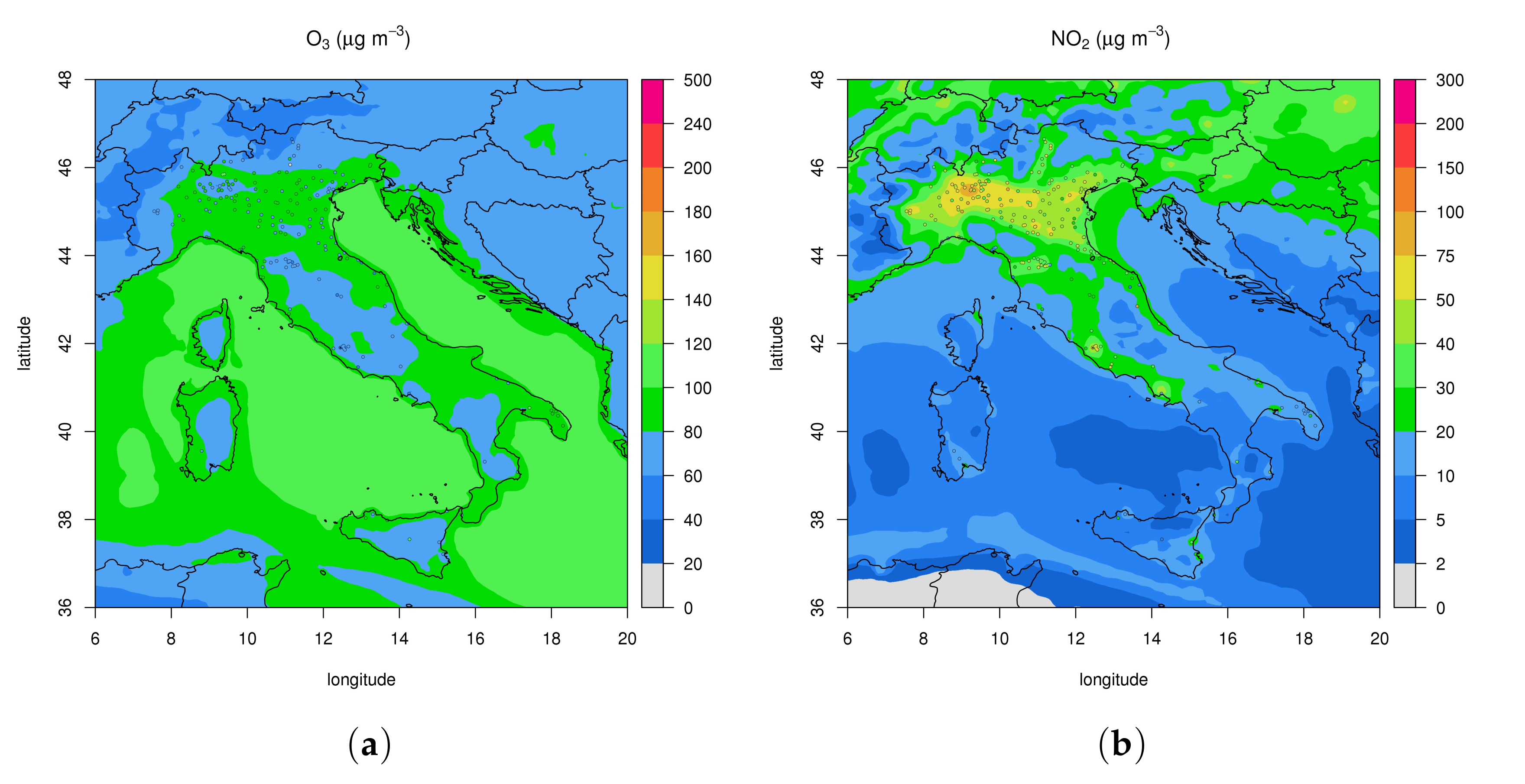
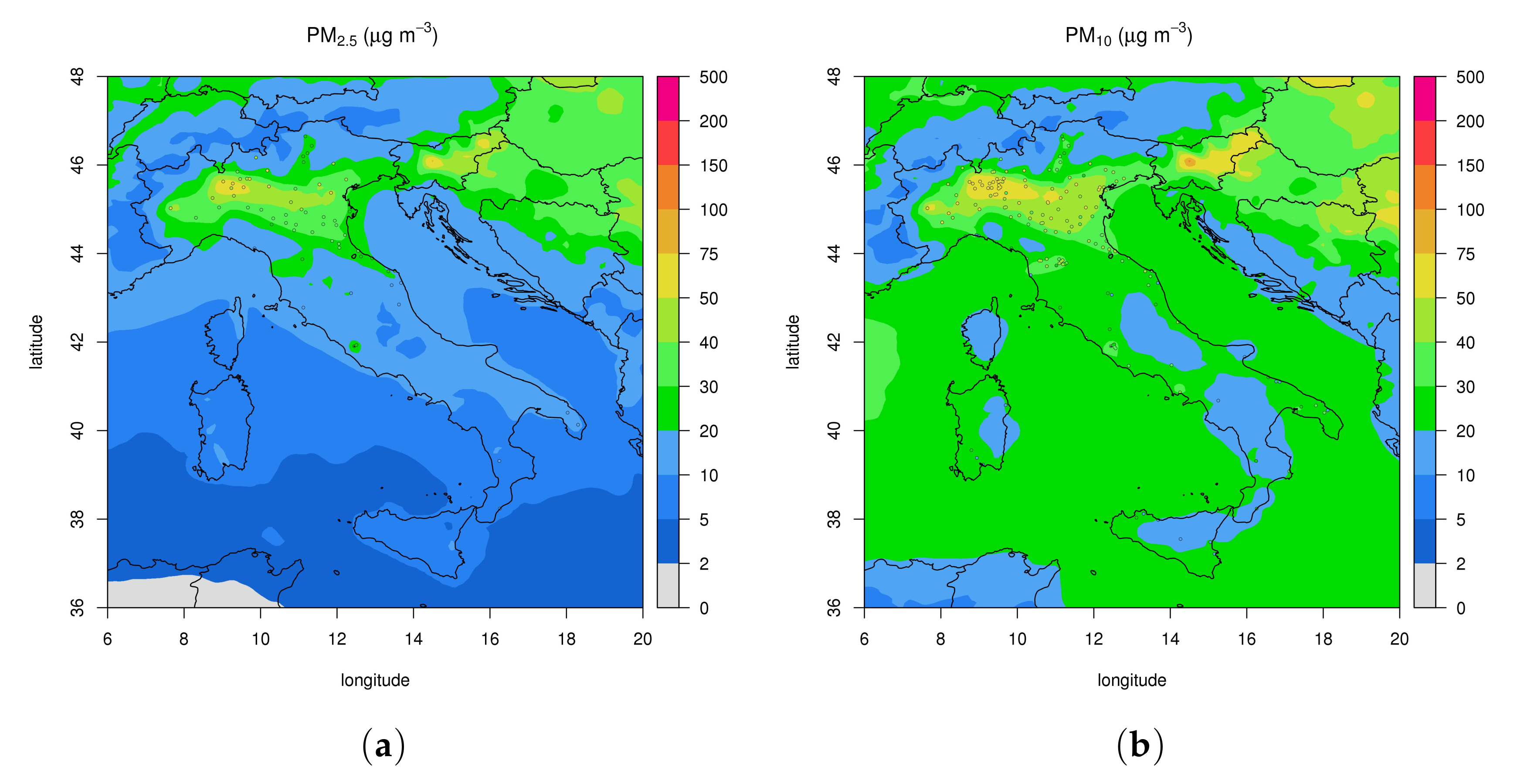
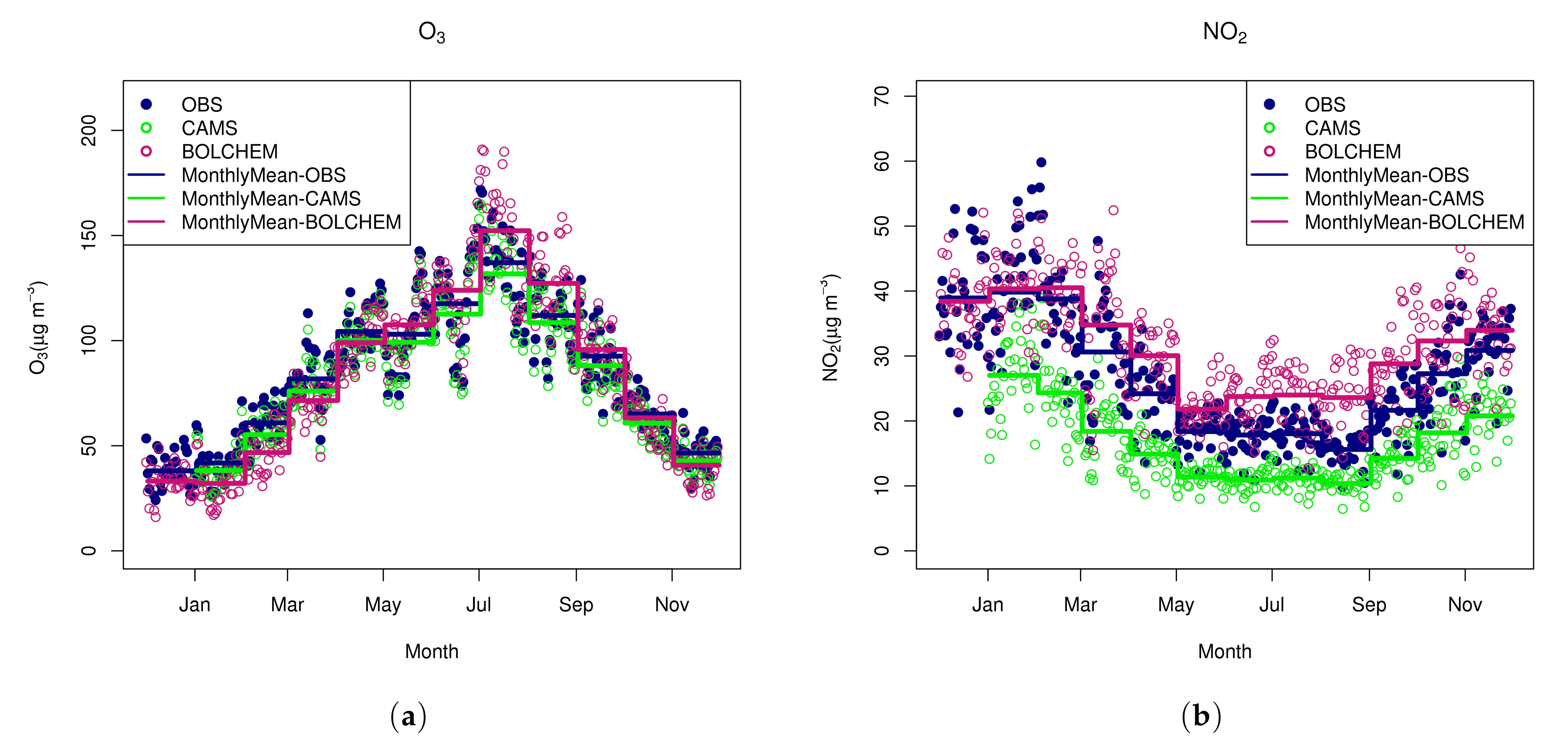
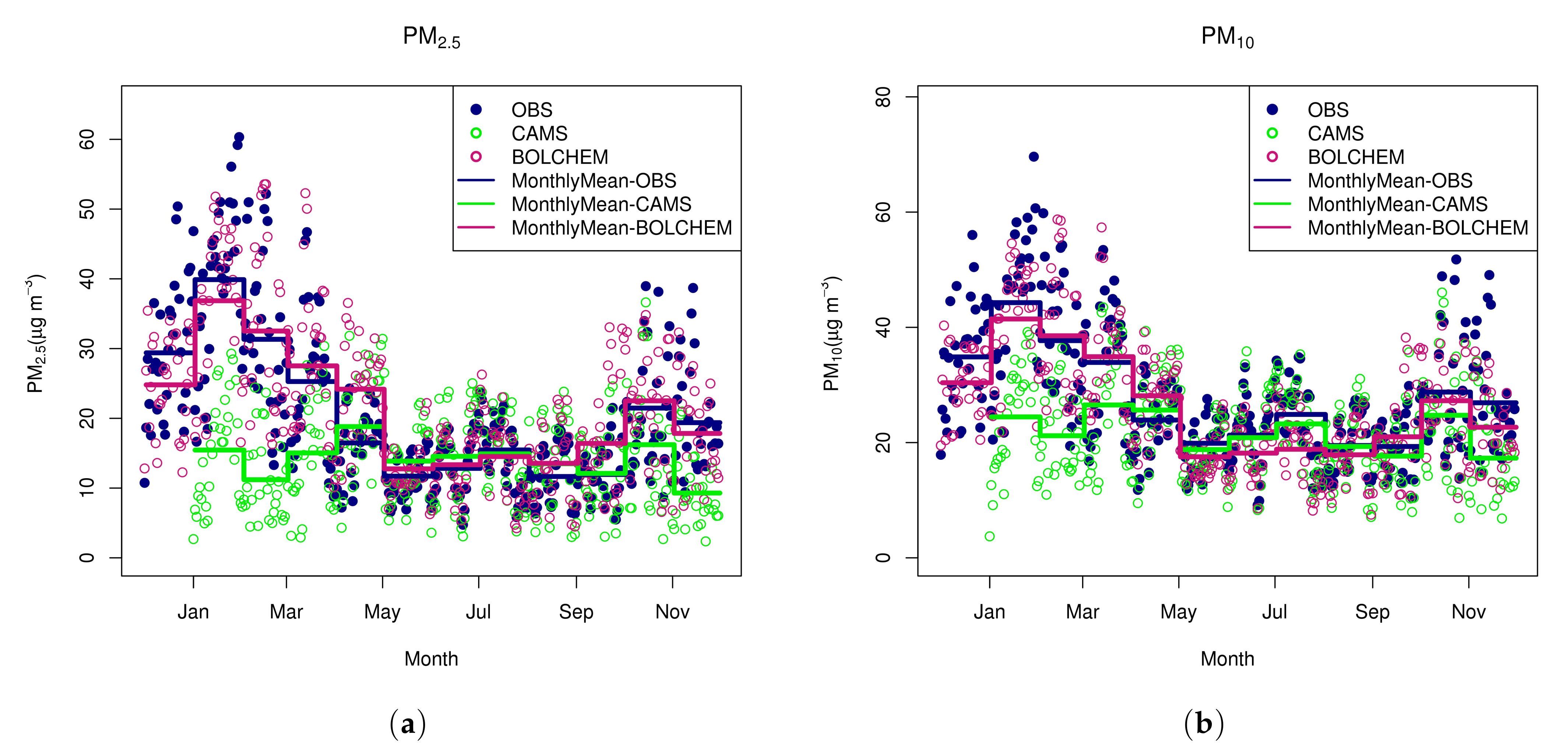
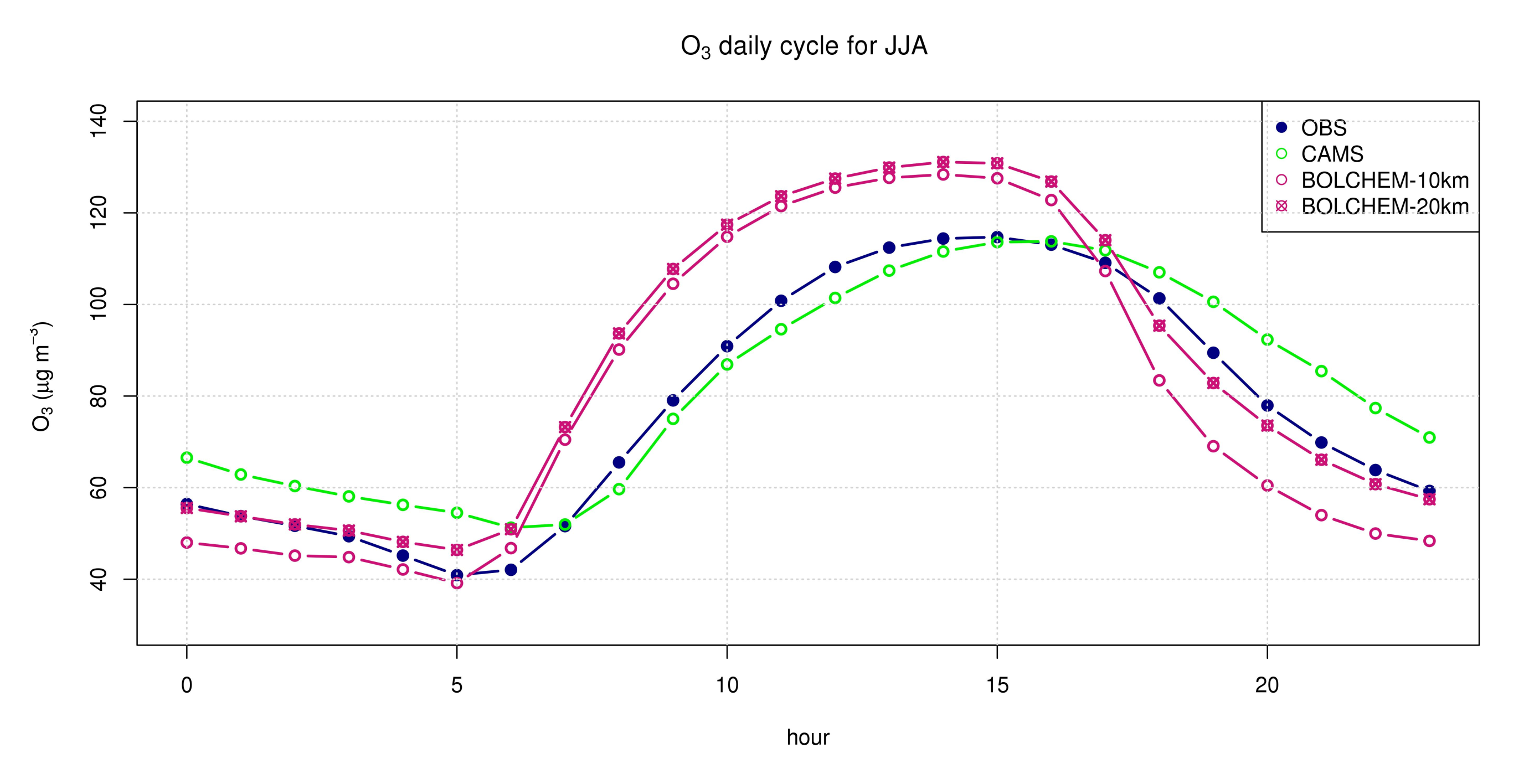

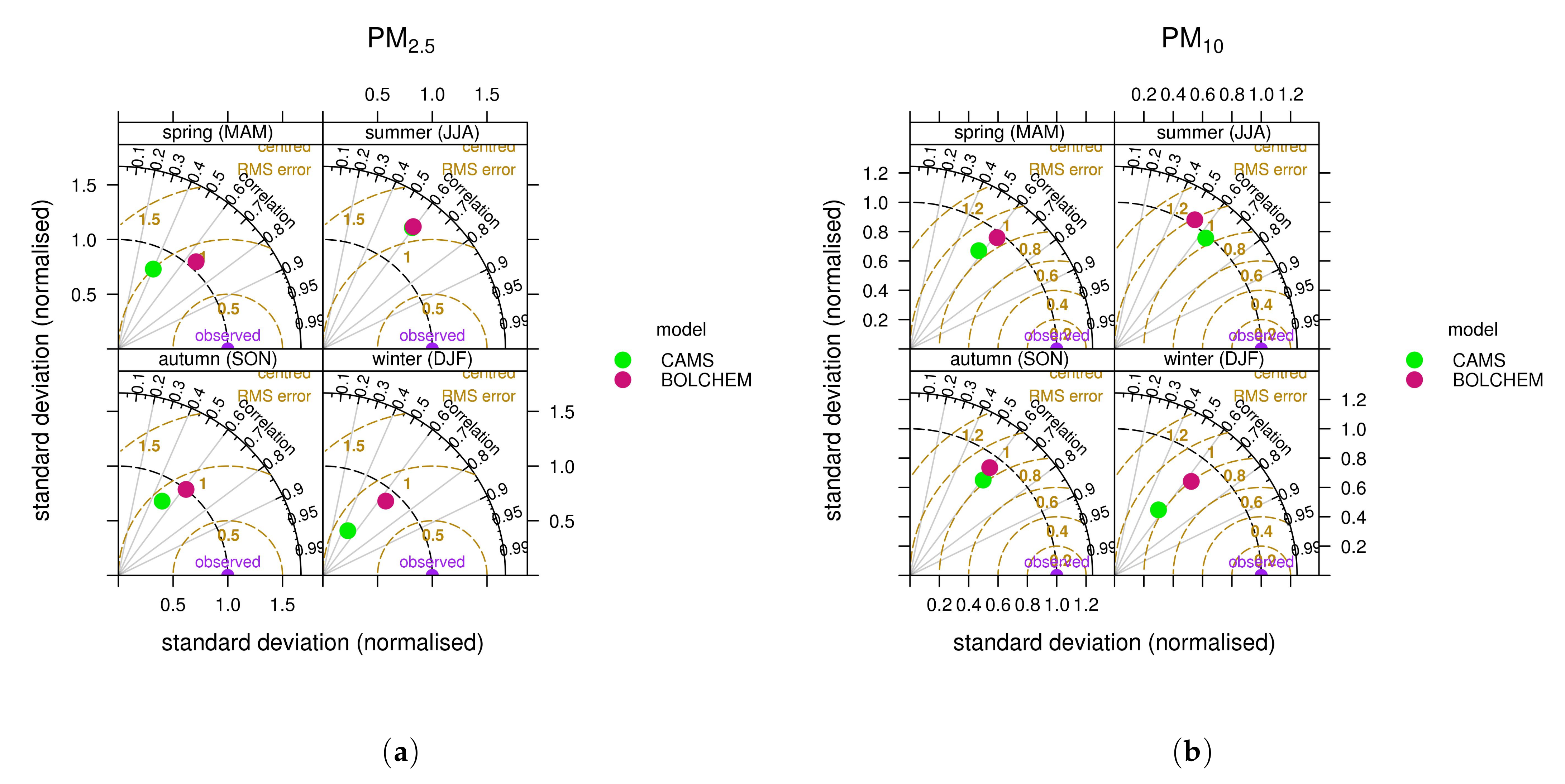
| Season | O3 | NO2 | PM2.5 | PM10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | RMSE | MB | R | RMSE | MB | R | RMSE | MB | R | RMSE | MB | |
| MAM | 0.64 | 25.13 | −5.38 | 0.50 | 21.01 | 3.67 | 0.65 | 9.42 | 2.15 | 0.56 | 13.72 | 0.18 |
| JJA | 0.72 | 26.36 | 2.15 | 0.44 | 19.53 | 3.49 | 0.51 | 7.20 | −1.24 | 0.47 | 12.05 | −5.22 |
| SON | 0.71 | 20.37 | −4.21 | 0.49 | 19.65 | 4.47 | 0.61 | 10.35 | 1.03 | 0.52 | 15.48 | −0.21 |
| DJF | 0.59 | 24.99 | −14.96 | 0.47 | 22.09 | 5.47 | 0.66 | 17.84 | 0.35 | 0.53 | 25.72 | 0.16 |
| Season | O3 BOLCHEM | O3 CAMS | NO2 BOLCHEM | NO2 CAMS | ||||||||
| R | RMSE | MB | R | RMSE | MB | R | RMSE | MB | R | RMSE | MB | |
| MAM | 0.62 | 30.14 | −6.44 | 0.84 | 18.20 | 3.61 | 0.42 | 26.26 | 4.43 | 0.56 | 19.33 | −9.59 |
| JJA | 0.67 | 34.82 | 2.36 | 0.85 | 20.97 | 4.48 | 0.35 | 26.55 | 6.50 | 0.48 | 13.89 | −6.40 |
| SON | 0.70 | 23.25 | −2.41 | 0.86 | 15.21 | 3.17 | 0.47 | 23.79 | 5.10 | 0.61 | 17.72 | −8.97 |
| DJF | 0.62 | 20.97 | −9.18 | 0.83 | 13.59 | 2.08 | 0.47 | 25.15 | 0.54 | 0.61 | 24.16 | −13.71 |
| Season | PM2.5 BOLCHEM | PM2.5 CAMS | PM10 BOLCHEM | PM10 CAMS | ||||||||
| R | RMSE | MB | R | RMSE | MB | R | RMSE | MB | R | RMSE | MB | |
| MAM | 0.66 | 11.31 | 3.60 | 0.40 | 12.75 | −1.78 | 0.61 | 12.97 | 0.92 | 0.57 | 13.05 | −2.27 |
| JJA | 0.59 | 7.49 | 0.48 | 0.59 | 7.49 | 1.00 | 0.53 | 10.58 | −3.60 | 0.63 | 8.52 | −0.73 |
| SON | 0.62 | 11.05 | 1.32 | 0.51 | 12.45 | −5.07 | 0.59 | 13.20 | −1.37 | 0.61 | 13.46 | −5.07 |
| DJF | 0.64 | 16.59 | −2.13 | 0.49 | 29.12 | −22.30 | 0.63 | 18.98 | −2.18 | 0.56 | 27.45 | −18.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cesari, R.; Landi, T.C.; D’Isidoro, M.; Mircea, M.; Russo, F.; Malguzzi, P.; Tampieri, F.; Maurizi, A. The On-Line Integrated Mesoscale Chemistry Model BOLCHEM. Atmosphere 2021, 12, 192. https://doi.org/10.3390/atmos12020192
Cesari R, Landi TC, D’Isidoro M, Mircea M, Russo F, Malguzzi P, Tampieri F, Maurizi A. The On-Line Integrated Mesoscale Chemistry Model BOLCHEM. Atmosphere. 2021; 12(2):192. https://doi.org/10.3390/atmos12020192
Chicago/Turabian StyleCesari, Rita, Tony Christian Landi, Massimo D’Isidoro, Mihaela Mircea, Felicita Russo, Piero Malguzzi, Francesco Tampieri, and Alberto Maurizi. 2021. "The On-Line Integrated Mesoscale Chemistry Model BOLCHEM" Atmosphere 12, no. 2: 192. https://doi.org/10.3390/atmos12020192
APA StyleCesari, R., Landi, T. C., D’Isidoro, M., Mircea, M., Russo, F., Malguzzi, P., Tampieri, F., & Maurizi, A. (2021). The On-Line Integrated Mesoscale Chemistry Model BOLCHEM. Atmosphere, 12(2), 192. https://doi.org/10.3390/atmos12020192








