Analyzing and Improving the Performance of a Particulate Matter Low Cost Air Quality Monitoring Device

Abstract

Air quality (AQ) in urban areas is deteriorating, thus having negative effects on people’s everyday lives. Official air quality monitoring stations provide the most reliable information, but do not always depict air pollution levels at scales reflecting human activities. They also have a high cost and therefore are limited in number. This issue can be addressed by deploying low cost AQ monitoring devices (LCAQMD), though their measurements are of far lower quality. In this paper we study the correlation of air pollution levels reported by such a device and by a reference station for particulate matter, ozone and nitrogen dioxide in Thessaloniki, Greece. On this basis, a corrective factor is modeled via seven machine learning algorithms in order to improve the quality of measurements for the LCAQMD against reference stations, thus leading to its on-field computational improvement. We show that our computational intelligence approach can improve the performance of such a device for PM10 under operational conditions.

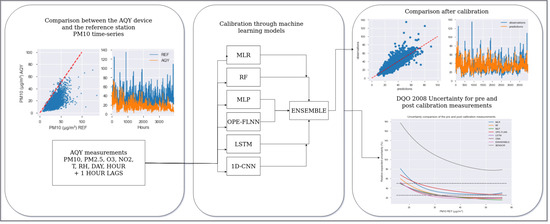
1. Introduction

Air pollution is characterized as the single most threatening environmental health risk. The World Health Organization (WHO) estimated that 4.2 million deaths worldwide were related to air pollution in 2016 [1]. Additionally, it bears economic implications because of increased medical costs and reduced productivity. Lately, particulate matter (PM) has drawn attention due to studies providing evidence that its high concentrations in breathed air correlate with adverse health effects [2]. The fact that more than 80% of the population in Europe lives in cities where the levels of PM exceed the WHO air quality guidelines points out the necessity for action regarding the proper identification and the reduction of pollution levels.

Currently, air quality monitoring stations are sparse and have a representative rather than an actual delineation ability of the air pollutant concentrations away from the measuring site. This is because of the diverse human activities taking place, especially in urban environments. Reference stations are expensive to build and maintain. Meanwhile, low cost air quality monitoring devices (LCAQMDs) have gained a lot of attention due to increased availability and lower cost. With the rise of the Internet of Things (IoT) and the interest for smart cities, these devices may provide the means for achieving increased spatiotemporal monitoring resolution. However, relevant measurements are of poor quality in terms of their uncertainty as set by the European Air Quality Directive [3]. This demonstrates that in-factory calibrations as well as operational principle limitations render LCAQMDs inadequate to capture the variability for on-site air pollution concentrations, indicating the need for on-site calibration. A number of studies [4,5,6,7] have investigated calibration methods based on computational intelligence (CI) and concluded that an additional calibration layer improves the performance on all examined sensors and can be implemented on any air quality monitoring system that uses them.

The main goal of this study is to develop, apply and evaluate CI-oriented algorithms for the modeling of the LCAQMD’s PM10 sensor behavior towards its operational improvement. Complementally to this improvement, we also investigate the performance of the specific device in terms of measurement correlation with a reference instrument.

2. Experiments

2.1. Experimental Setup

Thessaloniki has a Mediterranean climate with average monthly temperatures spanning from 5.2 °C in January to 26.5 °C in July, an annual average temperature around 15.9 °C and approximately 445 mm of annual precipitation [8]. The LCAQMD [9] used in this study is the AQY, manufactured by Aeroqual Limited; it was placed alongside the Agia Sofia air quality (AQ) reference station. The latter is located in the city center where the most significant source of emissions is traffic. The experiment took place from 27 March 2019 until 8 September 2019 (i.e., spanning a seven-month calendar period), measuring hourly concentrations of gaseous pollutants (nitrogen dioxide, NO₂, and Ozone, O₃), particulate matter (PM2.5 and PM10) and also meteorological variables (temperature, T, and relative humidity, RH). Concerning the reference station, PM10 levels were measured with the aid of an analyzer (Eberline FH 62 I-R, reference equivalence with European Standard EN 12341) that used β-attenuation; O₃ was measured with the aid of UV photometry according to European Standard EN 14625; NO₂ was measured via chemiluminescence (standard EN 14211) (manufacturer: Horiba). Values were averaged over 1 h, based on 1 min intervals. AQY, on the other hand, measured PM2.5 and PM10 number concentrations with the aid of an optical particle counter (model SDS011 by Nova Fitness Ltd.) based on a red laser scattering at an 90° angle, which were later converted into mass concentrations using embedded algorithms. The device also provided auto-correction of humidity effects for the PM measurements. NO₂ and O₃ were measured via a gas-sensitive electrochemical and a gas-sensitive semiconductor sensor, respectively, while temperature and relative humidity were also recorded [9].

2.2. Exploratory Data Analysis and Preprocessing

Preliminary analysis was conducted to determine the performance of the AQY LCAQMD before the computational calibration procedure was applied. We used standard correlation analysis to explore the linear relationships between the variables for two reasons: initially, to compare the data from the two AQ measuring devices, and second, to investigate whether the AQY variables could be used as input for the data driven modeling that we wanted to develop in order to improve the devices’ overall performance.

Although missing values in the data set were as low as 0.2% of the whole data set, we believed that an imputation approach based on k-Nearest Neighbors (KNN) algorithm [10] would yield better results than dropping temporal sensitive data or filling with an average/median. Feature scaling in the range (0, 1) was applied for the model, which took advantage of the Chebyshev orthogonal polynomials. This step was necessary because the expansion to high degree polynomials returns huge values, making the training of the data-driven models impossible to converge. We used a k-fold-like approach to evaluate the models. A train-test split was applied six times in order to have each time represent one month for testing, while using the other six months for training. This procedure created seven datasets, named after the month in which they were tested. For improving the regression results, we used the current hour and day as time features after transforming them via the following equation:

$$x\prime =sin\left(\frac{\pi x}{\frac{T}{2}}\right)$$

(1)

where T is the period of the year in (i) days for the day feature and (ii) hours for the hour feature. Finally, we chose 1 h lag features for O₃ AQY, PM10 AQY and HOUR as input variables to impose the persistent nature of the pollutant variables in the training set. In total, 11 features were employed as predictors for the CI on-site calibration of the target.

2.3. Advanced Data Analysis: Self-Organizing Maps (SOMs)

SOMs, introduced in [11], are an unsupervised learning technique based on artificial neural networks. They project the high dimensional input vectors into two- or three-dimensional maps while preserving the topology of the input space. These maps, which are created from the prototype vectors that fit the data, are capable of depicting relationships between features. They are often used for visualization purposes, nonlinear correlation analysis, dimensionality reduction, and clustering. We employed SOMs for analyzing AQ monitoring data, selected for both their low cost as well as the reference instruments, in order to reveal relationships among parameters of interest.

2.4. Statistical Machine Learning Algorithms

For the computational calibration of the LCAQMD, we employed a number of algorithms, which are briefly described in the following subsections. Specifically, the artificial neural network architectures of multilayer perceptron (MLP), long short-term memory (LSTM), one-dimensional convolutional neural networks (CNNs) and orthogonal polynomial expanded-functional link neural networks (OPE-FLNNs) were compared with the multiple linear regression (MLR) and random forest (RF) algorithms. Furthermore, an averaging ensemble of the models was evaluated. We reformulated the problem as a regression problem and used the measurements from the AQY device as predictors for the PM10 measurements of the reference instrument. Finally, we compared the results in terms of root mean square distance (RMSE), mean absolute error (MAE), bias (B), unbiased root mean squared distance (uRMSE) and coefficient of determination (R²). All the neural networks were trained with backpropagation using the MSE loss function and the ADAM optimizer.

2.4.1. Multiple Linear Regression (MLR)

MLR is the most widely used technique for on-site calibration. In this approach we considered the target y to be the weighted sum of the predictor variables x, and the weights were learned by the minimization of the mean squared error cost function. We implemented this model as a reference to compare with it the other machine learning models considered.

2.4.2. Random Forest (RF)

This is an ensemble-based meta-classifier, introduced in [12], which exploits the feature space by randomly transforming it and using it as a pool for extracting diversified data sets. This is accomplished by randomly choosing features (columns) and resampling throughout the time stamped records (rows) with replacement (bootstrap). Then, a regression tree is trained for each data set and the average of their predictions is the output of the model. Because regression trees have high variance, they are considered weak classifiers, but through the RF ensemble schema, the overall variance decreases and extrapolation results improve. In this study, due to the small number of features, we avoided using the random feature selection step and instead included all the features for every tree that was fitted, therefore using a total of 100 estimators.

2.4.3. Multilayer Perceptron (MLP)

Artificial Neural Networks (ANNs) [13] are characterized as nonlinear universal function approximators. The network is organized in layers (input, hidden, output), each containing a fixed number of nodes. Every node from one layer is connected with every node from the next layer, and so forth. The nodes, trying to simulate the biological neurons, only propagate the information forward if a threshold is exceeded. This threshold is determined by passing the computed response of a neuron through a nonlinear activation function.

The number of hidden layers, the number of nodes in each layer, the learning rate and the activation functions are hyperparameters that must be tuned correctly to avoid under-/over-fitting. In this study, the ANN consisted of the input layer with 11 nodes, each representing one variable, three hidden layers with 80, 64 and 32 nodes, and the output layer with one node. The three hidden layers were activated via the softplus activation function. The output layer is usually linearly activated for regression problems. The network was trained for 30 epochs before it started overfitting, marking the stopping point.

2.4.4. Convolutional Neural Networks for Time Series (CNNs)

Recently, CNN architectures were successfully applied for the modeling of sequential data, such as text [14], sound [15] and timeseries [16]. In our approach, we used convolutions to extract features and then used an MLP regressor to predict the next value in the sequence. The architecture of the CNN included an input convolutional layer with 11 nodes, two hidden convolutional layers with 32 filters each and window size of 2, a flattening layer that reshapes the feature vectors into one vector, and the output layer. All layers were activated through the softplus function. Each example that was “fed” into the CNN consisted of the last five hours’ measurements, including the present measurements. The model was trained for 50 epochs, with a batch size of 32.

2.4.5. Long Short-Term Memory Neural Networks (LSTMs)

LSTM [17] ANN models are considered state of the art for sequential data modeling. They have the ability to capture short- and long-term dependencies while resolving the exploding/vanishing gradient problem of recurrent neural networks (RNNs) by introducing the concept of memory. Natural language processing (NLP) [18], financial market predictions [19] and epileptic seizure predictions [20] as well as PM10 and PM2.5 forecasting [21] are some of the fields that exhibit superior performance compared to other machine learning algorithms. The network used in this study consisted of the input layer with 11 nodes, one LSTM layer with 45 nodes activated with the rectified linear unit (relu) function, followed by the output layer, which was linearly activated. The network was trained for 30 epochs, with examples holding the present and the last hour of data (measurements of 2 h) and a batch size of 16.

2.4.6. Orthogonal Polynomial Expanded, Functional Link, Neural Networks (OPE-FLNNs)

The OPE-FLNN consists of two sub-architectures. The first one is a standard MLP with one hidden layer, and the other one is a direct link from the input layer to the output layer. It also exploits the orthogonal polynomials to transform and expand the input vector in order to capture higher order information. The authors of [22] conducted a comprehensive analysis and concluded that the orthogonal polynomial transformation, with Chebyshev polynomials, significantly improves the regression network performance. The architecture of this model was as follows: Input layer with 11 nodes, expanding layer that implemented the orthogonal polynomial expansion using the first six Chebyshev polynomials, two densely connected layers with 35 nodes each and softplus activation, a concatenation layer that merged the input data with the processed data and an output layer connected with the concatenated layer.

2.4.7. Averaging Ensemble (ENSEMBLE)

The most straightforward way to produce an ensemble of seemingly different models is to average their predictions. This can potentially reduce the variance and result in improved estimations. An exhaustive grid search was performed to determine the best combination of the individual models’ predictions.

2.5. Metrics

Evaluation metrics, as well as metrics used in the target diagram, are presented in

Table 1. Regression evaluation metrics.

Scheme 2.	Symbol	Formula
Coefficient of determination	$R^2$	$1-\frac{{\sum }_{i=1}^n\left(y_i-\overline{y}\right)}{{\sum }_{i=1}^n{\left(y_i-\widehat{y}\right)}^2}$
Mean absolute error	MAE	$\frac{1}{n}{\displaystyle \sum _{i=1}^n}\left|y_i-\overline{y}\right|$
Root mean square error	RMSE	$\frac{1}{\sqrt{n}}\sqrt{{\displaystyle \sum _{i=1}^n}{\left(x_i-y_i\right)}^2}$
Unbiased root mean squared distance	uRMSD	$\frac{1}{\sqrt{n}}\sqrt{{\displaystyle \sum _{i=1}^n}{\left(\left(x_i-\overline{x}\right)-\left(y_i-\overline{y}\right)\right)}^2}$
Bias	B	$\overline{x}-\overline{y}$

.

2.6. Target Diagram

The target diagram [23] is derived from the equation RMSE² = B² + uRMSD². Since the relationship of the statistics obeys the Pythagorean theorem, the target diagram is placed on a Cartesian plane where the x-axis represents the uRMSD and the y-axis represents the bias. The error performance as quantified by the RMSE, is represented as the distance from the origin. The normalized target diagram can be plotted when B, RMSE, and uRMSD are normalized with the reference instrument standard deviation. Models within the target circle of unit radius are better predictors of the reference measurements than mean concentrations represented by the circle. In this study, we used the normalized target diagram in order to compare all the calibration techniques that we employed in terms of RMSE.

2.7. Relative Expanded Uncertainty

In order to evaluate the capability of the computational calibration methods to improve the operational performance of the AQY device for PM10 monitoring, the relevant uncertainty was calculated on the basis of the methodology described by [24] and making use of Equations (2) and (3).

$$U_r\left(y_i\right)=\frac{2{\left(\frac{RSS}{n-2}-u^2\left(x_i\right)+{\left[b_0+\left(b_1-1\right)x_i\right]}^2\right)}^{\left(1/2\right)}}{y_i}$$

(2)

$$RSS={\displaystyle \sum }{\left(y_i-b_0-b_1{x}_i\right)}^2,$$

(3)

where U_r(y_i), is the relative expanded uncertainty, u²(x_i), is the random uncertainty of the standard method, here set equal to 0.67, RSS represents the sum of (relative) residuals, x_i is the average result of the reference method over period i, y_i is the average result of the model over period i, and b₀ and b₁, are the coefficients of the regression y = b₁x + b₀. For PM10 and PM2.5 measurements to be accepted as indicative or fixed, the U_r(y_i) should be below 50% and 25%, respectively, for daily averages.

3. Results

3.1. Exploratory Data Analysis (EDA)

Table 2. Correlation matrix between the AQY and REF pollutants and meteorological variables (Pearson). Correlations between target variable and predictors are denoted with bold.

	NO2 REF	NO2 AQY	O3 REF	O3 AQY	PM2.5 AQY	PM10 REF	PM10 AQY	TEMP	RH
NO2 REF	1	0.04	−0.65	−0.42	0.20	0.43	0.26	0	−0.01
NO2 AQY	0.04	1	0.35	−0.05	−0.08	0.03	−0.10	0.61	−0.45
O3 REF	−0.65	0.35	1	0.62	−0.21	−0.29	−0.25	0.30	−0.42
O3 AQY	−0.42	−0.05	0.62	1	−0.08	−0.36	−0.12	−0.21	−0.27
PM2.5 AQY	0.20	−0.08	−0.21	−0.08	1	0.49	0.92	−0.31	0.21
PM10 REF	0.43	0.03	−0.29	−0.36	0.49	1	0.64	0.03	0.06
PM10 AQY	0.26	−0.10	−0.25	−0.12	0.92	0.64	1	−0.32	0.17
TEMP	0	0.61	0.30	−0.21	−0.31	0.03	−0.32	1	−0.49
RH	−0.01	−0.45	−0.42	−0.27	0.21	0.06	0.17	−0.49	1

summarizes the results of the EDA. Even though the measurements of PM10 and O₃ of the AQY device had the highest correlation with their reference counterparts, it is evident that the AQY device underestimated the values of the pollutants’ concentration, since the mean and the maximum values were lower for both cases. NO₂ AQY had almost zero correlation with NO₂ REF. PM2.5 AQY and PM10 AQY had a high linear correlation as expected. For modeling purposes, we also investigated the correlations of PM10 REF (target) with all AQY variables (predictors). PM10 REF was moderately correlated with PM10 AQY and PM2.5 AQY. We can see that it also had a small, yet non-negligible, dependence on O₃. On the other hand, PM10 REF had almost zero correlation with the meteorological variables, RH and T. Interestingly, PM10 REF showed moderate correlation with NO₂ REF but no correlation at all with NO₂ AQY. Even though the correlations with RH and T were negligible, it has been demonstrated in the literature that the former affects the PM levels [25] while the latter affects O₃ [26], thus we did not exclude any variables. However we took into account the correlations to choose lagged variables for the modeling phase: If a variable had negligible correlation with the target then we did not consider this variable as a candidate to extract lags. Nevertheless, the original variable was still included in the predictors.

3.2. LCAQMD Evaluation

Figure 1, Figure 2 and Figure 3 and

Table 3. Comparison of the AQY and REF instruments. The table is divided in three parts. In the left part, the behavior for the full time series is evaluated, in the center the sensor performance indices for the first half (March–June) of the series are presented, and in the right part the second half (July–September) of the series is evaluated.

	R2	R	MAE	RMSE	R2	R	MAE	RMSE	R2	R	MAE	RMSE
NO2	−3.02	0.04	16.76	19.84	−3.32	0.14	17.49	20.03	−2.71	0.0	15.96	19.58
O3	0.20	0.62	18.16	22.17	0.11	0.77	20.71	24.35	0.31	0.61	15.73	19.84
PM10	−1.28	0.64	15.39	17.77	−0.31	0.79	12.55	14.65	−2.68	0.50	18.22	20.41

display the performance of the microsensor against the reference station instruments. Regarding the full time series data (left), out of the three pollutants, NO₂ demonstrated the worst performance, with negative coefficient of determination and almost zero correlation. Ozone (O₃) had a moderate correlation R but very low coefficient of determination. For PM10 we could see a slightly higher R, even though R² was negative [27]. Both O₃ and PM10 exhibited drifting behaviors as time passed, leading to further underestimation. Regarding all three pollutants, the measurements were scattered far from the regression line (red line). Lastly, the values of MAE and RMSE indicated over 15 and 17 μg/m³ average errors for all pollutants, respectively.

In order to investigate the drifting behavior of the sensors, we further split the data into two segments, taking into account the transition from spring to summer. In the first period (March–June) there was little photochemical activity, so the O₃ sensor showed adequate performance in terms of correlation; however, in the second period (July–September) the photochemical activity was much higher, which is possibly one of the reasons that the AQY O₃ sensor performance decreased. An additional parameter that causes ozone underestimation has already been reported in literature and should be taken into account: particulate deposition in the inlet and on the sensor causes ozone decomposition and therefore diminution in the air inflow [28]. It should be noted that for both O₃ and NO₂, the remaining three sensor performance indices appeared to improve in the second period; however, these “improvements” were not real, but rather random and were regarded as numerical artefacts. Furthermore, in the second period the NO₂ sensor visually appeared to improve (Figure 3, right side), but this was hardly regarded as improvement based on the statistical indices. Part of the explanation is that the sensors suffer from cross sensitivity issues when measuring NO₂ and O₃, which is a known issue for these types of devices, especially in environments with rich photochemical activity. PM10 demonstrated reduced sensor performance indices in the second period, confirming the drifting effects that exist, potentially due to dust accumulation on the sensor’s surface, and the subsequent reduction in the detection capabilities of the optical sensor.

Karagulian et al. [29] reviewed 110 on-site calibrated and uncalibrated LCAQMDs and concluded that most of them, including the AQY device, underestimate the PM10 hourly concentrations, which is in accordance with our results. Another study [30] evaluated a stand-alone SDS011 sensor (during winter and spring), which is used by the AQY device enhanced with RH corrections, in Santiago, Chile, with similar meteorological conditions as Thessaloniki, and found R² in the range (0.24–0.56) for PM10 concentrations against a similar β-attenuation reference instrument. They concluded that the sensor is suitable for monitoring PM2.5 daily levels after RH corrections, but not for PM10 levels. It should be underlined that we were unable to compare PM2.5 levels due to lack of relevant reference measurements, and therefore, we were also unable to estimate the influence of the “real” PM2.5/PM10 ratio in the sensor’s performance. What we observed was that PM10 levels lacked sufficient quality even after RH corrections, under the specific conditions. Despite this, the PM10 levels exhibited good correlation with the reference instrument, taking into account that the metrics were influenced by factors other than data quality; this is indicative that an on-site calibration is needed and should be applied to obtain data of sufficient quality.

3.3. Self-Organizing Maps

To further investigate the performance of the AQY device, we compared the SOMs for each pollutant, as is shown in Figure 4. Comparing the NO₂ REF map with the NO₂ AQY map reflects the inconsistency of the measurements of the AQY device. While the first shows high values on the left lower region, the latter shows high values at the upper left region. Regarding O₃, the two maps show overlapping regions for high and low values. Even though the region in which the two maps differ corresponds to high temperatures, which favors the production of ground level O₃, this is reflected only on the reference measurements. Finally, the PM10 REF, PM10 AQY and PM2.5 AQY show the same patterns across their maps; however, the different range of the values confirms that the AQY device underestimated the PM10 levels.

3.4. Computational Intelligence Calibration

The statistical indices for the evaluation are presented in Figure 5. Overall, the calibration was successful in significantly improving the coefficient of determination from −1.28 to the range (0.557 to 0.818) for all the months except September, where the best individual model yielded R² = 0.298. The standard calibration method MLR was outperformed in most cases, except for May, where MLR yielded R² = 0.63 and MAE = 4.579. The best results overall were obtained for April by the CNN model, with R² = 0.818 and MAE = 4.467. Additionally, the CNN model yielded the best results for June, with R² = 0.603 and MAE = 5.159. The LSTM model outperformed the CNN model for March in terms of R² and RMSE, but displayed lower MAE than the CNN. Regarding July and August, the RF algorithm was preferred, with R² = 0.557 in both cases and MAE = 5.015 and MAE = 5.441, respectively. RF also had the highest R² and the lowest RMSE (= 8.503) for September, as mentioned above, but MLP had the lowest MAE (= 5.943); thus, the best model could not be determined with these indices alone. Lastly, the MLP architecture performed quite well and was stable for all months and approaches; however, it never outperformed the other (best) models. Averaging the predictions from the best models for each month consistently reduced the error metrics and improved the coefficient of determination 2–7%, except for May and June, where there was no gain from averaging. Finally, the drifting behavior of the AQY device measurements was reflected by the ability of the models to reconstruct the PM10 levels. It is expected that the information content of input variables was not evenly distributed among the time interval of investigation. Thus, for example, in the first two months, AQY demonstrated good performance in terms of O₃ against reference measurements, and therefore relevant models were expected to benefit from such an agreement.

3.5. Relative Expanded Uncertainty and Target Diagram

As can be seen in Figure 6, the initial PM10 measurements of AQY never reached an uncertainty below 75%, while they should be below 50% to be considered as compliant with the Data Quality Objectives (DQO) imposed by the European Air Quality Directive (AQD) for indicative measurements. However, the post-calibration measurements were well below the DQO limit for all the models. Furthermore, the uncertainty from the RF, MLP, LSTM, CNN, and AVG models dropped below 25%, which corresponds to the DQO limit for fixed measurements. The average performance of the models is depicted in Figure 7. All models except OPE-FLNN, which showed poor performance, were close to one another, with the best being the CNN neural network, with R² = 0.624, RMSE = 7.2 and MAE = 5.07. The averaging of the model predictions outperformed the CNN architecture, with R² = 0.667, RMSE = 6.77 and MAE = 4.76. In Figure 8, the calibrated output is compared with the reference and the sensor uncalibrated output. A 15th degree polynomial is fitted to clearly demonstrate the improvement of the calibration method.

4. Conclusions

On-site calibration of LCAQMDs is a crucial component to improve their performance against reference instruments. With improved performance, these microsensors can be used as complementary to the reference stations and IoT nodes, to increase the spatiotemporal air quality monitoring in urban areas. From the comparison of the Aeroqual AQY device against the reference instrument readings, we showed that the device’s performance deteriorates with time in terms of measurement correlation. Furthermore, we suggest that seasonal variations in meteorological conditions and cross-sensitivity play a significant role in the data quality offered by LCAQMDs. A nonlinear relationship between the temperature, relative humidity and the pollutants is observed with the aid of the SOMs, pointing out the need for nonlinear calibration methods. Taking into account the two-period analysis, where we observed a decrease in the performance during the second period, as well as the SOM results, in which the difference in the O₃ maps corresponded to high temperatures, we conclude that increased photochemical activity is not reflected in the AQY O₃ measurements.

The computational calibration procedure proposed in this paper (correlation analysis, feature extraction and machine learning processes) is transferable to other similar multi-sensor devices, on the basis of data availability. Out of the seven dataset folds evaluated for PM10, the standard calibration method MLR outperformed the other models only when predicting the May measurements. RF showed great potential as a calibration method, giving the best results on three datasets (July, August, and September). Predictions from the CNN architecture correlated highly with observations for April and June, while also competing with LSTM for March. Overall, the CNN architecture yielded the best results against all other individual models. Moreover, averaging the predictions from multiple good estimators greatly improved the metrics. Finally, our CI-calibration techniques reduced the relative expanded uncertainty and improved the measurements to be compliant with the DQO guidelines for indicative and for fixed measurements, rendering the device appropriate for expanding the official network of air pollution monitoring stations under the assumption that it will be recalibrated as needed.