Analysis of the Precipitable Water Vapor Observation in Yunnan–Guizhou Plateau during the Convective Weather System in Summer
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Introduction
2.2. Data Processing
3. Results and Discussion
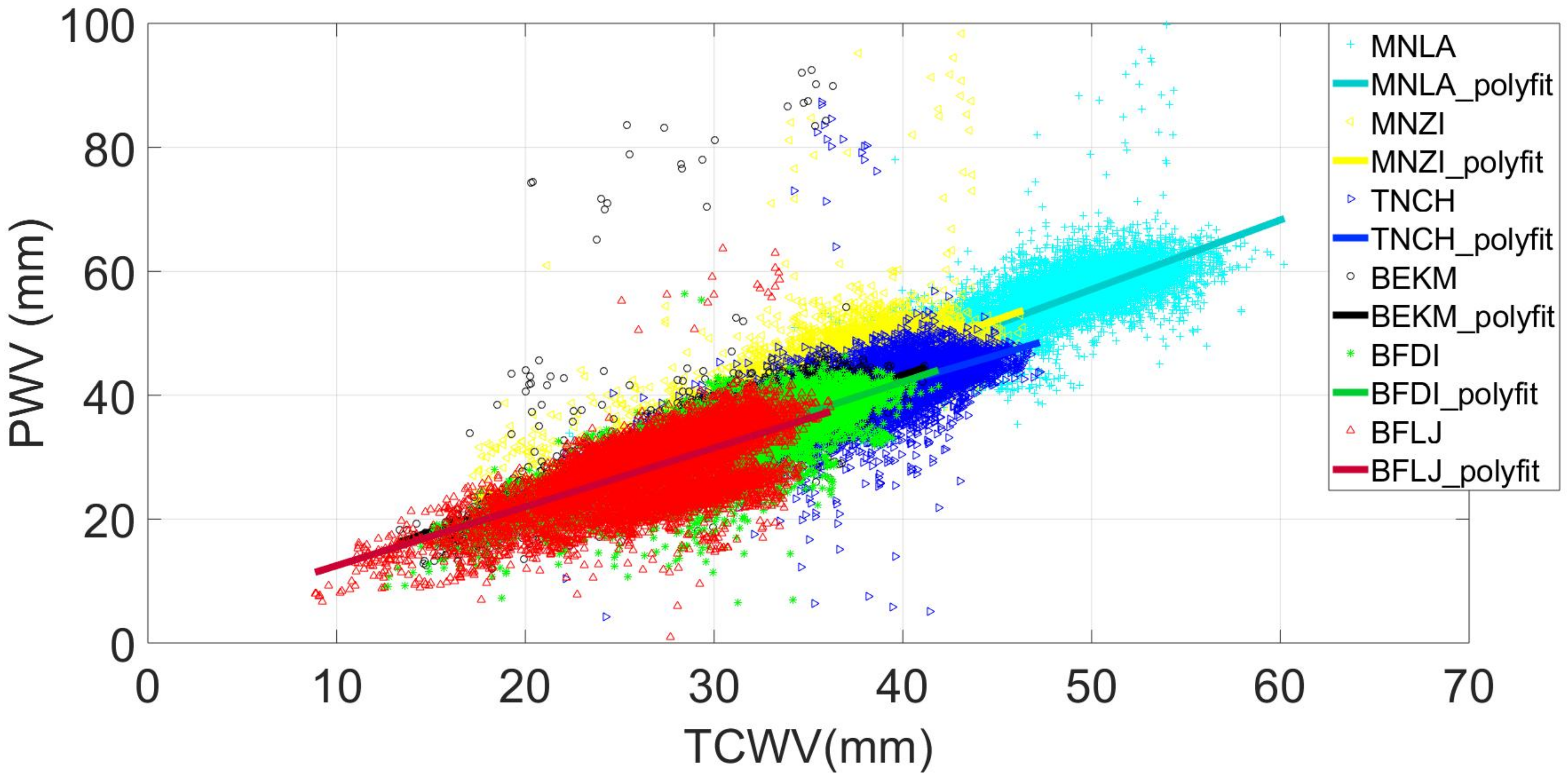
3.1. PWV Feature Analysis
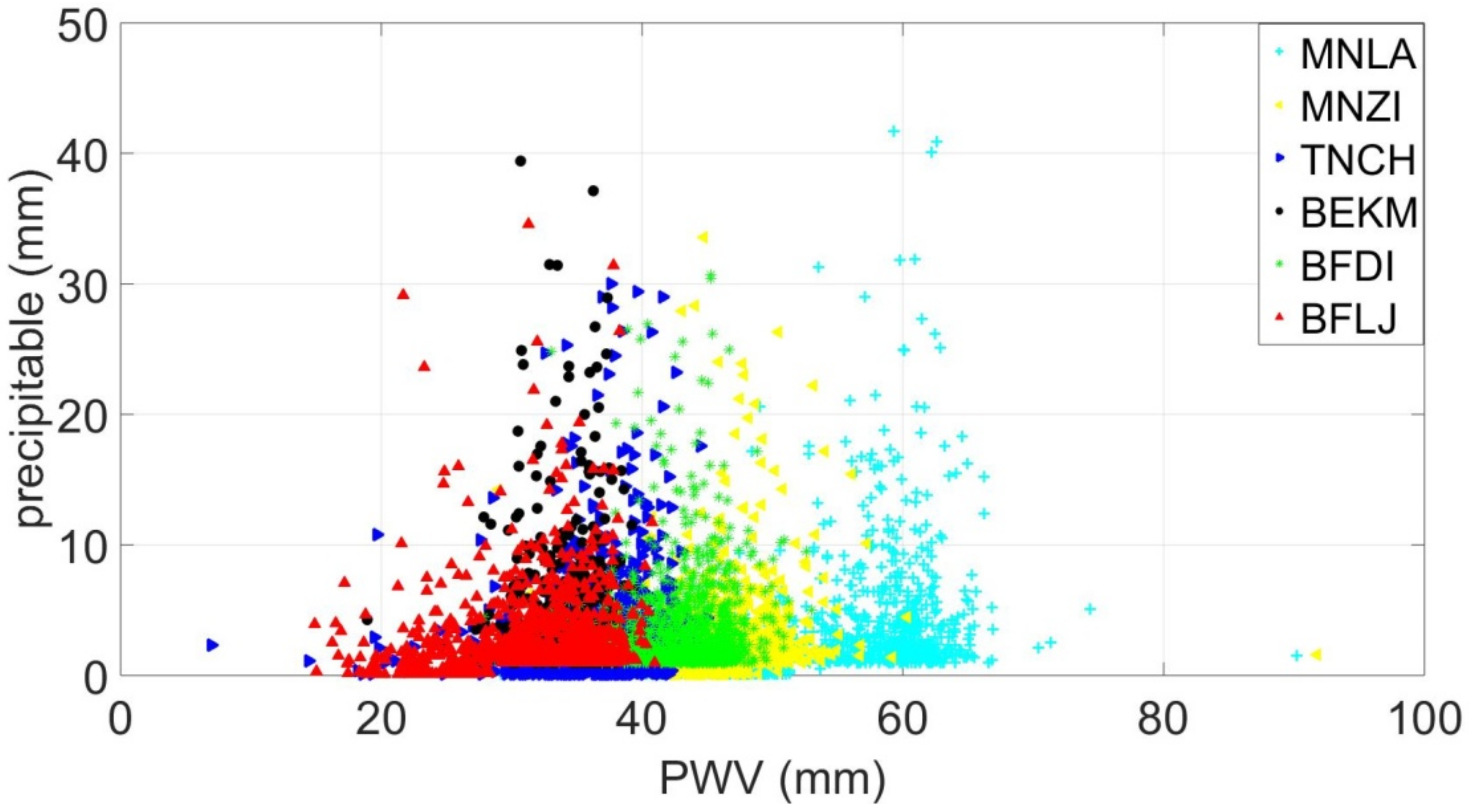
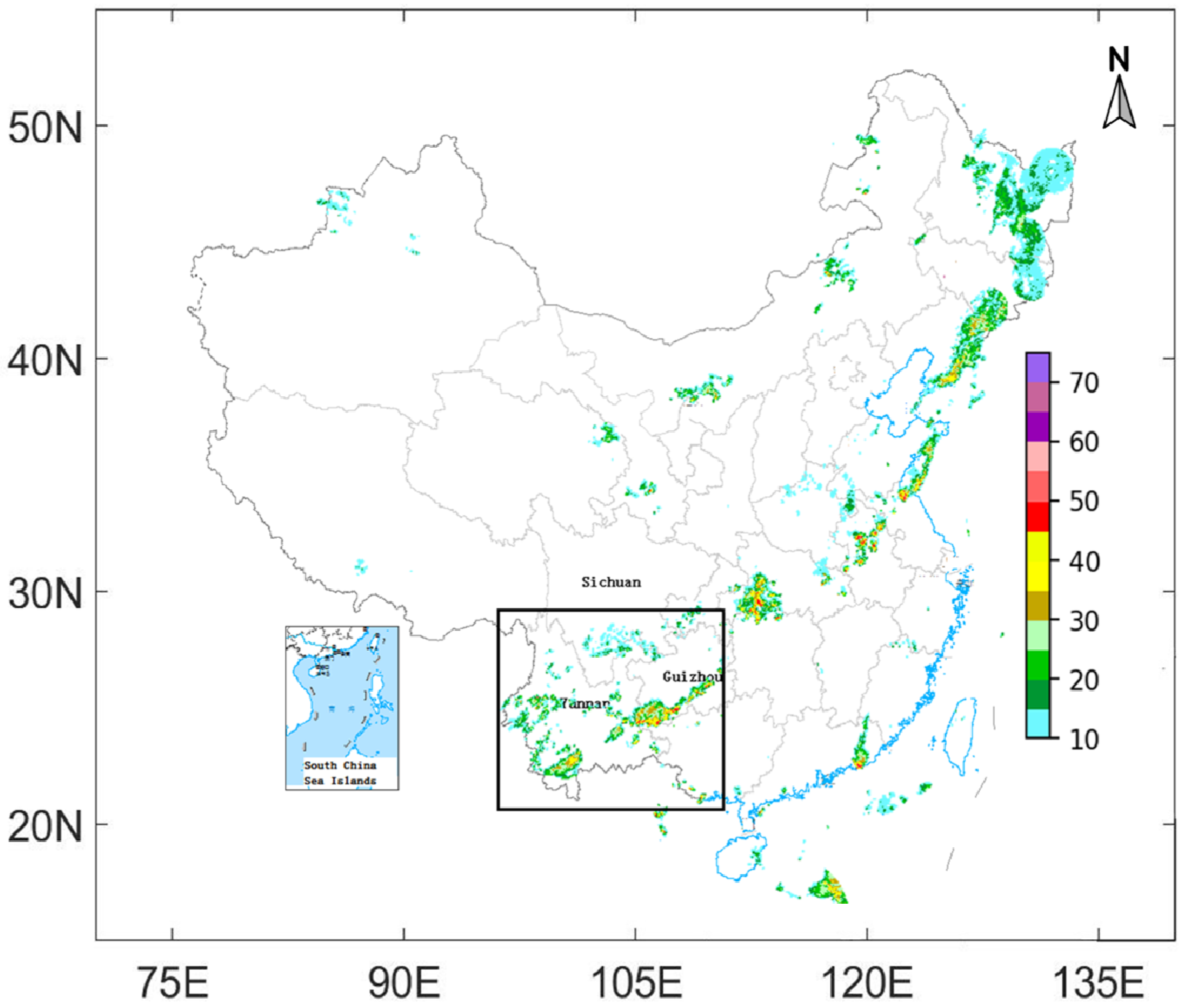
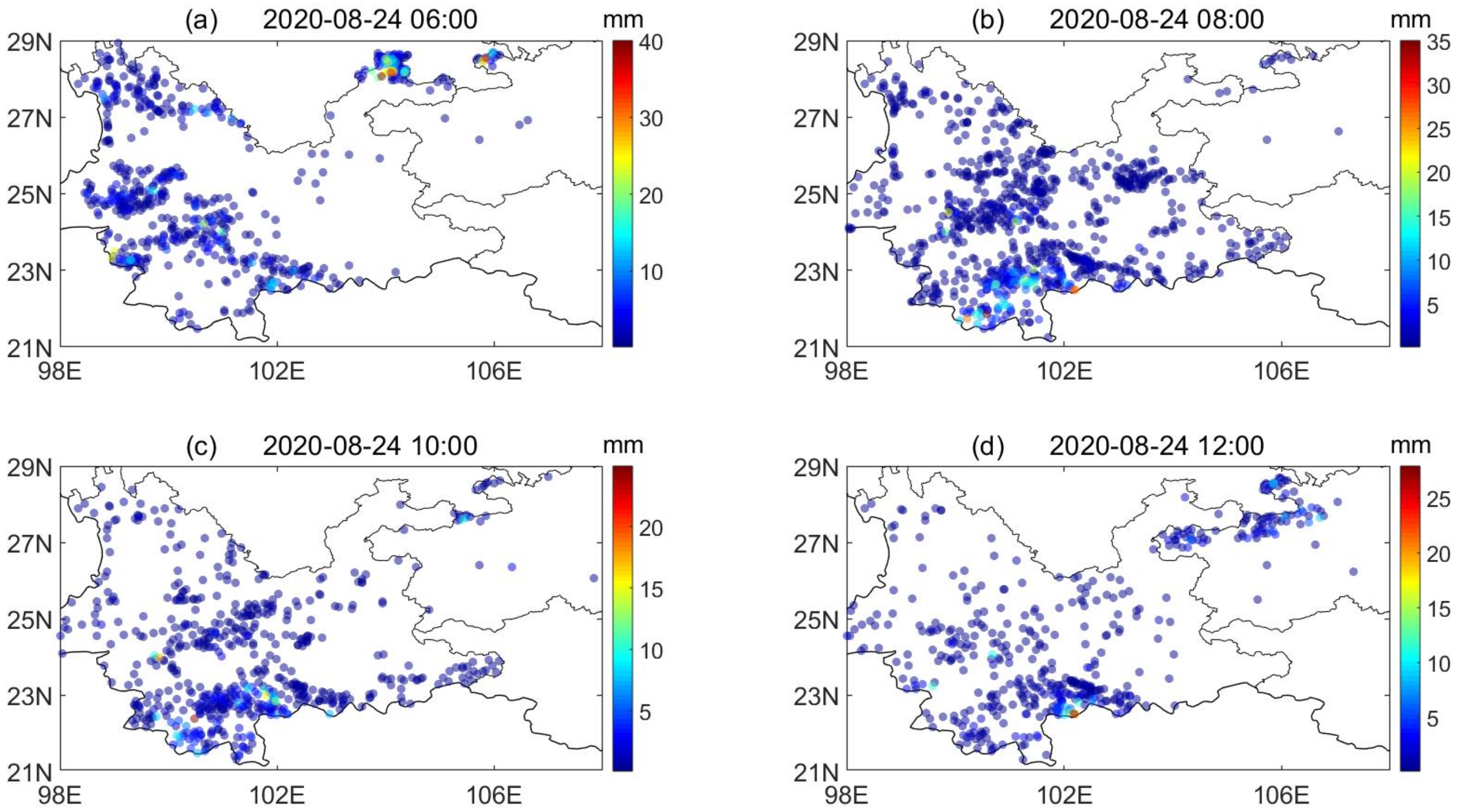
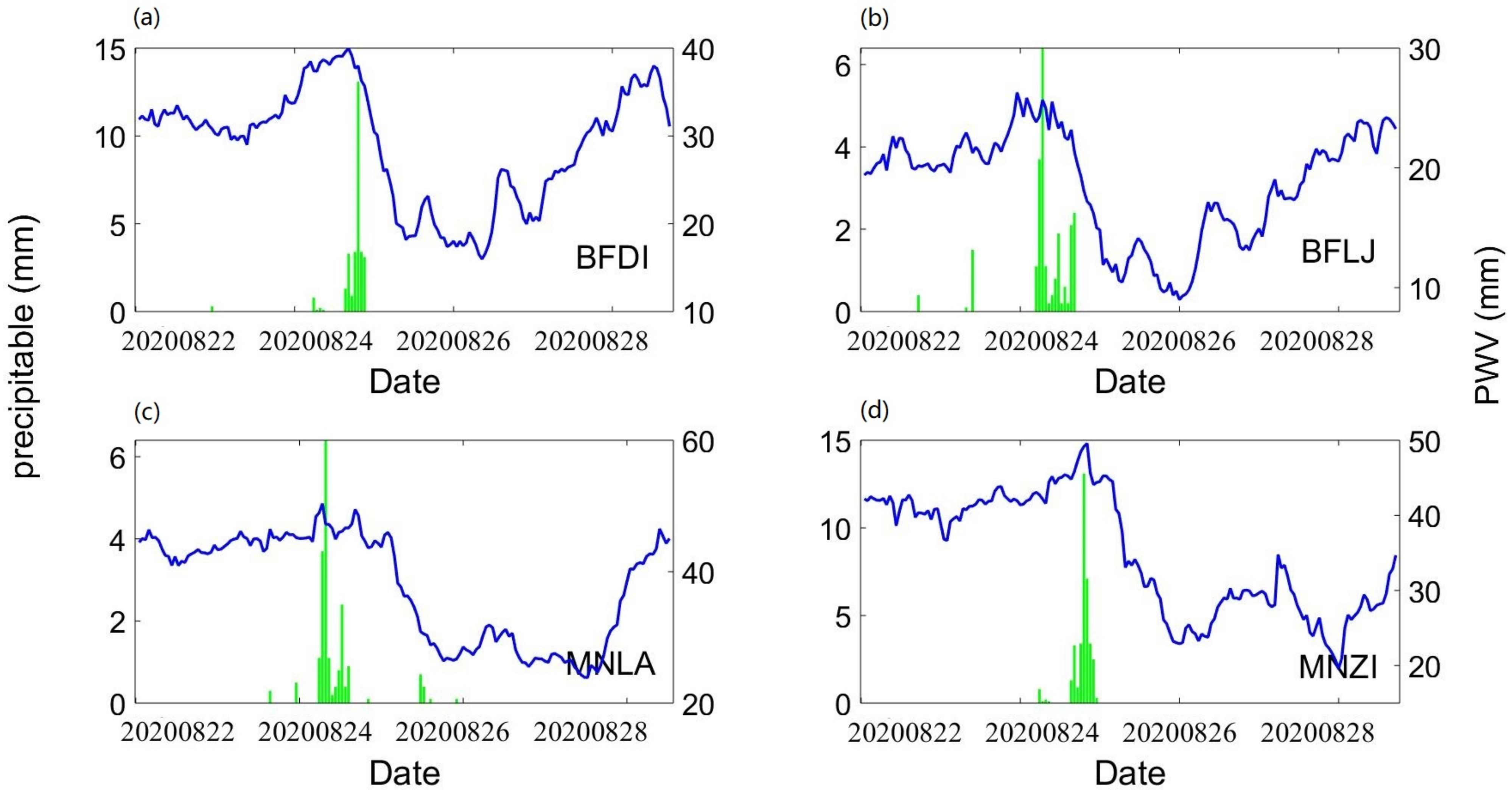
3.2. Analysis of Deep Convection Process
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kiehl, J.T.; Trenberth, K.E. Earth’s Annual Global Mean Energy Budget. Bull Am. Meteorol. Soc. 1997, 109, 197–208. [Google Scholar] [CrossRef] [Green Version]
- Held, I.M.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef] [Green Version]
- Anand, K.; Inamdar, V.; Ramanathan, N.; Loeb, G. Satellite observations of the water vapor greenhouse effect and column longwave cooling rates: Relative roles of the continuum and vibration-rotation to pure rotation bands. J. Geophys. Res. Atmos. 2004, 109, 1–9. [Google Scholar]
- Trenberth, K.E.; Dai, A. Effects of Mount Pinatubo volcanic eruption on the hydrological cycle as an analog of geoengineering. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s Global Energy Budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–323. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Chen, Q.; Zeng, Z.; Liu, H.; Wang, Y.; Zheng, Y.; Sun, T.; Liao, T.; Wang, H.; et al. Evaluation of radiosonde, MODIS-NIR-clear, and AERONET precipitable water vapor using IGS ground-based GPS measurements over China. Atmos. Res. 2017, 197, 461–473. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 228–232. [Google Scholar] [CrossRef]
- Rong, W. Prccipitable Water Vapor Retrieval Technology Research andAppliactions of Ground Based GPS Observation. Ph.D. Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2012; pp. 1–137. [Google Scholar]
- Zhou, R.R.; Wang, G.L.; Zhaxi, S.L. Cloud vertical structure measurements from a ground-based cloud radar over the southeastern Tibetan Plateau. Atmos. Res. 2021, 258, 105629. [Google Scholar] [CrossRef]
- Zhan, W.; Heki, K.; Arief, S.; Yoshida, M. Topographic Amplification of Crustal Subsidence by the Rainwater Load of the 2019 Typhoon Hagibis in Japan. J. Geophys. Res.-Solid Earth 2021, 126, e2021JB021845. [Google Scholar] [CrossRef]
- Zhao, T.B.; Dai, A.G.; Wang, J.H. Trends in Tropospheric Humidity from 1970 to 2008 over China from a Homogenized Radiosonde Dataset. J. Clim. 2012, 25, 4549–4567. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.H.; Zhang, L.Y.; Dai, A.G.; Immler, F.; Sommer, M.; Vomel, H. Radiation Dry Bias Correction of Vaisala RS92 Humidity Data and Its Impacts on Historical Radiosonde Data. J. Atmos. Ocean. Technol. 2013, 30, 197–214. [Google Scholar] [CrossRef]
- Jin, S.K.; Ma, Y.Y.; Gong, W.; Liu, B.M.; Lei, L.F.; Fan, R.N. Characteristics of vertical atmosphere based on five-year microwave remote sensing data over Wuhan region. Atmos. Res. 2021, 260, 105710. [Google Scholar] [CrossRef]
- Urban, J.; Baron, P.; Lautie, N.; Schneider, N.; Dassas, K.; Ricaud, P.; De La Noe, J. Moliere (v5): A versatile forward- and inversion model for the millimeter and sub-millimeter wavelength range. J. Quant. Spectrosc. Radiat. Transf. 2004, 83, 529–554. [Google Scholar] [CrossRef]
- Vespe, F.; Persia, T. Derivation of the water vapor content from the GNSS radio occultations observations. J. Atmos. Ocean. Technol. 2006, 23, 936–943. [Google Scholar] [CrossRef]
- Srivastava, A.; Kumar, A. Retrieval of total columnar precipitable water vapour using radio occultation technique over the Indian region. J. Atmos. Sol.-Terr. Phys. 2021, 219, 105652. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote sensing of atmospheric water vapor using the Global Position System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Braun, J.; Rocken, C.; Ware, R. Validation of line-of-sight water vapor measurements with GPS. Radio Sci. 2001, 36, 459–472. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.X. Water Vapor Retrieval, Variation Analysis and Applications over China using Ground-based GNSS and Multiple Data. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016; pp. 1–128. [Google Scholar]
- Garand, L.; Grassotti, C.; Halle, J.; Klein, G.L. On differences in radiosonde humidity-reporting practices and their implications for numerical weather prediction and remote sensing. Bull. Am. Meteorol. Soc. 1992, 73, 1417–1423. [Google Scholar] [CrossRef] [Green Version]
- António, P.; Ferreira, R.N.; Gimeno, L. Completeness of radiosonde humidity observations based on the Integrated Global Radiosonde Archive. Earth Syst. Sci. Data 2019, 11, 603–627. [Google Scholar]
- Song, S.L. Sensing Three Dimensional Water Vapor Structure with Ground-Based GPS Network and the Application in Meteorology. Ph.D. Thesis, Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai, China, 2004; pp. 1–122. [Google Scholar]
- Haefele, A.; De Wachter, E.; Hocke, K.; Kampfer, N.; Nedoluha, G.E.; Gomez, R.M.; Eriksson, P.; Forkman, P.; Lambert, A.; Schwartz, M.J. Validation of ground-based microwave radiometers at 22 GHz for stratospheric and mesospheric water vapor. J. Geophys. Res. Space Phys. 2009, 114, 23305. [Google Scholar] [CrossRef] [Green Version]
- Divakala, M.G.; Barnet, C.D.; Goldberg, M.D.; McMillin, L.M.; Wolf, W.; Zhou, L.; Liu, X. Validation of Atmospheric Infrared Sounder temperature and water vapor retrievals with matched radiosonde measurements and forecasts. J. Geophys. Res. 2006, 111, D09S15. [Google Scholar]
- Deeter, M.N. A new satellite retrieval method for precipitable water vapor land and ocean. Geophys. Res. Lett. 2007, 34, L02815. [Google Scholar] [CrossRef]
- Bauer, P.; Radnoti, G.; Healy, S.; Cardinali, C. GNSS Radio Occultation Constellation Observing System Experiments. Mon. Weather. Rev. 2014, 142, 555–572. [Google Scholar] [CrossRef]
- Hajj, G.A.; Ao, C.O.; Iijima, B.A.; Kuang, D.; Kursinski, E.R.; Mannucci, A.J.; Meehan, T.K.; Romans, L.J.; Juarez, M.D.; Yunck, T.P. CHAMP and SAC-C atmospheric occultation results and intercomparisons. J. Geophys. Res.-Atmos. 2004, 109, D06109. [Google Scholar] [CrossRef]
- Larsen, G.B.; Lauritsen, K.B.; Rubek, F. Processing of CHAMP Radio Occultation Data Using GRAS SAF Software. Earth Observation with Champ: Results from Three Years Orbit; Springer: Berlin/Heidelberg, Germany, 2005; pp. 543–548. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.; Anthes, R.; Rocken, C.; Ware, R. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Wang, J.H.; Dai, A.G.; Mear, C. Global Water Vapor Trend from 1988 to 2011 and Its Diurnal Asymmetry Based on GPS, Radiosonde, and Microwave Satellite Measurements. J. Clim. 2016, 29, 5205–5222. [Google Scholar] [CrossRef]
- Elgered, G.; Johansson, J.; Rönnäng, B.O.; Davis, J.L. Measuring regional atmospheric water vapor using the Swedish Permanent GPS Network. Geophys. Res. Lett. 1997, 24, 2663–2666. [Google Scholar] [CrossRef] [Green Version]
- Haase, J.; Ge, M.R.; Vedel, H.; Calais, E. Accuracy and variability of GPS tropospheric delay measurements of water vapor in the western Mediterranean. J. Appl. Meteorol. 2003, 42, 1547–1568. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, J.; Dai, A. Evaluation of atmospheric precipitable water from reanalysis products using homogenized radiosonde observation over China. J. Geophys. Res. Atmos. 2015, 120, 10703–10727. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhang, L. Systematic errors in global radiosonde precipitable water data from comparisons with groundbased GPS measurements. J. Clim. 2008, 21, 2218–2238. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Zou, X.; Guo, Y.R. Variational Assimilation of Precipitable Water Using a Nonhydrostatic Mesoscale Adjoint Model. Part I: Moisture Retrieval and Sensitivity Experiments. Mon. Weather Rev. 1996, 124, 122–147. [Google Scholar] [CrossRef] [Green Version]
- Gutman, S.I.; Holub, K.L.; Sahm, S.R.; Stewart, J.Q.; Smith, T.L.; Benjamin, S.G.; Schwartz, B.E. Rapid retrieval and assimilation of ground based GPS-Met Observations at NOAA Forecast System Laboratory: Impact on Weather Forecasts. J. Meteorol. Soc. Jpn. 2004, 8, 51–360. [Google Scholar]
- Xie, Y.; Wei, F.; Chen, G.; Zhang, T.; Hu, L. Analysis of the 2008 heavy snowfall over South China using GPS PWV measurements from the Tibetan Plateau. Ann. Geophys. 2010, 28, 1369–1376. [Google Scholar] [CrossRef]
- Radhakrishna, B.; Fabry, F.; Braun, J.J.; Van Hove, T. Precipitable water from GPS over the continental United States: Diurnal cycle, intercomparisons with NARR, and link with convective initiation. J. Clim. 2015, 28, 2584–2599. [Google Scholar] [CrossRef]
- Xiangde, X.; Shiyan, T.; Jizhi, W.; Lianshou, C.; Li, Z.; Xiurong, W. The relationship between Water Vapor Transport Features of Tibetan Plateau-Monsoon “Large Triangle” Affecting Region and Drought-flood Abnormality of China. Acta Meteorol. Sin. 2002, 60, 257–266. [Google Scholar]
- Xu, X.; Dong, L.; Zhao, Y.; Wang, Y. Effect of the Asian Water Tower over the Qinghai-Tibet Plateau and the characteristics of atmospheric water circulation. Sci. China Press 2019, 64, 2830–2841. [Google Scholar]
- Xinzhu, Z. Analysis on the Feature of Moisture Flux over Southwest China. Ph.D. Thesis, Hunan Normal University, Hunan, China, 2011; pp. 1–145. [Google Scholar]
- Xiangde, X.; Lianshou, C.; Xiurong, W.; Qiuju, M.; Shiyan, T. The structure of the source and sink of water vapor transportation in the Meiyu belt of the Yangtze River Basin. Sci. China Press 2003, 48, 2288–2294. [Google Scholar]
- Xingwen, J.; Yueqing, L.; Xin, W. Water vapor transport over China and its relationship with drought and flood in Yangtze River Basin. J. Geogr. Sci. 2009, 19, 153–163. [Google Scholar]
- Xiaoying, S.; Xiangde, X.; Hao, W.; Dayong, Q. Characteristics of moisture transport in middle and lower reaches of Yangtze River and its variation trend. J. Hydraul. Eng. 2008, 39, 596–603. [Google Scholar]
- Weijia, W.; Xinjia, Z. Retrieve the precipitable water vapor of the atmospheric in Southwestern China from the COSMIC data. In Proceedings of the 29th Annual Meeting of the Chinese Meteorological Society, Shenyang, China, 12 September 2012. [Google Scholar]
- Wang, J.; Han, S.; Bian, H.; Liu, X.; Sun, D.; Zhao, C. Characteristics of Three-Dimensional GPS tomography water vapor field during the rainstorm. Acta Sci. Nat. Univ. Pekin. 2014, 50, 1053–1064. [Google Scholar]
- Adams, D.K.; Fernandes, R.M.; Maia, J.M. GNSS Precipitable Water Vapor from an Amazonian Rain Forest Flux Tower. J. Atmos. Ocean. Technol. 2011, 28, 1192–1198. [Google Scholar] [CrossRef]
- Adams, D.K.; Fernandes, R.M.; Kursinski, E.R.; Maia, J.M.; Sapucci, L.F.; Machado, L.A.; Vitorello, I.; Monico, J.F.G.; Holub, K.L.; Gutman, S.I.; et al. A dense GNSS meteorological network for observing deep convection in the Amazon. Atmos. Sci. Lett. 2015, 12, 207–212. [Google Scholar] [CrossRef] [Green Version]
- Adams, D.K.; Fernandes, R.M.; Holub, K.L.; Gutman, S.I.; Barbosa, H.M.; Machado, L.A.; Calheiros, A.J.; Bennett, R.A.; Kursinski, E.R.; Sapucci, L.F.; et al. The Amazon Dense GNSS Meteorological Network: A New Approach for Examining Water Vapor and Deep Convection Interactions in the Tropics. Bull. Am. Meteorol. Soc. 2017, 96, 12. [Google Scholar] [CrossRef]
- The Copernicus Climate Change Service. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form (accessed on 15 April 2021).
- The Copernicus Climate Change Service. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=form (accessed on 20 April 2021).
- Fengyun Satellite Remote Sensing Data Service Network. Available online: http://satellite.nsmc.org.cn/PortalSite/Data/Satellite.aspx (accessed on 20 May 2021).
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelength. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Thayer, D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to theory of atmospheric refraction. J. Geod. 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Liou, Y.A.; Teng, Y.T.; Van Hove, T.; Liljegren, J.C. Comparison of Precipitable Water Observations in the Near Tropics by GPS, Microwave Radiometer, and Radiosondes. J. Appl. Meteorol. Climatol. 2001, 40, 5–15. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Z.; Liang, H.; Xu, X.; Wu, P. Precipitable water vapor on the Tibetan Plateau estimated by GPS, water vapor radiometer, radiosonde, and numerical weather prediction analysis and its impact on the radiation budget. J. Geophys. Res. 2005, 110, D17106. [Google Scholar] [CrossRef]
- Esteban Vázquez, G.; Dorota, B.; Grejner-Brzezinska, A. GPS-PWV estimation and validation with radiosonde data and numerical weather prediction model in Antarctic. GPS Solut. 2013, 17, 29–39. [Google Scholar] [CrossRef]
- Bock, O.; Bosser, P.; Flamant, C.; Doerflinger, E.; Jansen, F.; Fages, R.; Bony, S.; Schnitt, S. Integrated water vapour observations in the Caribbean arc from a network of ground-based GNSS receivers during EUREC(4)A. Earth Syst. Sci. Data 2021, 13, 2407–2436. [Google Scholar] [CrossRef]






| Station | Latitude | Longitude | Altitude(m) |
|---|---|---|---|
| MNLA | 101.58 | 21.47 | 631.39 |
| MNZI | 103.33 | 23.44 | 1320.47 |
| TNCH | 98.50 | 25.02 | 1665.99 |
| BEKM | 102.65 | 25.01 | 1896.61 |
| BFDI | 100.18 | 25.71 | 1986.25 |
| BFLJ | 100.22 | 26.85 | 2395.95 |
| Station | Data Volume | Correlation Coefficient | Standard Deviation (mm) | Mean Deviation (mm) |
|---|---|---|---|---|
| MNLA | 11,895 | 0.878 | 7.338 | 6.647 |
| MNZI | 13,393 | 0.824 | 6.406 | 6.748 |
| TNCH | 14,002 | 0.828 | 4.730 | 2.360 |
| BEKM | 10,964 | 0.817 | 5.470 | 3.170 |
| BFDI | 14,029 | 0.805 | 4.790 | 2.213 |
| BFLJ | 13,496 | 0.804 | 4.686 | 2.775 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Cao, Y.; Shi, C.; Lei, Y.; Wen, H.; Liang, H.; Tu, M.; Wan, X.; Wang, H.; Liang, J.; et al. Analysis of the Precipitable Water Vapor Observation in Yunnan–Guizhou Plateau during the Convective Weather System in Summer. Atmosphere 2021, 12, 1085. https://doi.org/10.3390/atmos12081085
Hu H, Cao Y, Shi C, Lei Y, Wen H, Liang H, Tu M, Wan X, Wang H, Liang J, et al. Analysis of the Precipitable Water Vapor Observation in Yunnan–Guizhou Plateau during the Convective Weather System in Summer. Atmosphere. 2021; 12(8):1085. https://doi.org/10.3390/atmos12081085
Chicago/Turabian StyleHu, Heng, Yunchang Cao, Chuang Shi, Yong Lei, Hao Wen, Hong Liang, Manhong Tu, Xiaomin Wan, Haishen Wang, Jingshu Liang, and et al. 2021. "Analysis of the Precipitable Water Vapor Observation in Yunnan–Guizhou Plateau during the Convective Weather System in Summer" Atmosphere 12, no. 8: 1085. https://doi.org/10.3390/atmos12081085
APA StyleHu, H., Cao, Y., Shi, C., Lei, Y., Wen, H., Liang, H., Tu, M., Wan, X., Wang, H., Liang, J., & Zhao, P. (2021). Analysis of the Precipitable Water Vapor Observation in Yunnan–Guizhou Plateau during the Convective Weather System in Summer. Atmosphere, 12(8), 1085. https://doi.org/10.3390/atmos12081085





