Spatiotemporal Modes Characteristics and SARIMA Prediction of Total Column Water Vapor over China during 2002–2022 Based on AIRS Dataset
Abstract
:1. Introduction
2. Data and Method
2.1. Data
2.2. Research Methods
2.2.1. Empirical Orthogonal Function (EOF) Analysis Method
2.2.2. Linear Regression
2.2.3. Mann-Kendall Mutation Test
2.2.4. Seasonal Autoregressive Integrated Moving Average (SARIMA) Forecast Analysis
- (1)
- To judge the stationarity of a sequence, this paper uses the Dickey-Fuller (DF) unit root test to judge whether the sequence is stationarity.
- (2)
- If the sequence is non stationary, it is processed by difference, eliminating the fluctuation of the sequence to make the data tend to be stationary, and extracting the effective information in the sequence.
- (3)
- Order the model. In this paper, the autocorrelation, partial correlation and criterion functions are used.
- (4)
- Test the model, including residual DF unit root test, residual Ljung-Box Q (LBQ) test and residual white noise test. If there are insignificant parameters, it is necessary to eliminate them and readjust the model structure [35,36]. The white noise test ensures that the model can fully extract the relevant information of the sequence.
2.2.5. Pearson Correlation Coefficient
3. Results
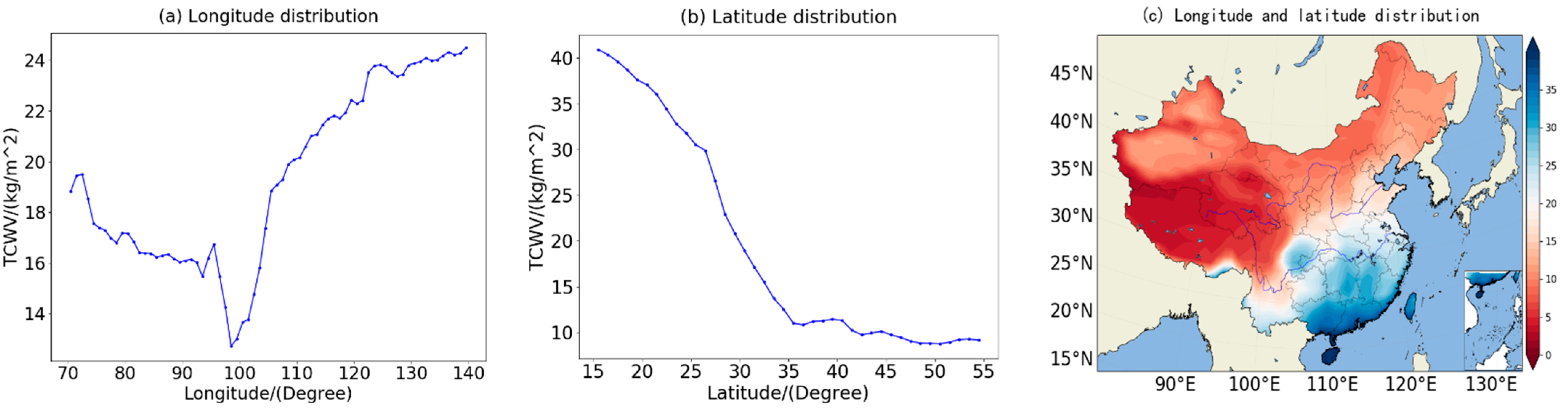
3.1. Spatial Distribution Characteristics of TCWV in China
3.1.1. Spatial Distribution Characteristics of Annual mean TCWV in China
3.1.2. Seasonal Spatial Distribution Characteristics of TCWV
3.1.3. EOF Analysis of TCWV Spatial Distribution in China
3.2. Temporal Variation Characteristics of TCWV in China
3.2.1. The Annual Variation Characteristics and Abrupt Change Analysis of TCWV in China
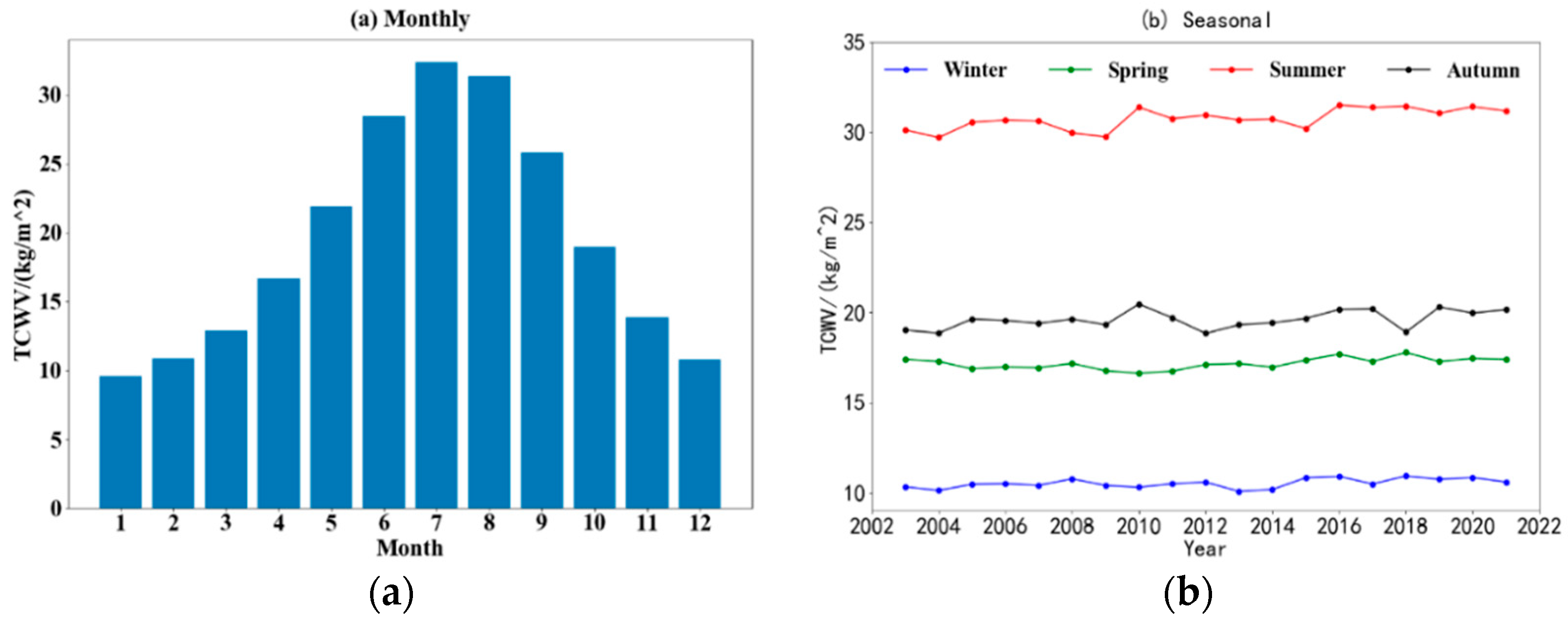
3.2.2. Monthly, Seasonal Variation Characteristics and Abrupt Change Analysis of TCWV in China
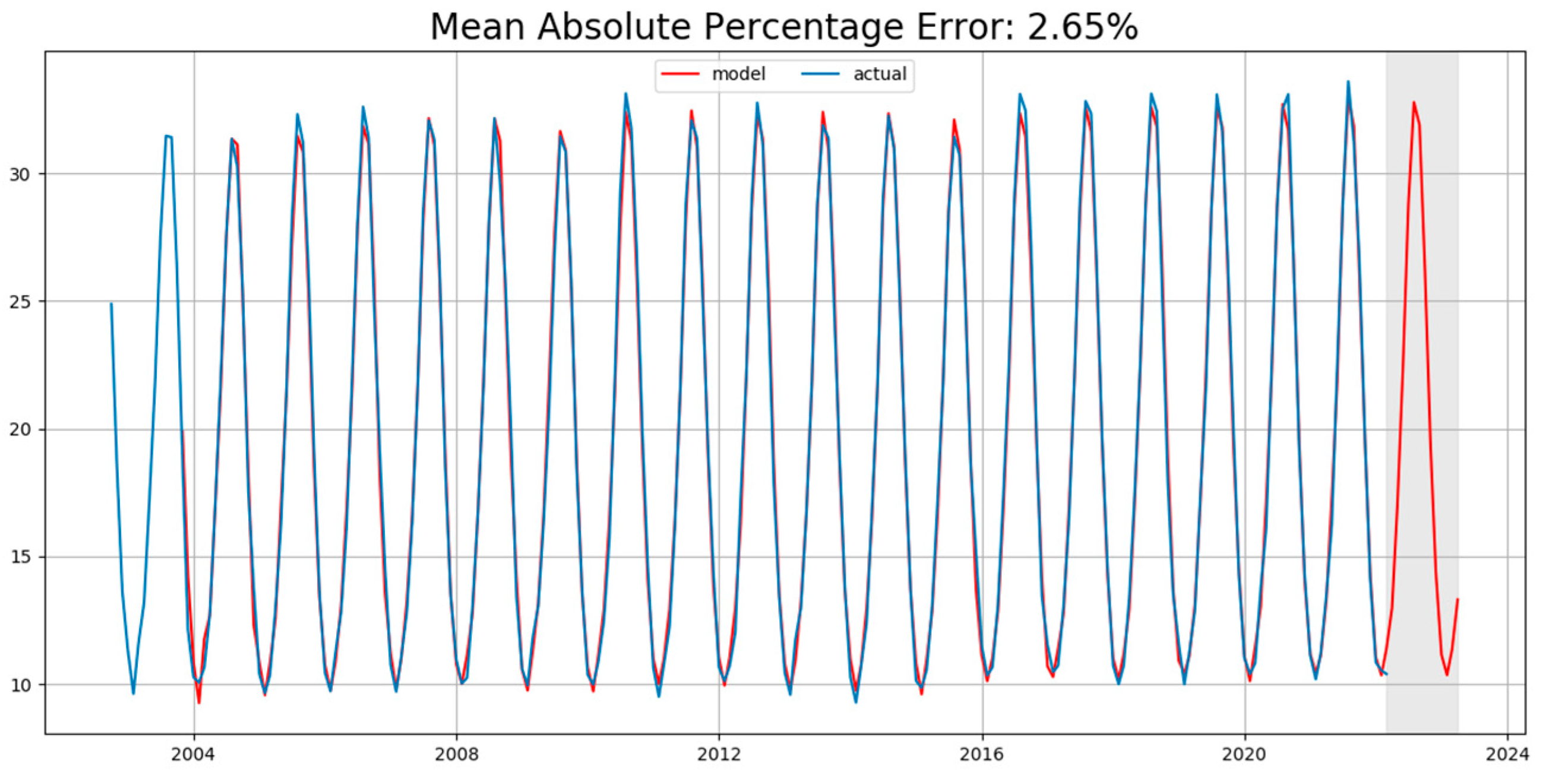
3.2.3. Prediction of TCWV in China Based on SARIMA
4. Discussions
5. Summary
- (1)
- The annual and seasonal distribution of TCWV in China are roughly the same, and have obvious longitude and latitude distribution characteristics. That is, the variation trend of TCWV in China with longitude shows a “V” shape as a whole and the TCWV in China decreases with the increase of latitude. The spatial distribution of TCWV in China has an obvious southeast-northwest direction. Generally, the seasonal variation of the TCWV in the same area is summer > autumn > spring > winter.
- (2)
- By performing EOF decomposition of the TCWV in China, the contribution rate of variance of the first mode is 31.47%, indicating that it can reflect the typical spatial distribution pattern of the TCWV in China, that is, the positive distribution from southeast to northwest.
- (3)
- The TCWV in China showed an overall growth trend, and the M-K mutation test found that there was a significant mutation after 2014. After 2017, the UF value was greater than 1.96, and the upward trend was more obvious. The monthly variation curve shows a slightly positive deviation of the ‘bell-shaped’ curve, while the four seasons M-K curve shows that each has different mutation points.
- (4)
- Using the SARIMA model, considering the trend and seasonality of TCWV time series, the optimal model is obtained. The average absolute error percentage (MAPE), mean square error (MSE), and R2-score are 2.65%, 0.3229 and 0.9949, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varamesh, S.; Hosseini, S.M.; Rahimzadegan, M. Estimation of atmospheric water vapor using MODIS data. J. Mater. Environ. Sci. 2017, 8, 1690–1695. [Google Scholar]
- Moradizadeh, M.; Momeni, M.; Saradjian, M.R. Estimation and validation of atmospheric water vapor content using a MODIS NIR band ratio technique based on AIRS water vapor products. Arab. J. Geosci. 2014, 7, 1891–1897. [Google Scholar] [CrossRef]
- Chang, L.; Gao, G.; Li, Y.; Zhang, Y.; Zhang, C.; Feng, G. Variations in water vapor from AIRS and MODIS in response to Arctic sea ice change in December 2002–November 2016. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7395–7405. [Google Scholar] [CrossRef]
- Skliris, N.; Zika, J.D.; Nurser, G.; Josey, S.A.; Marsh, R. Global water cycle amplifying at less than the Clausius-Clapeyron rate. Sci. Rep. 2016, 6, 38752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raval, A.; Ramanathan, V. Observational determination of the greenhouse effect. Nature 1989, 342, 758–761. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, L.; Gao, T.; Wang, Q.; Lu, C.; Song, Y.; Hua, D. Investigation and Analysis of All-Day Atmospheric Water Vapor Content over Xi’an Using Raman Lidar and Sunphotometer Measurements. Remote Sens. 2018, 10, 951. [Google Scholar] [CrossRef] [Green Version]
- Held, I.M.; Soden, B.J. Robust Responses of the Hydrological Cycle to Global Warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, M.; Yao, X.; Zhang, L.; Zhang, H. Spatiotemporal Variations of Water Vapor Content and Its Relationship with Meteorological Elements in the Third Pole. Water 2021, 13, 1856. [Google Scholar] [CrossRef]
- Gong, S.; Hagan, D.F.T.; Wu, X.; Wang, G. Spatio-temporal analysis of precipitable water vapour over northwest china utilizing MERSI/FY-3A products. Int. J. Remote Sens. 2018, 39, 3094–3110. [Google Scholar] [CrossRef]
- Lu, J.; Xie, F.; Sun, C.; Luo, J.; Cai, Q.; Zhang, J.; Li, J.; Tian, H. Analysis of factors influencing tropical lower stratospheric water vapor during 1980–2017. Npj Clim. Atmos. Sci. 2020, 3, 35. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H. Temporal and Spatial Variations of Precipitation Change from Southeast to Northwest China during the Period 1961–2017. Water 2020, 12, 2622. [Google Scholar] [CrossRef]
- Su, T.; Feng, G. The characteristics of the summer atmospheric water cycle over China and comparison of ERA-Interim and MERRA reanalysis. Acta Phys. Sin. 2014, 63, 249201. [Google Scholar] [CrossRef]
- Hao, W.; Jianxin, H. Temporal and Spatial Evolution Features of Precipitable Water in China during a Recent 65-Year Period (1951–2015). Adv. Meteorol. 2017, 2017, 9156737. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, T. Asian water tower evinced in total column water vapor: A comparison among multiple satellite and reanalysis data sets. Clim. Dyn. 2020, 54, 231–245. [Google Scholar] [CrossRef] [Green Version]
- Tuo, W.; Zhang, X.; Song, C.; Hu, D.; Liang, T. Annual precipitation analysis and forecasting–taking Zhengzhou as an example. Water Supply 2020, 20, 1604–1616. [Google Scholar] [CrossRef] [Green Version]
- Hellen, W.K.; John, M.K.; George, O.O.; Yodah, W.O. Forecasting Precipitation Using SARIMA Model: A Case Study of Mt. Kenya Region. Math. Theory Modeling 2014, 4, 50–58. [Google Scholar]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Alraddawi, D.; Sarkissian, A.; Keckhut, P.; Bock, O.; Noël, S.; Bekki, S.; Irbah, A.; Meftah, M.; Claud, C. Comparison of total water vapour content in the Arctic derived from GNSS, AIRS, MODIS and SCIAMACHY. Atmos. Meas. Tech. 2018, 11, 2949–2965. [Google Scholar] [CrossRef] [Green Version]
- Parkinson, C.L. Aqua: An Earth-Observing Satellite mission to examine water and other climate variables. IEEE Trans. Geosci. Remote Sens. 2003, 41, 173–183. [Google Scholar] [CrossRef]
- Tobin, D.C.; Revercomb, H.E.; Knuteson, R.O.; Lesht, B.M.; Larrabee Strow, L.L.; Hannon, S.E.; Feltz, W.F.; Moy, L.A.; Fetzer, E.J.; Cress, T.S. Atmospheric Radiation Measurement site atmospheric state best estimates for Atmospheric Infrared Sounder temperature and water vapor retrieval validation. J. Geophys. Res. Atmos. 2006, 111, 17884115. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Hagan, D.F.T.; Liu, Y. Global land surface temperature change (2003–2017) and its relationship with climate drivers: Airs, MODIS, and ERA5-land based analysis. Remote Sens. 2020, 13, 44. [Google Scholar] [CrossRef]
- Bi, S.; Qiu, X.; Wang, G.; Gong, Y.; Wang, L.; Xu, M. Spatial distribution characteristics of drought disasters in Hunan Province of China from 1644 to 1911 based on EOF and REOF methods. Environ. Earth Sci. 2021, 80, 533. [Google Scholar] [CrossRef]
- Qinzheng, L.; Peng, C.; Sun, L.; Ma, X. A global weighted mean temperature model based on empirical orthogonal function analysis. Adv. Space Res. 2018, 61, 1398–1411. [Google Scholar] [CrossRef]
- Fu, D.; Huang, Y.; Liu, D.; Liao, S.; Yu, G.; Zhang, X. Analysis of the regional spectral properties in northwestern South China Sea based on an empirical orthogonal function. Acta Oceanol. Sin. 2020, 39, 107–114. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Wei, J.; Kang, B.; Li, T.; Wang, G. Spatial and temporal characteristics of atmospheric water vapour content and its relationship with precipitation conversion in China during 1980–2016. Int. J. Climatol. 2021, 41, 1747–1766. [Google Scholar] [CrossRef]
- Kendall, M. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend Analysis in Reference Evapotranspiration Using Mann-Kendall and Spearman’s Rho Tests in Arid Regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.B.; Wang, Q. The definition and detection of the abrupt climate change. Atmos. Sci. 1992, 16, 482–492. [Google Scholar]
- Xing, L.; Huang, L.; Chi, G.; Yang, L.; Li, C.; Hou, X. A dynamic study of a karst spring based on wavelet analysis and the Mann-Kendall Trend Test. Water 2018, 10, 698. [Google Scholar] [CrossRef] [Green Version]
- Dubey, A.K.; Kumar, A.; García-Díaz, V.; Kumar Sharma, A.; Kanhaiya, K. Study and analysis of SARIMA and LSTM in forecasting time series data. Sustain. Energy Technol. Assess. 2021, 47, 101474. [Google Scholar] [CrossRef]
- Song, Z.; Guo, Y.; Wu, Y.; Ma, J. Short-term traffic speed prediction under different data collection time intervals using a SARIMA-SDGM hybrid prediction model. PLoS ONE 2019, 14, e0218626. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Melkumian, A.V. Forecasting Australian Red Wine Sales with SARIMA and ANNs. In Proceedings of the 2020 International Symposium on Frontiers of Economics and Management Science (FEMS 2020), Dalian, China, 20–21 March 2020; Wuhan University of Technology: Wuhan, China, 2020; pp. 147–151. [Google Scholar] [CrossRef]
- Yaya, O.S.; Fashae, O.A. Seasonal fractional integrated time series models for rainfall data in Nigeria. Theor. Appl. Climatol. 2015, 120, 99–108. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, N.; Liu, S.; Jiang, Q.; Zhang, N. Application of time series model and LSTM model in water quality prediction. Miniat. Microcomput. Syst. 2022, 42, 5. [Google Scholar]
- Dimri, T.; Ahmad, S.; Sharif, M. Time series analysis of climate variables using seasonal ARIMA approach. J. Earth Syst. Sci. 2020, 129, 149. [Google Scholar] [CrossRef]
- Moeeni, H.; Bonakdari, H.; Ebtehaj, I. Monthly reservoir inflow forecasting using a new hybrid SARIMA genetic programming approach. J. Earth Syst. Sci. 2017, 126, 18. [Google Scholar] [CrossRef]
- Wypych, A.; Bochenek, B.; Różycki, M. Atmospheric moisture content over Europe and the Northern Atlantic. Atmosphere 2018, 9, 18. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Yan, Z.; Li, Z. Spatial and Temporal Variations of Extreme Precipitation in Central Asia during 1982–2020. Atmosphere 2021, 13, 60. [Google Scholar] [CrossRef]
- Gaffen, D.J.; Elliott, W.P.; Robock, A. Relationships between tropospheric water vapor and surface temperature as observed by radiosondes. Geophys. Res. Lett. 1992, 19, 1839–1842. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhao, T. Historical and future changes of atmospheric precipitable water over China simulated by CMIP5 models. Clim. Dyn. 2019, 52, 6969–6988. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Shi, X.; Gao, S. World water tower: An atmospheric perspective. Geophys. Res. Lett. 2008, 35, L20815. [Google Scholar] [CrossRef]
- Jiang, Z.; Jiang, S.; Shi, Y.; Liu, Z.; Li, W.; Li, L. Impact of moisture source variation on decadal-scale changes of precipitation in North China from 1951 to 2010. J. Geophys. Res. Atmos. 2017, 122, 600–613. [Google Scholar] [CrossRef]
- Jia, X.J.; You, Y.J.; Wu, R.G.; Yang, Y. Interdecadal changes in the dominant modes of the interannual variation of spring precipitation over China in the mid-1980s. J. Geophys. Res. Atmos. 2019, 124, 10676–10695. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, S.; Lin, H.; Wei, Y.; Tang, C. Spatiotemporal Modes Characteristics and SARIMA Prediction of Total Column Water Vapor over China during 2002–2022 Based on AIRS Dataset. Atmosphere 2022, 13, 885. https://doi.org/10.3390/atmos13060885
Shangguan S, Lin H, Wei Y, Tang C. Spatiotemporal Modes Characteristics and SARIMA Prediction of Total Column Water Vapor over China during 2002–2022 Based on AIRS Dataset. Atmosphere. 2022; 13(6):885. https://doi.org/10.3390/atmos13060885
Chicago/Turabian StyleShangguan, Shanshan, Han Lin, Yuanyuan Wei, and Chaoli Tang. 2022. "Spatiotemporal Modes Characteristics and SARIMA Prediction of Total Column Water Vapor over China during 2002–2022 Based on AIRS Dataset" Atmosphere 13, no. 6: 885. https://doi.org/10.3390/atmos13060885
APA StyleShangguan, S., Lin, H., Wei, Y., & Tang, C. (2022). Spatiotemporal Modes Characteristics and SARIMA Prediction of Total Column Water Vapor over China during 2002–2022 Based on AIRS Dataset. Atmosphere, 13(6), 885. https://doi.org/10.3390/atmos13060885





