The Impact of Assimilating Winds Observed during a Tropical Cyclone on a Forecasting Model
Abstract
:1. Introduction
2. Methodology
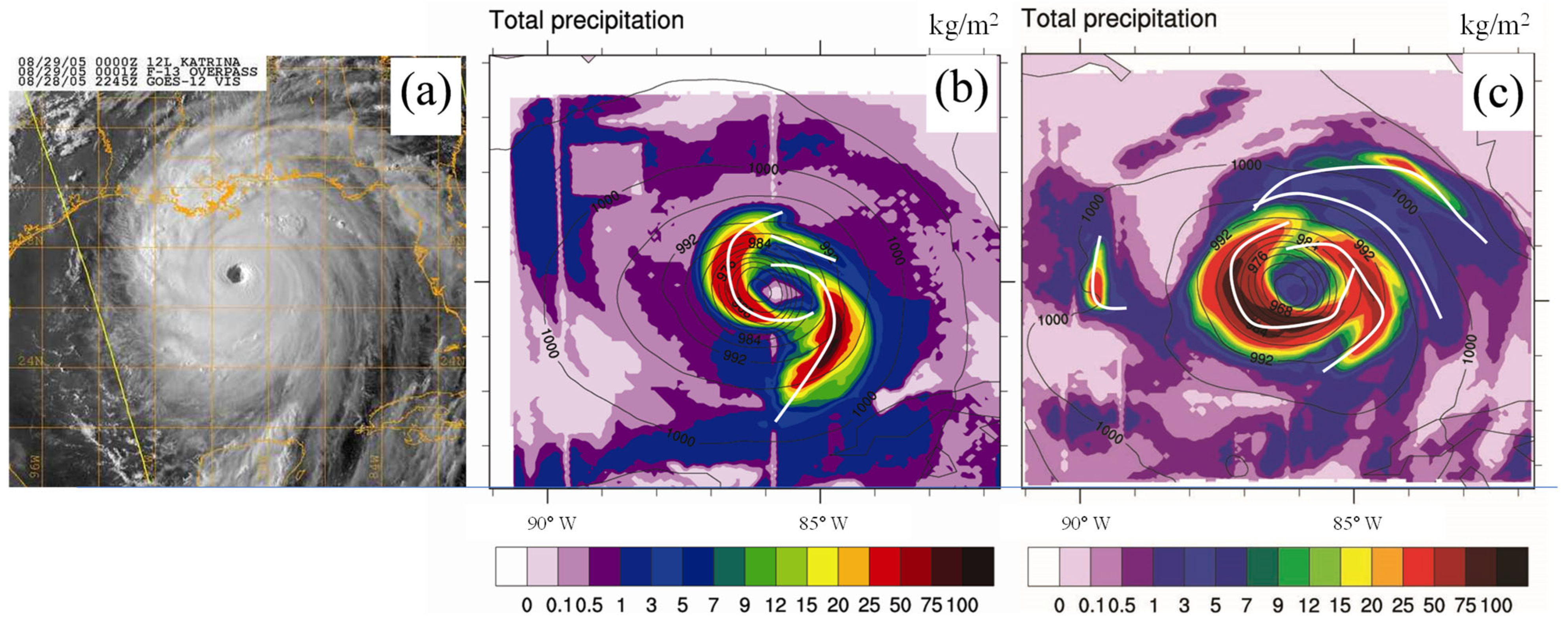
2.1. Brief Description of Hurricanes Katrina and Dennis (2005)
2.2. Hurricane Local Analysis and Prediction System
2.3. Hurricane Research System
2.4. Validation Data
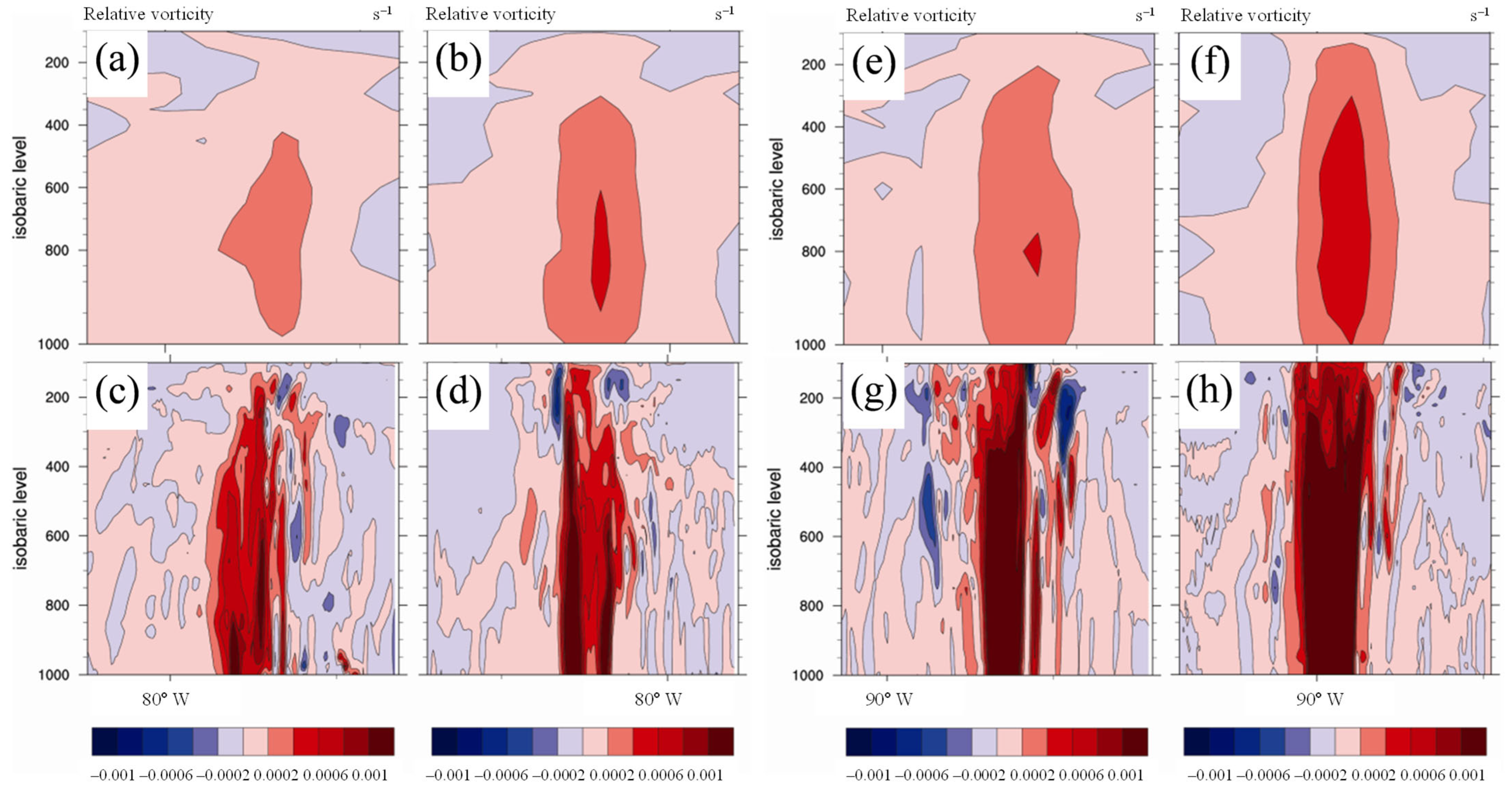
3. Results
3.1. Model Initialization
3.2. Impact of Data Assimilation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frank, W.M.; Young, G.S. The interannual variability of tropical cyclones. Mon. Weather Rev. 2007, 135, 3587–3598. [Google Scholar] [CrossRef]
- Pielke, J.R.A.; Gratz, J.; Landsea, C.W.; Collins, D.; Saunders, M.A.; Musulin, R. Normalized hurricane damage in the United States: 1900–2005. Nat. Hazards Rev. 2008, 9, 30–42. [Google Scholar] [CrossRef]
- Weinkle, J.; Maue, R.; Pielke, J.R. Historical global tropical cyclone landfalls. J. Clim. 2012, 25, 4729–4735. [Google Scholar] [CrossRef]
- Done, J.M.; Simmons, K.M.; Czajkowski, J. Relationship between residential losses and hurricane winds: Role of the Florida building code. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civ. Eng. 2018, 4, 04018001. [Google Scholar] [CrossRef]
- Munich, R. Topics Geo Natural Catastrophes 2017: Analyses, Assessments, Positions. Available online: www.readkong.com/page/a-stormy-year-topics-geo-natural-catastrophes-2017-6234005 (accessed on 16 August 2022).
- Liu, K.S.; Chang, J.C.L. Recent increase in extreme intensity of tropical cyclones making landfall in South Korea. Clim. Dyn. 2020, 55, 1059–1074. [Google Scholar] [CrossRef]
- Elsberry, R.L.; Marks, F.D. The Hurricane Landfall Workshop summary. Bull. Am. Meteorol. Soc. 1999, 80, 683–685. [Google Scholar]
- Aberson, S.D.; Etherton, B.J. Targeting and data assimilation studies during Hurricane Humberto (2001). J. Atmos. Sci. 2006, 63, 175–186. [Google Scholar] [CrossRef]
- Davis, C.; Wang, W.; Chen, S.; Chen, Y.; Corbosiero, K.; DeMaria, M.; Dudhia, J.; Holland, G.; Klenmp, J.; Michalakes, J.; et al. Prediction of landfalling hurricanes with the advanced hurricane WRF model. Mon. Weather Rev. 2008, 136, 1990–2005. [Google Scholar] [CrossRef]
- Zhang, F.; Sippel, J.A. Effects of moist convection on hurricane predictability. J. Atmos. Sci. 2009, 66, 1944–1961. [Google Scholar] [CrossRef]
- Pattanayak, S.; Mohanty, U.C.; Osuri, K.K. Impact of Parameterization of Physical Processes on Simulation of Track and Intensity of Tropical Cyclone Nargis (2008) with WRF-NMM Model. Sci. World J. 2012, 2012, 671437. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Z.; Zhang, F.; Weng, Y. Predictability of tropical cyclone intensity evaluated through 5-yr forecasts with a convection-permitting regional-scale model in the Atlantic Basin. Weather Forecast. 2014, 29, 1003–1023. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Li, Y.; Tong, M.; Ma, X. GSI-based ensemble-variational hybrid data assimilation for HWRF for hurricane initialization and prediction: Impact of various error covariances for airborne radar observation assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 223–239. [Google Scholar] [CrossRef]
- Zhu, P.; Zhu, Z.; Gopalakrishnan, S.; Black, R.; Marks, F.D.; Tallapragada, V.; Zhang, J.A.; Zhang, X.; Gao, C. Impact of subgrid-scale processes on eyewall replacement cycle of tropical cyclones in HWRF system. Geophys. Res. Lett. 2015, 42, 10,027–10,036. [Google Scholar] [CrossRef]
- Pu, Z.; Li, X.; Sun, J. Impact of airborne Doppler radar data assimilation on the numerical simulation of intensity changes of Hurricane Dennis near a landfall. J. Atmos. Sci. 2009, 66, 3351–3365. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, F. Assimilating airborne Dopplr radar observations with ensemble Kalman filter for convection-permitting hurricane initialization and prediction: Katrina (2005). Mon. Weather Rev. 2012, 140, 841–859. [Google Scholar] [CrossRef]
- Aksoy, A.; Lorsolo, S.; Vukicevic, T.; Sellwood, K.J.; Aberson, S.D.; Zhang, F. The HWRF Hurricane Ensemble Data Assimilation System (HEDAS) for high-resolution data: The impact of airborne Doppler radar observations in an OSSE. Mon. Weather Rev. 2012, 140, 1843–1862. [Google Scholar] [CrossRef]
- Du, N.; Xue, M.; Zhao, K.; Min, J. Impact of assimilating airborne Doppler radar velocity data using the ARPS 3DVAR on the analysis and prediction of Hurricane Ike (2008). J. Geophys. Res. 2012, 117, D18113. [Google Scholar] [CrossRef]
- Tong, M.; Sippel, J.A.; Tallagragada, V.; Liu, E.; Kieu, C.; Kwon, I.H.; Wang, W.; Liu, Q.; Ling, Y.; Zhang, B. Impact of Assimilating Aircraft Reconnaissance Observations on Tropical Cyclone Initialization and Prediction Using Operational HWRF and GSI Ensemble-Variational Hybrid Data Assimilation. Mon. Weather Rev. 2018, 146, 4155–4177. [Google Scholar] [CrossRef]
- Elsberry, R.L.; Hendricks, E.A.; Velden, C.S.; Bell, M.M.; Peng, M.; Casas, E.; Zhao, Q. Demonstration with special TCI-15 datasets of potential impacts of new-generation satellite atmospheric motion vectors on Navy regional and global models. Weather Forecast. 2018, 33, 1617–1637. [Google Scholar] [CrossRef]
- Minanmide, M.; Zhang, F. Assimilation of all-sky infrared radiances from Himawari-8 and impacts of moisture and hydrometer initialization on convection-permitting tropical cyclone prediction. Mon. Weather Rev. 2018, 146, 3241–3258. [Google Scholar] [CrossRef]
- Sawada, M.; Ma, Z.; Mehra, A.; Tallapragada, V.; Oyama, R.; Shimoji, K. Assimilation of himawari-8 rapid-scan atmospheric motion vectors on tropical cyclone in HWRF system. Atmosphere 2020, 11, 601. [Google Scholar] [CrossRef]
- Tian, X.; Zou, X. A comprehensive 4D-Var vortex initialization using a nonhydrostatic axisymmetric TC model with convection accounted for. Tellus A Dyn. Meteorol. Oceanogr. 2019, 71, 1653138. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, Z. Numerical simulation of rapid weakening of Hurricane Joaquin with assimilation of high-definition sounding system dropsondes during the tropical cyclone intensity experiment: Comparison of three- and four-dimensional ensemble-variational data assimilation. Weather Forecast. 2019, 34, 521–538. [Google Scholar] [CrossRef]
- Chang, Y.P.; Yang, S.C.; Lin, K.J.; Lien, G.Y.; Wu, C.M. Osse assessment of underwater glider arrays to improve ocean model initialization for tropical cyclone prediction. J. Atmos. Sci. 2010, 77, 467–487. [Google Scholar]
- Dong, J.; Xue, M. Assimilation of radial velocity and reflectivity data from coastal WSR-88D radars using an ensemble Kalman filter for the analysis and forecast of landfalling hurricane Ike (2008). Q. J. R. Meteorol. Soc. 2013, 139, 467–487. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Gamache, J.F.; Marks, F.D. Performance of convection-permitting hurricane initialization and prediction during 2008–2010 with ensemble data assimilation of inner-core airborne Doppler radar observations. Geophys. Res. Lett. 2011, 38, L15810. [Google Scholar] [CrossRef]
- Beven, J. Tropical Cyclone Report Hurricane Dennis 4–13 July 2005. Available online: https://www.nhc.noaa.gov/data/tcr/AL042005_Dennis.pdf (accessed on 16 August 2022).
- Knabb, R.D.; Rhome, J.R.; Brown, D.P. Tropical Cyclone Report Hurricane Katrina 23–30 August 2005. Available online: https://www.nhc.noaa.gov/data/tcr/AL122005_Katrina.pdf (accessed on 16 August 2022).
- Snook, J.S.; Cram, J.M. Schmidt JM. LAPS/RAMS. A nonhydrostatic mesoscale numerical modeling system configured for operational use. Tellus A Dyn. Meteorol. Oceanogr. 1995, 47, 864–875. [Google Scholar] [CrossRef]
- Jian, G.J.; McGinley, J.A. Evaluation of a short-range forecast system on quantitative precipitation forecasts associated with tropical cyclones of 2003 near Taiwan. J. Meteorol. Soc. Jpn. 2005, 83, 657–681. [Google Scholar] [CrossRef]
- Gregow, E.; Pressi, A.; Mäkelä, A.; Saltikoff, E. Improving the precipitation accumulation analysis using lightning measurements and different integration periods. Hydrol. Earth Syst. Sci. 2017, 21, 267–279. [Google Scholar] [CrossRef]
- Albers, S.C.; McGinley, J.A.; Birkenheuer, D.L.; Smart, J.R. The Local Analysis and Prediction System (LAPS): Analyses of Clouds, Precipitation, and Temperature. Weather Forecast. 1996, 11, 273–287. [Google Scholar] [CrossRef]
- Xie, Y.; Koch, S.; McGinley, J.; Albers, S.; Beringer, P.; Wolfson, M.; Chang, M. A space-time multiscale analysis system: A sequential variational analysis approach. Mon. Weather Rev. 2011, 139, 1224–1240. [Google Scholar] [CrossRef]
- Kim, O.Y.; Lu, C.; McGinley, J.A.; Albers, S.C.; Oh, J.H. Experiments of LAPS wind and temperature analysis with background error statistics obtained using ensemble methods. Atmos. Res. 2013, 122, 250–269. [Google Scholar] [CrossRef]
- Jiang, H.; Albers, S.; Xie, Y.; Toth, Z.; Jankove, I.; Scotten, M.; Picca, J.; Stumpf, G.; Kingfield, D.; Birkenheuer, D. Real-Time Applications of the Variational Version of the Local Analysis and Prediction System (vLAPS). Bull. Am. Meteorol. Soc. 2016, 80, 683–685. [Google Scholar] [CrossRef]
- McGinley, J.A.; Albers, S.C.; Stamus, P.A. Validation of a Composite Convective Index as Defined by a Real-Time Local Analysis System. Weather Forecast. 1991, 6, 337–356. [Google Scholar] [CrossRef]
- Rogers, R.; Aberson, S.; Aksoy, A.; Annane, B.; Black, M.; Cione, J.; Dorst, N.; Dunion, J.; Gamache, J.; Goldenberg, S.; et al. NOAA’S Hurricane Intensity Forecasting Experiment: A Progress Report. Bull. Am. Meteorol. Soc. 2013, 94, 859–882. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Liu, Q.; Marchok, T.; Sheinin, D.; Surgi, N.; Tuleya, R.; Yablonski, R.; Zhang, X. Hurricane Weather Research and Forecasting (HWRF) Scientific Documentation. Available online: https://dtcenter.org/sites/default/files/community-code/hwrf/docs/scientific_documents/HWRFv4.0a_ScientificDoc.pdf (accessed on 16 August 2022).
- Gopalakrishnan, S.G.; Bacon, D.P.; Ahmad, N.N.; Boybeyi, Z.; Dunn, T.J.; Hall, M.S.; Jin, Y.; Lee, P.C.S.; Mays, D.E.; Madala, R.V.; et al. An operational multiscale hurricane forecasting system. Mon. Weather Rev. 2002, 130, 1830–1847. [Google Scholar] [CrossRef]
- Ferrier, B.S.; Tao, W.-K.; Simpson, J. A double-moment multiplephase four-class bulk ice scheme. Part II: Simulations of convective storms in different large-scale environments and comparisons with other bulk parameterizations. J. Atmos. Sci. 1995, 52, 1001–1033. [Google Scholar] [CrossRef]
- Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer sensitivity to surface evaporation. Bound.-Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Janjić, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model; Office Note No. 437; National Centers for Environmental Prediction: Washington, DC, USA, 2001; p. 61.
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J. Clough SA. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Phillips, N.A.; Shukla, J. On the strategy of combining coarse and fine grid meshes in numerical weather prediction. J. Appl. Meteorol. Climatol. 1973, 12, 763–770. [Google Scholar] [CrossRef]
- Bielli, S.; Barthe, C.; Bousquet, O.; Tulet, P.; Pianezze, J. The Effect of Atmosphere-Ocean Coupling on the Structure and Intensity of Tropical Cyclone Bejisa in the Southwest Indian Ocean. Atmosphere 2021, 12, 688. [Google Scholar] [CrossRef]
- Manaster, A.; Ricciardulli, L.; Meissner, T. Tropical Cyclone Winds from WindSat, AMSR2, and SMAP: Comparison with the HWRF Model. Remote Sens. 2021, 13, 2347. [Google Scholar] [CrossRef]
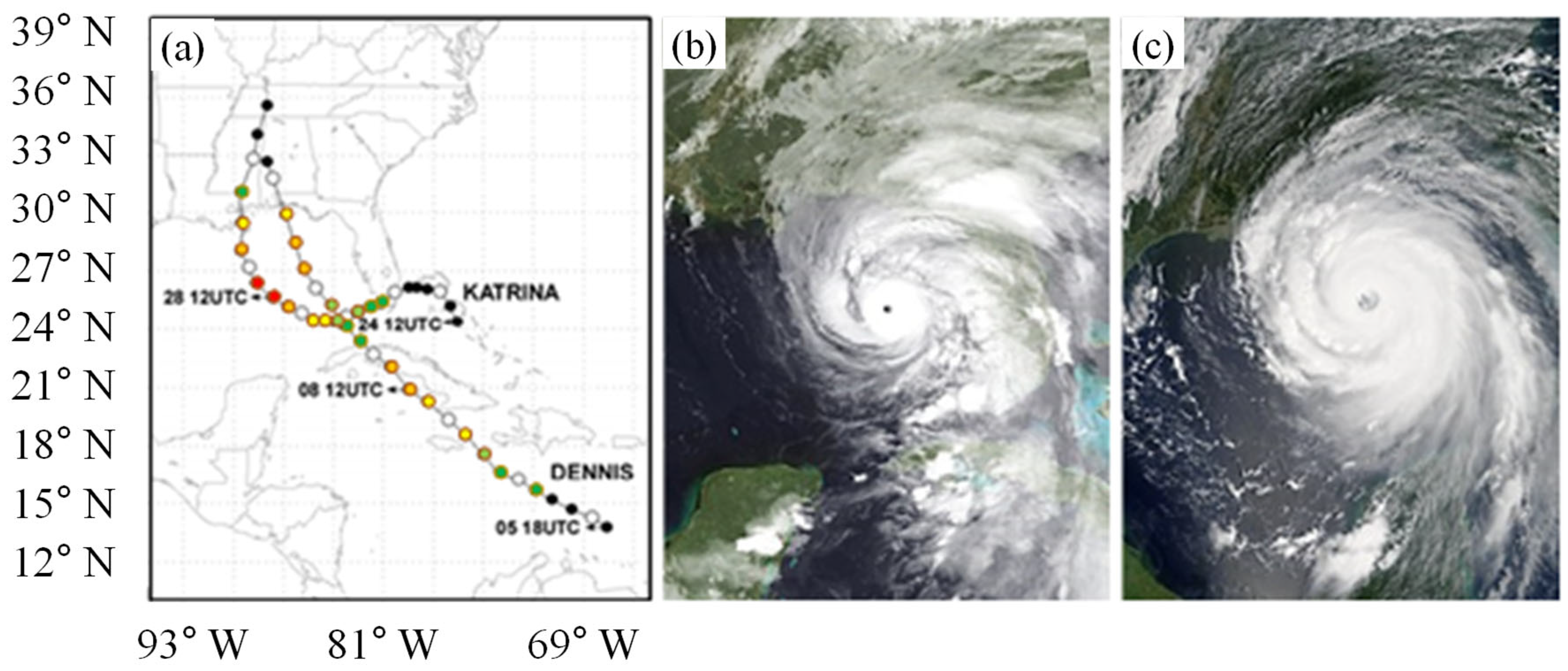
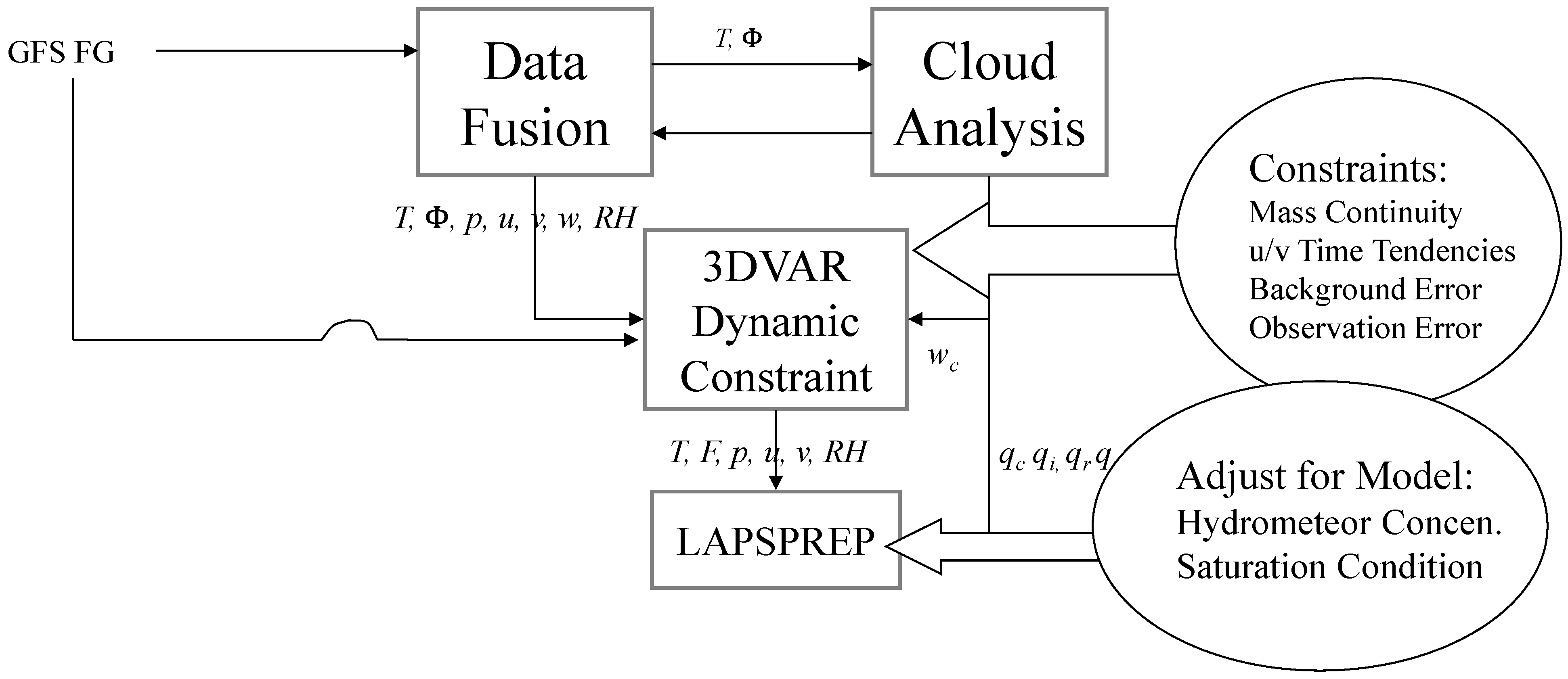
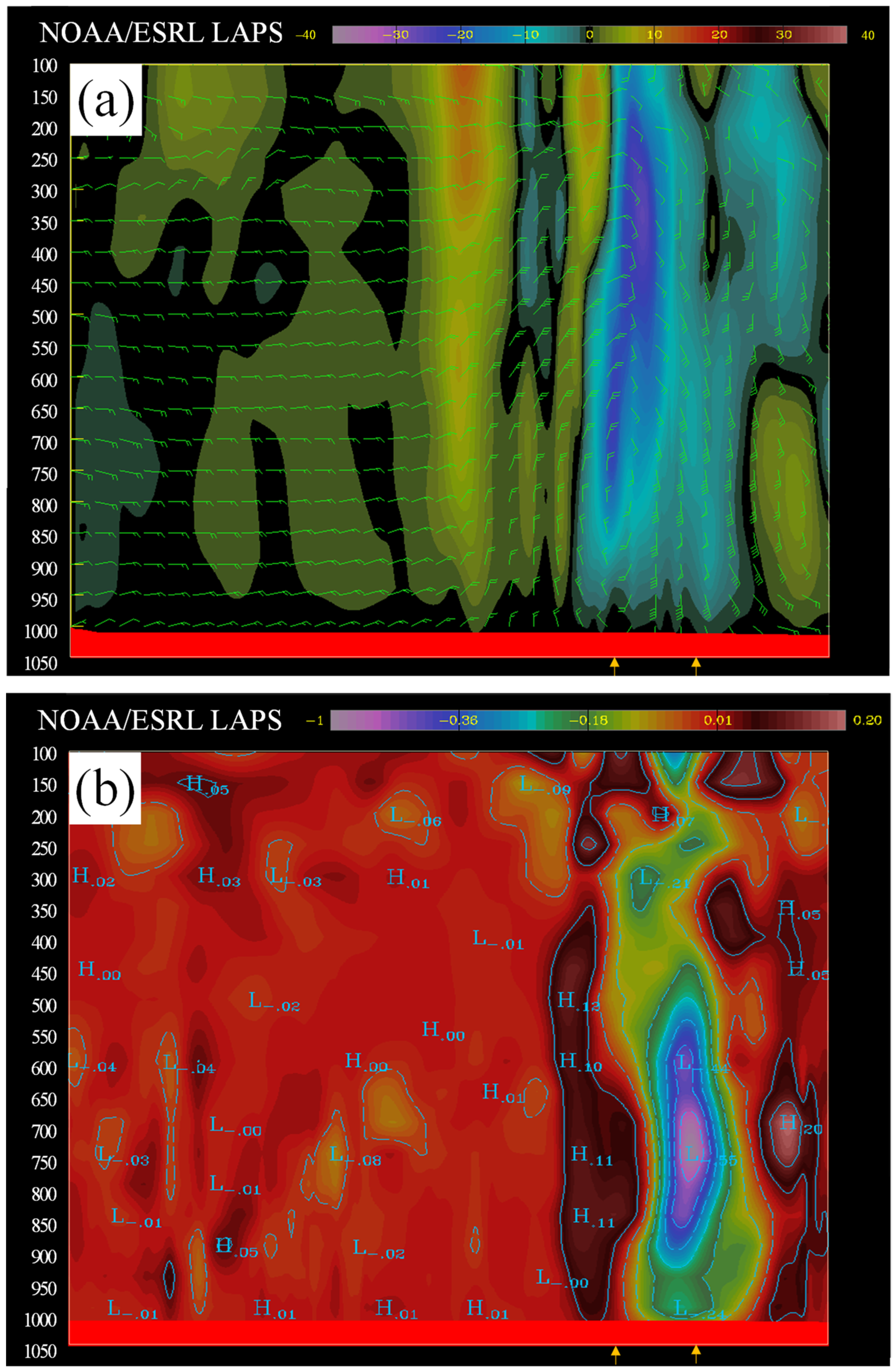




| Category | Description | |
|---|---|---|
| Grid dimensions | 309 × 317 | 133 × 157 |
| Horizontal-grid increments | 19.8 km | 6.6 km |
| Vertical levels | 41, top at 50 hPa | |
| Physical parameterization | ||
| Thermodynamics | Ferrier (new Eta) microphysics | |
| Radiation parameterization | RRTM longwave and Dudhia shortwave scheme | |
| Cumulus parameterization | Simplified Arakawa–Schubert (SAS) scheme | |
| PBL parameterization | Mellor–Yamada–Janjic TKE scheme | |
| Initial conditions | Hurricane Local Analysis and Prediction System | |
| Lateral boundary conditions | Global Forecasting System | |
| TC | Variable | 0 h | 6 h | 12 h | 18 h | 24 h | 48 h | 72 h |
|---|---|---|---|---|---|---|---|---|
| Dennis | ||||||||
| GFS | Dist (km) MLSP (hPa) MWS (knots) | 19.46 24.67 25.05 | 58.25 38.00 1.65 | 59.29 39.67 −15.50 | 69.51 46.34 −23.85 | 88.97 49.00 −57.25 | 89.17 37.00 −23.85 | 88.72 48.80 −66.70 |
| HRS | Dist (km) MLSP (hPa) MWS (knots) | 19.46 9.00 −7.25 | 94.47 25.00 −22.75 | 75.62 30.70 −46.70 | 117.53 31.60 −43.30 | 200.70 36.90 −79.45 | 204.58 26.30 −57.25 | 239.33 34.20 −67.25 |
| HRS/HLAPS | Dist (km) MLSP (hPa) MWS (knots) | 5.56 8.00 −7.00 | 65.11 16.50 −1.65 | 63.03 25.30 −28.90 | 100.77 34.60 −29.00 | 140.95 40.60 −51.10 | 203.56 29.30 −39.45 | 142.20 15.70 −23.95 |
| Katrina | ||||||||
| GFS | Dist (km) MLSP (hPa) MWS (knots) | 27.38 54.50 −37.60 | 53.20 45.50 −38.60 | 8.40 39.00 −38.40 | 42.53 50.00 −64.60 | 22.44 70.50 −83.35 | 190.78 40.50 −48.35 | 349.35 14.00 27.80 |
| HRS | Dist (km) MLSP (hPa) MWS (knots) | 23.67 33.50 −33.40 | 14.10 9.50 −33.90 | 47.60 15.50 −11.10 | 63.47 24.00 −37.10 | 96.98 29.00 −53.35 | 131.93 −22.00 40.00 | 170.73 −24.50 26.70 |
| HRS/HLAPS | Dist (km) MLSP (hPa) MWS (knots) | 14.45 1.00 −12.30 | 33.79 14.00 −13.80 | 37.52 20.00 −7.25 | 53.01 31.00 −36.10 | 97.93 32.00 −51.15 | 49.36 −3.00 11.65 | 98.57 −1.50 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-Y.; Albers, S.; Sen, P.; Kim, H.-G.; Kim, K.; Hwang, S.-J. The Impact of Assimilating Winds Observed during a Tropical Cyclone on a Forecasting Model. Atmosphere 2022, 13, 1302. https://doi.org/10.3390/atmos13081302
Kim J-Y, Albers S, Sen P, Kim H-G, Kim K, Hwang S-J. The Impact of Assimilating Winds Observed during a Tropical Cyclone on a Forecasting Model. Atmosphere. 2022; 13(8):1302. https://doi.org/10.3390/atmos13081302
Chicago/Turabian StyleKim, Jin-Young, Steve Albers, Purnendranath Sen, Hyun-Goo Kim, Keunhoon Kim, and Su-Jin Hwang. 2022. "The Impact of Assimilating Winds Observed during a Tropical Cyclone on a Forecasting Model" Atmosphere 13, no. 8: 1302. https://doi.org/10.3390/atmos13081302






