Evaluating Soil Temperature Variations for Enhanced Radon Monitoring in Volcanic Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement Site
2.2. Measurement Method
2.3. Numerical Modelling
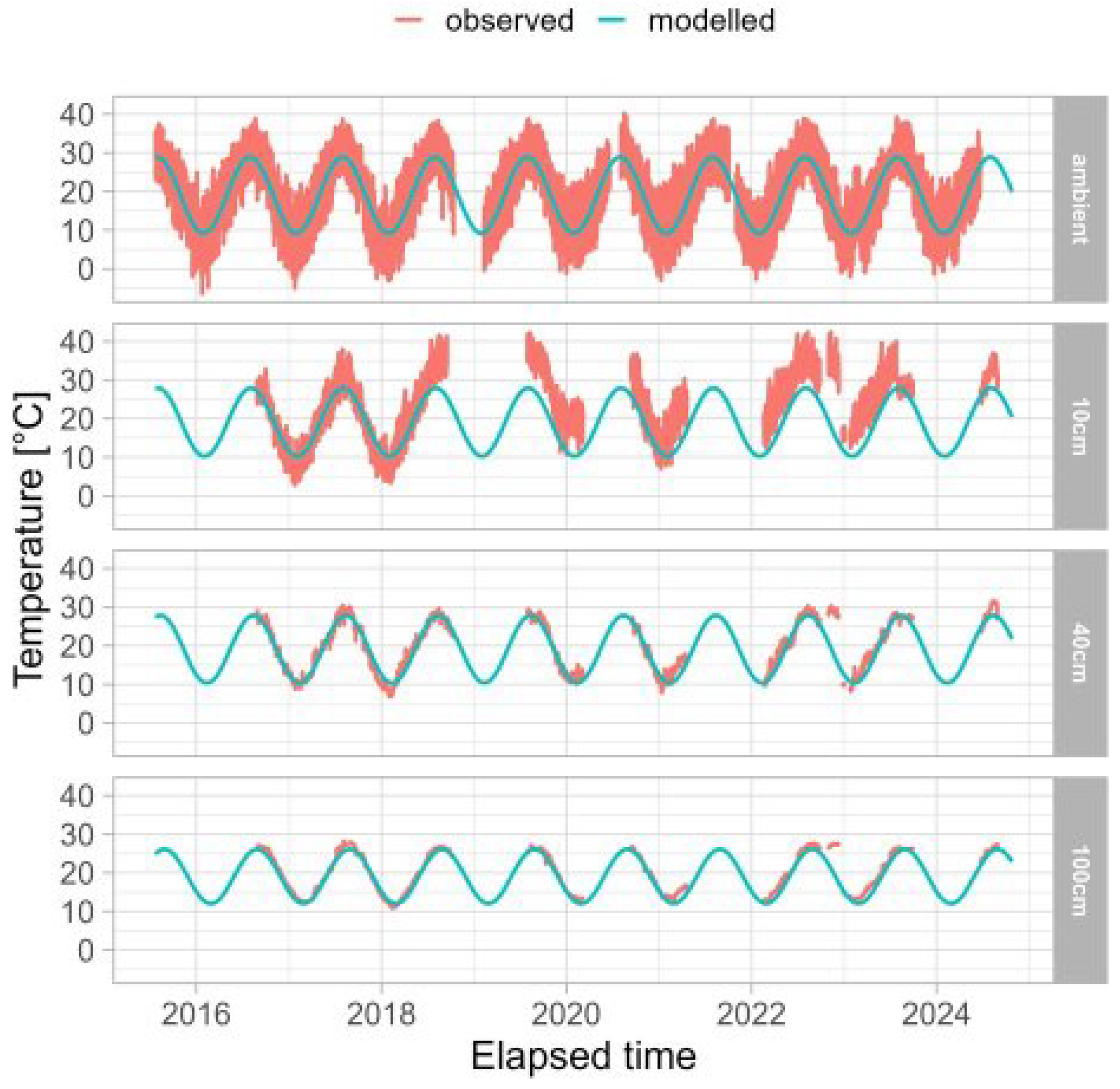
3. Results and Data Analysis
3.1. Data Analysis
3.2. Modelling
3.3. Temperature Model Application
3.4. Limitations
4. Conclusions
- Soil temperature models can be refined by incorporating the observed depth-dependent thermal diffusivity, leading to more accurate predictions of subsurface thermal regimes.
- Furthermore, there is a need to investigate the complex interplay between soil moisture, meteorological parameters, and subsurface temperature variations.
- Exploration of the correlation between volcanic activity and measured temperature fluctuations is recommended, with the aim of improving our understanding of subsurface thermal responses to volcanic processes.
- The optimal sensor placement depths identified in this study should be utilized for enhanced monitoring of various subsurface processes, including but not limited to gas transport and heat flow.
- Addressing discrepancies observed at shallow depths (10 cm) by conducting targeted investigations into potential sensor malfunctions or localized soil condition effects to ensure the robustness of future datasets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sousa, J.J.; Liu, G.; Fan, J.; Perski, Z.; Steger, S.; Bai, S.; Wei, L.; Salvi, S.; Wang, Q.; Tu, J.; et al. Geohazards Monitoring and Assessment Using Multi-Source Earth Observation Techniques. Remote Sens. 2021, 13, 4269. [Google Scholar] [CrossRef]
- Wang, C.Y.; Manga, M. Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources. Water 2023, 15, 1327. [Google Scholar] [CrossRef]
- Koizumi, N.; Sato, T.; Kitagawa, Y.; Ochi, T. Groundwater pressure changes and crustal deformation before and after the 2007 and 2014 eruptions of Mt. Ontake the Phreatic Eruption of Mt. Ontake Volcano in 2014 5. Volcanology. Earth Planets Space 2016, 68, 6–11. [Google Scholar] [CrossRef]
- Kotsarenko, A.; Yutsis, V.; Grimalsky, V.; Koshevaya, S.; Kotsarenko, Y. Anomalous temperature regimen in the near-surface soil layer of Tlamacas hill and its relation to activity of Popocatepetl Volcano, Mexico. BSGF-Earth Sci. Bull. 2020, 191, 3. [Google Scholar] [CrossRef]
- Yang, T.F.; Wen, H.Y.; Fu, C.C.; Lee, H.F.; Lan, T.F.; Chen, A.T.; Hong, W.L.; Lin, S.J.; Walia, V. Soil radon flux and concentrations in hydrothermal area of the Tatun Volcano Group, Northern Taiwan. Geochem. J. 2011, 45, 483–490. [Google Scholar] [CrossRef]
- Cigolini, C.; Poggi, P.; Ripepe, M.; Laiolo, M.; Ciamberlini, C.; Delle Donne, D.; Ulivieri, G.; Coppola, D.; Lacanna, G.; Marchetti, E.; et al. Radon surveys and real-time monitoring at Stromboli volcano: Influence of soil temperature, atmospheric pressure and tidal forces on 222Rn degassing. J. Volcanol. Geotherm. Res. 2009, 184, 381–388. [Google Scholar] [CrossRef]
- Hosoda, M.; Tokonami, S.; Suzuki, T.; Janik, M. Machine learning as a tool for analysing the impact of environmental parameters on the radon exhalation rate from soil. Radiat. Meas. 2020, 138, 106402. [Google Scholar] [CrossRef]
- Geological Survey of Japan AIST. Geological map of Japan, Kagoshima. Available online: https://www.gsj.jp/Map/EN/geology4-15.html (accessed on 1 April 2025).
- Janik, M.; Gomez, C.; Kodaira, S.; Grzadziel, D. Development of a new tool to simultaneously measure soil-gas permeability and CO2 concentration as important parameters for geogenic radon potential assessment. Environ. Monit. Assess. 2025, 197, 124. [Google Scholar] [CrossRef] [PubMed]
- ENVCO Global. WatchDog Soil Temperature Sensor. Available online: https://envcoglobal.com/catalog/water/water-quality-sensors/digital-sensors/digital-water-temperature-sensors/watchdog-soil/ (accessed on 1 April 2025).
- ENVCO Global. WatchDog 1000 Series Data Loggers. Available online: https://envcoglobal.com/catalog/agriculture/plant/disease-and-pests/barometric-1/ (accessed on 3 April 2025).
- Onset Computer Corporation. HOBO U30 USB Weather Station. Available online: https://www.onsetcomp.com/products/data-loggers/u30-nrc (accessed on 2 April 2025).
- Onset Computer Corporation. 12-Bit Temperature Smart Sensor. Available online: https://www.onsetcomp.com/products/sensors/s-tmb-m0xx (accessed on 2 April 2025).
- Florides, G.; Kalogirou, S. Annual ground temperature measurements at various depths. In Proceedings of the 8th REHVA World Congress, Clima, Lausanne, Switzerland, 9–12 October 2005; pp. 1–6. [Google Scholar]
- Florides, G.; Kalogirou, S. Measurements of Ground Temperature at Various Depths. In Proceedings of the 3rd International Conference on Sustainable Energy Technologies, University of Nottingham, Nottingham, UK, 27–29 June 2004. [Google Scholar]
- Kasuda, T.; Achenbach, P. Earth Temperature and Thermal Diffusivity at Selected Stations in the United States; Technical Report NBS REPORT 8972; National Berau of Standards: Gaithersburg, MD, USA, 1965. [Google Scholar]
- Boukhriss, M.; Zhani, K.; Ghribi, R. Study of thermophysical properties of a solar desalination system using solar energy. Desalin. Water Treat. 2013, 51, 1290–1295. [Google Scholar] [CrossRef]
- Ochsner, T. Rain or Shine: An Introduction to Soil Physical Properties and Processes; Oklahoma State University Libraries: Stillwater, OK, USA, 2019. [Google Scholar] [CrossRef]
- de Jong van Lier, Q.; Durigon, A. Soil thermal diffusivity estimated from data of soil temperature and single soil component properties. Revista Brasileira de Ciência do Solo 2013, 37, 106–112. [Google Scholar] [CrossRef]
- Xie, X.; Lu, Y.; Ren, T.; Horton, R. An empirical model for estimating soil thermal diffusivity from texture, bulk density, and degree of saturation. J. Hydrometeorol. 2018, 19, 445–457. [Google Scholar] [CrossRef]
- Romio, L.C.; Zimmer, T.; Bremm, T.; Buligon, L.; Herdies, D.L.; Roberti, D.R. Influence of Different Methods to Estimate the Soil Thermal Properties from Experimental Dataset. Land 2022, 11, 1960. [Google Scholar] [CrossRef]
- Kasubuchi, T. The effect of soil moisture on thermal properties in some typical Japanese upland soils. Soil Sci. Plant Nutr. 1975, 21, 107–112. [Google Scholar] [CrossRef]
- Suzuki, S.; Iiduka, K.; Sanada, A.; Ito, H.; Watanabe, F. Effects of thermal conductivity and diffusivity of a volcanic ash soil in central Ethiopian Rift Valley on soil temperatures. J. Arid. Land Stud. 2019, 29, 91–101. [Google Scholar] [CrossRef]
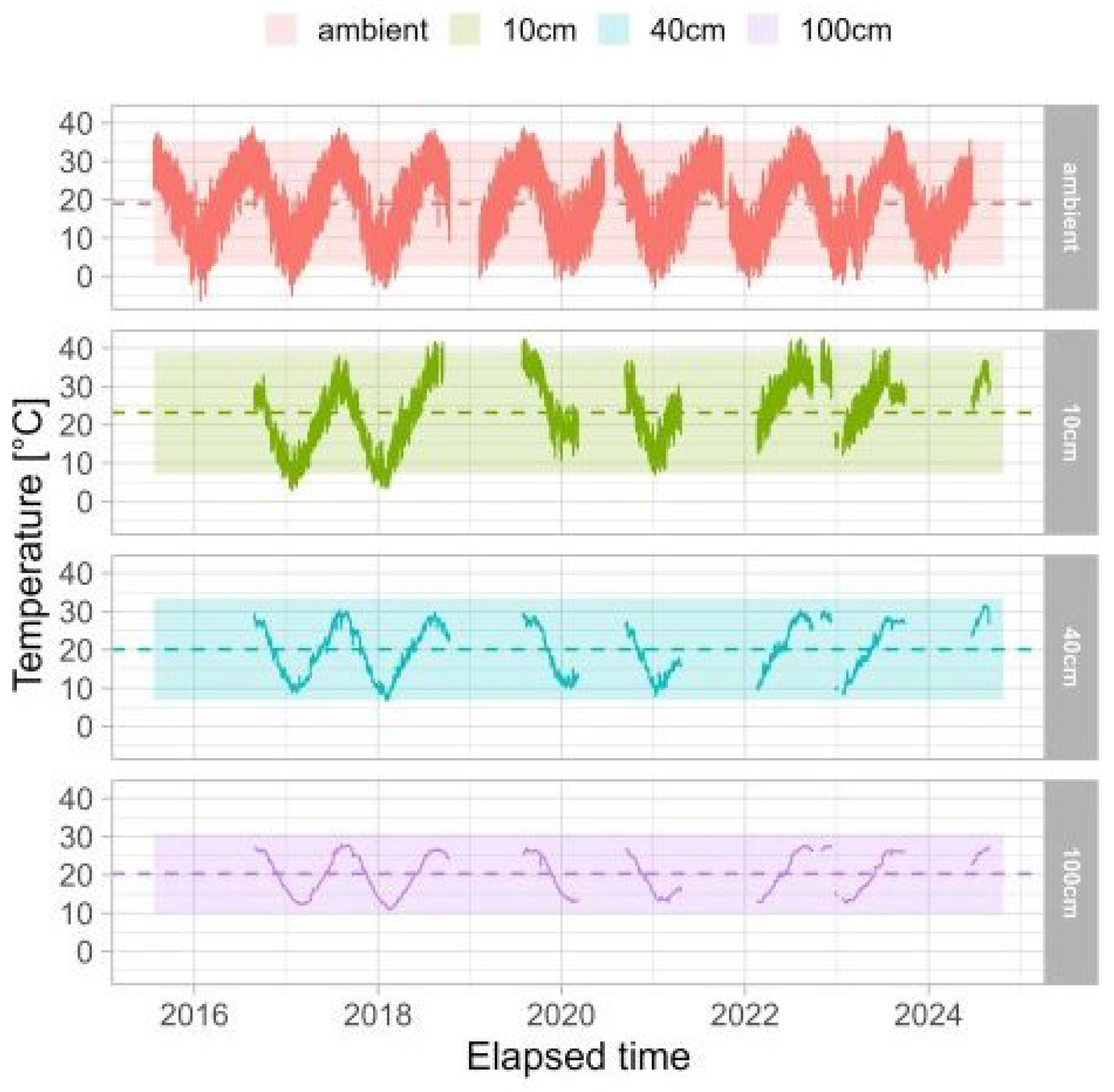
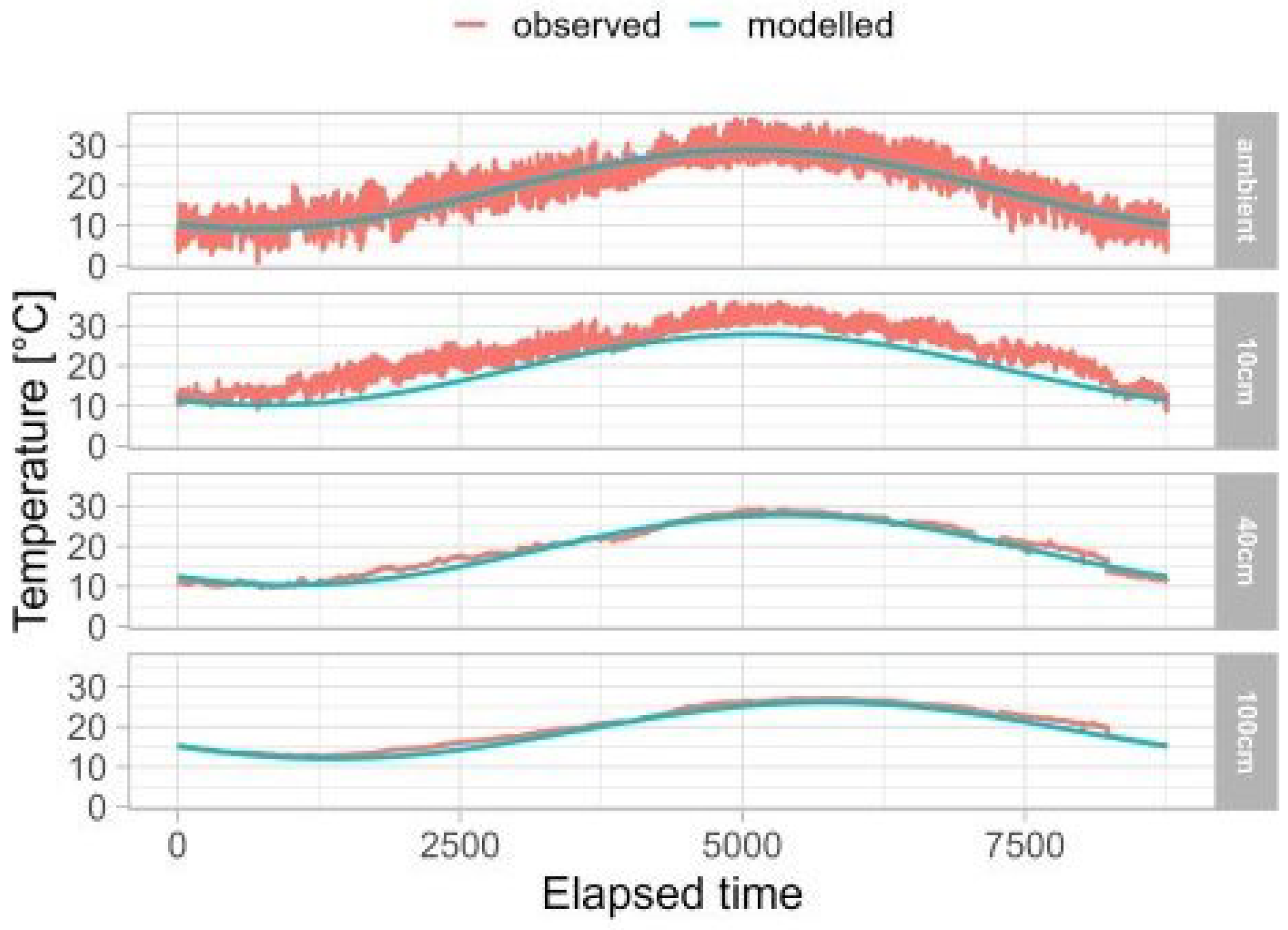

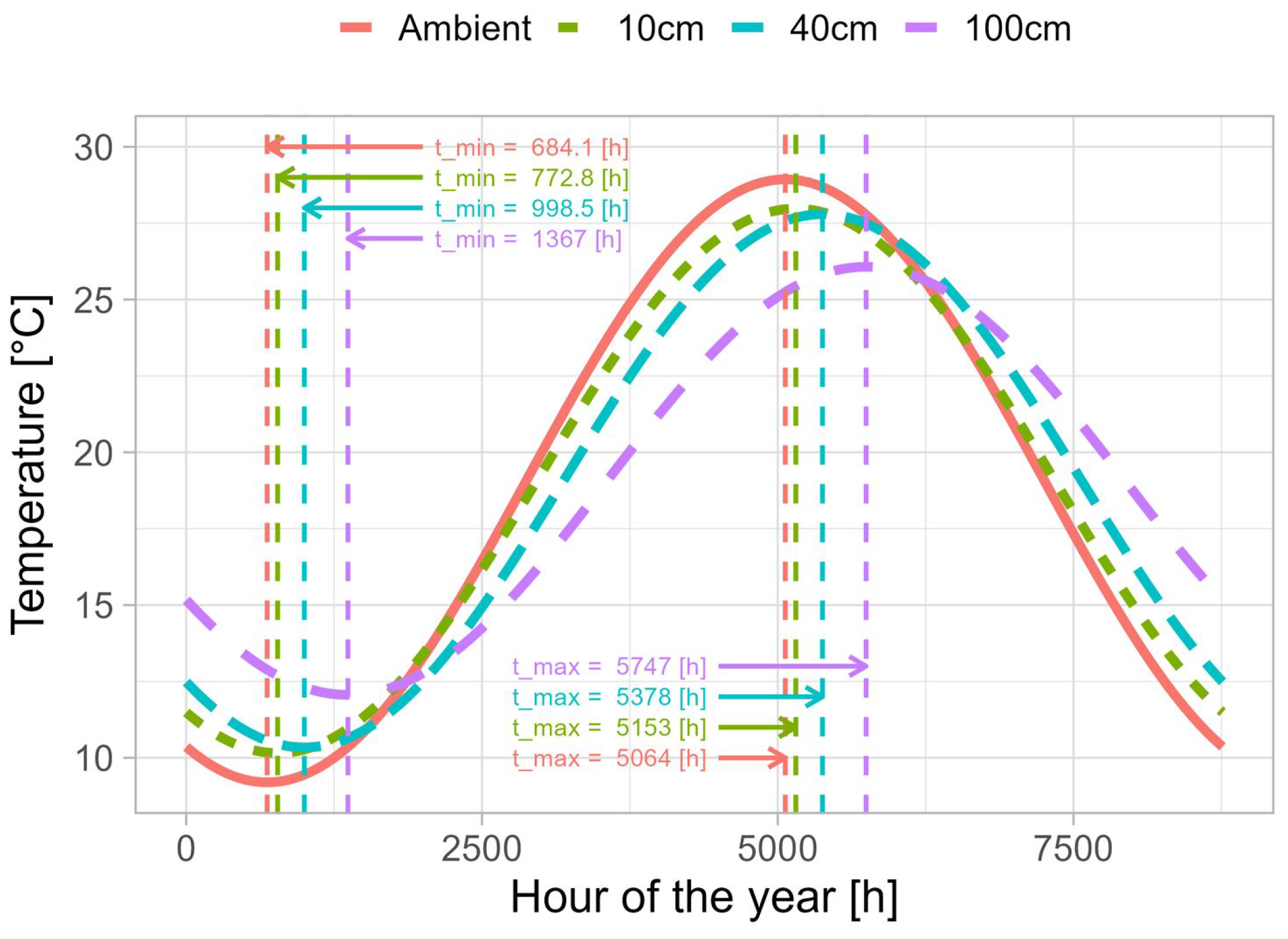

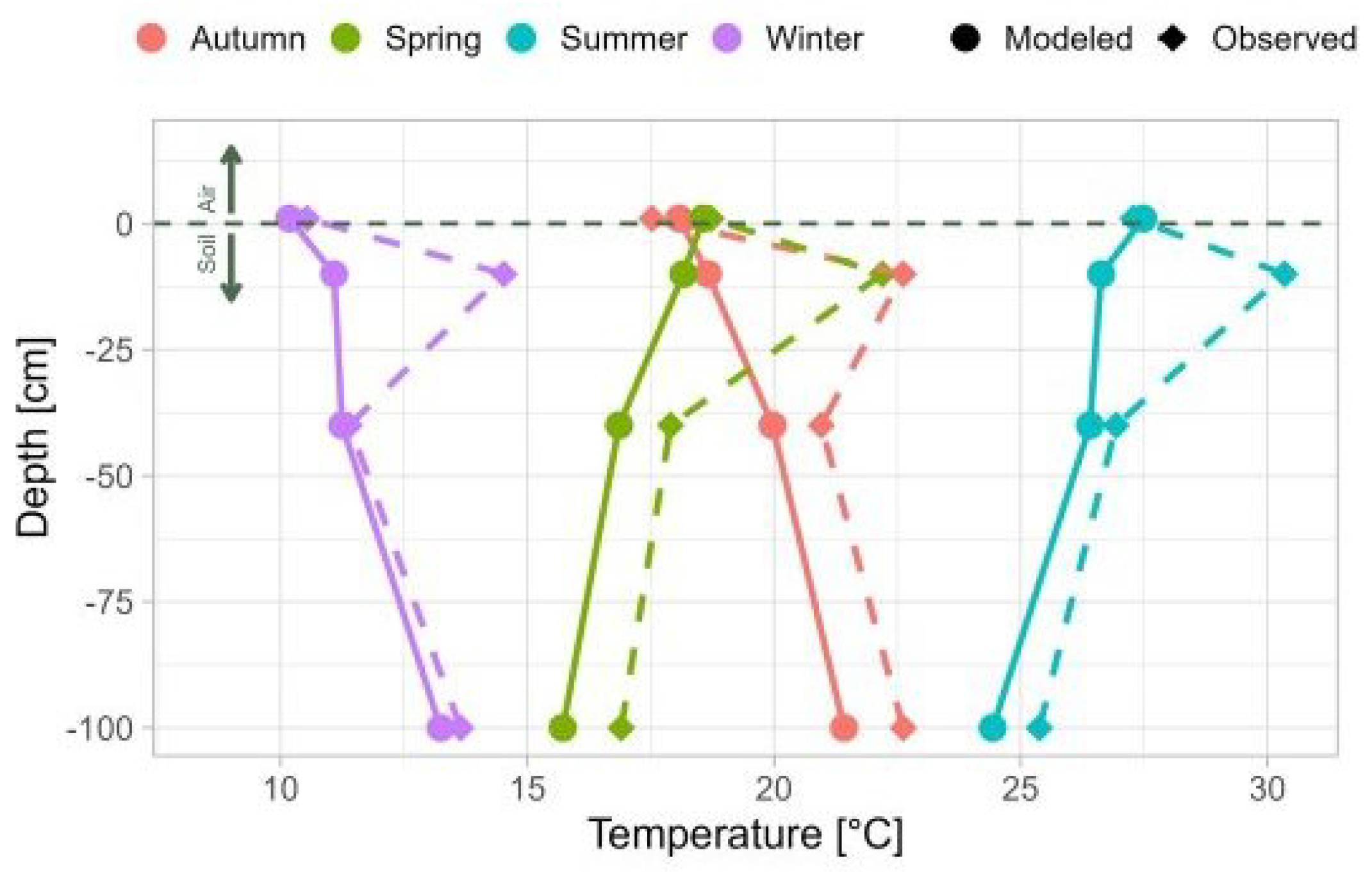
| Parameter | Ambient | Z = 10 cm | Z = 40 cm | Z = 100 cm |
|---|---|---|---|---|
| Min (°C) | −6.4 | 2.8 | 6.9 | 10.9 |
| Med (°C) | 19.5 | 24.0 | 20.3 | 20.5 |
| Mean (°C) | 19.0 | 23.2 | 20.1 | 20.3 |
| SD (°C) | 8 | 8 | 7 | 5 |
| Max (°C) | 40.2 | 42.4 | 31.6 | 28.1 |
| Range (°C) | 46.6 | 39.6 | 24.7 | 17.2 |
| Skewness | −0.13 | −0.35 | −0.13 | −0.12 |
| Kurtosis | −0.71 | −0.66 | −1.36 | −1.50 |
| Level | (m2 h−1) | (h) | (h) | (h) |
|---|---|---|---|---|
| Ambient | 7.45 * | 683 | 5063 | 2873 |
| Z = 10 cm | 1.66 | 763 | 5143 | 2953 |
| Z = 40 cm | 2.54 | 994 | 5374 | 3184 |
| Z = 100 cm | 7.43 | 1364 | 5744 | 3554 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janik, M.; Hosoda, M.; Tokonami, S.; Omori, Y.; Akata, N. Evaluating Soil Temperature Variations for Enhanced Radon Monitoring in Volcanic Regions. Atmosphere 2025, 16, 460. https://doi.org/10.3390/atmos16040460
Janik M, Hosoda M, Tokonami S, Omori Y, Akata N. Evaluating Soil Temperature Variations for Enhanced Radon Monitoring in Volcanic Regions. Atmosphere. 2025; 16(4):460. https://doi.org/10.3390/atmos16040460
Chicago/Turabian StyleJanik, Miroslaw, Mashiro Hosoda, Shinji Tokonami, Yasutaka Omori, and Naofumi Akata. 2025. "Evaluating Soil Temperature Variations for Enhanced Radon Monitoring in Volcanic Regions" Atmosphere 16, no. 4: 460. https://doi.org/10.3390/atmos16040460
APA StyleJanik, M., Hosoda, M., Tokonami, S., Omori, Y., & Akata, N. (2025). Evaluating Soil Temperature Variations for Enhanced Radon Monitoring in Volcanic Regions. Atmosphere, 16(4), 460. https://doi.org/10.3390/atmos16040460









