A Novel GIS-SWMM-ABM Approach for Flood Risk Assessment in Data-Scarce Urban Drainage Systems
Abstract
1. Introduction
1.1. Research Background
1.2. Motivation and Objectives
2. Materials and Methods
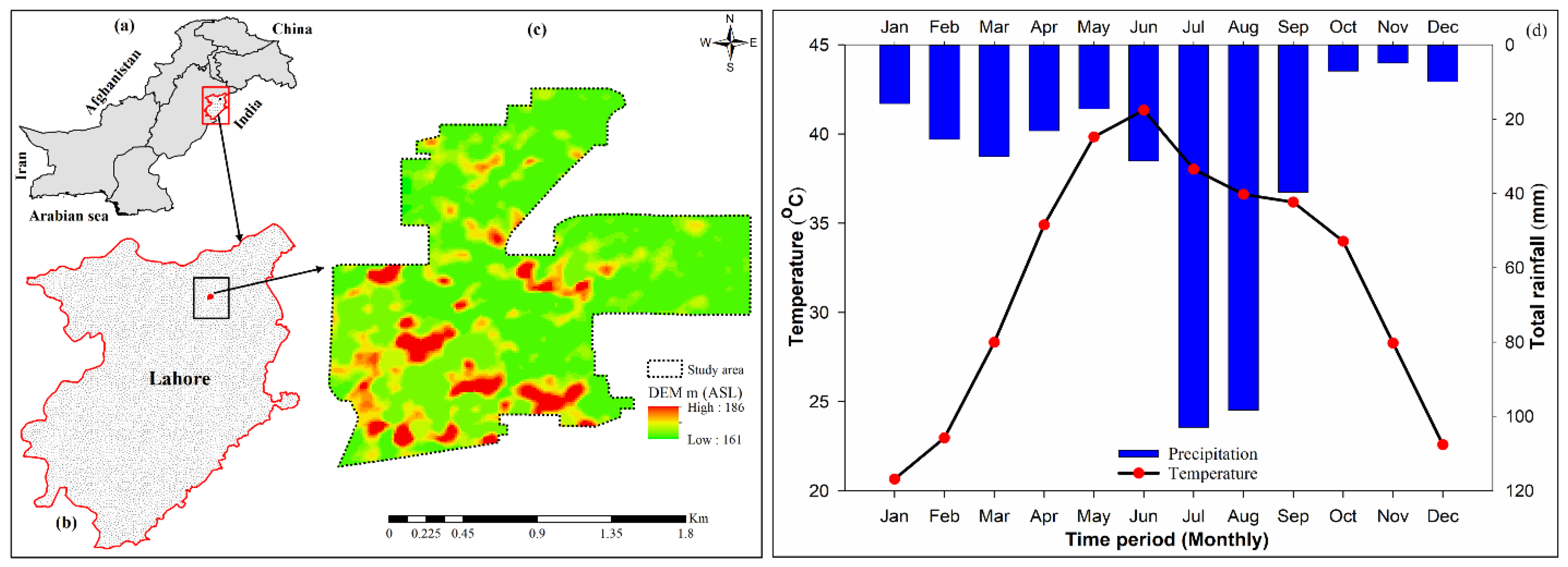
2.1. Study Area
2.2. Data Collection
2.3. Data Integration and Preparation
2.4. Model Selection
2.5. Model Development
2.5.1. Model Input Parameters
2.5.2. Sensitivity Analysis of Model Input Parameters
2.5.3. Model Calibration and Validation
2.6. Estimation of Hyetograph
2.6.1. Analysis of Rainfall Data
2.6.2. Log-Pearson Type III Distribution
2.6.3. Generation of Shorter-Duration Events
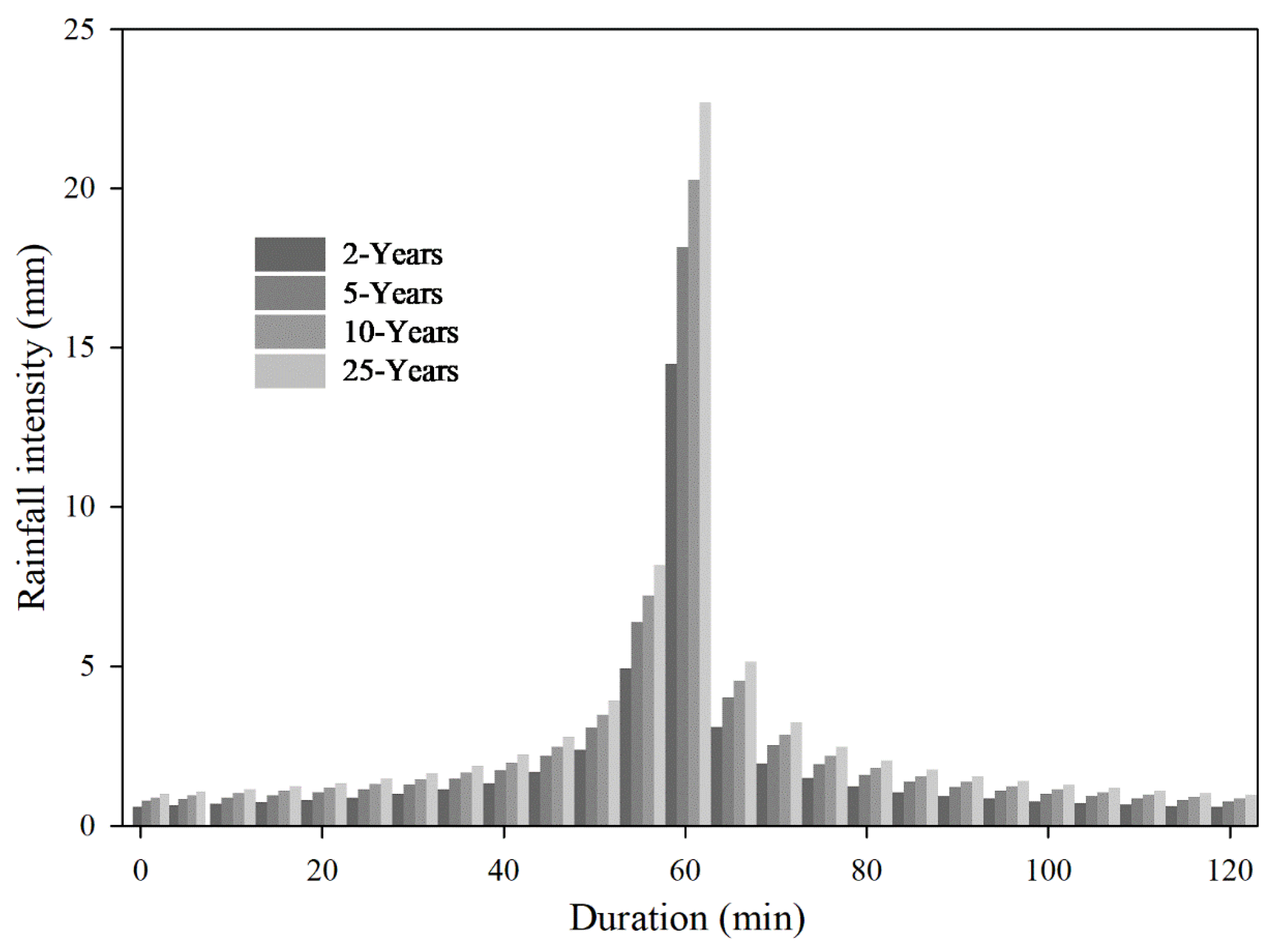
2.6.4. Alternating Block Method
2.7. Spatial Distribution of Flood Risk in Sub-Catchments
3. Results
3.1. Model Calibration and Validation
| Model Calibration | Model Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Event 1 | Event 2 | Event 3 | Event 4 | ||||||
| Statistical analysis | Obs | Sim | Obs | Sim | Obs | Sim | Obs | Sim | |
| Average inflow (CFS) | 0.63 | 0.48 | 0.88 | 0.64 | 0.60 | 0.50 | 1.10 | 0.81 | |
| Evaluation statistics | NSE | 0.72 | 0.76 | 0.71 | 0.78 | ||||
| RMSE | 0.43 | 0.44 | 0.28 | 0.41 | |||||
| R2 | 0.85 | 0.86 | 0.84 | 0.89 | |||||
3.2. Assessment of the Current Drainage System
3.3. Flood Risk Density
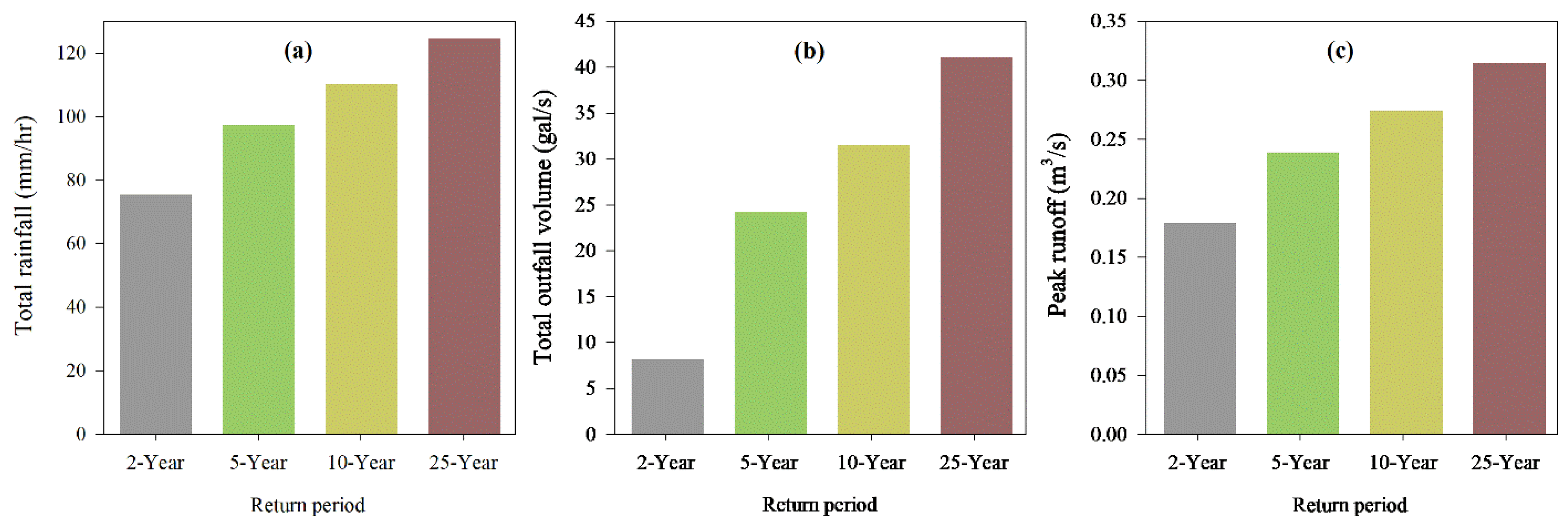
3.4. Assessment Based on Design Rainfall Events
3.5. Total Flooded Volume and Area Based on Different Design Rainfall Event Conditions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SWMM | Storm water management model |
| CFS | Cubic feet per second |
| LPT-III | Log-Pearson type III |
| GIS | Geographic information system |
| LID | Low-impact development |
| PMD | Pakistan Meteorological Department |
| NHA | National Highway Authority |
| DEM | Digital elevation model |
| ABM | Alternating block method |
| RMSE | Root mean square error |
| NSE | Nash–Sutcliffe efficiency |
References
- Parkinson, J. Urban drainage in developing countries—Challenges and opportunities. WATERLINES 2002, 20, 2–5. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, J.; Yin, H.; Jin, W.; Li, H.; He, Z. Urban river pollution control in developing countries. Nat. Sustain. 2019, 2, 158–160. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, Z.; Cai, Y.; Qiu, J.; Huang, B. Impacts of Climate Change on Urban Drainage Systems by Future Short-Duration Design Rainstorms. Water 2021, 13, 2718. [Google Scholar] [CrossRef]
- Yadav, B.; Gupta, P.K.; Patidar, N.; Himanshu, S.K. Ensemble modelling framework for groundwater level prediction in urban areas of India. Sci. Total Environ. 2020, 712, 135539. [Google Scholar] [CrossRef] [PubMed]
- Anees, M.; Sajjad, S.; Joshi, P.K. Characterizing urban area dynamics in historic city of Kurukshetra, India, using remote sensing and spatial metric tools. Geocarto Int. 2019, 34, 1584–1607. [Google Scholar] [CrossRef]
- Vemula, S.; Raju, K.S.; Veena, S.S.; Kumar, A.S. Urban floods in Hyderabad, India, under present and future rainfall scenarios: A case study. Nat. Hazards 2019, 95, 637–655. [Google Scholar] [CrossRef]
- Bisht, S.; Chatterjee, C.; Kalakoti, S.; Upadhyay, P.; Sahoo, M.; Panda, A. Modeling urban floods and drainage using SWMM and MIKE URBAN: A case study. Nat. Hazards 2016, 84, 749–776. [Google Scholar] [CrossRef]
- Paul, S.; Ghosh, S.; Mathew, M.; Devanand, A.; Karmakar, S.; Niyogi, D. Increased Spatial Variability and Intensification of Extreme Monsoon Rainfall due to Urbanization. Sci. Rep. 2018, 8, 3918. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.C.; Kendon, E.J.; Fowler, H.J.; Youngman, B.D.; Dale, M.; Short, C. New extreme rainfall projections for improved climate resilience of urban drainage systems. Clim. Serv. 2023, 30, 100375. [Google Scholar] [CrossRef]
- D’Ambrosio, R.; Longobardi, A.; Schmalz, B. SuDS as a climate change adaptation strategy: Scenario-based analysis for an urban catchment in northern Italy. Urban. Clim. 2023, 51, 101596. [Google Scholar] [CrossRef]
- Ji, X.; Dong, W.; Wang, W.; Dai, X.; Huang, H. Impacts of Climate Change on Extreme Precipitation Events and Urban Waterlogging: A Case Study of Beijing. Nat. Hazards Rev. 2024, 25, 05023014. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Shao, Z.; Javed, A. Mapping impervious surface area increase and urban pluvial flooding using Sentinel Application Platform (SNAP) and remote sensing data. Environ. Sci. Pollut. Res. 2023, 30, 125774–125789. [Google Scholar] [CrossRef] [PubMed]
- Chan, F.K.S.; Wang, Z.; Chen, J.; Lu, X.; Nafea, T.; Montz, B.; Adekola, O.; Pezzoli, A.; Griffiths, J.; Peng, Y.; et al. Selected global flood preparation and response lessons: Implications for more resilient Chinese Cities. Nat. Hazards 2023, 118, 1767–1796. [Google Scholar] [CrossRef]
- Idowu, D.; Zhou, W. Global Megacities and Frequent Floods: Correlation between Urban Expansion Patterns and Urban Flood Hazards. Sustainability 2023, 15, 2514. [Google Scholar] [CrossRef]
- Xu, T.; Xie, Z.; Jiang, F.; Yang, S.; Deng, Z.; Zhao, L.; Wen, G.; Du, Q. Urban flooding resilience evaluation with coupled rainfall and flooding models: A small area in Kunming City, China as an example. Water Sci. Technol. 2023, 87, 2820–2839. [Google Scholar] [CrossRef]
- Zhong, C.; Guo, H.; Swan, I.; Gao, P.; Yao, Q.; Li, H. Evaluating trends, profits, and risks of global cities in recent urban expansion for advancing sustainable development. Habitat Int. 2023, 138, 102869. [Google Scholar] [CrossRef]
- Balbastre-Soldevila, R.; García-Bartual, R.; Andrés-Doménech, I. A Comparison of Design Storms for Urban Drainage System Applications. Water 2019, 11, 757. [Google Scholar] [CrossRef]
- Salinas-Rodriguez, C.; Gersonius, B.; Zevenbergen, C.; Serrano, D.; Ashley, R. A Semi Risk-Based Approach for Managing Urban Drainage Systems under Extreme Rainfall. Water 2018, 10, 384. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, Z.; Chen, X.; He, P. Approach for evaluating inundation risks in urban drainage systems. Sci. Total Environ. 2016, 553, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Leng, G.; Su, J.; Ren, Y. Comparison of urbanization and climate change impacts on urban flood volumes: Importance of urban planning and drainage adaptation. Sci. Total Environ. 2019, 658, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Guptha, G.C.; Swain, S.; Al-Ansari, N.; Taloor, A.K.; Dayal, D. Evaluation of an urban drainage system and its resilience using remote sensing and GIS. Remote Sens. Appl. Soc. Environ. 2021, 23, 100601. [Google Scholar] [CrossRef]
- Adugna, D.; Lemma, B.; Jensen, M.B.; Gebrie, G.S. Evaluating the hydraulic capacity of existing drain systems and the management challenges of stormwater in Addis Ababa, Ethiopia. J. Hydrol. Reg. Stud. 2019, 25, 100626. [Google Scholar] [CrossRef]
- Bulti, T.; Abebe, B.G. Analyzing the impacts of urbanization on runoff characteristics in Adama city, Ethiopia. SN Appl. Sci. 2020, 2, 1151. [Google Scholar] [CrossRef]
- Sambeto, B.; Reddythta, D.; Kebebew, A.S. Assessment of the drainage systems performance in response to future scenarios and flood mitigation measures using stormwater management model. City Environ. Interact. 2023, 19, 100111. [Google Scholar] [CrossRef]
- Miller, J.D.; Hutchins, M. The impacts of urbanisation and climate change on urban flooding and urban water quality: A review of the evidence concerning the United Kingdom. J. Hydrol. Reg. Stud. 2017, 12, 345–362. [Google Scholar] [CrossRef]
- Akter, A.; Tanim, A.H. Estimating urban flood hazard zones using SWMM in Chittagong City. Tech. J. River Res. Inst. 2016, 13, 87–101. [Google Scholar]
- Jiang, L.; Chen, Y.; Wang, H. Urban flood simulation based on the SWMM model. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 186–191. [Google Scholar] [CrossRef]
- Shao, Z.; Ahmad, M.N.; Javed, A.; Islam, F.; Jahangir, Z.; Ahmad, I. Expansion of Urban Impervious Surfaces in Lahore (1993–2022) Based on Gee and Remote Sensing Data. Photogramm. Eng. Remote Sens. 2023, 89, 479–486. [Google Scholar] [CrossRef]
- Shrestha, B.Z. A Fusion of Remotely Sensed Data to Map the Impervious Surfaces of Growing Cities of Punjab, Pakistan. Master Dissertation, University of Nevada, Las Vegas, NV, USA, 2021. [Google Scholar]
- Rana, I.A.; Asim, M.; Aslam, A.B.; Jamshed, A. Disaster management cycle and its application for flood risk reduction in urban areas of Pakistan. Urban. Clim. 2021, 38, 100893. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Zhang, G.J.; Gong, P.; Wei, L.Y.; He, Y.J.; Li, L.J.; Wang, B. Effects of Urbanization in China on the East Asian Summer Monsoon as Revealed by Two Global Climate Models. J. Geophys. Res.-Atmos. 2024, 129, e2023JD039737. [Google Scholar] [CrossRef]
- Omer, S. Lahore’s Population Witnesses Steady Annual Growth of Three Percent. 18 October 2023. Available online: https://www.pakistantoday.com.pk/2023/05/16/lahores-population-witnesses-steady-annual-growth-of-three-percent/ (accessed on 18 October 2023).
- Zia, S.; Nasar-u-Minallah, M.; Zahra, N.; Hanif, A. The Effect of Urban Green Spaces in Reducing Urban Flooding in Lahore, Pakistan, Using Geospatial Techniques. Geogr. Environ. Sustain. 2022, 15, 47–55. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.D.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Yin, H.; Zheng, F.; Duan, H.-F.; Savic, D.; Kapelan, Z. Estimating Rainfall Intensity Using an Image-Based Deep Learning Model. Engineering 2023, 21, 162–174. [Google Scholar] [CrossRef]
- Johannessen, G.; Hamouz, V.; Gragne, A.S.; Muthanna, T.M. The transferability of SWMM model parameters between green roofs with similar build-up. J. Clean. Prod. 2019, 569, 816–828. [Google Scholar] [CrossRef]
- Tuomela, C.; Sillanpää, N.; Koivusalo, H. Assessment of stormwater pollutant loads and source area contributions with storm water management model (SWMM). J. Environ. Manag. 2019, 233, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Rossman, L.A.; Michelle, S.A. Storm Water Management Model User’s Manual, Version 5.2; National Risk Management Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Washington, DC, USA, 2022.
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual Volume I–Hydrology; U.S. EPA Office of Research and Development: Washington, DC, USA, 2016.
- James, W.; Rossman, L.A.; James, W.R.C. User’s Guide to SWMM 5: [Based on Original USEPA SWMM Documentation], 13th ed.; CHI: Guelph, ON, Canada, 2010. [Google Scholar]
- Randall, M.; Sun, F.; Zhang, Y.; Jensen, M.B. Evaluating Sponge City volume capture ratio at the catchment scale using SWMM. J. Environ. Manag. 2019, 246, 745–757. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Jia, H.; Wang, Z.; Mao, X.; Xu, C. SWMM-based methodology for block-scale LID-BMPs planning based on site-scale multi-objective optimization: A case study in Tianjin. Front. Environ. Sci. Eng. 2017, 11, 1. [Google Scholar] [CrossRef]
- Jia, H.; Liu, Z.; Xu, C.; Chen, Z.; Zhang, X.; Xia, J.; Yu, S.L. Adaptive pressure-driven multi-criteria spatial decision-making for a targeted placement of green and grey runoff control infrastructures. Water Res. 2022, 212, 118126. [Google Scholar] [CrossRef] [PubMed]
- Jia, H.; Ma, H.; Sun, Z.; Yu, S.; Ding, Y.; Liang, Y. A closed urban scenic river system using stormwater treated with LID-BMP technology in a revitalized historical district in China. Ecol. Eng. 2014, 71, 448–457. [Google Scholar] [CrossRef]
- Evans, I.S. General geomorphometry, derivatives of altitude, and descriptive statistics. In Spatial Analysis in Geomorphology; Routledge: Oxfordshire, UK, 1972; pp. 17–90. [Google Scholar]
- Chow, V.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Giudice, G.; Padulano, R. Sensitivity Analysis and Calibration of a Rainfall-Runoff Model with the Combined Use of EPA-SWMM and Genetic Algorithm. Acta Geophys. 2016, 64, 1755–1778. [Google Scholar] [CrossRef]
- Knighton, J.; Lennon, E.; Bastidas, L.; White, E. Stormwater Detention System Parameter Sensitivity and Uncertainty Analysis Using SWMM. J. Hydrol. Eng. 2016, 21, 05016014. [Google Scholar] [CrossRef]
- Annus, I.; Vassiljev, A.; Kändler, N.; Kaur, K. Automatic Calibration Module for an Urban Drainage System Model. Water 2021, 13, 1419. [Google Scholar] [CrossRef]
- Rosa, L.; Della Libera, S.; Iaconelli, M.; Donia, D.; Cenko, F.; Xhelilaj, G.; Cozza, P.; Divizia, M. Human bocavirus in children with acute gastroenteritis in Albania. J. Med. Virol. 2016, 88, 906–910. [Google Scholar] [CrossRef] [PubMed]
- Rosa, D.J.; Clausen, J.C.; Dietz, M.E. Calibration and Verification of SWMM for Low Impact Development. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 746–757. [Google Scholar] [CrossRef]
- Rawls, J.; Brakensiek, L.; Miller, N. Green-ampt Infiltration Parameters from Soils Data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Chen, Y.-R.; Yu, B. Impact assessment of climatic and land-use changes on flood runoff in southeast Queensland. Hydrol. Sci. J. 2015, 60, 1759–1769. [Google Scholar] [CrossRef]
- Yu, D.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Clean. Prod. 2015, 524, 385–400. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Clean. Prod. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N. Goodness-of-fit criteria for hydrological models: Model calibration and performance assessment. J. Clean. Prod. 2021, 600, 126674. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Clean. Prod. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- KlemeŠ, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Mishra, S.; Akhil, D.-G. Data-Driven Modeling. In Applied Statistical Modeling and Data Analytics; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Brown, S.A.; Schall, J.D.; Morris, J.L.; Stein, S.; Warner, J.C. Urban Drainage Design Manual: Hydraulic Engineering Circular; National Highway Institute (US): Arlington, VA, USA, 2009.
- Rasmussen, P.P.; Perry, C.A. Estimation of Peak Streamflows for Unregulated Rural Streams in Kansas; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2008.
- Russo, M.M. Extreme Precipitation Events in East Baton Rouge Parish: An Areal Rainfall Frequency/Magnitude Analysis; Louisiana State University and Agricultural & Mechanical College: Baton Rouge, LA, USA, 2004. [Google Scholar]
- Elsebaie, I.H. Developing rainfall intensity–duration–frequency relationship for two regions in Saudi Arabia. J. King Saud. Univ.—Eng. Sci. 2012, 24, 131–140. [Google Scholar] [CrossRef]
- Mudashiru, R.B.; Abustan, I.; Sabtu, N.; Mukhtar, H.B.; Balogun, W. Choosing the best fit probability distribution in rainfall design analysis for Pulau Pinang, Malaysia. Model. Earth Syst. Environ. 2023, 9, 3217–3227. [Google Scholar] [CrossRef]
- Rulfová, Z.; Buishand, A.; Roth, M.; Kyselý, J. A two-component generalized extreme value distribution for precipitation frequency analysis. J. Clean. Prod. 2016, 534, 659–668. [Google Scholar] [CrossRef]
- Baah, K.; Dubey, B.; Harvey, R.; McBean, E. A risk-based approach to sanitary sewer pipe asset management. Sci. Total Environ. 2015, 505, 1011–1017. [Google Scholar] [CrossRef] [PubMed]
- Caradot, N.; Granger, D.; Chapgier, J.; Cherqui, F.; Chocat, B. Urban flood risk assessment using sewer flooding databases. Water Sci. Technol. 2011, 64, 832–840. [Google Scholar] [CrossRef] [PubMed]
- Shahed Behrouz, M.; Zhu, Z.; Matott, L.S.; Rabideau, A.J. A new tool for automatic calibration of the Storm Water Management Model (SWMM). J. Hydrol. 2020, 581, 124436. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Ekmekcioğlu, Ö.; Yılmaz, M.; Özger, M.; Tosunoğlu, F. Investigation of the low impact development strategies for highly urbanized area via auto-calibrated Storm Water Management Model (SWMM). Water Sci. Technol. 2021, 84, 2194–2213. [Google Scholar] [CrossRef] [PubMed]
- Koc, K.; Ekmekcioğlu, Ö.; Özger, M. An integrated framework for the comprehensive evaluation of low impact development strategies. J. Environ. Manag. 2021, 294, 113023. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Strong, C.; Wang, J.; Burian, S. An Event-Based Resilience Index to Assess the Impacts of Land Imperviousness and Climate Changes on Flooding Risks in Urban Drainage Systems. Water 2023, 15, 2663. [Google Scholar] [CrossRef]
- Neumann, J.; Scheid, C.; Dittmer, U. Potential of Decentral Nature-Based Solutions for Mitigation of Pluvial Floods in Urban Areas—A Simulation Study Based on 1D/2D Coupled Modeling. Water 2024, 16, 811. [Google Scholar] [CrossRef]
- Wilson, E.M. Engineering Hydrology. In Engineering Hydrology: Solutions to Problems; Wilson, E.M., Ed.; Macmillan Education: London, UK, 1990; pp. 1–49. [Google Scholar]
- Haan, C.T. Statistical Methods in Hydrology, 1st ed.; Iowa State University Press: Ames, IA, USA, 1977. [Google Scholar]






| S. No | Data Type | Period | Source |
|---|---|---|---|
| 1 | Rainfall data (hourly) | 2001–2020 | PMD |
| 2 | Sub-catchments, links, and junction | 2021 | NHA |
| 3 | DEM (12.5 m × 12.5 m) | https://search.asf.alaska.edu/#/ (accessed on 15 October 2022) |
| Parameter | Initial Value | Calibrated Value/Range (For Each Sub-Catchment) | Source of Data |
|---|---|---|---|
| Area of sub-catchments (ha) | GIS-calculated | Original value | GIS-calculated |
| Width | GIS-calculated | Original value | GIS-calculated |
| Slope (%) | 0.5 | 0.11–1.5 | [38] |
| % Impervious | 50 | 0.4–11.104 | [38] |
| N-imperv. | 0.01 | 0.01 | [38] |
| N-perv. | 0.10 | 0.1 | [38] |
| Dstore-imperv (mm) | 0.05 | 0.05 | [38] |
| Dstore-perv (mm) | 0.05 | 10.5 | [38] |
| % Zero-imperv | 50 | 25 | [38] |
| Infiltration model (modified Green–Ampt) | |||
| Suction head (mm) | 3.5 | 20 | [38,52] |
| Conductivity (mm/h) | 0.5 | 10 | [38,52] |
| Initial soil moisture Deficit (fraction) | 0.26 | 0.5 | [38,52] |
| Design Storm (Years) | 2 Years | 5 Years | 10 Years | 25 Years |
|---|---|---|---|---|
| Total rainfall (mm/hr) | 75.44 | 97.46 | 110.11 | 124.51 |
| Peak runoff (m³/s) | 0.18 | 0.24 | 0.27 | 0.31 |
| Total outfall volume (gal/s) | 8.16 | 24.21 | 31.53 | 41.06 |
| Number of flooded nodes | 64 | 64 | 64 | 65 |
| Design Rainfall Event (2 h) Simulation | |||
|---|---|---|---|
| Return Period | Total Flood Volume (106 gal) | Total Flooding Area (%) | Total Area (km2) |
| 2 years | 0.07 | 59.86 | 2.71 |
| 5 years | 0.09 | 78.22 | |
| 10 years | 0.10 | 88.69 | |
| 25 years | 0.11 | 99.94 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.; Jia, H.; Ashraf, A.; Yin, D.; Chen, Z.; Ahmed, R.; Israr, M. A Novel GIS-SWMM-ABM Approach for Flood Risk Assessment in Data-Scarce Urban Drainage Systems. Water 2024, 16, 1464. https://doi.org/10.3390/w16111464
Ahmad S, Jia H, Ashraf A, Yin D, Chen Z, Ahmed R, Israr M. A Novel GIS-SWMM-ABM Approach for Flood Risk Assessment in Data-Scarce Urban Drainage Systems. Water. 2024; 16(11):1464. https://doi.org/10.3390/w16111464
Chicago/Turabian StyleAhmad, Shakeel, Haifeng Jia, Anam Ashraf, Dingkun Yin, Zhengxia Chen, Rasheed Ahmed, and Muhammad Israr. 2024. "A Novel GIS-SWMM-ABM Approach for Flood Risk Assessment in Data-Scarce Urban Drainage Systems" Water 16, no. 11: 1464. https://doi.org/10.3390/w16111464
APA StyleAhmad, S., Jia, H., Ashraf, A., Yin, D., Chen, Z., Ahmed, R., & Israr, M. (2024). A Novel GIS-SWMM-ABM Approach for Flood Risk Assessment in Data-Scarce Urban Drainage Systems. Water, 16(11), 1464. https://doi.org/10.3390/w16111464











