Copula-Probabilistic Flood Risk Analysis with an Hourly Flood Monitoring Index
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset
2.3. Development of the Hourly Flood Index and Vine Copula Model
2.3.1. Hourly Flood Index and Flood Characteristics
2.3.2. Joint Exceedance Probability between Flood Characteristics
2.3.3. Copula Analytical Approach
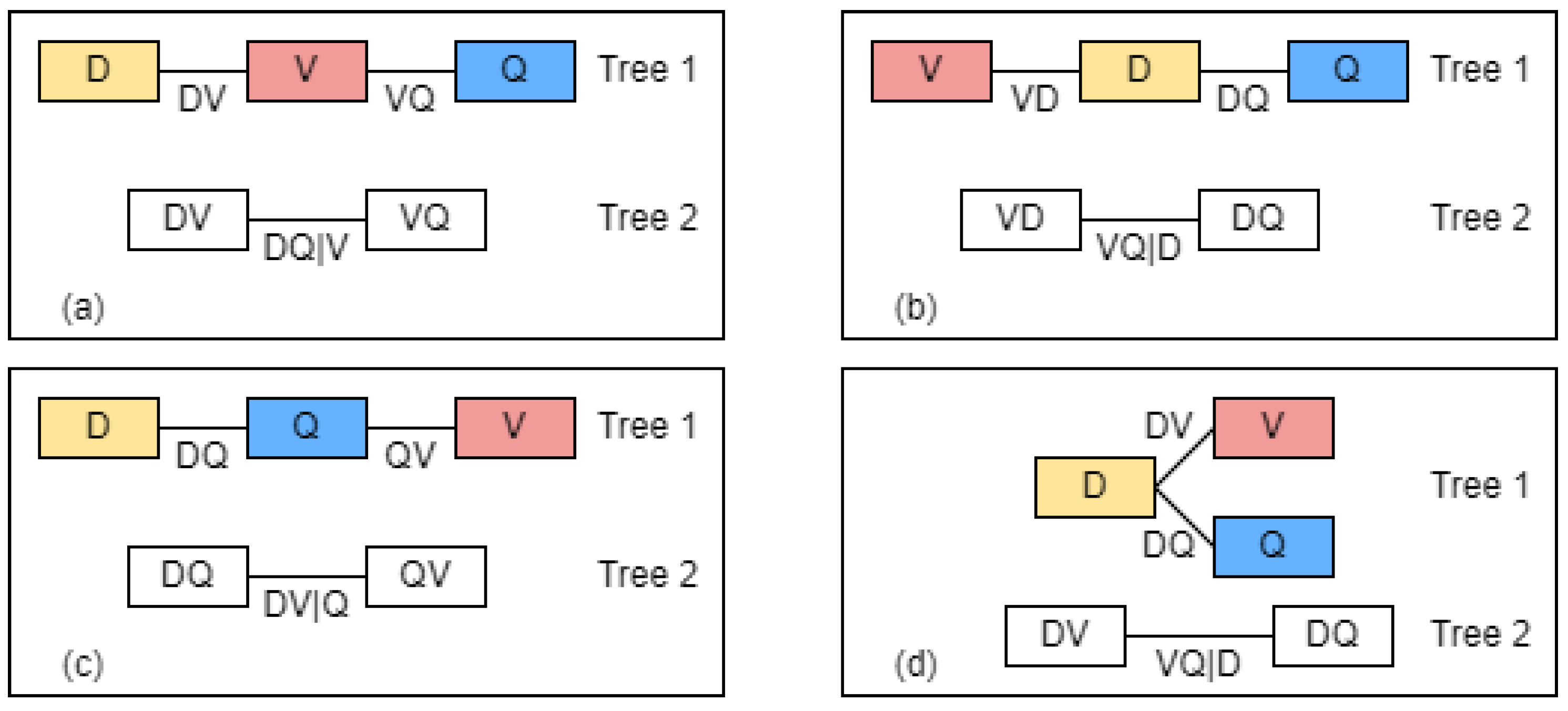
2.3.4. Vine Copulas
3. Results and Discussion
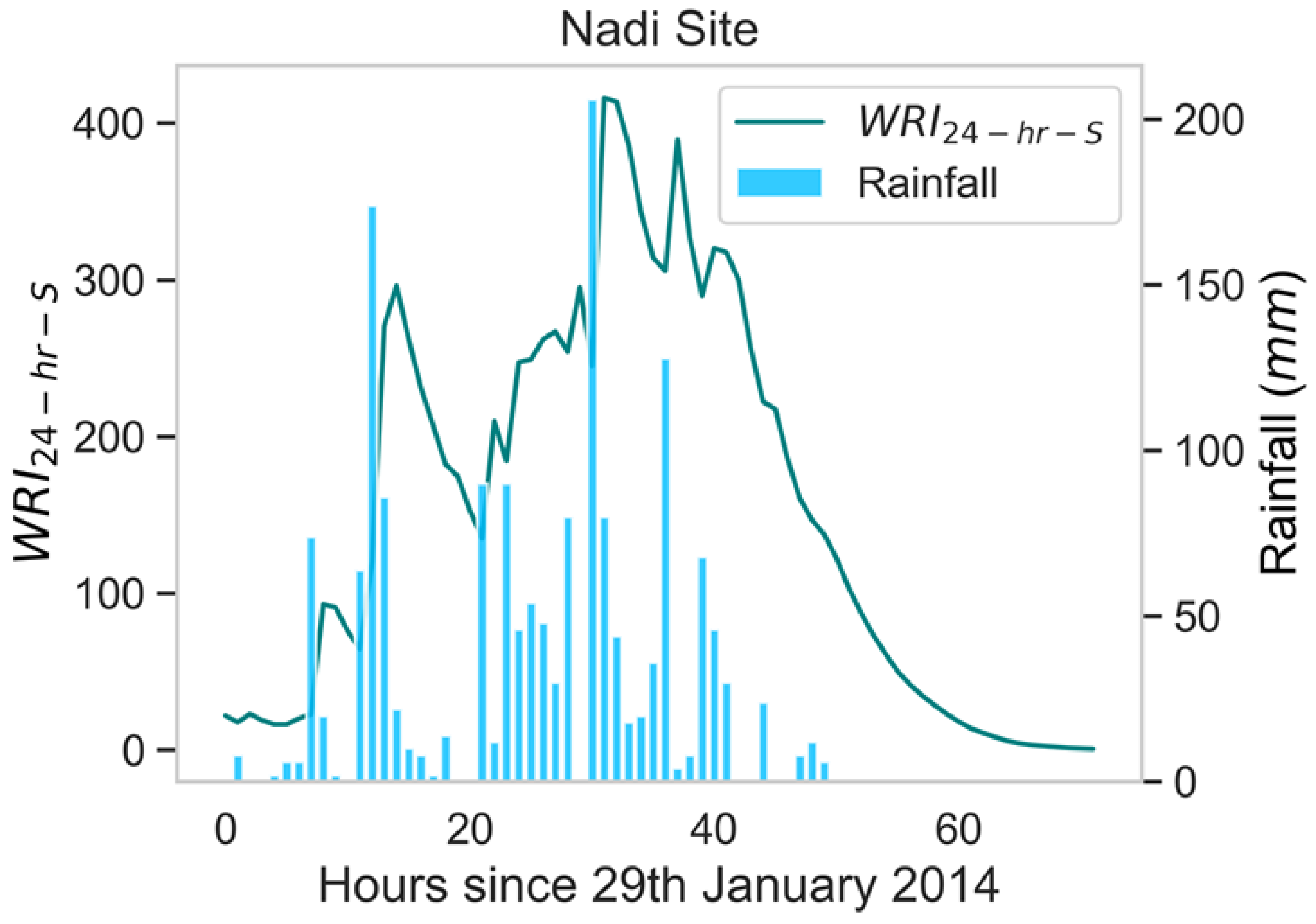
3.1. Application of the Hourly Flood Index for Flood Event Analysis
3.2. Application of the Vine Copula Model for Probabilistic Flood Risk Analysis
4. Conclusions, Limitations of the Study and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| API | Antecedent Precipitation Index |
| AWRI | Available Water Resources Index |
| BIC | Bayesian Information Criterion |
| D | Flood Duration |
| FFGS | Flash Flood Guidance System |
| FJD | Fijian Dollar |
| FMS | Fiji Meteorological Services |
| GDP | Gross Domestic Product |
| Daily Flood Index | |
| IQR | Interquartile Range |
| JCDF | Joint Cumulative Distribution Function |
| JPDF | Joint Density Distribution Function |
| logLik | Log-Likelihood |
| mBICv | Modified Vine Copula Bayesian Information Criteria |
| NDMO | Fiji’s National Disaster Management Office |
| Probability Density Function | |
| PSIDS | Pacific Small Island Developing State |
| Q | Flood Peak |
| r | Pearson’s Correlation Coefficient |
| SAPI | Standardised Antecedent Precipitation Index |
| SPCZ | South Pacific Convergence Zone |
| SPI | Standardised Precipitation Index |
| SWAP | Standardised Weighted Average of Precipitation |
| Hourly Flood Index | |
| USD | United States Dollar |
| V | Flood Volume |
| WAP | Weighted Average of Precipitation |
| 24-Hourly Water Resources Index | |
| Spearman’s Rank Correlation Coefficient | |
| Kendall’s Tau Correlation Coefficient |
Appendix A
| Copula Type | Bivariate Copula Family | Name |
|---|---|---|
| Parametric | Elliptical | Gaussian |
| Student-t | ||
| Archimedean | Frank | |
| Gumble | ||
| Rotated Gumbel 90 degrees | ||
| Rotated Gumbel 180 degrees (Survival Gumbel) | ||
| Rotated Gumbel 270 degrees | ||
| Clayton | ||
| Rotated Clayton 90 degrees | ||
| Rotated Clayton 180 degrees (Survival Clayton) | ||
| Rotated Clayton 270 degrees | ||
| Joe | ||
| Rotated Joe 90 degrees | ||
| Rotated Joe 180 degrees (Survival Joe) | ||
| Rotated Joe 270 degrees | ||
| Clayton-Gumbel (BB1) | ||
| Rotated BB1 90 degrees | ||
| Rotated BB1 180 degrees (Survival BB1) | ||
| Rotated BB1 270 degrees | ||
| Joe-Gumbel (BB6) | ||
| Rotated BB6 90 degrees | ||
| Rotated BB6 180 degrees (Survival BB6) | ||
| Rotated BB6 270 degrees | ||
| Joe- Clayton (BB7) | ||
| Rotated BB7 90 degrees | ||
| Rotated BB7 180 degrees (Survival BB7) | ||
| Rotated BB7 270 degrees | ||
| Joe-Frank (BB8) | ||
| Rotated BB8 90 degrees | ||
| Rotated BB8 180 degrees (Survival BB8) | ||
| Rotated BB8 270 degrees | ||
| Non-parametric | - | Transformation kernel |
| - | - | Independence |
References
- Taherizadeh, M.; Khushemehr, J.H.; Niknam, A.; Nguyen-Huy, T.; Mezosi, G. Revealing the effect of an industrial flash flood on vegetation area: A case study of Khusheh Mehr in Maragheh-Bonab Plain, Iran. Remote Sens. Appl. Soc. Environ. 2023, 32, 101016. [Google Scholar] [CrossRef]
- Taherizadeh, M.; Niknam, A.; Nguyen-Huy, T.; Mezosi, G.; Sarli, R. Flash flood-risk areas zoning using integration of decision-making trial and evaluation laboratory, GIS-based analytic network process and satellite-derived information. Nat. Hazards 2023, 118, 2309–2335. [Google Scholar] [CrossRef]
- Associated Programme on Flood Management. Management of Flash Floods. Integrated Flood Management Tools Series No. 16, World Meteorological Organization. 2012. Available online: https://www.floodmanagement.info/publications/tools/APFM_Tool_16.pdf (accessed on 11 January 2024).
- Shah, V.; Kirsch, K.R.; Cervantes, D.; Zane, D.F.; Haywood, T.; Horney, J.A. Flash flood swift water rescues, Texas, 2005–2014. Clim. Risk Manag. 2017, 17, 11–20. [Google Scholar] [CrossRef]
- Dordevic, M.; Mutic, P.; Kim, H. Flash Flood Guidance System: Response to One of the Deadliest Hazards. WMO Bulletin 1, World Meteorological Organization. 2020. Available online: https://www.imgw.pl/sites/default/files/2020-04/wmo_klimat_woda_en-min.pdf (accessed on 11 January 2024).
- Moishin, M.; Deo, R.C.; Prasad, R.; Raj, N.; Abdulla, S. Development of Flood Monitoring Index for daily flood risk evaluation: Case studies in Fiji. Stoch. Environ. Res. Risk Assess. 2021, 35, 1387–1402. [Google Scholar] [CrossRef]
- Sharma, K.K.; Verdon-Kidd, D.C.; Magee, A.D. A decision tree approach to identify predictors of extreme rainfall events–a case study for the Fiji Islands. Weather Clim. Extrem. 2021, 34, 100405. [Google Scholar] [CrossRef]
- Davis, J.; Henion, D.; Murro, M.J. The Impacts of Coastal Flooding on Physical Infrastructure: Case Studies in Fiji, Kiribati, and Papua New Guinea; Report; Center for Excellence in Disaster Management & Humanitarian Assistance: Ford Island, HI, USA, 2022. [Google Scholar]
- Government of Fiji. Climate Vulnerability Assessment: Making Fiji Climate Resilient. Report, Government of Fiji. 2017. Available online: https://reliefweb.int/report/fiji/climate-vulnerability-assessment-making-fiji-climate-resilient (accessed on 11 January 2024).
- The World Bank Group. Data. 2024. Available online: https://data.worldbank.org/country/fiji?view=chart (accessed on 11 January 2024).
- Leonard, M.; Westra, S.; Phatak, A.; Lambert, M.; van den Hurk, B.; McInnes, K.; Risbey, J.; Schuster, S.; Jakob, D.; Stafford-Smith, M. A compound event framework for understanding extreme impacts. Wiley Interdiscip. Rev. Clim. Change 2014, 5, 113–128. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.R.; et al. Changes in Climate Extremes and their Impacts on the Natural Physical Environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V., Stocker, T.F., Dahe, Q., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.K., Allen, S.K., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; pp. 109–230. [Google Scholar] [CrossRef]
- Seiler, R.; Hayes, M.; Bressan, L. Using the standardized precipitation index for flood risk monitoring. Int. J. Climatol. J. R. Meteorol. Soc. 2002, 22, 1365–1376. [Google Scholar] [CrossRef]
- Byun, H.R.; Lee, D.K. Defining three rainy seasons and the hydrological summer monsoon in Korea using available water resources index. J. Meteorol. Soc. Jpn. 2002, 80, 33–44. [Google Scholar] [CrossRef]
- Lu, E. Determining the start, duration, and strength of flood and drought with daily precipitation: Rationale. Geophys. Res. Lett. 2009, 36, L12707. [Google Scholar] [CrossRef]
- Lu, E.; Cai, W.; Jiang, Z.; Zhang, Q.; Zhang, C.; Higgins, R.W.; Halpert, M.S. The day-to-day monitoring of the 2011 severe drought in China. Clim. Dyn. 2014, 43, 1–9. [Google Scholar] [CrossRef]
- Deo, R.C.; Byun, H.R.; Adamowski, J.F.; Kim, D.W. A real-time flood monitoring index based on daily effective precipitation and its application to Brisbane and Lockyer Valley flood events. Water Resour. Manag. 2015, 29, 4075–4093. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Kath, J.; Nagler, T.; Khaung, Y.; Aung, T.S.S.; Mushtaq, S.; Marcussen, T.; Stone, R. A satellite-based Standardized Antecedent Precipitation Index (SAPI) for mapping extreme rainfall risk in Myanmar. Remote Sens. Appl. Soc. Environ. 2022, 26, 100733. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; Yaseen, Z.M.; Prasad, R.; Mushtaq, S. Bayesian Markov chain Monte Carlo-based copulas: Factoring the role of large-scale climate indices in monthly flood prediction. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation: Theory and Practice of Hazard Mitigation; Deo, R.C., Kisi, O., Samui, P., Yaseen, Z.M., Eds.; Springer Nature: Singapore, 2021; pp. 29–47. [Google Scholar] [CrossRef]
- Prasad, R.; Charan, D.; Joseph, L.; Nguyen-Huy, T.; Deo, R.C.; Singh, S. Daily flood forecasts with intelligent data analytic models: Multivariate empirical mode decomposition-based modeling methods. In Intelligent Data Analytics for Decision-Support Systems in Hazard Mitigation: Theory and Practice of Hazard Mitigation; Deo, R.C., Kisi, O., Samui, P., Yaseen, Z.M., Eds.; Springer Nature: Singapore, 2021; pp. 359–381. [Google Scholar] [CrossRef]
- Nosrati, K.; Saravi, M.M.; Shahbazi, A. Investigation of flood event possibility over Iran using Flood Index. In Survival and Sustainability: Environmental Concerns in the 21st Century; Gökçekus, H., Türker, U., LaMoreaux, J.W., Eds.; Environmental Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1355–1361. [Google Scholar]
- Deo, R.C.; Adamowski, J.F.; Begum, K.; Salcedo-Sanz, S.; Kim, D.W.; Dayal, K.S.; Byun, H.R. Quantifying flood events in Bangladesh with a daily-step flood monitoring index based on the concept of daily effective precipitation. Theor. Appl. Climatol. 2019, 137, 1201–1215. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Farheen, S.; Nguyen-Huy, T.; Raj, N.; Jui, S.J.J.; Farzana, S. Real-time prediction of the week-ahead flood index using hybrid deep learning algorithms with synoptic climate mode indices. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Deo, R.C.; Byun, H.R.; Kim, G.B.; Adamowski, J.F. A real-time hourly water index for flood risk monitoring: Pilot studies in Brisbane, Australia, and Dobong Observatory, South Korea. Environ. Monit. Assess. 2018, 190, 1–27. [Google Scholar] [CrossRef]
- Chebana, F.; Ouarda, T.B. Index flood–based multivariate regional frequency analysis. Water Resour. Res. 2009, 45, W10435. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Ann. l’ISUP 1959, 8, 229–231. [Google Scholar]
- Daneshkhah, A.; Remesan, R.; Chatrabgoun, O.; Holman, I.P. Probabilistic modeling of flood characterizations with parametric and minimum information pair-copula model. J. Hydrol. 2016, 540, 469–487. [Google Scholar] [CrossRef]
- Shafaei, M.; Fakheri-Fard, A.; Dinpashoh, Y.; Mirabbasi, R.; De Michele, C. Modeling flood event characteristics using D-vine structures. Theor. Appl. Climatol. 2017, 130, 713–724. [Google Scholar] [CrossRef]
- Tosunoglu, F.; Gürbüz, F.; İspirli, M.N. Multivariate modeling of flood characteristics using Vine copulas. Environ. Earth Sci. 2020, 79, 1–21. [Google Scholar] [CrossRef]
- Kuleshov, Y.; McGree, S.; Jones, D.; Charles, A.; Cottrill, A.; Prakash, B.; Atalifo, T.; Nihmei, S.; Seuseu, F.L.S.K. Extreme weather and climate events and their impacts on island countries in the Western Pacific: Cyclones, floods and droughts. Atmos. Clim. Sci. 2014, 4, 803. [Google Scholar] [CrossRef]
- Feresi, J.; Kenny, G.J.; de Wet, N.; Limalevu, L.; Bhusan, J.; Ratukalou, I. Climate Change Vulnerability and Adaptation Assessment for Fiji; Technical Report; The International Global Change Institute (IGCI), University of Waikato: Hamilton, New Zealand, 2000. [Google Scholar]
- Kumar, R.; Stephens, M.; Weir, T. Rainfall trends in Fiji. Int. J. Climatol. 2014, 34, 1501–1510. [Google Scholar] [CrossRef]
- McGree, S.; Yeo, S.W.; Devi, S. Flooding in the Fiji Islands between 1840 and 2009; Risk Frontiers Technical Report, Risk Frontiers; Macquarie University: Macquarie Park, Australia, 2010. [Google Scholar]
- Lo Presti, R.; Barca, E.; Passarella, G. A methodology for treating missing data applied to daily rainfall data in the Candelaro River Basin (Italy). Environ. Monit. Assess. 2010, 160, 1–22. [Google Scholar] [CrossRef]
- Oriani, F.; Stisen, S.; Demirel, M.C.; Mariethoz, G. Missing data imputation for multisite rainfall networks: A comparison between geostatistical interpolation and pattern-based estimation on different terrain types. J. Hydrometeorol. 2020, 21, 2325–2341. [Google Scholar] [CrossRef]
- Yevjevich, V.M. Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1967. [Google Scholar]
- FMS. Fiji Annual Climate Summary 2014. Report, Fiji Meteorological Service. 2015. Available online: https://www.met.gov.fj/aifs_prods/ACS-2014.pdf (accessed on 11 January 2024).
- Nguyen-Huy, T.; Deo, R.C.; Mushtaq, S.; Kath, J.; Khan, S. Copula-based agricultural conditional value-at-risk modelling for geographical diversifications in wheat farming portfolio management. Weather Clim. Extrem. 2018, 21, 76–89. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; Khan, S.; Devi, A.; Adeyinka, A.A.; Apan, A.A.; Yaseen, Z.M. Student performance predictions for advanced engineering mathematics course with new multivariate copula models. IEEE Access 2022, 10, 45112–45136. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; Mushtaq, S.; Kath, J.; Khan, S. Copula statistical models for analyzing stochastic dependencies of systemic drought risk and potential adaptation strategies. Stoch. Environ. Res. Risk Assess. 2019, 33, 779–799. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Kath, J.; Mushtaq, S.; Cobon, D.; Stone, G.; Stone, R. Integrating El Niño-Southern Oscillation information and spatial diversification to minimize risk and maximize profit for Australian grazing enterprises. Agron. Sustain. Dev. 2020, 40, 4. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J.; Xie, F. Vine copula selection using mutual information for hydrological dependence modeling. Environ. Res. 2020, 186, 109604. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; Mushtaq, S.; Khan, S. Probabilistic seasonal rainfall forecasts using semiparametric d-vine copula-based quantile regression. In Handbook of Probabilistic Models; Samui, P., Chakraborty, S., Bui, D.T., Deo, R.C., Eds.; Elsevier: Oxford, UK, 2020; pp. 203–227. [Google Scholar] [CrossRef]
- Cheng, Y.; Du, J.; Ji, H. Multivariate joint probability function of earthquake ground motion prediction equations based on vine copula approach. Math. Probl. Eng. 2020, 2020, 1697352. [Google Scholar] [CrossRef]
- Lü, T.J.; Tang, X.S.; Li, D.Q.; Qi, X.H. Modeling multivariate distribution of multiple soil parameters using vine copula model. Comput. Geotech. 2020, 118, 103340. [Google Scholar] [CrossRef]
- Latif, S.; Mustafa, F. Parametric vine copula construction for flood analysis for Kelantan river basin in Malaysia. Civ. Eng. J. 2020, 6, 1470–1491. [Google Scholar] [CrossRef]
- Latif, S.; Simonovic, S.P. Parametric Vine copula framework in the trivariate probability analysis of compound flooding events. Water 2022, 14, 2214. [Google Scholar] [CrossRef]
- Latif, S.; Simonovic, S.P. Trivariate Joint Distribution Modelling of Compound Events Using the Nonparametric D-Vine Copula Developed Based on a Bernstein and Beta Kernel Copula Density Framework. Hydrology 2022, 9, 221. [Google Scholar] [CrossRef]
- Czado, C.; Bax, K.; Sahin, Ö.; Nagler, T.; Min, A.; Paterlini, S. Vine copula based dependence modeling in sustainable finance. J. Financ. Data Sci. 2022, 8, 309–330. [Google Scholar] [CrossRef]
- Jeong, H.; Dey, D. Application of a vine copula for multi-line insurance reserving. Risks 2020, 8, 111. [Google Scholar] [CrossRef]
- Allen, D.E.; McAleer, M.; Singh, A.K. Risk measurement and risk modelling using applications of vine copulas. Sustainability 2017, 9, 1762. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; Chapman & Hall/CRC: Boca Raton, FL, USA, 1997. [Google Scholar]
- Nagler, T.; Krüger, D.; Min, A. Stationary vine copula models for multivariate time series. J. Econom. 2022, 227, 305–324. [Google Scholar] [CrossRef]
- Nagler, T.; Vatter, T. Rvinecopulib: High Performance Algorithms for Vine Copula Modeling. R Package Version 3, CRAN. 2023. Available online: https://cran.r-project.org/web/packages/rvinecopulib/rvinecopulib.pdf (accessed on 11 January 2024).
- Nagler, T.; Czado, C. Evading the curse of dimensionality in nonparametric density estimation with simplified vine copulas. J. Multivar. Anal. 2016, 151, 69–89. [Google Scholar] [CrossRef]
- Nagler, T.; Schellhase, C.; Czado, C. Nonparametric estimation of simplified vine copula models: Comparison of methods. Depend. Model. 2017, 5, 99–120. [Google Scholar] [CrossRef]
- Nagler, T.; Bumann, C.; Czado, C. Model selection in sparse high-dimensional vine copula models with an application to portfolio risk. J. Multivar. Anal. 2019, 172, 180–192. [Google Scholar] [CrossRef]
- FMS. Fiji Annual Climate Summary 2016. Report, Fiji Meteorological Service. 2017. Available online: https://www.met.gov.fj/Summary2.pdf (accessed on 11 January 2024).
- FMS. Fiji Annual Climate Summary 2015. Report, Fiji Meteorological Service. 2016. Available online: https://www.met.gov.fj/aifs_prods/ACS-2015.pdf (accessed on 11 January 2024).
- FMS. Fiji’s Climate in 2018. Report, Fiji Meteorological Service. 2019. Available online: https://www.met.gov.fj/aifs_prods/Climate_Products/December%202019annualSum2020.02.05%2012.35.54.pdf (accessed on 11 January 2024).
- FMS. Fiji Climate Summary January 2018. Report, Fiji Meteorological Service. 2018. Available online: https://www.met.gov.fj/aifs_prods/FSCJAN18.pdf (accessed on 11 January 2024).
- FMS. Fiji Annual Climate Summary 2017. Report, Fiji Meteorological Service. 2018. Available online: https://www.met.gov.fj/aifs_prods/Climate_Products/2017annualSum2020.01.28%2012.40.27.pdf (accessed on 11 January 2024).
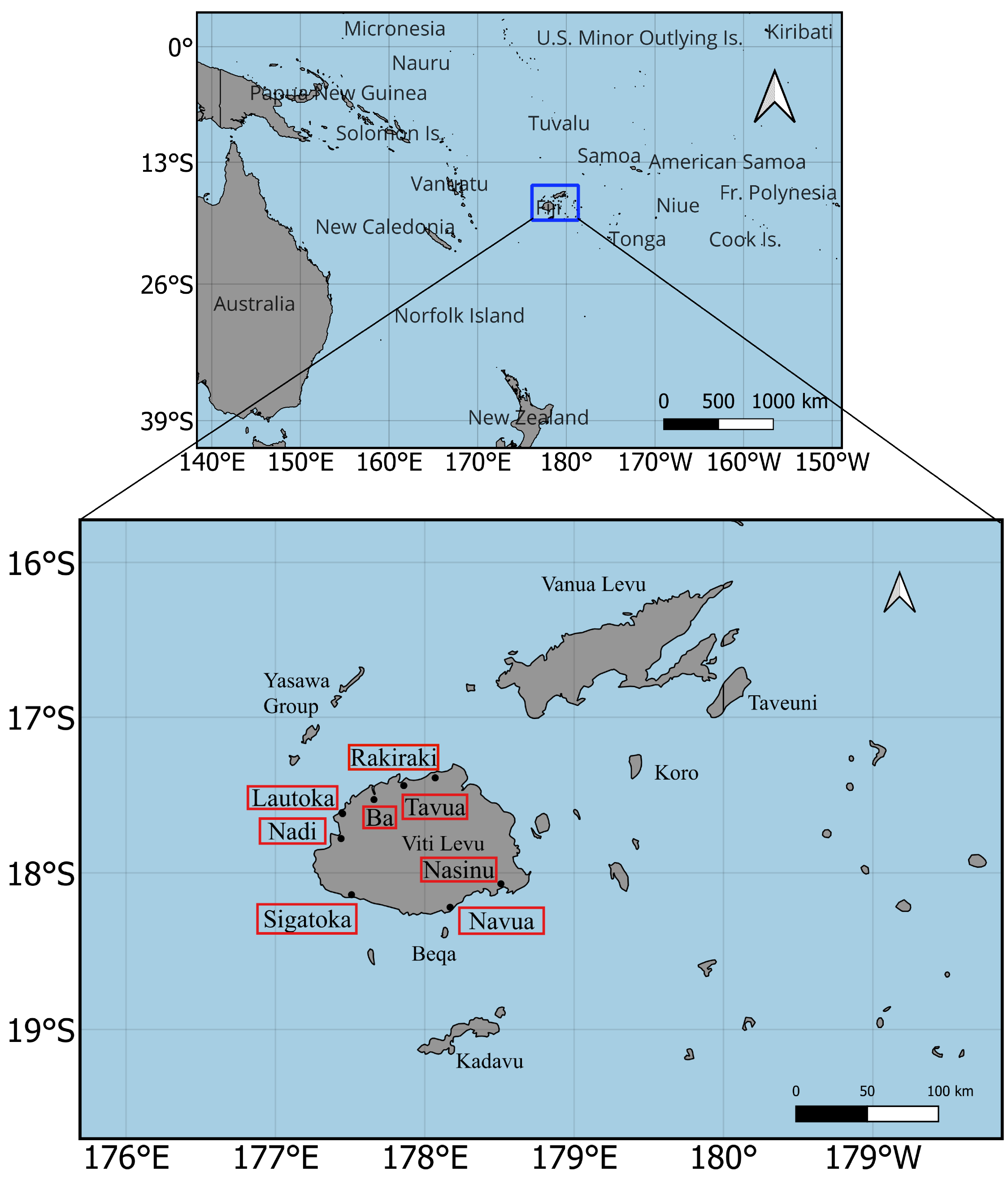



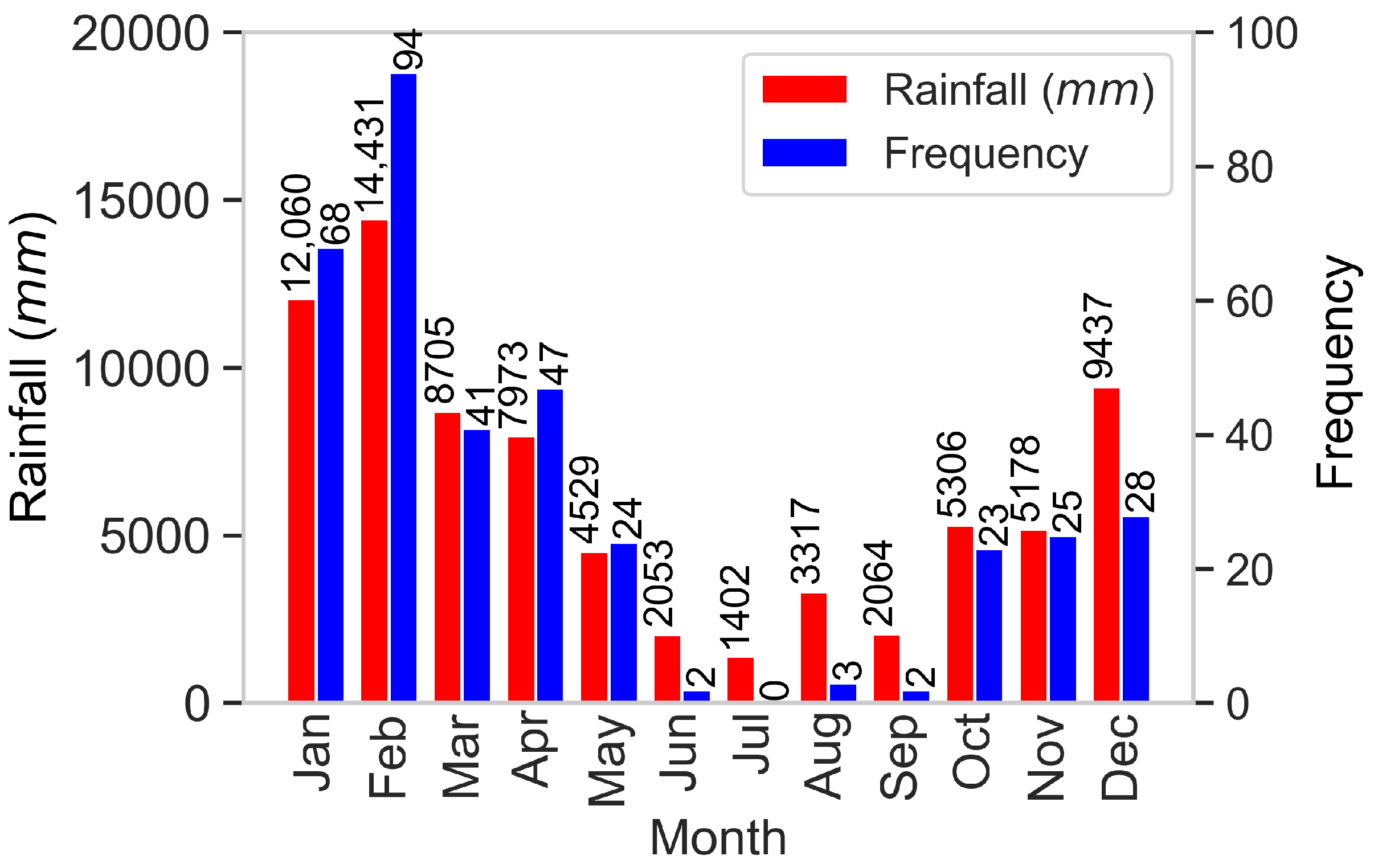
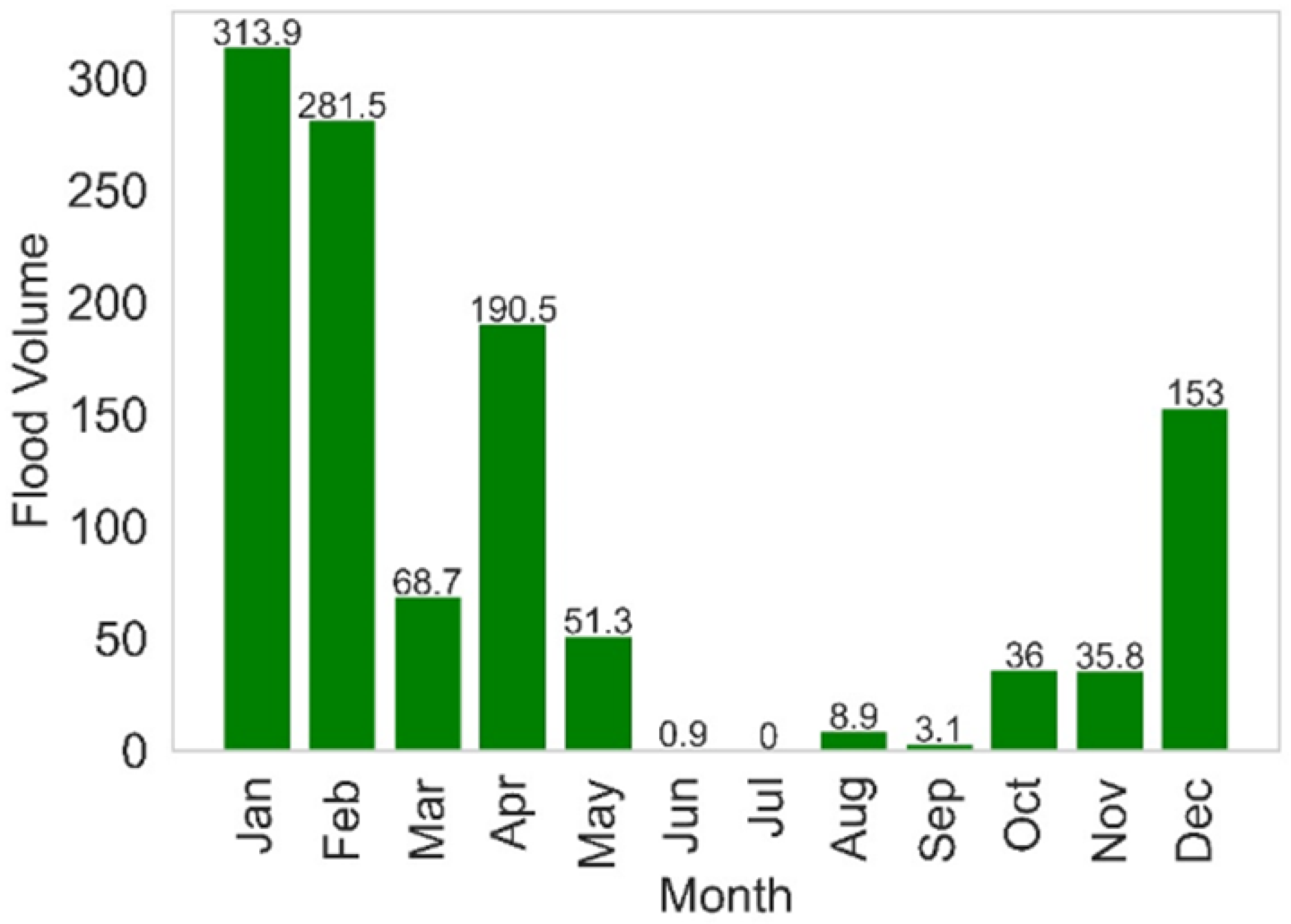
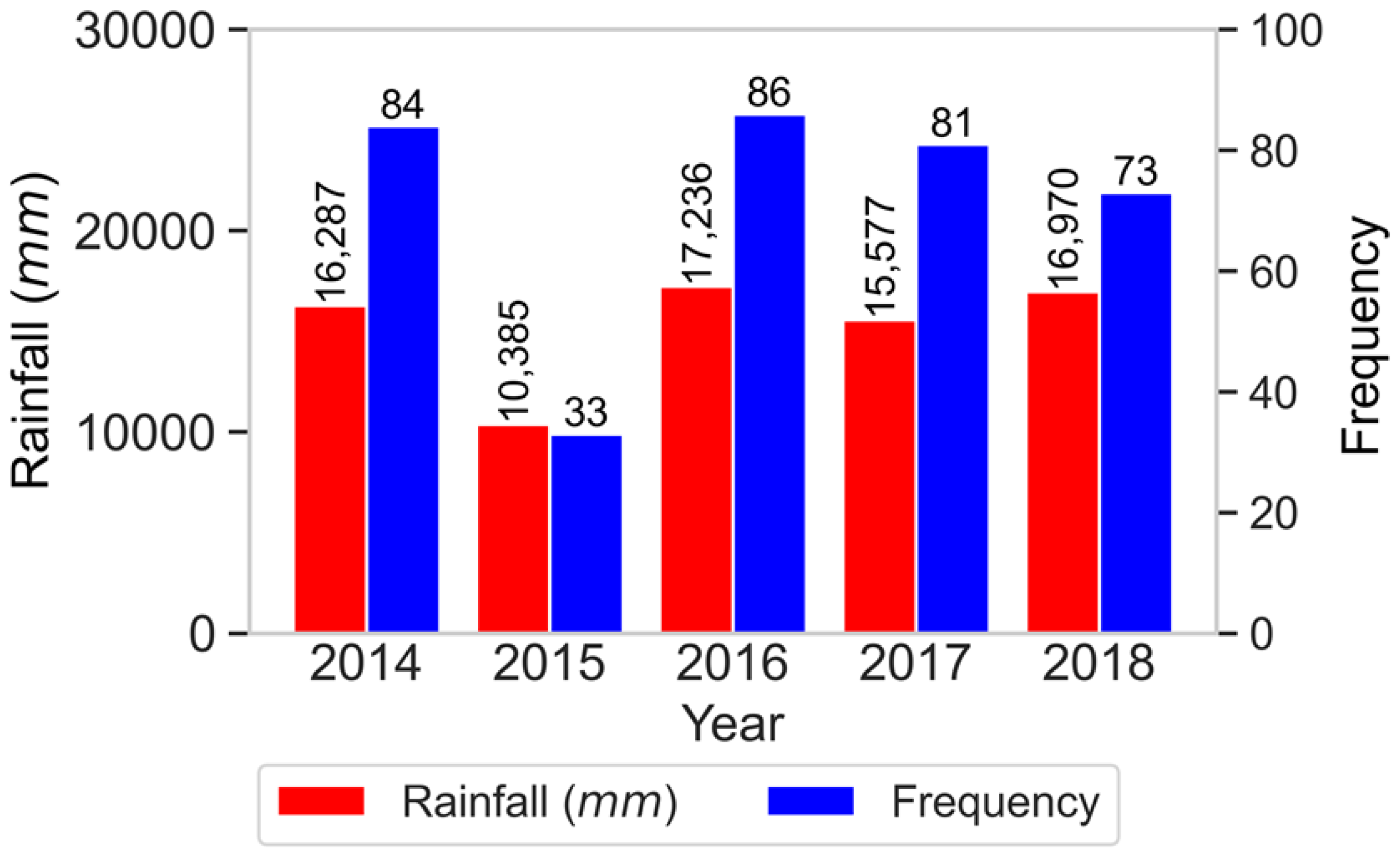
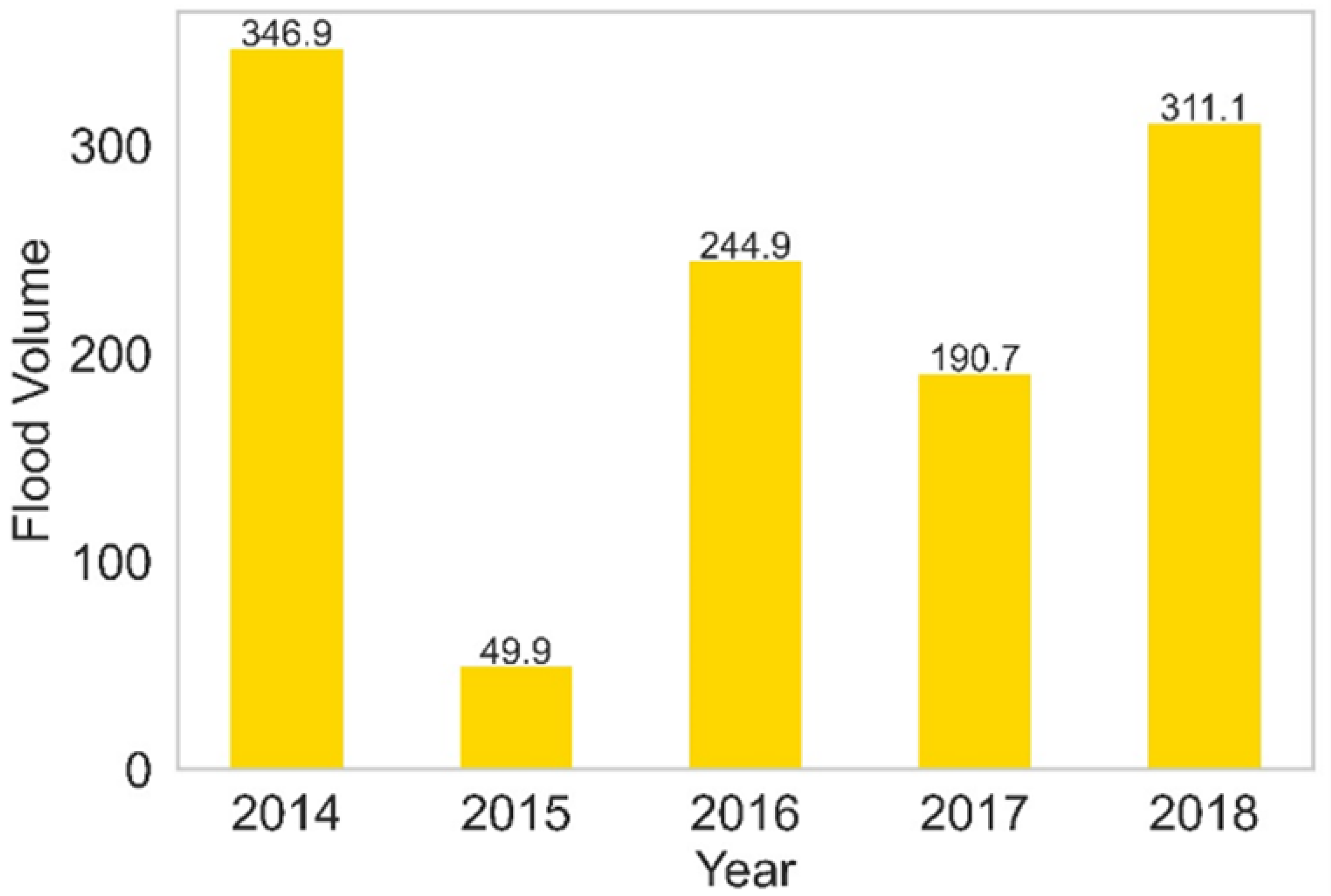

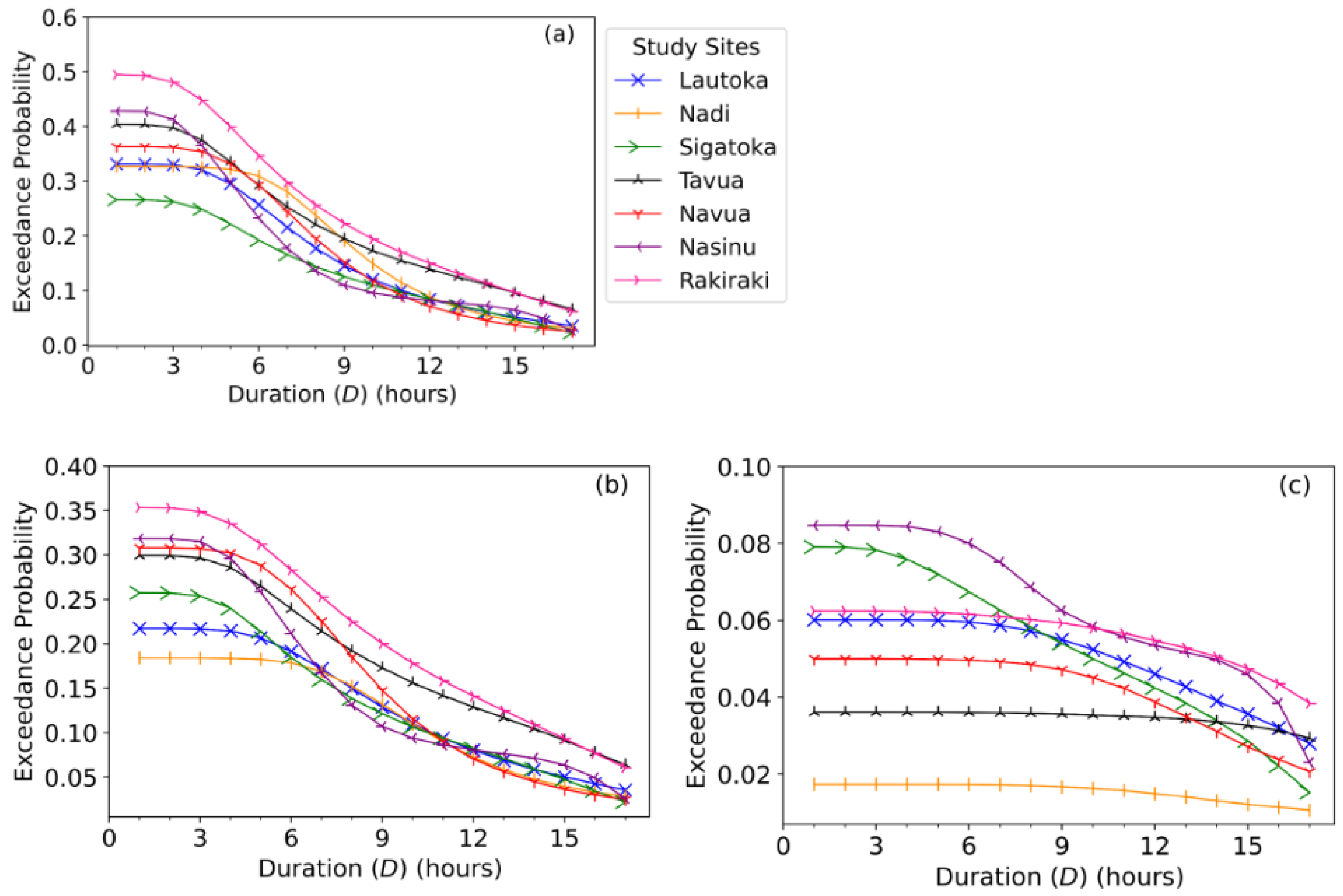
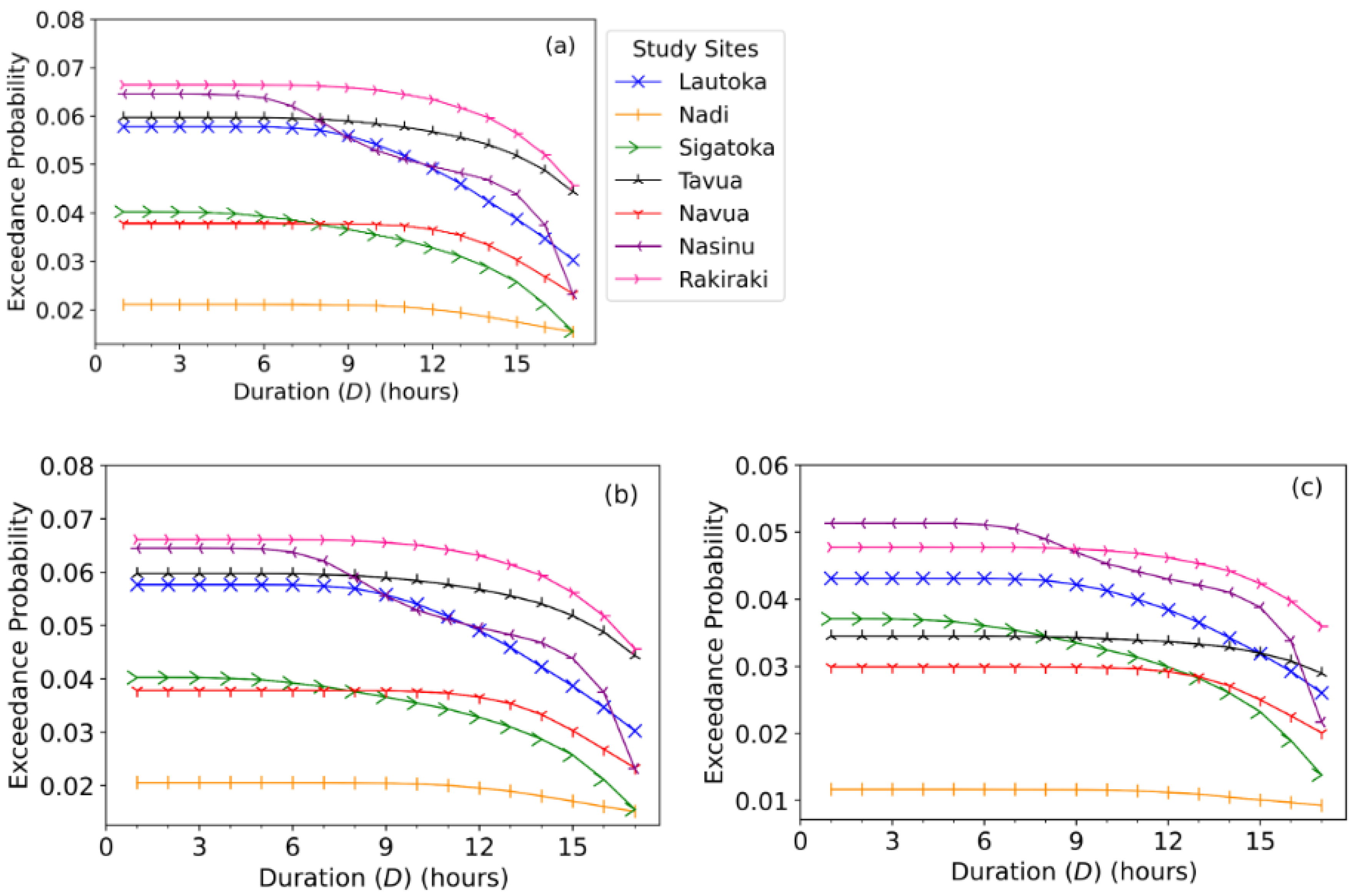
| Study Site | Location | Missing Data | Average | Maximum |
|---|---|---|---|---|
| (%) | Hourly Rainfall (mm) | Hourly Rainfall (mm) | ||
| Ba | 17.53° S, 177.66° E | 23.76 | 0.24 | 56.00 |
| Lautoka | 17.62° S, 177.45° E | 0.83 | 0.19 | 83.50 |
| Nadi | 17.78° S, 177.44° E | 1.17 | 0.27 | 260.00 |
| Nasinu | 18.07° S, 178.51° E | 1.18 | 0.33 | 72.00 |
| Navua | 18.22° S, 178.17° E | 1.57 | 0.36 | 62.50 |
| Rakiraki | 17.39° S, 178.07° E | 3.76 | 0.23 | 68.50 |
| Sigatoka | 18.14° S, 177.51° E | 1.99 | 0.21 | 59.00 |
| Tavua | 17.44° S, 177.86° E | 3.45 | 0.16 | 57.50 |
| Study Site | Onset Time | Volume | Duration (hrs) | Peak | Total | Total Rain (mm) | Maximum | |
|---|---|---|---|---|---|---|---|---|
| a | Nadi | |||||||
| 1 | 29 January 2014 at 8 a.m. | 157.28 | 49 | 6.80 | 10,557.06 | 1590 | 416.05 | |
| 2 | 8 February 2017 at 4 a.m. | 11.88 | 18 | 1.31 | 1316.32 | 195.40 | 109.56 | |
| 3 | 4 April 2016 at 8 a.m. | 6.86 | 20 | 0.87 | 1108.52 | 161.40 | 84.87 | |
| 4 | 7 January 2014 at 6 p.m. | 6.31 | 10 | 1.73 | 715.09 | 84 | 133.10 | |
| 5 | 15 January 2014 at 6 p.m. | 5.77 | 13 | 1.18 | 794.02 | 84 | 102.03 | |
| b | Lautoka | |||||||
| 1 | 14 January 2018 at 2 p.m. | 25.05 | 19 | 3.29 | 1315.15 | 175 | 126.10 | |
| 2 | 6 April 2016 at 2 a.m. | 23.95 | 19 | 2.27 | 1283.34 | 180 | 96.59 | |
| 3 | 1 April 2014 at 7 a.m. | 18.39 | 13 | 3.49 | 935.98 | 109 | 131.92 | |
| 4 | 6 February 2017 at 3 p.m. | 11.48 | 20 | 1.53 | 954.55 | 131.50 | 75.40 | |
| 5 | 8 February 2017 at 9 a.m. | 10.85 | 13 | 1.49 | 718.16 | 98 | 74.18 | |
| c | Nasinu | |||||||
| 1 | 27 February 2014 at 9 a.m. | 24.90 | 18 | 2.83 | 1388.83 | 173 | 115.53 | |
| 2 | 21 February 2015 at 6 p.m. | 23.15 | 16 | 2.48 | 1261.37 | 163.50 | 106.16 | |
| 3 | 6 December 2014 at 4 a.m. | 19.15 | 16 | 2.92 | 1155.37 | 140 | 117.79 | |
| 4 | 11 November 2018 at 11 p.m. | 7.46 | 8 | 1.91 | 521.64 | 37 | 91.16 | |
| 5 | 28 May 2018 at 8 a.m. | 7.20 | 7 | 2.10 | 474.23 | 21 | 96.15 | |
| d | Navua | |||||||
| 1 | 15 December 2016 at 6 a.m. | 56.98 | 28 | 4.29 | 2732.99 | 392.50 | 161.35 | |
| 2 | 17 March 2017 at 4 a.m. | 16.37 | 14 | 2.10 | 1023.68 | 114.50 | 99.48 | |
| 3 | 16 January 2014 at 1 a.m. | 9.82 | 14 | 1.16 | 838.28 | 123.50 | 72.87 | |
| 4 | 2 May 2016 at 6 a.m. | 8.15 | 13 | 1.38 | 751.01 | 110 | 79.03 | |
| 5 | 27 February 2014 at 3 p.m. | 7.98 | 10 | 1.61 | 626.25 | 83.50 | 85.60 | |
| e | Rakiraki | |||||||
| 1 | 19 December 2016 at 5 a.m. | 33.99 | 21 | 4.28 | 1783.89 | 265.50 | 170.39 | |
| 2 | 14 January 2018 at 2 p.m. | 19.89 | 17 | 2 | 1199.35 | 156.50 | 97.02 | |
| 3 | 20 February 2016 at 8 p.m. | 16.89 | 17 | 2.68 | 1103.01 | 112.50 | 119.05 | |
| 4 | 17 December 2016 at 4 p.m. | 11.28 | 19 | 1.25 | 989.33 | 145.50 | 73.09 | |
| 5 | 5 March 2017 at 9 a.m. | 10.06 | 15 | 1.52 | 818.03 | 114.50 | 81.73 | |
| f | Sigatoka | |||||||
| 1 | 30 January 2014 at 10 a.m. | 23.32 | 16 | 2.84 | 999.93 | 121 | 92.83 | |
| 2 | 3 February 2018 at 3 p.m. | 15 | 12 | 2.25 | 695.39 | 93 | 79.78 | |
| 3 | 1 May 2018 at 6 p.m. | 11.10 | 14 | 1.67 | 671.12 | 65 | 67.25 | |
| 4 | 4 April 2016 at 12 a.m. | 10.91 | 18 | 1.33 | 789.16 | 103 | 59.79 | |
| 5 | 1 April 2018 at 6 a.m. | 9.74 | 11 | 1.55 | 549.66 | 73 | 64.62 | |
| g | Tavua | |||||||
| 1 | 8 February 2017 at 10 a.m. | 45.88 | 23 | 4.04 | 1612.79 | 238 | 117.34 | |
| 2 | 3 April 2016 at 5 p.m. | 20.37 | 23 | 2.36 | 1023.74 | 154 | 78.55 | |
| 3 | 17 May 2014 at 10 a.m. | 17.16 | 17 | 1.81 | 805.30 | 103.50 | 65.93 | |
| 4 | 6 February 2017 at 11 a.m. | 14.77 | 18 | 1.69 | 774.08 | 89.50 | 63.11 | |
| 5 | 6 March 2017 at 1 p.m. | 14.23 | 17 | 1.75 | 737.52 | 98.50 | 64.47 |
| Flood Characteristic | Site | Min. | Lower Quartile (Q1) | Median (Q2) | Upper Quartile (Q3) | Max. | Mean | Standard Dev. | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|---|---|---|
| Duration (D) (hours) | Lautoka | 1 | 1 | 3 | 6 | 20 | 4.796 | 4.791 | 1.771 | 5.511 |
| Nadi | 1 | 1 | 3 | 7 | 49 | 5.424 | 7.135 | 4.286 | 24.981 | |
| Rakiraki | 1 | 1 | 3 | 8 | 21 | 5.681 | 5.801 | 1.248 | 3.243 | |
| Tavua | 1 | 2 | 3 | 7 | 23 | 5.525 | 5.749 | 1.590 | 4.492 | |
| Sigatoka | 1 | 1 | 3 | 5 | 18 | 4.413 | 4.578 | 1.746 | 4.848 | |
| Navua | 1 | 1 | 3 | 5 | 28 | 4.367 | 5.003 | 2.753 | 11.676 | |
| Nasinu | 1 | 2 | 3 | 6 | 18 | 4.415 | 4.153 | 1.962 | 6.236 | |
| Volume (V) | Lautoka | 0.003 | 0.204 | 0.633 | 1.983 | 25 | 2.746 | 5.473 | 3.022 | 11.168 |
| Nadi | 0.002 | 0.132 | 0.517 | 2.271 | 157.276 | 4.156 | 20.404 | 7.538 | 55.625 | |
| Rakiraki | 0.005 | 0.097 | 0.529 | 3.038 | 33.993 | 3.272 | 6.329 | 3.257 | 13.998 | |
| Tavua | 0.016 | 0.185 | 0.617 | 2.272 | 45.879 | 3.190 | 7.123 | 4.230 | 22.984 | |
| Sigatoka | 0.021 | 0.220 | 0.632 | 2.834 | 23.316 | 2.826 | 4.777 | 2.523 | 9.293 | |
| Navua | 0.005 | 0.167 | 0.557 | 2.058 | 56.983 | 3.012 | 8.495 | 5.656 | 34.803 | |
| Nasinu | 0.033 | 0.159 | 0.886 | 2.854 | 24.903 | 3.028 | 5.853 | 2.951 | 10.098 | |
| Peak (Q) | Lautoka | 0.003 | 0.179 | 0.348 | 0.701 | 3.490 | 0.597 | 0.725 | 2.519 | 9.356 |
| Nadi | 0.002 | 0.108 | 0.244 | 0.674 | 6.803 | 0.527 | 0.940 | 5.369 | 35.042 | |
| Rakiraki | 0.005 | 0.097 | 0.323 | 0.816 | 4.282 | 0.606 | 0.809 | 2.663 | 10.954 | |
| Tavua | 0.016 | 0.124 | 0.338 | 0.799 | 4.040 | 0.573 | 0.688 | 2.719 | 12.339 | |
| Sigatoka | 0.021 | 0.207 | 0.393 | 1.121 | 2.841 | 0.718 | 0.714 | 1.369 | 3.945 | |
| Navua | 0.005 | 0.167 | 0.401 | 0.723 | 4.289 | 0.601 | 0.747 | 2.924 | 13.398 | |
| Nasinu | 0.033 | 0.139 | 0.419 | 0.916 | 2.915 | 0.720 | 0.763 | 1.566 | 4.596 |
| Site | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MI | MI | MI | ||||||||||
| Lautoka | 0.895 | 0.941 | 0.831 | 1.051 | 0.860 | 0.877 | 0.738 | 0.584 | 0.931 | 0.971 | 0.883 | 1.044 |
| Nadi | 0.863 | 0.950 | 0.849 | 0.966 | 0.929 | 0.891 | 0.740 | 0.619 | 0.924 | 0.978 | 0.890 | 0.771 |
| Rakiraki | 0.855 | 0.934 | 0.828 | 0.823 | 0.842 | 0.902 | 0.760 | 0.647 | 0.949 | 0.987 | 0.926 | 1.123 |
| Sigatoka | 0.895 | 0.929 | 0.820 | 0.851 | 0.810 | 0.869 | 0.721 | 0.616 | 0.887 | 0.979 | 0.888 | 1.129 |
| Tavua | 0.838 | 0.946 | 0.836 | 0.983 | 0.859 | 0.902 | 0.698 | 0.651 | 0.942 | 0.960 | 0.859 | 1.103 |
| Navua | 0.891 | 0.937 | 0.838 | 1.066 | 0.937 | 0.892 | 0.752 | 0.616 | 0.899 | 0.982 | 0.903 | 0.933 |
| Nasinu | 0.942 | 0.945 | 0.831 | 0.903 | 0.895 | 0.844 | 0.687 | 0.501 | 0.896 | 0.964 | 0.844 | 0.904 |
| Site | D-Vine Structure (Conditioning Variable) | Tree Level | Flood Characteristic Pairs | Best-Fitted Copula | Copula Dependence Parameter (s) | logLik | AIC | BIC | |
|---|---|---|---|---|---|---|---|---|---|
| Lautoka | D-V-Q (V is placed in the centre) | Tree 1 | D-V | Gaussian | 0.77 | 102.58 | −199.16 | −193.19 | |
| V-Q | Gaussian | 0.78 | |||||||
| Tree 2 | DQ|V | Gumbel | 0.08 | ||||||
| Nadi | Tree 1 | D-V | Frank | 0.77 | 142.45 | −278.89 | −272.66 | ||
| V-Q | BB7 | ; | 0.81 | ||||||
| Tree 2 | DQ|V | Independence | NA | 0 | |||||
| Nasinu | Tree 1 | D-V | Gaussian | 0.75 | 2.98 | −141.96 | −138.53 | ||
| V-Q | Gaussian | 0.75 | |||||||
| Tree 2 | DQ|V | Independence | NA | 0 | |||||
| Navua | Tree 1 | D-V | Frank | 0.78 | 111.65 | −219.29 | −215.51 | ||
| V-Q | Survival Gumbel (Rotated Gumbel 180 degrees) | 0.84 | |||||||
| Tree 2 | DQ|V | Independence | NA | 0 | |||||
| Rakiraki | Tree 1 | D-V | Gaussian | 0.75 | 118.13 | −230.25 | −224.70 | ||
| V-Q | BB7 | ; | 0.83 | ||||||
| Tree 2 | DQ|V | Independence | NA | 0 | |||||
| Sigatoka | Tree 1 | D-V | Frank | 0.82 | 123.88 | −241.76 | −236.27 | ||
| V-Q | Survival Gumbel (Rotated Gumbel 180 degrees) | 0.86 | |||||||
| Tree 2 | DQ|V | Frank | −0.36 | ||||||
| Tavua | Tree 1 | D-V | Survival BB7 (Rotated BB7 180 degrees) | ; | 0.77 | 148.44 | −288.87 | −280.43 | |
| V-Q | BB7 | ; | 0.82 | ||||||
| Tree 2 | DQ|V | Independence | NA | 0 |
| Flood Characteristic | Study Site | 50th Quantile | 75th Quantile | 95th Quantile |
|---|---|---|---|---|
| D (hours) | Lautoka | 3 | 6 | 15 |
| Nadi | 3 | 7 | 13 | |
| Rakiraki | 3 | 8 | 17 | |
| Tavua | 3 | 7 | 17 | |
| Sigatoka | 3 | 5 | 16 | |
| Navua | 3 | 5 | 14 | |
| Nasinu | 3 | 6 | 16 | |
| Average | 3 | 6 | 15 | |
| V | Lautoka | 0.633 | 1.983 | 13.898 |
| Nadi | 0.517 | 2.271 | 6.365 | |
| Rakiraki | 0.529 | 3.038 | 15.205 | |
| Tavua | 0.617 | 2.272 | 14.767 | |
| Sigatoka | 0.632 | 2.834 | 11.054 | |
| Navua | 0.557 | 2.058 | 9.149 | |
| Nasinu | 0.866 | 2.854 | 19.153 | |
| Average | 0.622 | 2.473 | 12.799 | |
| Q | Lautoka | 0.348 | 0.701 | 1.840 |
| Nadi | 0.244 | 0.674 | 1.365 | |
| Rakiraki | 0.323 | 0.816 | 1.976 | |
| Tavua | 0.338 | 0.799 | 1.750 | |
| Sigatoka | 0.393 | 1.121 | 2.305 | |
| Navua | 0.401 | 0.723 | 1.694 | |
| Nasinu | 0.419 | 0.916 | 2.477 | |
| Average | 0.352 | 0.821 | 1.915 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chand, R.; Nguyen-Huy, T.; Deo, R.C.; Ghimire, S.; Ali, M.; Ghahramani, A. Copula-Probabilistic Flood Risk Analysis with an Hourly Flood Monitoring Index. Water 2024, 16, 1560. https://doi.org/10.3390/w16111560
Chand R, Nguyen-Huy T, Deo RC, Ghimire S, Ali M, Ghahramani A. Copula-Probabilistic Flood Risk Analysis with an Hourly Flood Monitoring Index. Water. 2024; 16(11):1560. https://doi.org/10.3390/w16111560
Chicago/Turabian StyleChand, Ravinesh, Thong Nguyen-Huy, Ravinesh C. Deo, Sujan Ghimire, Mumtaz Ali, and Afshin Ghahramani. 2024. "Copula-Probabilistic Flood Risk Analysis with an Hourly Flood Monitoring Index" Water 16, no. 11: 1560. https://doi.org/10.3390/w16111560
APA StyleChand, R., Nguyen-Huy, T., Deo, R. C., Ghimire, S., Ali, M., & Ghahramani, A. (2024). Copula-Probabilistic Flood Risk Analysis with an Hourly Flood Monitoring Index. Water, 16(11), 1560. https://doi.org/10.3390/w16111560







