Method of Wavelet-Decomposition to Research Cosmic Ray Variations: Application in Space Weather
Abstract
:1. Introduction
2. Materials and Methods
2.1. Identification of Informative Signal Structures and Noise Reduction
2.2. Anomaly Detection and Estimate of Their Intensity
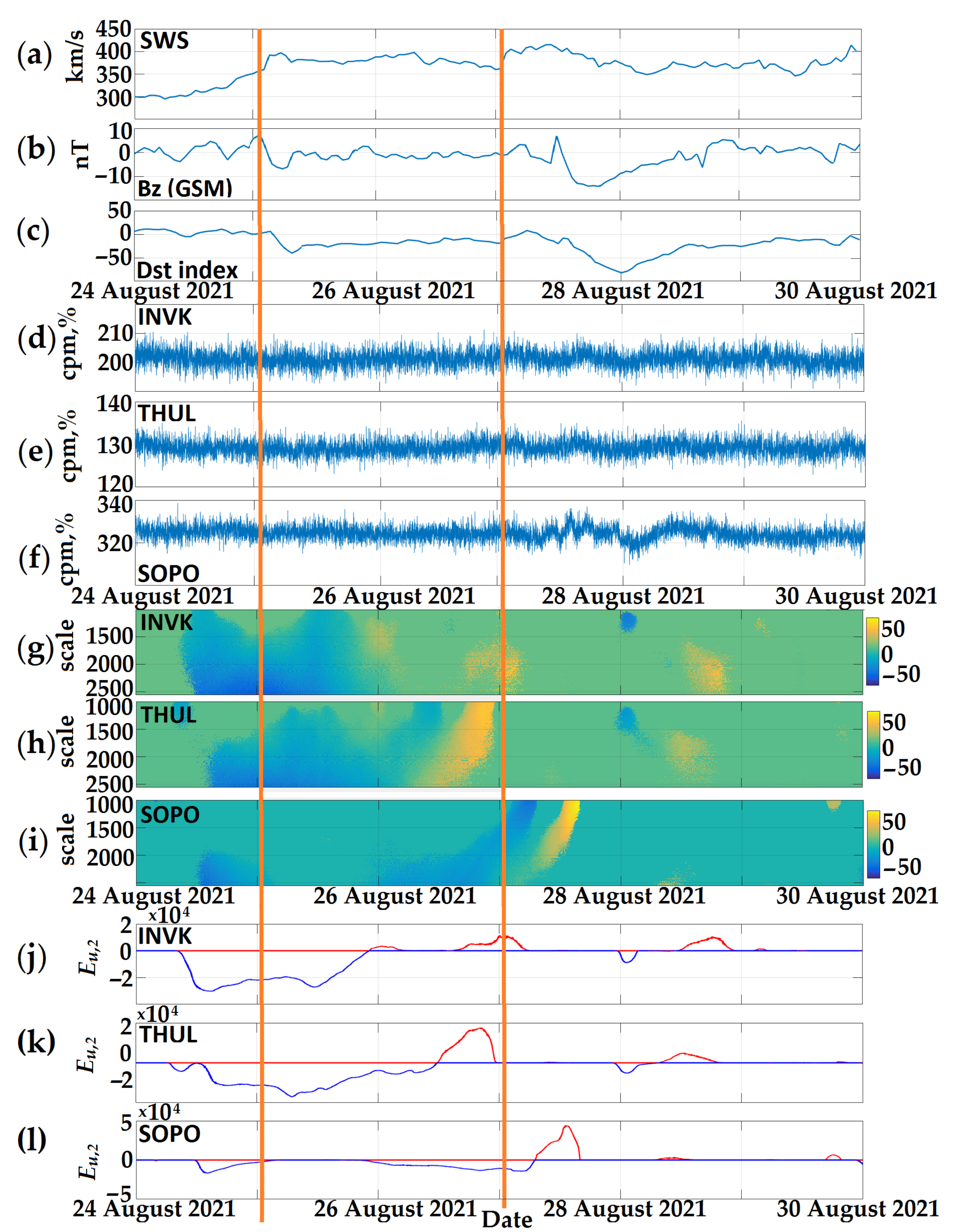
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Owens, A.J. The effects of fluctuations and noise on the neutron monitor diurnal anisotropy. J. Geophys. Res. Space Phys. 1977, 82, 1066–1070. [Google Scholar] [CrossRef]
- Aghion, S.; Amsler, C.; Bonomi, G.; Brusa, R.S.; Caccia, M.; Caravita, R.; Castelli, F.; Cerchiari, G.; Comparat, D.; Consolati, G.; et al. Compression of a mixed antiproton and electron non-neutral plasma to high densities. Eur. Phys. J. D 2018, 72, 1–11. [Google Scholar] [CrossRef]
- Andrei, C.-O.; Lahtinen, S.; Nordman, M.; Näränen, J.; Koivula, H.; Poutanen, M.; Hyyppä, J. GPS Time Series Analysis from Aboa the Finnish Antarctic Research Station. Remote Sens. 2018, 10, 1937. [Google Scholar] [CrossRef] [Green Version]
- Gaisser, T. Cosmic rays and particle physics at extremely high energies. J. Frankl. Inst. 1974, 298, 271–287. [Google Scholar] [CrossRef]
- Schlickeiser, R. Cosmic Ray Astrophysics; Springer GmbH & Co., KG.: Berlin/Heidelberg, Germany, 2002; p. 519. [Google Scholar]
- Yermolaev, Y.I.; Lodkina, I.G.; Dremukhina, L.A.; Yermolaev, M.Y.; Khokhlachev, A.A. What Solar–Terrestrial Link Researchers Should Know about Interplanetary Drivers. Universe 2021, 7, 138. [Google Scholar] [CrossRef]
- Iglesias-Martínez, M.E.; Castro-Palacio, J.C.; Scholkmann, F.; Milián-Sánchez, V.; Fernandez de Cordoba, P.; Mocholí-Salcedo, A.; Mocholi Belenguer, F.; Kolombet, V.A.; Panchelyuga, V.A.; Verdú, G. Correlations between Background Radiation Inside a Mul-tilayer Interleaving Structure, Geomagnetic Activity, and Cosmic Radiation: A Fourth-Order Cumulant-Based Correlation Analysis. Mathematics 2020, 8, 344. [Google Scholar] [CrossRef] [Green Version]
- Homola, P.; Beznosko, D.; Bhatta, G.; Bibrzycki, Ł.; Borczyńska, M.; Bratek, Ł.; Budnev, N.; Burakowski, D.; Alvarez-Castillo, D.; Cheminant, K.A.; et al. Cosmic-Ray Extremely Distributed Observatory. Symmetry 2020, 12, 1835. [Google Scholar] [CrossRef]
- Abunin, A.A.; Abunina, M.A.; Belov, A.V.; Eroshenko, E.A.; Oleneva, V.A.; Yanke, V.G. Forbush effects with a sudden and gradual onset. Geomagn. Aeron. 2012, 52, 292–299. [Google Scholar] [CrossRef]
- Bychkov, A.; Guskov, A. Search for correlations between the solar-flare disturbances of the earth’s magnetosphere and a flux of cosmic rays detected by the RUSALKA setup. Phys. Part. Nucl. Lett. 2012, 9, 578–581. [Google Scholar] [CrossRef]
- Badruddin, B.; Aslam, O.P.M.; Derouich, M.; Asiri, H.; Kudela, K. Forbush decreases and geomagnetic storms during a highly disturbed solar and interplanetary period, 4–10 September 2017. Space Weather 2019, 17, 487. [Google Scholar] [CrossRef]
- Kudela, K.; Rybak, J.; Antalová, A.; Storini, M. Time Evolution of low-Frequency Periodicities in Cosmic ray Intensity. Sol. Phys. 2002, 205, 165–175. [Google Scholar] [CrossRef]
- Badruddin, B.H.; Derouich, M. Study of the geoeffectiveness of interplanetary magnetic clouds. Planet. Space Sci. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Akiyama, S.; Yashiro, S.; Michalek, G.; Lepping, R.P. Solar sources and geospace consequences of inter-planetary magnetic clouds observed during solar cycle 23. J. Atmos. Sol. Terr. Phys. 2008, 70, 245–253. [Google Scholar] [CrossRef]
- Lara, A.; Gopalswamy, N.; Caballero-Lopez, R.A.; Yashiro, S.; Xie, H.; Valdes-Galicia, J.F. Coronal mass ejections and galactic cosmic ray modulation. Astrophys. J. 2005, 625, 441–450. [Google Scholar] [CrossRef]
- Livada, M.; Mavromichalaki, H.; Plainaki, C. Galactic cosmic ray spectral index: The case of Forbush decreases of March 2012. Astrophys. Space Sci. 2017, 363, 8. [Google Scholar] [CrossRef]
- E Carlson, B.; Brobeck, E.; Jillings, C.J.; Larson, M.B.; Lynn, T.W.; McKeown, R.D.; E Hill, J.; Falkowski, B.J.; Seki, R.; Sepikas, J.; et al. Search for correlated high energy cosmic ray events with CHICOS. J. Phys. G Nucl. Part. Phys. 2005, 31, 409–416. [Google Scholar] [CrossRef] [Green Version]
- Papailiou, M.; Mavromichalaki, H.; Belov, A.; Eroshenko, E.; Yanke, V. Precursor Effects in Different Cases of Forbush Decreases. Sol. Phys. 2011, 276, 337–350. [Google Scholar] [CrossRef]
- Paul, A.B.K.; Antia, H.; Dugad, S.; Gupta, S.K.; Hayashi, Y.; Kawakami, S.; Mohanty, P.K.; Oshima, A.; Subramanian, P. Forbush decrease precursors observed using GRAPES-3. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 44. [Google Scholar] [CrossRef]
- Dorman, L.I. Space weather and dangerous phenomena on the Earth: Principles of great geomagnetic storms forcasting by online cosmic ray data. Ann. Geophys. 2005, 23, 2997–3002. [Google Scholar] [CrossRef] [Green Version]
- Munakata, K.; Bieber, J.W.; Yasue, S.-I.; Kato, C.; Koyama, M.; Akahane, S.; Fujimoto, K.; Fujii, Z.; Humble, J.E.; Duldig, M.L. Precursors of geomagnetic storms observed by the muon detector network. J. Geophys. Res. Space Phys. 2000, 105, 27457–27468. [Google Scholar] [CrossRef]
- Kudela, K.; Brenkus, R. Cosmic ray decreases and geomagnetic activity: List of events 1982–2002. J. Atmos. Sol. Terr. Phys. 2004, 66, 1121–1126. [Google Scholar] [CrossRef]
- Thomas, S.; Owens, M.; Lockwood, M.; Barnard, L.; Scott, C. Near-earth cosmic ray decreases associated with remote coronal mass ejections. Astrophys. J. 2015, 801, 5. [Google Scholar] [CrossRef] [Green Version]
- Uryson, A. Studying Cosmic Ray Sources Using Intergalactic Electromagnetic Cascades. Universe 2021, 7, 287. [Google Scholar] [CrossRef]
- Grigoriev, V.G. Global survey method in real time and space weather forecast. Izvestiya RAN. Physics 2015, 79, 703–707. [Google Scholar]
- Belov, A.V.; Dorman, L.I.; Gushchina, R.T.; Yanke, V.G. Temporal and latitudinal dependence of the temperature effect for neutron component of cosmic ray. Proc. Int. Cosmic Ray Conf. 1995, 4, 1141–1144. [Google Scholar]
- SWS Australian Antarctic Division. Available online: http://www.sws.bom.gov.au/Geophysical/1/4 (accessed on 1 October 2020).
- Mandrikova, O.; Mandrikova, B.; Rodomanskay, A. Method of Constructing a Nonlinear Approximating Scheme of a Complex Signal: Application Pattern Recognition. Mathematics 2021, 9, 737. [Google Scholar] [CrossRef]
- Geppener, V.; Mandrikova, B. Method for cosmic ray variation analysis based on the data from global network of neutron monitors. In Proceedings of the 2020 International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Geppener, V.V.; Mandrikova, B.S. Automated Method for Cosmic Ray Data Analysis and Detection of Sporadic Effects. Comput. Math. Math. Phys. 2021, 61, 1129–1139. [Google Scholar] [CrossRef]
- Astafyeva, N.M.; Bazilevskaya, G.A. Long-Term Changes of Cosmic Ray Intensity: Spectral Behaviour and 27-Day Variations. Phys. Chem. Earth 1999, 25, 129–132. [Google Scholar] [CrossRef]
- Kudela, K.; Storini, M.; Antalova, A.; Rybak, J. On the wavelet approach to cosmic ray variability. In Proceedings of the 27th International Cosmic Ray Conference, Hamburg, Germany, 7–15 August 2001; pp. 3773–3776. Available online: https://articles.adsabs.harvard.edu//full/2001ICRC....9.3773K/0003776.000.html (accessed on 15 August 2021).
- Mandrikova, O.V.; Rodomanskaya, A.I.; Mandrikova, B.S. Application of the New Wavelet-Decomposition Method for the Analysis of Geomagnetic Data and Cosmic Ray Variations. Geomagn. Aeron. 2021, 61, 492–507. [Google Scholar] [CrossRef]
- Stamper, R.; Lockwood, M.; Wild, M.N.; Clark, T.D.G. Solar causes of the long-term increase in geomagnetic activity. J. Geophys. Res. 1999, 104, 325. [Google Scholar] [CrossRef] [Green Version]
- Mallat, S.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation via wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Mandrikova, O.V.; Solovev, I.S.; Zalyaev, T.L. Methods of analysis of geomagnetic field variations and cosmic ray data. Earth Planet Sp. 2014, 66, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Ten Lectures on Wavelets; CBMS-NSF Lecture Notes; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Real Time Data Base for the Measurements of High-Resolution Neutron Monitor. Available online: www.nmdb.eu (accessed on 1 October 2020).
- Mertens, J.-F.; Neyman, A. Minimax Theorems for Undiscounted Stochastic Games. Game Theory Math. Econ. 1981, 83–87. [Google Scholar]
- Chui, C.K. An Introduction in Wavelets; Academic Press: New York, NY, USA, 1992; p. 264. [Google Scholar]
- IZMIRAN Space Weather Forecast Center. Catalog of Forbush Effects and Interplanetary Disturbances. Available online: http://spaceweather.izmiran.ru/rus/fds2019.html (accessed on 11 October 2020).
- Institute of Applied Geophysics. Available online: http://ipg.geospace.ru/ (accessed on 11 October 2020).
- Chiaha, S.O.; Ugonabo, O.J.; Okpala, K.C. A study on the effects of solar wind and interplanetary magnetic field on geo-magnetic H-component during geomagnetic storms. Int. J. Phys. Sci. 2018, 13, 230–234. [Google Scholar]
| Year | Number of FE/Number of False FEs (No Storm) | Method Results |
|---|---|---|
| 2013–2015 (high SA) | 285/32 | Detected: ~86% |
| Not detected: ~14% | ||
| False alarm 1 (no FE): ~13% False alarm 2 (no GS): ~9% | ||
| 2019 (low SA) | 97/15 | Detected: ~89% |
| Not detected: ~11% | ||
| False alarm 1 (no FE): ~11% False alarm 2 (the presence of a FE, but no GS): ~8% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandrikova, O.; Mandrikova, B. Method of Wavelet-Decomposition to Research Cosmic Ray Variations: Application in Space Weather. Symmetry 2021, 13, 2313. https://doi.org/10.3390/sym13122313
Mandrikova O, Mandrikova B. Method of Wavelet-Decomposition to Research Cosmic Ray Variations: Application in Space Weather. Symmetry. 2021; 13(12):2313. https://doi.org/10.3390/sym13122313
Chicago/Turabian StyleMandrikova, Oksana, and Bogdana Mandrikova. 2021. "Method of Wavelet-Decomposition to Research Cosmic Ray Variations: Application in Space Weather" Symmetry 13, no. 12: 2313. https://doi.org/10.3390/sym13122313
APA StyleMandrikova, O., & Mandrikova, B. (2021). Method of Wavelet-Decomposition to Research Cosmic Ray Variations: Application in Space Weather. Symmetry, 13(12), 2313. https://doi.org/10.3390/sym13122313





