Towards New Chiroptical Transitions Based on Thought Experiments and Hypothesis
Abstract
1. Introduction
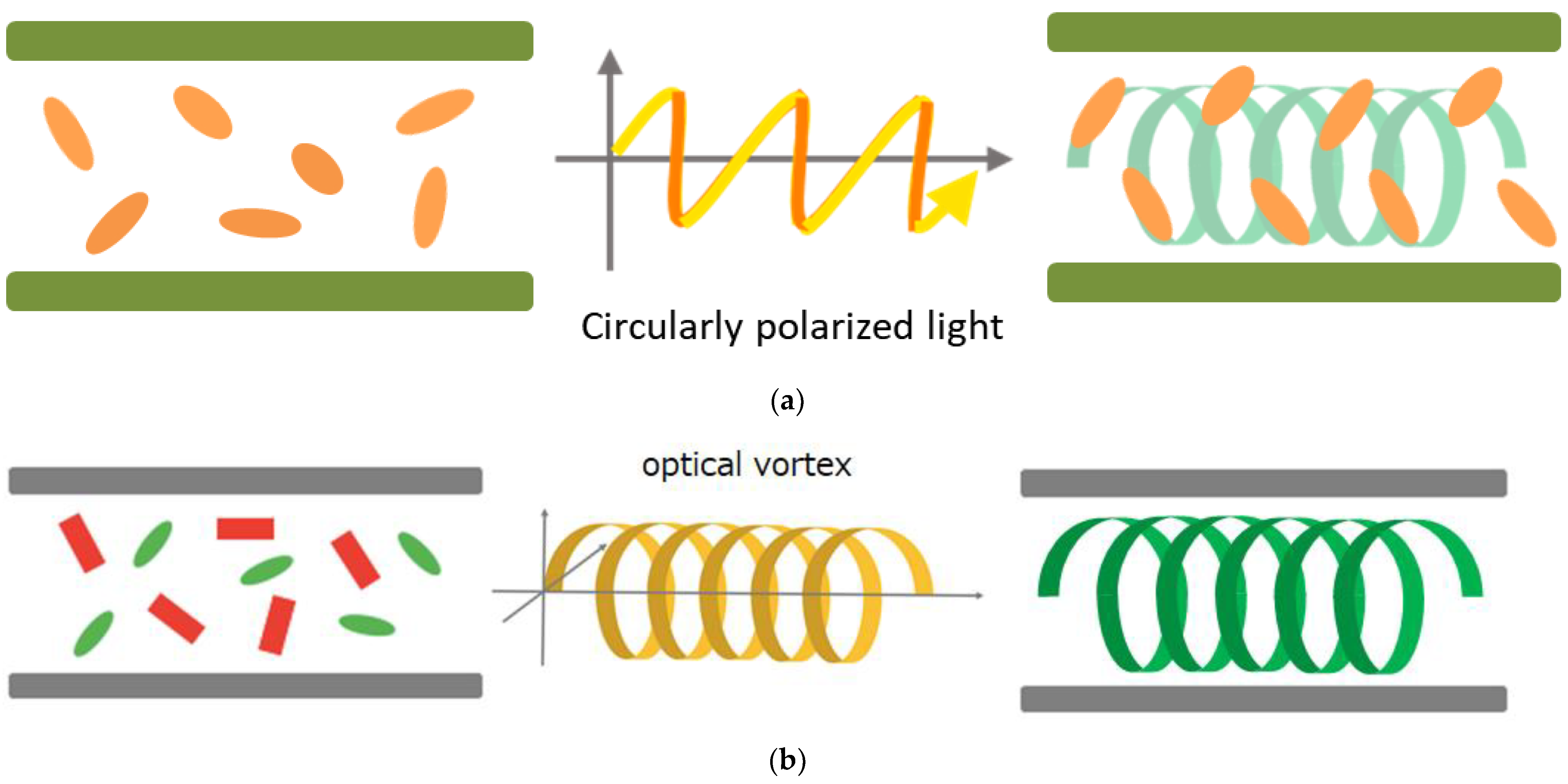
2. Thought Experiments of Optical Vortex Applied for Some Cases of Known Systems
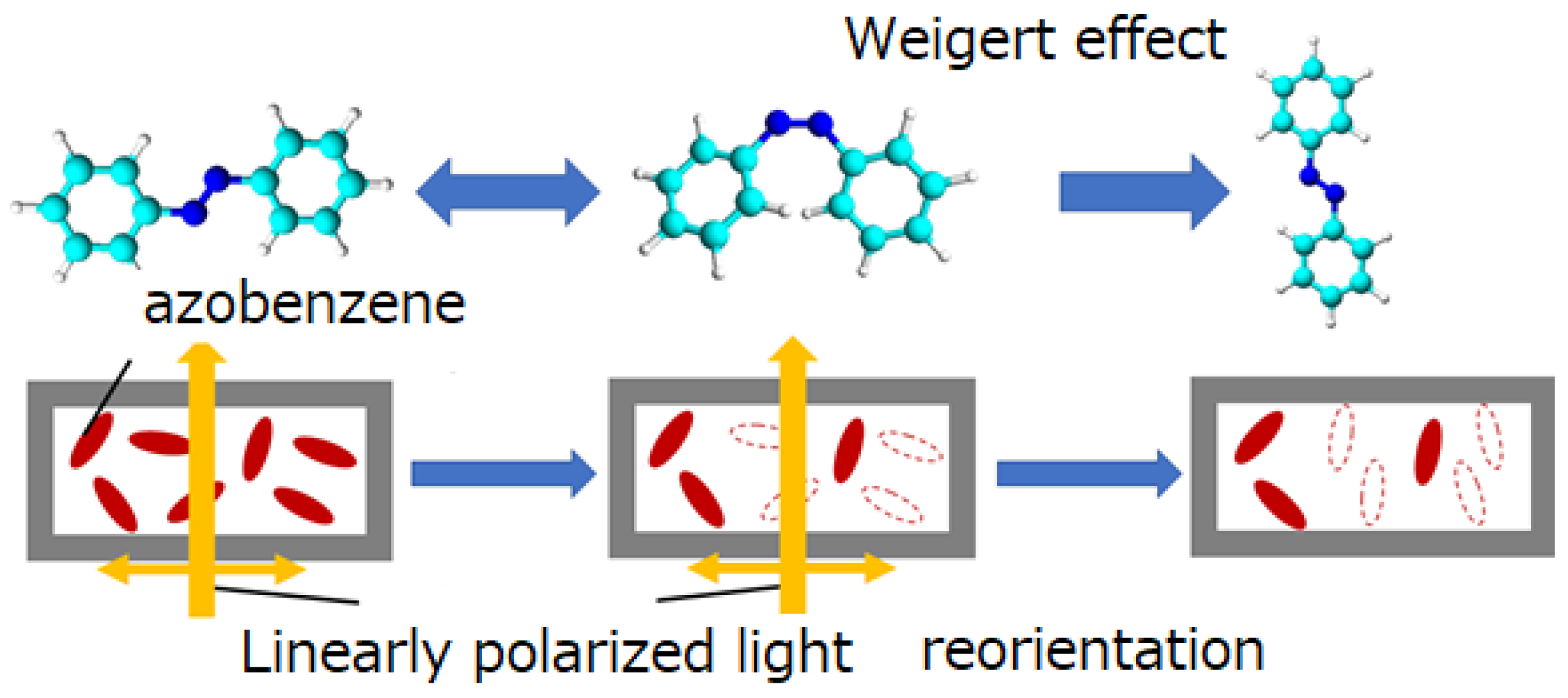
2.1. Separated Azobenzene and Schiff Base Metal Complexes
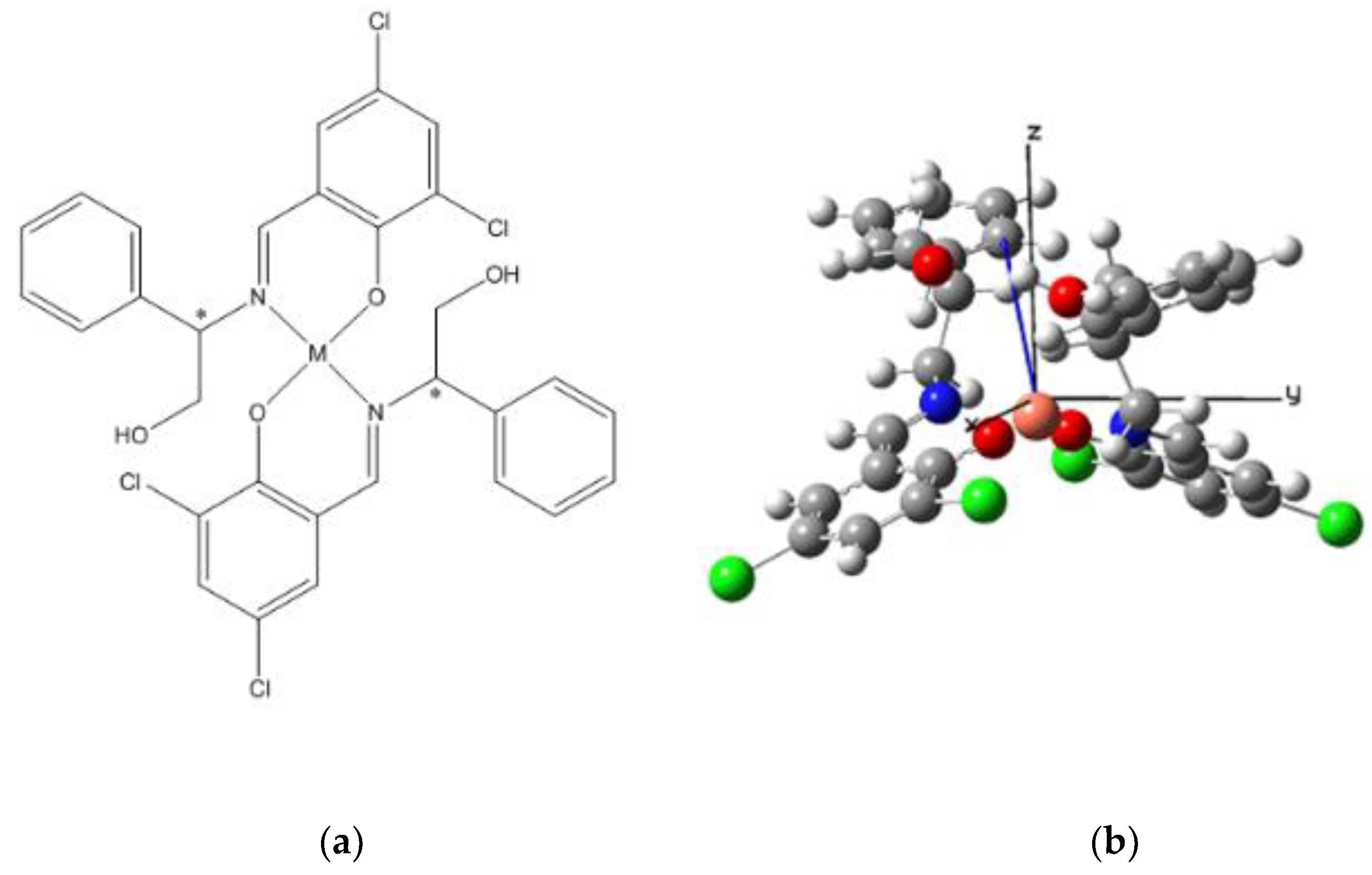
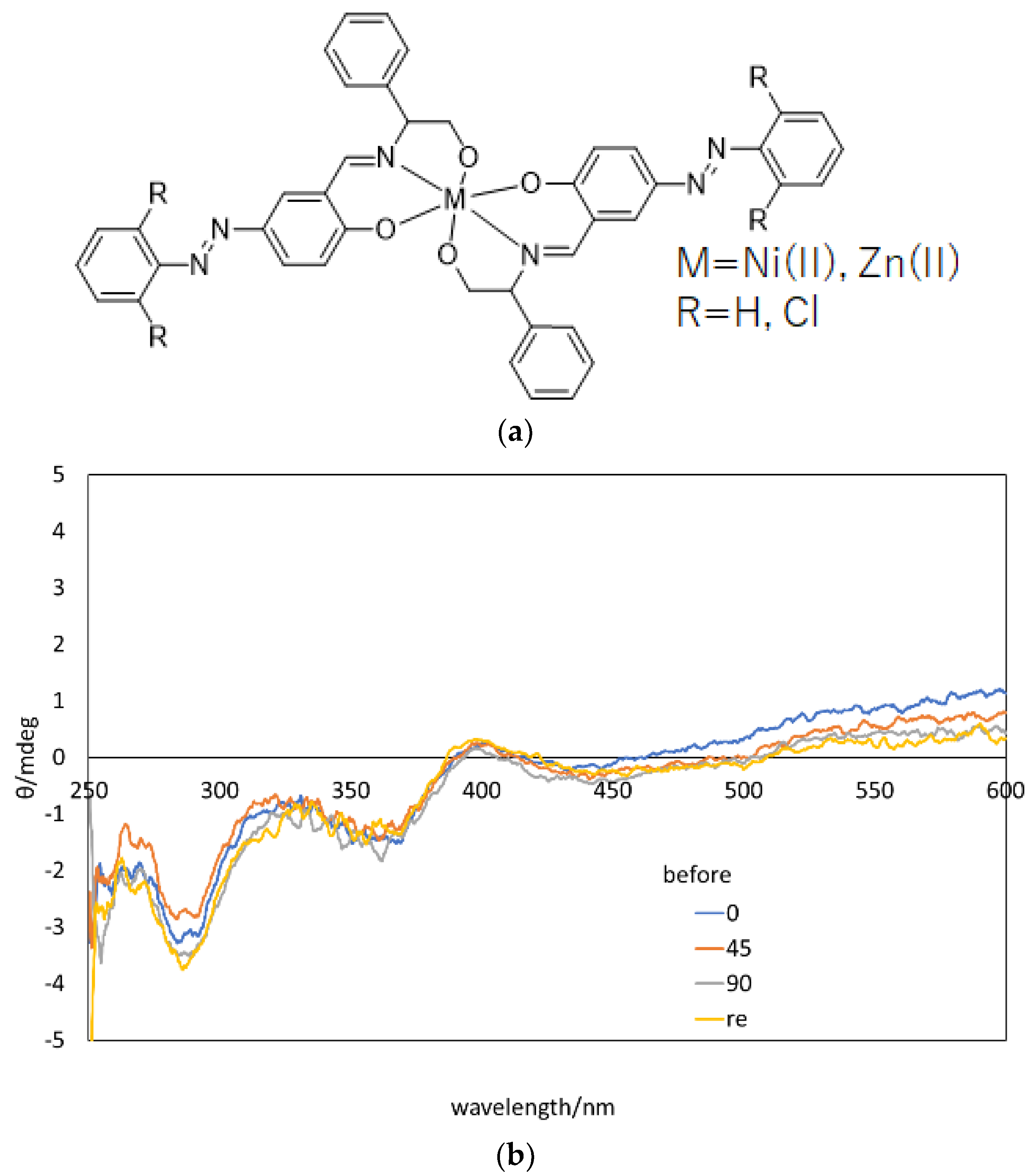
2.2. Azobenzene Containing Schiff Base Metal Complexes
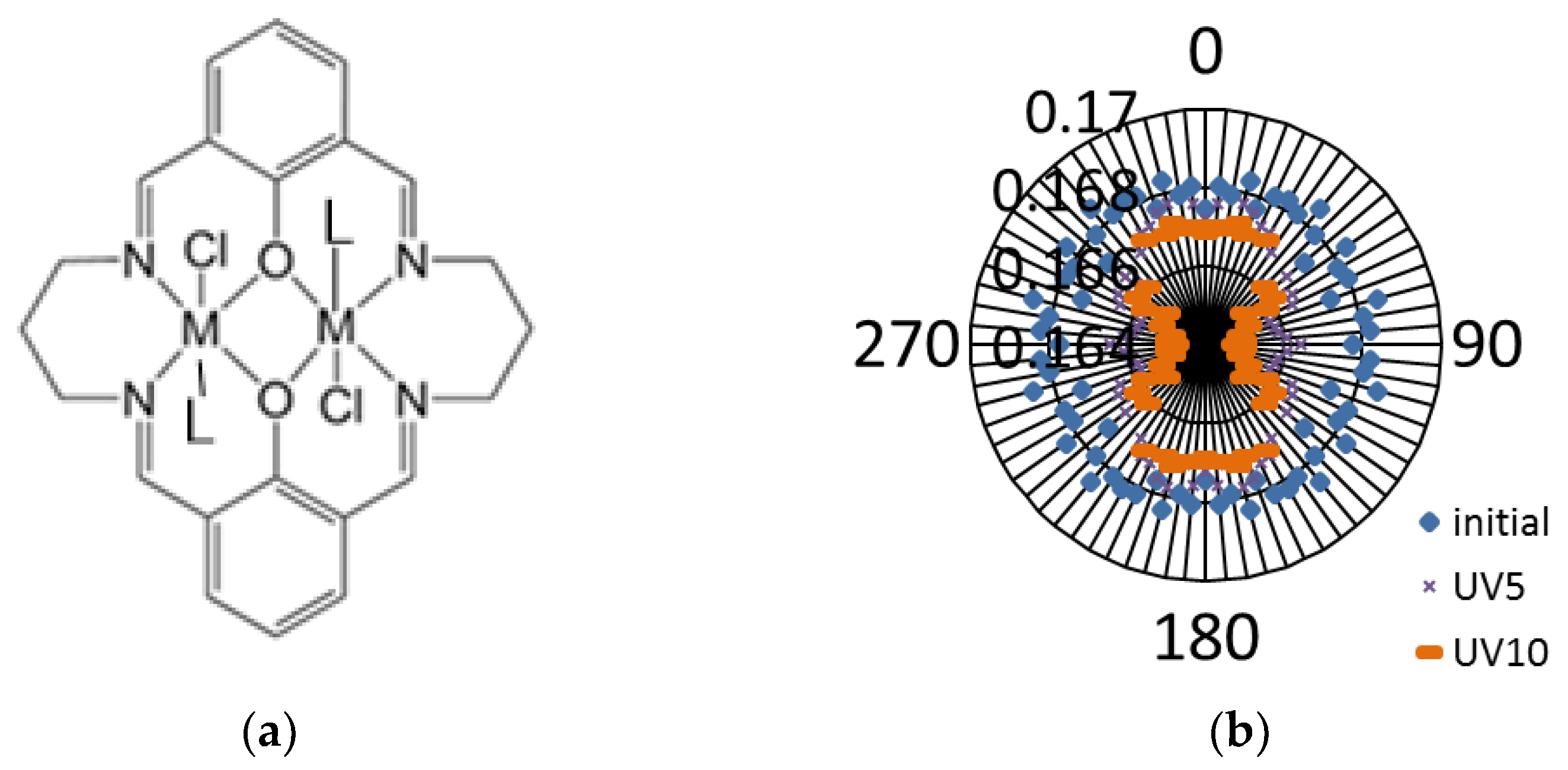
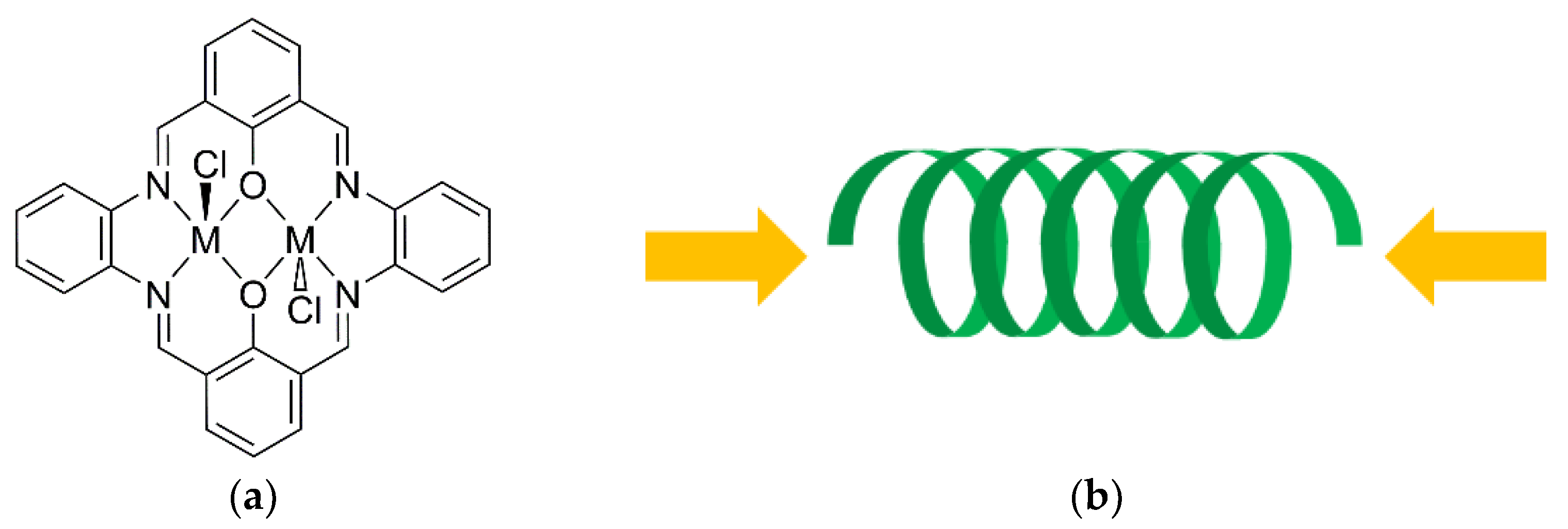
2.3. Mechanical Effect of the Light for Complexes without Azobenzene
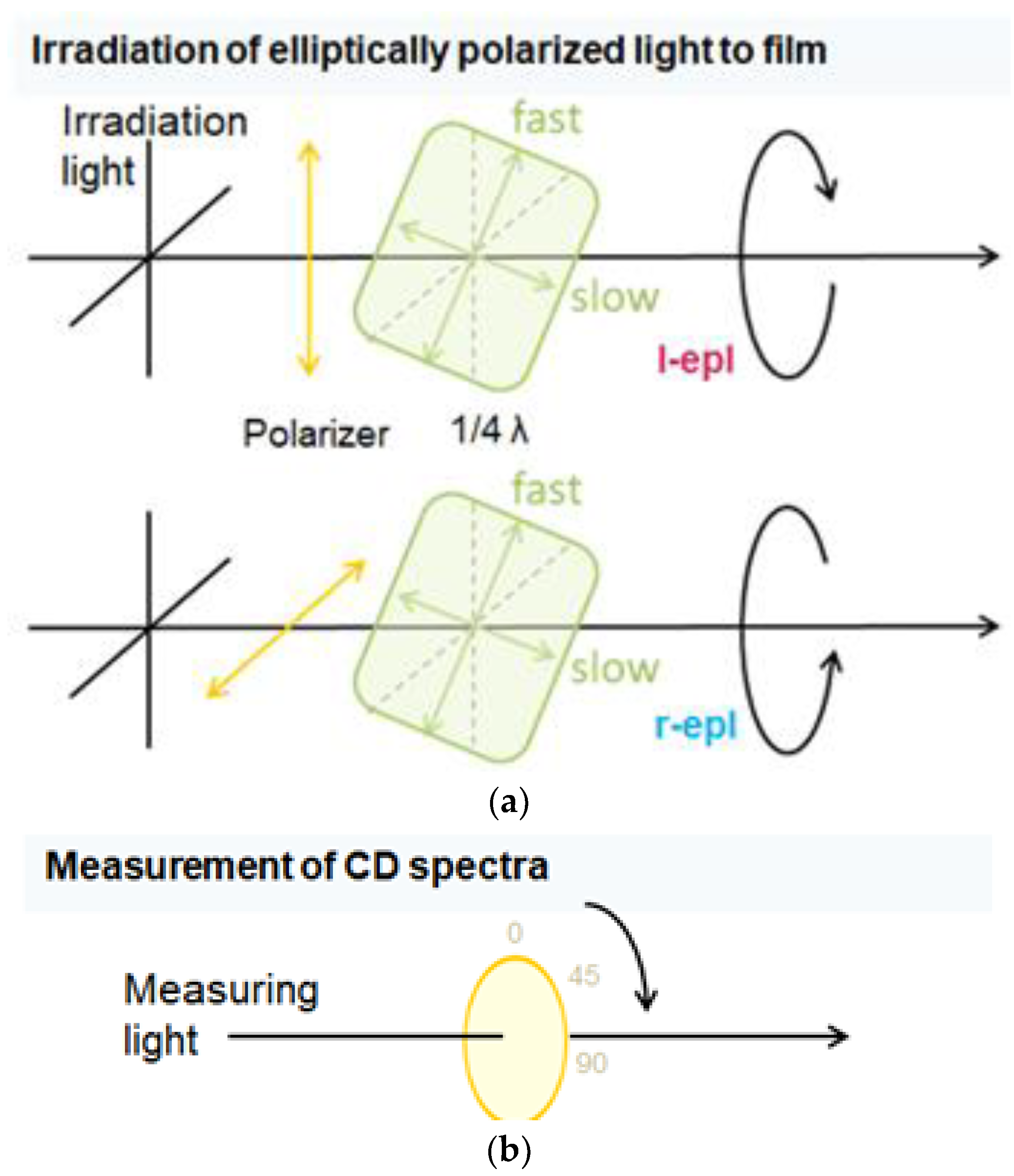
3. Theoretical Consideration of Topological Factors for CD
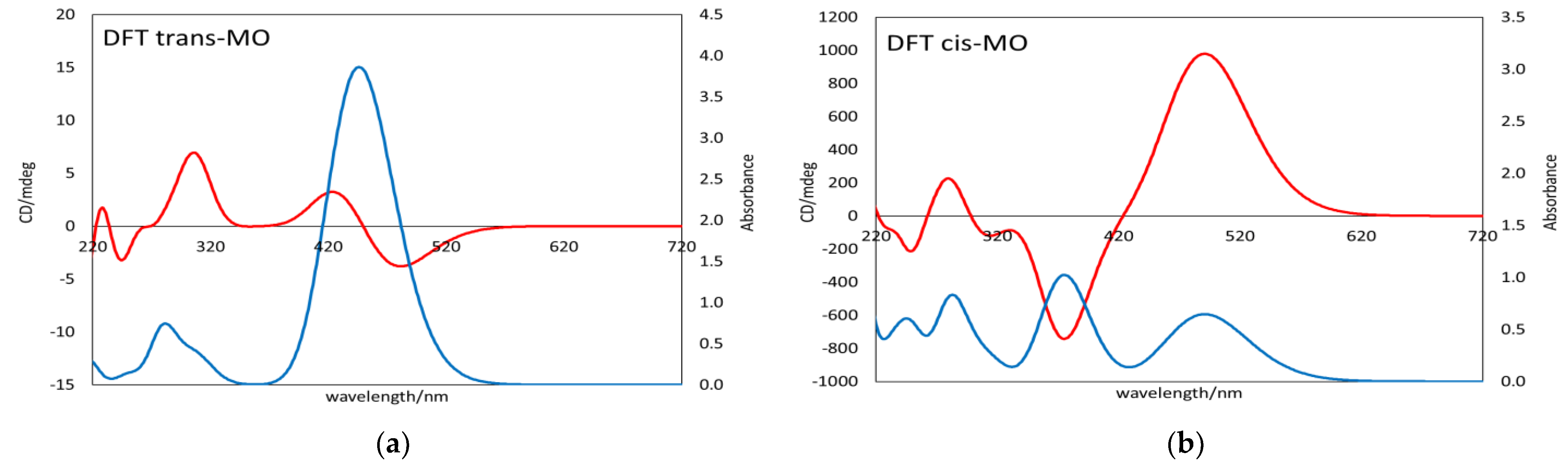
4. Computational Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Natansohn, A.; Rochon, P. Photoinduced Motions in Azo-Containing Polymers. Chem. Rev. 2002, 102, 4139–4175. [Google Scholar] [CrossRef]
- Ichimura, K. Photoalignment of Liquid-Crystal Systems. Chem. Rev. 2000, 100, 1847–1874. [Google Scholar] [CrossRef] [PubMed]
- Fujiki, M. Supramolecular Chirality: Solvent Chirality Transfer in Molecular Chemistry and Polymer Chemistry. Symmetry 2014, 6, 677–703. [Google Scholar] [CrossRef]
- Fujiki, M. Mirror Symmetry Breaking in Helical Polysilanes: Preference between Left and Right of Chemical and Physical Origin. Symmetry 2010, 2, 1625–1652. [Google Scholar] [CrossRef]
- Li, S.; Feng, Y.; Long, P.; Qin, C.; Feng, W. The light-switching conductance of an anisotropic azobenzene-based polymer close-packed on horizontally aligned carbon nanotubes. J Mater. Chem. C 2017, 5, 5068–5075. [Google Scholar] [CrossRef]
- Akitsu, T.; Itoh, T. Polarized spectroscopy of hybrid materials of chiral Schiff base cobalt(II), nickel(II), copper(II), and zinc(II) complexes and photochromic azobenzenes in PMMA films. Polyhedron 2010, 29, 477–487. [Google Scholar] [CrossRef]
- Aritake, Y.; Akitsu, T. The role of chiral dopants in organic/inorganic hybrid materials containing chiral Schiff base Ni(II), Cu(II), and Zn(II) complexes. Polyhedron 2012, 31, 278–284. [Google Scholar] [CrossRef]
- Yamazaki, A.; Akitsu, T. Polarized spectroscopy and polarized UV light-induced molecular orientation of chiral diphenyl Schiff base Ni(II) and Cu(II) complexes and azobenzene in a PMMA film. RSC Adv. 2012, 2, 2975–2980. [Google Scholar] [CrossRef]
- Cantatore, T.; Granucci, G.; Persico, M. The Photo-orientation of azobenzene in viscous solutions, simulated by a stochastic model. Phys. Chem. Chem. Phys. 2014, 16, 25081–25092. [Google Scholar] [CrossRef]
- Bogdanov, A.V.; Vorobiev, A.K. Photo-Orientation of Azobenzene-Containing Liquid-Crystalline Materials by Means of Domain Structure Rearrangement. J. Phys. Chem. B 2013, 117, 13936–13945. [Google Scholar] [CrossRef]
- Kimizuka, N.; Kawasaki, T.; Kunitake, T. Spectral Characteristics and Molecular Orientation of Azobenzene-Containing Hydrogen-Bond-Mediated Bilayer Membranes. Chem. Lett. 1994, 23, 1399–1402. [Google Scholar] [CrossRef]
- Hestand, N.J.; Spano, F.C. Expanded Theory of H- and J-Molecular Aggregates: The Effects of Vibronic Coupling and Intermolecular Charge Transfer. Chem. Rev. 2018, 118, 7069–7163. [Google Scholar] [CrossRef]
- Peakra, H.M.D.; Burdette, S.C. Photoisomerization in different classes of azobenzene. Chem. Soc. Rev. 2012, 41, 1809–1825. [Google Scholar] [CrossRef]
- Hicks, M.R.; Kowalski, J.; Rodger, A. LD spectroscopy of natural and syntetic biomaterials. Chem. Soc. Rev. 2010, 39, 3380–3393. [Google Scholar] [CrossRef] [PubMed]
- Jameson, D.M.; Ross, J.A. Fluorescense Polariation/Anisotropy in Diagnostics and Imaging. Chem. Rev. 2010, 110, 2685–2708. [Google Scholar] [CrossRef] [PubMed]
- Ito, M.; Akitsu, T.; Palafox, M.A. Theoretical interpretation of polarized light-induced supramolecular orientation on the basis of normal mode analysis of azobenzene as hybrid materials in PMMA with chiral Schiff base Ni(II), Cu(II), and Zn(II) complexes. J. Appl. Solut. Chem. Model. 2016, 5, 30–47. [Google Scholar] [CrossRef]
- Wen, Y.; Yi, W.; Meng, L.; Feng, M.; Jiang, G.; Yuan, W.; Zhang, Y.; Gao, H.; Jiang, L.; Song, Y. Photochemical-Controlled Switching Based on Azobenzene Monolayer Modified Silicon (111) Surface. J. Phys. Chem. B 2005, 109, 14465–14468. [Google Scholar] [CrossRef]
- Miao, T.; Yin, L.; Cheng, X.; Zhao, Y.; Hou, W.; Zhang, W.; Zhu, X. Chirality Construction from Preferred π−π Stacks of Achiral Azobenzene Units in Polymer: Chiral Induction, Transfer and Memory. Polymers 2018, 10, 612. [Google Scholar] [CrossRef]
- Thomas, R.; Tamaoki, N. Chirality transfer from chiral solvents and its memory in an azobenzene derivative exhibiting photo-switchable racemization. Org. Biomol. Chem. 2011, 9, 5389–5939. [Google Scholar] [CrossRef]
- Aritake, Y.; Takanashi, T.; Yamazaki, A.; Akitsu, T. Polarized spectroscopy and hybrid materials of chiral Schiff base Ni(II), Cu(II), Zn(II) complexes with included or separated azo-groups. Polyhedron 2011, 30, 886–894. [Google Scholar] [CrossRef]
- Akitsu, T.; Yamazaki, A.; Kobayashi, K.; Haraguchi, T.; Endo, K. Computational treatments of hybrid dye materials of azobenzene and chiral Schiff base metal complexes. Inorganics 2018, 6, 37. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Katoh, M.; Fujimoto, M.; Kawaguchi, H.; Tsuchiya, K.; Ohmi, K.; Kaneyasu, T.; Taira, Y.; Hosaka, M.; Mochihashi, A.; Takashima, Y. Angular Momentum of Twisted Radiation from an Electron in Spiral Motion. Phys. Rev. Lett. 2017, 118, 094801. [Google Scholar] [CrossRef] [PubMed]
- Hikosaka, Y.; Kaneyasu, T.; Fujimoto, M.; Iwayama, H.; Katoh, M. Coherent control in the extreme ultraviolet and attosecond regime by synchrotron radiation. Nat. Commun. 2019, 10, 4988. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Courtial, J.; Allen, L. Light’s Orbital Angular Momentum. Phys. Today 2004, 57, 35–40. [Google Scholar] [CrossRef]
- Cameron, R.P.; Gotte, J.B.; Barnett, S.M.; Yao, A.M. Chrality and the angular momentum of light. Phil. Trans. R. Soc. A 2017, 375, 20150433. [Google Scholar] [CrossRef] [PubMed]
- Forbes, A. Controlling light’s helicity at the source: Orbital angular momentum states from lasers. Phil. Trans. R. Soc. A 2017, 375, 20150436. [Google Scholar] [CrossRef]
- Ambrosio, A.; Marrucci, L.; Borbone, F.; Roviello, A.; Maddalena, P. Light-induced spiral mass transport in azo-polymer films under vortex-beam illumination. Nat. Commun. 2012, 3, 989. [Google Scholar] [CrossRef]
- Watabe, M.; Juman, G.; Miyamato, K.; Omatsu, T. Light induced conch-shaped relief in an azo-polymer film. Sci. Rep. 2014, 4, 4281. [Google Scholar] [CrossRef]
- Andrews, D.L.; Romero, L.C.D.; Babiker, M. On optical vortex interactions with chiral matter. Opt. Commun. 2004, 237, 133–139. [Google Scholar] [CrossRef]
- Friedrich, B.; Herschbach, D. Polarization of Molecules Induced byIntense Nonresonant Laser Fields. J. Phys. Chem. 1995, 99, 15686–15693. [Google Scholar] [CrossRef]
- Fujita, H.; Sato, M. Ultrafast generation of skyrmionic defects with vortex beam: Printing laser profiles on magnets. Phys. Rev. B 2017, 95, 054421. [Google Scholar] [CrossRef]
- Fujita, H.; Sato, M. Encoding orbital angular momentum of light in magnets. Phys. Rev. B 2017, 95, 060407. [Google Scholar] [CrossRef]
- Fujiki, M.; Yoshida, K.; Suzuki, N.; Zhang, J.; Zhang, W.; Zhu, X. Mirror symmetry breaking and restoration within μm-sized polymer particles in optofluidic media by pumping circularly polaised light. RSC Adv. 2013, 3, 5213–5219. [Google Scholar] [CrossRef]
- Fujiki, M.; Donguri, Y.; Zhao, Y.; Nakao, A.; Suzuki, N.; Yoshida, K.; Zhang, W. Photon magic: Chroptical polarization, depolarization, inversion, retention and switching of non-photochromic light-emitting polymers in optofludic medium. Polym. Chem. 2015, 6, 1627–1638. [Google Scholar] [CrossRef]
- Barboza, R.; Bortolozzo, U.; Clerc, M.G.; Residori, S.; Vidal-Henriquez, E. Optical vortex induction via light-matter interaction in liquid-crystal media. Adv. Opt. Photonics. 2015, 7, 635–683. [Google Scholar] [CrossRef]
- Bin, J.; Oates, W.S. A Unified Material Description for Light Induced Deformation in Azobenzene Polymers. Sci. Rep. 2015, 5, 14654. [Google Scholar] [CrossRef]
- Rananaware, A.; Samanta, M.; Bhosale, R.S.; Kobaisi, M.; Roy, B.; Bheemireddy, V.; Bhosale, S.V.; Peakyopadhyay, S.; Bhosale, S.V. PHotomodulation of fluoride ion binding through anion-p inteactions using a photoswitchable azobenzene system. Sci. Rep. 2016, 6, 22928. [Google Scholar] [CrossRef]
- Schellman, J.; Jensen, H.P. Optical spectroscopy of oriented molecules. Chem. Rev. 1987, 87, 1359–1399. [Google Scholar] [CrossRef]
- Kuball, H.-G.; Karstens, T.; Schonhofer, A. Optical Activity of Oriented Molecules. Chem. Phys. 1976, 12, 1–13. [Google Scholar] [CrossRef]
- Morrow, S.M.; Bissette, A.J.; Fletcher, S.P. Transmission of chirality through space and across length scales. Nat. Nanotechnol. 2017, 12, 410–419. [Google Scholar] [CrossRef]
- Nuckolls, C.; Katz, T.J.; Verbiest, T.; Elshocht, S.V.; Kuball, H.-G.; Kieswwalter, S.; Lovinger, A.J.; Persoons, A. Circular Dichroism and UV-Visible Apsorption Spectra of the Langmuir-Blodgett Films of an Aggregating Helicence. J. Am. Chem. Soc. 1998, 120, 8656–8660. [Google Scholar] [CrossRef]
- Kuroda, R.; Harada, T.; Shindo, Y. A solid-state dedicated circular dichroism spectrophotometer: Development and application. Rev. Sci. Instr. 2001, 72, 3802–3810. [Google Scholar] [CrossRef]
- Okamoto, Y.; Nidaira, K.; Akitsu, T. Environmental Dependence of Artifact CD Peaks of Chiral Schiff Base 3d-4f Complexes in Softmater PMMA Matrix. Int. J. Mol. Sci. 2011, 12, 6966–6979. [Google Scholar] [CrossRef] [PubMed]
- Burck, J.; Wadhwani, P.; Fanhanel, S.; Ulrich, A.S. Oriented Circular Dichroism: A Method to Characterize Membrane-Active Peptides in Oriented Lipid Bilayers. Acc. Chem. Res. 2016, 49, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Sunaga, N.; Furuya, S.; Ito, M.; Kominato, C.; Akitsu, T. Interpretaion of chiral ordering of hybrid system of several azo dyes and chiral Schiff base Co(II) complex induced by circularly polarized light. In Computational Chemistry: Theories, Methods and Applications; Nova Science Publishers, Inc.: Houppauge, NY, USA, 2014; pp. 85–104. ISBN 978-1-63321-354-8. [Google Scholar]
- Sunaga, N.; Kominato, C.; Ishida, N.; Ito, M.; Akitsu, T.; Konomi, T.; Katoh, M. Wavelength dependence of polarized UV light induced supramolecular orientation of azobenzene-containing organic/inorganic hybrid materials of chiral Schiff base Ni(II), Cu(II), and Zn(II) complexes. In Azobenzene: Aspects, Applications and Research; Nova Science Publishers, Inc.: Houppauge, NY, USA, 2017; pp. 117–136. ISBN 978-1-53610-673-2. [Google Scholar]
- Sunaga, N.; Akitsu, T.; Konomi, T.; Katoh, M. The theoretical interpretation of the Linear/circularly polarized light-induced molecular orientation of the azo group-containing trans-Achiral Schiff base dinuclear complex composite material. MATEC Web Conf. 2017, 130, 07004. [Google Scholar] [CrossRef][Green Version]
- Takano, H.; Takase, M.; Sunaga, N.; Ito, M.; Akitsu, T. Viscosity and intermolecular interaction of organic/inorganic hybrid systems composed of chiral Schiff base Ni(II), Cu(II), Zn(II) complexes having long ligands, azobenzene and PMMA. Inorganics 2016, 4, 20–29. [Google Scholar] [CrossRef]
- Akitsu, T.; Yagi, S.; Kim, S.; Yoshida, M.; Haraguchi, T. Interaction between Polarized UV Light and Hybrid Materials of Chiral Schiff base Octahedral Cu(II) complexes with Azobenzene. In The Fundamentals of Polarized Light; Terry, A., Ed.; Nova Science Publishers, Inc.: Houppauge, NY, USA, 2021; pp. 119–142. ISBN 978-1-53618-977-3. [Google Scholar]
- Yagi, S.; Haraguchi, T.; Lo, C.-T.; Akitsu, T. Polarized Light-Induced Orientaion of Chiral Schiff Base Ni(II) and Zn(II) Complexes Having Substituted Azobenzene Moiety. In The Fundamentals of Polarized Light; Terry, A., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2021; pp. 143–166. ISBN 978-1-53618-977-3. [Google Scholar]
- Toyoda, K.; Miyamoto, K.; Aoki, N.; Morita, R.; Omatsu, T. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Lett. 2012, 12, 3645–3649. [Google Scholar] [CrossRef]
- Yan, Z.; Scherer, N.F. Optical Vortex Induced Rotation of Silver Nanowires. J. Phys. Chem. Lett. 2013, 4, 2937–2942. [Google Scholar] [CrossRef]
- Mechau, N.; Saphiannikova, M.; Neher, D. Dielectric and Mechanical Properties of Azobenzene Polymer Layers under Visible and Ultraviolet Irradiation. Macromolecules 2005, 38, 3894–3902. [Google Scholar] [CrossRef]
- Barrett, C.J.; Mamiya, J.-I.; Yager, K.G.; Ikeda, T. Photo-mechanical effects in azobenzene-containing soft materials. Soft Matter 2007, 3, 1249–1261. [Google Scholar] [CrossRef] [PubMed]
- Omatsu, T.; Miyamoto, K.; Toyoda, K.; Morita, R.; Arita, Y.; Dholakia, K. A New Twist for Materials Science: The Formation of Chiral Structures Using the Angular Momentum of Light. Adv. Opt. Mater. 2019, 7, 1801672. [Google Scholar] [CrossRef]
- He, L.; Li, H.; Li, M. Optomechanical measurement of photon spin angular momentum and optical torque in integrated photonic devices. Sci. Adv. 2016, 6, e1600485. [Google Scholar] [CrossRef]
- Nakatori, H.; Haraguchi, T.; Akitsu, T. Polarized light induced molecular orientation control of rigid Schiff base Ni(II), Cu(II), Zn(II) binuclear complexes as polymer composites. Symmetry 2018, 10, 147. [Google Scholar] [CrossRef]
- Takase, M.; Yagi, S.; Haraguchi, T.; Noor, S.; Akitsu, T. Linearly Polarized UV Light-Induced Optical Anisotropy of PVA Films and Flexible Macrocycle Schiff Base Ni(II), Cu(II), Zn(II) Dinuclear Complexes. Symmetry 2018, 10, 760. [Google Scholar] [CrossRef]
- Lavery, M.P.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a Spinning Object Using Light’s Orbital Angular Momentum. Science 2017, 341, 537–540. [Google Scholar] [CrossRef]
- Yamazaki, S.; Haraguchi, T.; Lo, C.-T.; Akitsu, T. Polarized Light Induced Chiral Molearular Alignment of Achiral Zn(II) and Zu(II) Complexes for Depth Problem. In The Fundamentals of Polarized Light; Terry, A., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2021; pp. 166–192. ISBN 978-1-53618-977-3. [Google Scholar]
- Karimi, E.; Schulz, S.A.; DeLeon, I.; Qassim, H.; Upham, J.; Boyd, R.W. Generating optical orbital angular momentum at visible wavelengths using a plasmonic metasurface. Light Sci. Appl. 2014, 3, e167. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Cchmidt-Kaler, F. Transfer of Optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef]
- Bauer, T.; Banzer, P.; Karimi, E.; Oriov, S.; Rubano, A.; Marrucci, L.; Santamato, E.; Boyd, R.W.; Leuchs, G. Observation of optical polarization Mobius Strips. Science 2015, 347, 964–966. [Google Scholar] [CrossRef]
- Eyring, H.; Liu, H.-C.; Caldwell, D. Optical Rottory Dispersion and Circular Dichroism. Chem. Rev. 1968, 68, 525–540. [Google Scholar] [CrossRef]
- Andrews, S.S.; Tretton, J. Physical Principles of Circular Dichroism. J. Chem. Educ. 2021, 97, 4370–4376. [Google Scholar] [CrossRef]
- Tang, Y.; Cook, T.A.; Cohen, A.E. Limits on Fluoresence Detected Circular Dichroism of Single Helicence Molecules. J. Phys. Chem. A 2009, 113, 6213–6216. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Cook, T.A.; Cohen, A.E. Optically Chirality and Its Interaction with Matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef]
- Andrews, S.S. Using Rotational Averaging to Calculate the Bulk Response of Isotropic and Anisotropic Samples from Molecular Parameters. J. Chem. Educ. 2004, 81, 877–885. [Google Scholar] [CrossRef]
- Sakai, K.; Nomura, K.; Yamamoto, T.; Sasaki, K. Excitation of Multipole Plasmons by Optical Vortex Beams. Sci. Rep. 2015, 5, 8431. [Google Scholar] [CrossRef] [PubMed]
- Garoli, D.; Zilio, P.; Gorodetski, Y.; Tantussi, F.; De Angelis, F. Optical votex beam generator at nanoscale level. Sci. Rep. 2016, 6, 29547. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akitsu, T.; Kim, S.; Nakane, D. Towards New Chiroptical Transitions Based on Thought Experiments and Hypothesis. Symmetry 2021, 13, 1103. https://doi.org/10.3390/sym13061103
Akitsu T, Kim S, Nakane D. Towards New Chiroptical Transitions Based on Thought Experiments and Hypothesis. Symmetry. 2021; 13(6):1103. https://doi.org/10.3390/sym13061103
Chicago/Turabian StyleAkitsu, Takashiro, Sanyobi Kim, and Daisuke Nakane. 2021. "Towards New Chiroptical Transitions Based on Thought Experiments and Hypothesis" Symmetry 13, no. 6: 1103. https://doi.org/10.3390/sym13061103
APA StyleAkitsu, T., Kim, S., & Nakane, D. (2021). Towards New Chiroptical Transitions Based on Thought Experiments and Hypothesis. Symmetry, 13(6), 1103. https://doi.org/10.3390/sym13061103





