Distributed Adaptive Formation Tracking Control under Fixed and Switching Topologies: Application on General Linear Multi-Agent Systems
Abstract
1. Introduction
2. Preliminaries and Problem Formulation
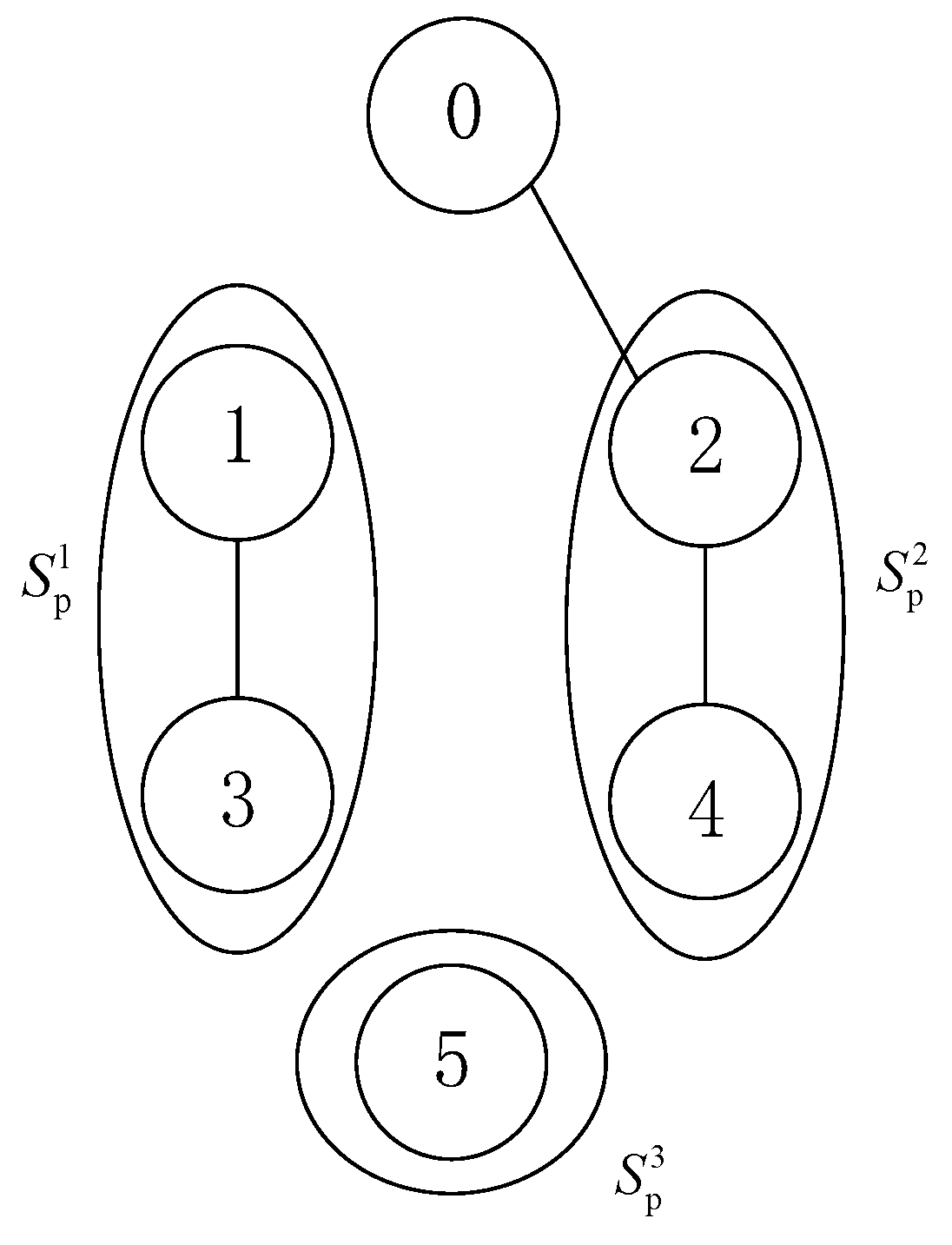
2.1. Basic Concepts of Algebraic Graph Theory and Relevant Notions
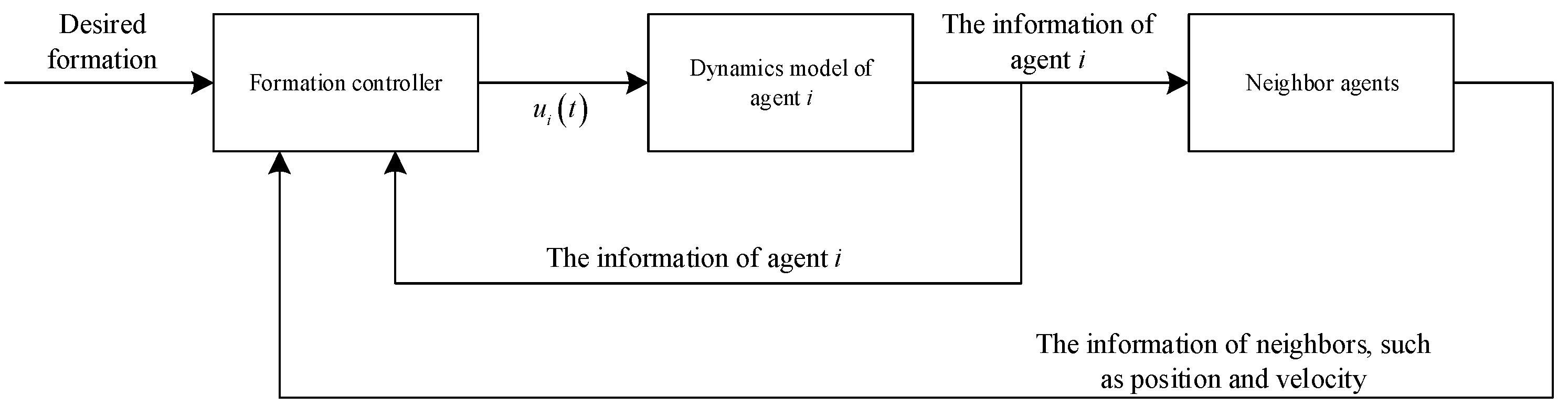
2.2. Leader–Follower Formation Control Problem
3. Main Results
3.1. Leader-Following Tracking Control under Fixed Topology
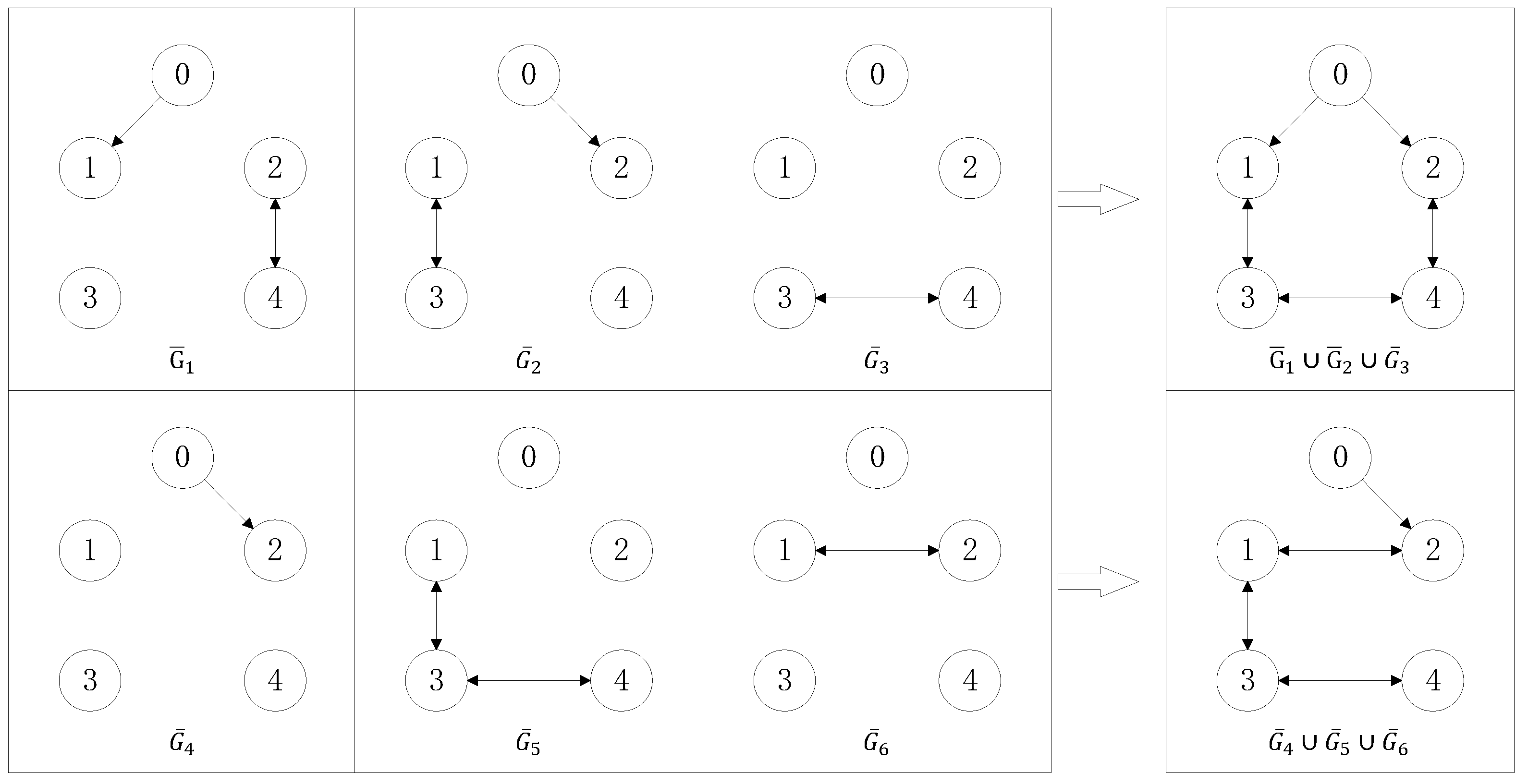
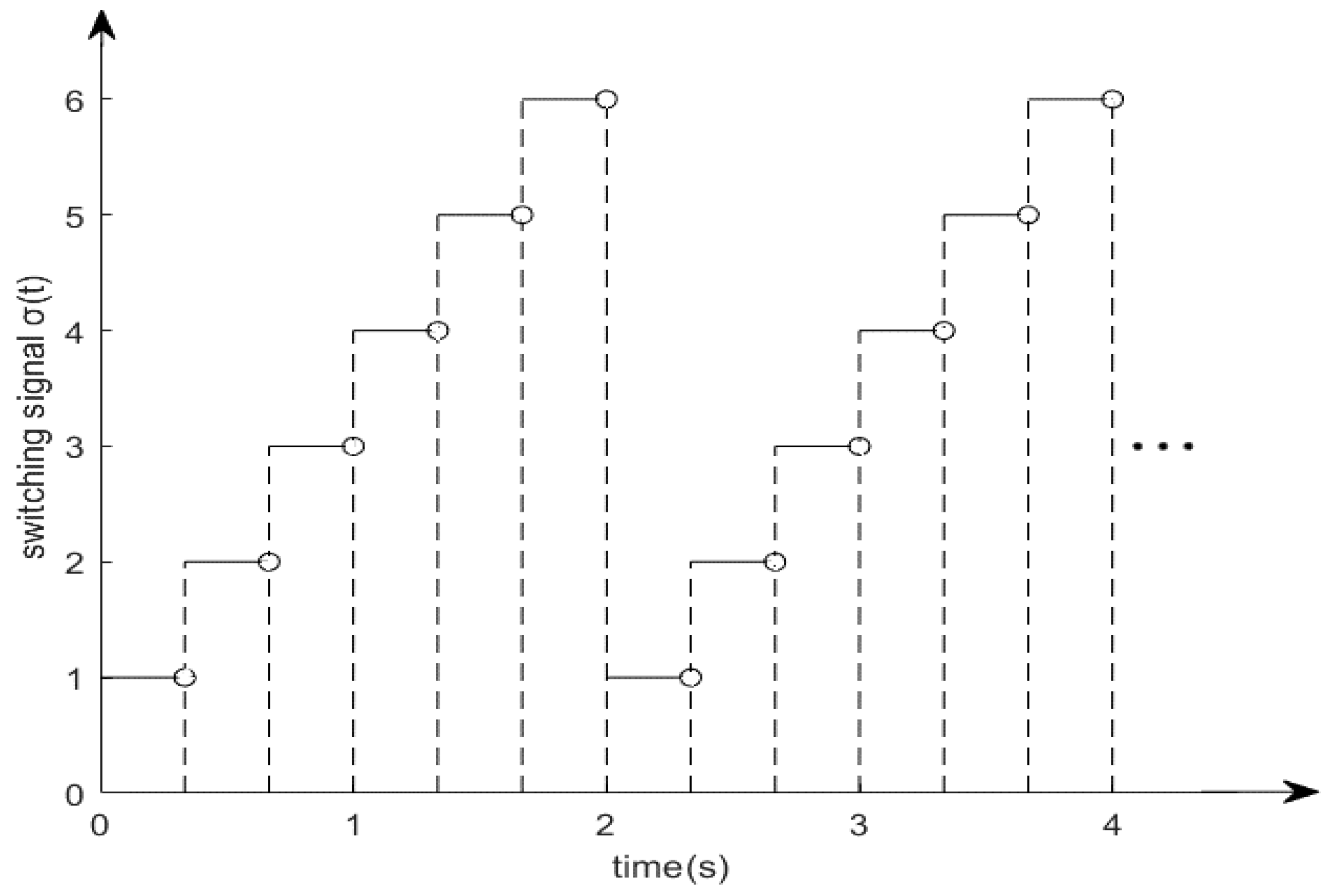
3.2. Leader-Following Tracking Control under Switching Topology
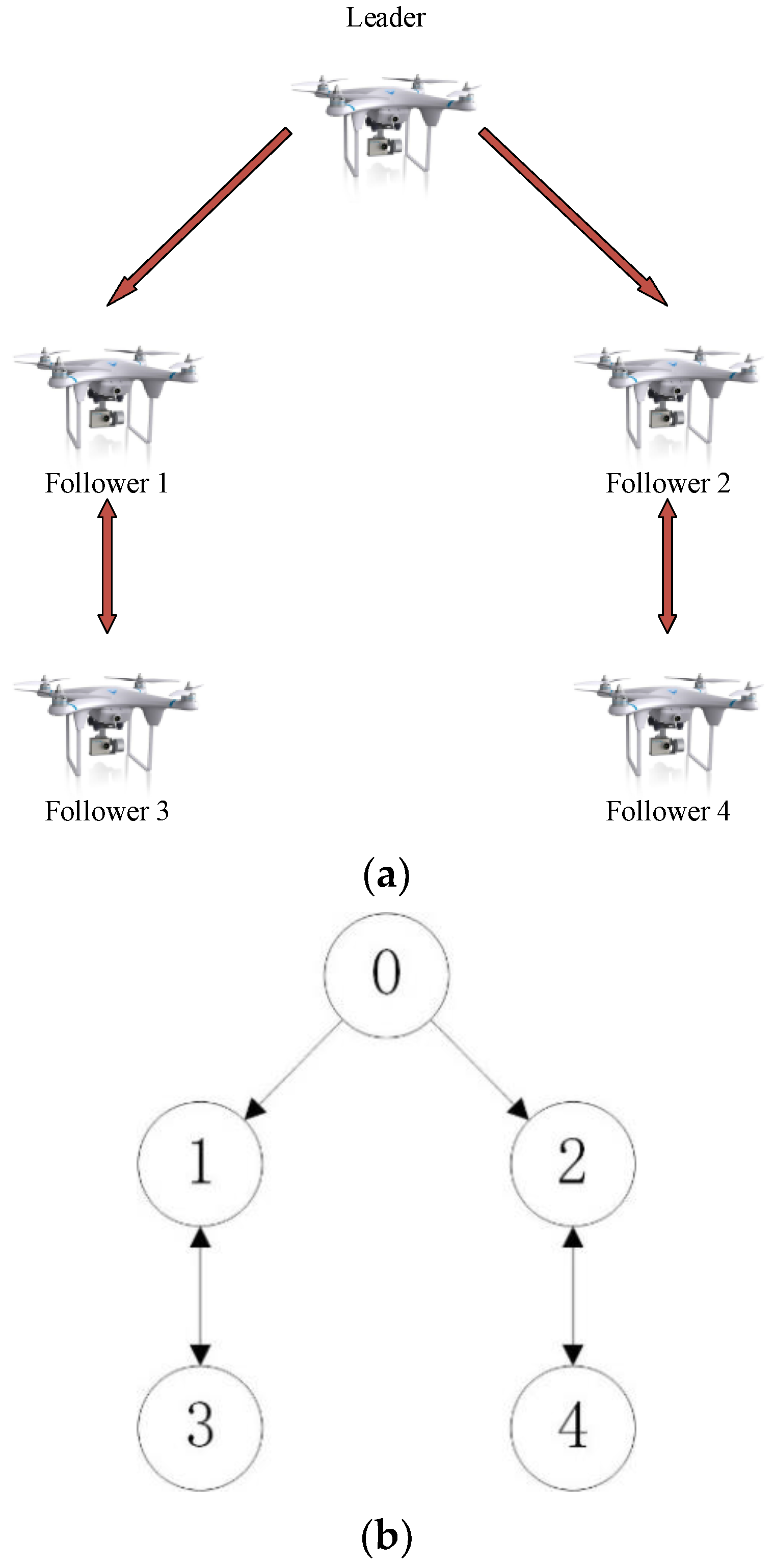
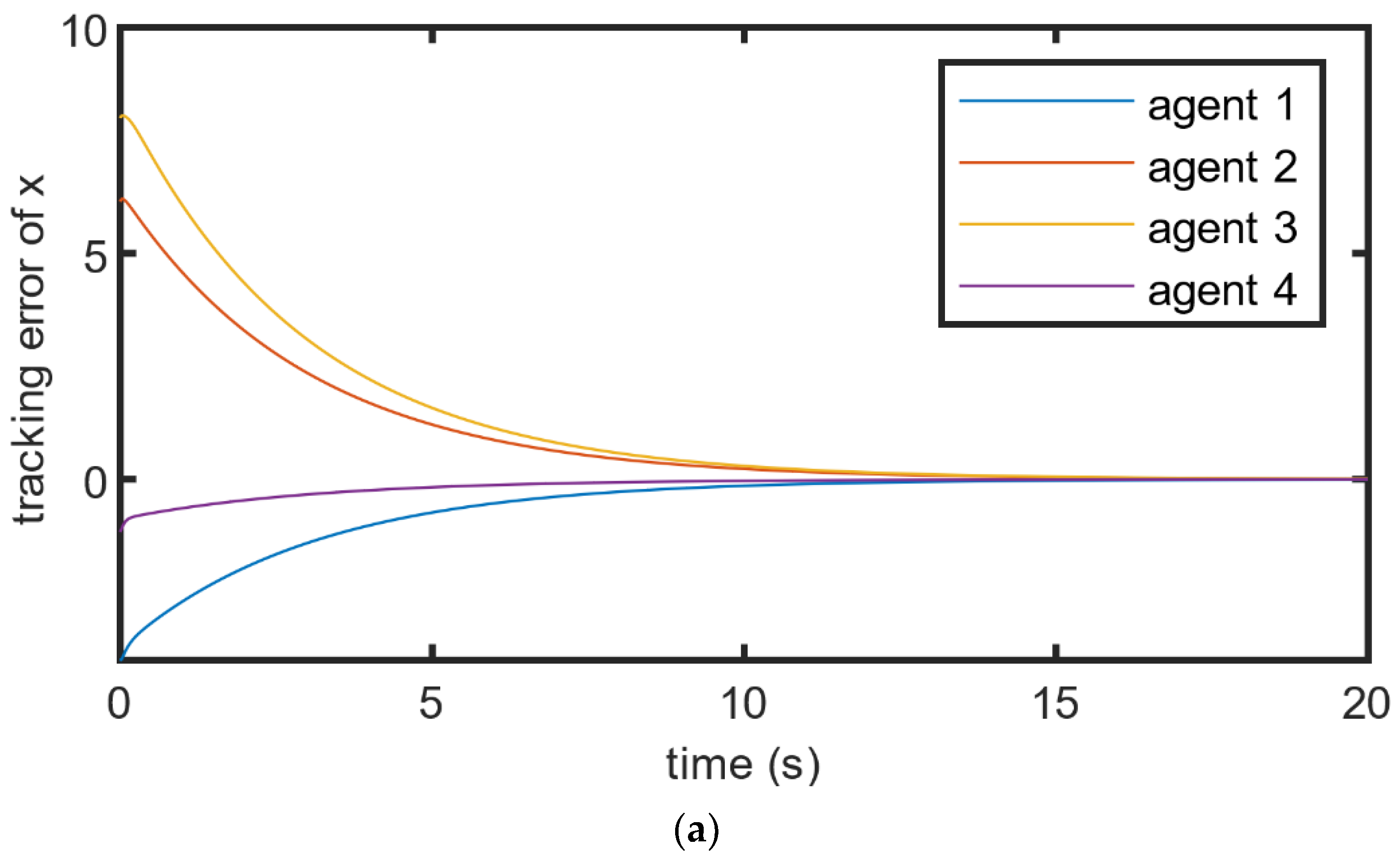
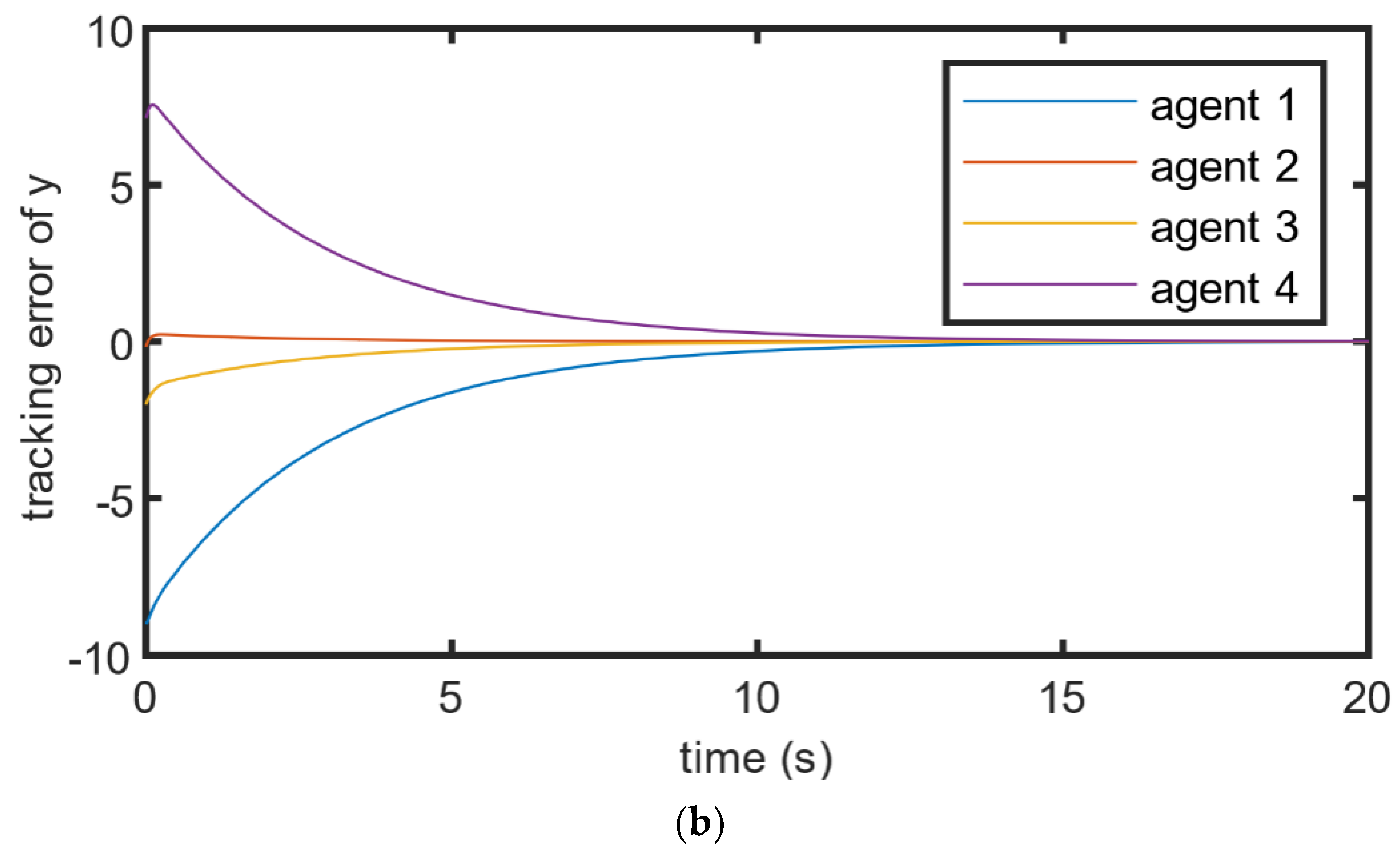
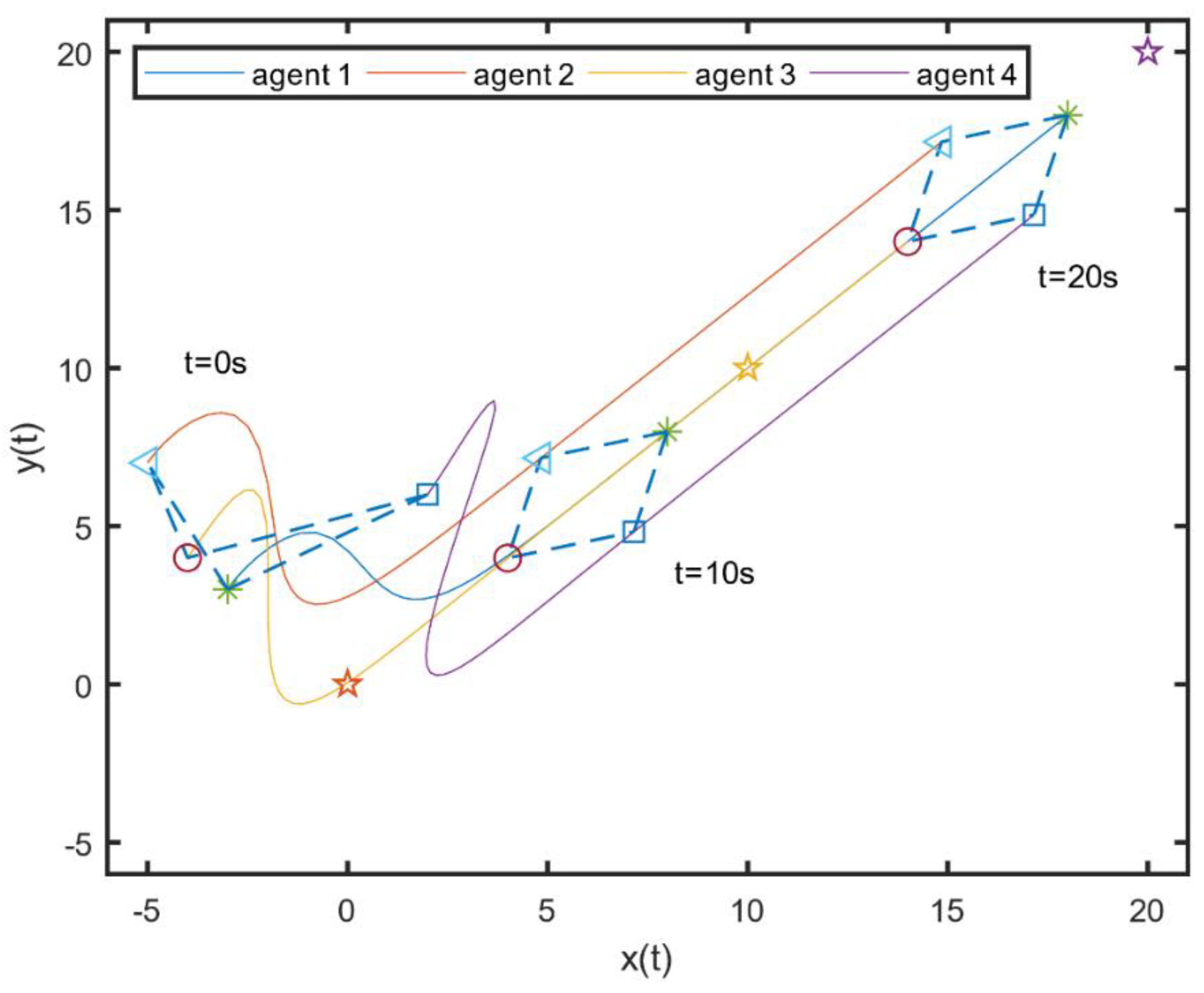
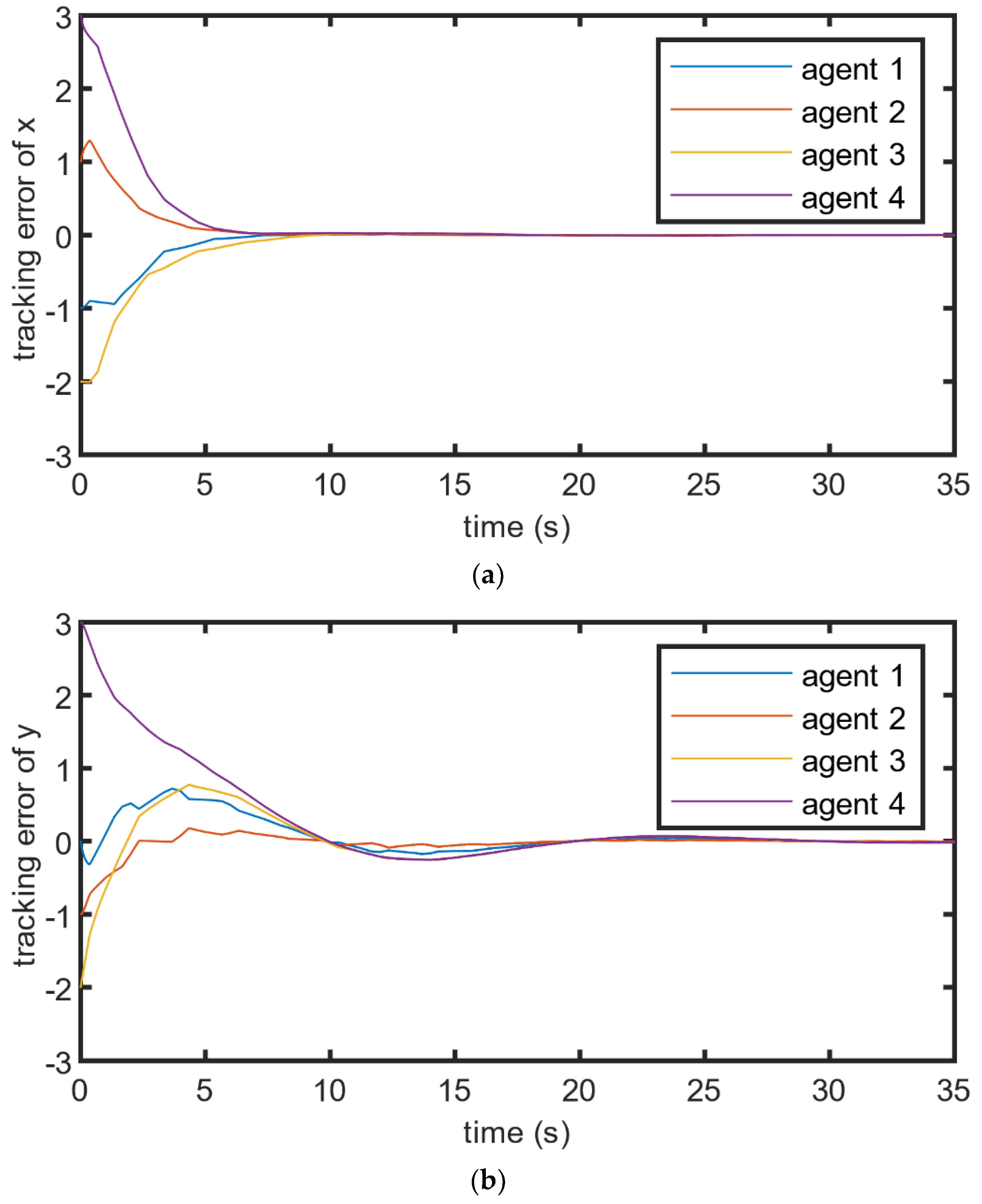
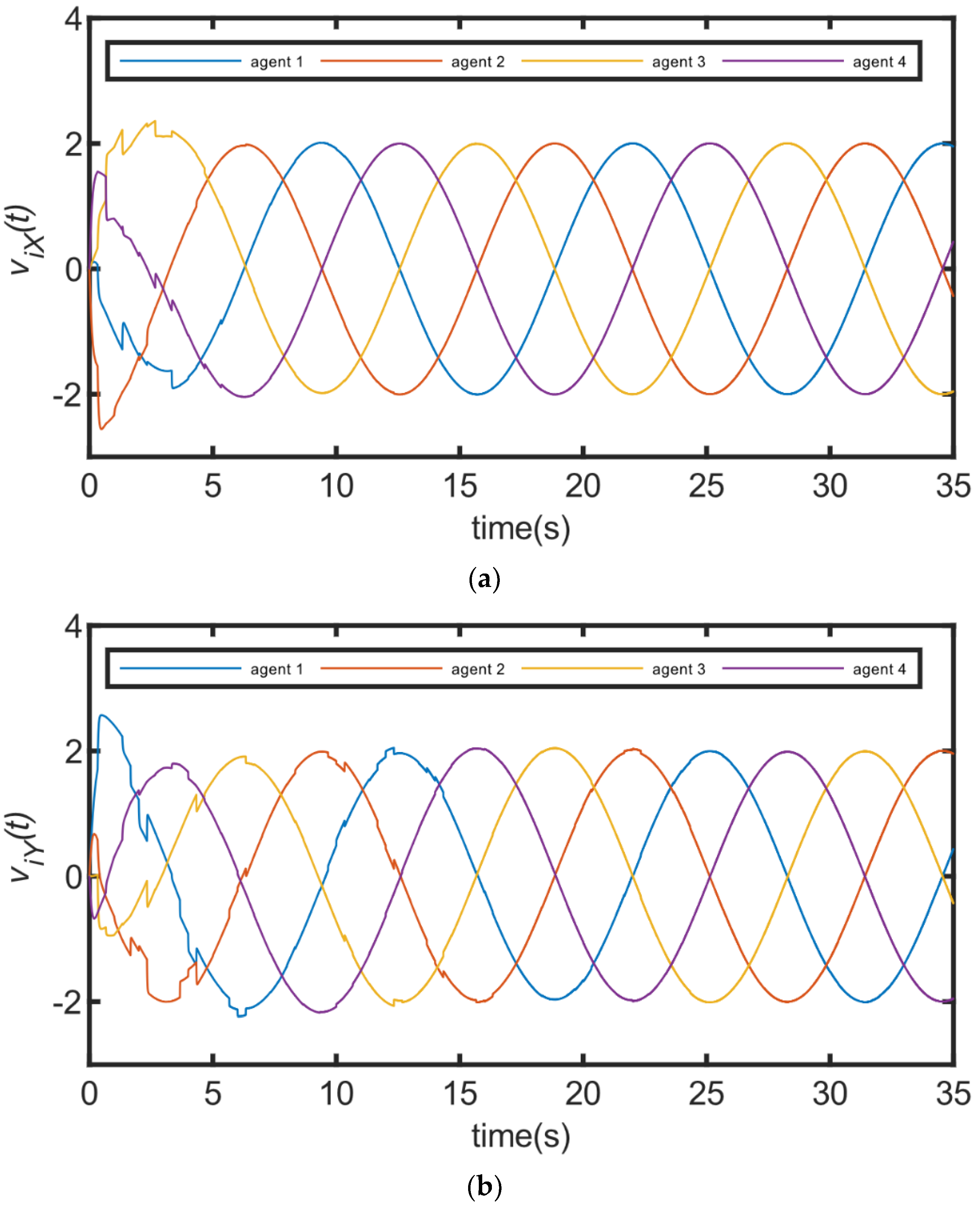
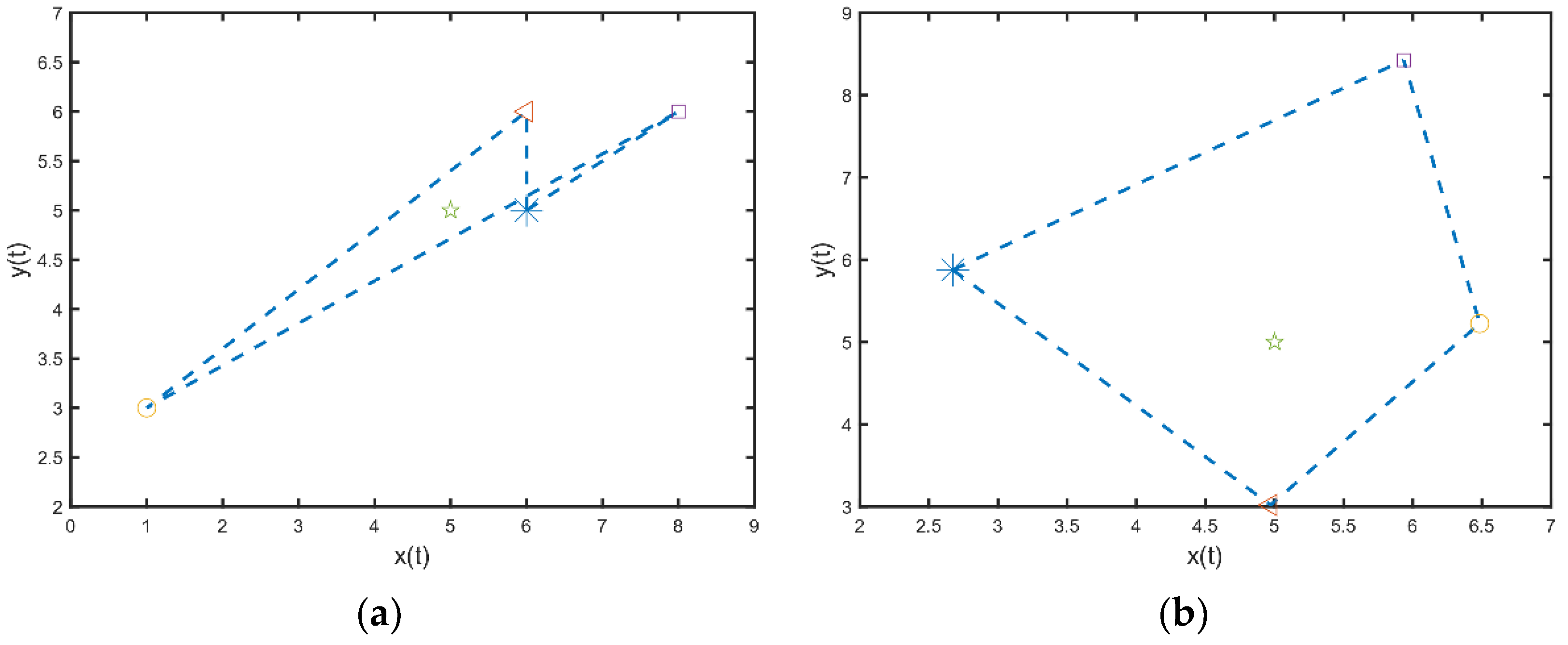
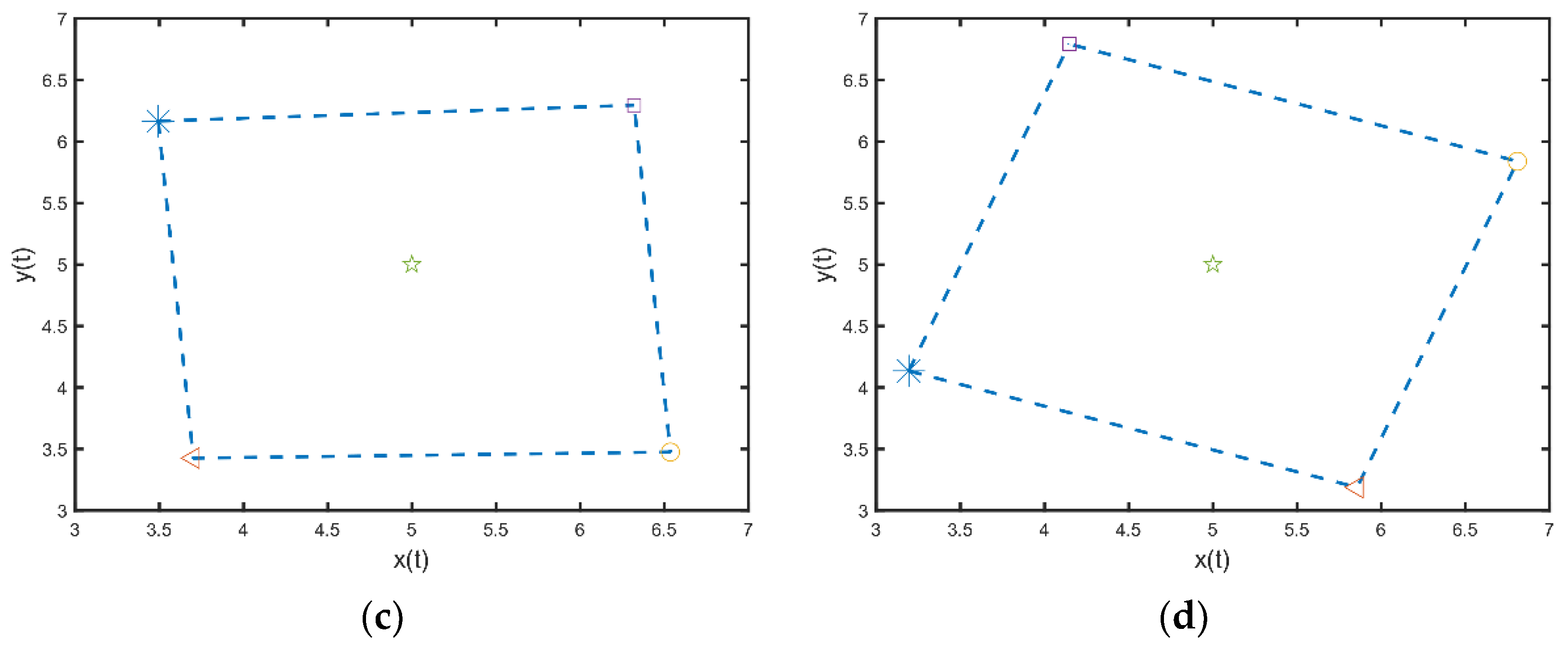
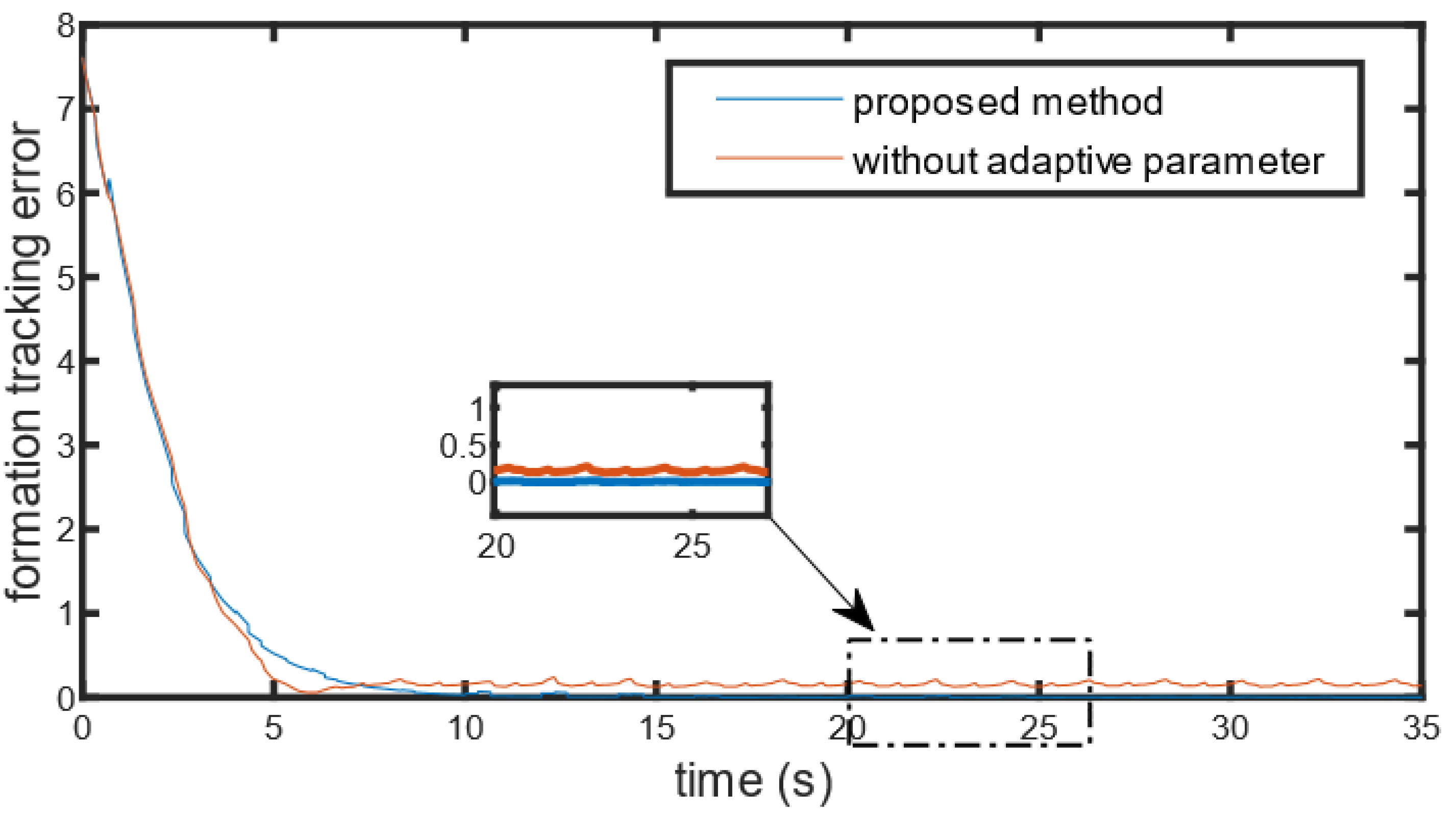
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, S.-L.; Sun, X.-M.; Cao, M.; Wang, W. Pursuing an evader through cooperative relaying in multi-agent surveillance networks. Automatica 2017, 83, 155–161. [Google Scholar] [CrossRef]
- Kada, B.; Khalid, M.; Shaikh, M.S. Distributed cooperative control of autonomous multi-agent UAV systems using smooth control. J. Syst. Eng. Electron. 2020, 31, 1297–1307. [Google Scholar] [CrossRef]
- Gui, H.; Vukovich, G. Distributed almost global finite-time attitude consensus of multiple spacecraft without velocity measurements. Aerosp. Sci. Technol. 2018, 75, 284–296. [Google Scholar] [CrossRef]
- Carli, R.; Cavone, G.; Epicoco, N.; Di Ferdinando, M.; Scarabaggio, P.; Dotoli, M. Consensus-Based Algorithms for Controlling Swarms of Unmanned Aerial Vehicles(Conference Paper). Lect. Notes Comput. Sci. 2020, 12338, 84–99. [Google Scholar]
- Zhang, S.; Li, Z.; Wang, X. Robust H2 Consensus for Multi-Agent Systems with Parametric Uncertainties. IEEE Trans. Circuits Syst. II Express Briefs 2021. [Google Scholar] [CrossRef]
- Dong, X.; Li, Q.; Ren, Z.; Zhong, Y. Formation-containment control for high-order linear time-invariant multi-agent systems with time delays. J. Frankl. Inst. 2015, 352, 3564–3584. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, Y.; Sun, C. Distributed event-based consensus control of multi-agent system with matching nonlinear uncertainties. Neurocomputing 2018, 272, 694–702. [Google Scholar] [CrossRef]
- Consolini, L.; Morbidi, F.; Prattichizzo, D.; Tosques, M. Leader-follower formation control of nonholonomic mobile robots with input constraints. Automatica 2008, 44, 1343–1349. [Google Scholar] [CrossRef]
- Abbaspour, A.; Moosavian, S.A.A.; Alipour, K. Formation control and obstacle avoidance of cooperative wheeled mobile robots. Int. J. Robot. Autom. 2015, 30, 418–428. [Google Scholar] [CrossRef]
- Lee, G.; Chwa, D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance. Intell. Serv. Robot. 2018, 11, 127–138. [Google Scholar] [CrossRef]
- Dong, X.; Zhou, Y.; Ren, Z.; Zhong, Y. Time-Varying Formation Tracking for Second-Order Multi-Agent Systems Subjected to Switching Topologies With Application to Quadrotor Formation Flying. IEEE Trans. Ind. Electron. 2017, 64, 5014–5024. [Google Scholar] [CrossRef]
- Djaidja, S.; Wu, Q. Consensus of double-integrator multi-agent systems without relative states derivative under relative-state dependent measurement noises. Int. J. Syst. Sci. 2019, 50, 777–790. [Google Scholar] [CrossRef]
- Mu, B.; Li, H.; Ding, J.; Shi, Y. Consensus in second-order multiple flying vehicles with random delays governed by a Markov chain. J. Frankl. Inst. Eng. Appl. Math. 2015, 352, 3628–3644. [Google Scholar] [CrossRef]
- Qin, J.; Yu, C. Cluster consensus control of generic linear multi-agent systems under directed topology with acyclic partition. Automatica 2013, 49, 2898–2905. [Google Scholar] [CrossRef]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Control Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y.; Kim, S.; Tsourdos, A. Consensus-based reconfigurable controller design for unmanned aerial vehicle formation flight. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 226, 817–829. [Google Scholar] [CrossRef]
- Dong, X.; Yu, B.; Shi, Z.; Zhong, Y. Time-Varying Formation Control for Unmanned Aerial Vehicles: Theories and Applications. IEEE Trans. Control Syst. Technol. 2015, 23, 340–348. [Google Scholar] [CrossRef]
- Dong, X.; Xiang, J.; Han, L.; Li, Q.; Ren, Z. Distributed Time-Varying Formation Tracking Analysis and Design for Second-Order Multi-Agent Systems. J. Intell. Robot. Syst. 2017, 86, 277–289. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of Multi-Agent Systems With General Linear and Lipschitz Nonlinear Dynamics Using Distributed Adaptive Protocols. IEEE Trans. Autom. Control 2013, 58, 1786–1791. [Google Scholar] [CrossRef]
- Chu, H.; Cai, Y.; Zhang, W. Consensus tracking for multi-agent systems with directed graph via distributed adaptive protocol. Neurocomputing 2015, 166, 8–13. [Google Scholar] [CrossRef]
- Ding, Z.; Li, Z. Distributed adaptive consensus control of nonlinear output-feedback systems on directed graphs. Automatica 2016, 72, 46–52. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, H.; Ma, H.; Zhou, Q.; Yu, Z. Distributed adaptive consensus tracking control for nonlinear multi-agent systems with state constraints. Appl. Math. Comput. 2018, 326, 16–32. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L. Adaptive cooperative tracking control of higher-order nonlinear systems with unknown dynamics. Automatica 2012, 48, 1432–1439. [Google Scholar] [CrossRef]
- Hong, Y.; Hu, J.; Gao, L. Tracking control for multi-agent consensus with an active leader and variable topology. Automatica 2006, 42, 1177–1182. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Trans. Autom. Control 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Su, Y.; Huang, J. Stability of a Class of Linear Switching Systems with Applications to Two Consensus Problems. IEEE Trans. Autom. Control 2012, 57, 1420–1430. [Google Scholar] [CrossRef]
- Mu, B.X.; Shi, Y. Distributed LQR Consensus Control for Heterogeneous Multiagent Systems: Theory and Experiments. IEEE-ASME Trans. Mechatron. 2018, 23, 434–443. [Google Scholar] [CrossRef]
- Deng, J.; Li, K.; Wu, S.; Wen, Y. Distributed Adaptive Time-Varying Formation Tracking Control for General Linear Multi-Agent Systems Based on Event-Triggered Strategy. IEEE Access 2020, 8, 13204–13217. [Google Scholar] [CrossRef]
- Ni, W.; Cheng, D. Leader-following consensus of multi-agent systems under fixed and switching topologies. Syst. Control Lett. 2010, 59, 209–217. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, T.; Liu, H.; Yao, Y.; Li, T.; Cheng, Z. Distributed Adaptive Formation Tracking Control under Fixed and Switching Topologies: Application on General Linear Multi-Agent Systems. Symmetry 2021, 13, 941. https://doi.org/10.3390/sym13060941
Sun T, Liu H, Yao Y, Li T, Cheng Z. Distributed Adaptive Formation Tracking Control under Fixed and Switching Topologies: Application on General Linear Multi-Agent Systems. Symmetry. 2021; 13(6):941. https://doi.org/10.3390/sym13060941
Chicago/Turabian StyleSun, Tianhao, Huiying Liu, Yongming Yao, Tianyu Li, and Zhibo Cheng. 2021. "Distributed Adaptive Formation Tracking Control under Fixed and Switching Topologies: Application on General Linear Multi-Agent Systems" Symmetry 13, no. 6: 941. https://doi.org/10.3390/sym13060941
APA StyleSun, T., Liu, H., Yao, Y., Li, T., & Cheng, Z. (2021). Distributed Adaptive Formation Tracking Control under Fixed and Switching Topologies: Application on General Linear Multi-Agent Systems. Symmetry, 13(6), 941. https://doi.org/10.3390/sym13060941







