Pseudo Almost Automorphic Solutions for Stochastic Differential Equations Driven by Lévy Noise and Its Optimal Control

Abstract

As we know, the periodic functions are symmetric within a cycle time, and it is meaningful to generalize the periodicity into more general cases, such as almost periodicity or almost automorphy. In this work, we introduce the concept of Poisson ${\mathbb{S}}_{\gamma }^2$-pseudo almost automorphy (or Poisson generalized Stepanov-like pseudo almost automorphy) for stochastic processes, which are almost-symmetric within a suitable period, and establish some useful properties of such stochastic processes, including the composition theorems. In addition, we apply a Krasnoselskii–Schaefer type fixed point theorem to obtain the existence of pseudo almost automorphic solutions in distribution for some semilinear stochastic differential equations driven by Lévy noise under ${\mathbb{S}}_{\gamma }^2$-pseudo almost automorphic coefficients. In addition, then we establish optimal control results on the bounded interval. Finally, an example is provided to illustrate the theoretical results obtained in this paper.

1. Introduction

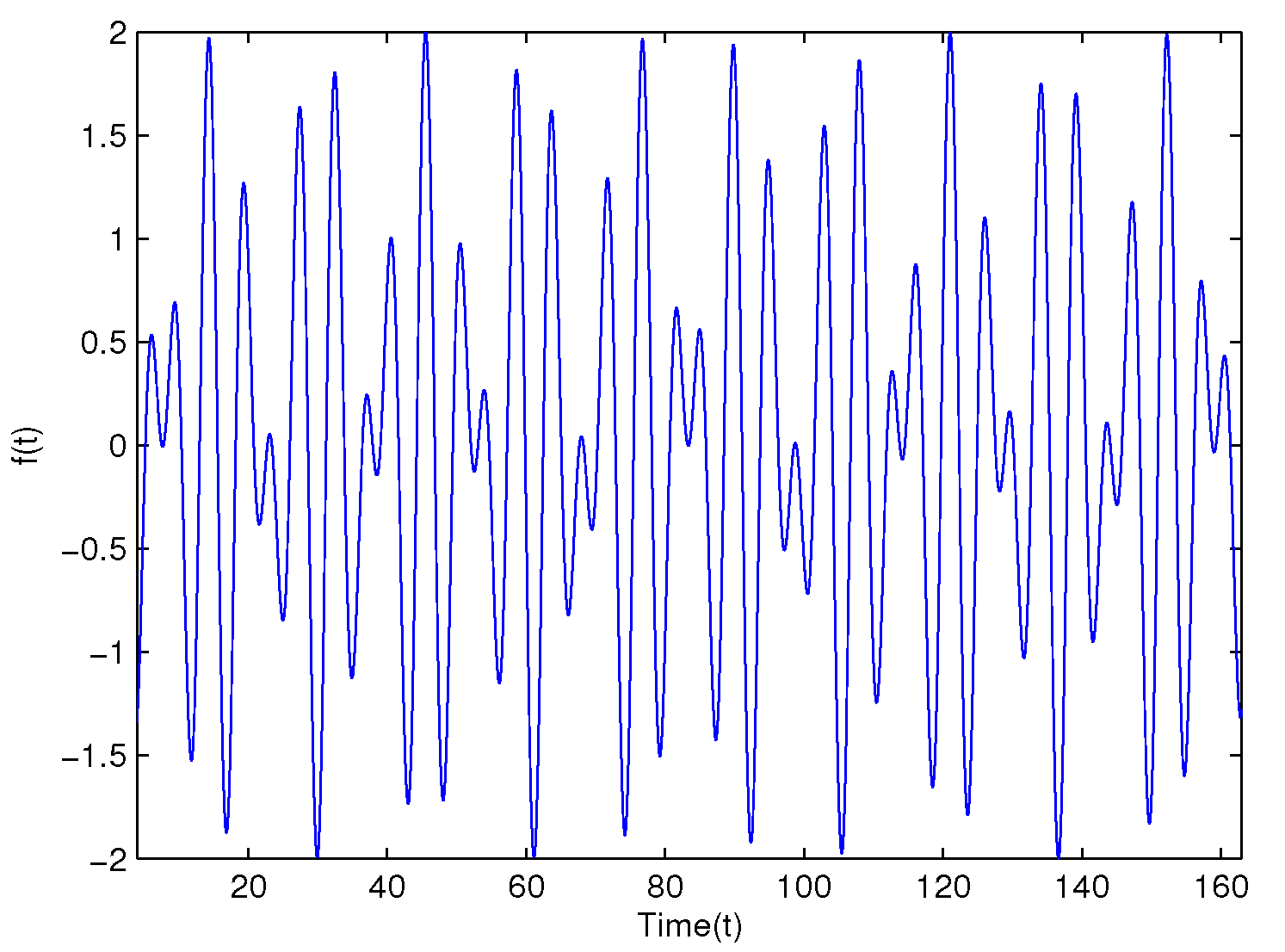
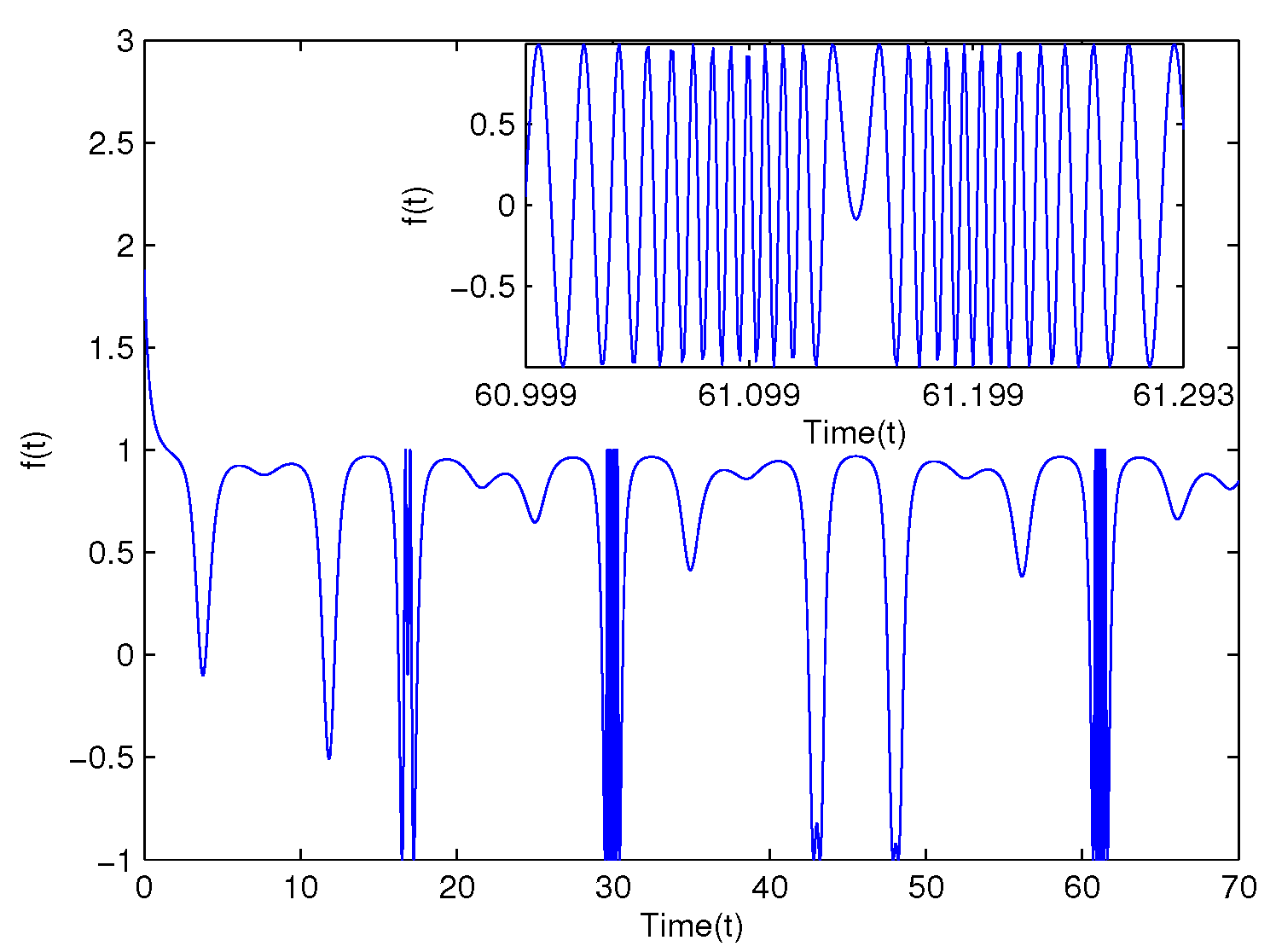
It is well known that symmetry exists in every corner of the world, which may help us explore the truth around our life. Particularly, if there is a periodic function F with a periodicity $\tau$, then it holds that $F(t)=F(t+\tau )$, which means the periodic functions are symmetric within a cycle time. However, the symmetry may not always appear in the accurate sense; it is meaningful to generalize the periodic functions into more general cases, for instance, almost periodicity or almost automorphy. For example, an almost periodic function $f(t)=sint+sin\sqrt{2}t$ and a pseudo almost automorphic function $f(t)=cos\left(\frac{1}{2+sint+sin\sqrt{2}t}\right)+\frac{e^{-\left|t\right|}}{{(1+|t|)}^2}$. (About the almost-symmetry, please see Figure 1 and Figure 2).

Figure 1. The trajectory of almost periodic function.

Figure 2. The trajectory of pseudo almost automorphic function.

In this paper, we will introduce the concept of Poisson ${\mathbb{S}}_{\gamma }^2$-PAA(or Poisson generalized Stepanov-like pseudo almost automorphy) for stochastic processes, which are almost-symmetric within a suitable period.

Liang et al. [1] established the concept of pseudo almost automorphy (PAA, for short) and also provided the composition theorems under a uniformly continuous condition. Diagana [2] generalized the concept of PAA into ${\mathbb{S}}^p$-PAA, and then obtained the asymptotic behavior of the solutions for some differential equations. Mao et al. [3] established the concept of square-mean PAA, which generalized the concept PAA into stochastic cases, and also obtained the square-mean PAA solutions. For more applications of ${\mathbb{S}}^p$-PAA, one can see [4] and the references therein. In 2012, the concept of ${\mathbb{S}}_{\gamma }^p$-PAA was investigated by Diagana [5], and then established the existence results of differential equations of Sobolev type. After this work, Tang et al. [6] introduced the concept of ${\mathbb{S}}_{\gamma }^p$-WPAA in stochastic cases, and proved some interesting results on local stability.

There is a lot of interest from researchers in almost periodic and almost automorphic solutions in stochastic cases; for more details, we refer to [7,8,9,10] and the references therein. Furthermore, stochastic equations driven by Lévy process was investigated by many researchers in the last decade. Wang and Liu [11] mainly studied the square-mean almost period stochastic processes; then, the well-posedness of stochastic evolution equations driven by Lévy noise was obtained. Liu and Sun [12] established the existence of almost automorphic solutions in distribution to some equations driven by Lévy noise. Li [13] established the existence results of WPAA solutions in distribution for some SPDEs driven by Lévy noise; for related works, we refer to [14,15,16]. Motivated by the works [5,6,12,15], we introduce the concept of Poisson ${\mathbb{S}}_{\gamma }^2$-PAA (or Poisson generalized Stepanov-like pseudo almost automorphy) and provide some composition theorems of such stochastic processes, and then study the existence of PAA solutions in distribution for some semilinear stochastic equations driven by Lévy noise under ${\mathbb{S}}_{\gamma }^2$-pseudo almost automorphic coefficients.

Optimal control problem has a wide impact on many fields in the real world, such as celestial mechanic, engineering, biology, economy, and so on; it always minimizes or maximizes a cost functional over some admissible control sets, see monographs [17,18]. In 2007, Mahmudov et al. [19] investigated the backward stochastic equations in infinite-dimensional spaces and obtained its optimal control. After that, fractional integro-differential systems are deeply studied by Wang et al. [20,21], and also some important optimal control problems are solved. In recent days, Rajivganthi-Muthukumar [22] mainly investigated some special optimal control problems and the control pairs were proved. However, to our best knowledge, there are only a few research works on the existence of optimal control pairs for stochastic equations driven by the Lévy process. Motivated by the works [19,20,22], we study a classic optimal control problem for stochastic equations driven by Lévy noise, and the existence of optimal control will be proved.

The outline of this paper is as follows: in Section 2, some definitions and basic properties are introduced, in particular, the concept of Poisson ${\mathbb{S}}_{\gamma }^2$-AA and Poisson ${\mathbb{S}}_{\gamma }^2$-PAA. The new composition theorem of such processes under some suitable conditions are also studied. After that, we investigate the asymptotic behavior of solutions for some semilinear stochastic equations driven by Lévy noise by the Krasnoselskii–Schaefer type fixed point theorem. In the 4th part, we establish the optimal control results on a bounded interval. In Section 5, an example is provided to illustrate our theoretic results.

2. Preliminaries

In the following, we introduce some basic notations and properties which will be used in the sequel. We suppose that $(\mathbb{H},\parallel ·\parallel )$ and $(\mathbb{V},|·|)$ are real separable Hilbert space throughout the paper. Later in Section 2.1, the $\mathbb{V}$-valued Lévy processes are introduced. $(\Omega ,\mathcal{F},P)$ is supposed to be a completed probability space and ${\mathcal{L}}^2(P,\mathbb{H})$ denotes the space of all $\mathbb{H}$-valued random variables Y such that

$${E\parallel Y\parallel }^2={\int }_{\Omega }{\parallel Y\parallel }^{2}dP<\infty$$

Note that, when equipped with the norm

$${\parallel Y\parallel }_2={(E\parallel Y\parallel }^2{)}^{\frac{1}{2}},$$

${\mathcal{L}}^2(P,\mathbb{H})$ is a Hilbert space.

In addition, $C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of all continuous functions from $\mathbb{R}$ into ${\mathcal{L}}^2(P,\mathbb{H})$, and $BC(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ stands for the collection of all bounded continuous functions from $\mathbb{R}$ into ${\mathcal{L}}^2(P,\mathbb{H})$. Note that $BC(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is a Banach space with the sup norm

$${\parallel Y\parallel }_{\infty }=\underset{t\in \mathbb{R}}{sup}{(E\parallel Y(t)\parallel }^2{)}^{\frac{1}{2}}$$

Furthermore, the spaces $C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H})$ and $BC(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H})$ can be explained in a similar way.

2.1. The Introduction of the Lévy Process

In this part, the Lévy process and the Lévy–Itô decomposition theorem are introduced, and we refer to the literature [12,23,24,25] for more details.

Definition 1

([23]). The Lévy process is called a $\mathbb{V}$-valued stochastic process $L=(L(t),t\ge 0)$, if

(i)

$L(0)=0$ a.s.;

(ii)

L has independent and stationary increments;

(iii)

For all $ϵ>0$ and $s>0$,

$$\underset{t\to s}{lim}{P(|L(t)-L(s)|}_{\mathbb{V}}>ϵ)=0$$

Poisson random measure. For a given Lévy process L, it is easy to define $\Delta L=(\Delta L(t),t\ge 0)$, which is a jump process satisfying

$$\Delta L(t)=L(t)-L(t-)$$

for each $t\ge 0$. Furthermore, by virtue of $\Delta L$, it can define the following random counting measure

$$N(t,B)(\omega ):=♯\{0\le s\le t:\Delta L(s)(\omega )\in B\}=\sum _{0\le s\le t}{\chi }_B(\Delta L(s)(\omega ))$$

for any Borel set B in $\mathbb{V}-0$, where ${\chi }_B$ is the indicator function.

Next, we introduce the Poisson random measure N and the compensated Poisson random measure $\tilde{N}$. Firstly, we suppose there is a bounded below Borel set B in $\mathbb{V}-0$, and $\nu (·)=\mathbf{E}(N(1,·))$ denotes the intensity measure, from which it holds that $N(t,B)<\infty$ almost surely for all $t\ge 0$ and $(N(t,B),t\ge 0)$ is a Poisson process with intensity $\nu (B)$. Meanwhile, the compensated Poisson random measure $\tilde{N}$ defined by

$$\tilde{N}(t,B)=N(t,B)-t\nu (B)$$

where the Poisson random measure N satisfies

$${\int }_{\mathbb{V}}{(|y|}_{\mathbb{V}}^2\wedge 1)\nu (dy)<\infty$$

(1)

Proposition 1

([23]). (Lévy–Itô decomposition) Suppose L is a$\mathbb{V}$-valued Lévy process; then, a $\mathbb{V}$-valued Wiener process W, an independent Poisson random measure N and also a constant a exist, such that

$$L(t)=at+W(t)+{\int }_{{\left|x\right|}_{\mathbb{V}}<1}x\tilde{N}(t,dx)+{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}xN(t,dx)$$

for each $t\ge 0$.

However, from Definition 1, L only is one-sided. In order to finish the research, we need a two-sided Lévy process, i.e.,

$$\begin{array}{c}\hfill L(t)=\left\{\begin{array}{cc}{L}_1(t),\hfill & fort\ge 0\hfill \\ -L_2(-t),\hfill & fort\le 0\hfill \end{array}\right.\end{array}$$

where $L_1$ and $L_2$ are two independent, identically distributed Lévy processes satisfying Proposition 1, and we assume L is defined on the filtered probability space ${(\Omega ,\mathcal{F},P,{\mathcal{F}}_t)}_{t\in \mathbb{R}}$.

Remark 1.

By (1), it holds that $b:={\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\nu (dx)<\infty$.

Remark 2.

Furthermore, the increment $\tilde{L}(t):=L(t+s)-L(s),s\in \mathbb{R}$ is also a two-sided Lévy process, which is identically distributed with L.

2.2. ${\mathbb{S}}_{\gamma }^2$-Almost Automorphy

Definition 2

([26]). Given a function $x:\mathbb{R}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, its Bochner transform $x^b(t,s)$ is, in the following sense,

$$x^b(t,s):=x(t+s)$$

where $t\in \mathbb{R}$, $s\in [0,1]$.

Remark 3.

(i) If $\phi (t,s)=f^b(t,s)$ is the Bochner transform of a certain function f, then $\phi (t+\tau ,s-\tau )=\phi (t,s)$, for all $t\in \mathbb{R},s\in [0,1]$ and $\tau \in [s-1,s]$; Similarly, the converse is also true.

(ii) It also follows that, if $f=l+m$, then $f^b=l^b+m^b$. In addition, ${(\lambda f)}^b=\lambda f^b$ for each scalar λ.

Definition 3

([27,28]). Given a function $f:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, for each $Y\in L^2(P,\mathbb{H})$, its Bochner transform is

$$f^b(t,s,Y):=f(t+s,Y)$$

Definition 4

([29]). A function $Y\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is called square-mean almost automorphic if, for every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exist a subsequence ${(s_n)}_{n\in \mathbb{N}}$ and a function $\tilde{Y}\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ such that

$$\underset{n\to \infty }{lim}E\parallel Y(t+s_n)-\tilde{Y}(t){\parallel }^2=0\mathrm{and}\underset{n\to \infty }{lim}E{\parallel \tilde{Y}(t-s_n)-Y(t)\parallel }^2=0$$

hold for each $t\in \mathbb{R}$. We use the notation $AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$ to denote the collection of all square-mean almost automorphic functions.

Definition 5

([30]). Let $\mathbb{T}=\{(t,s)\in \mathbb{R}\times \mathbb{R},t\ge s\}$. A continuous function $U:\mathbb{T}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ is called positively bi-almost automorphic if, for every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exist a subsequence ${(s_n)}_{n\in \mathbb{N}}$ and a function $\tilde{U}\in C(\mathbb{T},{\mathcal{L}}^2(P,\mathbb{H}))$ such that

$$\underset{n\to \infty }{lim}E\parallel U(t+s_n,s+s_n)-\tilde{U}(t,s){\parallel }^2=0\mathrm{and}\underset{n\to \infty }{lim}E{\parallel \tilde{U}(t-s_n,s-s_n)-U(t,s)\parallel }^2=0$$

hold for each $(t,s)\in \mathbb{T}$. The notation $bAA(\mathbb{T},{\mathcal{L}}^2(P,\mathbb{H})$ denotes the collection of all such functions.

Definition 6

([26]). The notation $B{S}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ stands for the collection of all Stepanov bounded functions, if the measurable functions $Y\in B{S}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, then $Y^b\in L^{\infty }(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),ds))$. If, with the norm

$$\parallel Y^b{\parallel }_{L^{\infty }(\mathbb{R},L^2)}=\underset{t\in \mathbb{R}}{sup}({\int }_t^{t+1}{E\parallel Y(s)\parallel }^2{ds)}^{\frac{1}{2}}=\underset{t\in \mathbb{R}}{sup}({\int }_0^1{E\parallel Y(t+s)\parallel }^2{ds)}^{\frac{1}{2}},$$

it is a Banach space.

Definition 7

([31]). A function $Y\in B{S}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is Stepanov-like almost automorphic (or ${\mathbb{S}}^2$-almost automorphic), if $Y^b\in AA(\mathbb{R},L^2((0,1);{\mathcal{L}}^2(P,\mathbb{H}),ds))$ that is to say, given a function $Y\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),ds)$, if its Bochner transform $Y^b:\mathbb{R}\mapsto L^2((0,1);{\mathcal{L}}^2(P,\mathbb{H}),ds)$ is almost automorphic, then it is ${\mathbb{S}}^2$-almost automorphic, i.e., for every sequence of real numbers $\left\{s_n^{\prime }\right\}$, there exist a subsequence $\left\{s_n\right\}$ and a function $\tilde{Y}\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),ds)$ such that

$$\begin{array}{c}\hfill {\int }_t^{t+1}E\parallel Y(s+s_n)-\tilde{Y}(s){\parallel }^{2}ds\to 0\mathrm{and}{\int }_t^{t+1}E{\parallel \tilde{Y}(s-s_n)-Y(s)\parallel }^{2}ds\to 0\end{array}$$

as $n\to \infty$ pointwise on $\mathbb{R}$. The notation $A{S}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

In the following, we introduce a measurable (weights) function $\gamma :(0,\infty )\mapsto (0,\infty )$, which satisfies

$${\gamma }_0:=\underset{\epsilon \to 0}{lim}{\int }_{\epsilon }^1\gamma (s)ds={\int }_0^1\gamma (s)ds<\infty \mathrm{and}{m}_0:=\underset{s\in (0,\infty )}{inf}\gamma (s)>0$$

Let $\mathbb{U}$ denote the collection of all such measurable (weights) functions and the collection of all such differentiable functions denoted by ${\mathbb{U}}_{\infty }$.

Definition 8.

Let $\gamma \in \mathbb{U}$. A $\gamma ds$-measurable functions Y on $\mathbb{R}$ with values in ${\mathcal{L}}^2(P,\mathbb{H})$ is called generalized Stepanov bounded, if its Bochner transform $Y^b\in L^{\infty }(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. If with the norm

$${\parallel Y\parallel }_{{\mathbb{S}}_{\gamma }^2}=\underset{t\in \mathbb{R}}{sup}({\int }_t^{t+1}{E\gamma (s-t)\parallel Y(s)\parallel }^2{ds)}^{\frac{1}{2}}=\underset{t\in \mathbb{R}}{sup}({\int }_0^1{E\gamma (s)\parallel Y(t+s)\parallel }^2{ds)}^{\frac{1}{2}},$$

it is a Banach space.

Definition 9

([31]). Suppose $\gamma \in \mathbb{U}$. A function $Y\in B{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is called a generalized Stepanov-like almost automorphic (or ${\mathbb{S}}_{\gamma }^2$-almost automorphic), if for a function $\tilde{Y}\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t)\parallel Y(s+s_n)-\tilde{Y}(s){\parallel }^{2}ds={\int }_0^1\gamma (s){\parallel Y(s+t+s_n)-\tilde{Y}(s+t)\parallel }^{2}ds\to 0\\ \hfill {\int }_t^{t+1}\gamma (s-t)\parallel \tilde{Y}(s-s_n)-Y(s){\parallel }^{2}ds={\int }_0^1\gamma (s){\parallel \tilde{Y}(s+t-s_n)-Y(s+t)\parallel }^{2}ds\to 0\end{array}$$

for each $t\in \mathbb{R}$, as $n\to \infty$.

Definition 10

([31]). Let $\gamma \in \mathbb{U}$. A function $f:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $(t,Y)\mapsto f(t,Y)$ with $f(·,Y)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, is called ${\mathbb{S}}_{\gamma }^2$-almost automorphic in $t\in \mathbb{R}$ uniformly in $Y\in {\mathcal{L}}^2(P,\mathbb{H})$ if $t\mapsto f(t,Y)$ is ${\mathbb{S}}_{\gamma }^2$-almost automorphic for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, that is, for a function $\tilde{f}(·,Y)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$${\int }_t^{t+1}\gamma (s-t){\parallel f(s+s_n,Y)-\tilde{f}(s,Y)\parallel }^{2}ds\to 0$$

$${\int }_t^{t+1}\gamma (s-t){\parallel \tilde{f}(s-s_n,Y)-f(s,Y)\parallel }^{2}ds\to 0$$

for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, as $n\to \infty$ pointwise on $\mathbb{R}$. The notation $A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of all ${\mathbb{S}}_{\gamma }^2$-almost automorphic functions.

Definition 11.

Let $\gamma \in \mathbb{U}$. A function $J:\mathbb{R}\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $(t,x)\mapsto J(t,x)$ with $J(·,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ for each $x\in \mathbb{V}$, is called Poisson ${\mathbb{S}}_{\gamma }^2$-almost automorphic in $t\in \mathbb{R}$ uniformly in $x\in \mathbb{V}$ if $t\mapsto J(t,x)$ is Poisson ${\mathbb{S}}_{\gamma }^2$-almost automorphic for each $x\in \mathbb{V}$, that is, for a function $\tilde{J}(·,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$${\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel J(s+s_n,x)-\tilde{J}(s,x)\parallel }^2\nu (dx)ds\to 0$$

$${\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \tilde{J}(s-s_n,x)-J(s,x)\parallel }^2\nu (dx)ds\to 0$$

for each $x\in \mathbb{V}$, as $n\to \infty$ pointwise on $\mathbb{R}$. The notation Poisson $A{S}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of all such functions.

Definition 12.

Let $\gamma \in \mathbb{U}$. A function $F:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $(t,Y,x)\mapsto F(t,Y,x)$ with $F(·,Y,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, is called Poisson ${\mathbb{S}}_{\gamma }^2$-almost automorphic uniformly in $Y\in {\mathcal{L}}^2(P,\mathbb{H})$ in $t\in \mathbb{R}$ if $t\mapsto F(t,Y,x)$ is Poisson ${\mathbb{S}}_{\gamma }^2$-almost automorphic for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, that is, for a function $\tilde{F}(·,Y,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$${\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s+s_n,Y,x)-\tilde{F}(s,Y,x)\parallel }^2\nu (dx)ds\to 0$$

$${\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \tilde{F}(s-s_n,Y,x)-F(s,Y,x)\parallel }^2\nu (dx)ds\to 0$$

for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, as $n\to \infty$ pointwise on $\mathbb{R}$. The notation Poisson $A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of all such functions.

Proposition 2

([32]). Suppose $Y\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and $K=\left\{\overline{Y(t):t\in \mathbb{R}}\right\}\subset {\mathcal{L}}^2(P,\mathbb{H})$ is a compact subset, where $\left\{\overline{Y(t):t\in \mathbb{R}}\right\}$ denotes the closure of the set. If $f\in A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ and there exists $L>$0 such that

$$\parallel f(t,u)-f(t,v)\parallel \le L\parallel u-v\parallel$$

(2)

for all $u,v\in {\mathcal{L}}^2(P,\mathbb{H})$ and $t\in \mathbb{R}$, then the mapping $t\mapsto f(t,Y(t))$ belongs to the space $A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

In this paper, we show the new composition theorem of ${\mathbb{S}}_{\gamma }^2$-almost automorphic functions under the following condition.

Suppose $L>$ 0 such that, for all $u,v\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and $t\in \mathbb{R}$,

$${\int }_t^{t+1}{\gamma (s-t)\parallel f(s,u)-f(s,v)\parallel }^{2}ds\le L{\int }_t^{t+1}\gamma (s-t){\parallel u-v\parallel }^{2}ds.$$

(3)

Theorem 1.

Suppose $Y\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ such that $K=\left\{\overline{Y(t):t\in \mathbb{R}}\right\}\subset {\mathcal{L}}^2(P,\mathbb{H})$ is a compact subset, where $\left\{\overline{Y(t):t\in \mathbb{R}}\right\}$ denotes the closure of the set. If $f\in A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ and satisfies $(3)$, then the function $D:\mathbb{R}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ given by $D(t)=f(t,Y(t))$ is $A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Let ${(s_n^{\prime })}_{n\in \mathbb{N}}$ be an arbitrary sequence of real numbers. Since $Y\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and $f\in A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$, there exist a subsequence ${(s_n)}_{n\in \mathbb{N}}$ and functions $\tilde{Y}\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$, $\tilde{f}(·,Y)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ such that

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t){\parallel Y(s+s_n)-\tilde{Y}(s)\parallel }^{2}ds\to 0\end{array}$$

(4)

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t){\parallel \tilde{Y}(s-s_n)-Y(s)\parallel }^{2}ds\to 0\end{array}$$

(5)

as $n\to \infty$ for each $t\in \mathbb{R}$.

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t){\parallel f(s+s_n,Y)-\tilde{f}(s,Y)\parallel }^{2}ds\to 0\end{array}$$

(6)

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t){\parallel \tilde{f}(s-s_n,Y)-f(s,Y)\parallel }^{2}ds\to 0\end{array}$$

(7)

for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, as $n\to \infty$ pointwise on $\mathbb{R}$.

Define the function $\tilde{D}:\mathbb{R}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $\tilde{D}(t)=\tilde{f}(t,\tilde{Y}(t))$. It holds that

$$D(s+s_n)-\tilde{D}(s)=f(s+s_n,Y(s+s_n))-f(s+s_n,\tilde{Y}(s))+f(s+s_n,\tilde{Y}(s))-\tilde{f}(s,\tilde{Y}(s))$$

Then, by virtue of the mean-value Inequalities and the Lipschitz condition (H1), we can obtain

$$\begin{array}{ccc}& & {\int }_t^{t+1}\gamma (s-t){\parallel D(s+s_n)-\tilde{D}(s)\parallel }^{2}ds\hfill \\ & \le & 2{\int }_t^{t+1}\gamma (s-t){\parallel f(s+s_n,Y(s+s_n))-f(s+s_n,\tilde{Y}(s))\parallel }^{2}ds\hfill \\ & & +2{\int }_t^{t+1}\gamma (s-t){\parallel f(s+s_n,\tilde{Y}(s))-\tilde{f}(s,\tilde{Y}(s))\parallel }^{2}ds\hfill \\ & \le & 2L{\int }_t^{t+1}\gamma (s-t){\parallel Y(s+s_n)-\tilde{Y}(s)\parallel }^{2}ds\hfill \\ & & +2{\int }_t^{t+1}\gamma (s-t){\parallel f(s+s_n,\tilde{Y}(s))-\tilde{f}(s,\tilde{Y}(s))\parallel }^{2}ds\hfill \end{array}$$

We can deduce from $(4)$, $(6)$ that

$${\int }_t^{t+1}\gamma (s-t){\parallel D(s+s_n)-\tilde{D}(s)\parallel }^{2}ds\to 0$$

pointwise on $\mathbb{R}$, as $n\to \infty$. Similarly, we can deduce from $(5)$, $(7)$ that

$${\int }_t^{t+1}\gamma (s-t){\parallel \tilde{D}(s-s_n)-D(s)\parallel }^{2}ds\to 0$$

pointwise on $\mathbb{R}$, as $n\to \infty$. Thus, $D(t)=f(t,Y(t))$ is $A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. □

Remark 4.

In the proof of Theorem 1, the similar techniques have been used in the study of diffusion processes in networks; for more details, please refer to the work [33], in which the authors investigate a logistic model, which is a dependent Markov chain and allows individual variation and time-dependent infection and recovery rates.

For the Poisson term, we need the following conditions: Assume $L>0$ such that, for all $t\in \mathbb{R}$ and $u,v\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$,

$${\int }_t^{t+1}{\int }_{\mathbb{V}}{\gamma (s-t)\parallel F(s,u,x)-F(s,v,x)\parallel }^2\nu (dx)ds\le L{\int }_t^{t+1}\gamma (s-t){\parallel u-v\parallel }^{2}ds$$

(8)

Theorem 2.

Suppose $Y\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ such that $K=\left\{\overline{Y(t):t\in \mathbb{R}}\right\}\subset {\mathcal{L}}^2(P,\mathbb{H})$ is a compact subset, where $\left\{\overline{Y(t):t\in \mathbb{R}}\right\}$ denotes the closure of the set. If $F\in A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ and satisfies $(8)$, then the function $D:\mathbb{R}\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ given by $D(t,x)=F(t,Y(t),x)$ is $A{S}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Please the proof of Theorem 2 in Appendix A.1. □

2.3. ${\mathbb{S}}_{\gamma }^2$-Pseudo Almost Automorphy

Define the classes of functions:

$PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})):=\left\{Y\in BC(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})):{lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\parallel Y(t)\parallel }^{2}dt=0\right\}$

$$\begin{gathered} PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H})):=\left\{f\in BC(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H})): \\ {lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\parallel f(t,Y)\parallel }^{2}dt=0,f(·,Y)\mathrm{is}\mathrm{bounded}\mathrm{for}\mathrm{each}Y\in {\mathcal{L}}^2(P,\mathbb{H})\right\} \end{gathered}$$

$PA{P}_0(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H})):=\left\{{lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\int }_{\mathbb{V}}{\parallel J(t,x)\parallel }^2\nu (dx)dt=0,whereJ\in BC(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))\right\}$

$PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H})):=\left\{F\in PA{P}_0(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H})):\mathrm{for}\mathrm{any}Y\in {\mathcal{L}}^2(P,\mathbb{H})\right\}$

Definition 13

([30]). A function $Y\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is called PAA if it can be given by $Y=x+z$, where $x\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and $z\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. The notation $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

Definition 14

([30]). A function $f\in C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ is called PAA if it can be written as $f=l+m$, where $l\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ and $m\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$. The notation $PAA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

Definition 15.

A function $F\in C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ is called Poisson PAA if it can be given by $F=h+\varphi$, where $h\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H})$ and $\varphi \in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$. The notation $PAA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

Proposition 3

([30]). The space $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is a Banach space when equipped with the sup norm ${\parallel ·\parallel }_{\infty }$.

Define the following collections:

$$\begin{gathered} PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)):=\left\{Y(·)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds): \\ {lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\int }_t^{t+1}\gamma (s-t){\parallel Y(s)\parallel }^{2}dsdt=0\right\}, \end{gathered}$$

$$\begin{gathered} PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)):=\left\{f(·,Y)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds): \\ {lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\int }_t^{t+1}\gamma (s-t){\parallel f(s,Y)\parallel }^{2}dsdt=0,f(·,Y)\mathrm{is}\mathrm{bounded}\mathrm{for}\mathrm{each}Y\in {\mathcal{L}}^2(P,\mathbb{H})\right\}, \end{gathered}$$

$$\begin{gathered} PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)):=\left\{J(·,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds): \\ {lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\int }_{\mathbb{V}}{\int }_t^{t+1}\gamma (s-t){\parallel J(s,x)\parallel }^{2}ds\nu (dx)dt=0\right\}, \end{gathered}$$

$PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)):=\left\{\mathrm{for}\mathrm{any}Y\in {\mathcal{L}}^2(P,\mathbb{H}),F\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))\right\}$

Definition 16

([5]). Let $\gamma \in {\mathbb{U}}_{\infty }$. A function $Y\in B{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is called ${\mathbb{S}}_{\gamma }^2$-PAA, if it can be given by $Y=x+z$, where $x^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and $z^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. The notation $PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

Remark 5.

By the definition, ${\mathbb{S}}_{\gamma }^2$-PAA spaces are translation-invariant. Moreover, the decomposition of ${\mathbb{S}}_{\gamma }^2$-PAA functions is unique.

Proposition 4

([5]). If $Y\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, then $Y\in PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ that is, $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\subset PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proposition 5

([5]). Let $\gamma \in {\mathbb{U}}_{\infty }$. The space $PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is a Banach space when equipped with the norm ${\parallel ·\parallel }_{{\mathbb{S}}_{\gamma }^2}$.

Definition 17

([5]). Let $\gamma \in {\mathbb{U}}_{\infty }$. A function $f:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $(t,Y)\mapsto f(t,Y)$ with $f(·,Y)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, is called ${\mathbb{S}}_{\gamma }^2$-PAA if there exist functions $l,m:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ such that $f=l+m$ where $l^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and $m^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. The notation $PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of all such functions.

Definition 18.

Let $\gamma \in {\mathbb{U}}_{\infty }$. A function $J:\mathbb{R}\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $(t,x)\mapsto J(t,x)$ with $J(·,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ for each $x\in \mathbb{V}$, is called Poisson ${\mathbb{S}}_{\gamma }^2$-PAA, if there exist functions $\phi ,\psi :\mathbb{R}\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ such that $J=\phi +\psi$ where ${\phi }^b\in AA(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and ${\psi }^b\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. The notation $PA{A}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

Definition 19.

Let ${\gamma }_{\infty }\in \mathbb{U}$. A function $F:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $(t,Y,x)\mapsto F(t,Y,x)$ with $F(·,Y,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, is called Poisson ${\mathbb{S}}_{\gamma }^2$-PAA, if there exist functions $h,\varphi :\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ such that $F=h+\varphi$ where $h^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and ${\varphi }^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. The notation $PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ denotes the collection of such functions.

Remark 6.

Actually, Poisson generalized Stepanov-like PAA(Poisson ${\mathbb{S}}_{\gamma }^2$-PAA) generalizes the concept of Poisson Stepanov-like almost automorphy [15], that is, if a stochastic process is Poisson Stepanov-like almost automorphy, then it is Poisson generalized Stepanov-like PAA, but the converse is not true, which means the function space becomes much bigger than ever before.

Proposition 6

([5]). Let $f=l+m\in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ such that $l^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and also $m^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Assume that l satisfies $(2)$ and m satisfies $(3)$. Furthermore, if $Y=x+z\in PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ with $x^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and $z^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and also $K=\left\{\overline{x(t):t\in \mathbb{R}}\right\}$ is compact, where $\overline{\{·\}}$ denotes the closure of the set, then $t\mapsto f(t,Y(t))$ belongs to $PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Theorem 3.

Let $f=l+m\in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$ such that its Bochner transform $l^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and also $m^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Assume that l and m satisfy $(3)$. Furthermore, if $Y=x+z\in PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ with $x^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and $z^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and also $K=\left\{\overline{x(t):t\in \mathbb{R}}\right\}$ is compact, where $\overline{\{·\}}$ denotes the closure of the set, then $t\mapsto f(t,Y(t))$ belongs to $PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

We have

$$\begin{array}{ccc}\hfill f(t,Y(t))& =& l(t,x(t))+f(t,Y(t))-l(t,x(t))\hfill \\ & =& l(t,x(t))+f(t,Y(t))-f(t,x(t))+m(t,x(t))\hfill \end{array}$$

Denote by

$$\begin{array}{ccc}\hfill {\Gamma }^b(·)& =& f^b(·,Y^b(·)\hfill \\ & =& l^b(·,x^b(·))+f^b(·,Y^b(·))-f^b(·,x^b(·))+m^b(·,x^b(·))\hfill \end{array}$$

Next, we shall show that ${\Gamma }^b(·)\in PAP(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ by several steps.

Step 1: we claim that $l^b(·,x^b(·))\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. In fact, we easily know that the function l satisfies $(H1)$ and its Bochner transform $l^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, $x^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$. Moreover, $K=\left\{\overline{x(t):t\in \mathbb{R}}\right\}$ is compact. Thus, by virtue of the Theorem 1, we have $l^b(·,x^b(·))\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$.

Step 2: On the other hand, we claim that ${\phi }^b(·)=f^b(·,Y^b(·))-f^b(·,x^b(·))\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Since $l,m$ satisfies $(3)$, we obtain

$$\begin{array}{ccc}& & {\int }_0^1\gamma (s){\parallel \phi (t+s)\parallel }^{2}ds\hfill \\ & =& {\int }_t^{t+1}\gamma (s-t){\parallel \phi (s)\parallel }^{2}ds\hfill \\ & =& {\int }_t^{t+1}\gamma (s-t){\parallel f(s,Y(s))-f(s,x(s))\parallel }^{2}ds\hfill \\ & \le & 2{\int }_t^{t+1}\gamma (s-t){\parallel l(s,Y(s))-l(s,x(s))\parallel }^{2}ds\hfill \\ & & 2{\int }_t^{t+1}\gamma (s-t){\parallel m(s,Y(s))-m(s,x(s))\parallel }^{2}ds\hfill \\ & \le & 4L{\int }_t^{t+1}\gamma (s-t){\parallel z(s)\parallel }^{2}ds\hfill \end{array}$$

Thus, for any $T>0$,

$$\frac{1}{2T}{\int }_{-T}^T{\int }_0^1{\gamma (s)\parallel \phi (t+s)\parallel }^{2}dsdt\le \frac{2L}{T}{\int }_{-T}^T{\int }_t^{t+1}\gamma (s-t){\parallel z(s)\parallel }^{2}dsdt$$

Since $z^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, we can obtain

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\int }_0^1\gamma (s){\parallel \phi (t+s)\parallel }^{2}dsdt=0$$

which implies ${\phi }^b(·)\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$.

Step 3: we also claim that $m^b(·,x^b(·))\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. There are finite open balls $O_k(k=1,2,...,n)$ with center $x_k\in K$ from the fact that $K=\left\{\overline{x(t):t\in \mathbb{R}}\right\}$ is compact. In addition, if the radius $\epsilon$ of $O_k(k=1,2,...,n)$ small enough, then $\{x(t);t\in \mathbb{R}\}\subset {\bigcup }_{k=1}^n{O}_k$, where $B_k=\{s\in \mathbb{R};x(s)\in O_k\}$ and $\mathbb{R}={\bigcup }_{k=1}^n{B}_k$. Suppose $E_1=B_1$, $E_k=B_k\setminus {\bigcup }_{j=1}^{k-1}{B}_j(2\le j\le n)$; then, $E_i\cap E_j=\varnothing$, when $i\ne j,1\le i,j\le n$.

On the other hand, given the step function $\overline{x}:\mathbb{R}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ by $\overline{x}(s)=x_k$, $s\in E_k,k=1,2,...,n$. Thus,

$$\parallel x(s)-\overline{x}(s)\parallel \le \epsilon$$

for all $s\in \mathbb{R}$. By replacing the variable in the integral, it holds that

$$\begin{array}{ccc}& & {\int }_t^{t+1}\gamma (s-t){\parallel m(s,x(s))\parallel }^{2}ds\hfill \\ & \le & 2{\int }_t^{t+1}\gamma (s-t)\parallel m(s,x(s))-m(s,\overline{x}(s)){\parallel }^{2}ds+2{\int }_t^{t+1}\gamma (s-t){\parallel m(s,\overline{x}(s))\parallel }^{2}ds\hfill \\ & \le & 2L{\int }_t^{t+1}\gamma (s-t)\parallel x(s)-\overline{x}{(s)\parallel }^{2}ds+2\sum _{k=1}^n{\int }_{[t,t+1]\cap E_k}\gamma (s-t){\parallel m(s,x_k)\parallel }^{2}ds\hfill \\ & \le & 2L{\gamma }_0{\epsilon }^2+2\sum _{k=1}^n{\int }_{[t,t+1]\cap E_k}\gamma (s-t){\parallel m(s,x_k)\parallel }^{2}ds\hfill \end{array}$$

Thus, for any $T>0$,

$$\begin{array}{ccc}& & \frac{1}{2T}{\int }_{-T}^T{\int }_t^{t+1}\gamma (s-t){\parallel m(s,x(s))\parallel }^{2}dsdt\hfill \\ & \le & 2L{\gamma }_0{\epsilon }^2+\frac{1}{T}{\int }_{-T}^T\sum _{k=1}^n{\int }_{[t,t+1]\cap E_k}\gamma (s-t){\parallel m(s,x_k)\parallel }^{2}dsdt\hfill \end{array}$$

Since the arbitrariness of $\epsilon$ and $m^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, we can obtain

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\int }_t^{t+1}\gamma (s-t){\parallel m(s,x(s))\parallel }^{2}dsdt=0$$

which implies $m^b(·,x^b(·))\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. The proof is complete. □

Theorem 4.

Let $F=h+\varphi \in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ such that $h^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and ${\varphi }^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Assume that h and ϕ satisfy $(3)$. Furthermore, if $Y=\alpha +\beta \in PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ with ${\alpha }^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and ${\beta }^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and such that $K=\left\{\overline{\alpha (t):t\in \mathbb{R}}\right\}$ is compact, where $\left\{\overline{\alpha (t):t\in \mathbb{R}}\right\}$ denotes the closure of the set, then $(t,x)\mapsto F(t,Y(t),x)$ belongs to $PA{A}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Please see the proof of Theorem 4 in Appendix A.2. □

3. Main Results

In this section, we consider the following abstract model:

$$\begin{array}{cc}\hfill dY(t)& =A(t)Y(t)dt+f(t,Y(t))dt+g(t,Y(t))dW(t)\hfill \\ \hfill & +{\int }_{{\left|x\right|}_{\mathbb{V}}<1}F(t,Y(t-),x)\tilde{N}(dt,dx)\hfill \\ \hfill & +{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}G(t,Y(t-),x)N(dt,dx),t\in \mathbb{R}\hfill \end{array}$$

(9)

It supposes that

(i)

The coefficients in the above model satisfy that $f:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\mapsto {\mathcal{L}}^2(P,\mathbb{H})$, $g:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\mapsto L(\mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$, $F,G:\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$;

(ii)

W is a Brownian motion, N and $\tilde{N}$ are Poisson random measure and compensated Poisson random measure, respectively.

(iii)

$A(t)$ satisfies the “Acquistapace–Terrani” condition.

Definition 20.

Suppose $U(t,s):t\ge switht,s\in \mathbb{R}$ is a set of bounded linear operators on ${\mathcal{L}}^2(P,\mathbb{H})$, if

(i)

$U(s,s)=Q$, $U(t,s)=U(t,r)U(r,s)$ for $t\ge r\ge s$ and $t,r,s\in \mathbb{R}$;

(ii)

The strongly continuous mapping $(t,s)\mapsto U(t,s)$∈ $\{(\tau ,\sigma )\in {\mathbb{R}}^2:\tau \ge \sigma \}$.

Thus, $U(t,s)$ is an evolution family.

Definition 21.

The mild solution of (9) is listed in the following:

$$\begin{array}{ccc}\hfill Y(t)& =& {\int }_{-\infty }^{t}U(t,s)f(s,Y(s))ds+{\int }_{-\infty }^{t}U(t,s)g(s,Y(s))dW(s)\hfill \\ & & +{\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx),t\in \mathbb{R}\hfill \end{array}$$

where $Y:\mathbb{R}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ is a continuous function.

Almost automorphy in distribution Let real $\mathbb{H}$-valued functions f are Lipschitz continuous and equipped with the norms

$${\parallel f\parallel }_{BL}={\parallel f\parallel }_L+{\parallel f\parallel }_{\infty }{,\parallel f\parallel }_L=\underset{x\ne y}{sup}\frac{|f(x)-f(y)|}{\parallel x-y\parallel }{,\parallel f\parallel }_{\infty }=\underset{x\in \mathbb{H}}{sup}\left|f\right|$$

Then, define a metric in the following sense:

$$\beta (\mu ,\nu ):=sup\left\{\right|\int fd\mu -\int fd\nu |:\parallel f{\parallel }_{BL}\le 1\},\mu ,\nu \in \mathcal{P}(\mathbb{H})$$

and assume $\mathcal{P}(\mathbb{H})$ to be the space of all Borel probability measure on $\mathbb{H}$ endowed with the $\beta$ metric.

Definition 22

([12]). For a $\mathcal{P}(\mathbb{H})$-valued almost automorphic mapping $\tilde{\mu }(t)$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\underset{n\to \infty }{lim}\beta (\mu (t+s_n),\tilde{\mu }(t))=0,\underset{n\to \infty }{lim}\beta (\tilde{\mu }(t-s_n),\mu (t))=0$$

holds for each $t\in \mathbb{R}$. Then, $\mathbb{H}$-valued $Y(t)$ with law $\mu (t)$ is called almost automorphy in distribution.

Remark 7

([12]). A square-mean automorphic function is necessarily almost automorphy in distribution from the fact that, for a sequence of random variables, ${\mathcal{L}}^2$ converge implies convergence in distribution, but the converse is not true.

Definition 23.

An $\mathbb{H}$-valued function $Y(t)$ is called pseudo almost automorphy in distribution if it can be expressed as $Y=x+z$, where x is almost automorphy in distribution and $z\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

In order to study the asymptotic behavior of the solutions, the following hypotheses are needed: $\left[Hf\right]$$f\in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))\cap C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$, f satisfies the assumption of the Theorem 3, and

$$K_f=\underset{s\in (t,t+1)}{sup}{\int }_t^{t+1}\gamma (s-t){\parallel f(s,0)\parallel }^{2}ds,t\in \mathbb{R}$$

$\left[Hg\right]$$g\in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))\cap C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}),{\mathcal{L}}^2(P,\mathbb{H}))$, g satisfies the assumption of the Theorem 3, and

$$K_g=\underset{s\in (t,t+1)}{sup}{\int }_t^{t+1}\gamma (s-t){\parallel g(s,0)\parallel }^{2}ds,t\in \mathbb{R}$$

$\left[HF\right]$$F\in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))\cap C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$, F satisfies the assumption of the Theorem 4, and

$$K_F=\underset{s\in (t,t+1)}{sup}{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s,0,x)\parallel }^2\nu (dx)ds,t\in \mathbb{R}$$

$\left[HG\right]$$G\in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))\cap C(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$, G satisfies the assumption of the Theorem 4, and

$$K_G=\underset{s\in (t,t+1)}{sup}{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel G(s,0,x)\parallel }^2\nu (dx)ds,t\in \mathbb{R}$$

$\left[HU\right]$

(i)

$U(t,s)$ satisfies $\parallel U(t,s)\parallel \le M{e}^{-\delta (t-s)}$, where $M,\delta >0$ are constants.

(ii)

The mapping $(t,s)\mapsto U(t,s)x$$\in bAA(\mathbb{T},{\mathcal{L}}^2(P,\mathbb{H}))$ uniformly for $x\in {\mathcal{L}}^2(P,\mathbb{H})$.

Lemma 1.

Under assumptions $(Hf,HU)$, then the integral operator ${\Lambda }_1$ defined by

$${\Lambda }_{1}Y(t):={\int }_{-\infty }^{t}U(t,s)f(s,Y(s))ds$$

maps $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ into $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Let $Y\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\subset PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. By Theorem 3, it holds that $D_1(t):=f(t,Y(t))\in PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Now, let $D_1=l+m$, where their Bochner transform $l^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and $m^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. For each $k=1,2,...$, the integral

$$\begin{array}{ccc}\hfill {\Phi }_k(t)& =& {\int }_{k-1}^{k}U(t,t-\xi )D_1(t-\xi )d\xi \hfill \\ & =& {\int }_{k-1}^{k}U(t,t-\xi )l(t-\xi )d\xi +{\int }_{k-1}^{k}U(t,t-\xi )m(t-\xi )d\xi \hfill \end{array}$$

and set $X_k(t):={\int }_{k-1}^{k}U(t,t-\xi )l(t-\xi )d\xi$ and $Z_k(t):={\int }_{k-1}^{k}U(t,t-\xi )m(t-\xi )d\xi$.

Let us show that $X_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$. For that, letting $\sigma =t-\xi$, we obtain

$$X_k(t)={\int }_{t-k}^{t-k+1}U(t,\sigma )l(\sigma )d\sigma ,t\in \mathbb{R}$$

By virtue, the Cauchy–Schwarz inequality and $(HU(i))$, we have

$$\begin{array}{ccc}\hfill E\parallel X_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{U(t,\sigma )l(\sigma )d\sigma \parallel }^2\hfill \\ & \le & {\left({\int }_{t-k}^{t-k+1}\parallel U(t,\sigma )l(\sigma )\parallel d\sigma \right)}^2\hfill \\ & \le & {\int }_{t-k}^{t-k+1}{M}^2{e}^{-2\delta (t-\sigma )}\gamma {(\sigma -t+k)}^{-1}d\sigma ·{\int }_{t-k}^{t-k+1}\gamma (\sigma -t+k){\parallel l(\sigma )\parallel }^{2}d\sigma \hfill \\ & \le & \frac{M^2}{2m_0\delta }{e}^{-2\delta (k-1)}{\parallel l\parallel }_{{\mathbb{S}}_{\gamma }^2}^2\hfill \end{array}$$

Using the fact that

$$\frac{M^2}{2m_0\delta }\sum _{k=1}^{\infty }{e}^{-2\delta (k-1)}<\infty$$

We deduce that the series ${\sum }_{k=1}^{\infty }{X}_k(t)$ is uniformly convergent on $\mathbb{R}$ by the Weirstrass theorem. Furthermore,

$$X(t):={\int }_{-\infty }^{t}U(t,\sigma )l(\sigma )d\sigma =\sum _{k=1}^{\infty }{X}_k(t)$$

$X(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, and

$$\begin{array}{ccc}\hfill {E\parallel X(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }{X}_k{(t)\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}\sum _{k=1}^{\infty }\{k^{2}E\parallel X_k(t){\parallel }^2\}\hfill \\ & \le & \frac{M^2}{2m_0\delta }{\parallel l\parallel }_{{\mathbb{S}}_{\gamma }^2}^2\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<\infty \hfill \end{array}$$

We deduce that $X(t)$ is bounded from the Weirstrass theorem. Here, it can be noted that a similar estimation has been done in the study of random system control processes [34], and this helps to motivate the methodology of the above estimation.

Since $l\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and $U(t,s)x\in bAA(\mathbb{T},{\mathcal{L}}^2(P,\mathbb{H}))$, then, for functions $\tilde{U}$, $\tilde{l}\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\parallel U(t+s_n,s+s_n)x-\tilde{U}(t,s)x\parallel }^2=0\end{array}$$

(10)

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\parallel \tilde{U}(t-s_n,s-s_n)x-U(t,s)x\parallel }^2=0\end{array}$$

(11)

and

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel l(t+s_n)-\tilde{l}(t){\parallel }_{{\mathbb{S}}_{\gamma }^2}^2=0,\underset{n\to \infty }{lim}{\parallel \tilde{l}(t-s_n)-l(t)\parallel }_{{\mathbb{S}}_{\gamma }^2}^2=0\end{array}$$

(12)

Let

$$\widetilde{X_k}(t):={\int }_{k-1}^k\tilde{U}(t,t-\xi )\tilde{l}(t-\xi )d\xi$$

Next, by the Cauchy–Schwarz inequality, it follows that

$$\begin{array}{ccc}& & E\parallel X_k(t+s_n)-\widetilde{X_k}(t){\parallel }^2\hfill \\ & =& E\parallel {\int }_{k-1}^{k}U(t+s_n,t+s_n-\xi )l(t+s_n-\xi )-\tilde{U}(t,t-\xi )\tilde{l}(t-\xi ){d\xi \parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{k-1}^{k}U(t+s_n,t+s_n-\xi )[l(t+s_n-\xi )-\tilde{l}(t-\xi )]{d\xi \parallel }^2\hfill \\ & & +2E\parallel {\int }_{k-1}^k[U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{l}(t-\xi ){d\xi \parallel }^2\hfill \\ & \le & \frac{M^2}{m_0\delta }{e}^{-2\delta (k-1)}{\int }_{k-1}^k\gamma (\xi -k+1){\parallel l(t+s_n-\xi )-\tilde{l}(t-\xi )\parallel }^{2}d\xi \hfill \\ & & +2{\int }_{k-1}^k{\parallel [U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{l}(t-\xi )\parallel }^{2}d\xi \hfill \end{array}$$

Now, from Lebesgue dominated convergence theorem and $(10)$, $(12)$, it holds that

$$\parallel X_k(t+s_n)-\widetilde{X_k}(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Similarly, using $(11)$, $(12)$, we have

$$\parallel \widetilde{X_k}(t-s_n)-X_k(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Thus, each $X_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$ for each k. Hence, $X(t)\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Let us show that $Z_k\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Using the Cauchy–Schwarz inequality, we can obtain

$$\begin{array}{ccc}\hfill E\parallel Z_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{U(t,\sigma )m(\sigma )d\sigma \parallel }^2\hfill \\ & \le & \frac{M^2}{2m_0\delta }{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}\gamma (\sigma -t+k){\parallel m(\sigma )\parallel }^{2}d\sigma \hfill \end{array}$$

Thus, for any $T>0$,

$$\frac{1}{2T}{\int }_{-T}^T\parallel Z_k{(t)\parallel }^{2}dt\le \frac{M^2}{4T{m}_0\delta }{e}^{-2\delta (k-1)}{\int }_{-T}^T{\int }_{t-k}^{t-k+1}\gamma (\sigma -t+k){\parallel m(\sigma )\parallel }^{2}d\sigma dt$$

Since $m^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, then

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel Z_k(t)\parallel }^{2}dt=0,$$

that is, $Z_k\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Furthermore,

$$Z(t):={\int }_{-\infty }^{t}U(t,\sigma )m(\sigma )d\sigma =\sum _{k=1}^{\infty }{Z}_k(t)$$

$Z(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, and

$$\begin{array}{ccc}\hfill {E\parallel Z(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }{Z}_k{(t)\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel Z_k(t){\parallel }^2\}\hfill \end{array}$$

Then,

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel Z(t)\parallel }^{2}dt=0$$

Consequently, the uniform limit $Z(t)\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Thus, ${\Lambda }_{1}Y(t)=X(t)+Z(t)\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. □

Lemma 2.

Under assumptions $(Hg,HU)$, then ${\Lambda }_2$ defined by

$${\Lambda }_{2}Y(t):={\int }_{-\infty }^{t}U(t,s)g(s,Y(s))dW(s)$$

maps $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ into $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Let $Y\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\subset PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. By Theorem 3, $D_2(t):=g(t,Y(t))\in PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Now, let $D_2=p+q$, where its Bochner transform $p^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and $q^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Next,

$$\begin{array}{ccc}\hfill {\Psi }_k(t)& =& {\int }_{k-1}^{k}U(t,t-\xi )D_2(t-\xi )dW(\xi )\hfill \\ & =& {\int }_{k-1}^{k}U(t,t-\xi )p(t-\xi )dW(\xi )+{\int }_{k-1}^{k}U(t,t-\xi )q(t-\xi )dW(\xi )\hfill \end{array}$$

and set $V_k(t):={\int }_{k-1}^{k}U(t,t-\xi )p(t-\xi )dW(\xi )$ and $W_k(t):={\int }_{k-1}^{k}U(t,t-\xi )q(t-\xi )dW(\xi )$ for each $k=1,2,...$.

Let us show that $V_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$. Assuming $\sigma =t-\xi$, we obtain

$$V_k(t)={\int }_{t-k}^{t-k+1}U(t,\sigma )p(\sigma )dW(\sigma ),t\in \mathbb{R}$$

By the mean value theorem of integrals and Itô’s isometry, we have

$$\begin{array}{ccc}\hfill E\parallel V_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{U(t,\sigma )p(\sigma )dW(\sigma )\parallel }^2\hfill \\ & \le & {\int }_{t-k}^{t-k+1}E{\parallel U(t,\sigma )p(\sigma )\parallel }^{2}d\sigma \hfill \\ & \le & \frac{M^2}{m_0}{e}^{-2\delta (t-\epsilon )}{\int }_{t-k}^{t-k+1}\gamma (\sigma -t+k){\parallel p(\sigma )\parallel }^{2}d\sigma ,\epsilon \in [t-k,t-k+1]\hfill \\ & \le & \frac{M^2}{m_0}{e}^{-2\delta (k-1)}{\parallel p\parallel }_{{\mathbb{S}}_{\gamma }^2}^2\hfill \end{array}$$

Using the fact that

$$\frac{M^2}{m_0}\sum _{k=1}^{\infty }{e}^{-2\delta (k-1)}<\infty ,$$

We deduce the series ${\sum }_{k=1}^{\infty }{V}_k(t)$ is uniformly convergent on $\mathbb{R}$ by virtue of the Weirstrass theorem. Meanwhile,

$$V(t):={\int }_{-\infty }^{t}U(t,\sigma )p(\sigma )dW(\sigma )=\sum _{k=1}^{\infty }{V}_k(t)$$

$V(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, and

$$\begin{array}{ccc}\hfill {E\parallel V(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }{V}_k{(t)\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel V_k(t){\parallel }^2\}\hfill \\ & \le & \frac{M^2}{m_0}{\parallel p\parallel }_{{\mathbb{S}}_{\gamma }^2}^2\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<\infty \hfill \end{array}$$

We deduce that $V(t)$ is bounded by the Weirstrass theorem.

Since $p\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, then, for a function $\tilde{p}\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel p(t+s_n)-\tilde{p}(t){\parallel }_{{\mathbb{S}}_{\gamma }^2}^2=0\mathrm{and}\underset{n\to \infty }{lim}{\parallel \tilde{p}(t-s_n)-p(t)\parallel }_{{\mathbb{S}}_{\gamma }^2}^2=0\end{array}$$

(13)

Let

$$\widetilde{V_k}(t):={\int }_{k-1}^k\tilde{U}(t,t-\xi )\tilde{p}(t-\xi )dW(\xi )$$

Thus, from the Itô’s isometry and the mean value theorem of integrals, it follows that

$$\begin{array}{ccc}& & E\parallel V_k(t+s_n)-\widetilde{V_k}(t){\parallel }^2\hfill \\ & =& E\parallel {\int }_{k-1}^{k}U(t+s_n,t+s_n-\xi )p(t+s_n-\xi )-\tilde{U}(t,t-\xi )\tilde{p}(t-\xi )dW(\xi ){\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{k-1}^{k}U(t+s_n,t+s_n-\xi )[p(t+s_n-\xi )-\tilde{p}(t-\xi )]dW(\xi ){\parallel }^2\hfill \\ & & +2E\parallel {\int }_{k-1}^k[U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{p}(t-\xi )dW(\xi ){\parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{k-1}^k\gamma (\xi -k+1){\parallel p(t+s_n-\xi )-\tilde{p}(t-\xi )\parallel }^{2}d\xi \hfill \\ & & +2{\int }_{k-1}^k{\parallel [U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{p}(t-\xi )\parallel }^{2}d\xi \hfill \end{array}$$

Now, from the Lebesgue dominated convergence theorem and $(10)$, $(13)$, we have

$$\parallel V_k(t+s_n)-\widetilde{V_k}(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Similarly, using $(11)$, $(13)$, it follows that

$$\parallel \widetilde{V_k}(t-s_n)-V_k(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Thus, each $V_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$ for each k. Hence, $V(t)\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Let us show that $W_k\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Using the Itô’s isometry, we can obtain

$$\begin{array}{ccc}\hfill E\parallel W_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{U(t,\sigma )q(\sigma )dW(\sigma )\parallel }^2\hfill \\ & \le & \frac{M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}\gamma (\sigma -t+k){\parallel q(\sigma )\parallel }^{2}d\sigma \hfill \end{array}$$

Thus, for any $T>0$,

$$\frac{1}{2T}{\int }_{-T}^T\parallel W_k{(t)\parallel }^{2}dt\le \frac{M^2}{2T{m}_0}{e}^{-2\delta (k-1)}{\int }_{-T}^T{\int }_{t-k}^{t-k+1}\gamma (\sigma -t+k){\parallel q(\sigma )\parallel }^{2}d\sigma dt$$

Since $q^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, then

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel W_k(t)\parallel }^{2}dt=0,$$

that is, $W_k\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Furthermore,

$$W(t):={\int }_{-\infty }^{t}U(t,\sigma )q(\sigma )dW(\sigma )=\sum _{k=1}^{\infty }{W}_k(t)$$

$W(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$; then,

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel W(t)\parallel }^{2}dt=0$$

Consequently, the uniform limit $W(t)\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Thus, ${\Lambda }_{2}Y(t)=V(t)+W(t)\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. □

Lemma 3.

Under assumptions $(HF,HU)$, then ${\Lambda }_3$ is defined by

$${\Lambda }_{3}Y(t):={\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)$$

maps $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ into $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Let $Y\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\subset PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. By Theorem 4, it follows that $D_3(t,x):=F(t,Y(t),x)\in PA{A}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$. Now, let $D_3=h+\varphi$, where $h^b\in AA(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and ${\varphi }^b\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Next,

$$\begin{array}{ccc}\hfill {\Omega }_k(t)& =& {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,t-\xi )D_3(t-\xi ,x)\tilde{N}(d\xi ,dx)\hfill \\ & =& {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,t-\xi )h(t-\xi ,x)\tilde{N}(d\xi ,dx)\hfill \\ & & +{\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,t-\xi )\varphi (t-\xi ,x)\tilde{N}(d\xi ,dx)\hfill \end{array}$$

and set

$$T_k(t):={\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,t-\xi )h(t-\xi ,x)\tilde{N}(d\xi ,dx)$$

and

$$Q_k(t):={\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,t-\xi )\varphi (t-\xi ,x)\tilde{N}(d\xi ,dx)$$

Next, we prove $T_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$. Assuming $\sigma =t-\xi$, we obtain

$$T_k(t)={\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,\sigma )h(\sigma ,x)\tilde{N}(d\sigma ,dx),t\in \mathbb{R}$$

By the mean value theorem of integrals and the Itô’s isometry, we have

$$\begin{array}{ccc}\hfill E\parallel T_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,\sigma )h(\sigma ,x)\tilde{N}{(d\sigma ,dx)\parallel }^2\hfill \\ & \le & {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}E{\parallel U(t,\sigma )h(\sigma ,x)\parallel }^2\nu (dx)d\sigma \hfill \\ & \le & \frac{M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (\sigma -t+k){\parallel h(\sigma ,x)\parallel }^2\nu (dx)d\sigma \hfill \\ & \le & \frac{M^2}{m_0}{e}^{-2\delta (k-1)}{\parallel h\parallel }_{{\mathbb{S}}_{\gamma }^2}^2\hfill \end{array}$$

Using the fact that

$$\frac{M^2}{m_0}\sum _{k=1}^{\infty }{e}^{-2\delta (k-1)}<\infty ,$$

We deduce that the series ${\sum }_{k=1}^{\infty }{T}_k(t)$ is uniformly convergent on $\mathbb{R}$ by the Weirstrass theorem. Meanwhile,

$$T(t):={\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,\sigma )h(\sigma ,x)\tilde{N}(d\sigma ,dx)=\sum _{k=1}^{\infty }{T}_k(t)$$

$T(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, and

$$\begin{array}{ccc}\hfill {E\parallel T(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }{T}_k{(t)\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel T_k(t){\parallel }^2\}\hfill \\ & \le & \frac{M^2}{m_0}{\parallel h\parallel }_{{\mathbb{S}}_{\gamma }^2}^2\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<\infty \hfill \end{array}$$

We deduce $T(t)$ is bounded by the Weirstrass theorem.

Since $h\in A{S}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$, then, for a function $\tilde{h}\in A{S}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\begin{array}{c}\hfill {\int }_0^1{\int }_{\mathbb{V}}\gamma (t){\parallel h(t+s_n,x)-\tilde{h}(t,x)\parallel }^2\nu (dx)dt\to 0,\mathrm{as}n\to \infty \end{array}$$

(14)

$$\begin{array}{c}\hfill {\int }_0^1{\int }_{\mathbb{V}}\gamma (t){\parallel \tilde{h}(t-s_n,x)-h(t,x)\parallel }^2\nu (dx)dt\to 0,\mathrm{as}n\to \infty \end{array}$$

(15)

Let

$$\widetilde{T_k}(t):={\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\tilde{U}(t,t-\xi )\tilde{h}(t-\xi ,x)\tilde{N}(d\xi ,dx)$$

Then, from the mean value theorem of integrals and the Itô’s isometry, we have

$$\begin{array}{ccc}& & E\parallel T_k(t+s_n)-\widetilde{T_k}(t){\parallel }^2\hfill \\ & =& E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t+s_n,t+s_n-\xi )h(t+s_n-\xi ,x)-\tilde{U}(t,t-\xi )\tilde{h}(t-\xi ,x)\tilde{N}(d\xi ,dx){\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t+s_n,t+s_n-\xi )[h(t+s_n-\xi ,x)-\tilde{h}(t-\xi ,x)]\tilde{N}(d\xi ,dx){\parallel }^2\hfill \\ & & +2E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}[U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{h}(t-\xi ,x)\tilde{N}(d\xi ,dx){\parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (\xi -k+1){\parallel h(t+s_n-\xi ,x)-\tilde{h}(t-\xi ,x)\parallel }^2\nu (dx)d\xi \hfill \\ & & +2{\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}<1}{\parallel [U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{h}(t-\xi ,x)\parallel }^2\nu (dx)d\xi \hfill \end{array}$$

Now, by the Lebesgue dominated convergence theorem and $(10)$, $(14)$, we have

$$\parallel T_k(t+s_n)-\widetilde{T_k}(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Similarly, using $(11)$, $(15)$, we have

$$\parallel \widetilde{T_k}(t-s_n)-T_k(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Thus, each $T_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$ for each k. Hence, $T(t)\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$.

Let us show that $Q_k\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Using the Itô’s isometry, we can obtain

$$\begin{array}{ccc}\hfill E\parallel Q_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,\sigma )\varphi (\sigma ,x)\tilde{N}{(d\sigma ,dx)\parallel }^2\hfill \\ & \le & \frac{M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (\sigma -t+k){\parallel \varphi (\sigma ,x)\parallel }^2\nu (dx)d\sigma \hfill \end{array}$$

Thus, for any $T>0$,

$$\frac{1}{2T}{\int }_{-T}^T\parallel Q_k{(t)\parallel }^{2}dt\le \frac{M^2}{2T{m}_0}{e}^{-2\delta (k-1)}{\int }_{-T}^T{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (\sigma -t+k){\parallel \varphi (\sigma ,x)\parallel }^2\nu (dx)d\sigma dt$$

Since ${\varphi }^b\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, then

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel Q_k(t)\parallel }^{2}dt=0,$$

that is, $Q_k\in PA{P}_0(\mathbb{R}\times ,{\mathcal{L}}^2(P,\mathbb{H}))$. Furthermore,

$$Q(t):={\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,\sigma )\varphi (\sigma ,x)\tilde{N}(d\sigma ,dx)=\sum _{k=1}^{\infty }{Q}_k(t)$$

$Q(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$; then,

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel Q(t)\parallel }^{2}dt=0$$

Consequently, the uniform limit $Q(t)\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Thus, ${\Lambda }_{3}Y(t)=T(t)+Q(t)\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. □

Lemma 4.

Under assumptions $(HG,HU)$, then ${\Lambda }_4$ defined by

$${\Lambda }_{4}Y(t):={\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx)$$

maps $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ into $PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$.

Proof. 

Let $Y\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\subset PA{A}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. By Theorem 4, $D_4(t,x):=G(t,Y(t),x)\in PA{A}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$. Now, let $D_4=\alpha +\beta$, where ${\alpha }^b\in AA(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and ${\beta }^b\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Next,

$$\begin{array}{ccc}\hfill {\Gamma }_k(t)& =& {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,t-\xi )D_4(t-\xi ,x)N(d\xi ,dx)\hfill \\ & =& {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,t-\xi )\alpha (t-\xi ,x)N(d\xi ,dx)\hfill \\ & & +{\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,t-\xi )\beta (t-\xi ,x)N(d\xi ,dx)\hfill \end{array}$$

and set

$$S_k(t):={\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,t-\xi )\alpha (t-\xi ,x)N(d\xi ,dx)$$

and

$$O_k(t):={\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,t-\xi )\beta (t-\xi ,x)N(d\xi ,dx)$$

Let us show that $S_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$. Assuming $\sigma =t-\xi$, we obtain

$$S_k(t)={\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,\sigma )\alpha (\sigma ,x)N(d\sigma ,dx),t\in \mathbb{R}$$

By Itô’s isometry and Cauchy–Schwarz inequality, we have

$$\begin{array}{ccc}\hfill E\parallel S_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,\sigma )\alpha (\sigma ,x)N(d\sigma ,dx)\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,\sigma )\alpha (\sigma ,x)\tilde{N}{(d\sigma ,dx)\parallel }^2\hfill \\ & & +2E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,\sigma )\alpha (\sigma ,x)\nu (dx)d\sigma \parallel }^2\hfill \\ & \le & \frac{M^2}{m_0}(2+\frac{b}{\delta })e^{-2\delta (k-1)}{\parallel \alpha \parallel }_{{\mathbb{S}}_{\gamma }^2}^2\hfill \end{array}$$

From

$$\frac{M^2}{m_0}(2+\frac{b}{\delta })\sum _{k=1}^{\infty }{e}^{-2\delta (k-1)}<\infty ,$$

We deduce that the series ${\sum }_{k=1}^{\infty }{S}_k(t)$ is uniformly convergent on $\mathbb{R}$ by the Weirstrass theorem. Moreover,

$$S(t):={\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,\sigma )\alpha (\sigma ,x)N(d\sigma ,dx)=\sum _{k=1}^{\infty }{S}_k(t)$$

$S(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, and

$$\begin{array}{ccc}\hfill {E\parallel S(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }{S}_k{(t)\parallel }^2\le \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel S_k(t){\parallel }^2\}\hfill \\ & \le & \frac{M^2}{m_0}(2+\frac{b}{\delta }){\parallel \alpha \parallel }_{{\mathbb{S}}_{\gamma }^2}^2\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<\infty \hfill \end{array}$$

We deduce that $S(t)$ is bounded, by the Weirstrass theorem.

Next, since $\alpha \in A{S}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$, then, for a function $\tilde{\alpha }\in A{S}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ and every sequence of real numbers ${(s_n^{\prime })}_{n\in \mathbb{N}}$, there exists a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\begin{array}{c}\hfill {\int }_0^1{\int }_{\mathbb{V}}\gamma (t){\parallel \alpha (t+s_n,x)-\tilde{\alpha }(t,x)\parallel }^2\nu (dx)dt\to 0,\mathrm{as}n\to \infty \end{array}$$

(16)

$$\begin{array}{c}\hfill {\int }_0^1{\int }_{\mathbb{V}}\gamma (t){\parallel \tilde{\alpha }(t-s_n,x)-\alpha (t,x)\parallel }^2\nu (dx)dt\to 0,\mathrm{as}n\to \infty \end{array}$$

(17)

Let

$$\widetilde{S_k}(t):={\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\tilde{U}(t,t-\xi )\tilde{\alpha }(t-\xi ,x)N(d\xi ,dx)$$

Then, by Cauchy–Schwartz inequality and Ito isometry, from $\tilde{N}(t,B)=N(t,B)-t\nu (B)$, it follows that

$$\begin{array}{ccc}& & E\parallel S_k(t+s_n)-\widetilde{S_k}(t){\parallel }^2\hfill \\ & =& E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t+s_n,t+s_n-\xi )\alpha (t+s_n-\xi ,x)-\tilde{U}(t,t-\xi )\tilde{\alpha }(t-\xi ,x)N(d\xi ,dx){\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t+s_n,t+s_n-\xi )[\alpha (t+s_n-\xi ,x)-\tilde{\alpha }(t-\xi ,x)]N(d\xi ,dx){\parallel }^2\hfill \\ & & +2E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}[U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{\alpha }(t-\xi ,x)N(d\xi ,dx){\parallel }^2\hfill \\ & \le & 4E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t+s_n,t+s_n-\xi )[\alpha (t+s_n-\xi ,x)-\tilde{\alpha }(t-\xi ,x)]\tilde{N}(d\xi ,dx){\parallel }^2\hfill \\ & & +4E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t+s_n,t+s_n-\xi )[\alpha (t+s_n-\xi ,x)-\tilde{\alpha }(t-\xi ,x)]\nu (dx){d\xi \parallel }^2\hfill \\ & & +4E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}[U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{\alpha }(t-\xi ,x)\tilde{N}(d\xi ,dx){\parallel }^2\hfill \\ & & +4E\parallel {\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}[U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{\alpha }(t-\xi ,x)\nu (dx){d\xi \parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0}(2+\frac{b}{\delta })e^{-2\delta (k-1)}{\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (\xi -k+1){\parallel \alpha (t+s_n-\xi ,x)-\tilde{\alpha }(t-\xi ,x)\parallel }^2\nu (dx)d\xi \hfill \\ & & +4(1+b){\int }_{k-1}^k{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{\parallel [U(t+s_n,t+s_n-\xi )-\tilde{U}(t,t-\xi )]\tilde{\alpha }(t-\xi ,x)\parallel }^2\nu (dx)d\xi \hfill \end{array}$$

Now, by the Lebesgue dominated convergence theorem and $(10)$, $(16)$, we have

$$\parallel S_k(t+s_n)-\widetilde{S_k}(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Similarly, using $(11)$, $(17)$, we have

$$\parallel \widetilde{S_k}(t-s_n)-S_k(t){\parallel }^2\to 0,\mathrm{as}n\to \infty$$

Thus, each $S_k\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$ for each k. Hence, $S(t)\in AA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H})$. Next, we prove $O_k\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Thus,

$$\begin{array}{ccc}\hfill E\parallel O_k{(t)\parallel }^2& =& E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,\sigma )\beta (\sigma ,x)N(d\sigma ,dx)\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,\sigma )\beta (\sigma ,x)\tilde{N}{(d\sigma ,dx)\parallel }^2\hfill \\ & & +2E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,\sigma )\beta (\sigma ,x)\nu (dx)d\sigma \parallel }^2\hfill \\ & \le & \frac{M^2}{m_0}(2+\frac{b}{\delta })e^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (\sigma -t+k){\parallel \beta (\sigma ,x)\parallel }^2\nu (dx)d\sigma \hfill \end{array}$$

Thus, for any $T>0$,

$$\begin{array}{ccc}& & \frac{1}{2T}{\int }_{-T}^T{\parallel O_k(t)\parallel }^{2}dt\hfill \\ & \le & \frac{M^2}{2T{m}_0}(2+\frac{b}{\delta })e^{-2\delta (k-1)}{\int }_{-T}^T{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (\sigma -t+k){\parallel \beta (\sigma ,x)\parallel }^2\nu (dx)d\sigma dt\hfill \end{array}$$

Since ${\beta }^b\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, then

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel O_k(t)\parallel }^{2}dt=0$$

that is, $O_k\in PA{P}_0(\mathbb{R}\times ,{\mathcal{L}}^2(P,\mathbb{H}))$. Furthermore,

$$O(t):={\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,\sigma )\beta (\sigma ,x)N(d\sigma ,dx)=\sum _{k=1}^{\infty }{O}_k(t)$$

$O(t)\in C(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, then

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\parallel O(t)\parallel }^{2}dt=0$$

Consequently, the uniform limit $O(t)\in PA{P}_0(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. Thus, ${\Lambda }_{4}Y(t)=S(t)+O(t)\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. □

Theorem 5.

Supposing that the assumptions $(Hf,Hg,HF,HG,HU)$ hold, then Equation (9) has at least one PAA solution in distribution, if

$$K:=\frac{4M^{2}L{\gamma }_0}{m_0}(\frac{1}{\delta }+2)\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<1$$

Proof. 

For any $Y(t)\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$, define $\Phi$

$$\begin{array}{ccc}\hfill \Phi Y(t)& :=& {\int }_{-\infty }^{t}U(t,s)f(s,Y(s))ds+{\int }_{-\infty }^{t}U(t,s)g(s,Y(s))dW(s)\hfill \\ & & +{\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx)\hfill \\ & =& {\Lambda }_{1}Y(t)+{\Lambda }_{2}Y(t)+{\Lambda }_{3}Y(t)+{\Lambda }_{4}Y(t)\hfill \end{array}$$

for each $t\in \mathbb{R}$. By virtue of Lemma 1–4, we deduce that $\Phi :PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\mapsto PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ is continuous and well-defined.

Next, we shall use the Krasnoselskii–Schaefer-type fixed point theorem [35] to verify the existence of solutions. Consider the space $\mathbb{B}:=\{Y(t)\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))\}$ that is the operator: $\Phi :\mathbb{B}\mapsto \mathbb{B}$. Now, we decompose $\Phi$ as ${\Phi }_1+{\Phi }_2$ where

$${\Phi }_{1}Y(t)={\int }_{-\infty }^{t}U(t,s)f(s,Y(s))ds+{\int }_{-\infty }^{t}U(t,s)g(s,Y(s))dW(s),t\in \mathbb{R}$$

$$\begin{array}{ccc}\hfill {\Phi }_{2}Y(t)& =& {\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{-\infty }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx),t\in \mathbb{R}\hfill \end{array}$$

In order to obtain the main results, we will verify that ${\Phi }_1$ is a contraction and ${\Phi }_2$ is a complete operator. For better readability, we prove it step by step.

Step 1: ${\Phi }_1$ is a contraction on $\mathbb{B}$. Consider for each $k=1,2,...,$ the integral

$${\Phi }_{1k}Y(t)={\int }_{t-k}^{t-k+1}U(t,s)f(s,Y(s))ds+{\int }_{t-k}^{t-k+1}U(t,s)g(s,Y(s))dW(s)$$

Since $\chi =\zeta +\xi \in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H},{\mathcal{L}}^2(P,\mathbb{H}))$ (where $\chi =f$ or g), and $\chi$ satisfies $\left[H\chi \right]$, for all $u,v\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H},\gamma ds)$ and $t\in \mathbb{R}$, we have

$$\begin{array}{cc}\hfill & {\int }_{t-k}^{t-k+1}{\gamma (s-t+k)\parallel \chi (s,u)-\chi (s,v)\parallel }^{2}ds\le 2{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel \zeta (s,u)-\zeta (s,v)\parallel }^{2}ds\hfill \\ \hfill & +2{\int }_{t-k}^{t-k+1}{\gamma (s-t+k)\parallel \xi (s,u)-\xi (s,v)\parallel }^{2}ds\le 4L{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel u-v\parallel }^{2}ds\hfill \end{array}$$

(18)

Let $t\in \mathbb{R}$, $Y_1,Y_2\in \mathbb{B}$. From Itô’s isometry, Cauchy–Schwarz inequality, and (18), we have

$$\begin{array}{ccc}& & E\parallel {\Phi }_{1k}{Y}_1(t)-{\Phi }_{1k}{Y}_2{(t)\parallel }^2\hfill \\ & =& E\parallel {\int }_{t-k}^{t-k+1}U(t,s)[f(s,Y_1(s))-f(s,Y_2(s))]ds\hfill \\ & & +{\int }_{t-k}^{t-k+1}U(t,s)[g(s,Y_1(s))-g(s,Y_2(s))]{dW(s)\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{t-k}^{t-k+1}U(t,s)[f(s,Y_1(s))-f(s,Y_2(s))]{ds\parallel }^2\hfill \\ & & +2E\parallel {\int }_{t-k}^{t-k+1}U(t,s)[g(s,Y_1(s))-g(s,Y_2(s))]{dW(s)\parallel }^2\hfill \\ & \le & \frac{M^2}{m_0\delta }{e}^{-2\delta (k-1)}\parallel {\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel f(s,Y_1(s))-f(s,Y_2(s))\parallel }^{2}ds\hfill \\ & & +\frac{2M^2}{m_0}{e}^{-2\delta (k-1)}\parallel {\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel g(s,Y_1(s))-g(s,Y_2(s))\parallel }^{2}ds\hfill \\ & \le & \frac{4M^{2}L}{m_0}(\frac{1}{\delta }+2)e^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel Y_1(s)-Y_2(s)\parallel }^{2}ds\hfill \\ & \le & K^{\prime }{e}^{-2\delta (k-1)}{\parallel Y_1(\sigma )-Y_2(\sigma )\parallel }^2,\sigma \in [t-k,t-k+1]\hfill \end{array}$$

where $K^{\prime }=\frac{4M^{2}L{\gamma }_0}{m_0}(\frac{1}{\delta }+2)$. Using the Cauchy–Schwarz inequality and the mean value theorem of integrals, it follows that

$$\begin{array}{ccc}\hfill E\parallel {\Phi }_1{Y}_1(t)-{\Phi }_1{Y}_2{(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }\frac{1}{k}·k[{\Phi }_{1k}{Y}_1(t)-{\Phi }_{1k}{Y}_2(t)]{\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel {\Phi }_{1k}{Y}_1(t)-{\Phi }_{1k}{Y}_2(t){\parallel }^2\}\hfill \\ & \le & K^{\prime }\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^2{e}^{-2\delta (k-1)}\parallel Y_1(\sigma )-Y_2(\sigma ){\parallel }^2\}\hfill \\ & \le & K\parallel Y_1(\epsilon )-Y_2{(\epsilon )\parallel }^2,\epsilon \in \mathbb{R}\hfill \end{array}$$

where $K<1$. Thus, ${\Phi }_1$ is a contraction on $\mathbb{B}$.

Step 2: ${\Phi }_2:\mathbb{B}\mapsto \mathbb{B}$ is continuous. For each $k=1,2,...$, the integral

$$\begin{array}{ccc}\hfill {\Phi }_{2k}Y(t)& =& {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx)\hfill \end{array}$$

Since ${\rm Y}=\Sigma +\Delta \in PA{A}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ (where ${\rm Y}=F$ or G), and ${\rm Y}$ satisfies $[H{\rm Y}]$, for all $u,v\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H},\gamma ds)$ and $t\in \mathbb{R}$, it follows that

$$\begin{array}{cc}\hfill & {\int }_{t-k}^{t-k+1}{\int }_{\mathbb{V}}\gamma (s-t+k){\parallel {\rm Y}(s,u,x)-{\rm Y}(s,v,x)\parallel }^2\nu (dx)ds\hfill \\ \hfill & \le 2{\int }_{t-k}^{t-k+1}{\int }_{\mathbb{V}}\gamma (s-t+k){\parallel \Sigma (s,u,x)-\Sigma (s,v,x)\parallel }^2\nu (dx)ds\hfill \\ \hfill & +2{\int }_{t-k}^{t-k+1}{\int }_{\mathbb{V}}\gamma (s-t+k){\parallel \Delta (s,u,x)-\Delta (s,v,x)\parallel }^2\nu (dx)ds\hfill \\ \hfill & \le 4L{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel u-v\parallel }^{2}ds\hfill \end{array}$$

(19)

Let $\left\{Y^{(n)}\right\}$ with $Y^{(n)}\to Y(\mathrm{as}n\to \infty )$ in $\mathbb{B}$. From Itô’s isometry, Cauchy–Schwarz inequality, and (19), we have

$$\begin{array}{ccc}& & E\parallel {\Phi }_{2k}{Y}^{(n)}(t)-{\Phi }_{2k}{Y(t)\parallel }^2\hfill \\ & =& E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)[F(s,Y^{(n)}(s-),x)-F(s,Y(s-),x)]\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)[G(s,Y^{(n)}(s-),x)-G(s,Y(s-),x)]{N(ds,dx)\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)[F(s,Y^{(n)}(s-),x)-F(s,Y(s-),x)]\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)[G(s,Y^{(n)}(s-),x)-G(s,Y(s-),x)]\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)[G(s,Y^{(n)}(s-),x)-G(s,Y(s-),x)]{\nu (dx)ds\parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (s-t+k){\parallel F(s,Y^{(n)}(s-),x)-F(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +\frac{4M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (s-t+k){\parallel G(s,Y^{(n)}(s-),x)-G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +\frac{2M^{2}b}{m_0\delta }{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (s-t+k){\parallel G(s,Y^{(n)}(s-),x)-G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & \frac{8M^{2}L}{m_0}(3+\frac{b}{\delta })e^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel Y^{(n)}(s-)-Y(s-)\parallel }^{2}ds\hfill \end{array}$$

Thus,

$$\parallel {\Phi }_{2k}{Y}^{(n)}(t)-{\Phi }_{2k}{Y(t)\parallel }^2\to 0,\mathrm{as}{Y}^{(n)}\to Y(\mathrm{as}n\to \infty )$$

Then,

$$\begin{array}{ccc}\hfill E\parallel {\Phi }_2{Y}^{(}n{)(t)-{\Phi }_{2}Y(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }\frac{1}{k}·k[{\Phi }_{2k}{Y}^{(n)}(t)-{\Phi }_{2k}Y(t)]{\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel {\Phi }_{2k}{Y}^{(}n)(t)-{\Phi }_{2k}Y(t){\parallel }^2\}\hfill \end{array}$$

Then,

$$\parallel {\Phi }_2{Y}^{(n)}(t)-{\Phi }_2{Y(t)\parallel }^2\to 0,\mathrm{as}{Y}^{(n)}\to Y(\mathrm{as}n\to \infty )$$

Thus, ${\Phi }_2:\mathbb{B}\mapsto \mathbb{B}$ is continuous.

Step 3: ${\Phi }_2$ maps bounded sets into bounded sets in $\mathbb{B}$. By the formula (19), we can obtain

$$\begin{array}{cc}\hfill & {\int }_{t-k}^{t-k+1}{\int }_{\mathbb{V}}\gamma (s-t+k){\parallel {\rm Y}(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ \hfill & \le 2{\int }_{t-k}^{t-k+1}{\int }_{\mathbb{V}}\gamma (s-t+k){\parallel {\rm Y}(s,Y(s-),x)-{\rm Y}(s,0,x)\parallel }^2\nu (dx)ds\hfill \\ \hfill & +2{\int }_{t-k}^{t-k+1}{\int }_{\mathbb{V}}\gamma (s-t+k){\parallel {\rm Y}(s,0,x)\parallel }^2\nu (dx)ds\hfill \\ \hfill & \le {8L\parallel Y\parallel }_{{\mathbb{S}}_{\gamma }^2}^2+2K_{{\rm Y}}\hfill \end{array}$$

(20)

Let ${\mathbb{B}}_r:={\{Y(t):\parallel Y(t)\parallel }^2\le r,Y(t)\in \mathbb{B}\}$. For each $Y(t)\in {\mathbb{B}}_r$, by Itô’s isometry, Cauchy–Schwarz inequality, and (20), we have

$$\begin{array}{ccc}& & E\parallel {\Phi }_{2k}{Y(t)\parallel }^2\hfill \\ & =& E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,s)G(s,Y(s-),x)N(ds,dx)\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,s)G(s,Y(s-),x)\nu (dx)ds\parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (s-t+k){\parallel F(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +\frac{2M^2}{m_0}(2+\frac{b}{\delta })e^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (s-t+k){\parallel G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & \{C_1(M,L,m_0,b,\delta ){\parallel Y\parallel }_{{\mathbb{S}}_{\gamma }^2}^2+C_2(M,L,m_0,b,\delta ,K_F,K_G)\}{e}^{-2\delta (k-1)}\hfill \end{array}$$

Then, there exists a uniformly constant $M^{*}$ (not about k), such that

$$\begin{array}{ccc}\hfill E\parallel {\Phi }_2{Y(t)\parallel }^2& =& E\parallel \sum _{k=1}^{\infty }\frac{1}{k}·k{\Phi }_{2k}{Y(t)\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel {\Phi }_{2k}Y(t){\parallel }^2\}\hfill \\ & \le & M^{*}\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<\infty \hfill \end{array}$$

Step 4: ${\Phi }_2$ maps bounded sets into equicontinuous sets of $\mathbb{B}$. For each $Y\in {\mathbb{B}}_r,t_2\ge t_1\in \mathbb{R}$, by the Itô’s isometry, Cauchy–Schwarz inequality, we have

$$\begin{array}{ccc}& & E\parallel {\Phi }_{2}Y(t_2)-{\Phi }_{2}Y(t_1){\parallel }^2\hfill \\ & =& E\parallel {\int }_{-\infty }^{t_1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}[U(t_1,s)-U(t_2,s)]F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t_2,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{-\infty }^{t_1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}[U(t_1,s)-U(t_2,s)]G(s,Y(s-),x)N(ds,dx)\hfill \\ & & +{\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t_2,s)G(s,Y(s-),x)N(ds,dx){\parallel }^2\hfill \\ & \le & {3E\parallel \Theta \parallel }^2+3E{\parallel {\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t_2,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\parallel }^2\hfill \\ & & +6E\parallel {\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t_2,s)G(s,Y(s-),x)\tilde{N}(ds,dx){\parallel }^2\hfill \\ & & +6E\parallel {\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t_2,s)G(s,Y(s-),x)\nu (dx){ds\parallel }^2\hfill \\ & \le & 3\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel {\Theta }_k{\parallel }^2\}\hfill \\ & & +\frac{3M^2}{m_0}{\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (s-t_1){\parallel F(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +\frac{3M^2}{m_0}(2+\frac{b}{\delta }){\int }_{t_1}^{t_2}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (s-t_1){\parallel G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill \Theta & =& {\int }_{-\infty }^{t_1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}[U(t_1,s)-U(t_2,s)]F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{-\infty }^{t_1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}[U(t_1,s)-U(t_2,s)]G(s,Y(s-),x)N(ds,dx)\hfill \\ & =& \sum _{k=1}^{\infty }{\Theta }_k\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\Theta }_k& =& {\int }_{t_1-k}^{t_1-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}[U(t_1,s)-U(t_2,s)]F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t_1-k}^{t_1-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}[U(t_1,s)-U(t_2,s)]G(s,Y(s-),x)N(ds,dx)\hfill \end{array}$$

By Itô’s isometry, Cauchy–Schwarz inequality, we have

$$\begin{array}{ccc}& & E\parallel {\Theta }_k{\parallel }^2\hfill \\ & \le & 2E{\int }_{t_1-k}^{t_1-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}{\parallel [U(t_1,s)-U(t_2,s)]F(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +4E{\int }_{t_1-k}^{t_1-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{\parallel [U(t_1,s)-U(t_2,s)]G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +4bE{\int }_{t_1-k}^{t_1-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{\parallel [U(t_1,s)-U(t_2,s)]G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \end{array}$$

Since $U(t,s)$ is strongly continuous, so $\parallel U(t_1,s)-U(t_2,s){\parallel }^2\to 0$, as $t_1\to t_2$, then $\parallel {\Theta }_k{\parallel }^2\to 0$. Hence, $\parallel {\Phi }_{2}Y(t_2)-{\Phi }_{2}Y(t_1){\parallel }^2\to 0$, as $t_1\to t_2$. Thus, ${\Phi }_2$ maps bounded sets into equicontinuous sets of $\mathbb{B}$.

Step 5: ${\Phi }_2$ maps bounded sets into a relatively compact set in $\mathbb{B}$. Define an operator ${\Phi }_2^{\epsilon }$ on ${\mathbb{B}}_r$ by

$$\begin{array}{ccc}\hfill {\Phi }_2^{\epsilon }Y(t)& :=& {\int }_{-\infty }^{t-\epsilon }{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{-\infty }^{t-\epsilon }{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx)\hfill \end{array}$$

For each $Y(t)\in {\mathbb{B}}_r$, it follows that

$$\begin{array}{ccc}& & E\parallel {\Phi }_{2}Y(t)-{\Phi }_2^{\epsilon }{Y(t)\parallel }^2\hfill \\ & =& E\parallel {\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,s)G(s,Y(s-),x)N(ds,dx)\parallel }^2\hfill \\ & \le & 2E\parallel {\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,s)G(s,Y(s-),x)\nu (dx)ds\parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0}{\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (s-t+\epsilon ){\parallel F(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +\frac{2M^2}{m_0}(2+\frac{b}{\delta }){\int }_{t-\epsilon }^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (s-t+\epsilon ){\parallel G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \end{array}$$

Then,

$$\parallel {\Phi }_{2}Y(t)-{\Phi }_2^{\epsilon }{Y(t)\parallel }^2\to 0,\mathrm{as}\epsilon \to 0$$

Thus, ${\Phi }_2$ maps bounded sets into a relatively compact set in $\mathbb{B}$.

Step 6: We shall show that the set

$$G=\{Y\in \mathbb{B}:\lambda {\Phi }_1(\frac{Y}{\lambda })+\lambda {\Phi }_2(Y)=Y,\mathrm{for}\mathrm{some}\lambda \in (0,1)\}$$

is bounded on $t\in \mathbb{R}$. To do this, from [35], consider the following equation:

$$Y(t)=\lambda \Phi Y(t),0<\lambda <1$$

Next, we give a priori estimate. By the formula (18), we can obtain

$$\begin{array}{cc}\hfill {\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel \chi (s,Y(s))\parallel }^{2}ds& \le 2{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel \chi (s,Y(s))-\chi (s,0)\parallel }^{2}ds\hfill \\ \hfill & +2{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel \chi (s,0)\parallel }^{2}ds\hfill \\ \hfill & \le {8L\parallel Y\parallel }_{{\mathbb{S}}_{\gamma }^2}^2+2K_{\chi }\hfill \end{array}$$

(21)

Thus,

$$\begin{array}{ccc}& & E\parallel {\Phi }_k{Y(t)\parallel }^2\hfill \\ & =& E\parallel {\int }_{t-k}^{t-k+1}U(t,s)f(s,Y(s))ds+{\int }_{t-k}^{t-k+1}U(t,s)g(s,Y(s))dW(s)\hfill \\ & & +{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,s)G(s,Y(s-),x)N(ds,dx)\parallel }^2\hfill \\ & \le & 4E\parallel {\int }_{t-k}^{t-k+1}{U(t,s)f(s,Y(s))ds\parallel }^2+4E{\parallel {\int }_{t-k}^{t-k+1}U(t,s)g(s,Y(s))dW(s)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +8E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +8E\parallel {\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}{U(t,s)G(s,Y(s-),x)\nu (dx)ds\parallel }^2\hfill \\ & \le & \frac{2M^2}{m_0\delta }{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel f(s,Y(s))\parallel }^{2}ds\hfill \\ & & +\frac{4M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}\gamma (s-t+k){\parallel g(s,Y(s))\parallel }^{2}ds\hfill \\ & & +\frac{4M^2}{m_0}{e}^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}\gamma (s-t+k){\parallel F(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & & +\frac{4M^2}{m_0}(2+\frac{b}{\delta })e^{-2\delta (k-1)}{\int }_{t-k}^{t-k+1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}\gamma (s-t+k){\parallel G(s,Y(s-),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & \{C_1(M,L,m_0,b,\delta ){\parallel Y\parallel }_{{\mathbb{S}}_{\gamma }^2}^2+C_2(M,L,m_0,b,\delta ,K_f,K_g,K_F,K_G)\}{e}^{-2\delta (k-1)}\hfill \end{array}$$

Then, there exists a uniformly constant $M^{*}$ (not about k), such that

$$\begin{array}{ccc}\hfill {E\parallel Y(t)\parallel }^2& \le & {E\parallel \Phi Y(t)\parallel }^2\hfill \\ & \le & \sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\{k^{2}E\parallel {\Phi }_{k}Y(t){\parallel }^2\}\hfill \\ & \le & M^{*}\sum _{k=1}^{\infty }\frac{1}{k^2}·\sum _{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<\infty \hfill \end{array}$$

Thus, this implies that G is bounded. Consequently, by the Krasnoselskii–Schaefer-type fixed point theorem, $\Phi$ has a fixed point $Y\in PAA(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$. From Remark 5 and the similar approach in ([6], Theorem 4.1), Y is necessarily pseudo almost automorphy in distribution. □

4. Optimal Control Results

Let $\mathbb{K}$ be a reflexive Banach space and the control u is $\mathbb{K}$-valued. The multi-valued map $\mathcal{U}:[0,T]\rightrightarrows 2^{\mathbb{K}}\setminus \varnothing$ is graph measurable, and $\mathcal{U}(·)\subseteq \Omega$ is a bounded set in $\mathbb{K}$ and has bounded, closed, and convex values. Let the admissible set $U_{ad}:=\{u(·)\in L^2(\Omega ):u(t)\in \mathcal{U}(t),a.e.\}$. Obviously, $U_{ad}\ne 0$, and $U_{ad}\subset L^2([0,T],\mathbb{K})$ is bounded, closed, and convex. For the stochastic controlled systems:

$$\begin{array}{cc}\hfill dY(t)& =A(t)Y(t)dt+f(t,Y(t))dt+B(t)u(t)dt+g(t,Y(t))dW(t)\hfill \\ \hfill & +{\int }_{{\left|x\right|}_{\mathbb{V}}<1}F(t,Y(t-),x)\tilde{N}(dt,dx)\hfill \\ \hfill & +{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}G(t,Y(t-),x)N(dt,dx),t\in [0,T]\hfill \end{array}$$

(22)

By Definition 21, for each $u\in U_{ad}$, the solution of the Equation (22) is in the following sense:

$$\begin{array}{ccc}\hfill Y(t)& =& {\int }_0^{t}U(t,s)f(s,Y(s))ds+{\int }_0^{t}U(t,s)B(s)u(s)ds+{\int }_0^{t}U(t,s)g(s,Y(s))dW(s)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y(s-),x)N(ds,dx),t\in [0,T]\hfill \end{array}$$

Let $Y^u$ denote the mild solution of Equation (22). Next, the following problem will be investigated:

Problem 1.

$(P)$ Find an optimal pair $(Y^0,u^0)\in \mathbb{B}\times U_{ad}$ such that $\mathcal{J}(Y^0,u^0)\le \mathcal{J}(Y^u,u),\mathrm{for}\mathrm{all}u\in U_{ad}$ where

$$\mathcal{J}(Y^u,u)=E{\int }_0^{T}L(t,Y^u(t),u(t))dt$$

In order to study the Problem 1, the following hypotheses are needed: $\left[HL\right]$

(i)

The function $L:[0,T]\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{K}\mapsto \mathbb{R}\cup \{\infty \}$ is Borel measurable;

(ii)

For almost all $t\in [0,T]$, $L(t,·,·)$ is sequentially lower semicontinuous on ${\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{K}$;

(iii)

For almost all $t\in [0,T]$, $L(t,Y,·)$ is convex on $\mathbb{K}$ for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$;

(iv)

There exists $a\ge 0$, $b>0$, c is nonegative and $c\in L^1([0,T],\mathbb{R})$ such that

$$L(t,Y,u)\ge c(t)+{a\parallel Y\parallel }_{{\mathcal{L}}^2(P,\mathbb{H})}+b{\parallel u\parallel }_{\mathbb{K}}^2$$

Theorem 6.

Equation (22) has an optimal control pair, if the hypotheses $(HL)$ and Theorem 5 hold; meanwhile, B is a strongly continuous operator.

Proof. 

Next, we shall minimize the cost function $\mathcal{J}(Y,u)$. In particular, the results are obvious if $inf\left\{\mathcal{J}(Y,u)\right|u\in U_{ad}\}=+\infty$. Then, assume that $inf\left\{\mathcal{J}(Y,u)\right|u\in U_{ad}\}=\kappa <+\infty$, using the hypothesis $(HL(iv))$, we can obtain $\kappa >-\infty$.

Then, there exists a minimizing sequence of feasible pair $\left\{(Y^n,u^n)\right\}\subset A_{ad}$ by infimum, (where $A_{ad}=\left\{(Y,u)\right|Y$ is a solution of Equation (22) corresponding to $u\in U_{ad}\}$), such that $\mathcal{J}(Y^n,u^n)\to \kappa$ as $n\to +\infty$. Suppose $U_{ad}$ is a bounded subset of the separable reflexive Banach space $L^2([0,T],\mathbb{K})$ then $\left\{u^n\right\}\subseteq U_{ad}$, there exists a subsequence $u^n$ and $u^0\in L^2([0,T],\mathbb{K})$ such that $u^n\stackrel{w}{\to }{u}^0$. Furthermore, by Marzur lemma, $u^0\in U_{ad}$ and $U_{ad}$ is also closed and convex.

Assume that $Y^n$ is the mild solution of Equation (22) corresponding to $u^n$ and

$$\begin{array}{ccc}\hfill Y^n(t)& =& {\int }_0^{t}U(t,s)f(s,Y^n(s))ds+{\int }_0^{t}U(t,s)B(s)u^n(s)ds+{\int }_0^{t}U(t,s)g(s,Y^n(s))dW(s)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y^n(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y^n(s-),x)N(ds,dx),t\in [0,T]\hfill \end{array}$$

Similarly,

$$\begin{array}{ccc}\hfill Y^0(t)& =& {\int }_0^{t}U(t,s)f(s,Y^0(s))ds+{\int }_0^{t}U(t,s)B(s)u^0(s)ds+{\int }_0^{t}U(t,s)g(s,Y^0(s))dW(s)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)F(s,Y^0(s-),x)\tilde{N}(ds,dx)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)G(s,Y^0(s-),x)N(ds,dx),t\in [0,T]\hfill \end{array}$$

Using the Cauchy–Schwarz inequality and the Itô’s isometry, we have

$$\begin{array}{ccc}\hfill {E\parallel \Pi \parallel }^2& =& E\parallel {\int }_{t-k}^{t-k-1}U(t,s)[f(s,Y^n(s))-f(s,Y^0(s))]ds\hfill \\ & & +{\int }_{t-k}^{t-k-1}U(t,s)[g(s,Y^n(s))-g(s,Y^n(s))]dW(s)\hfill \\ & & +{\int }_{t-k}^{t-k-1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)[F(s,Y^n(s-),x)-F(s,Y^n(s-),x)]\tilde{N}(ds,dx)\hfill \\ & & +{\int }_{t-k}^{t-k-1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)[G(s,Y^n(s-),x)-G(s,Y^n(s-),x)]{N(ds,dx)\parallel }^2\hfill \\ & \le & 4E\parallel {\int }_{t-k}^{t-k-1}U(t,s)[f(s,Y^n(s))-f(s,Y^0(s))]{ds\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k-1}U(t,s)[g(s,Y^n(s))-g(s,Y^n(s))]{dW(s)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k-1}{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)[F(s,Y^n(s-),x)-F(s,Y^n(s-),x)]\tilde{N}{(ds,dx)\parallel }^2\hfill \\ & & +4E\parallel {\int }_{t-k}^{t-k-1}{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)[G(s,Y^n(s-),x)-G(s,Y^n(s-),x)]{N(ds,dx)\parallel }^2\hfill \\ & \le & C(M,L,m_0,\delta ,{\gamma }_0)e^{-2\delta (k-1)}{\parallel Y^n(\sigma )-Y^0(\sigma )\parallel }^2,\sigma \in [t-k,t-k+1]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill E\parallel {\int }_0^{t}U(t,s)B(s)[u^n(s)-u^0(s)]{ds\parallel }^2& \le & {\int }_0^t{\parallel U(t,s)\parallel }^{2}ds·{\int }_0^t{\parallel B(s)[u^n(s)-u^0(s)]\parallel }^{2}ds\hfill \\ & \le & M^{2}T{\int }_0^t{\parallel B(s)[u^n(s)-u^0(s)]\parallel }^{2}ds\hfill \end{array}$$

Thus,

$$\begin{array}{ccc}& & E\parallel Y^n(t)-Y^0{(t)\parallel }^2\hfill \\ & =& E\parallel {\int }_0^{t}U(t,s)[f(s,Y^n(s))-f(s,Y^0(s))]ds\hfill \\ & & +{\int }_0^{t}U(t,s)B(s)[u^n(s)-u^0(s)]ds\hfill \\ & & +{\int }_0^{t}U(t,s)[g(s,Y^n(s))-g(s,Y^n(s))]dW(s)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}<1}U(t,s)[F(s,Y^n(s-),x)-F(s,Y^n(s-),x)]\tilde{N}(ds,dx)\hfill \\ & & +{\int }_0^t{\int }_{{\left|x\right|}_{\mathbb{V}}\ge 1}U(t,s)[G(s,Y^n(s-),x)-G(s,Y^n(s-),x)]{N(ds,dx)\parallel }^2\hfill \\ & \le & 2E\parallel \sum _{k=1}^{\lceil T\rceil }{\Pi }_k{\parallel }^2+2E{\parallel {\int }_0^{t}U(t,s)B(s)[u^n(s)-u^0(s)]ds\parallel }^2\hfill \\ & \le & C(M,L,m_0,\delta ,{\gamma }_0)\sum _{k=1}^{\lceil T\rceil }\frac{1}{k^2}·\sum _{k=1}^{\lceil T\rceil }\{k^2{e}^{-2\delta (k-1)}\parallel Y^n(\sigma )-Y^0(\sigma ){\parallel }^2\}\hfill \\ & & +M^{2}T{\int }_0^t{\parallel B(s)[u^n(s)-u^0(s)]\parallel }^{2}ds\hfill \\ & \le & C_1\parallel Y^n(t)-Y^0{(t)\parallel }^2+C_2{\parallel B(s)[u^n(t)-u^0(t)]\parallel }_{L^2([0,T],\mathbb{K})}^2\hfill \end{array}$$

There exists $M^{*}$ such that

$$E\parallel Y^n(t)-Y^0{(t)\parallel }^2\le M^{*}{\parallel B(t)[u^n(t)-u^0(t)]\parallel }_{L^2([0,T],\mathbb{K})}^2$$

It is easy to obtain $\parallel B(t)[u^n(t)-u^0(t)]{\parallel }_{L^2([0,T],\mathbb{K})}^2\to 0$ as $n\to 0$ from B is strongly continuous. Then,

$$E\parallel Y^n(t)-Y^0{(t)\parallel }^2\to 0\mathrm{as}n\to 0$$

We obtain that $\mathcal{J}(Y,u)$ is sequentially lower semicontinuous in $L^1([0,T],\mathbb{K})$ by Balder’s theorem [36]. Hence, $\mathcal{J}(Y,u)$ is weakly lower semicontinuous in $L^2([0,T],\mathbb{K})$. Since $(HL(iv))$, $\kappa >-\infty$, $\mathcal{J}$ obtains its infimum at $u^0\in U_{ad}$, that is,

$$\kappa =\underset{n\to \infty }{lim}{\int }_0^{T}L(t,Y^n(t),u^n(t))dt\ge {\int }_0^{T}L(t,Y^0(t),u^0(t))dt=\kappa$$

Thus, it completes the proof. □

Remark 8.

Here, it should be noted that the developed result above can be potentially applicable to other problems including epidemic spreading problems; for more details, please refer to the work [37].

5. An Example

In this part, we consider the stochastic heat equation in the following, for more details, please refer to the work [13] and, for some relevant background about the stochastic heat equation, please refer to [23,38],

$$\left\{\begin{array}{cc}\hfill \frac{\partial y}{\partial t}(t,\xi )& =\frac{{\partial }^{2}y}{\partial {\xi }^2}(t,\xi )+y(t,\xi )sin\frac{1}{2+sint+sin\pi t}+\frac{(sin\sqrt{2}t+cos\sqrt{3}t)y(t,\xi )}{6(y^2(t,\xi )+1)}\hfill \\ \hfill & +\frac{sin\sqrt{2}t·y(t,\xi )}{3(cos\sqrt{3}t+2)}\frac{\partial W}{\partial t}(t,\xi )+\frac{cos\sqrt{2}tsinu(t,\xi )}{4(Z^2(t,\xi )+1)}\frac{\partial Z}{\partial t}(t,\xi ),t\in \mathbb{R},\xi \in (0,1)\hfill \\ \hfill & :=A(t)y+f(t,y)+g(t,y)\frac{\partial W}{\partial t}+h(t,y,Z)\frac{\partial Z}{\partial t}\hfill \\ \hfill y(t,0)& =y(t,1)=0,t\in \mathbb{R}\hfill \end{array}\right.$$

(23)

where Z is a Lévy pure jump process on $L^2(0,1)$, and W is a Q-Wiener process on $L^2(0,1)$ with $TrQ<\infty$. From [13], we have

Let $A_1$ be the Laplace operator, and

$$\begin{array}{ccc}\hfill D(A_1)& =& \{\tau \in C^1[0,1]|{\tau }^{\prime }(s)\mathrm{is}\mathrm{absolutely}\mathrm{continuous}\mathrm{on}[0,1],\hfill \\ & & {\tau }^{\prime }(s)\in L^2(0,1),\tau (0)=\tau (1)=0\}\hfill \end{array}$$

$A_1$ generates a $C_0$-semigroup ${(T(t))}_{t\ge 0}$ on $L^2(0,1)$, which is

$$(T(t)\tau )(s)=\sum _{n=1}^{\infty }{e}^{-n^2{\pi }^{2}t}(\tau ,e_n)e_n(s)$$

where $(·,·)$ denotes the inner product on $L^2(0,1)$, $e_n(s)=\sqrt{2}sin(n\pi s),n=1,2,...$, and $\parallel T(t)\parallel \le e^{-{\pi }^{2}t}$ for $t\ge 0$. Then,

$$\begin{array}{ccc}& & D(A(t))=D(A_1),t\in \mathbb{R}\hfill \\ & & A(t)\tau =(A_1+sin\frac{1}{2+sint+sin\pi t})\tau ,\tau \in D(A(t))\hfill \end{array}$$

$A{(t)}_{t\in \mathbb{R}}$ generates an evolution family ${\left\{U(t,s)\right\}}_{t\ge s}$ such that

$$U(t,s)\tau =T(t-s)e^{{\int }_s^{t}sin\frac{1}{2+sin\theta +sin\pi \theta }d\theta }\tau ,\tau \in {\mathcal{L}}^2(P,L^2(0,1))$$

Denote $\mathbb{H}=\mathbb{V}=L^2(0,1)$, Equation (20) listed as the abstract form

$$dY=A(t)Ydt+F(t,Y)dt+G(t,Y)dW+{\int }_{\mathbb{V}<1}H(t,Y,z)\tilde{N}(dt,dz)+{\int }_{\mathbb{V}\ge 1}H(t,Y,z)N(dt,dz)$$

where $Y:=y$, $F(t,Y):=f(t,y)$, $G(t,Y):=g(t,y)$

$$h(t,y,Z)dZ:={\int }_{\mathbb{V}<1}H(t,Y,z)\tilde{N}(dt,dz)+{\int }_{\mathbb{V}\ge 1}H(t,Y,z)N(dt,dz)$$

with

$$Z(t,\xi )={\int }_{\mathbb{V}<1}z\tilde{N}(t,dz)+{\int }_{\mathbb{V}\ge 1}zN(t,dz),H(t,Y,z)=h(t,y,z)z$$

Here, by $\parallel T(t)\parallel \le e^{-{\pi }^{2}t}$, we get $\parallel U(t,s)\parallel \le e^{-({\pi }^2-1)(t-s)},t\ge s$, i.e., $M=1,\delta ={\pi }^2-1$. By the almost automorphic property of $sin\frac{1}{2+sin\theta +sin\pi \theta }$ and

$$\begin{array}{ccc}\hfill U(t+s_n,s+s_n)\tau & =& T(t-s)e^{{\int }_{s+s_n}^{t+s_n}sin\frac{1}{2+sin\theta +sin\pi \theta }d\theta }\tau \hfill \\ & =& T(t-s)e^{{\int }_s^{t}sin\frac{1}{2+sin(\theta +s_n)+sin\pi (\theta +s_n)}d\theta }\tau ,\tau \in {\mathcal{L}}^2(P,\mathbb{H}),\hfill \end{array}$$

we get that $U(t,s)\tau \in bAA(\mathbb{T},{\mathcal{L}}^2(P,\mathbb{H}))$ uniformly for all $\tau$ in any bounded subset of ${\mathcal{L}}^2(P,\mathbb{H})$.

Choose $\gamma (t)=e^{-t}+1$; then, ${\gamma }_0=2-e^{-1}$, $m_0=1$, $K_F=K_G=K_H=0$. Note that F, G, H satisfy the new composition theorem, with constant $L=max\{\frac{1}{6^2},\frac{{\parallel Q\parallel }_{L(\mathbb{V},\mathbb{V})}}{6^2},\frac{\nu (B(0))}{8^2},\frac{b}{8^2}\}$. If L satisfies the inequality $\frac{4M^{2}L{\gamma }_0}{m_0}(\frac{1}{\delta }+1){\sum }_{k=1}^{\infty }\frac{1}{k^2}·{\sum }_{k=1}^{\infty }\left\{k^2{e}^{-2\delta (k-1)}\right\}<1$, then, by Theorem 5, the stochastic heat Equation (20) has a mild solution.

Taking into consideration the optimal control problem and defining $B(t)u(t)={\int }_{[0,1]}p(\xi ,\tau )u(t,\tau )d\tau ,\xi \in (0,1)$, we have

$$\begin{array}{ccc}\hfill dY& =& A(t)Ydt+F(t,Y)dt+B(t)u(t)dt+G(t,Y)dW\hfill \\ & & +{\int }_{\mathbb{V}<1}H(t,Y,z)\tilde{N}(dt,dz)+{\int }_{\mathbb{V}\ge 1}H(t,Y,z)N(dt,dz),t\in [0,T]\hfill \end{array}$$

$t\mapsto u(t,·)$ defined from $[0,T]$ into $\mathbb{K}$ is measurable from the fact that $u\in L^2([0,T]\times (0,1))$. Set $U_{ad}=\{u\in L^2([0,T]\times (0,1))$, such that ${\parallel u(t,·)\parallel }^2\le \sigma (t)a.e$, where $\sigma (t)\in L^2([0,T],{\mathbb{R}}^{+})$}. Consider the following cost function:

$$\mathcal{J}(Y^u,u)=E{\int }_0^{T}L(t,Y^u(t),u(t))dt$$

Here, $L:[0,T]\times C([0,T]\times (0,1))\times L^2([0,T]\times (0,1))\mapsto \mapsto \mathbb{R}\cup \{+\infty \}$

$$\begin{array}{ccc}\hfill L(t,Y^u(t),u(t))& =& {\int }_{[0,1]}{\int }_{-\infty }^0\parallel Y^u{(t+s,\xi )\parallel }^{2}dsd\xi +{\int }_{[0,1]}{\parallel Y^u(t,\xi )\parallel }^{2}d\xi \hfill \\ & & +{\int }_{[0,1]}{\parallel u(t,\xi )\parallel }_{\mathbb{K}}^{2}d\xi \hfill \end{array}$$

From [22], the hypotheses $(HL)$ stated in Section 4 are satisfied, and assumptions of Theorem 6; then, Theorem 6 holds. Thus, there exists an admissible control $u^0\in U_{ad}$ such that $\mathcal{J}(Y^0,u^0)\le \mathcal{J}(Y^u,u)$, for all $u\in U_{ad}$.

6. Conclusions

In this paper, we introduce the concept of Poisson ${\mathbb{S}}_{\gamma }^2$-PAA (or Poisson generalized Stepanov-like PAA) for stochastic processes, which generalizes the concept of Poisson Stepanov-like PAA in [6,15]. In addition, we provide some composition theorems of such stochastic processes, and then the existence of PAA solutions in distribution for some semilinear stochastic differential equations driven by Lévy noise by virtue of the Krasnoselskii–Schaefer type fixed point theorem is obtained, which is the main contribution throughout the paper. Finally, some sufficient conditions for ensuring the existence of optimal control pairs for stochastic differential equations driven by Lévy noise are established, which enriches our research. On the other hand, it is meaningful to generalize the Poisson ${\mathbb{S}}_{\gamma }^2$-pseudo almost automorphy into more general cases, for instance, Poisson ${\mathbb{S}}_{\gamma }^2$-weighted PAA or Poisson $\mu$-PAA, which will be the research in the future.

Appendix A.1. Proof of Theorem 2

Proof. 

Since $Y\in A{S}_{\gamma }^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}))$ and $F\in A{S}_{\gamma }^2(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$, for the functions $\tilde{Y}\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$, $\tilde{F}(·,Y,x)\in L_{loc}^2(\mathbb{R},{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$ and a subsequence ${(s_n)}_{n\in \mathbb{N}}$ such that

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t){\parallel Y(s+s_n)-\tilde{Y}(s)\parallel }^{2}ds\to 0\end{array}$$

(A1)

$$\begin{array}{c}\hfill {\int }_t^{t+1}\gamma (s-t){\parallel \tilde{Y}(s-s_n)-Y(s)\parallel }^{2}ds\to 0\end{array}$$

(A2)

for each $t\in \mathbb{R}$, as $n\to \infty$.

$$\begin{array}{c}\hfill {\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s+s_n,Y,x)-\tilde{F}(s,Y,x)\parallel }^2\nu (dx)ds\to 0\end{array}$$

(A3)

$$\begin{array}{c}\hfill {\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \tilde{F}(s-s_n,Y,x)-F(s,Y,x)\parallel }^2\nu (dx)ds\to 0\end{array}$$

(A4)

for each $Y\in {\mathcal{L}}^2(P,\mathbb{H})$, as $n\to \infty$ pointwise on $\mathbb{R}$.

Suppose $\tilde{D}(t,x)=\tilde{F}(t,\tilde{Y}(t),x)$. Then,

$$\begin{array}{ccc}& & D(s+s_n,x)-\tilde{D}(s,x)\hfill \\ & =& F(s+s_n,Y(s+s_n),x)-F(s+s_n,\tilde{Y}(s),x)+F(s+s_n,\tilde{Y}(s),x)-\tilde{F}(s,\tilde{Y}(s),x)\hfill \end{array}$$

Then, we can obtain

$$\begin{array}{ccc}& & {\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel D(s+s_n,x)-\tilde{D}(s,x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s+s_n,Y(s+s_n),x)-F(s+s_n,\tilde{Y}(s),x)\parallel }^2\nu (dx)ds\hfill \\ & & +2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s+s_n,\tilde{Y}(s),x)-\tilde{F}(s,\tilde{Y}(s),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 2L{\int }_t^{t+1}\gamma (s-t){\parallel Y(s+s_n)-\tilde{Y}(s)\parallel }^{2}ds\hfill \\ & & +2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s+s_n,\tilde{Y}(s),x)-\tilde{F}(s,\tilde{Y}(s),x)\parallel }^2\nu (dx)ds\hfill \end{array}$$

From (A1) and (A3), we have

$${\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel D(s+s_n,x)-\tilde{D}(s,x)\parallel }^2\nu (dx)ds\to 0$$

as $n\to \infty$ pointwise on $\mathbb{R}$. Similarly, from (A2) and (A4), we have

$${\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \tilde{D}(s-s_n,x)-D(s,x)\parallel }^2\nu (dx)ds\to 0$$

pointwise on $\mathbb{R}$, as $n\to \infty$, which completes the proof. □

Appendix A.2. Proof of Theorem 4

Proof. 

We have

$$\begin{array}{ccc}\hfill F(t,Y(t),x)& =& h(t,\alpha (t),x)+F(t,Y(t),x)-h(t,\alpha (t),x)\hfill \\ & =& h(t,\alpha (t),x)+F(t,Y(t),x)-F(t,\alpha (t),x)+\varphi (t,\alpha (t),x)\hfill \end{array}$$

In the following, we shall show that $F(t,Y(t),x)\in PA{P}_{\gamma }^2(\mathbb{R}\times \mathbb{V},{\mathcal{L}}^2(P,\mathbb{H}))$ by several steps.

Step 1: we claim that $h^b(·,{\alpha }^b(·),x)\in AA(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. In fact, the function h satisfies $(8)$ and $h^b\in AA(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, ${\alpha }^b\in AA(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds)$. Moreover, $K=\left\{\overline{\alpha (t):t\in \mathbb{R}}\right\}$ is compact. Thus, by Theorem 2, we have $h^b(·,{\alpha }^b(·),x)\in AA(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$.

Step 2: At this moment, we claim that $F^b(·,Y^b(·),x)-F^b(·,{\alpha }^b(·),x)\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. Since $h,\varphi$ satisfies $(8)$, we obtain

$$\begin{array}{ccc}& & {\int }_0^1{\int }_{\mathbb{V}}\gamma (s){\parallel F(t+s,Y(t+s),x)-F(t+s,\alpha (t+s),x)\parallel }^2\nu (dx)ds\hfill \\ & =& {\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel F(s,Y(s),x)-F(s,\alpha (s),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel h(s,Y(s),x)-h(s,\alpha (s),x)\parallel }^2\nu (dx)ds\hfill \\ & & 2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,Y(s),x)-\varphi (s,\alpha (s),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 4L{\int }_t^{t+1}\gamma (s-t){\parallel \beta (s)\parallel }^{2}ds\hfill \end{array}$$

Thus, for any $T>0$,

$$\begin{array}{ccc}& & \frac{1}{2T}{\int }_{-T}^T{\int }_0^1{\int }_{\mathbb{V}}\gamma (s){\parallel F(t+s,Y(t+s),x)-F(t+s,\alpha (t+s),x)\parallel }^2\nu (dx)dsdt\hfill \\ & \le & \frac{2L}{T}{\int }_{-T}^T{\int }_t^{t+1}\gamma (s-t){\parallel \beta (s)\parallel }^{2}dsdt\hfill \end{array}$$

Since ${\beta }^b\in PA{P}_0(\mathbb{R},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$, we obtain

$$\underset{T\to \infty }{lim}\frac{1}{2T}{\int }_{-T}^T{\int }_0^1{\int }_{\mathbb{V}}\gamma (s){\parallel F(t+s,Y(t+s),x)-F(t+s,\alpha (t+s),x)\parallel }^2\nu (dx)dsdt=0,$$

which implies $F^b(·,Y^b(·),x)-F^b(·,{\alpha }^b(·),x)\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$.

Step 3: we also claim that ${\varphi }^b(·,{\alpha }^b(·),x)\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. There are finite open balls $O_k(k=1,2,...,n)$ with center ${\alpha }_k\in K$ from the fact that $K=\left\{\overline{\alpha (t):t\in \mathbb{R}}\right\}$ is compact. Then, $\{\alpha (t);t\in \mathbb{R}\}\subset {\bigcup }_{k=1}^n{O}_k$, $B_k=\{s\in \mathbb{R};\alpha (s)\in O_k\}$ and $\mathbb{R}={\bigcup }_{k=1}^n{B}_k$, if the radius $\epsilon$ is small enough. Assume $E_1=B_1$, $E_k=B_k\setminus {\bigcup }_{j=1}^{k-1}{B}_j(2\le j\le n)$; then, $E_i\cap E_j=\varnothing$, when $i\ne j,1\le i,j\le n$.

Define $\overline{\alpha }:\mathbb{R}\mapsto {\mathcal{L}}^2(P,\mathbb{H})$ by $\overline{\alpha }(s)={\alpha }_k$, $s\in E_k,k=1,2,...,n$ is the step function. Thus, $\parallel \alpha (s)-\overline{\alpha }(s)\parallel \le \epsilon$ for all $s\in \mathbb{R}$. We have

$$\begin{array}{ccc}& & {\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,\alpha (s),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,\alpha (s),x)-\varphi (s,\overline{\alpha }(s),x)\parallel }^2\nu (dx)ds\hfill \\ & & +2{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,\overline{\alpha }(s),x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 2L{\int }_t^{t+1}\gamma (s-t){\parallel \alpha (s)-\overline{\alpha }(s)\parallel }^{2}ds\hfill \\ & & +2\sum _{k=1}^n{\int }_{[t,t+1]\cap E_k}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,{\alpha }_k,x)\parallel }^2\nu (dx)ds\hfill \\ & \le & 2L{\gamma }_0{\epsilon }^2+2\sum _{k=1}^n{\int }_{[t,t+1]\cap E_k}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,{\alpha }_k,x)\parallel }^2\nu (dx)ds\hfill \end{array}$$

Thus, for any $T>0$,

$$\begin{array}{ccc}& & \frac{1}{2T}{\int }_{-T}^T{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,\alpha (s),x)\parallel }^2\nu (dx)dsdt\hfill \\ & \le & 2L{\gamma }_0{\epsilon }^2+\frac{1}{T}{\int }_{-T}^T\sum _{k=1}^n{\int }_{[t,t+1]\cap E_k}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,{\alpha }_k,x)\parallel }^2\nu (dx)dsdt\hfill \end{array}$$

Since ${\varphi }^b\in PA{P}_0(\mathbb{R}\times {\mathcal{L}}^2(P,\mathbb{H})\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$ and the arbitrariness of $\epsilon$, we can obtain ${lim}_{T\to \infty }\frac{1}{2T}{\int }_{-T}^T{\int }_t^{t+1}{\int }_{\mathbb{V}}\gamma (s-t){\parallel \varphi (s,\alpha (s),x)\parallel }^2\nu (dx)dsdt=0,$ which implies ${\varphi }^b(·,{\alpha }^b(·),x)\in PA{P}_0(\mathbb{R}\times \mathbb{V},L^2(0,1;{\mathcal{L}}^2(P,\mathbb{H}),\gamma ds))$. The proof is complete. □