Constraints on Cosmic Ray Acceleration Capabilities of Black Holes in X-ray Binaries and Active Galactic Nuclei
Abstract
:1. Introduction
2. Astrophysical Black Holes: Rotating and Magnetized
2.1. Energy Extraction from Black Holes
2.2. Magnetosphere of Rotating BHs: Magnetic Field—BH Mass Relation
| Source | Refs. | Spin a | Log | Log | |
|---|---|---|---|---|---|
| GX 339-4 | [25,37] | 5.8 ± 0.5 | 0.92 ± 0.06 | 8.07 ± 0.18 | |
| V404 Cygni | [25,38] | 0.97 ± 0.02 | 7.84 ± 0.24 | ||
| XTE J1118+480 | [25,39] | ||||
| A0620-00 | [25,40] | ||||
| GRS 1915+105 | [41,42,43,44] | ||||
| XTE J1650-500 | [45,46] | ||||
| XTE J1550-564 | [44,47,48] | ≈7.70 | |||
| H 1743-322 | [49,50] | ≈6.88 |
| Source | d (Mpc) | Log | Spin a | Log | Log |
|---|---|---|---|---|---|
| Sgr A* | (GC) 0.008 | 6.63 | 0.6 | 2 | 15.64 |
| NGC 1052 | 19 | 8.19 | ≲1 | 4.8 | 20.11 |
| NGC 1068/M77 | 15 | 6.9 | ≲1 | 4.54 | 18.56 |
| NGC 1365 | 17 | 6.3 | ≲1 | 4.70 | 18.12 |
| NGC 2273 | 29 | 6.9 | 0.97 | 4.58 | 18.41 |
| NGC 2787 | 8 | 7.6 | ≲1 | 3.73 | 18.45 |
| NGC 3079 | 22 | 6.4 | ≲1 | 4.06 | 17.58 |
| NGC 3516 | 42 | 7.4 | 0.64 | 4.88 | 19.37 |
| NGC 3783 | 41 | 7.5 | 0.98 | 4.15 | 18.77 |
| NGC 3998 | 15 | 8.9 | 0.54 | 3.58 | 19.52 |
| NGC 4151 | 14 | 7.8 | 0.84 | 4.6 | 19.53 |
| NGC 4258/M106 | 8 | 7.6 | 0.38 | 4.14 | 18.65 |
| NGC 4261 | 32 | 8.7 | ≲1 | 3.51 | 19.33 |
| NGC 4374/M84 | 20 | 9 | 0.98 | 3 | 19.12 |
| NGC 4388 | 18 | 6.9 | 0.51 | 5.19 | 19.11 |
| NGC 4486/M87 | 17 | 9.7 | ≲1 | 2.84 | 19.66 |
| NGC 4579 | 18 | 8 | 0.82 | 4.11 | 19.23 |
| NGC 4594 | 11 | 8.8 | 0.6 | 3.18 | 19.05 |
| NGC 5033 | 20 | 7.2 | 0.68 | 4.47 | 18.77 |
| NGC 5194/M51 | 8 | 6.0 | 0.57 | 4.51 | 17.57 |
| MCG-6-30-15 | 33 | 7.3 | 0.98 | 4.74 | 19.16 |
| NGC 5548 | 75 | 7.8 | 0.58 | 4.48 | 19.34 |
| NGC 6251 | 102 | 8.8 | ≲1 | 3.70 | 19.62 |
| NGC 6500 | 43 | 8.6 | ≲1 | 3.60 | 19.32 |
| IC 1459 | 31 | 9.4 | ≲1 | 3.20 | 19.72 |
3. Black Hole Rotating in Magnetic Field as CR Accelerator
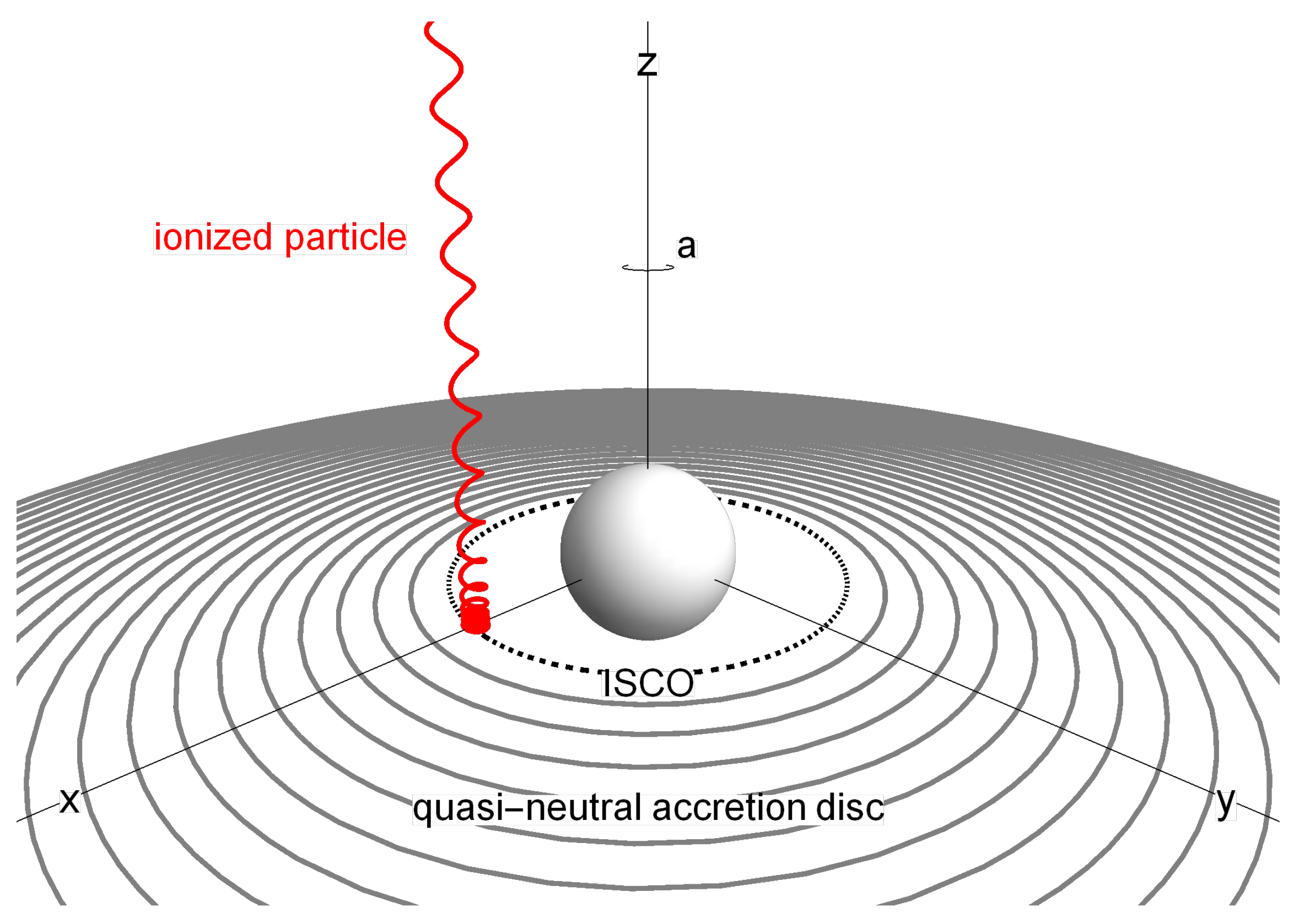
3.1. Generalized Formalism
3.2. Mean Energy of Cosmic Rays Accelerated by Various BH Candidates
3.3. CR Propagation: GZK and Synchrotron Losses
4. Conclusions and Future Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BH | Black hole |
| CR | Cosmic ray |
| AGNs | Active galactic nuclei |
| GBHs | Galactic black holes |
| SMBH | Supermassive black hole |
| UHECR | Ultrahigh-energy cosmic ray |
| CREDO | Cosmic Ray Extremely Distributed Observatory |
| Log | Log |
References
- Pierre Auger Collaboration. An Indication of Anisotropy in Arrival Directions of Ultra-high-energy Cosmic Rays through Comparison to the Flux Pattern of Extragalactic Gamma-Ray Sources. Astrophys. J. Lett. 2018, 853, L29. [Google Scholar] [CrossRef]
- Stecker, F.W. Effect of Photomeson Production by the Universal Radiation Field on High-Energy Cosmic Rays. Phys. Rev. Lett. 1968, 21, 1016–1018. [Google Scholar] [CrossRef] [Green Version]
- Greisen, K. End to the cosmic ray spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuzmin, V.A. Upper limit of the spectrum of cosmic rays. JETP Lett. 1966, 4, 78–80. [Google Scholar]
- Bykov, A.M.; Ellison, D.C.; Marcowith, A.; Osipov, S.M. Cosmic Ray Production in Supernovae. Space Sci. Rev. 2018, 214, 41. [Google Scholar] [CrossRef] [Green Version]
- Nagar, N.M.; Matulich, J. Ultra-high energy cosmic rays detected by the Pierre Auger observatory. First direct evidence, and its implications, that a subset originate in nearby radiogalaxies. Astron. Astrophys. 2008, 488, 879–885. [Google Scholar] [CrossRef]
- Garrappa, S.; Buson, S.; Franckowiak, A.; Shappee, B.J.; Beacom, J.F.; Dong, S.; Holoien, T.S.; Kochanek, C.S.; Prieto, J.L.; Stanek, K.Z.; et al. Investigation of Two Fermi-LAT Gamma-Ray Blazars Coincident with High-energy Neutrinos Detected by IceCube. Astrophys. J. 2019, 880, 103. [Google Scholar] [CrossRef] [Green Version]
- Blandford, R.D. Acceleration of Ultra High Energy Cosmic Rays. Phys. Scr. Vol. T 2000, 85, 191–194. [Google Scholar] [CrossRef] [Green Version]
- Tursunov, A.; Stuchlík, Z.; Kološ, M.; Dadhich, N.; Ahmedov, B. Supermassive Black Holes as Possible Sources of Ultrahigh-energy Cosmic Rays. Astrophys. J. 2020, 895, 14. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Nuovo Cimento Riv. Ser. 1969, 1, 252. [Google Scholar]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Wald, R.M. Energy Limits on the Penrose Process. Astrophys. J. 1974, 191, 231–234. [Google Scholar] [CrossRef]
- Ruffini, R.; Wilson, J.R. Relativistic magnetohydrodynamical effects of plasma accreting into a black hole. Phys. Rev. D 1975, 12, 2959–2962. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. Revival of the Penrose process for astrophysical applications. Astrophys. J. 1985, 290, 12–14. [Google Scholar] [CrossRef]
- Parthasarathy, S.; Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. High efficiency of the Penrose process of energy extraction from rotating black holes immersed in electromagnetic fields. Astrophys. J. 1986, 307, 38–46. [Google Scholar] [CrossRef]
- Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. [Google Scholar] [CrossRef] [Green Version]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef] [Green Version]
- Stuchlík, Z.; Kološ, M.; Tursunov, A. Penrose Process: Its Variants and Astrophysical Applications. Universe 2021, 7, 416. [Google Scholar] [CrossRef]
- Koide, S.; Baba, T. Causal Extraction of Black Hole Rotational Energy by Various Kinds of Electromagnetic Fields. Astrophys. J. 2014, 792, 88. [Google Scholar] [CrossRef] [Green Version]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef] [Green Version]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Radiative Penrose process: Energy gain by a single radiating charged particle in the ergosphere of rotating black hole. Phys. Rev. D 2021, 103, 024021. [Google Scholar] [CrossRef]
- Tursunov, A.; Juraev, B.; Stuchlík, Z.; Kološ, M. Electric Penrose process: High-energy acceleration of ionized particles by nonrotating weakly charged black hole. Phys. Rev. D 2021, 104, 084099. [Google Scholar] [CrossRef]
- Daly, R.A. Black Hole Spin and Accretion Disk Magnetic Field Strength Estimates for More Than 750 Active Galactic Nuclei and Multiple Galactic Black Holes. Astrophys. J. 2019, 886, 37. [Google Scholar] [CrossRef]
- Piotrovich, M.Y.; Mikhailov, A.G.; Buliga, S.D.; Natsvlishvili, T.M. Determination of magnetic field strength on the event horizon of supermassive black holes in active galactic nuclei. Mon. Not. R. Astron. Soc. 2020, 495, 614–620. [Google Scholar] [CrossRef]
- Eckart, A.; Hüttemann, A.; Kiefer, C.; Britzen, S.; Zajaček, M.; Lämmerzahl, C.; Stöckler, M.; Valencia-S, M.; Karas, V.; García-Marín, M. The Milky Way’s Supermassive Black Hole: How Good a Case Is It? Found. Phys. 2017, 47, 553–624. [Google Scholar] [CrossRef] [Green Version]
- Gal’tsov, D.V.; Petukhov, V.I. Black hole in an external magnetic field. Sov. J. Exp. Theor. Phys. 1978, 47, 419. [Google Scholar]
- Tursunov, A.; Stuchlík, Z.; Kološ, M. Circular orbits and related quasiharmonic oscillatory motion of charged particles around weakly magnetized rotating black holes. Phys. Rev. D 2016, 93, 084012. [Google Scholar] [CrossRef] [Green Version]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Bicak, J.; Janis, V. Magnetic fluxes across black holes. Mon. Not. R. Astron. Soc. 1985, 212, 899–915. [Google Scholar] [CrossRef] [Green Version]
- Petterson, J.A. Magnetic field of a current loop around a Schwarzschild black hole. Phys. Rev. D 1974, 10, 3166–3170. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S. On the charge of the Galactic centre black hole. Mon. Not. R. Astron. Soc. 2018, 480, 4408–4423. [Google Scholar] [CrossRef]
- Komissarov, S.S. Electrodynamics of black hole magnetospheres. Mon. Not. R. Astron. Soc. 2004, 350, 427–448. [Google Scholar] [CrossRef] [Green Version]
- Punsly, B. Black Hole Gravitohydromagnetics; Springer Science & Business Media: Cham, Switzerland, 2001. [Google Scholar]
- Beskin, V.S. REVIEWS OF TOPICAL PROBLEMS: Axisymmetric stationary flows in compact astrophysical objects. Phys. Uspekhi 1997, 40, 659–688. [Google Scholar] [CrossRef]
- Hynes, R.I.; Steeghs, D.; Casares, J.; Charles, P.A.; O’Brien, K. Dynamical Evidence for a Black Hole in GX 339-4. Astrophys. J. Lett. 2003, 583, L95–L98. [Google Scholar] [CrossRef] [Green Version]
- Khargharia, J.; Froning, C.S.; Robinson, E.L. Near-infrared Spectroscopy of Low-mass X-ray Binaries: Accretion Disk Contamination and Compact Object Mass Determination in V404 Cyg and Cen X-4. Astrophys. J. 2010, 716, 1105–1117. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M.; Katysheva, N.A.; Khruzina, T.S.; Shugarov, S.Y.; Tatarnikov, A.M.; Bogomazov, A.I. Optical, J and K light curves of XTE J1118 + 480 = KV UMa: The mass of the black hole and the spectrum of the non-stellar component. Mon. Not. R. Astron. Soc. 2019, 490, 3287–3308. [Google Scholar] [CrossRef]
- Cantrell, A.G.; Bailyn, C.D.; Orosz, J.A.; McClintock, J.E.; Remillard, R.A.; Froning, C.S.; Neilsen, J.; Gelino, D.M.; Gou, L. The Inclination of the Soft X-ray Transient A0620-00 and the Mass of its Black Hole. Astrophys. J. 2010, 710, 1127–1141. [Google Scholar] [CrossRef]
- Hurley, D.J.; Callanan, P.J.; Elebert, P.; Reynolds, M.T. The mass of the black hole in GRS 1915+105: New constraints from infrared spectroscopy. Mon. Not. R. Astron. Soc. 2013, 430, 1832–1838. [Google Scholar] [CrossRef] [Green Version]
- Török, G.; Kotrlová, A.; Šrámková, E.; Stuchlík, Z. Confronting the models of 3:2 quasiperiodic oscillations with the rapid spin of the microquasar GRS 1915+105. Astron. Astrophys. 2011, 531, A59. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.M.; Raymond, J.; Fabian, A.C.; Gallo, E.; Kaastra, J.; Kallman, T.; King, A.L.; Proga, D.; Reynolds, C.S.; Zoghbi, A. The Accretion Disk Wind in the Black Hole GRS 1915+105. Astrophys. J. Lett. 2016, 821, L9. [Google Scholar] [CrossRef] [Green Version]
- Kološ, M.; Tursunov, A.; Stuchlík, Z. Possible signature of the magnetic fields related to quasi-periodic oscillations observed in microquasars. Eur. Phys. J. C 2017, 77, 860. [Google Scholar] [CrossRef]
- Orosz, J.A.; McClintock, J.E.; Remillard, R.A.; Corbel, S. Orbital Parameters for the Black Hole Binary XTE J1650-500. Astrophys. J. 2004, 616, 376–382. [Google Scholar] [CrossRef] [Green Version]
- Slaný, P.; Stuchlík, Z. Mass estimate of the XTE J1650-500 black hole from the extended orbital resonance model for high-frequency QPOs. Astron. Astrophys. 2008, 492, 319–322. [Google Scholar] [CrossRef] [Green Version]
- Chaty, S.; Dubus, G.; Raichoor, A. Near-infrared jet emission in the microquasar XTE J1550-564. Astron. Astrophys. 2011, 529, A3. [Google Scholar] [CrossRef] [Green Version]
- Steiner, J.F.; Reis, R.C.; McClintock, J.E.; Narayan, R.; Remillard, R.A.; Orosz, J.A.; Gou, L.; Fabian, A.C.; Torres, M.A.P. The spin of the black hole microquasar XTE J1550-564 via the continuum-fitting and Fe-line methods. Mon. Not. R. Astron. Soc. 2011, 416, 941–958. [Google Scholar] [CrossRef]
- Tursunov, A.A.; Kološ, M. Constraints on Mass, Spin and Magnetic Field of Microquasar H 1743-322 from Observations of QPOs. Phys. At. Nucl. 2018, 81, 279–282. [Google Scholar] [CrossRef] [Green Version]
- Aneesha, U.; Mandal, S. Spectral and accretion evolution of H1743-322 during outbursts in RXTE era. Astron. Astrophys. 2020, 637, A47. [Google Scholar] [CrossRef] [Green Version]
- Tursunov, A.; Kološ, M.; Stuchlík, Z.; Gal’tsov, D.V. Radiation Reaction of Charged Particles Orbiting a Magnetized Schwarzschild Black Hole. Astrophys. J. 2018, 861, 2. [Google Scholar] [CrossRef]
- Homola, P.; Beznosko, D.; Bhatta, G.; Bibrzycki, Ł.; Borczyńska, M.; Bratek, Ł.; Budnev, N.; Burakowski, D.; Alvarez-Castillo, D.E.; Almeida Cheminant, K.; et al. Cosmic-Ray Extremely Distributed Observatory. Symmetry 2020, 12, 1835. [Google Scholar] [CrossRef]
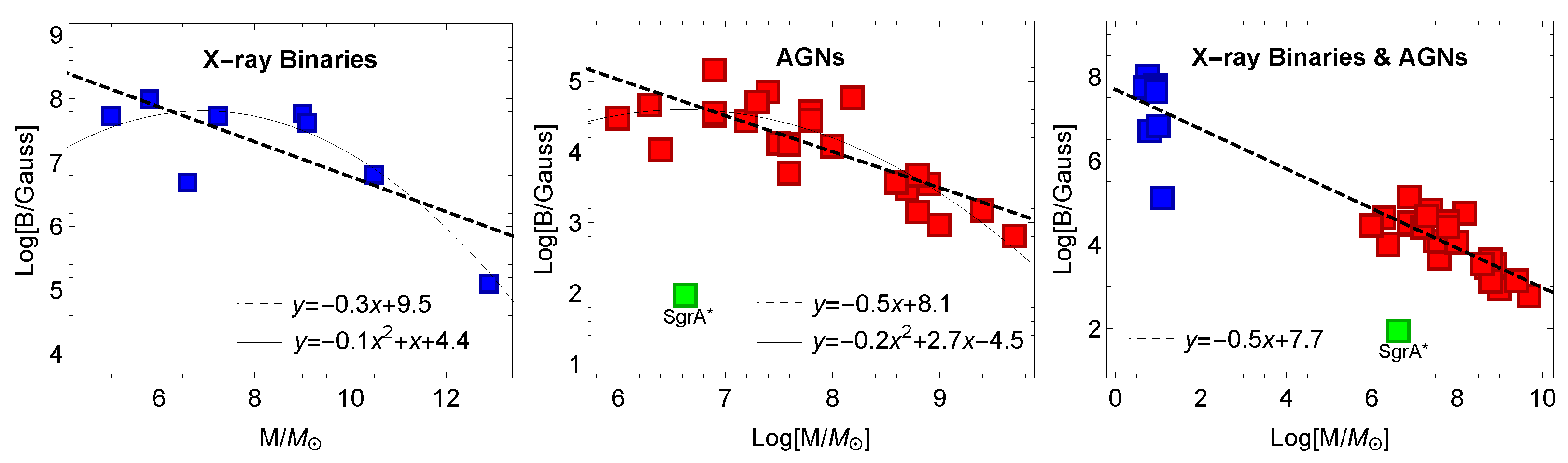
| B (Gauss) | 1 | ||||
| (s) | 1 | ||||
| (s) | |||||
| (s) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tursunov, A.; Kološ, M.; Stuchlík, Z. Constraints on Cosmic Ray Acceleration Capabilities of Black Holes in X-ray Binaries and Active Galactic Nuclei. Symmetry 2022, 14, 482. https://doi.org/10.3390/sym14030482
Tursunov A, Kološ M, Stuchlík Z. Constraints on Cosmic Ray Acceleration Capabilities of Black Holes in X-ray Binaries and Active Galactic Nuclei. Symmetry. 2022; 14(3):482. https://doi.org/10.3390/sym14030482
Chicago/Turabian StyleTursunov, Arman, Martin Kološ, and Zdeněk Stuchlík. 2022. "Constraints on Cosmic Ray Acceleration Capabilities of Black Holes in X-ray Binaries and Active Galactic Nuclei" Symmetry 14, no. 3: 482. https://doi.org/10.3390/sym14030482
APA StyleTursunov, A., Kološ, M., & Stuchlík, Z. (2022). Constraints on Cosmic Ray Acceleration Capabilities of Black Holes in X-ray Binaries and Active Galactic Nuclei. Symmetry, 14(3), 482. https://doi.org/10.3390/sym14030482







