Asymptotic Approximations of Higher-Order Apostol–Frobenius–Genocchi Polynomials with Enlarged Region of Validity
Abstract
1. Introduction
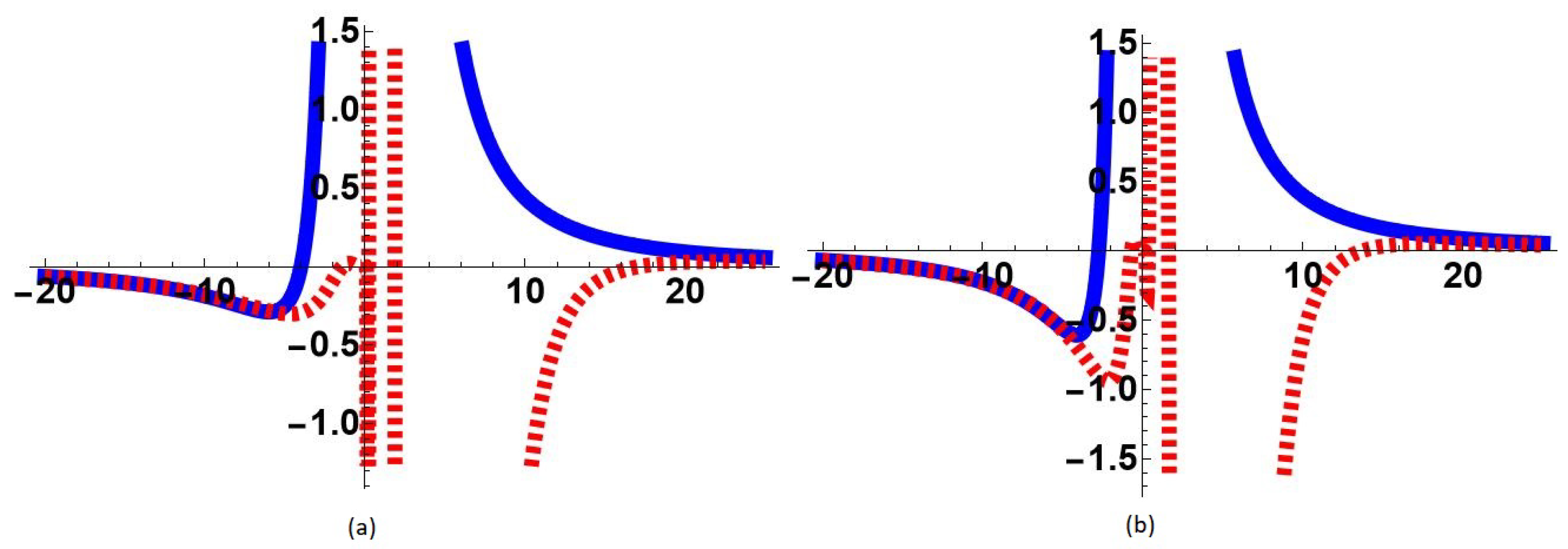
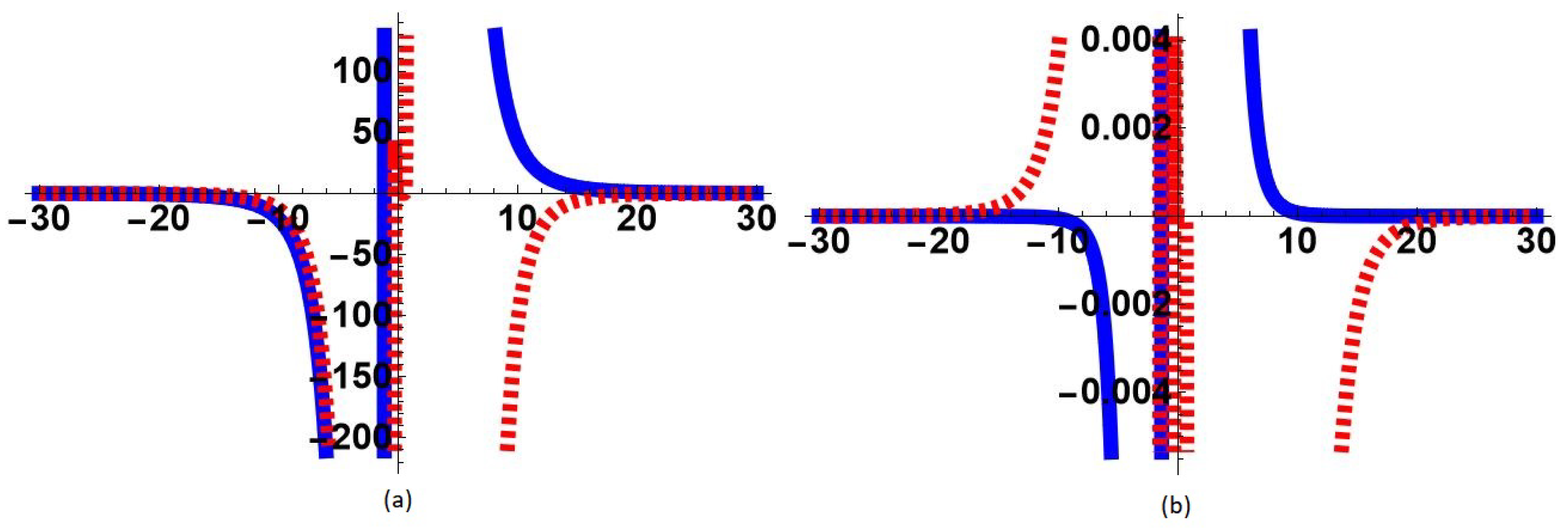
2. Uniform Approximation
3. Enlarged Region of Validity
4. Generalized Apostol-Type Frobenius–Genocchi Polynomials
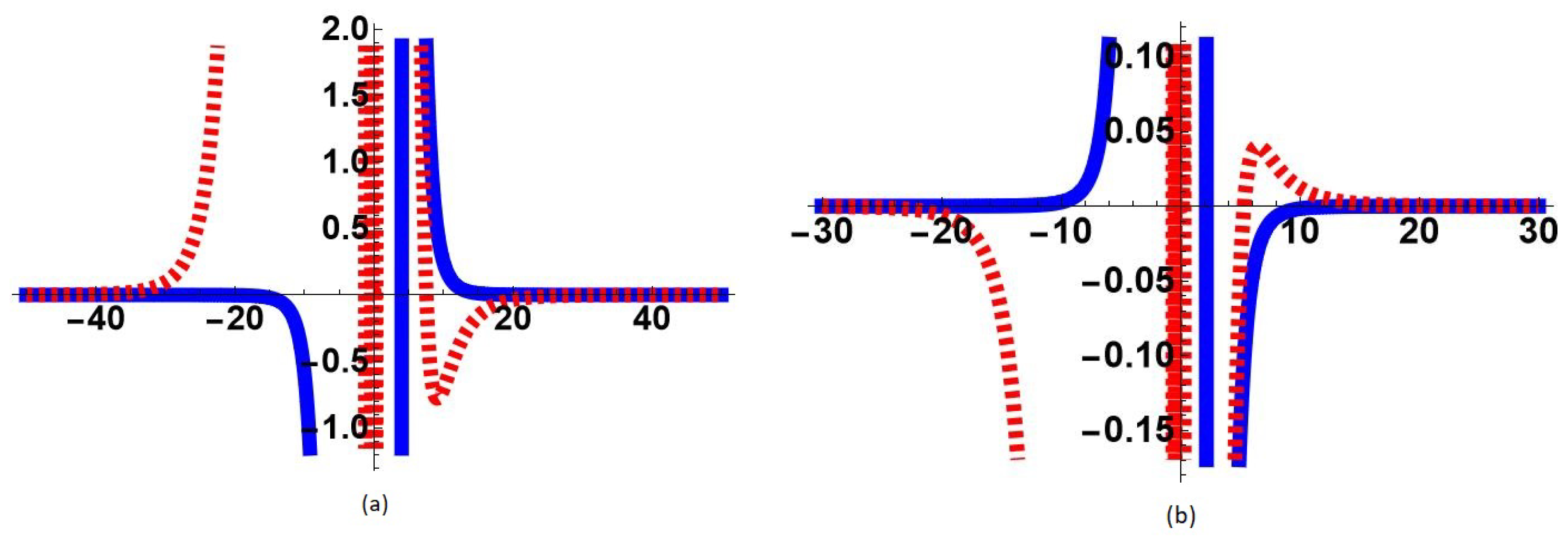
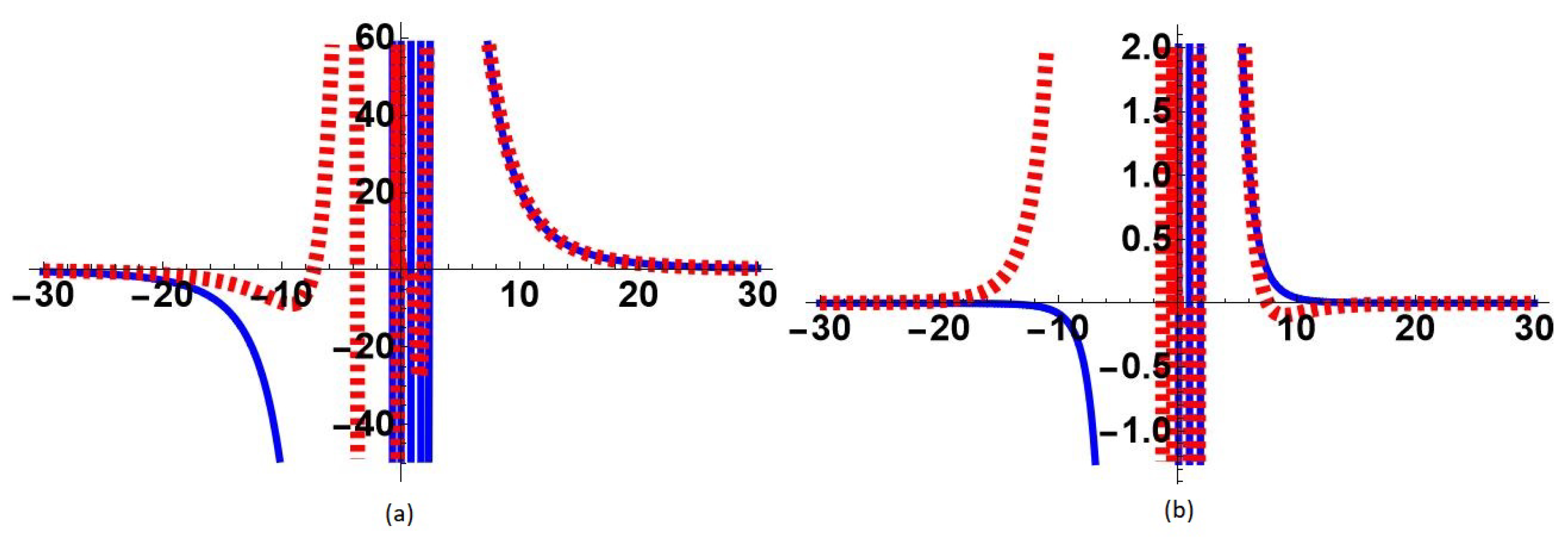
4.1. Uniform Approximations
4.2. Enlarged Region of Validity
5. Apostol–Frobenius-Type Poly-Genocchi Polynomials of Order with Parameters a, b, and c
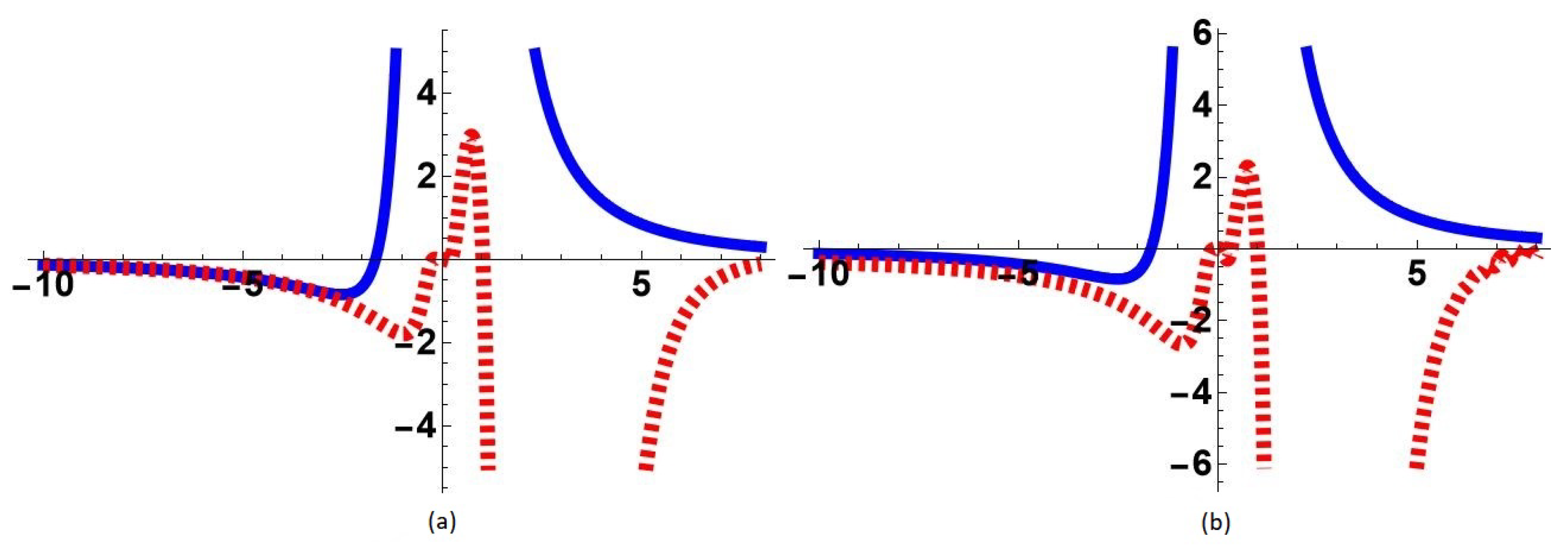
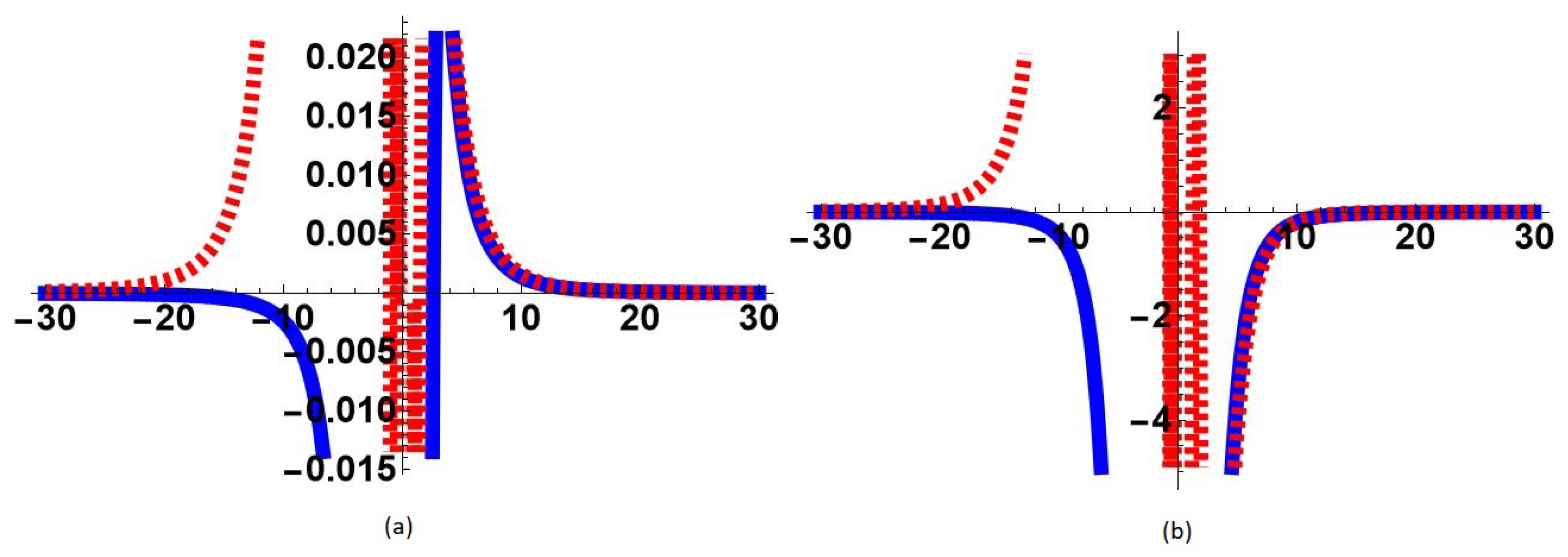
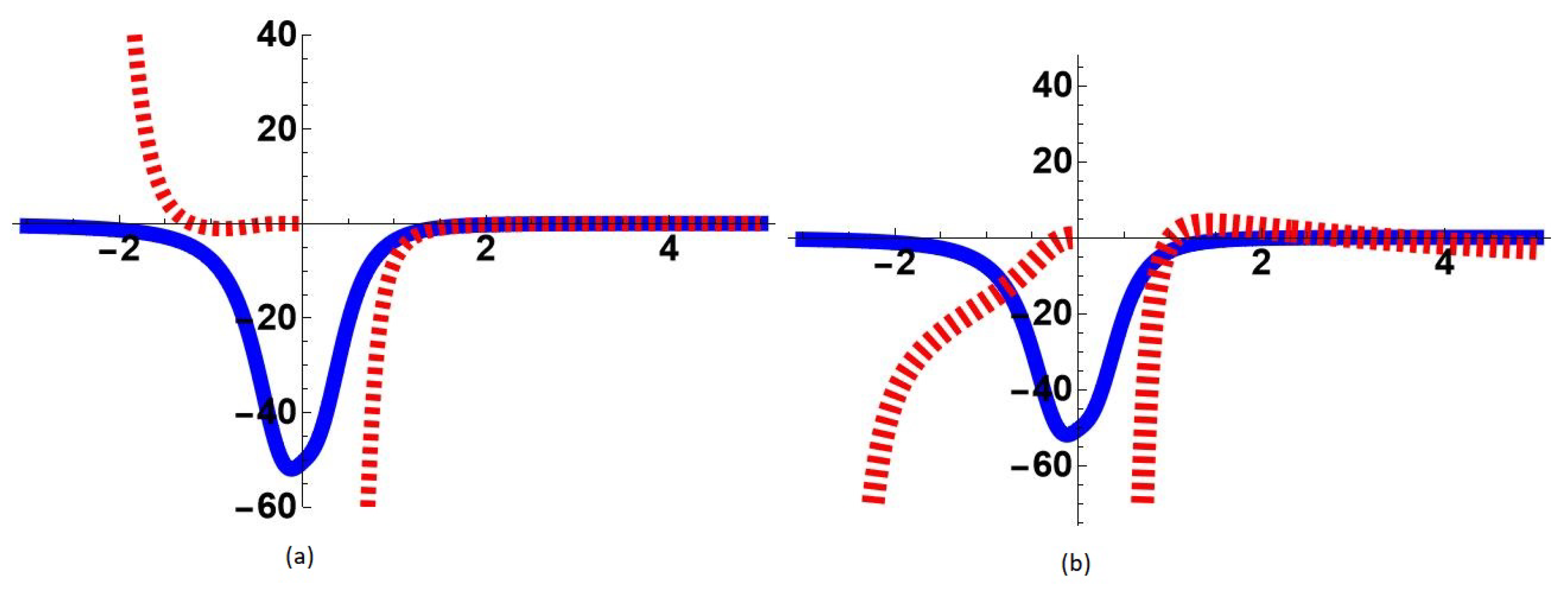
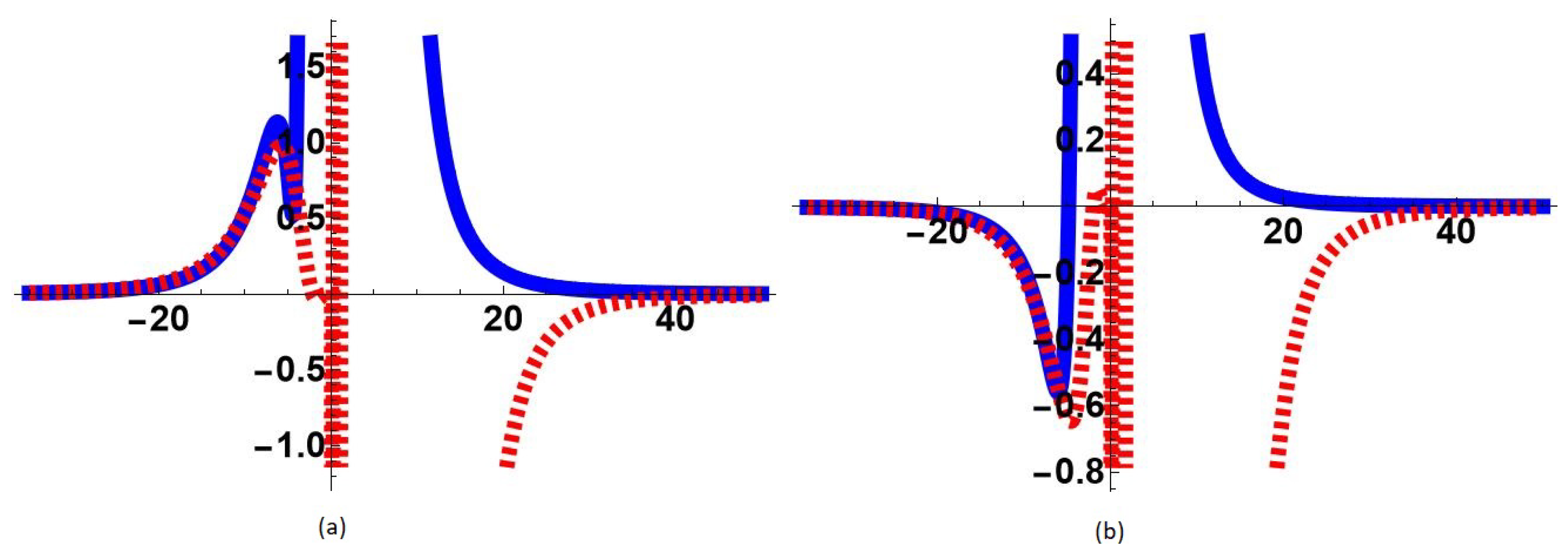
5.1. Uniform Approximations
5.2. Enlarged Region of Validity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Araci, S.; Acikgoz, M. Construction of Fourier expansion of Apostol Frobenius–Euler polynomials and its applications. Adv. Differ. Equ. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Wani, S.A.; Riyasat, M. Integral transforms and extended Hermite-Apostol type Frobenius- Genocchi polynomials. Kragujev. J. Math. 2021, 48, 41–53. [Google Scholar]
- Yaşar, B.Y.; Özarslan, M.A. Frobenius-Euler and Frobenius-Genocchi polynomials and their differential equations. New Trends Math. Sci. 2015, 3, 172–180. [Google Scholar]
- Jolany, H.; Sharifi, H. Some results for the Apostol-Genocchi polynomials of higher order. Bull. Malays. Math. Sci. Soc. 2013, 36, 465–479. [Google Scholar]
- Duran, U.; Acikgoz, M.; Araci, S. Construction of the type 2 poly-Frobenius–Genocchi polynomials with their certain applications. Adv. Differ. Equ. 2020, 2020, 432. [Google Scholar] [CrossRef]
- Tomaz, G.; Malonek, H.R. Matrix Approach to Frobenius-Euler Polynomials. In International Conference on Computational Science and Its Applications; Springer: Cham, Switzerland, 2014; pp. 75–86. [Google Scholar]
- Araci, S.; Acikgoz, M.; Şen, E. Some new formulae for Genocchi numbers and polynomials involving Bernoulli and Euler polynomials. Int. J. Math. Math. Sci. 2014, 2014, 760613. [Google Scholar] [CrossRef]
- Appell, P. Sur une classe de polynômes. Ann. Sci. L’éCole Norm. SupéRieure 1880, 9, 119–144. [Google Scholar] [CrossRef]
- Levi, D.; Tempesta, P.; Winternitz, P. Umbral calculus, difference equations and the discrete Schrödinger equation. J. Math. Phys. 2004, 45, 4077–4105. [Google Scholar] [CrossRef]
- Corcino, C.B.; Castañeda, W.; Corcino, R.B. Asymptotic Approximations of Apostol-Tangent Polynomials in terms of Hyperbolic Functions. Comput. Eng. Sci. 2022, 132, 133–151. [Google Scholar] [CrossRef]
- Corcino, C.B.; Corcino, R.B.; Ontolan, J.; Castañeda, W. Approximations of Genocchi polynomials in terms of hyperbolic functions. J. Math. Anal. 2019, 10, 76. [Google Scholar]
- Corcino, C.B.; Corcino, R.B.; Ontolan, J. Approximations of Tangent Polynomials, Tangent–Bernoulli and Tangent–Genocchi Polynomials in terms of Hyperbolic Functions. J. Appl. Math. 2021, 2021, 1–10. [Google Scholar] [CrossRef]
- Wong, R. Asymptotic Approximations of Integrals; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Lopez, J.L.; Temme, N.M. Uniform Approximations of Bernoulli and Euler polynomials in terms of hyperbolic functions. Stud. Appl. Math. 1999, 103, 241–258. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers; Dover Publications, Inc.: Mineola, NY, USA, 2013. [Google Scholar]
- Solomentsev, E.D. Encyclopedia of Mathematics: Mittag-Leffler Theorem. 2017. Available online: http://encyclopediaofmath.org/index.php?title=Mittag-Leffler_theorem&oldid=41565 (accessed on 28 March 2023).
- Khan, W.A.; Srivastava, D. On the generalized Apostol-type Frobenius-Genocchi polynomials. Filomat 2019, 33, 1967–1977. [Google Scholar] [CrossRef]
- Belbachir, H.; Souddi, N. Some explicit formulas for the generalized Frobenius-Euler polynomials of higher order. Filomat 2019, 33, 211–220. [Google Scholar] [CrossRef]
- Kim, T.; Jang, Y.S.; Seo, J.J. A note on poly-Genocchi numbers and polynomials. Appl. Math. Sci. 2014, 8, 4775–4781. [Google Scholar] [CrossRef]
- Corcino, R.B.; Corcino, C.B. Higher Order Apostol-Frobenius-Type Poly-Genocchi Polynomials with parameters a, b and c. J. Inequalities Spec. Funct. 2021, 12, 54–72. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corcino, C.; Castañeda, W.D., Jr.; Corcino, R. Asymptotic Approximations of Higher-Order Apostol–Frobenius–Genocchi Polynomials with Enlarged Region of Validity. Symmetry 2023, 15, 876. https://doi.org/10.3390/sym15040876
Corcino C, Castañeda WD Jr., Corcino R. Asymptotic Approximations of Higher-Order Apostol–Frobenius–Genocchi Polynomials with Enlarged Region of Validity. Symmetry. 2023; 15(4):876. https://doi.org/10.3390/sym15040876
Chicago/Turabian StyleCorcino, Cristina, Wilson D. Castañeda, Jr., and Roberto Corcino. 2023. "Asymptotic Approximations of Higher-Order Apostol–Frobenius–Genocchi Polynomials with Enlarged Region of Validity" Symmetry 15, no. 4: 876. https://doi.org/10.3390/sym15040876
APA StyleCorcino, C., Castañeda, W. D., Jr., & Corcino, R. (2023). Asymptotic Approximations of Higher-Order Apostol–Frobenius–Genocchi Polynomials with Enlarged Region of Validity. Symmetry, 15(4), 876. https://doi.org/10.3390/sym15040876