Power Transformer On-Load Capacity-Regulating Control and Optimization Based on Load Forecasting and Hesitant Fuzzy Control
Abstract
:1. Introduction
- A multi-strategy enhanced dung beetle optimizer (MSDBO), named the MSDBO–CNN–LSTM model for load forecasting, is proposed to adjust the hyperparameters of a CNN−LSTM. This adjustment enhances the model’s accuracy. Additionally, different optimization algorithms are compared to validate that the proposed MSDBO algorithm achieves the highest accuracy and the fewest iterations.
- Due to the difficulty of accurately analyzing the importance of various factors for transformer capacity-regulating control and the lack of weights on different factors, conventional fuzzy control methods perform poorly. For multifactor problems with unknown weights, hesitant fuzzy control combines the different opinions of multiple decision-makers for a more comprehensive analysis, resulting in decisions that are more relevant to the integrated opinions of multiple control. Compared to conventional fuzzy control, hesitant fuzzy control provides more accurate and comprehensive results.
- The effectiveness of the proposed capacity control method is assessed through simulation using the MATLAB/SIMULINK platform. The simulation results show that transformers using load forecasting models can accurately and promptly switch capacities. Transformers that combine load forecasting with hesitant fuzzy control can reduce the number of daily capacity switch operations while ensuring low power and economic losses.
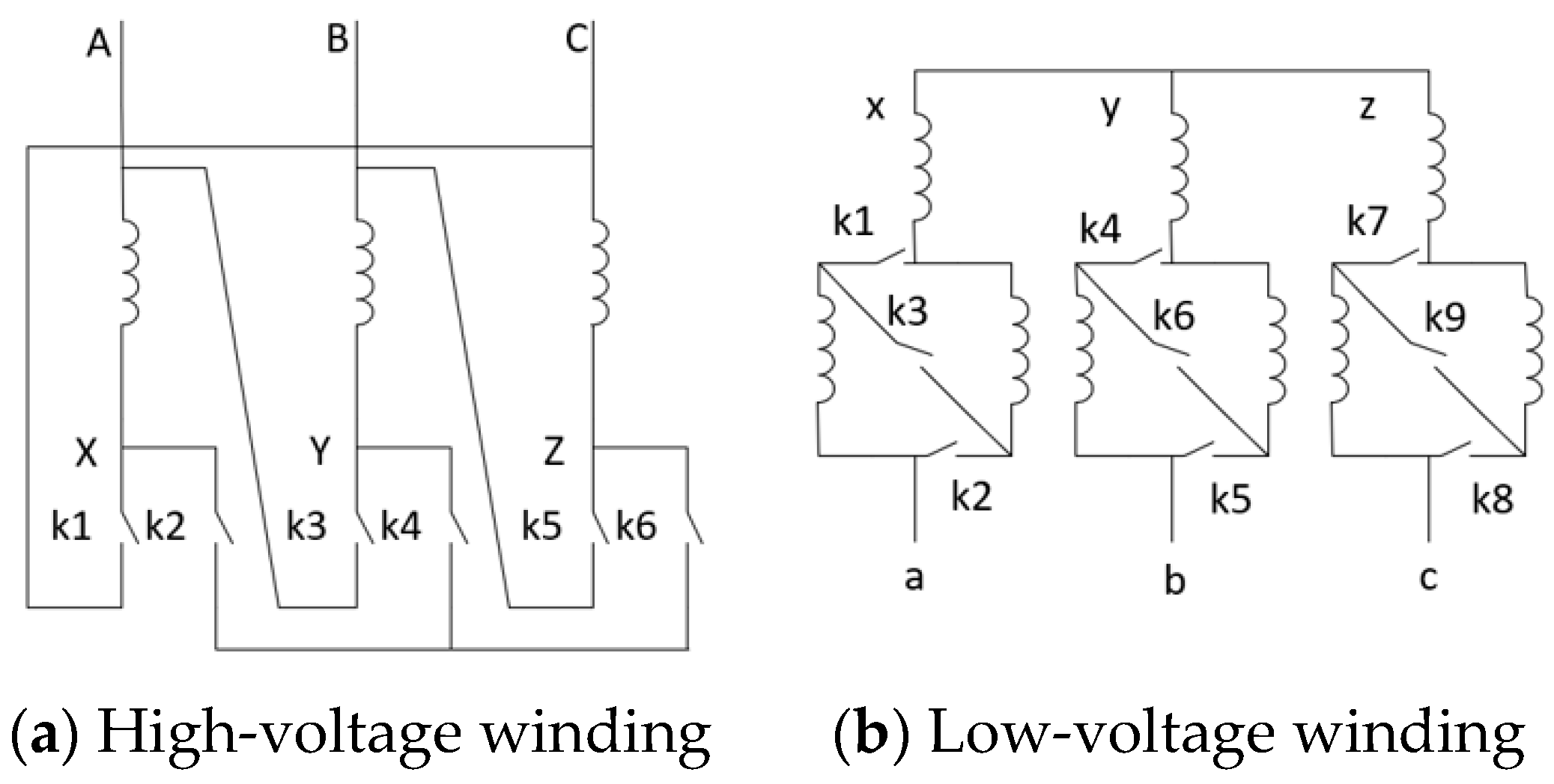
2. On-Load Capacity-Regulating Transformer Operating Principles
3. On-Load Capacity-Regulating Control Based on Load Forecasting
3.1. Load Forecasting Based on CNN−LSTM
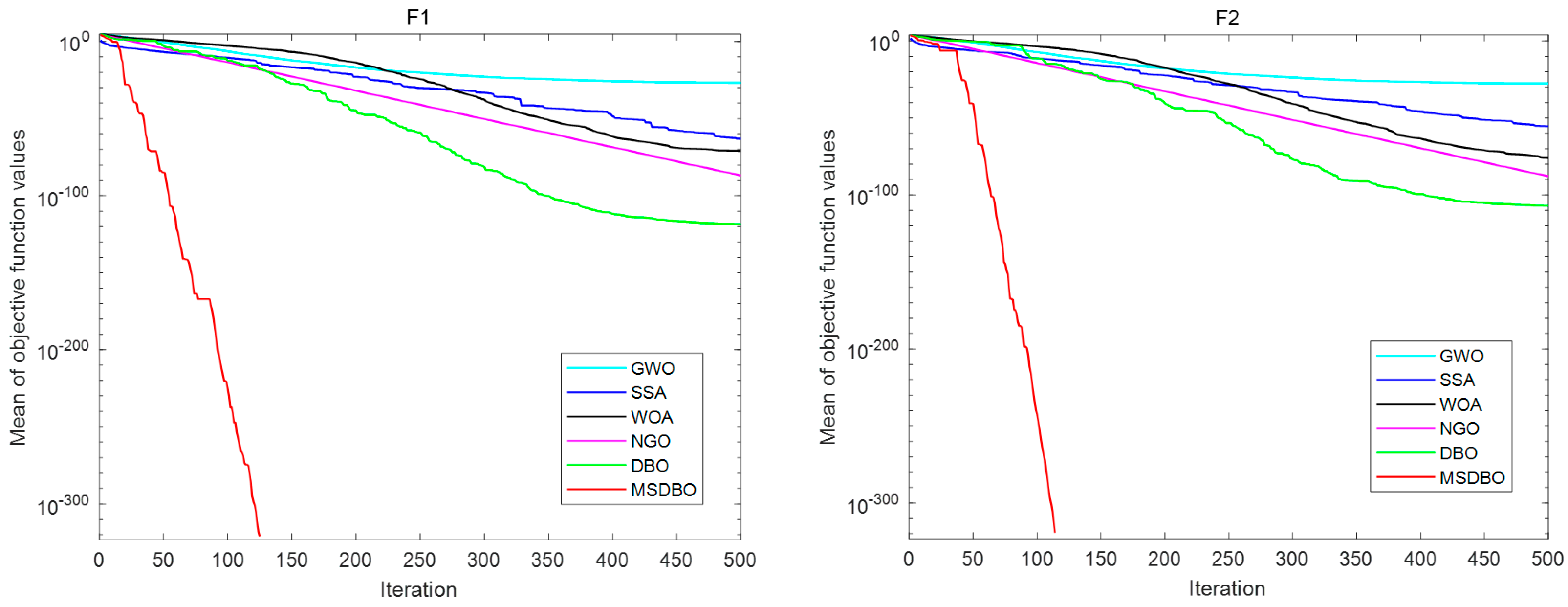
3.2. The Multi-Strategy Enhanced Dung Beetle Optimizer
3.2.1. Dung Beetle Optimizer
- (1)
- When the dung beetle encounters no obstacles, it navigates using the sun. The repositioning of the dung beetle rolling dung balls is influenced bywhere represents the number of iterations, represents the position of the th dung beetle, represents the degree of offset caused by natural factors, represents the perturbation coefficient , and represents the change in light intensity, where a larger value indicates a lower light intensity and represents the worst position.
- (2)
- When a dung beetle encounters an obstacle and cannot move forward, it repositions itself through a dance, and its new position is updated towhere represents the perturbation angle; when is 0 or , the position remains unchanged. represents the offset of the th dung beetle’s position.
- (3)
- The breeding area is simulated using a boundary selection strategy, defined aswhere represents the global best position; and are two independent random vectors of size , where represents the dimension of the optimization problem; and represent the lower and upper bounds of the breeding area, respectively.
- (4)
- When dung beetles forage, the formula for position change iswhere and represent the lower and upper bounds of the foraging area, respectively, represents random numbers drawn from a normal distribution, and represents random vectors of size .
- (5)
- When dung beetles steal, the formula for position change iswhere represents the best food source, represents a constant value, and is a random vector of size drawn from a normal distribution.
3.2.2. The Multi-Strategy Enhanced Dung Beetle Optimizer (MSDBO)
- (1)
- Bernoulli chaos mapping
- (2)
- Levy flight strategy
3.2.3. MSDBO Testing
3.3. MSDBO−CNN−LSTM
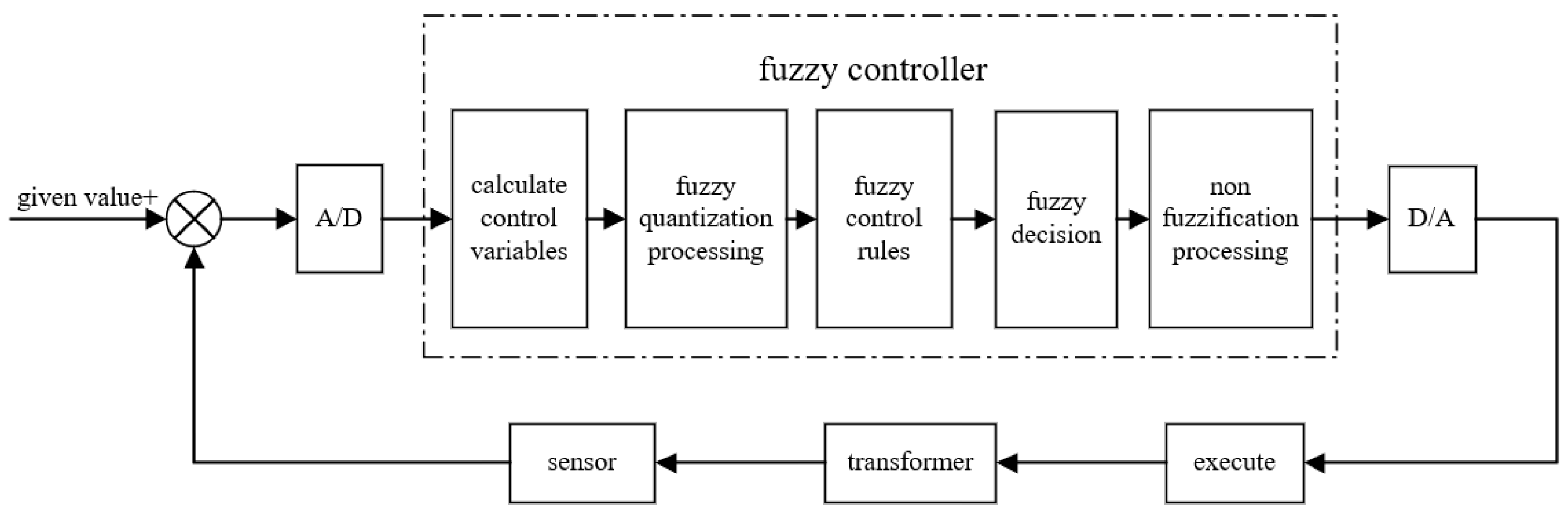
4. On-Load Capacity Regulation and Optimization Based on Fuzzy Control
4.1. Calculation and Economic Analysis of Capacity-Regulating Nodes
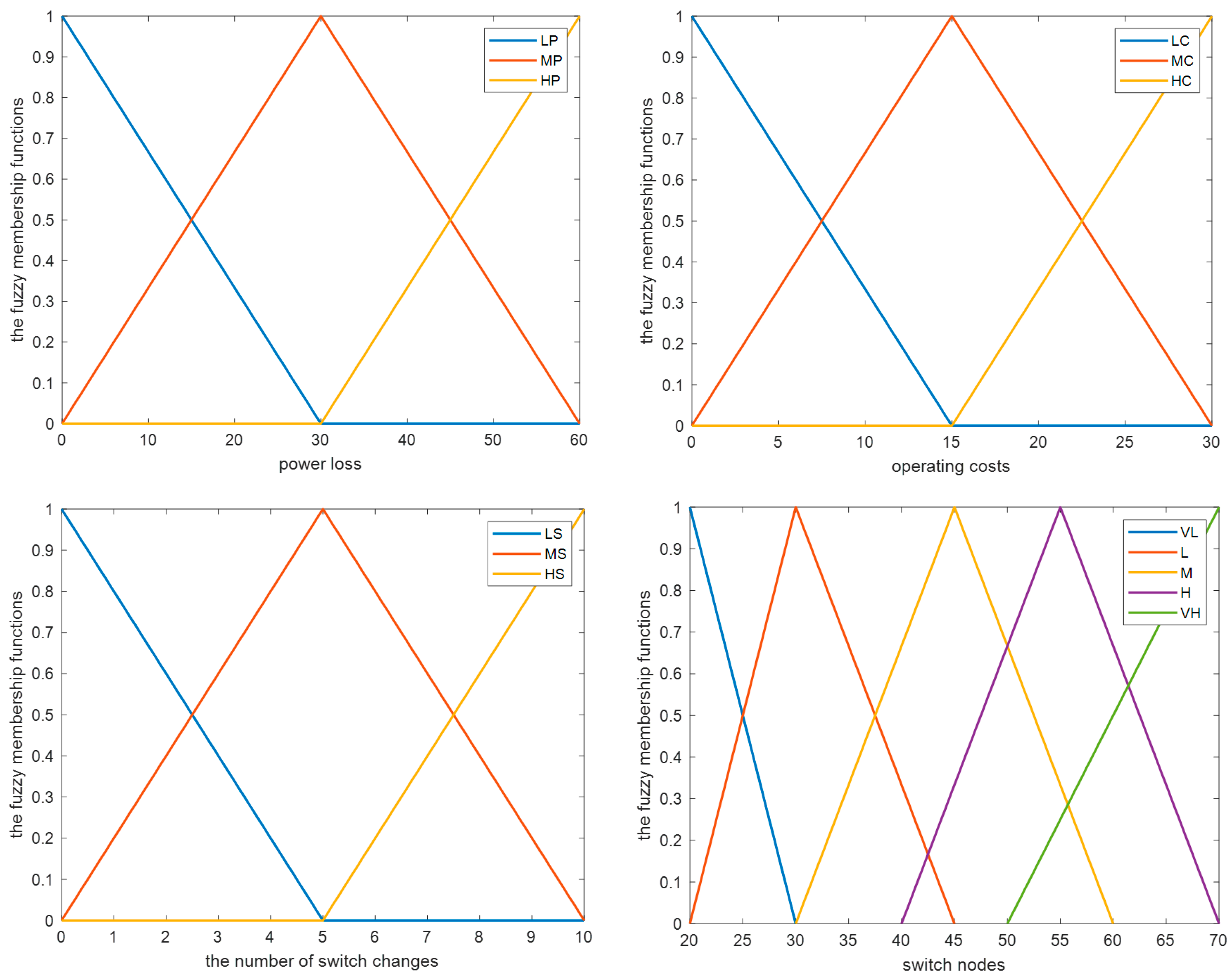
4.2. Hesitant Fuzzy Control Making for Capacity-Regulating Nodes
- (1)
- Generate the hesitant fuzzy control matrix based on the decision-maker’s evaluations of the options, and obtain matrix by standardizing the matrix.
- (2)
- Calculate the optimal weight vector based on Formula (12).
- (3)
- Select the operator-related weight vector based on the value of n.
- (4)
- Using the new hesitant fuzzy control weighted aggregation operator (NGHFHWA), integrate into the hesitant fuzzy element for each option .
- (5)
- Calculate the score function based on . If the score functions are equal, differentiate them through the hesitant fuzzy-order central aggregation function for sorting.
- (6)
- Arrange the options according to the score function and then choose the one with the highest score as the best option.
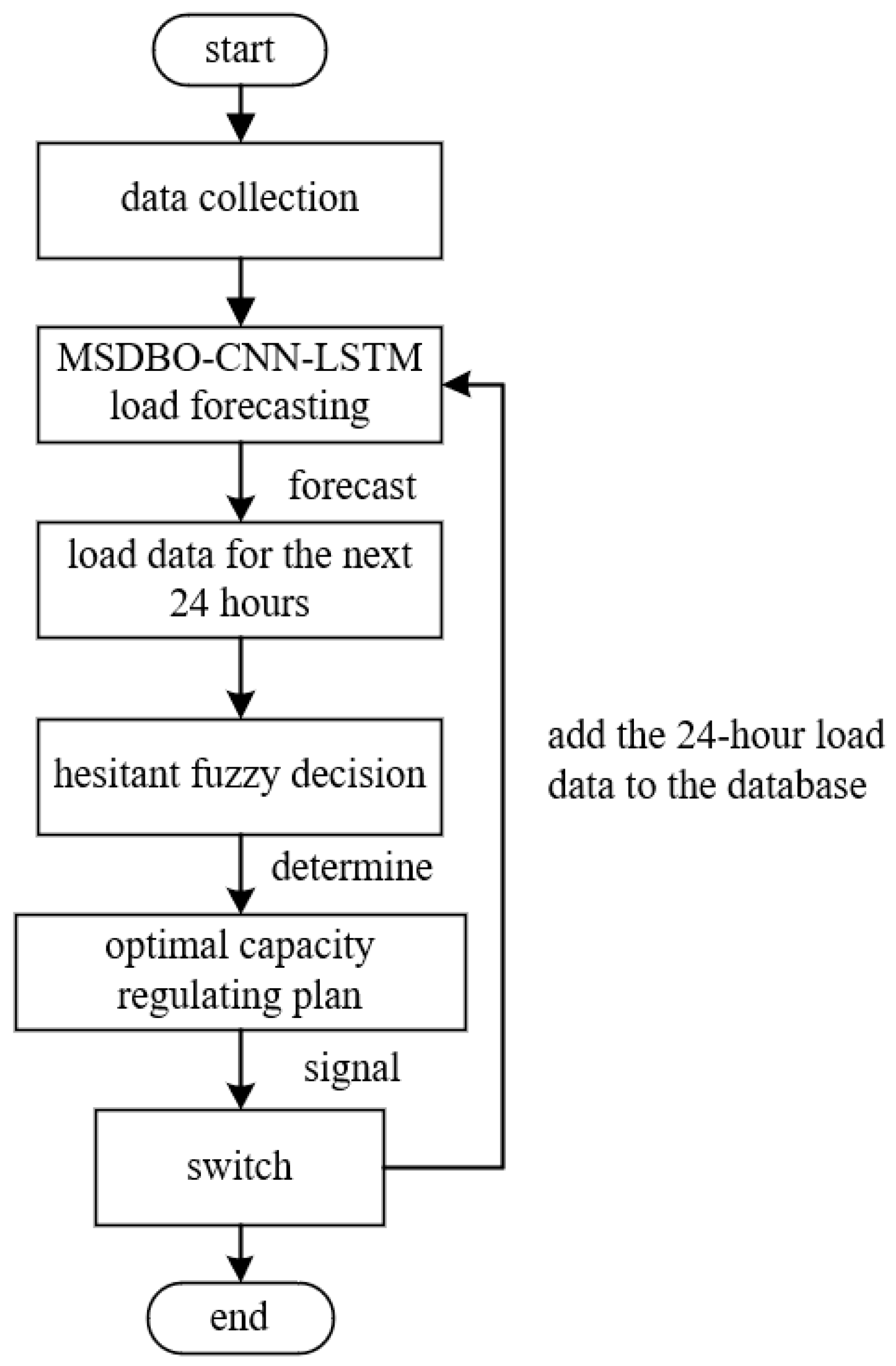
5. On-Load Capacity-Regulating Control Strategy and Methodology
- Step 1. Data collection:
- Step 2. Load forecasting:
- Step 3. Hesitant fuzzy control:
- (1)
- Define the evaluation criteria for selecting the optimal adjustment scheme, including the number of switch times, power losses, and operating costs.
- (2)
- Design a fuzzy controller with inputs of the number of switch changes, power loss, and operating costs, and an output of adjustment node value.
- (3)
- Define the fuzzy subsets and membership functions for each input and output variable.
- (4)
- Develop fuzzy rules based on expert knowledge and the fuzzy rule base table to determine the adjustment node value.
- Step 4. Optimal capacity-regulating plan:
- (1)
- Develop a detailed capacity adjustment schedule for the 24-h period based on the optimal adjustment nodes obtained through load forecasting and hesitant fuzzy decision-making methods.
- (2)
- Reduce power losses and operating costs through the capacity adjustment schedule while minimizing the number of switch changes as much as possible.
- Step 5. Action and analysis:
- (1)
- Control the switching of OLCR transformer capacity by implementing the optimal capacity-regulating plan in the form of signals.
- (2)
- Compare the performance of the conventional OLCR transformer with the proposed method in terms of the number of switching times, power losses, and operating costs.
- (3)
- Analyze the results of different scenarios to demonstrate the effectiveness and superiority of the proposed method in capacity regulation.
6. Case Studies and Results Analysis
6.1. Example Introduction
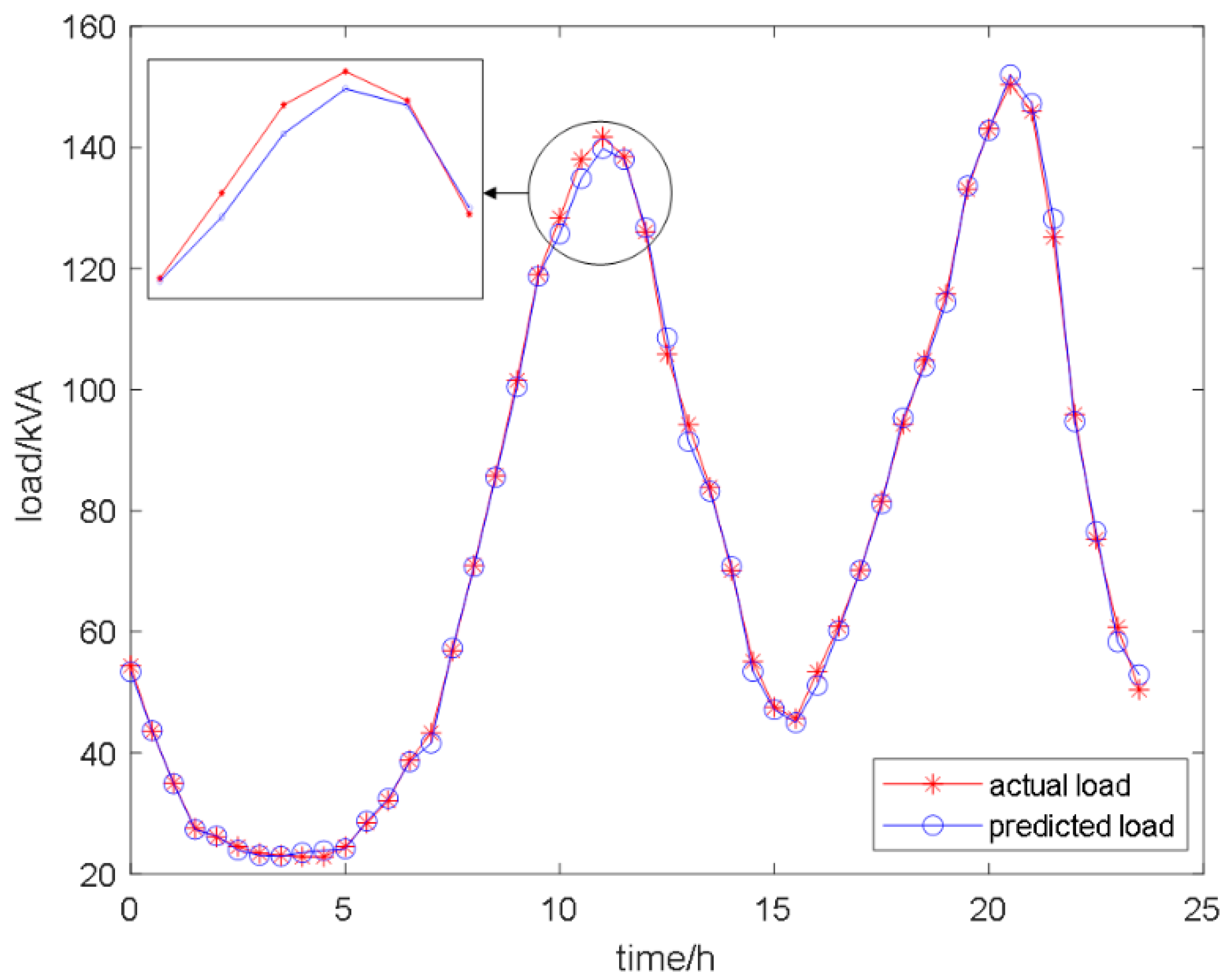
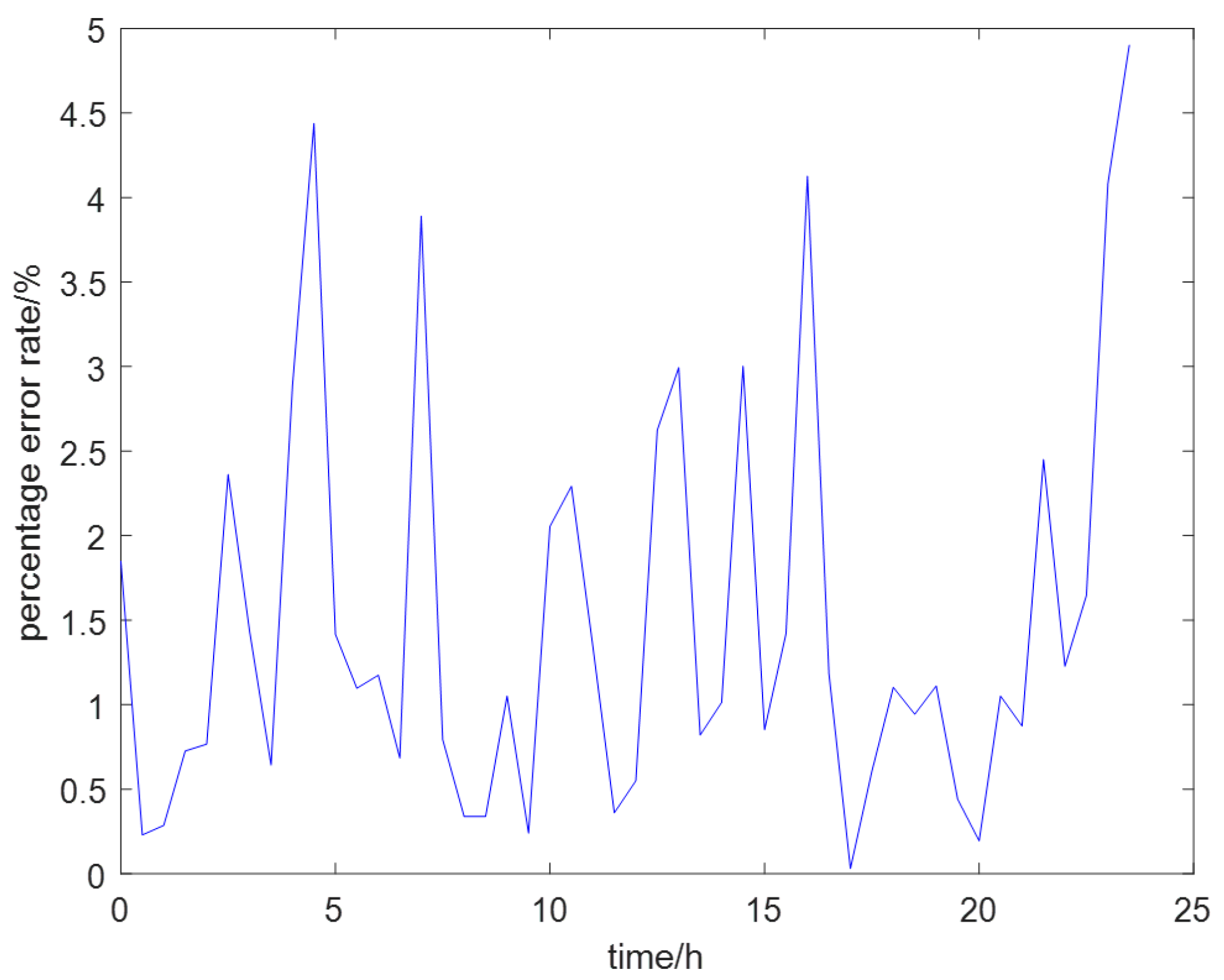
6.2. Load Forecasting Based on an MSDBO−CNN−LSTM Model
6.3. Capacity-Regulating Control Based on Hesitant Fuzzy Control
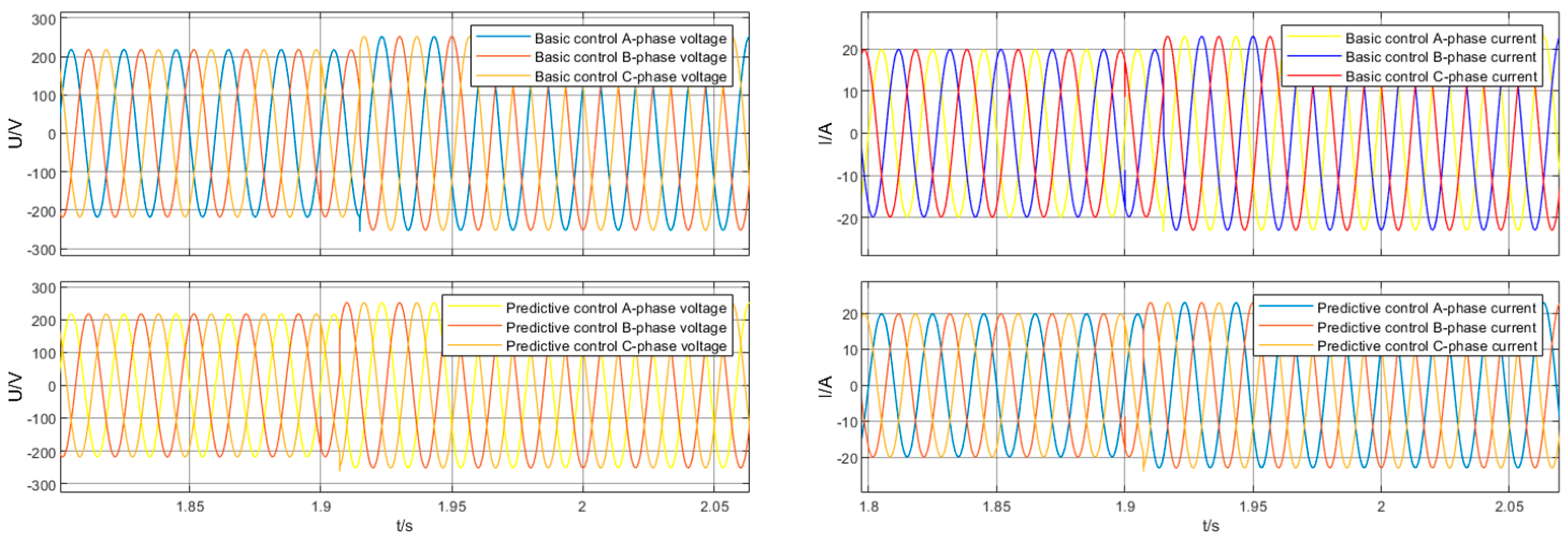
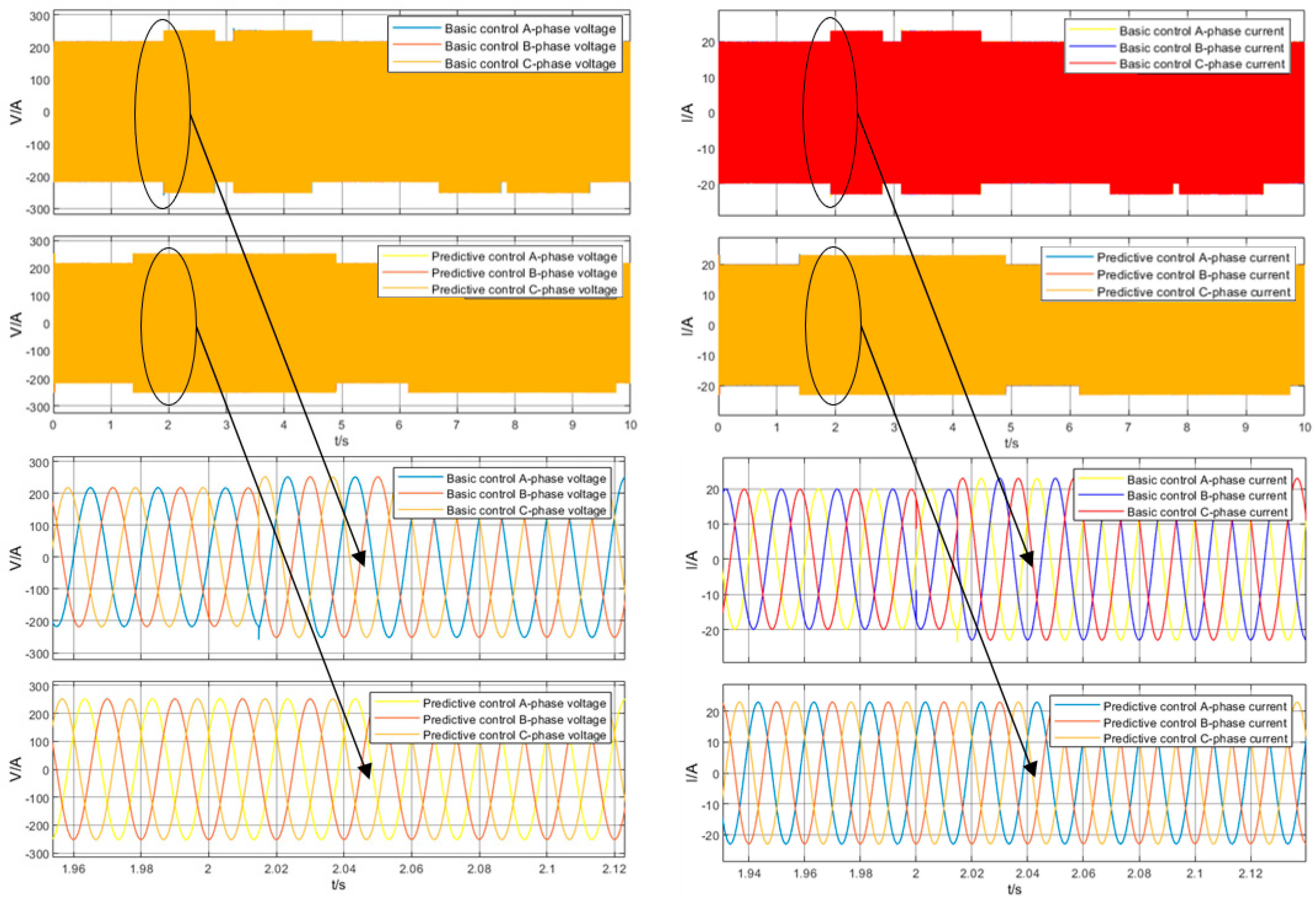
6.4. Simulation Results and Analysis
6.5. Scene Analysis
- (1)
- Scenario 1: During the busy agricultural season, electricity consumption in rural power grids is concentrated, leading to significant load fluctuations and severe overloading of transformers.
- (2)
- Scenario 2: During the idle agricultural season, electricity consumption in rural power grids is more dispersed. Transformers operate in no-load or light-load conditions for extended periods, leading to higher no-load losses.
- (3)
- Scenario 3: Urban residents’ electricity consumption follows daily life rhythms, resulting in large peak–valley differences in electricity usage.
- (1)
- Both the conventional OLCR transformer and the OLCR transformer controlled by the method proposed in this paper can effectively reduce power loss and operating costs, with the reduction effect significantly increasing as the load decreases. For the idle agricultural season in rural power grids, using the method proposed in this paper reduces daily power loss and daily economic loss by an average of 56.3% and 50.8%, respectively. For the busy agricultural season in rural power grids, using the method proposed in this paper reduces daily power loss and daily economic loss by an average of 28.5% and 25.4%, respectively. For urban residents’ electricity consumption, using the method proposed in this paper reduces daily power loss and daily economic loss by an average of 46.8% and 39%, respectively.
- (2)
- Compared to a conventional OLCR transformer, an OLCR transformer controlled by load prediction and fuzzy hesitant decision-making can significantly reduce the daily number of switch operations while sacrificing some loss reduction capability. For the three scenarios mentioned above, the method used in this paper can sacrifice 3.5% to 9.2% of the loss reduction capability in exchange for reducing the number of switch operations by 28.6% to 57.1%. This significantly extends the lifespan of the switches, thereby increasing the operational lifespan of the transformer.
7. Conclusions
- (1)
- The utilization of an MSDBO−CNN−LSTM neural network in this study for forecasting the load conditions for the next 24 h enables accurate switching of the transformer capacity mode. This helps avoid prolonged periods of overload or light-load conditions for the transformer. By reducing losses, it extends the operational lifespan of the on-load variable transformer, thereby enhancing the security and stability of the power grid.
- (2)
- In this study, a hesitant fuzzy control approach is employed to select the variable-capacity regulating nodes. Considering the three major factors of loss, economy, and switching frequency, the approach aims to minimize power loss and operating cost while reducing the number of switching operations. This strategy helps avoid a decrease in the operational lifespan of the transformer due to frequent capacity switch operations.
- (3)
- This control method demonstrates good capacity adjustment effects for OLCR transformers in rural distribution networks with seasonal loads and in urban residential networks with symmetric loads. It is applicable in various scenarios and exhibits superior performance. For the three scenarios mentioned above, the method reduces daily power loss by 28.5% to 56.3% and daily operating costs by 25.4% to 50.8%. The method used in this paper can sacrifice 3.5% to 9.2% of the loss reduction capability in exchange for reducing the number of switch operations by 28.6% to 57.1%. This significantly extends the lifespan of the switches, thereby increasing the operational lifespan of the transformer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Jiang, J.; Li, B. Residual lifetime evaluation of power transformers based on data fusion and wiener model. IEEE Trans. Power Deliv. 2023, 38, 4189–4201. [Google Scholar] [CrossRef]
- Yao, D.; Li, L.; Zhang, S.; Zhang, D.; Chen, D. The vibroacoustic characteristics analysis of transformer core faults based on multi-physical field coupling. Symmetry 2022, 14, 544. [Google Scholar] [CrossRef]
- Wang, S.; Gao, M.; Zhuo, R. Research on high efficient order reduction algorithm for temperature coupling simulation model of transformer. High Volt. Appar. 2023, 59, 115–126. [Google Scholar]
- Chen, T.; Chen, Y.; Li, X. Prediction for dissolved gas concentration in power transformer oil based on CEEMDAN-SG-BiLSTM. High Volt. Appar. 2023, 59, 168–175. [Google Scholar]
- Zang, C.; Zeng, J.; Li, P. Intelligent diagnosis model of mechanical fault for power transformer based on SVM algorithm. High Volt. Appar. 2023, 59, 216–222. [Google Scholar]
- Xia, Y.; Guo, C.; Chen, Y. Evaluation model of transformer overload capacity considering multi-factor. J. Mech. Electr. Eng. 2017, 34, 509–514. [Google Scholar]
- Zheng, Y.; Hao, Z.; Xue, Z. Exploration of safe operation and active protection technology for large power transformers. Autom. Electr. Power Syst. 2023, 40, 1–12. [Google Scholar]
- Wang, Q.; Guo, Y.; Mo, F. Optimal load distribution of urban high voltage distribution network considering short term emergency load of transformers. Automat. Electron. Power Syst. 2023, 47, 106–115. [Google Scholar]
- Shi, M.; Xu, H.; Li, H. A graded warning model for oil immersed distribution transformers based on multimodal data fusion. Guangdong Electr. Power 2022, 35, 110–117. [Google Scholar]
- Zhang, H.; Chen, X.; Li, Z. Study on thermal circuit model of ONAN transformer with auxiliary heat dissipation equipment. Guangdong Electr. Power 2022, 35, 95–103. [Google Scholar]
- Wang, J.; Sheng, W.; Wang, L.; Yang, H. Study on technical and economical efficiency of amorphous alloy transformer and on-load capacity regulating transformer in distribution network application. In Proceedings of the 2014 China International Conference on Electricity Distribution (CICED), Shenzhen, China, 23–25 September 2014. [Google Scholar]
- Yang, S.; Li, K. Study on synthesis loss reduction optimization method considering for rural distribution network planning. J. Agric. Mech. Res. 2015, 37, 250–253. [Google Scholar]
- Wang, J.; Sheng, W. Simulation analysis of capacity regulating transformer. Transformer 2009, 46, 19–23. [Google Scholar]
- Wang, J. Application and integrated economic analysis of on-load capacity regulating transformer. High Volt. Appar. 2009, 45, 32–35. [Google Scholar]
- Yang, T.; Zhao, Y.; Jiang, Z. Study on the technology of non-contact on-load automatic capacity regulating of the distribution transformer in rural power network. J. Agric. Mech. Res. 2016, 38, 239–244. [Google Scholar]
- Han, S.; Guo, X.; Tang, Q. Analysis and calculation of the best capacitive set-point of on-load adjustable capacitive transformer in operation. Transformer 2013, 50, 1–6. [Google Scholar]
- Fan, W.; Han, S. A Control strategy for secure and economic operation of on-load capacity regulating transformer. Automat. Electron. Power Syst. 2011, 35, 98–102. [Google Scholar]
- Meng, Z.; Piao, Z.; Wang, D. Design of switchover strategy and control system for arc-less on-load automatic capacity regulating distribution transformer. Trans. Chin. Soc. Agric. Eng. 2013, 29, 158–165. [Google Scholar]
- Huo, J.; Zhao, Q.; Wang, X. Analysis and selection of optimal capacity adjustment point of on-load capacity regulating transformer. Transformer 2018, 55, 38–42. [Google Scholar]
- Wang, R.; Zhao, W. A Fuzzy decision-based method to evaluate planning scheme for urban high voltage transmission network. Power Syst. Technol. 2013, 37, 488–492. [Google Scholar]
- Wang, Q.; Zhao, Q.; Wang, X. Research on load capacity control strategy based on load forecasting. Transformer 2019, 56, 23–26. [Google Scholar]






| Test Function | Value Range |
|---|---|
| The Number of Switch Changes | |||||
|---|---|---|---|---|---|
| LS | MS | HS | |||
| Power loss and operating costs | LP | LC | VH | H | H |
| LP | MC | H | H | M | |
| LP | HC | H | M | M | |
| MP | LC | H | H | M | |
| MP | MC | H | M | M | |
| MP | HC | M | M | L | |
| HP | LC | H | M | M | |
| HP | MC | M | M | L | |
| HP | HC | M | L | VL | |
| n | Operator-Related Weight Vector |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 5 |
| Rated Capacity (kVA) | No-Load Loss (kW) | Load Loss (kW) | No-Load Current (%) | Short-Circuit Impedance (%) | Critical Value (kVA) |
|---|---|---|---|---|---|
| 315/100 | 0.48 | 3.65 | 1.1 | 4 | 49.73 |
| 0.2 | 1.5 | 1.6 | 4 |
| Rated Capacity (kVA) | Operating Cost of the OLCR Transformer (CNY) | Rated Capacity (kVA) | Operating Cost of the Fixed-Tap Transformer (CNY) | Cost Savings with OLCR Transformer (CNY) | Cost Savings with OLCR Transformer (%) |
|---|---|---|---|---|---|
| 315/100 | 16.61 | 315 | 20.68 | 4.07 | 19.68 |
| Rated Capacity (kVA) | Operating Cost of the OLCR Transformer (CNY) | Rated Capacity (kVA) | Operating Cost of the Fixed-Tap Transformer (CNY) | Cost Savings with OLCR Transformer (CNY) | Cost Savings with OLCR Transformer (%) |
|---|---|---|---|---|---|
| 315/100 | 4334.80 | 315 | 8240.50 | 3905.70 | 47.40 |
| G1 | G2 | G3 | |
|---|---|---|---|
| {0.7, 0.8, 0.9} | {0.4, 0.6} | {0.5, 0.6, 0.7} | |
| {0.5, 0.6} | {0.7, 0.8, 0.9} | {0.4, 0.5} | |
| {0.3, 0.4, 0.5} | {0.6, 0.7} | {0.7, 0.8} |
| G1 | G2 | G3 | |
|---|---|---|---|
| {0.7, 0.8, 0.9} | {0.4, 0.6, 0.6} | {0.5, 0.6, 0.7} | |
| {0.5, 0.6, 0.6} | {0.7, 0.8, 0.9} | {0.4, 0.5, 0.5} | |
| {0.3, 0.4, 0.5} | {0.6, 0.7, 0.7} | {0.7, 0.8, 0.8} |
| Case | The Number of Switch Changes | Power Loss (kWh) | Operating Costs (CNY) | |||
|---|---|---|---|---|---|---|
| Conventional Method | New Method | Conventional Method | New Method | Conventional Method | New Method | |
| 1 | 2 | 1 | 17.6 | 19.2 | 10.9 | 11.8 |
| 2 | 2 | 1 | 21.2 | 23.4 | 12.6 | 14.0 |
| 3 | 4 | 3 | 31.7 | 33.6 | 18.0 | 19.3 |
| 4 | 1 | 1 | 16.7 | 19.1 | 10.3 | 11.7 |
| 5 | 4 | 3 | 34.5 | 36.8 | 19.3 | 20.8 |
| 6 | 4 | 2 | 30.5 | 32.1 | 17.3 | 18.5 |
| 7 | 3 | 1 | 25.6 | 27.5 | 14.9 | 16.2 |
| 8 | 3 | 1 | 27.4 | 29.4 | 15.8 | 17.2 |
| 9 | 2 | 1 | 20.8 | 21.8 | 12.4 | 13.1 |
| 10 | 3 | 2 | 25.0 | 28.1 | 14.5 | 16.4 |
| The Number of Switch Changes | Power Loss (kWh) | Operating Costs (CNY) | |
|---|---|---|---|
| Fixed-tap transformer | / | 37.9 | 21.3 |
| Conventional method | 2.8 | 25.1 | 14.6 |
| New method | 1.6 | 27.1 | 15.9 |
| The Number of Switch Changes | Power Loss (kWh) | Operating Costs (CNY) | |
|---|---|---|---|
| Fixed-tap transformer | / | 84.3 | 42.1 |
| Conventional method | 6.3 | 33.7 | 19.2 |
| New method | 2.7 | 36.8 | 20.7 |
| The Number of Switch Changes | Power Loss (kWh) | Operating Costs (CNY) | |
|---|---|---|---|
| Fixed-tap transformer | / | 58.5 | 29.2 |
| Conventional method | 3.7 | 29.8 | 17.2 |
| New method | 2.1 | 31.1 | 17.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, D.; Sun, X.; Quan, H.; Yin, J.; Peng, Q.; Wang, S.; Dai, W.; Hong, Z. Power Transformer On-Load Capacity-Regulating Control and Optimization Based on Load Forecasting and Hesitant Fuzzy Control. Symmetry 2024, 16, 679. https://doi.org/10.3390/sym16060679
Zou D, Sun X, Quan H, Yin J, Peng Q, Wang S, Dai W, Hong Z. Power Transformer On-Load Capacity-Regulating Control and Optimization Based on Load Forecasting and Hesitant Fuzzy Control. Symmetry. 2024; 16(6):679. https://doi.org/10.3390/sym16060679
Chicago/Turabian StyleZou, Dexu, Xinyu Sun, Hao Quan, Jianhua Yin, Qingjun Peng, Shan Wang, Weiju Dai, and Zhihu Hong. 2024. "Power Transformer On-Load Capacity-Regulating Control and Optimization Based on Load Forecasting and Hesitant Fuzzy Control" Symmetry 16, no. 6: 679. https://doi.org/10.3390/sym16060679
APA StyleZou, D., Sun, X., Quan, H., Yin, J., Peng, Q., Wang, S., Dai, W., & Hong, Z. (2024). Power Transformer On-Load Capacity-Regulating Control and Optimization Based on Load Forecasting and Hesitant Fuzzy Control. Symmetry, 16(6), 679. https://doi.org/10.3390/sym16060679






