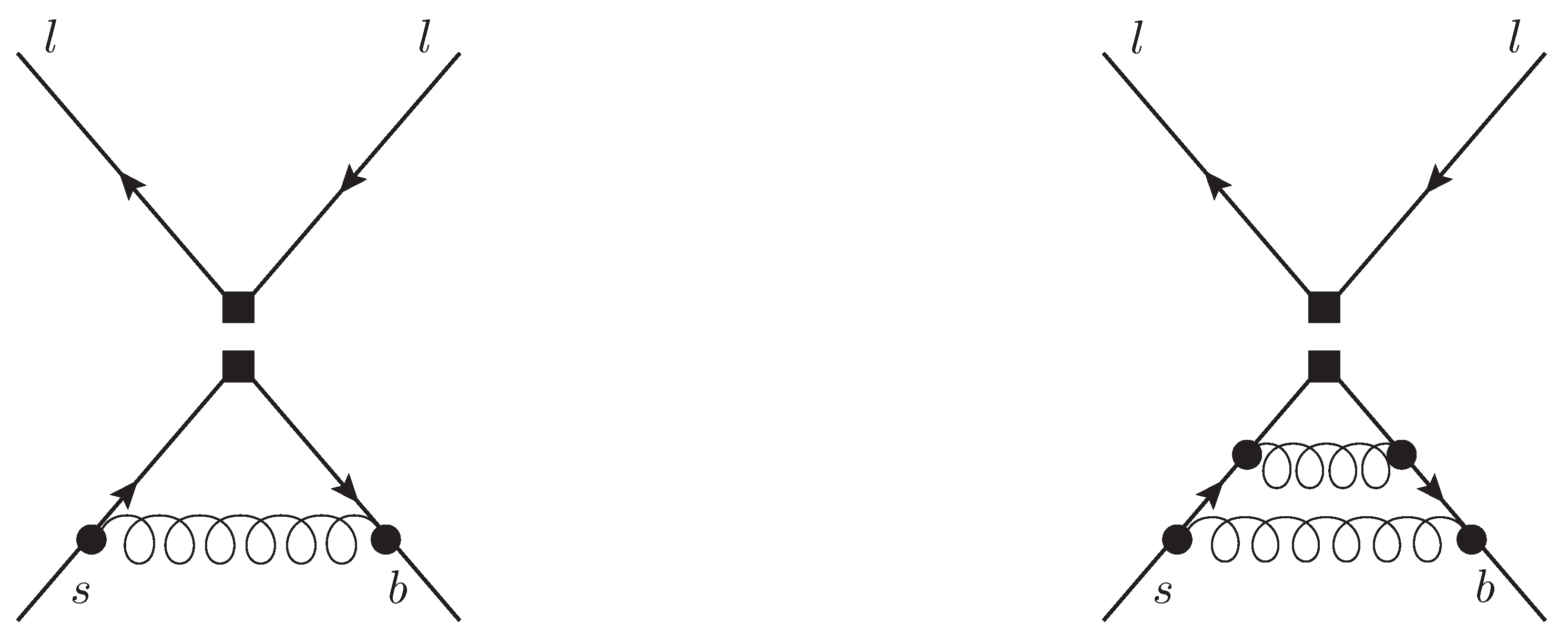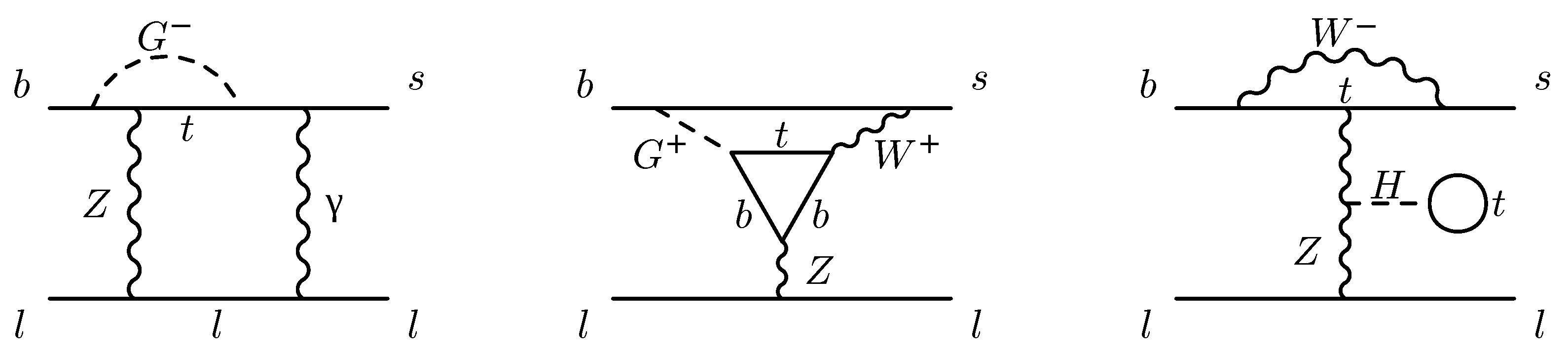Abstract
The rare decay provides an important constraint on possible deviations from the Standard Model in b-s-ℓ-ℓ interactions. The present weighted average of its branching ratio measurements amounts to , which remains in good agreement with the theoretical prediction of within the Standard Model. In the present paper, we review calculations that have contributed to this prediction and discuss the associated uncertainties.
1. Introduction
The Higgs boson discovery [1,2] through direct production at the LHC completed the experimental search for the Standard Model (SM) particle content. Since then, no clear signal for Beyond-Standard Model (BSM) particle production has been seen at the high-energy frontier of experimental particle physics. Consequently, more and more focus is being shifted towards precise studies of rare processes that are sensitive to corrections from BSMs.
In particular, decays of the B meson mediated through Flavor-Changing Neutral Currents (FCNCs) have been a very active area of research. Theoretical studies of the B mesons are greatly aided by the framework of Heavy Quark Expansion which, in many cases, allows us to parameterize the effects of their hadronic structure through a series of non-perturbative matrix elements suppressed by powers of . Moreover, while the FCNC-mediated processes are loop-suppressed in the SM, they can receive sizable tree-level contributions from BSMs, which underlines them as primary candidates for observables where indirect signals from new particles may be detected [3]. The rich phenomenology of rare B meson decays is being actively studied by LHC experiments and Belle II that follow and extend past investigations at CLEO, Belle, and BABAR. To fully take advantage of the current and future experimental data, improvements in the precision of the SM predictions are often necessary.
One of the most interesting rare decays of the B meson and the focus of this review is the channel that was first observed over a decade ago [4]. Since then, the experimental precision for its average time-integrated branching ratio has reached [5,6,7,8]. The current world average reads [9]
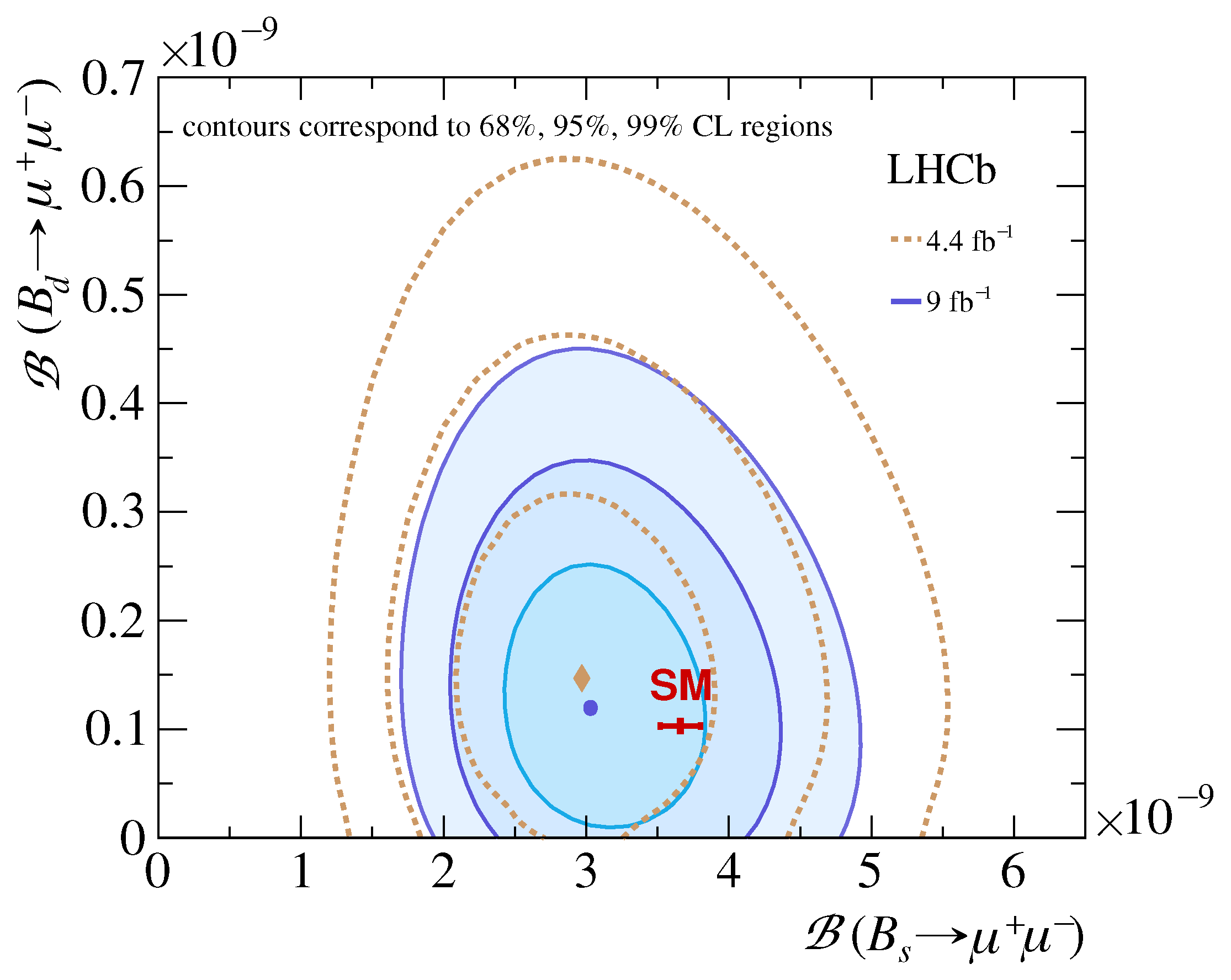
The similar channel is suppressed by a factor , which has a negative effect on experimental precision due to significantly reduced statistics, as illustrated in Figure 1.
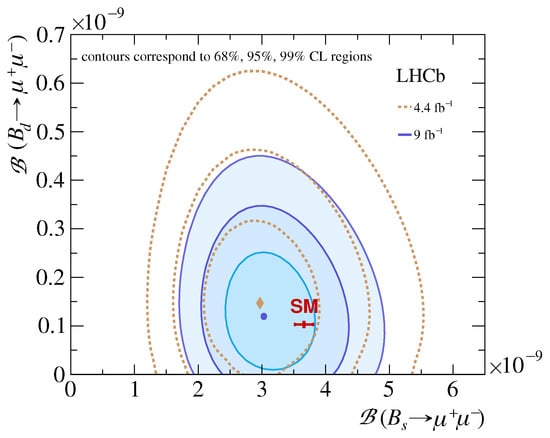
Figure 1.
LHCb measurements of and at 4.4 and 9 integrated luminosity, compared to the current SM predictions. Plot from Figure 2 of Ref. [7].
The SM description of is greatly simplified by a factorization of long- and short-distance Quantum Chromodynamics (QCD) effects. In contrast to many other B decays, the SM decay amplitude of depends, to a very good approximation, only on a single non-perturbative hadronic quantity, namely the -meson decay constant . Its determinations from lattice simulations (see below) are mature and precise. Moreover, the hard QCD and electroweak (EW) corrections are, to a very good approximation, contained within a single Wilson coefficient , which can be calculated in a standard, perturbative matching procedure as a series in the strong and electromagnetic couplings and . Thanks to these properties, SM calculations have reached the accuracy of a few percent. The current SM prediction for the branching ratio reads
We describe its evaluation in the next sections. The numerical value in Equation (2) has been obtained by updating the input parameters in the semi-numerical expressions of Ref. [10] and including the power-enhanced QED correction from Refs. [11,12] that amounts to around . A difference with respect to in Ref. [12] is due to the parameter update. The above SM prediction is well in agreement with each individual measurement [5,6,7,8], as well as with their average in Equation (1).
In the SM, on top of the aforementioned FCNC loop suppression, receives a helicity suppression by the mass-squared ratio . One or both of these suppressions may be lifted in models with additional Higgs doublets or with a . In effect, one finds restrictions on allowed parameter spaces in, among others, Two Higgs Doublet Models (2HDMs) [13] and the Minimal Supersymmetric Standard Model [14]. In addition, several time-dependent observables in can be used to study potential BSM -violation mechanisms [15].
The present review is organized as follows. In Section 2, we present the effective Lagrangian and the branching ratio formula for in the SM. Section 3 and Section 4 are devoted to describing, respectively, the perturbative QCD and EW corrections to the Wilson coefficient . At the end of Section 4, the power-enhanced QED correction to is discussed. In Section 5, we summarize the current parameter update and evaluate the SM prediction for (2) together with the corresponding uncertainty. We conclude in Section 6. In Appendix A, we recall the derivation of the branching ratio formula. In Appendix B, we present the current SM prediction for , i.e., the average time-integrated branching ratio of .
2. The Effective Lagrangian and the Branching Ratio Formula
The effective Lagrangian used to describe in the SM is obtained through simultaneous integrating out of all fields heavier than the b quark at the scale . It has the form
where
are the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements, is the Fermi constant, while is the W-boson mass defined in the on-shell renormalization scheme. The local operators are polynomials in the light fields and their derivatives. The Wilson coefficients can be treated as real-valued (up to negligible corrections) once the global normalization factor N is set as in Equation (4). The operators are of mass-dimension 5 or higher and have to be suppressed by powers of necessary to make the overall mass-dimension of equal to 4. At the leading order in and , it is sufficient to consider the operators , where a flavor-changing quark current multiplies a lepton current. Moreover, the quark current must violate parity to annihilate the pseudoscalar meson. Once the Lorentz invariance is imposed, one is left with the following four operators only (no tensor current needs to be considered because no antisymmetric tensor could be formed from alone in the corresponding matrix element, analogous to the one in Equation (7)):
The Lagrangian (3) can be used to derive the formula for . A sketch of the derivation is given in Appendix A. While evaluating the contribution of there, it becomes clear that does not contribute at the leading order in . As far as and are concerned, their Wilson coefficients are computed in a matching to full SM amplitudes with the quark and lepton currents exchanging Higgs bosons. Such contributions are suppressed by and can be neglected as being of the same order as dimension-8 operator effects. Hence, neglecting these tiny effects, in the SM depends on only. The explicit expression reads
where , , while is the heavier mass eigenstate width in the – system. Finally, the decay constant is defined through the relation
It is calculated using lattice QCD methods with errors at a sub-percent level. The current world average based on simulations [16,17,18,19] alone amounts to [20]
In several popular BSMs, the Wilson coefficients and can become comparable in size to . For example, in the 2HDM-II with large (the ratio of the vacuum expectation values of the two Higgs doublets), one finds [21],
where . The SM suppression factor of can be compensated by values of or larger. The branching ratio formula in the 2HDM becomes (see Appendix A)
where , and is the lighter mass eigenstate width in the – system.
Coming back to the SM expression for in Equation (6), several comments concerning the terms are necessary. First, all the corrections of this order to are already known and included in the numerical result in Equation (2). They will be discussed in Section 4.1. Some of them are enhanced by , or , where is the weak mixing angle. Second, some of the remaining electromagnetic corrections in the term in Equation (6) receive a power enhancement by [11]. They come from virtual photons emitted by the s quark and absorbed by the leptons. We shall comment on them in Section 4.2. Their evaluation requires extending the operator basis to include the effects of other dimension-6 operators, not present in Equation (5), such as
where . Third, the dependence of on the renormalization scale (that arises due to QED effects only) induces around uncertainty in [10]. Such a dependence must be compensated by the yet unknown corrections that receive no extra enhancement factors.
3. The QCD Corrections to
As described in the previous section, at the leading order in and , the only significant short-distance parameter entering the SM branching ratio formula is the Wilson coefficient, where we specifically indicate its dependence on the low-energy renormalization scale . It is evaluated by demanding the equality of corresponding Green’s functions in the SM and the effective theory (3) at the renormalization scale at which the electroweak degrees of freedom are decoupled. Computationally, the simplest choice of a Green’s function for the extraction of is with vanishing external momenta:
At the matching scale , QCD on both sides is treated perturbatively. This equation is then solved for order-by-order in and , resulting in a double series
where are the running couplings renormalized in the scheme at the scale . In this section, we focus on the leading terms in , namely .
As we work at the leading order in , all light masses in the matching Equation (12) can be set to 0. In dimensional regularization, all scaleless loop integrals vanish. In consequence, on the effective theory side, one is left only with tree diagrams, including the UV-counterterm ones. On the SM side, partially massive tadpoles have to be calculated. Removing light masses from propagators in the SM Green’s function leads to spurious infrared divergences in loop integrals evaluated in dimensions. The resulting additional -poles are not removed by the renormalization constants of the SM. Instead, they cancel in the matching Equation (12) against the tree-level UV counterterms in the effective theory.
Once such a procedure is applied in our case, one has to supplement the effective Lagrangian with additional operators that vanish when due to the Dirac algebra identities. Such operators are called evanescent. The UV-counterterms with these operators cancel against some of the spurious infrared divergence effects on the SM side. Moreover, their Wilson coefficients evaluated at lower orders affect the physical operator Wilson coefficients at higher orders. For the terms, it is sufficient to introduce only one evanescent operator [22]:
The bare fields, couplings, and Wilson coefficients on the effective side are replaced by the renormalized ones, with mixing occurring between the physical and evanescent operators:
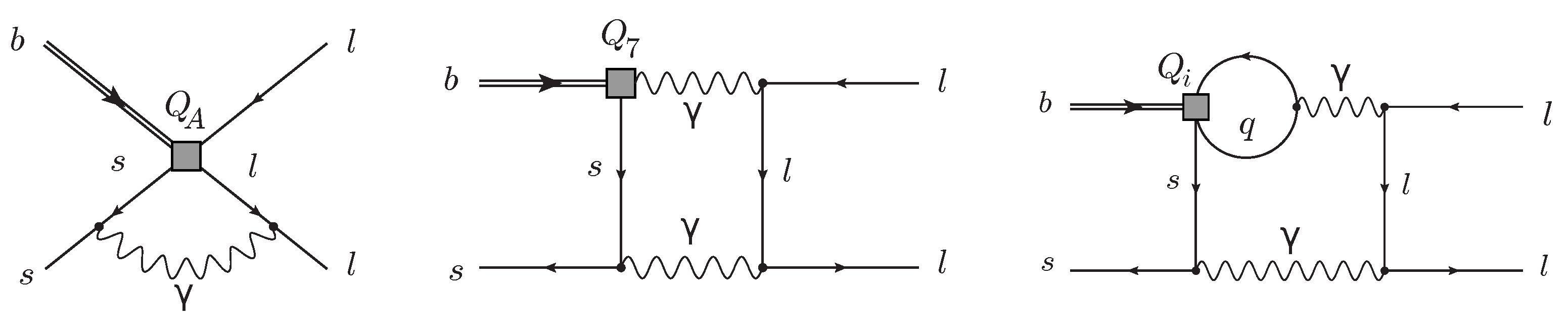
where and are the quark- and lepton-field renormalization constants, respectively, with . To fix the renormalization constants , one demands that in the renormalized Green’s functions, the terms proportional to are finite when , while those proportional to vanish in this limit [23]. Examples of diagrams contributing to at and are shown in Figure 2. Results for the relevant up to are given in Equation (15) of Ref. [24].
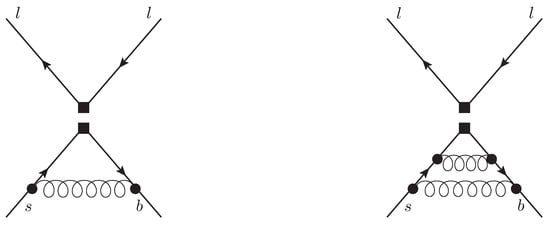
Figure 2.
Examples of the Feynman diagrams appearing in the calculation of . The double square in the middle denotes an insertion of either or . Diagrams from Figure 2 of Ref. [24].
It is important to emphasize that to all orders in QCD, once higher-dimensional operators and effects are neglected. Therefore, the Renormalization Group Equation (RGE) for is trivial at this level:
Consequently, there is no RG evolution of at the leading order in :
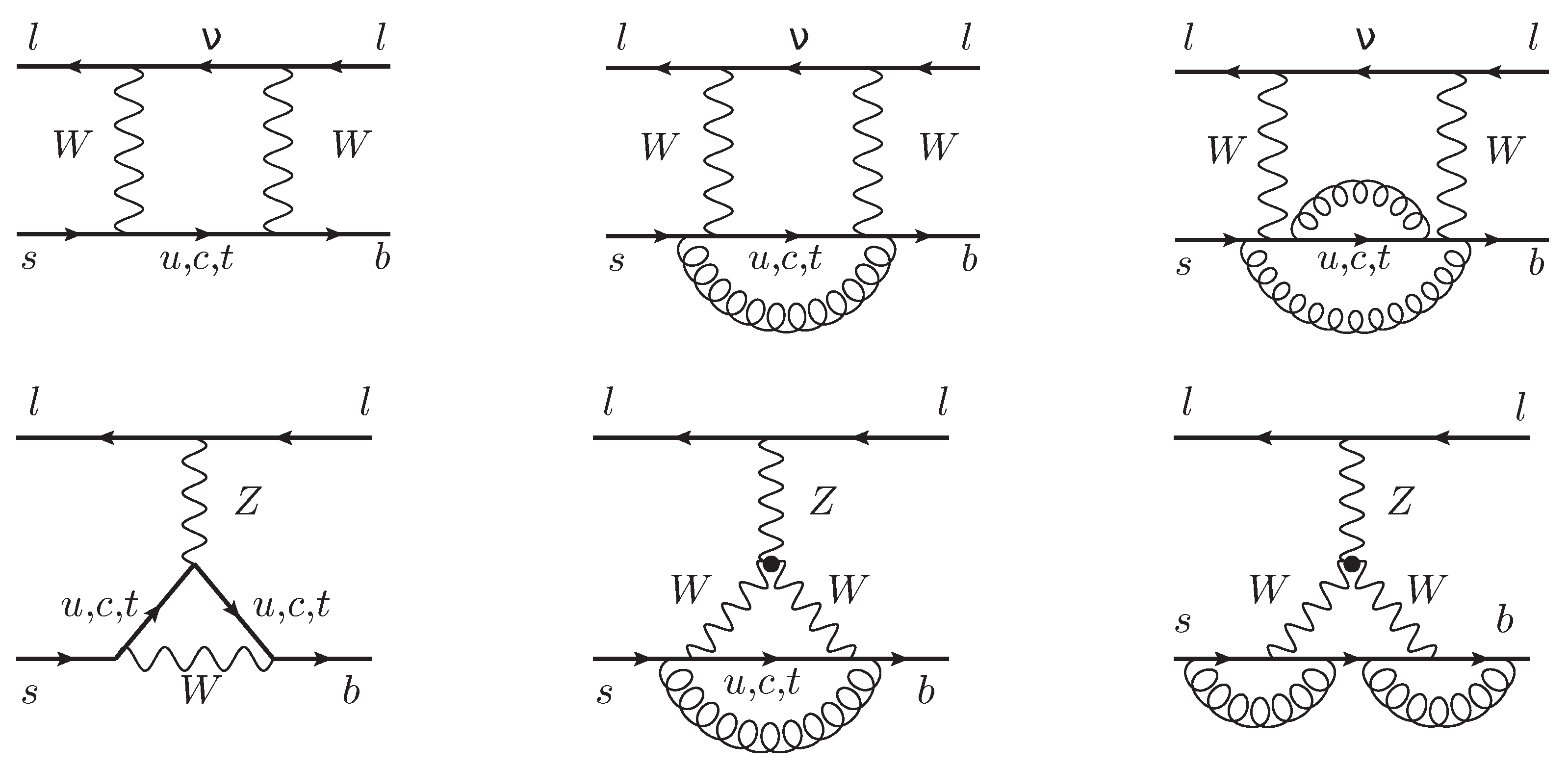
The SM Green’s function in Equation (12) receives QCD corrections from two classes of diagrams: W-boxes and Z-penguins, shown in Figure 3. Such bare diagrams are renormalized using lower-loop SM diagrams with counterterms. The QCD coupling constant renormalization has to be modified by an appropriate threshold correction to match the coupling constant of the effective theory with only five active flavors (see Section 3 in Ref. [25]). Similarly, the light-field wave-function renormalization constants have to be shifted to account for the decoupling threshold (see Section 4 in Ref. [26]). Heavy fields and masses are renormalized in the scheme.
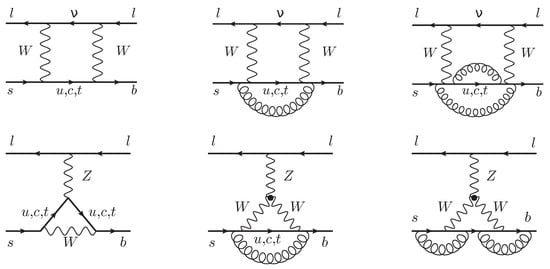
Figure 3.
Examples of diagrams entering the SM side of the matching Equation (12) at various orders in QCD. The W-boxes and Z-penguins are shown in the top and bottom rows, respectively. Contributions of the orders , , and are arranged from left to right. Diagrams from Figures 1 and 4 of Ref. [24].
Once both sides of the matching Equation (12) have been properly renormalized, the value of can be extracted. All the Dirac structures appearing on the SM side are mapped onto either or and their coefficients compared to the ones on the effective side.
The procedure described in this section was completed in Ref. [27] at the leading order, followed by Refs. [22,28,29] and [24] for the and corrections, respectively. In the latter case, high-order expansions in and were computed, and their combination was used to obtain a numerical result at the physical value of .
4. The Electroweak Corrections
4.1. The Correction
The next-to-leading order EW correction was first obtained in Ref. [30] (Let us note that it was called in that paper due to different notational conventions). Its calculation follows a similar pattern to the one described in the previous section. The main difference comes from additional Dirac structures appearing in the corrections on the SM side of the matching equation, which necessitate including additional operators in the effective Lagrangian. For the complete matching at the scale , at the leading order in and including terms, one has to retain all the operators from Equation (5), and supplement them with defined in Equation (11). The cancellation of spurious infrared divergence effects requires also the inclusion of additional evanescent operators (see Appendix A of Ref. [30]). The renormalization constants of all resulting Wilson coefficients are then calculated in a way analogous to the calculation.
Examples of diagrams contributing to on the SM side are shown in Figure 4. Before this correction can be extracted, the UV divergences on the SM side have to be renormalized. For a discussion of different renormalization schemes for the electroweak boson and top-quark masses, we refer to the original article [30]. Here, we will continue the analysis in the OS-2 scheme defined therein, as it was used in the subsequent phenomenological analysis [10]. In this scheme, all the QCD corrections to mass renormalization constants are defined in the , but the corrections to , , and are defined on-shell. In practice, the calculation is first performed fully in the scheme, and the finite terms in these three renormalization constants are subsequently added to the renormalized results.
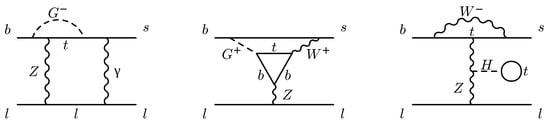
Figure 4.
Examples of diagrams contributing to the EW correction on the SM side of the matching Equation (12). Diagrams from Figure 1 of Ref. [30].
The value of extracted at the scale must then be RG-evolved down to the scale of the decay. The renormalized Wilson coefficients of the extended set of effective operators are related to the bare ones through a relation similar to Equation (15):
The one-loop RGE for Wilson coefficients has a general form
where the Anomalous Dimension Matrices (ADMs) and are obtained from the renormalization constants of Wilson coefficients. Once we restrict to non-evanescent operators only, the necessary MS-scheme relation reads
For the RGE (19) to close, one has to extend the set of operators in the effective Lagrangian further (see the discussion under Equation (15) in Ref. [30]). Analytical expressions for the evolution operator associated with Equation (19) can be found, e.g., in Ref. [31]. The details and results of the numerical solution can be found in Appendix B of Ref. [30].
4.2. Power-Enhanced QED Corrections
Within the effective theory framework, the S-matrix element corresponding to the decay receives contributions from diagrams with tree-level Wilson coefficients and a virtual photon exchanged between the fermions. In particular, there is a class of diagrams with a photon emitted from the spectator s quark and absorbed by one of the outgoing muons (see Figure 5). The leading terms of the power series in of this correction were computed in Ref. [11]. It was observed that its helicity suppression by the factor of in the tree-level branching ratio (6) is partially lifted due to a relative enhancement by .
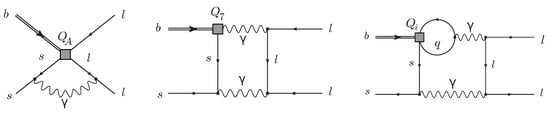
Figure 5.
Examples of diagrams with virtual photon exchanges that are responsible for the power-enhanced QED correction in Equation (23). Diagrams from Figure 1 of Ref. [11].
Effects of hard virtual photons with energies and virtualities above the scale are contained in the Wilson coefficients . The remaining virtual photons need to be taken into account in the physical matrix elements that are evaluated at the scale . In particular, virtual photons exchanged in the diagrams in Figure 5 probe the inner structure of the meson, smearing the annihilation point of the valence quarks over a distance , which corresponds to inverse virtuality of the off-shell s quark. Such long-distance QCD effects cannot be parameterized solely by , as at the leading order. Instead, one has to estimate the effects of matrix elements like
where is the time-ordering operator. They involve the B meson light-cone distribution amplitude [32] and its first logarithmic moments.
Virtual photon exchanges leading to power-enhanced QED corrections were thoroughly studied in the formalism of the Soft-Collinear Effective Theory by Beneke, Bobeth, and Szafron in Ref. [12]. Their effect can be included in the SM prediction through a replacement
with
The main uncertainty in comes from poorly known values of hadronic parameters [33]. We have extracted the numerical value of as well as its uncertainty in Equation (23) from Equations (8.8) and (8.10) of Ref. [12]. One can observe there that the relatively small central value of the correction () arises as an effect of partial cancellation between potentially unrelated contributions from the and operators. Thanks to this cancellation, the overall effect remains below the non-parametric uncertainty estimated in Ref. [10]. That uncertainty was primarily due to unknown effects, although the possibility of their power enhancement remained unknown at the time.
The contribution of to the considered corrections was reanalyzed in Ref. [34]. Despite several differences in the analytical expressions with respect to the earlier analysis of Ref. [12], the numerical results of the two papers remain in qualitative agreement, and no modification of the factor in Equation (23) is necessary.
5. Numerical Analysis
In this section, we update the SM prediction for based on Equation (6), including the complete and corrections to , as well as the QED correction factor in Equation (23). In practice, it is sufficient to use the semi-numerical expressions from Equation (6) of Ref. [10], which gives
where
In the above expressions, all the explicitly displayed input parameters are normalized to their 2013 central values. In Table 1, we update these central values together with the corresponding uncertainties. All the remaining parameters are retained unaltered with respect to Table I of Ref. [10], as their update would not affect in a noticeable manner—they are either very precisely measured or have little effect on .

Table 1.
Numerical values of the updated input parameters.
As already mentioned in Equation (2), we find . The overall uncertainty is now almost a factor of two smaller than that found in Ref. [10], while the central value remains almost unchanged. The latter fact can be attributed to an approximate cancellation of shifts stemming from the parameter updates and , as in the following sum:
As far as the uncertainty breakdown is concerned, its current version is compared to the 2013 one [10] in Table 2. In its last column, the uncertainties are combined in quadrature.

Table 2.
The current uncertainty breakdown in , as compared to the 2013 one.
One can observe a significant improvement in the first four columns where the dominant parametric uncertainties originate from, in particular in the case of , which is determined on the lattice. As far as the top-quark mass is concerned, let us recall that the PDG [9] value is treated as the on-shell mass, which is not strictly correct. However, the overall non-parametric uncertainty of is understood to contain a contribution from such an approximation. As is evident from Table 1 and Table 2, a shift in implies a shift in .
At present, the most important uncertainty originates from , in which case we use the inclusive determination only [35]. A combination with exclusive determinations would not lead to an improvement, given the persistent discrepancy between the inclusive and exclusive results [9]. Our preference is the same as in Ref. [10], i.e., we treat the inclusive determination as theoretically cleaner and more reliable.
As already mentioned in Ref. [10], one can get rid of in the ratio of to the measured - mass difference, at the cost of introducing an extra uncertainty from lattice determinations of the “bag parameter” . Such an approach is likely to become relevant once the experimental accuracy in (currently in Equation (1)) becomes closer to the theoretical one.
6. Conclusions
In this review, we analyzed the current SM prediction for the branching ratio of the rare decay. This channel continues to be among the most promising candidates for detecting BSM physics without the direct production of new particles, due to its SM suppression and possible BSM enhancements.
The SM analysis is, to a very good approximation, contained in the perturbative calculation of the Wilson coefficient and the lattice calculation of the long-distance QCD parameter . The perturbative part was already complete up to and including next-to-next-to-leading QCD and next-to-leading EW effects.
The currently dominant theoretical uncertainty originates from the CKM-matrix element . The next-to-dominant uncertainty is already non-parametric, stemming mainly from the unknown higher-order electromagnetic corrections at the scale . They depend on non-perturbative effects that are not contained in . The current result for changes by around when is varied between and . However, since it provides a lower bound only on the possible size of unknown electromagnetic effects, the actual uncertainty estimate should be somewhat more conservative. Here, we have retained the overall non-parametric uncertainty at the same level as in Ref. [10], namely .
The experimental error is currently much larger, around 8%, which sets a limit on the power of as a means for testing various BSM theories. The situation is expected to improve with time, when higher statistics are collected at the LHC and future experiments.
A final message that we would like to share with the reader is as follows. Our numerical result in Equation (2) will become outdated as soon as any of the input parameters are determined in a new analysis. Performing another update of does not require being an expert. It is sufficient to substitute new inputs into the simple formula (24).
Author Contributions
Both authors have equally contributed. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Science Center, Poland, under the research project 2020/37/B/ST2/02746.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Branching Ratio Formula
In this appendix, we sketch the derivation of the branching ratio formula (10) that holds in models with SM-like -violation, including the SM and the 2HDM. We work at the leading order in QED throughout, i.e., the final-state muons are understood to be emitted directly from the operator vertex (, , or ).
Let and denote the meson flavor eigenstates with valence quarks and , respectively. We fix conventions in their overall phases by demanding that , and . Once this is done, the heavier (H) and lighter (L) mass eigenstates (see Section 13 of Ref. [9]) can, respectively, be written as
where N has been defined in Equation (4). In the limit of no -violation (), and are -odd and -even, respectively.
From the form of the lepton currents in Equation (5), we observe that the and interactions can lead to production of -odd lepton pairs only (in the CM frame), while can lead to production of -even pairs only. In the case, it follows from the fact that the timelike component of the lepton current is -odd (see, e.g., the table below Equation (3.150) of Ref. [38]), while the spacelike components play no role, as they get contracted with the vanishing spacelike components of the meson momentum (see Equation (7)).
Let us now show that even in the presence of SM-like -violation, ( but real Wilson coefficients), the operators and have no effect on dimuonic decays of , while has no effect on such decays of . When the “” terms in the Lagrangian (3) are taken into account, the leading contribution to the decay amplitude is proportional to
where the matrix elements on the r.h.s. are the only two that do not vanish due to flavor conservation in QCD. Next, we observe that
where we have taken advantage of the fact that the dimuon state is -odd, as argued above. Consequently, the sum of the two matrix elements on the r.h.s. of Equation (A2) vanishes. An identical reasoning holds for . As far as and are concerned, we proceed by analogy:
where, this time, the dimuon state is -even. Consequently, the difference in the two matrix elements on the r.h.s. of Equation (A4) vanishes. As a by-product of the above reasoning, we can simplify the non-vanishing matrix elements as follows:
Both at the LHC and at machines, the production rates of and are practically equal. Thus, to a very good approximation, the heavy and light mass eigenstates are produced in the same quantities, as can be seen by inverting the relation (A1). Since the decay products of (-odd dimuons) and (-even dimuons) do not interfere, the average time-integrated branching ratio is simply given by
In each of the two cases, the decay rate is given by the well-known formula
with
Here, are the corresponding invariant matrix elements, has been defined below Equation (6), and we have neglected the tiny mass splitting between and . Summing over spins of the final-state muons is understood in Equation (A8). The two-body phase-space integral is trivial (see Section 3.2 of Ref. [39]), as is constant in the integration domain due to rotational symmetry in the decaying scalar rest frame.
The (and ) contribution to reads
where the identity (A6) has already been taken into account. Moreover, the state normalization has been adjusted to the one that is conventionally used in the decay-constant definition (7), namely
To verify that the global normalization in Equation (A10) is correct, one can begin with the relevant S matrix element
In its evaluation, the meson hadronic structure cannot be treated in a perturbative manner. Therefore, in the definition of the in/out states in the above equation, the interaction part of the Lagrangian that is switched off at timelike infinities consists only of the weak part . It is assumed that non-perturbative QCD effects have been solved beforehand and are contained in that is treated as an asymptotic state from the weak interaction perspective.
In practice, the right normalization in Equation (A10) can be determined with possibly least effort by considering an analogy with a certain purely perturbative theory. Suppose the muons interact with a massive real pseudoscalar via a dimension-five operator . Once the tree-level invariant matrix element for the decay is quickly determined, it should be expressed in terms of the free-field matrix element , with the free-particle state normalized as in Equation (A11). Finally, replacing
(see Equation (A6)), one obtains Equation (A10) with the proper overall normalization.
The r.h.s. of Equation (A10) can be further simplified by noticing that
where the identities and have been used in the last step. Let us note that our expression would vanish in the absence of , which is related to the vanishing divergence of the vectorlike current, the same one that enters the QED interactions of muons and photons. This is precisely the reason why we were allowed to skip in our initial operator list in Equation (5).
Let us now turn to the operators and . The pseudoscalar current that is present in both of them can be eliminated in favor of the axial current using Equations of Motion (EoMs) for the s- and -quark operator fields:
where g and e are the QCD and QED couplings, respectively, is the gluon field, is the photon field, and are the SU(3) generators. The effects on the r.h.s. of the above equations stand for higher-order weak-interaction effects that stem from the operators in Equation (). Such effects will be neglected below, as we are going to use the EoM to transform the weak operators and , while we work at the leading order in weak interactions. Operators that vanish by the EoM will commonly be denoted by . They can be skipped in evaluation of observables at the leading order in weak interactions, as their physical matrix elements vanish.
To proceed, we multiply the first equation in (A14) by from the left, the second one by from the right, take their difference, rearrange, and obtain
Using the above identity, one can express the following total derivative as
Consequently,
where commonly denotes total derivatives of operators that are invariant under QCD and QED gauge transformations. Similarly,
Since in the Lagrangian has no effect on physical observables, we are allowed to replace and by the first (explicit) terms in the above equations. After such replacements, the same quark current shows up in , , and , which means that only a single non-perturbative quantity, namely , is sufficient to describe their physical matrix elements at the leading order in QED.
Using Equations (A17) and (A18), and performing calculations along the same way as in the case of , one obtains
and
The total invariant matrix element for reads
It remains to take the moduli squared and perform the sums over spins:
Finally, after substitution to Equation (A8) and then (A7), we end up with the branching ratio formula quoted in Equation (10).
In BSM models with generic (not SM-like) -violation, the Wilson coefficients , , and are not necessarily real. Moreover, the mass eigenstates are not necessarily given by Equation (A1), as the phase factors may differ from and . The latter effect can be described by introducing an extra complex phase , see Section 2.2 of Ref. [15]. In such models, the branching ratio formula generalizes to
with r, , and u that have been defined below Equations (6) and (10), as well as
The above expressions for and have been derived from the results of Refs. [40,41] where an interesting discussion concerning time-dependent observables can be found.
Appendix B. Numerical Update for
Here, we present the current SM prediction for , i.e., the average time-integrated branching ratio of . The necessary formula is analogous to Equation (24), obtained by combining the semi-numerical expression from Equation (7) of Ref. [10] with (23) derived from Ref. [12]. It reads
where
As input, we need three more parameters in addition to those already listed in Table 1, namely the decay constant of the meson, the average lifetime of this meson , and the relevant CKM factor . Their current values are listed in Table A1. Our use of the well-measured instead of is a good approximation thanks to the very small width difference predicted in the SM for the - system: [42].

Table A1.
Numerical values of the extra input parameters that matter for .
Table A1.
Numerical values of the extra input parameters that matter for .
| Parameter | Value | Unit | Refs. |
|---|---|---|---|
| 190.0 (1.3) | MeV | [16,17,18,19,20] | |
| 0.00851 (10) | - | derived from Ref. [36] | |
| 1.517 (4) | ps | [37] |
After substituting all the numerical inputs to Equation (A25), we find
The uncertainty breakdown is presented in Table A2, in the same manner as it was done for in Table 2.

Table A2.
The current uncertainty breakdown in , as compared to the 2013 one.
Table A2.
The current uncertainty breakdown in , as compared to the 2013 one.
| CKM | Other | Non-Parametric | ∑ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2024 [this paper] | % | % | % | % | % | <0.1% | % | % | |
| 2013 [10] | % | % | % | % | % | <0.1% | % | % |
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 16565–16590. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Altmannshofer, W.; Stangl, P. New physics in rare B decays after Moriond 2021. Eur. Phys. J. C 2021, 81, 952. [Google Scholar] [CrossRef] [PubMed]
- Aaij, R.; Abellan Beteta, C.; Adametz, A.; Adeva, B.; Adinolfi, M.; Adrover, C.; Affolder, A.; Ajaltouni, Z.; Albrecht, J.; Alessio, F.; et al. First Evidence for the Decay → μ+μ−. Phys. Rev. Lett. 2013, 110, 021801. [Google Scholar] [CrossRef] [PubMed]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Brandstetter, J.; Dragicevic, M.; Erö, J.; Escalante Del Valle, A.; Flechl, M.; et al. Measurement of properties of → μ+μ− decays and search for B0 → μ+μ− with the CMS experiment. J. High Energy Phys. 2020, 2020, 188. [Google Scholar] [CrossRef]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Del Valle, A.E.; Hussain, P.S.; Jeitler, M.; et al. Measurement of the → μ+μ− decay properties and search for the B0 → μ+μ− decay in proton-proton collisions at s = 13 TeV. Phys. Lett. B 2023, 842, 137955. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Analysis of Neutral B-Meson Decays into Two Muons. Phys. Rev. Lett. 2022, 128, 041801. [Google Scholar] [CrossRef] [PubMed]
- Aaboud, M.; Aad, G.; Abbott, B.; Abbott, D.C.; Abdinov, O.; Abeloos, B.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; et al. Study of the rare decays of and B0 mesons into muon pairs using data collected during 2015 and 2016 with the ATLAS detector. J. High Energy Phys. 2019, 2019, 098. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. Review of Particle Physics. Phys. Rev. D 2024, 110, 030001. Available online: https://pdg.lbl.gov (accessed on 1 June 2024).
- Bobeth, C.; Gorbahn, M.; Hermann, T.; Misiak, M.; Stamou, E.; Steinhauser, M. Bs,d → l+l− in the Standard Model with Reduced Theoretical Uncertainty. Phys. Rev. Lett. 2014, 112, 101801. [Google Scholar] [CrossRef]
- Beneke, M.; Bobeth, C.; Szafron, R. Enhanced electromagnetic correction to the rare B-meson decay Bs,d → μ+μ−. Phys. Rev. Lett. 2018, 120, 011801. [Google Scholar] [CrossRef]
- Beneke, M.; Bobeth, C.; Szafron, R. Power-enhanced leading-logarithmic QED corrections to Bq → μ+μ−. J. High Energy Phys. 2019, 10, 232, Erratum in J. High Energy Phys. 2022, 11, 099. [Google Scholar] [CrossRef]
- Arbey, A.; Mahmoudi, F.; Stal, O.; Stefaniak, T. Status of the Charged Higgs Boson in Two Higgs Doublet Models. Eur. Phys. J. C 2018, 78, 182. [Google Scholar] [CrossRef]
- Arbey, A.; Battaglia, M.; Mahmoudi, F. Constraints on the MSSM from the Higgs Sector: A pMSSM Study of Higgs Searches, → μ+μ− and Dark Matter Direct Detection. Eur. Phys. J. C 2012, 72, 1906. [Google Scholar] [CrossRef]
- Buras, A.J.; Fleischer, R.; Girrbach, J.; Knegjens, R. Probing New Physics with the Bs → μ+μ− Time-Dependent Rate. J. High Energy Phys. 2013, 2013, 077. [Google Scholar] [CrossRef]
- Bazavov, A.; Bernard, C.; Brown, N.; DeTar, C.; El-Khadra, X.; Gámiz, E.; Gottlieb, S.; Heller, M.; Komijani, J.; Kronfeld, S.; et al. B- and D-meson leptonic decay constants from four-flavor lattice QCD. Phys. Rev. D 2018, 98, 074512. [Google Scholar] [CrossRef]
- Bussone, A.; Carrasco, N.; Dimopoulos, P.; Frezzotti, R.; Lami, P.; Lubicz, V.; Picca, E.; Riggio, L.; Rossi, G.C.; Simula, S.; et al. Mass of the b quark and B -meson decay constants from Nf=2+1+1 twisted-mass lattice QCD. Phys. Rev. D 2016, 93, 114505. [Google Scholar] [CrossRef]
- Dowdall, R.J.; Davies, C.T.H.; Horgan, R.R.; Monahan, C.J.; Shigemitsu, J. B-Meson Decay Constants from Improved Lattice Nonrelativistic QCD with Physical u, d, s, and c Quarks. Phys. Rev. Lett. 2013, 110, 222003. [Google Scholar] [CrossRef]
- Hughes, C.; Davies, C.T.H.; Monahan, C.J. New methods for B meson decay constants and form factors from lattice NRQCD. Phys. Rev. D 2018, 97, 054509. [Google Scholar] [CrossRef]
- Aoki, Y.; Blum, T.; Colangelo, G.; Collins, S.; Della Morte, M.; Dimopoulos, P.; Dürr, S.; Feng, X.; Fukaya, H.; Golterman, M.; et al. FLAG Review 2021. Eur. Phys. J. C 2022, 82, 869. [Google Scholar] [CrossRef]
- Logan, H.E.; Nierste, U. Bs,d → ℓ+ℓ− in a two Higgs doublet model. Nucl. Phys. B 2000, 586, 39–55. [Google Scholar] [CrossRef]
- Misiak, M.; Urban, J. QCD corrections to FCNC decays mediated by Z-penguins and W-boxes. Phys. Lett. B 1999, 451, 161–169. [Google Scholar] [CrossRef]
- Dugan, M.J.; Grinstein, B. On the vanishing of evanescent operators. Phys. Lett. B 1991, 256, 239–244. [Google Scholar] [CrossRef]
- Hermann, T.; Misiak, M.; Steinhauser, M. Three-loop QCD corrections to Bs → μ+μ−. J. High Energy Phys. 2013, 12, 097. [Google Scholar] [CrossRef]
- Steinhauser, M. Results and techniques of multiloop calculations. Phys. Rept. 2002, 364, 247–357. [Google Scholar] [CrossRef]
- Misiak, M.; Steinhauser, M. Three loop matching of the dipole operators for b → sγ and b → sg. Nucl. Phys. B 2004, 683, 277–305. [Google Scholar] [CrossRef][Green Version]
- Inami, T.; Lim, C.S. Effects of Superheavy Quarks and Leptons in Low-Energy Weak Processes KL → μ, K+ → π+ν and K0↔0. Prog. Theor. Phys. 1981, 65, 297–314. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. QCD corrections to rare K- and B-decays for arbitrary top quark mass. Nucl. Phys. B 1993, 400, 225–239. [Google Scholar] [CrossRef]
- Buchalla, G.; Buras, A.J. QCD corrections to the sdZ vertex for arbitrary top quark mass. Nucl. Phys. B 1993, 398, 285–300. [Google Scholar] [CrossRef]
- Bobeth, C.; Gorbahn, M.; Stamou, E. Electroweak Corrections to Bs,d → ℓ+ℓ−. Phys. Rev. D 2014, 89, 034023. [Google Scholar] [CrossRef]
- Huber, T.; Lunghi, E.; Misiak, M.; Wyler, D. Electromagnetic logarithms in → Xsl+l−. Nucl. Phys. B 2006, 740, 105–137. [Google Scholar] [CrossRef]
- Beneke, M.; Buchalla, G.; Neubert, M.; Sachrajda, C.T. QCD factorization for B → ππ decays: Strong phases and CP violation in the heavy quark limit. Phys. Rev. Lett. 1999, 83, 1914–1917. [Google Scholar] [CrossRef]
- Beneke, M.; Rohrwild, J. B meson distribution amplitude from B → γℓ. Eur. Phys. J. C 2011, 71, 1818. [Google Scholar] [CrossRef]
- Feldmann, T.; Gubernari, N.; Huber, T.; Seitz, N. Contribution of the electromagnetic dipole operator O7 to the s → μ+μ− decay amplitude. Phys. Rev. D 2023, 107, 013007. [Google Scholar] [CrossRef]
- Finauri, G.; Gambino, P. The q2 moments in inclusive semileptonic B decays. J. High Energy Phys. 2024, 2024, 206. [Google Scholar] [CrossRef]
- Charles, J.; Hocker, A.; Lacker, H.; Laplace, S.; Le Diberder, F.R.; Malcles, J.; Ocariz, J.; Pivk, M.; Roos, L. CP violation and the CKM matrix: Assessing the impact of the asymmetric B factories. Eur. Phys. J. C 2005, 41, 1–131. [Google Scholar] [CrossRef]
- Amhis, Y.S.; Banerjee, S.; Ben-Haim, E.; Bertholet, E.; Bernlochner, F.U.; Bona, M.; Bozek, A.; Bozzi, C.; Brodzicka, J.; Chobanova, V.; et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of 2021. Phys. Rev. D 2023, 107, 052008. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley: Reading, PA, USA, 1995. [Google Scholar] [CrossRef]
- Lang, M. Leptonic Decays of Neutral B Mesons in the Three-Spurion Two-Higgs-Doublet Model. Ph.D. Thesis, KIT, Karlsruhe, Germany, 2023. [Google Scholar] [CrossRef]
- De Bruyn, K.; Fleischer, R.; Knegjens, R.; Koppenburg, P.; Merk, M.; Pellegrino, A.; Tuning, N. Probing New Physics via the → μ+μ− Effective Lifetime. Phys. Rev. Lett. 2012, 109, 041801. [Google Scholar] [CrossRef]
- De Bruyn, K.; Fleischer, R.; Knegjens, R.; Koppenburg, P.; Merk, M.; Tuning, N. Branching Ratio Measurements of Bs Decays. Phys. Rev. D 2012, 86, 014027. [Google Scholar] [CrossRef]
- Asatrian, H.M.; Asatryan, H.H.; Hovhannisyan, A.; Nierste, U.; Tumasyan, S.; Yeghiazaryan, A. Penguin contribution to the width difference and CP asymmetry in Bq-q mixing at order Nf. Phys. Rev. D 2020, 102, 033007. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).