Operating Characteristic Analysis and Verification of Short-Stroke Linear Oscillating Actuators Considering Mechanical Load
Abstract
:1. Introduction
2. Analysis of LOAs
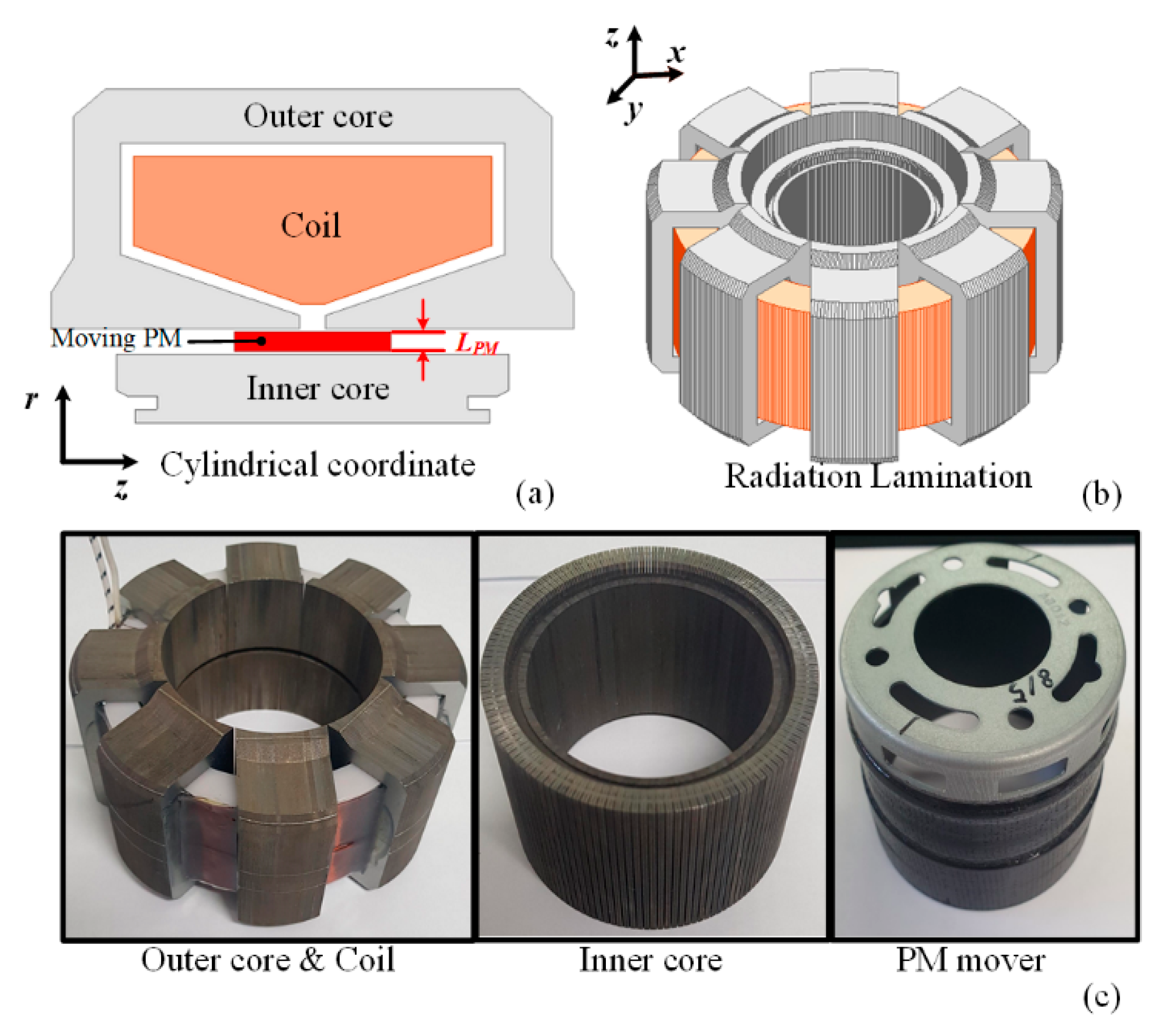
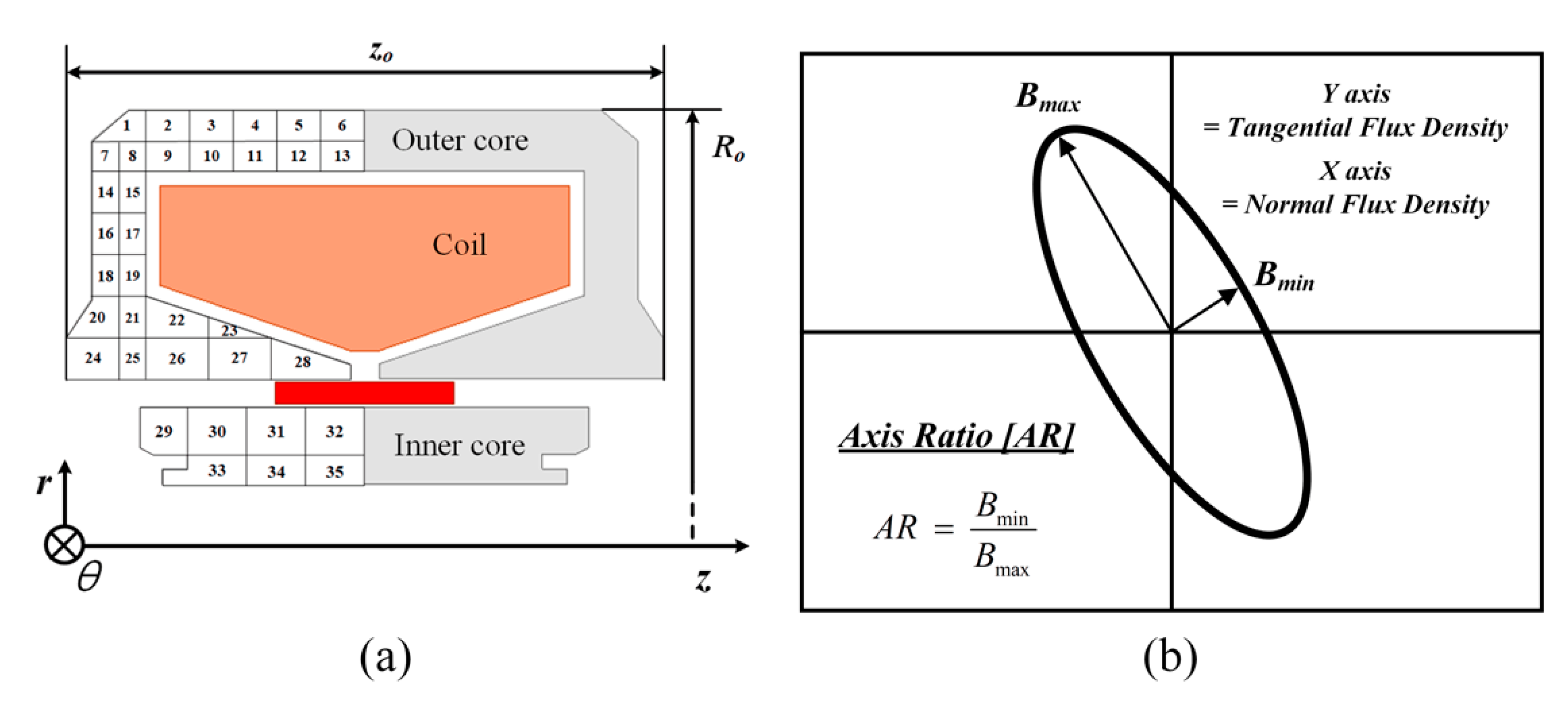
2.1. Topology and Features
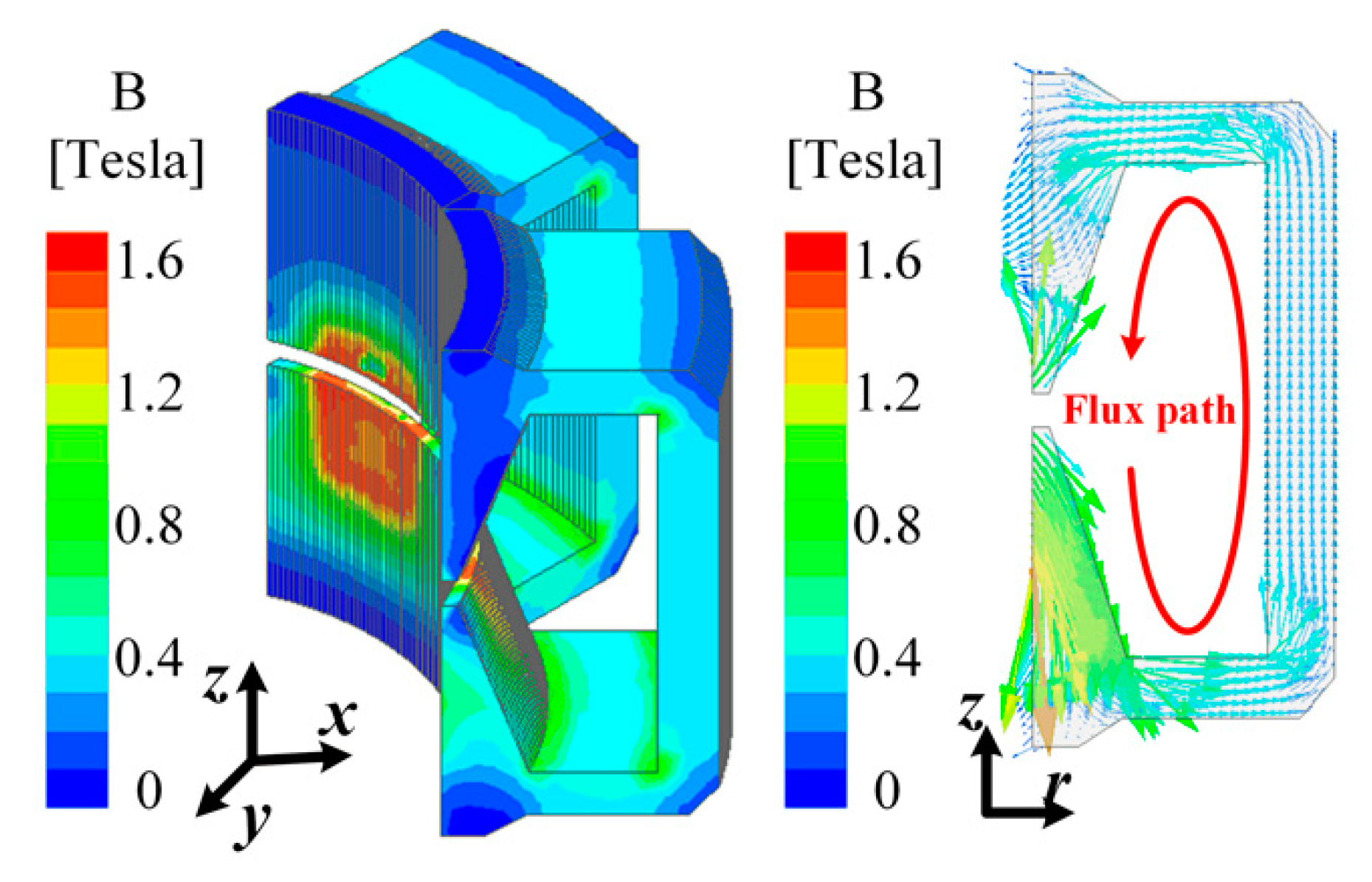
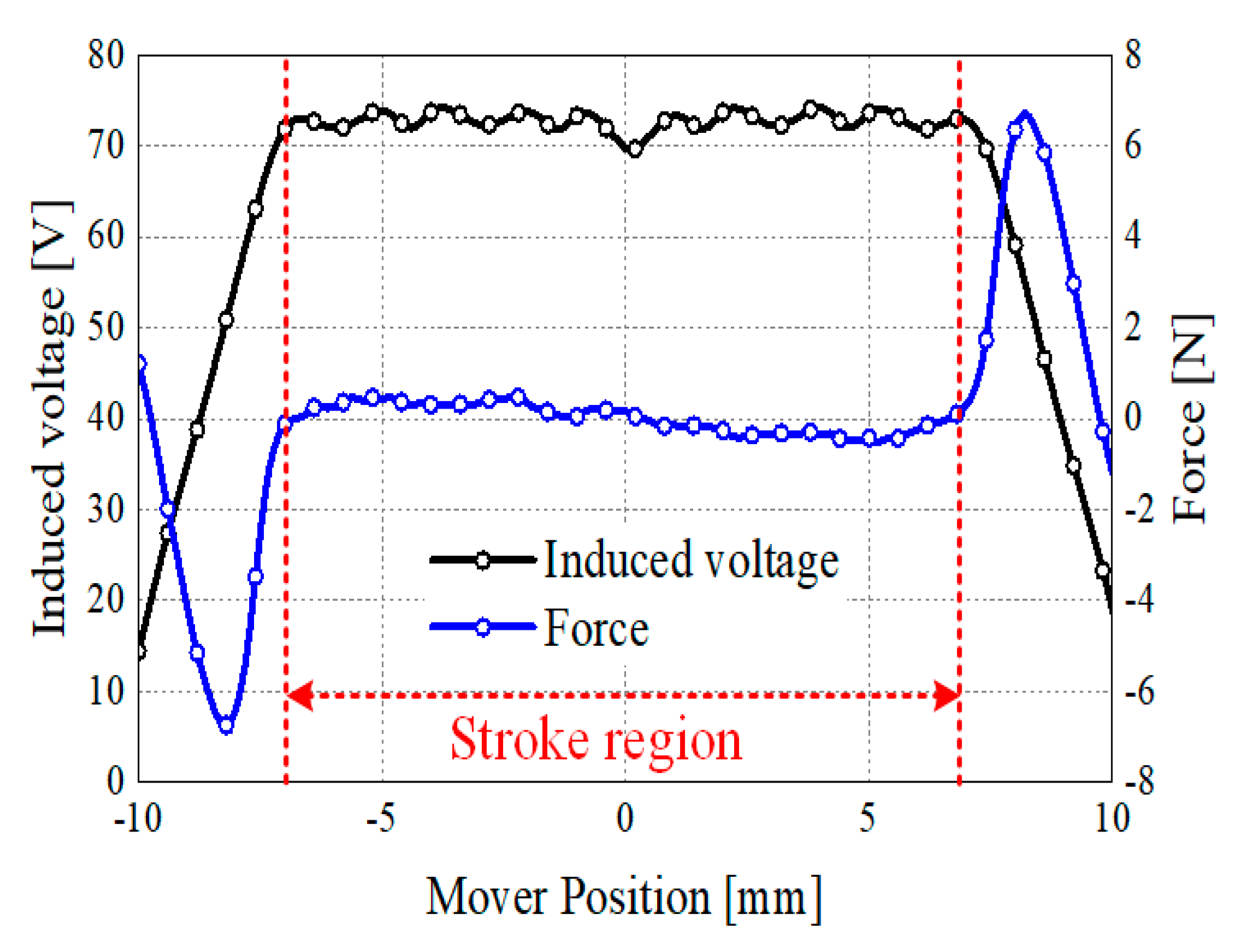
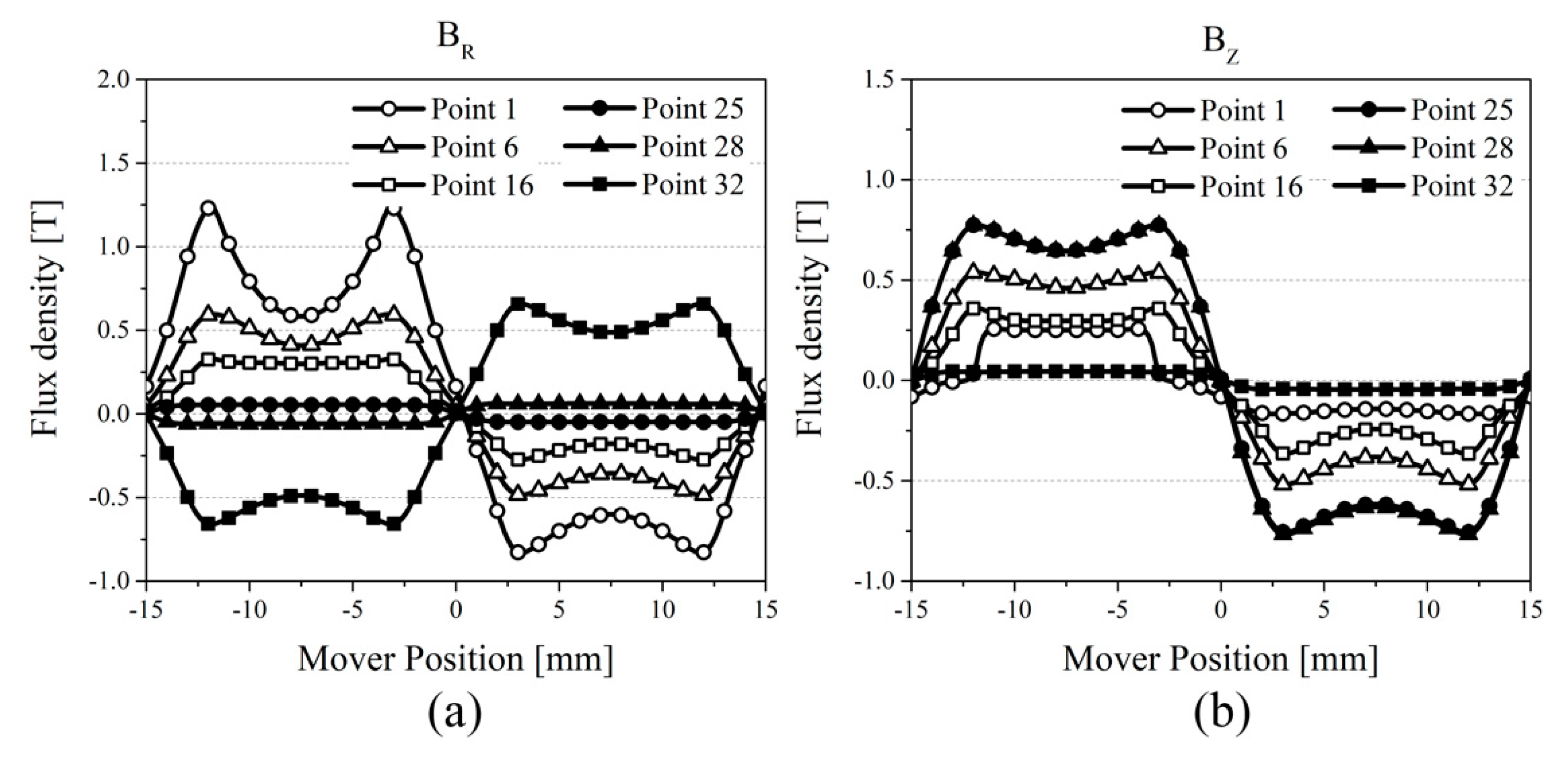
2.2. Electromagnetic Characteristic of LOM
2.3. Electromagnetic Loss Characteristic of LOM
2.3.1. Copper Loss
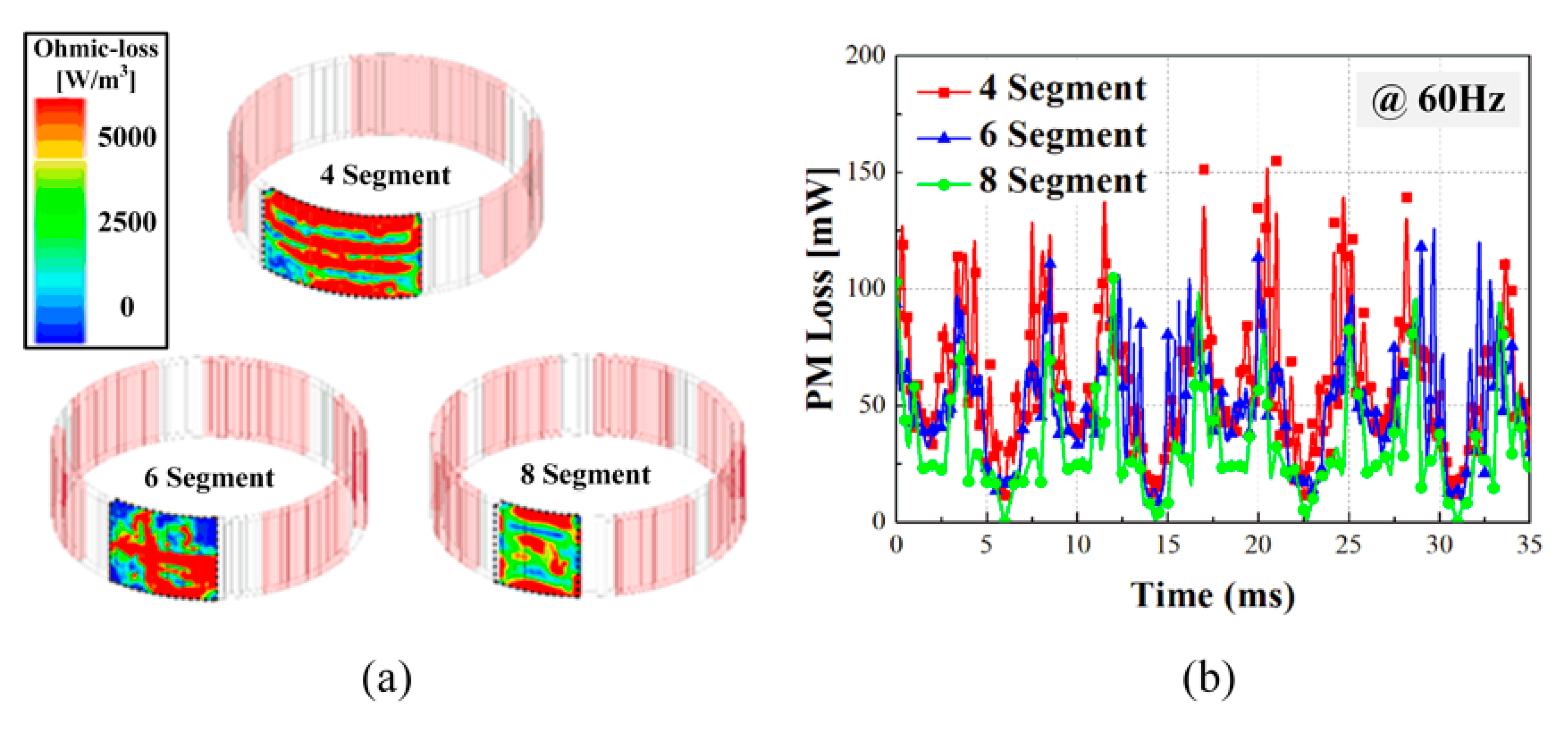
2.3.2. Eddy Current Loss
2.3.3. Core Loss
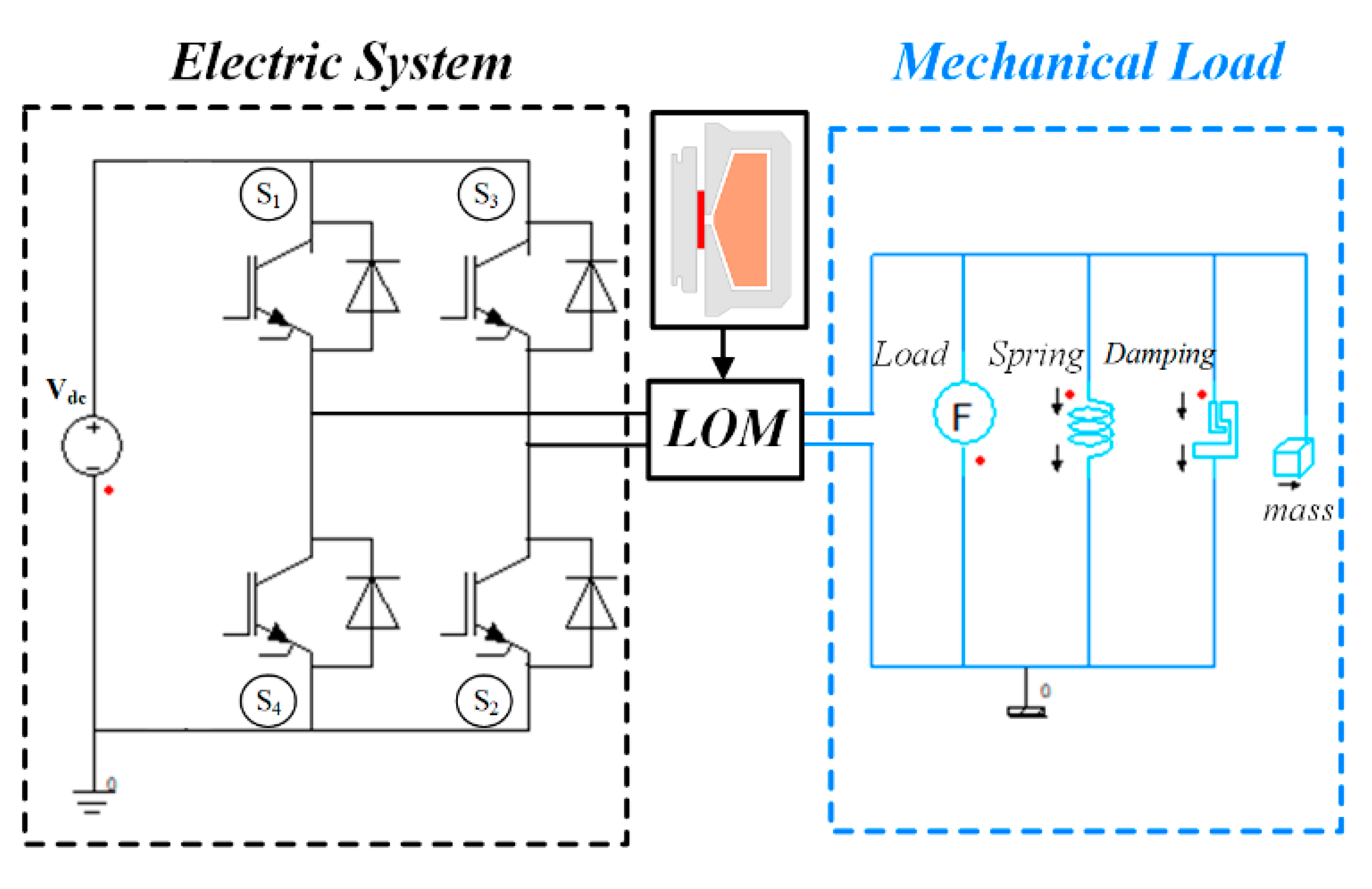
2.4. Dynamic Characteristic of LOM
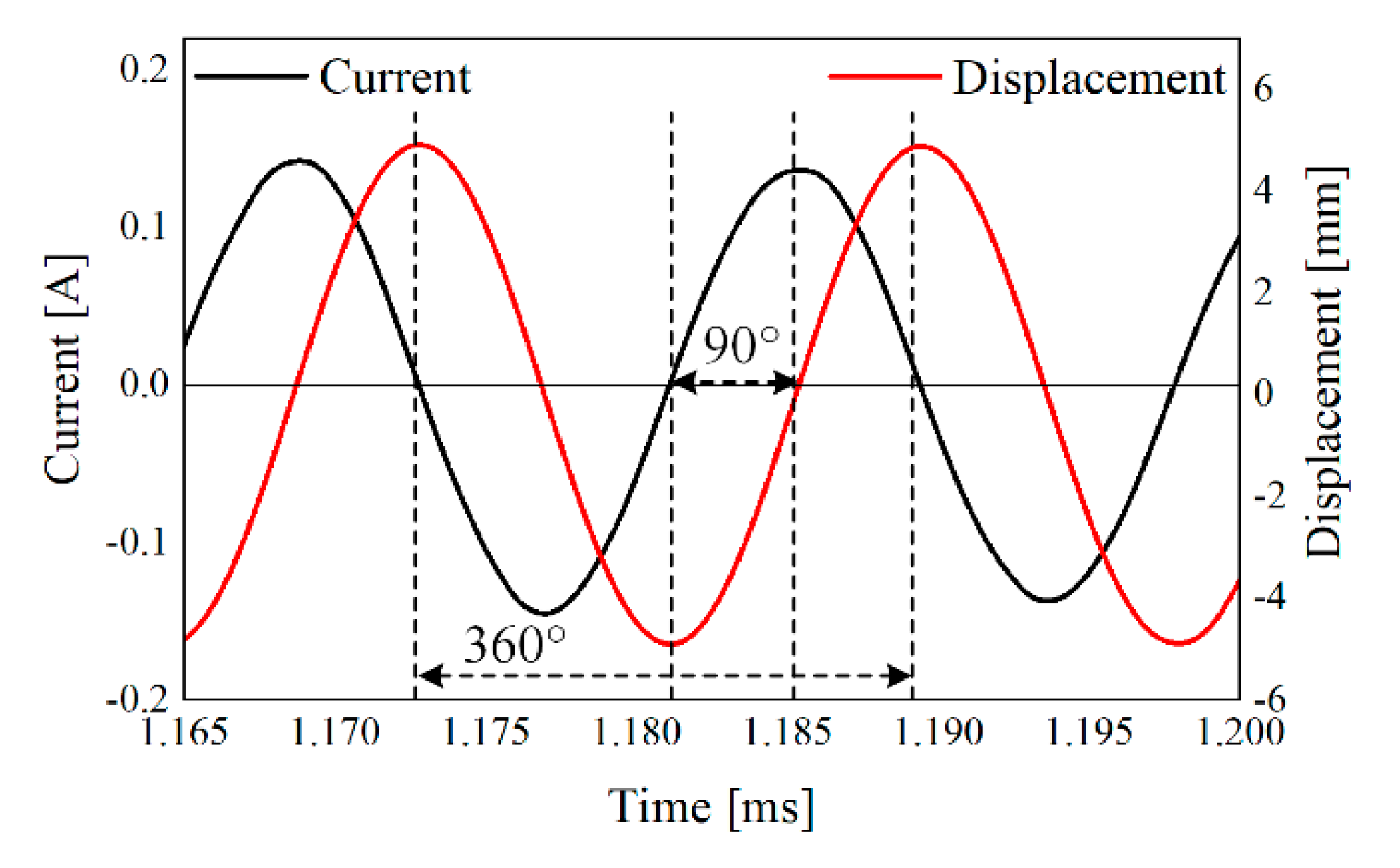
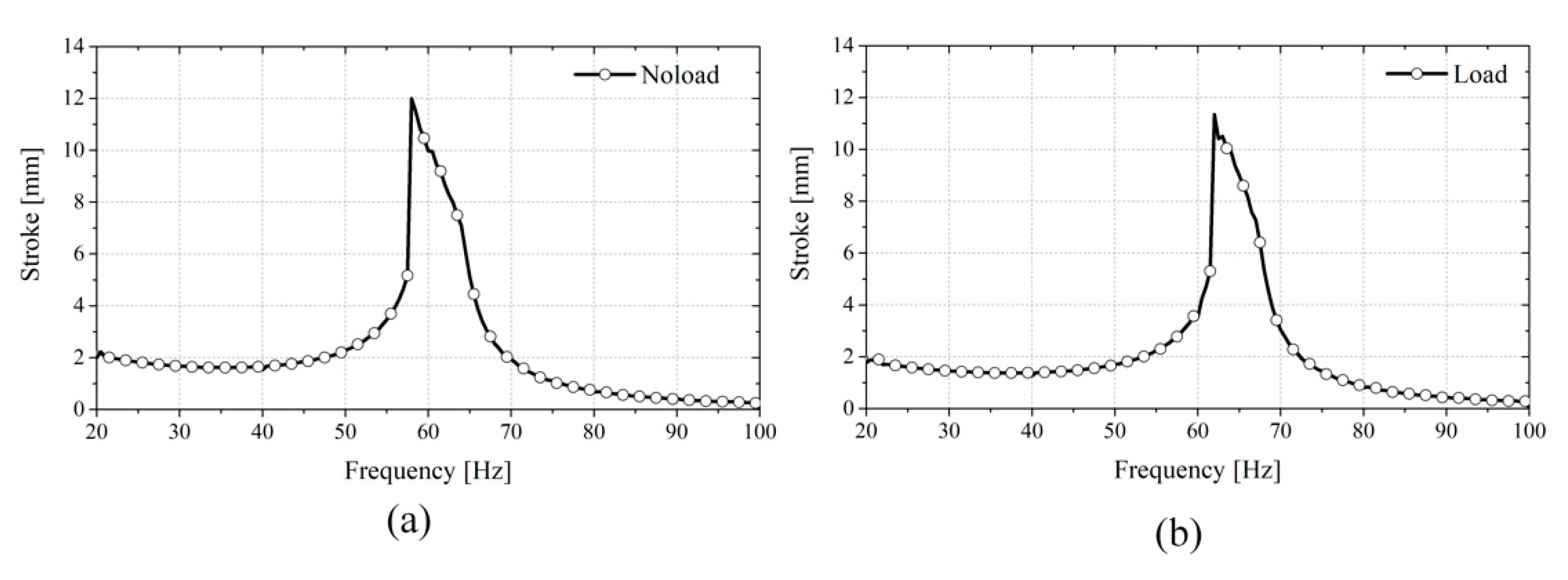
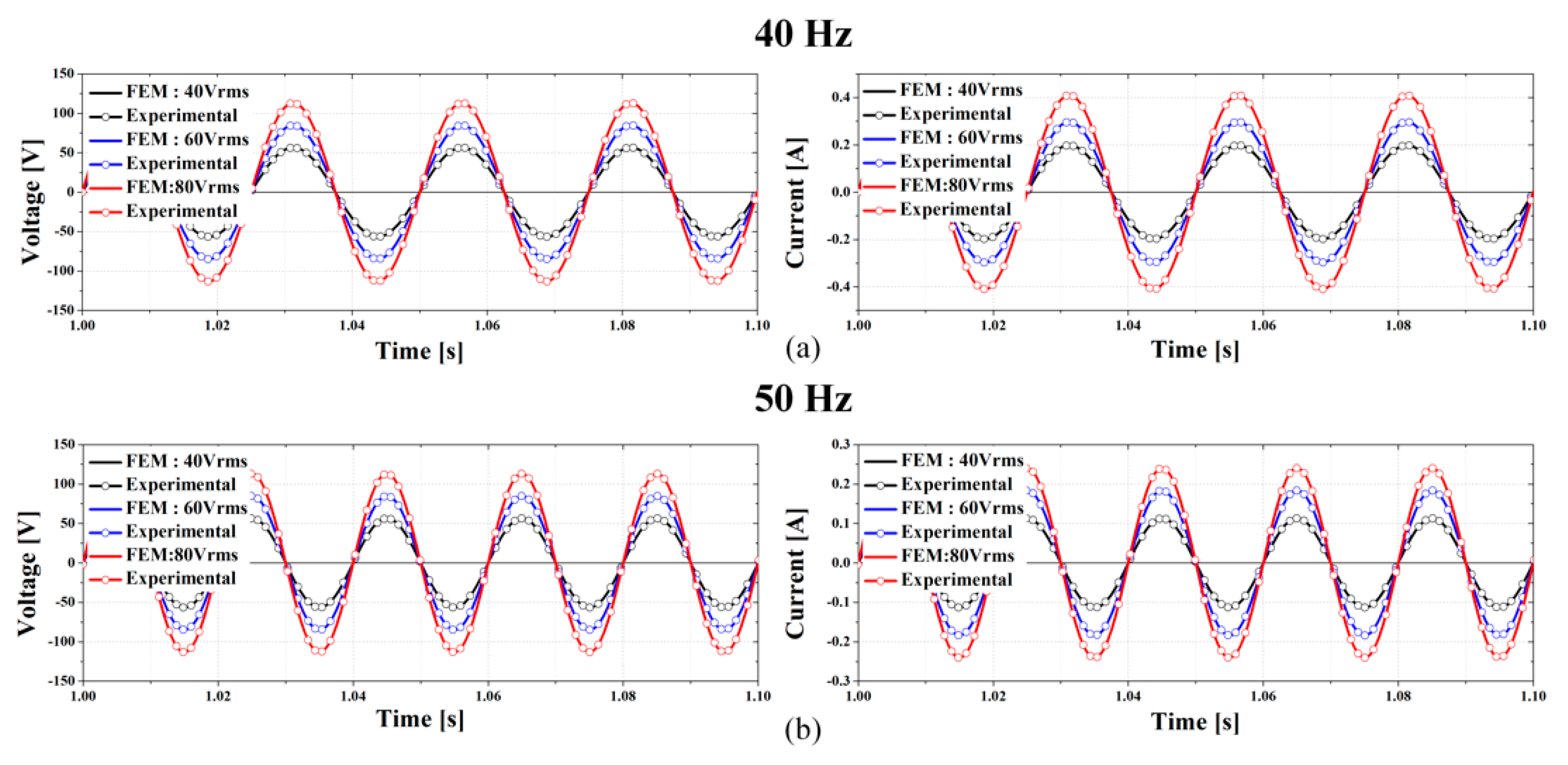
3. Experiment and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Howe, D.; Lin, Z. Design Optimization of Short-Stroke Single-Phase Tubular Permanent-Magnet Motor for Refriger-ation Applications. IEEE Trans. Ind. Electron. 2010, 57, 327–334. [Google Scholar] [CrossRef]
- Ibrahim, T.; Wang, J.; Howe, D. Analysis of a single phase, quasi-Halbach magnetised tubular permanent magnet motor with non-ferromagnetic supporting tube. In Proceedings of the 4th IET International Conference on Power Electronics, Machines and Drives (PEMD 2008), York, UK, 2–4 April 2008; pp. 762–766. [Google Scholar]
- Zhu, Z.; Chen, X.; Howe, D.; Iwasaki, S. Electromagnetic Modeling of a Novel Linear Oscillating Actuator. IEEE Trans. Magn. 2008, 44, 3855–3858. [Google Scholar] [CrossRef]
- Khalid, S.; Khan, F.; Ahmad, Z.; Ullah, B. Design and finite element analysis of modular C-Core stator tubular linear oscillating actuator for miniature compressor. World J. Eng. 2021, ahead-of-print. [Google Scholar] [CrossRef]
- Ahmad, Z.; Hassan, A.; Khan, F.; Ahmad, N.; Khan, B.; Ro, J.-S. Analysis and Design of a Novel Outer Mover Moving Magnet Linear Oscillating Actuator for a Refrigeration System. IEEE Access. 2021, 9, 121240–121252. [Google Scholar] [CrossRef]
- Chen, H.; Nie, R.; Yan, W. A Novel Structure Single-Phase Tubular Switched Reluctance Linear Motor. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Ahmad, Z.; Hassan, A.; Khan, F.; Lazoglu, I. Design of a high thrust density moving magnet linear actuator with magnetic flux bridge. IET Electr. Power Appl. 2020, 14, 1256–1262. [Google Scholar] [CrossRef]
- Xue, X.; Cheng, K.W.E.E.; Zhang, Z. Model, Analysis, and Application of Tubular Linear Switched Reluctance Actuator for Linear Compressors. IEEE Trans. Ind. Electron. 2018, 65, 9863–9872. [Google Scholar] [CrossRef]
- Asai, Y.; Ota, T.; Yamamoto, T.; Hirata, K. Proposed of Novel Linear Oscillating Actuator’s Structure Using Topology Optimi-zation. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Roemer, D.B.; Bech, M.M.; Johansen, P.; Pedersen, H.C. Optimum Design of a Moving Coil Actuator for Fast-Switching Valves in Digital Hydraulic Pumps and Motors. IEEE/ASME Trans. Mechatron. 2015, 20, 2761–2770. [Google Scholar] [CrossRef]
- Al-Otaibi, Z.S. Spring-less permanent magnet linear-resonant motor for compressor applications. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 420–423. [Google Scholar]
- Lee, K.-S.; Lee, S.-H.; Park, J.-H.; Choi, J.-Y.; Sim, K.-H. Design and Experimental Analysis of a 3 kW Single-Phase Linear Permanent Magnet Generator for Stirling Engines. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Atallah, K.; Howe, D.; Mellor, P.; Stone, D. Rotor loss in permanent magnet brushless AC machines. In Proceedings of the IEEE International Electric Machines and Drives Conference. IEMDC’99., Seattle, WA, USA, 9–12 May 1999; pp. 60–62. [Google Scholar] [CrossRef]
- Bertotti, G. General properties of power losses in soft ferromagnetic materials. IEEE Trans. Magn. 1988, 24, 621–630. [Google Scholar] [CrossRef]
- Nam, H.; Ha, K.-H.; Lee, J.-J.; Hong, J.-P.; Kang, G.-H. A study on iron loss analysis method considering the harmonics of the flux density waveform using iron loss curves tested on epstein samples. IEEE Trans. Magn. 2003, 39, 1472–1475. [Google Scholar] [CrossRef]






| Copper Loss | Core Loss | Solid Loss | Power | Efficiency |
|---|---|---|---|---|
| 1.18 W | 2.85 W | 0.04 W | 110 W | 96.4% |
| Parameter | Value |
|---|---|
| Spring Coefficient | 34,800 N/m |
| Damping Coefficient | 0.9 Ns/m |
| Mover Mass | 0.25 kg |
| Resonance Frequency | 60 Hz |
| Parameter | Value |
|---|---|
| Operating frequency | 60 Hz |
| Rated stroke | ±5 mm |
| Outer core radius | 59 mm |
| Stator type | Outer core |
| Mover type | PM mover |
| Rated power | 100 W |
| Resistance | 1.11 Ω |
| Inductance | 792 mH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, W.-H.; Kim, C.-W.; Shin, H.-S.; Shin, K.-H.; Choi, J.-Y. Operating Characteristic Analysis and Verification of Short-Stroke Linear Oscillating Actuators Considering Mechanical Load. Machines 2022, 10, 48. https://doi.org/10.3390/machines10010048
Kim W-H, Kim C-W, Shin H-S, Shin K-H, Choi J-Y. Operating Characteristic Analysis and Verification of Short-Stroke Linear Oscillating Actuators Considering Mechanical Load. Machines. 2022; 10(1):48. https://doi.org/10.3390/machines10010048
Chicago/Turabian StyleKim, Woo-Hyeon, Chang-Woo Kim, Hyo-Seob Shin, Kyung-Hun Shin, and Jang-Young Choi. 2022. "Operating Characteristic Analysis and Verification of Short-Stroke Linear Oscillating Actuators Considering Mechanical Load" Machines 10, no. 1: 48. https://doi.org/10.3390/machines10010048
APA StyleKim, W.-H., Kim, C.-W., Shin, H.-S., Shin, K.-H., & Choi, J.-Y. (2022). Operating Characteristic Analysis and Verification of Short-Stroke Linear Oscillating Actuators Considering Mechanical Load. Machines, 10(1), 48. https://doi.org/10.3390/machines10010048







