Gearbox Condition Monitoring and Diagnosis of Unlabeled Vibration Signals Using a Supervised Learning Classifier
Abstract
:1. Introduction
- Monitoring the behavior of a process (variables);
- Identifying faults, their characteristics, and their root causes.
- Steel-making plants continually switch between a load state (where they exert force for processing) and an idle state where they do not. Without a distinction between equipment operating conditions, it is difficult to detect changes in equipment status from the collected data. This difficulty can be overcome by eliminating noise in the data, recording the exact time of an occurrence (time stamping), and compiling event data.
- The data collected in the field on vibrations, temperatures, electric current, and debris inside the oil are often collected separately from the meta data (event data) that indicate the equipment’s operating condition. The equipment data collected cannot be labeled as failure or normal states, thus making it difficult to apply a supervised learning algorithm.
- When parts of the equipment are replaced, overhauled, or repaired, the characteristics of that equipment are altered. Because of this, the data on equipment status are not accurate, so they must be collected again to reflect the current normal status.
- Unlabeled vibration data can be pseudolabeled and used to monitor changes in equipment conditions using a supervised learning classifier.
- It is possible to reduce false alarms due to periodic changes in equipment operating under normal conditions.
- We confirm the timing of equipment condition changes.
- A quantitative analysis was performed, and relationships between independent and dependent variables are explained to determine which features affect equipment abnormalities.
2. Related Work
- When an artificial failure is created, labeled, and then analyzed, it is unlikely to produce the same results in the field.
- When a methodology cannot be applied directly at the production site because only vibration signals are collected without normal presence-and-absence labels.
- When fault alarms are inevitable if the equipment characteristics include repeated accelerations, decelerations, and stopping while operating, and they are subject to temporary influences from the surrounding environment.
- When normal states of the equipment constantly change, whether because of regular repairs, overhauls, oil replenishment, or minor repairs.
3. Equipment Condition Monitoring
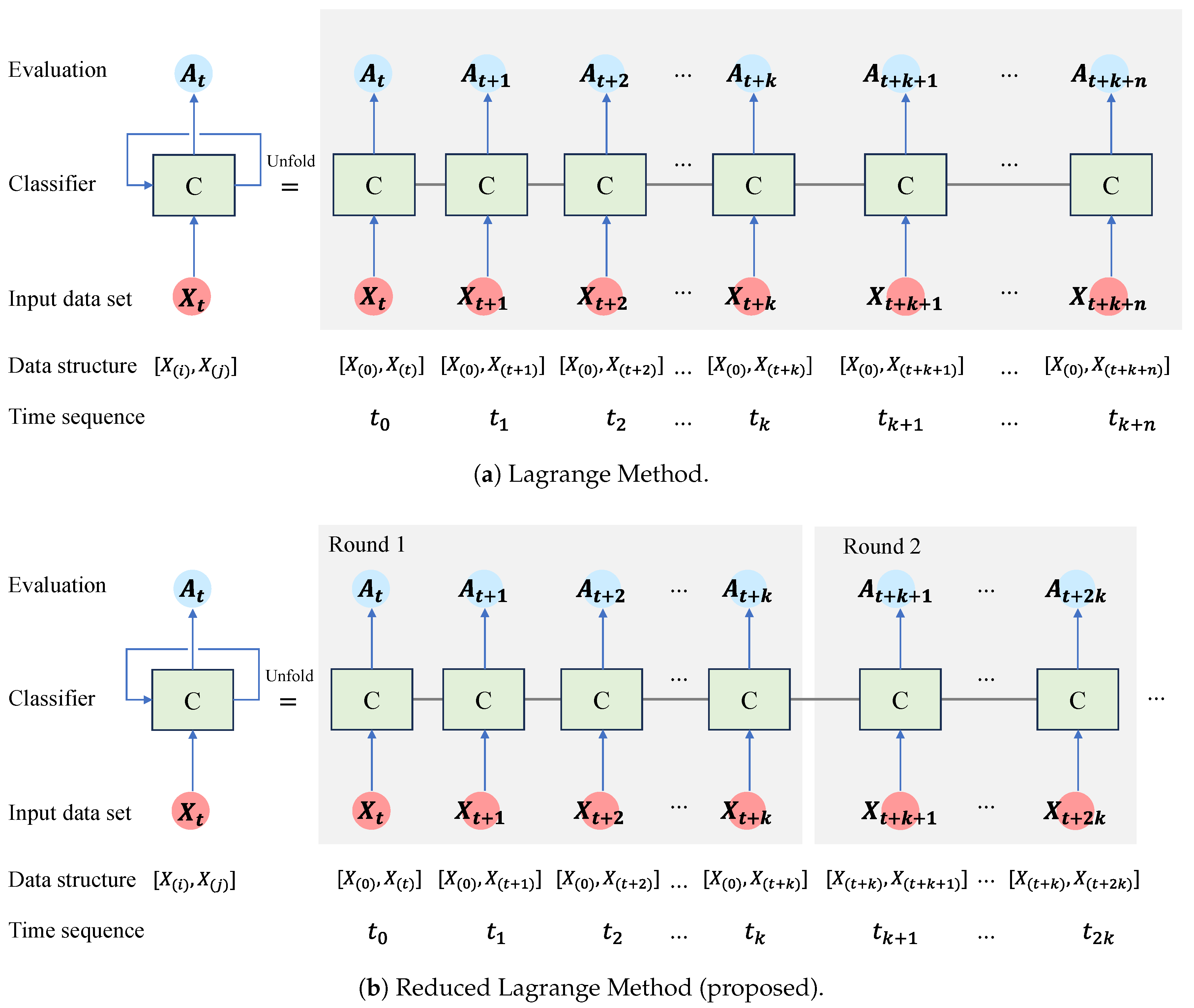
3.1. The Proposed Reduced Lagrange Method
- The first arrow indicates that the input data set is entered into the classifier (C). On the right side of Figure 1a, you can see the unfolded tasks for each time sequence. describes the structure of the input data set and refers to normal and abnormal data sets, respectively. Data set in the ith time sequence is labeled normal up front. Data set in the jth time sequence is labeled abnormal later. In the data structure, you can see that the first data sets are all the same, , which indicates that you have a data set that can be considered normal. The data sets prepared for each time sequence are considered abnormal and are used as input for the classifier.
- The second arrow indicates that the evaluation metric is created and stored in the classifier. A pseudolabeled data set is input, and the classifier stores the classification performance. represents the classification evaluation performance of the classifier at time sequence .
- The topmost arrows execute the classifier repeatedly. and denote the classifier and the nth time sequence, respectively.
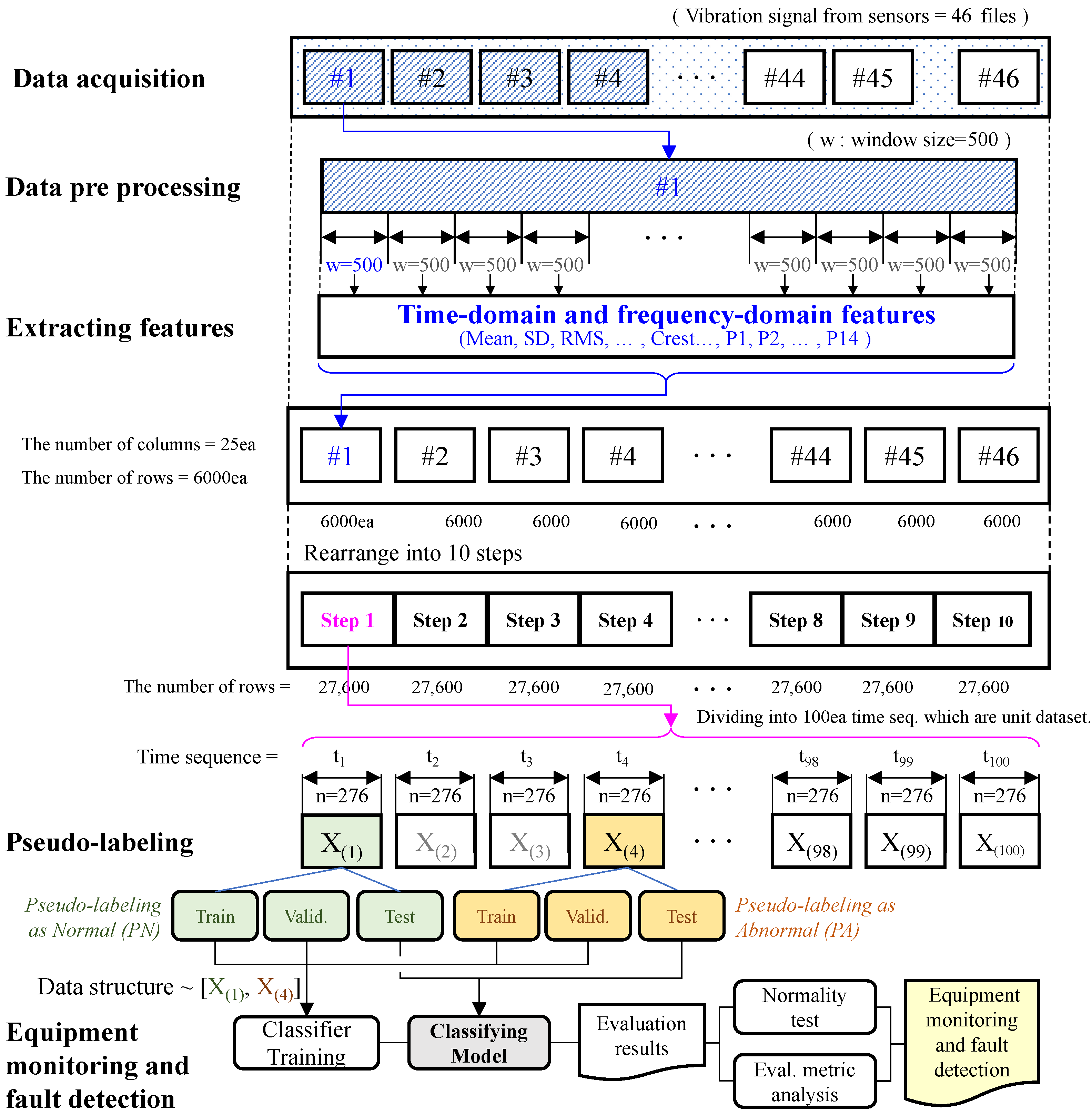
3.2. Procedure for Equipment Monitoring and Fault Detection
| Algorithm 1 Procedure for equipment condition monitoring based on the R-LM |
| Input: |
| Input data set structure defined as . |
| where is a data set pseudolabeled normal in the ith time sequence. |
| is a data set pseudolabeled abnormal in the th time sequence. |
| For each iteration k: |
| is fixed during k iterations |
| When kth iteration is completed, th data set is normal data set, |
| 1: Normalize data set and as |
| 2: Separate training, validation, and testing data at a certain rate |
| 3: Compute the variable importance using random forest, then sort in descending order |
| 4: Train supervised learning classifier using variables ranked in the top 10 |
| 5: Compute performance evaluation metrics and save result |
| 6: Iterate k processes |
| Perform normality test on evaluation results (). |
| Average evaluation results (): Alert if > 0.7, Alarm if > 0.8, Warning if > 0.9 |
| Output: |
| Alert, Alarm, Warning from normality test and averaged evaluation results |
4. Theoretical Background
4.1. Random Forest
- Bootstrap resampling is run k times on the original sample data set, thus collecting a fixed number of samples each time, taking them back out after each sampling, and then obtaining K subsample sets.
- The CART algorithm is used to generate a decision tree for each subsample set. If feature from the ith subsample set contains C categories, the Gini index is calculated as follows: In the case that the feature from the ith subsample set contains C categories, the Gini index is calculated as follows:where is the probability of category . As a result of Equation (3) below, a smaller Gini value indicates a higher level of purity. In the decision tree, the feature with the smallest Gini value is split.
- Based on Step 2, each subsample set generates a decision tree, and the decision trees of all the subsample sets form a random forest. Each decision tree is pruned according to the minimum Gini criterion by automatically selecting M features from feature set T containing M features as the attribute separation.
- A majority voting algorithm is used to analyze and vote on the results of the final RF algorithm.
4.2. Support Vector Machines
4.3. Model Performance Evaluation Metrics
4.4. Feature Extraction
5. Experiment Validation
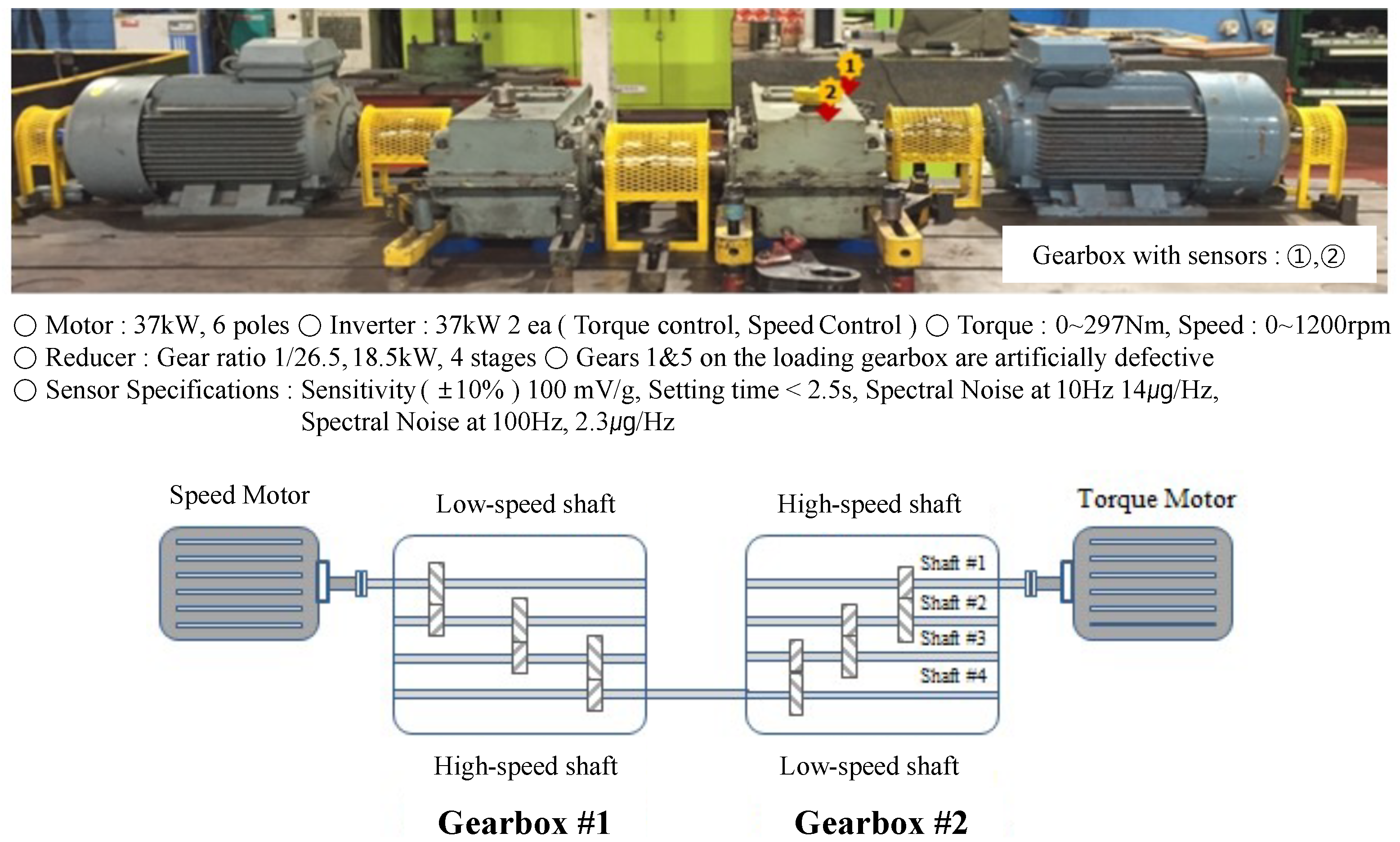
5.1. Data Acquisition and Preprocessing
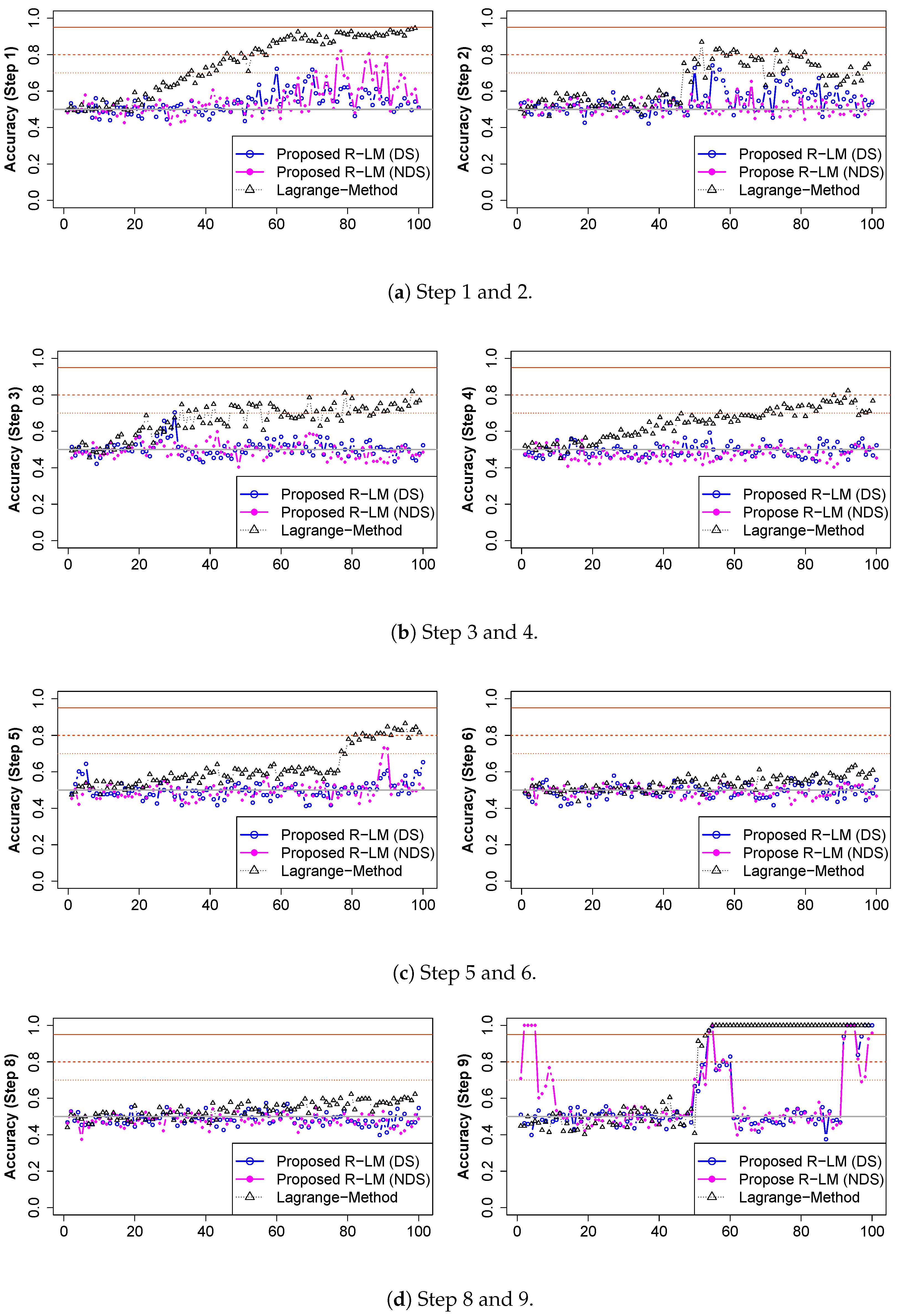
5.2. Experiment Results
5.3. Normality Test for Classification Evaluation Metrics
5.4. Variable Importance and Partial Dependence Plot
6. Discussion and Conclusions
- It is still necessary to find the optimal combination of hyper parameters used in pseudolabel analysis, such as the interval between normal and abnormal data sets (d), the data set window size (w), and the movement interval (s).
- There is a need for research on a hybrid LM, which monitors equipment conditions with R-LM under normal conditions and switches to LM under abnormal conditiosn to monitor accumulated changes. The advantages of R-LM and LM will be combined if a hybrid LM is successfully developed.
- Research that predicts equipment condition changes and categorizes them according to their type can reduce false alarms and contribute to the diagnosis of equipment problems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Autoencoder |
| AI | Artificial Intelligence |
| BM | Breakdown Maintenance |
| CART | Classification and Regression Tree |
| CBM | Condition-Based Maintenance |
| CNN | Convolutional Neural Networks |
| DS | Drive Side |
| FDD | Fault Detection and Diagnosis |
| GPUs | Graphics Processing Units |
| LM | Lagrange Method |
| ML | Machine Learning |
| NDS | Nondrive Side |
| PDP | Partial Dependence Plot |
| R-LM | Reduced Lagrange Method |
| RF | Random Forest |
| PM | Preventive Maintenance |
| SVM | Support Vector Machine |
References
- Yacout, S. Fault detection and Diagnosis for Condition Based Maintenance Using the Logical Analysis of Data. In Proceedings of the 40th International Conference on Computers and Industrial Engineering Computers and Industrial Engineering (CIE), Awaji, Japan, 25–28 July 2010; pp. 1–6. [Google Scholar]
- Farina, M.; Osto, E.; Perizzato, A.; Piroddi, L.; Scattolini, R. Fault detection and isolation of bearings in a drive reducer of a hot steel rolling mill. Control Eng. Pract. 2015, 39, 35–44. [Google Scholar] [CrossRef]
- Niu, G. Data-Driven Technology for Engineering Systems Health Management: Design Approach, Feature Construction, Fault Diagnosis, Prognosis, Fusion and Decisions; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kumar, S.; Goyal, D.; Dang, R.K.; Dhami, S.S.; Pabla, B.S. Condition based maintenance of bearings and gears for fault detection—A review. Mater. Today Proc. 2018, 5, 6128–6137. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J. Gear crack level identification based on weighted K nearest neighbor classification. Mech. Sys. Siganl Process. 2009, 23, 1535–1547. [Google Scholar] [CrossRef]
- Fan, S.; Cai, Y.; Zhang, Z.; Wang, J.; Shi, Y.; Li, X. Adaptive Convolution Sparse Filtering Method for the Fault Diagnosis of an Engine Timing Gearbox. Sensors 2023, 24, 169. [Google Scholar] [CrossRef]
- Tang, X.H.; Gu, X.; Rao, L.; Lu, J.G. A single fault detection method of gearbox based on random forest hybrid classifier and improved Dempster-Shafer information fusion. Comput. Electr. Eng. 2021, 92, 107101. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sanchez, R.V. Gearbox fault identification and classification with convolutional neural networks. Shock. Vib. 2015, 2015, 390134. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A CNN based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Lee, J.H.; Okwuosa, C.N.; Hur, J.W. Extruder Machine Gear Fault Detection Using Autoencoder LSTM via Sensor Fusion Approach. Inventions 2023, 8, 140. [Google Scholar] [CrossRef]
- Ramteke, D.S.; Parey, A.; Pachori, R.G. A New Automated Classification Framework for Gear Fault Diagnosis Using Fourier–Bessel Domain-Based Empirical Wavelet Transform. Machines 2023, 11, 1055. [Google Scholar] [CrossRef]
- Lupea, L.; Lupea, M. Detecting Helical Gearbox Defects from Raw Vibration Signal Using Convolutional Neural Networks. Sensors 2023, 23, 8769. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Zhao, C.; Huang, J.; Song, T. Intelligent and Small Samples Gear Fault Detection Based on Wavelet Analysis and Improved CNN. Processes 2023, 11, 2969. [Google Scholar] [CrossRef]
- Tran, V.T.; Yang, B.S. An intelligent condition-based maintenance platform for rotating machinery. Expret Syst. Appl. 2012, 39, 2977–2988. [Google Scholar] [CrossRef]
- Lee, S.H.; Youn, B.D. Industry 4.0 and direction of failure prediction and health management technology (PHM). J. Korean Soc. Noise Vib. Eng. 2015, 21, 22–28. [Google Scholar]
- Pecht, M.G.; Kang, M.S. Prognostics and Health Management of Electronics-Fundamentals Machine Learning, and the Internet of Things; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Choi, J.H. A review on prognostics and health management and its application. J. Aerosp. Syst. Eng. 2014, 38, 7–17. [Google Scholar]
- Yang, B.S.; Widodo, A. Introduction of Intelligent Machine Fault Diagnosis and Prognosis; Nova: Dongtan, Republic of Korea, 2009. [Google Scholar]
- Widodo, A.; Yang, B.-S. Support vector machine in machine condition monitoring and fault diagnosis. Mech. Syst. Signal Process 2007, 21, 2560–2574. [Google Scholar] [CrossRef]
- Banerjee, T.P.; Das, S. Multi-sensor data fusion using support vector machine for motor fault detection. Inf. Sci. 2012, 217, 96–107. [Google Scholar] [CrossRef]
- Park, J.; Kwon, I.H.; Kim, S.S.; Baek, J.G. Spline regression based feature extraction for semiconductor process fault detection using support vector machine. Expert Syst. Appl. 2011, 38, 5711–5718. [Google Scholar] [CrossRef]
- Wang, C.C.; Wu, T.Y.; Wu, C.W.; Wu, S.D. Multi-Scale Analysis Based Ball Bearing Defect Diagnostics Using Mahalanobis Distance and Support Vector Machine. Entropy 2013, 15, 416–433. [Google Scholar]
- Shin, I.S.; Lee, J.M.; Lee, J.Y.; Jung, K.S.; Kwon, D.I.; Youn, B.D.; Jang, H.S.; Choi, J.H. A Framework for prognostics and health management applications toward smart manufacturing system. Inter. J. Precis. Eng. Manuf.-Green Tech. 2018, 5, 535–554. [Google Scholar] [CrossRef]
- Hadi, R.H.; Hady, H.N.; Hasan, A.M.; Al-Jodah, A.; Humaidi, A.J. Improved Fault Classification for Predictive Maintenance in Industrial IoT Based on AutoML: A Case Study of Ball-Bearing Faults. Processes 2023, 11, 1507. [Google Scholar] [CrossRef]
- Santamaria-Bonfil, G.; Arroyo-Figueroa, G.; Zuniga-Garcia, M.A.; Ramos, C.G.A.; Bassam, A. Power Transformer Fault detection: A Comparision of Standard Machine Learning and autoML Approach. Energies 2023, 17, 77. [Google Scholar] [CrossRef]
- Brescia, E.; Vergallo, P.; Serafino, P.; Tipaldi, M.; Cascella, D.; Cascella, G.L.; Romano, F.; Polichetti, A. Online Condtion Monitoring of Industrial Loads Using AutoGMM and Decision Tree. Machines 2023, 11, 1082. [Google Scholar] [CrossRef]
- Hong, S.; Lu, Y.; Dunning, R.; Ahn, S.H.; Wang, Y. 2012 Adaptive fusion based on physics-constrained dictionary learning for fault diagnosis of rotating machinery. Manuf. Lett. 2023, 35, 999–1008. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, Y. A physics-constrained dictionary learning approach for compression of vibration signals. Mech. Syst. Signal Process. 2021, 153, 107434. [Google Scholar] [CrossRef]
- Miao, M.; Sun, Y.; Yu, J. Sparse representation convolutional autoencoder for feature learning of vibration signals and its applications in machinery fault diagnosis. IEEE Trans. Ind. Electron. 2021, 69, 13565–13575. [Google Scholar] [CrossRef]
- Seo, M.-K.; Yun, W.-Y. Clustering-based monitoring and fault detection in hot strip rolling mill. J. Korean Soc. Qual. Manag. 2017, 45, 298–307. [Google Scholar] [CrossRef]
- Seo, M.-K.; Yun, W.-Y. Clustering-based hot strip rolling mill diagnosis using Mahalanobis distance. J. Korean Inst. Ind. Eng. 2017, 43, 298–307. [Google Scholar]
- Seo, M.-K.; Yun, W.-Y. Condition Monitoring and Diagnosis of a Hot Strip Roughing Mill Using an Autoencoder. J. Korean Soc. Qual. Manag. 2019, 47, 75–86. [Google Scholar]
- Seo, M.-K.; Yun, W.-Y.; Seo, S.-K. Machine Learning Based Equipment Monitoring and Diagnosis Using Pseudo-Label Method. J. Korean Inst. Ind. Eng. 2020, 46, 517–526. [Google Scholar]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification And Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Yaqub, R.; Ali, H.; Wahab, M.H.B.A. Electrical Motor Fault Detection System using AI’s Random Forest Classifier Technique. In Proceedings of the 2023 IEEE International Conference on Advanced Systems and Emergent Technologies, Hammamet, Tunisia, 29 April–1 May 2023. [Google Scholar]
- Niu, G. Data-Driven Technology for Engineering Systems Health Management; Science Press, Springer: Beijing, China, 2017. [Google Scholar]
- Zhong, J.; Yang, Z.; Wong, S.F. Machine Condition Monitoring and Fault Diagnosis based on Support Vector Machine. In Proceedings of the 2010 IEEE International Conference on Industrial Engineering and Engineering Management, Macao, China, 7–10 December 2010. [Google Scholar]
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Seo, M.-K.; Yun, W.-Y. Hot Strip Mill Gearbox Monitoring and Diagnosis Based on Convolutional Neural Networks Using the Pseudo-Labeling Method. Appl. Sci. 2024, 14, 450. [Google Scholar] [CrossRef]


| Domain | Common Statistical Features | ||
|---|---|---|---|
| Time domain | |||
| Domain | Common Statistical Features | ||
|---|---|---|---|
| Frequency domain | |||
| Evaluation Metric | Kernel | Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | Step 6 | Step 7 | Step 8 | Step 9 | Step 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy (DS) | Radial | 0.6189 | 0.6384 | 0.5870 | 0.5527 | 0.5847 | 0.5657 | 0.5703 | 0.5745 | 0.9898 | 0.7791 |
| Linear | 0.6541 | 0.6842 | 0.5916 | 0.5587 | 0.6013 | 0.5578 | 0.5384 | 0.5518 | 0.9847 | 0.7800 | |
| Sigmoid | 0.5921 | 0.6097 | 0.5486 | 0.5625 | 0.5671 | 0.5486 | 0.5601 | 0.5532 | 0.9671 | 0.7763 | |
| Polynomial | 0.6111 | 0.6310 | 0.5842 | 0.5648 | 0.5717 | 0.5504 | 0.5578 | 0.5662 | 0.9833 | 0.7796 | |
| Accuracy (NDS) | Radial | 0.7523 | 0.5740 | 0.5754 | 0.5421 | 0.6138 | 0.5893 | 0.5851 | 0.5564 | 0.9884 | 0.7861 |
| Linear | 0.7476 | 0.5828 | 0.5712 | 0.5347 | 0.5949 | 0.5379 | 0.5370 | 0.5319 | 0.9921 | 0.7717 | |
| Sigmoid | 0.6546 | 0.5555 | 0.5587 | 0.5555 | 0.5759 | 0.5620 | 0.5550 | 0.5657 | 0.9773 | 0.7819 | |
| Polynomial | 0.6995 | 0.5675 | 0.5625 | 0.5486 | 0.5837 | 0.5995 | 0.5606 | 0.5657 | 0.9898 | 0.7819 | |
| Precision (DS) | Radial | 0.6235 | 0.6407 | 0.5858 | 0.5568 | 0.5878 | 0.5716 | 0.5772 | 0.5786 | 0.9872 | 0.7796 |
| Linear | 0.6667 | 0.6873 | 0.5889 | 0.5593 | 0.6224 | 0.5678 | 0.5427 | 0.5616 | 0.9791 | 0.7839 | |
| Sigmoid | 0.5932 | 0.6113 | 0.5500 | 0.5638 | 0.5678 | 0.5498 | 0.5586 | 0.5557 | 0.9643 | 0.7777 | |
| Polynomial | 0.6172 | 0.6440 | 0.5798 | 0.5640 | 0.5835 | 0.5537 | 0.5588 | 0.5664 | 0.9794 | 0.7823 | |
| Precision (NDS) | Radial | 0.7620 | 0.5833 | 0.5788 | 0.5680 | 0.6202 | 0.5950 | 0.5883 | 0.5635 | 0.9830 | 0.7868 |
| Linear | 0.7808 | 0.5815 | 0.5736 | 0.5344 | 0.6003 | 0.5412 | 0.5425 | 0.5286 | 0.9893 | 0.7753 | |
| Sigmoid | 0.6643 | 0.5568 | 0.5624 | 0.5567 | 0.5799 | 0.5632 | 0.5586 | 0.5651 | 0.9640 | 0.7858 | |
| Polynomial | 0.7226 | 0.5662 | 0.5619 | 0.5491 | 0.5871 | 0.6070 | 0.5620 | 0.5665 | 0.9916 | 0.7840 | |
| Specificity (DS) | Radial | 0.6769 | 0.6722 | 0.6463 | 0.7120 | 0.6796 | 0.6602 | 0.6454 | 0.6315 | 0.9870 | 0.8148 |
| Linear | 0.7176 | 0.7593 | 0.6694 | 0.6185 | 0.7176 | 0.6491 | 0.6472 | 0.6352 | 0.9778 | 0.8157 | |
| Sigmoid | 0.6287 | 0.6454 | 0.5880 | 0.6167 | 0.6028 | 0.6111 | 0.5778 | 0.5917 | 0.9639 | 0.8028 | |
| Polynomial | 0.6806 | 0.6954 | 0.6074 | 0.5870 | 0.6500 | 0.6176 | 0.6287 | 0.6380 | 0.9787 | 0.8306 | |
| Specificity (NDS) | Radial | 0.7722 | 0.6796 | 0.6759 | 0.7426 | 0.6769 | 0.6481 | 0.6426 | 0.6259 | 0.9824 | 0.8222 |
| Linear | 0.8157 | 0.6509 | 0.6463 | 0.5870 | 0.6824 | 0.6426 | 0.7380 | 0.5981 | 0.9889 | 0.8157 | |
| Sigmoid | 0.6981 | 0.6028 | 0.6167 | 0.5954 | 0.6102 | 0.6065 | 0.6157 | 0.6009 | 0.9667 | 0.8130 | |
| Polynomial | 0.7620 | 0.6194 | 0.6250 | 0.5861 | 0.6315 | 0.6602 | 0.6204 | 0.6046 | 0.9917 | 0.8259 | |
| Sensitivity (DS) | Radial | 0.6528 | 0.6722 | 0.6926 | 0.7444 | 0.6639 | 0.6361 | 0.6361 | 0.6306 | 0.9963 | 0.8157 |
| Linear | 0.7546 | 0.7685 | 0.6722 | 0.6454 | 0.6343 | 0.6250 | 0.6315 | 0.6500 | 0.9917 | 0.8176 | |
| Sigmoid | 0.6491 | 0.6565 | 0.5926 | 0.6130 | 0.6204 | 0.5944 | 0.6241 | 0.5889 | 0.9759 | 0.8065 | |
| Polynomial | 0.6806 | 0.6833 | 0.6500 | 0.5954 | 0.6296 | 0.6019 | 0.6333 | 0.6343 | 0.9880 | 0.8278 | |
| Sensitivity (NDS) | Radial | 0.7454 | 0.6657 | 0.6120 | 0.7565 | 0.6898 | 0.6481 | 0.6583 | 0.5963 | 0.9954 | 0.8269 |
| Linear | 0.7398 | 0.6463 | 0.6519 | 0.5935 | 0.6528 | 0.6009 | 0.6009 | 0.6546 | 0.9981 | 0.8213 | |
| Sigmoid | 0.6537 | 0.5981 | 0.5769 | 0.5806 | 0.6009 | 0.5981 | 0.5833 | 0.6056 | 0.9991 | 0.8083 | |
| Polynomial | 0.6944 | 0.6306 | 0.6481 | 0.5917 | 0.6157 | 0.6583 | 0.6222 | 0.6370 | 0.9917 | 0.8139 | |
| Alarm Signal * | R-LM ** | A | At | At | N | At | N | N | N | W | A |
| LM ** | A | A | A | A | A | N | N | N | W | A |
| Sensor Position | Test Method | Step 1 | Step 2 | Step 3 | Step 4 | Step 5 | Step 6 | Step 7 | Step 8 | Step 9 | Step 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
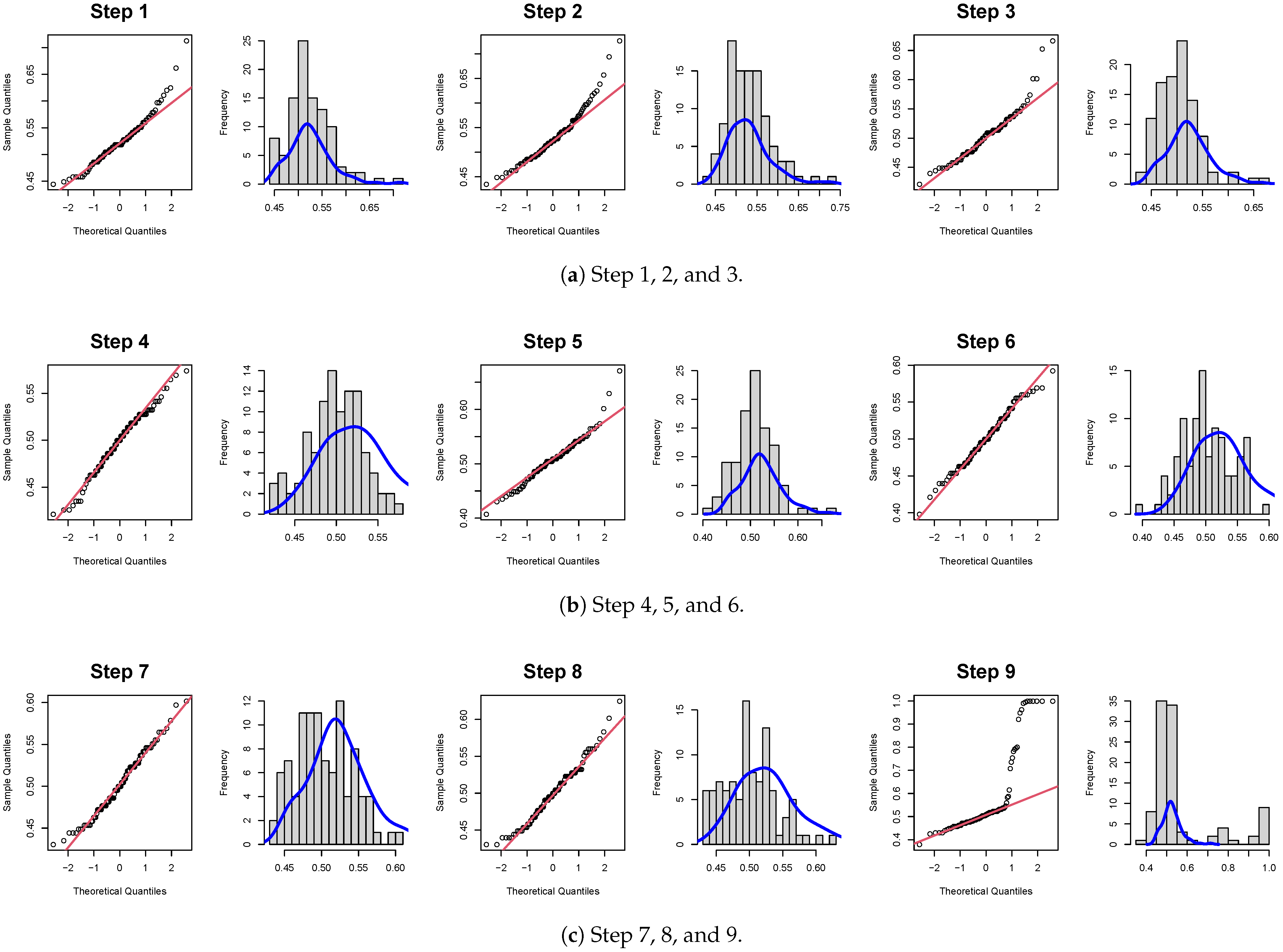
| Drive Side | Shapiro–Wilk | 0.0003 | 0.0002 | 0.0000 | 0.2677 | 0.0070 | 0.6323 | 0.1888 | 0.0585 | 0.0000 | 0.0000 |
| Anderson–D | 0.0094 | 0.0025 | 0.0038 | 0.2234 | 0.0736 | 0.5098 | 0.2506 | 0.2270 | 0.0000 | 0.0000 | |
| Lilliefors | 0.0506 | 0.0067 | 0.0168 | 0.3623 | 0.2790 | 0.7019 | 0.0768 | 0.1874 | 0.0000 | 0.0000 | |
| Nondrive Side | Shapiro–Wilk | 0.0000 | 0.2170 | 0.0156 | 0.6334 | 0.0001 | 0.7534 | 0.4786 | 0.7625 | 0.0000 | 0.0000 |
| Anderson–D | 0.0000 | 0.1185 | 0.0951 | 0.3435 | 0.0038 | 0.6461 | 0.5703 | 0.6068 | 0.0000 | 0.0000 | |
| Lilliefors | 0.0000 | 0.0926 | 0.0181 | 0.3217 | 0.0081 | 0.6831 | 0.5198 | 0.4042 | 0.0000 | 0.0000 | |
| Alarm Signal | Normality test * | A | A | A | N | A | N | N | N | A | A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, M.-K.; Yun, W.-Y. Gearbox Condition Monitoring and Diagnosis of Unlabeled Vibration Signals Using a Supervised Learning Classifier. Machines 2024, 12, 127. https://doi.org/10.3390/machines12020127
Seo M-K, Yun W-Y. Gearbox Condition Monitoring and Diagnosis of Unlabeled Vibration Signals Using a Supervised Learning Classifier. Machines. 2024; 12(2):127. https://doi.org/10.3390/machines12020127
Chicago/Turabian StyleSeo, Myung-Kyo, and Won-Young Yun. 2024. "Gearbox Condition Monitoring and Diagnosis of Unlabeled Vibration Signals Using a Supervised Learning Classifier" Machines 12, no. 2: 127. https://doi.org/10.3390/machines12020127
APA StyleSeo, M.-K., & Yun, W.-Y. (2024). Gearbox Condition Monitoring and Diagnosis of Unlabeled Vibration Signals Using a Supervised Learning Classifier. Machines, 12(2), 127. https://doi.org/10.3390/machines12020127







