Self-Calibration Method for Circular Encoder Based on Two Reading Heads with Adjustable Positions
Abstract
:1. Introduction
2. Self-Calibration Principle
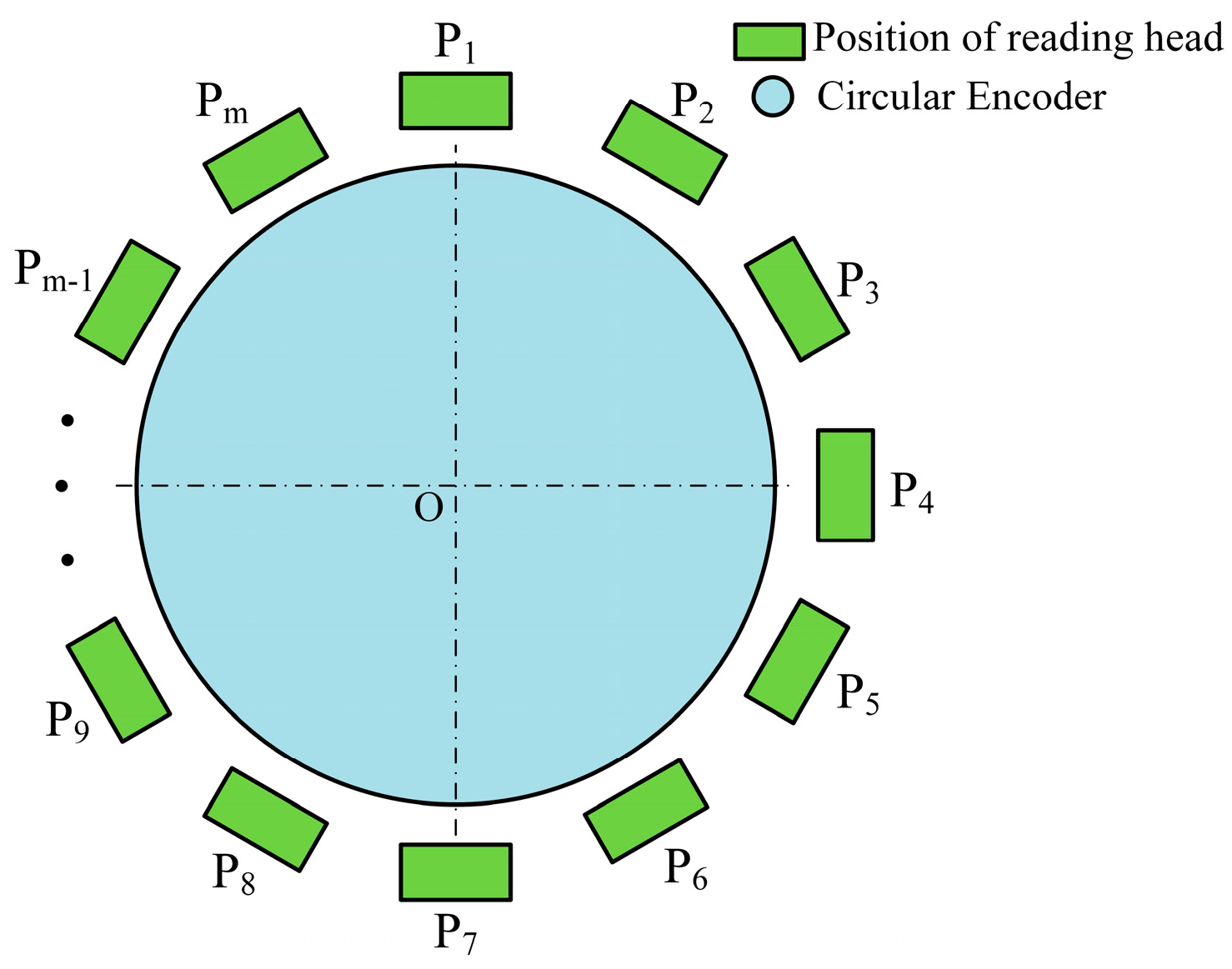
2.1. Calculation Method for Actual Angle between Reading Heads
2.2. Self-Calibration Principle Based on Two Reading Heads with Adjustable Positions
3. Design and Construction of Experimental System
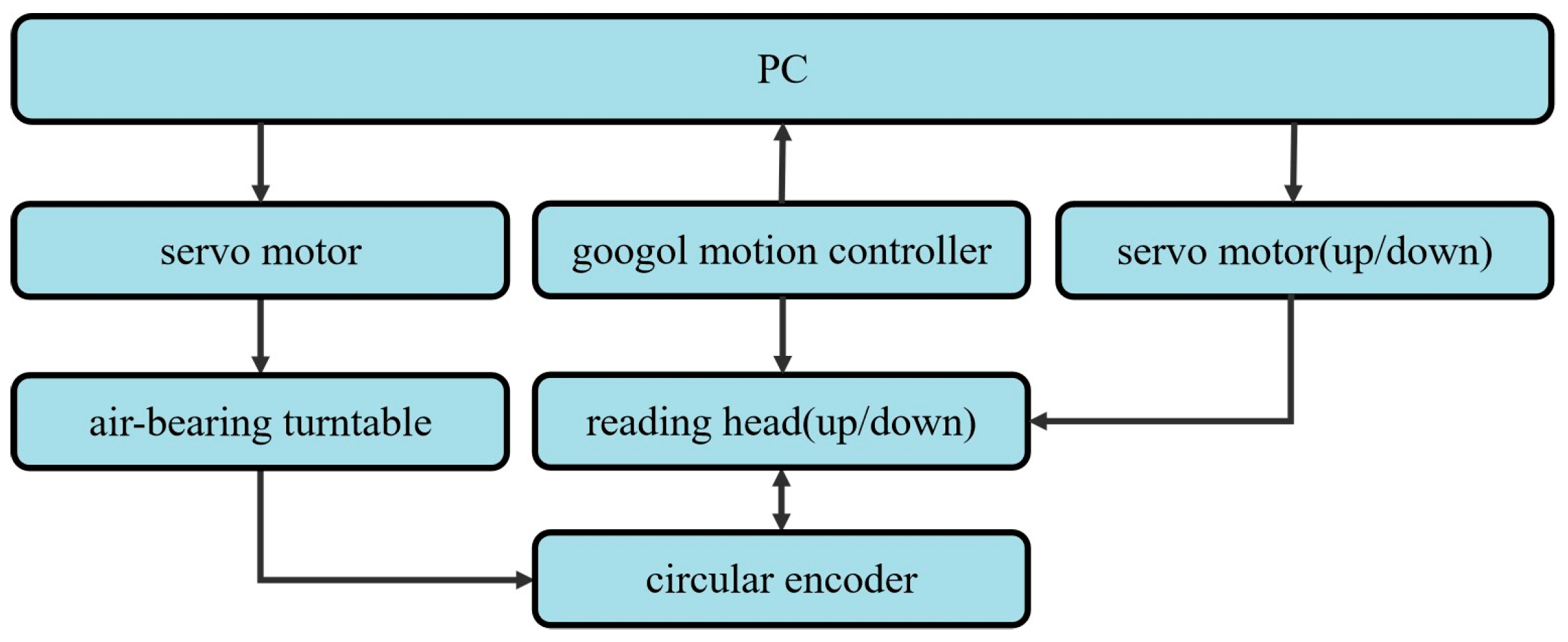
3.1. Structural Design of Self-Calibration Device
3.2. Design of Hardware Circuit and Software System
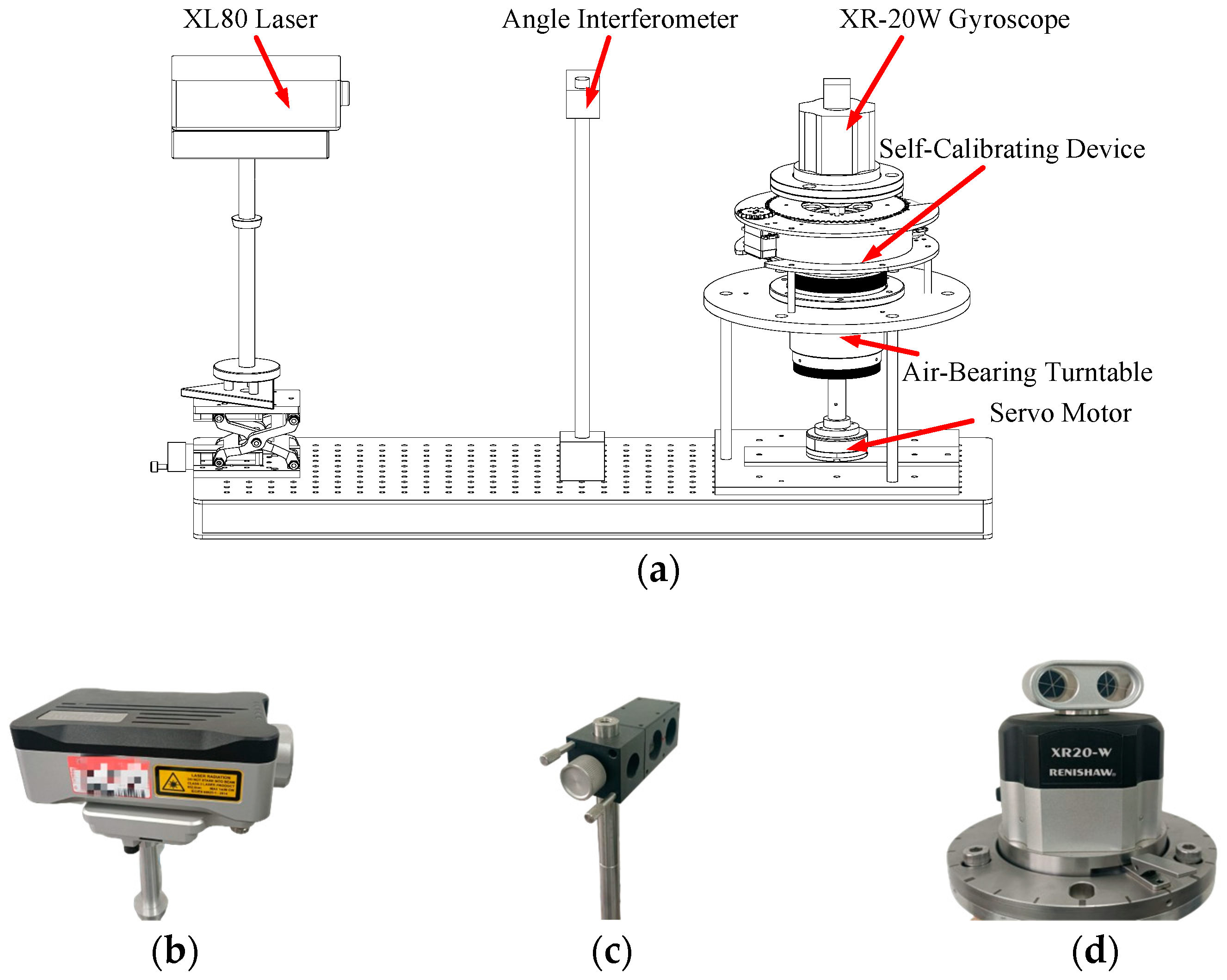
3.3. Construction of Experimental Platform
4. Experiment
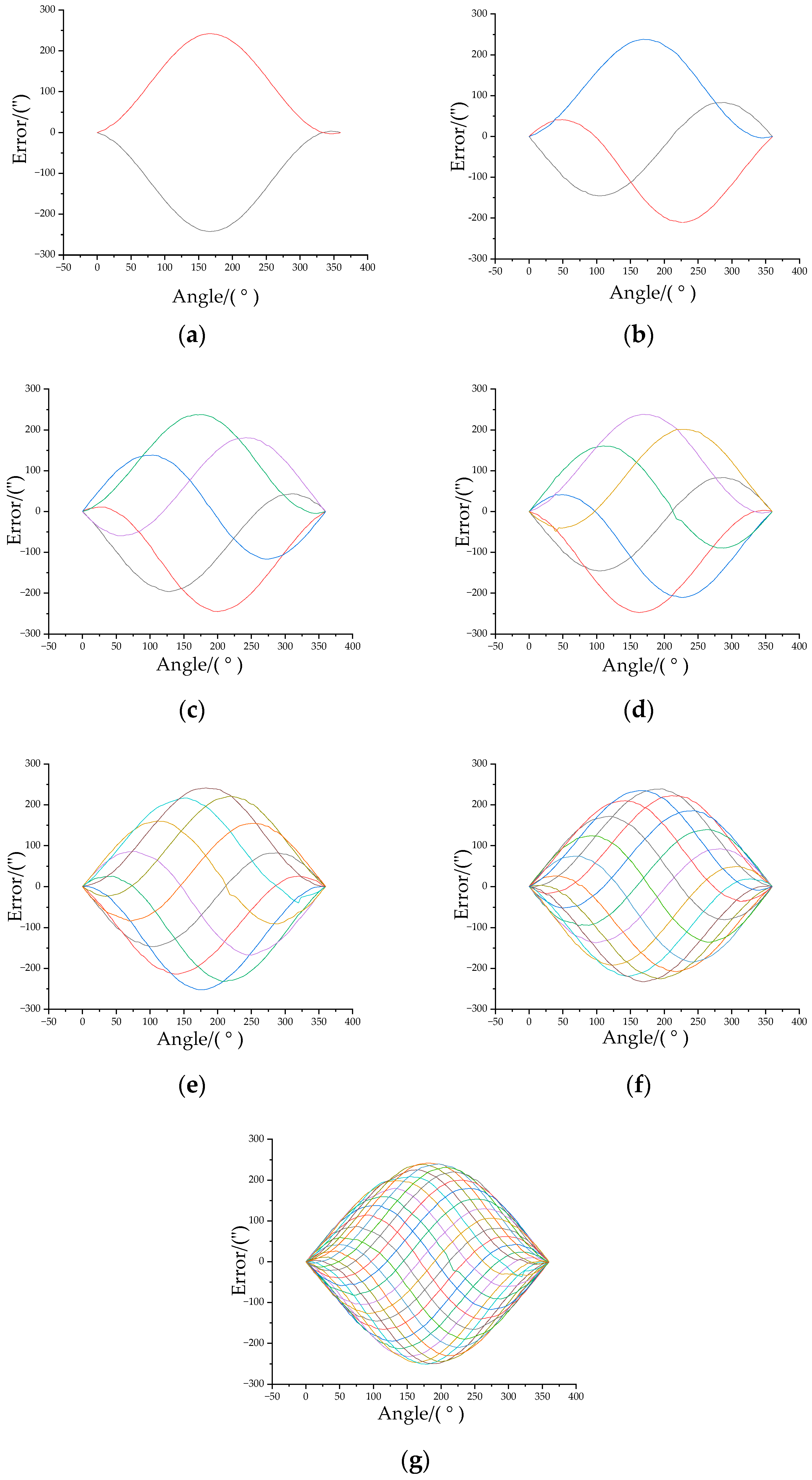
4.1. Experimental Process
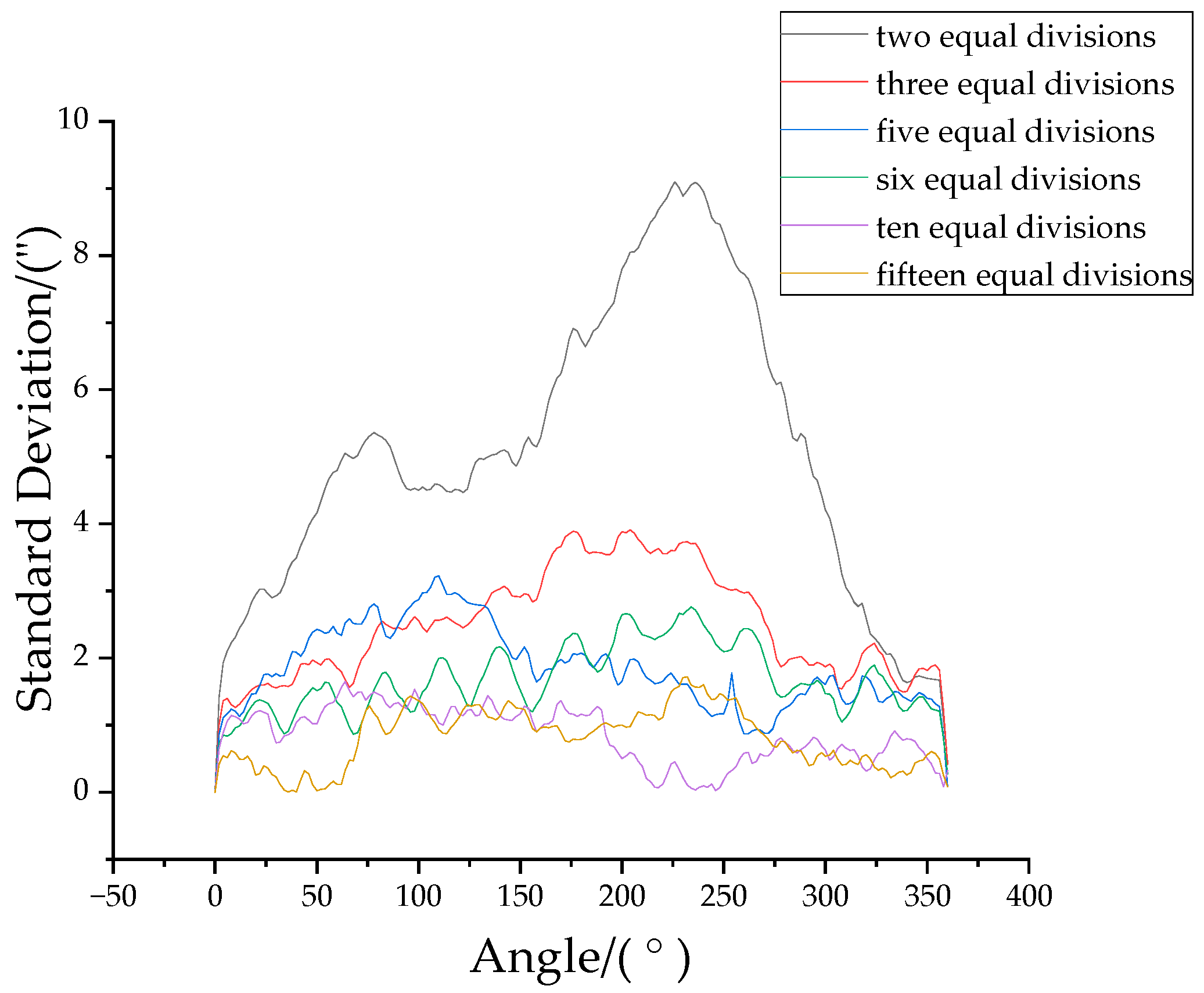
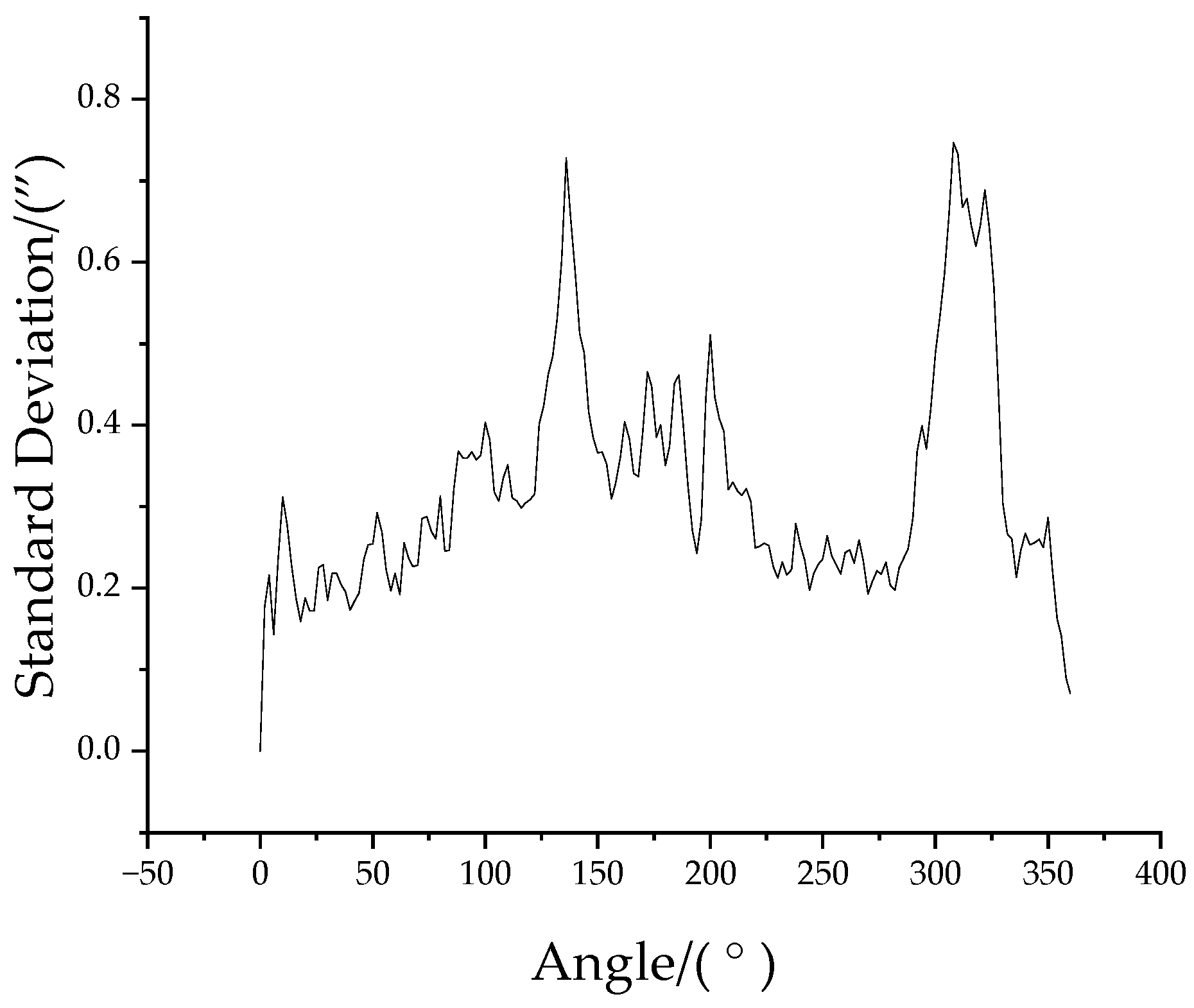
4.2. Analysis of Experimental Data
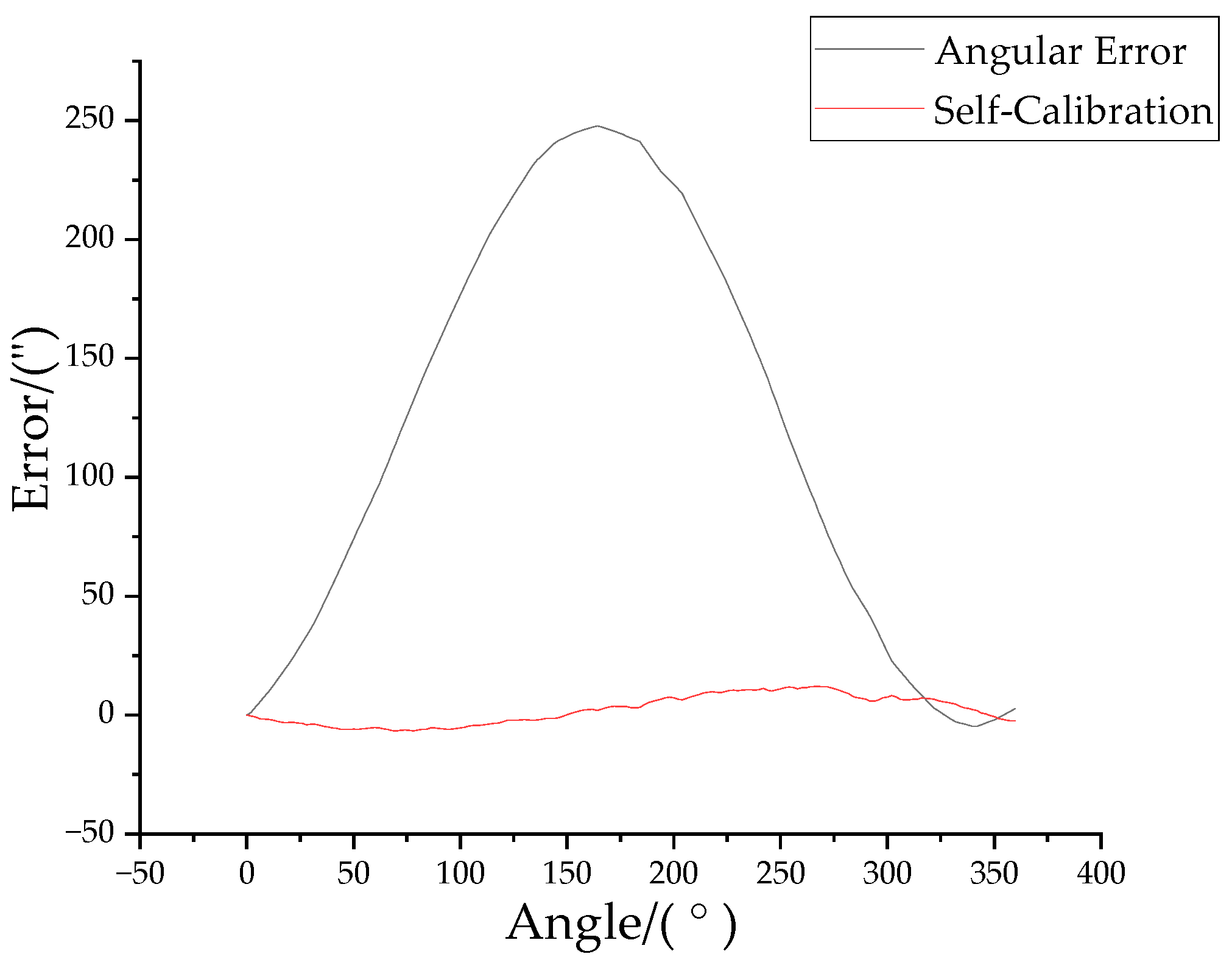
4.3. Comparison with Interferometric Measurements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, H.K.; Yu, L.D.; Zhao, H.N.; Jiang, Y.Z. A New Method of Angle Measurement Error Analysis of Rotary Encoders. Appl. Sci. 2019, 9, 3415. [Google Scholar] [CrossRef]
- Li, Y.T.; Fan, K.C. A novel method of angular positioning error analysis of rotary stages based on the Abbe principle. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 1885–1892. [Google Scholar] [CrossRef]
- Li, G.L.; Xue, Z.; Huang, Y.; Zhu, W.B.; Zou, W. Indication error analysis and compensation of circular grating angle measurement system. Chin. J. Sci. Instrum. 2021, 42, 59–65. [Google Scholar] [CrossRef]
- Zhang, S.Z. The principle of eliminating errors in the multi reading head structure of high-precision circular indexing measurement devices. Tool Eng. 1982, 6, 42–46. [Google Scholar] [CrossRef]
- Probst, R. Self-calibration of divided circles on the basis of a prime factor algorithm. Meas. Sci. Technol. 2008, 19, 015101. [Google Scholar] [CrossRef]
- Lu, X.D.; Trumper, D.L. Self-Calibration of On-Axis Rotary Encoders. CIRP Ann.-Manuf. Technol. 2007, 56, 499–504. [Google Scholar] [CrossRef]
- Lu, X.D.; Graetz, R.; Amin-Shahidi, D.; Smeds, K. On-axis self-calibration of angle encoders. CIRP Ann.-Manuf. Technol. 2010, 59, 529–534. [Google Scholar] [CrossRef]
- Feng, C.P.; Zhu, L.Q.; Pan, Z.K.; Guo, Y.K. New self-calibration method of circular grating eccentric parameters. Chin. J. Sci. Instrum. 2016, 37, 2459–2464. [Google Scholar] [CrossRef]
- Jiao, Y.; Dong, Z.G.; Ding, Y.; Liu, P.K. Optimal arrangements of scanning heads for self-calibration of angle encoders. Meas. Sci. Technol. 2017, 28, 105013. [Google Scholar] [CrossRef]
- Jiao, Y.; Dong, Z.G.; Huang, M.; Liu, P.K. Optimal-arrangement-based four-scanning-heads error separation technique for self-calibration of angle encoders. Meas. Sci. Technol. 2018, 29, 085005. [Google Scholar] [CrossRef]
- Wang, X.Q.; Yu, Y.; Zhu, G.L.; Jiang, Z.H.; Zhao, T.T. Multiple Reading Head Displacement Sensor Research Based on Arithmetic Phase. Instrum. Tech. Sens. 2016, 9, 1–4+63. [Google Scholar] [CrossRef]
- Wang, X.Q.; Zhao, T.T.; Wen, C.Y.; Wang, L.; Wang, P.Y. Error Correcting for Displacement Sensor Based on Multiple Reading Head. Tool Eng. 2017, 51, 121–126. [Google Scholar] [CrossRef]
- Ishii, N.; Taniguchi, K.; Yamazaki, K.; Aoyama, H. Development of super-accurate angular encoder system with multi-detecting heads using VEDA method. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, JAMDSM0106. [Google Scholar] [CrossRef]
- Ishii, N.; Taniguchi, K.; Yamazaki, K.; Aoyama, H. Super-Accurate Angular Encoder System with Multi-Detecting Heads Using VEDA Method. J. Jpn. Soc. Precis. Eng. 2018, 84, 717–723. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Lao, D.B.; Zhou, W.H.; Zhu, H.R. Development and experiment of online self-calibration system for circular grating angle sensor. Infrared Laser Eng. 2018, 47, 224–229. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Lao, D.B.; Zhou, W.H.; Zhu, H.R. Self-Calibration Method Based on Multi-head Reading Layout. Acta Opt. Sin. 2018, 38, 352–358. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Zhu, H.R.; Li, M.X.; Guo, Z.X.; Guo, M. Real-Time In-Situ Calibration for Angle Measuring Sensors Based on Autocollimator. Chin. J. Lasers 2019, 46, 166–172. [Google Scholar] [CrossRef]
- Zhang, R.; Bao, W.; Zhao, H.; Jia, H.; Yu, L. Self-calibration method of precision shafting angle measurement error based on multiple reading heads. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018. [Google Scholar] [CrossRef]
- Li, Z.M.; Li, Z.L.; Han, B.; Tang, Y.F.; Yang, Y.Q.; Ma, Y. Compensation Method of Circular Grating Angle Measurement Error. Instrum. Tech. Sens. 2021, 10, 56–59+89. [Google Scholar] [CrossRef]
- Masuda, T.; Kajitani, M. An automatic calibration system for angular encoders. Precis. Eng. 1989, 11, 95–100. [Google Scholar] [CrossRef]
- Just, A.; Krause, M.; Probst, R.; Bosse, H.; Haunerdinger, H.; Spaeth, C.; Metz, G.; Israel, W. Comparison of angle standards with the aid of a high-resolution angle encoder. Precis. Eng. 2009, 33, 530–533. [Google Scholar] [CrossRef]
- Sun, S.Z.; Zhang, Z.M.; Han, Y.; Tao, P.A.; He, Z.Y. Self-calibration study of the embedded angular displacement sensor based on single probe error phase shift method. Chin. J. Sci. Instrum. 2022, 43, 96–103. [Google Scholar] [CrossRef]
- Li, G.L.; Xue, Z.; Huang, Y.; Zhu, W.B.; Zou, W. System error separation and compensation of the continuous full circle angle standard device. Chin. J. Sci. Instrum. 2021, 42, 1–9. [Google Scholar] [CrossRef]
- Geckeler, R.D.; Link, A.; Krause, M.; Elster, C. Capabilities and limitations of the self-calibration of angle encoders. Meas. Sci. Technol. 2014, 25, 055003. [Google Scholar] [CrossRef]
- Probst, R.; Wittekopf, R.; Krause, M.; Dangschat, H.; Ernst, A. The new PTB angle comparator. Meas. Sci. Technol. 1998, 9, 1059–1066. [Google Scholar] [CrossRef]


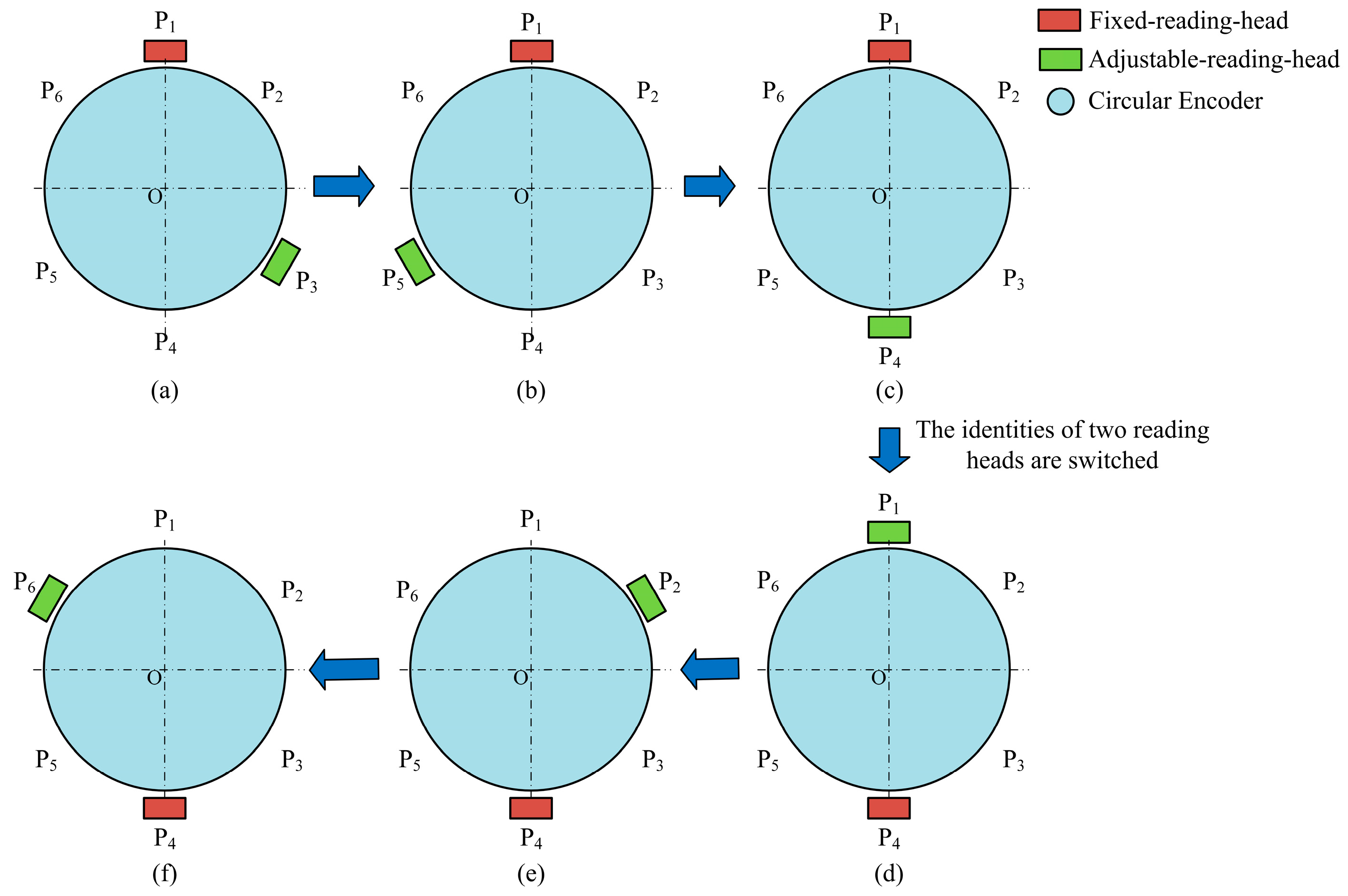

| Number of Measurements | Position of Fixed Reading Head | Position of Adjustable Reading Head | Measurements of Two Reading Heads | Position Marked as Measured |
|---|---|---|---|---|
| 1 | P1 | P3 | P1, P3 | |
| 2 | P1 | P5 | P1, P3, P5 | |
| 3 | P1 | P4 | P1, P3, P4, P5 | |
| 4 | P4 | P2 | P1, P2, P3, P4, P5 | |
| 5 | P4 | P6 | P1, P2, P3, P4, P5, P6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhao, C.; Xiao, L.; Zheng, K.; Liu, M.; Zhu, D.; Yao, T. Self-Calibration Method for Circular Encoder Based on Two Reading Heads with Adjustable Positions. Machines 2024, 12, 246. https://doi.org/10.3390/machines12040246
Wang X, Zhao C, Xiao L, Zheng K, Liu M, Zhu D, Yao T. Self-Calibration Method for Circular Encoder Based on Two Reading Heads with Adjustable Positions. Machines. 2024; 12(4):246. https://doi.org/10.3390/machines12040246
Chicago/Turabian StyleWang, Xiaoyi, Chengxiang Zhao, Longyuan Xiao, Kunlei Zheng, Mingkang Liu, Dongjie Zhu, and Tianyang Yao. 2024. "Self-Calibration Method for Circular Encoder Based on Two Reading Heads with Adjustable Positions" Machines 12, no. 4: 246. https://doi.org/10.3390/machines12040246
APA StyleWang, X., Zhao, C., Xiao, L., Zheng, K., Liu, M., Zhu, D., & Yao, T. (2024). Self-Calibration Method for Circular Encoder Based on Two Reading Heads with Adjustable Positions. Machines, 12(4), 246. https://doi.org/10.3390/machines12040246






