An Al-Biruni Earth Radius Optimization-Based Deep Convolutional Neural Network for Classifying Monkeypox Disease
Abstract
1. Introduction
- Offer machine learning techniques for predicting monkeypox disease;
- A new Al-Biruni Earth radius (BER) optimization-based stochastic fractal search (BERSFS) algorithm is suggested;
- To raise the tested dataset prediction accuracy, a BERSFS-based classifier is created.
- A comparison of the results of different algorithms to determine which is the most accurate is performed;
- The Wilcoxon rank-sum and ANOVA tests are used to determine the statistical significance of the BERSFS algorithm;
- It is possible to generalize and test the BERSFS-based classification algorithm for different kinds of datasets.
2. Literature Review
3. Materials and Methods
3.1. Convolutional Neural Network (CNN)
3.2. Al-Biruni Earth Radius (BER) Algorithm
| Algorithm 1 AL-Biruni Earth radius (BER) algorithm |
|
3.2.1. Exploration Operation
3.2.2. Exploitation Operation
3.2.3. Selection of the Best Solution
3.3. Stochastic Fractal Search (SFS) Algorithm
| Algorithm 2 Stochastic fractal search (SFS) algorithm |
|
3.4. Proposed BERSFS Algorithm
- Initialize the parameters of the BERSFS algorithm: O(1);
- Calculate for each agent : O(n);
- Obtain the best agent : O (n);
- Update positions to head toward the best solution: O();
- Update positions for the elitism of the best solution: O();
- Update the positions for investigating the area around the best solution: O();
- Mutate the solution: O();
- Calculate the updated best solution: O();
- Calculate for each agent : O();
- Update the BERSFS parameters: O();
- Obtain the best agent : O();
- Obtain the best agent : O(1).
| Algorithm 3 Proposed BERSFS algorithm |
|
4. Experimental Results
4.1. Dataset Description
4.2. Performance Metrics
4.3. Comparison with Basic Models
4.4. Comparison with Deep Learning Models
4.5. Comparison with Optimization-Based Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Somogyi, Z. The Application of Artificial Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Chakraborty, U. Artificial Intelligence for All: Transforming Every Aspect of Our Life; BPB Publications: Noida, India, 2020. [Google Scholar]
- Zhou, X.; Wang, S.; Chen, H.; Hara, T.; Yokoyama, R.; Kanematsu, M.; Fujita, H. Automatic localization of solid organs on 3D CT images by a collaborative majority voting decision based on ensemble learning. Comput. Med. Imaging Graph. 2012, 36, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.A.; Hamarneh, G.; Garbi, R. Cascaded Regression Neural Nets for Kidney Localization and Segmentation-free Volume Estimation. IEEE Trans. Med. Imaging 2021, 40, 1555–1567. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, X.; Yang, M.; Zhang, H.; Xu, X.S. Optimize Deep Learning Models for Prediction of Gene Mutations Using Unsupervised Clustering. arXiv 2022, arXiv:2204.01593. [Google Scholar]
- Habibi, K.; Tirdad, K.; Dela Cruz, A.; Wenger, K.; Mari, A.; Basheer, M.; Kuk, C.; van Rhijn, B.W.G.; Zlotta, A.R.; van der Kwast, T.H.; et al. ABC: Artificial Intelligence for Bladder Cancer grading system. Mach. Learn. Appl. 2022, 9, 100387. [Google Scholar] [CrossRef]
- Hunter, B.; Hindocha, S.; Lee, R.W. The Role of Artificial Intelligence in Early Cancer Diagnosis. Cancers 2022, 14, 1524. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Mirjalili, S.; Ibrahim, A.; Alrahmawy, M.; El-Said, M.; Zaki, R.M.; Eid, M.M. Advanced Meta-Heuristics, Convolutional Neural Networks, and Feature Selectors for Efficient COVID-19 X-Ray Chest Image Classification. IEEE Access 2021, 9, 36019–36037. [Google Scholar] [CrossRef]
- Basu, K.; Sinha, R.; Ong, A.; Basu, T. Artificial Intelligence: How is It Changing Medical Sciences and Its Future? Indian J. Dermatol. 2020, 65, 365–370. [Google Scholar] [CrossRef]
- The Handbook of Brain Theory and Neural Networks. Available online: https://mitpress.mit.edu/9780262511025/the-handbook-of-brain-theory-and-neural-networks/ (accessed on 2 October 2022).
- Fenner, F. Adventures with poxviruses of vertebrates. Fems Microbiol. Rev. 2000, 24, 123–133. [Google Scholar] [CrossRef]
- Poxviruses—An Overview | ScienceDirect Topics. Available online: https://www.sciencedirect.com/topics/neuroscience/poxviruses (accessed on 2 October 2022).
- Monkeypox Virus Infection in Humans across 16 Countries—April–June 2022 | NEJM. Available online: https://www.nejm.org/doi/full/10.1056/NEJMoa2207323 (accessed on 2 October 2022).
- Memariani, M.; Memariani, H. Multinational monkeypox outbreak: What do we know and what should we do? Ir. J. Med. Sci. 2022, 2022, 1–2. [Google Scholar] [CrossRef]
- Multi-Country Monkeypox Outbreak in Non-Endemic Countries. Available online: https://www.who.int/emergencies/disease-outbreak-news/item/2022-DON385 (accessed on 2 October 2022).
- Gong, Q.; Wang, C.; Chuai, X.; Chiu, S. Monkeypox virus: A re-emergent threat to humans. Virol. Sin. 2022, 37, 477–482. [Google Scholar] [CrossRef]
- Laboratory Testing for the Monkeypox Virus. Available online: https://apps.who.int/iris/bitstream/handle/10665/354488/WHO-MPX-Laboratory-2022.1-eng.pdf?sequence=1&isAllowed=y (accessed on 2 October 2022).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Lake Tahoe, NV, USA, 2012; Volume 25. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch ormalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Vienna, Austria, 29–30 October 2015; pp. 448–456. [Google Scholar]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist–level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Haenssle, H.A.; Fink, C.; Schneiderbauer, R.; Toberer, F.; Buhl, T.; Blum, A.; Kalloo, A.; Hassen, A.B.H.; Thomas, L.; Enk, A.; et al. Man against machine: Diagnostic performance of a deep learning convolutional neural network for dermoscopic melanoma recognition in comparison to 58 dermatologists. Ann. Oncol. 2018, 29, 1836–1842. [Google Scholar] [CrossRef]
- Hekler, A.; Utikal, J.S.; Enk, A.H.; Hauschild, A.; Weichenthal, M.; Maron, R.C.; Berking, C.; Haferkamp, S.; Klode, J.; Schadendorf, D.; et al. Superior skin cancer classification by the combination of human and artificial intelligence. Eur. J. Cancer 2019, 120, 114–121. [Google Scholar] [CrossRef]
- Akinola, O.O.; Ezugwu, A.E.; Agushaka, J.O.; Zitar, R.A.; Abualigah, L. Multiclass feature selection with metaheuristic optimization algorithms: A review. Neural Comput. Appl. 2022, 34, 19751–19790. [Google Scholar] [CrossRef]
- Eid, M.M.; El-kenawy, E.S.M.; Ibrahim, A. A binary Sine Cosine-Modified Whale Optimization Algorithm for Feature Selection. In Proceedings of the 2021 National Computing Colleges Conference (NCCC), Taif, Saudi Arabia, 27–28 March 2021. [Google Scholar] [CrossRef]
- Ibrahim, A.; Mirjalili, S.; El-Said, M.; Ghoneim, S.S.M.; Al-Harthi, M.M.; Ibrahim, T.F.; El-Kenawy, E.S.M. Wind Speed Ensemble Forecasting Based on Deep Learning Using Adaptive Dynamic Optimization Algorithm. IEEE Access 2021, 9, 125787–125804. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M. A new human-based metahurestic optimization method based on mimicking cooking training. Sci. Rep. 2022, 12, 14861. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Mirjalili, S.; Abdelhamid, A.A.; Ibrahim, A.; Khodadadi, N.; Eid, M.M. Meta-Heuristic Optimization and Keystroke Dynamics for Authentication of Smartphone Users. Mathematics 2022, 10, 2912. [Google Scholar] [CrossRef]
- Alhussan, A.A.; Khafaga, D.S.; El-Kenawy, E.S.M.; Ibrahim, A.; Eid, M.M.; Abdelhamid, A.A. Pothole and Plain Road Classification Using Adaptive Mutation Dipper Throated Optimization and Transfer Learning for Self Driving Cars. IEEE Access 2022, 10, 84188–84211. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; El-Kenawy, E.S.M.; Alotaibi, B.; Amer, G.M.; Abdelkader, M.Y.; Ibrahim, A.; Eid, M.M. Robust Speech Emotion Recognition Using CNN+LSTM Based on Stochastic Fractal Search Optimization Algorithm. IEEE Access 2022, 10, 49265–49284. [Google Scholar] [CrossRef]
- El-kenawy, E.S.M.; Abdelhamid, A.A.; Ibrahim, A.; Mirjalili, S.; Khodadad, N.; Al Duailij, M.A.; Alhussan, A.A.; Khafaga, D.S. Al-Biruni Earth Radius (BER) Metaheuristic Search Optimization Algorithm. Comput. Syst. Sci. Eng. 2023, 45, 1917–1934. [Google Scholar] [CrossRef]
- Abdelhamid, A.A.; El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Khafaga, D.S.; Alharbi, A.H.; Ibrahim, A.; Eid, M.M.; Saber, M. Classification of Monkeypox Images Based on Transfer Learning and the Al-Biruni Earth Radius Optimization Algorithm. Mathematics 2022, 10, 3614. [Google Scholar] [CrossRef]
- Salimi, H. Stochastic Fractal Search: A powerful metaheuristic algorithm. Knowl.-Based Syst. 2015, 75, 1–18. [Google Scholar] [CrossRef]
- Bello, R.; Gomez, Y.; Nowe, A.; Garcia, M.M. Two-Step Particle Swarm Optimization to Solve the Feature Selection Problem. In Proceedings of the Seventh International Conference on Intelligent Systems Design and Applications (ISDA 2007), Rio de Janeiro, Brazil, 20–24 October 2007; pp. 691–696. [Google Scholar] [CrossRef]
- Al-Tashi, Q.; Abdul Kadir, S.J.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Binary Optimization Using Hybrid Grey Wolf Optimization for Feature Selection. IEEE Access 2019, 7, 39496–39508. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jang, S.; Jang, Y.E.; Kim, Y.J.; Yu, H. Input initialization for inversion of neural networks using k-nearest neighbor approach. Inf. Sci. 2020, 519, 229–242. [Google Scholar] [CrossRef]
- Tharwat, A. Parameter investigation of support vector machine classifier with kernel functions. Knowl. Inf. Syst. 2019, 61, 1269–1302. [Google Scholar] [CrossRef]
- Han, J.; Zhang, D.; Cheng, G.; Liu, N.; Xu, D. Advanced Deep-Learning Techniques for Salient and Category-Specific Object Detection: A Survey. IEEE Signal Process. Mag. 2018, 35, 84–100. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Al-Dhamari, A.; Sudirman, R.; Mahmood, N.H. Transfer Deep Learning Along with Binary Support Vector Machine for Abnormal Behavior Detection. IEEE Access 2020, 8, 61085–61095. [Google Scholar] [CrossRef]
- Yu, S.; Xie, L.; Liu, L.; Xia, D. Learning Long-Term Temporal Features with Deep Neural Networks for Human Action Recognition. IEEE Access 2020, 8, 1840–1850. [Google Scholar] [CrossRef]
- Amarathunga, A.a.L.C.; Ellawala, E.P.W.C.; Abeysekara, G.N.; Amalraj, C.R.J. Expert System For Diagnosis Of Skin Diseases. Int. J. Sci. Technol. Res. 2015, 4, 174–178. [Google Scholar]
- Wei, L.s.; Gan, Q.; Ji, T. Skin Disease Recognition Method Based on Image Color and Texture Features. Comput. Math. Methods Med. 2018, 2018, 8145713. [Google Scholar] [CrossRef]
- Chatterjee, S.; Dey, D.; Munshi, S.; Gorai, S. Extraction of features from cross correlation in space and frequency domains for classification of skin lesions. Biomed. Signal Process. Control. 2019, 53, 101581. [Google Scholar] [CrossRef]
- Diagnosis of Skin Lesions Based on Dermoscopic Images Using Image Processing Techniques; IntechOpen: London, UK, 2022.
- Narayanan, S.J.; Jaiswal, P.R.; Chowdhury, A.; Joseph, A.M.; Ambar, S. A Computational Intelligence Approach for Skin Disease Identification Using Machine/Deep Learning Algorithms. In Computational Intelligence and Healthcare Informatics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 15; pp. 269–295. [Google Scholar] [CrossRef]
- Shamsul Arifin, M.; Golam Kibria, M.; Firoze, A.; Ashraful Amini, M.; Yan, H. Dermatological disease diagnosis using color-skin images. In Proceedings of the 2012 International Conference on Machine Learning and Cybernetics, Xi’an, China, 15–17 July 2012; Volume 5, pp. 1675–1680. [Google Scholar] [CrossRef]
- Yasir, R.; Rahman, M.A.; Ahmed, N. Dermatological disease detection using image processing and artificial neural network. In Proceedings of the 8th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 20–22 December 2014; pp. 687–690. [Google Scholar] [CrossRef]
- ALKolifi ALEnezi, N.S. A Method Of Skin Disease Detection Using Image Processing and Machine Learning. Procedia Comput. Sci. 2019, 163, 85–92. [Google Scholar] [CrossRef]
- Sandeep, R.; Vishal, K.P.; Shamanth, M.S.; Chethan, K. Diagnosis of Visible Diseases Using CNNs. In Proceedings of the International Conference on Communication and Artificial Intelligence; Goyal, V., Gupta, M., Mirjalili, S., Trivedi, A., Eds.; Lecture Notes in Networks and Systems; Springer Nature: Berlin/Heidelberg, Germany, 2022; pp. 459–468. [Google Scholar]
- Mejía Lara, J.V.; Arias Velásquez, R.M. Low-cost image analysis with convolutional neural network for herpes zoster. Biomed. Signal Process. Control 2022, 71, 103250. [Google Scholar] [CrossRef]
- Glock, K.; Napier, C.; Gary, T.; Gupta, V.; Gigante, J.; Schaffner, W.; Wang, Q. Measles Rash Identification Using Transfer Learning and Deep Convolutional Neural Networks. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021; pp. 3905–3910. [Google Scholar] [CrossRef]
- Ali, S.N.; Ahmed, M.T.; Paul, J.; Jahan, T.; Sani, S.M.S.; Noor, N.; Hasan, T. Monkeypox Skin Lesion Detection Using Deep Learning Models: A Feasibility Study. arXiv 2022, arXiv:2207.03342. [Google Scholar]
- Islam, T.; Hussain, M.A.; Chowdhury, F.U.H.; Islam, B.M.R. Can Artificial Intelligence Detect Monkeypox from Digital Skin Images? bioRxiv 2022. [Google Scholar] [CrossRef]
- Sitaula, C.; Shahi, T.B. Monkeypox virus detection using pre-trained deep learning-based approaches. arXiv 2022, arXiv:2209.04444. [Google Scholar] [CrossRef]
- Akin, K.D.; Gurkan, C.; Budak, A.; Karataş, H. Classification of Monkeypox Skin Lesion using the Explainable Artificial Intelligence Assisted Convolutional Neural Networks. Avrupa Bilim ve Teknoloji Dergisi 2022, 40, 106–110. [Google Scholar] [CrossRef]
- Bacanin, N.; Bezdan, T.; Tuba, E.; Strumberger, I.; Tuba, M. Optimizing Convolutional Neural Network Hyperparameters by Enhanced Swarm Intelligence Metaheuristics. Algorithms 2020, 13, 67. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Eid, M.M.; Saber, M.; Ibrahim, A. MbGWO-SFS: Modified Binary Grey Wolf Optimizer Based on Stochastic Fractal Search for Feature Selection. IEEE Access 2020, 8, 107635–107649. [Google Scholar] [CrossRef]
- El-kenawy, E.S.M.; Albalawi, F.; Ward, S.A.; Ghoneim, S.S.M.; Eid, M.M.; Abdelhamid, A.A.; Bailek, N.; Ibrahim, A. Feature Selection and Classification of Transformer Faults Based on Novel Meta-Heuristic Algorithm. Mathematics 2022, 10, 3144. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Mirjalili, S.; Alassery, F.; Zhang, Y.D.; Eid, M.M.; El-Mashad, S.Y.; Aloyaydi, B.A.; Ibrahim, A.; Abdelhamid, A.A. Novel Meta-Heuristic Algorithm for Feature Selection, Unconstrained Functions and Engineering Problems. IEEE Access 2022, 10, 40536–40555. [Google Scholar] [CrossRef]
- Khafaga, D.S.; Alhussan, A.A.; El-Kenawy, E.S.M.; Ibrahim, A.; Eid, M.M.; Abdelhamid, A.A. Solving Optimization Problems of Metamaterial and Double T-Shape Antennas Using Advanced Meta-Heuristics Algorithms. IEEE Access 2022, 10, 74449–74471. [Google Scholar] [CrossRef]
- Monkeypox Skin Images Dataset (MSID). Available online: https://www.kaggle.com/datasets/dipuiucse/monkeypoxskinimagedataset (accessed on 2 October 2022).
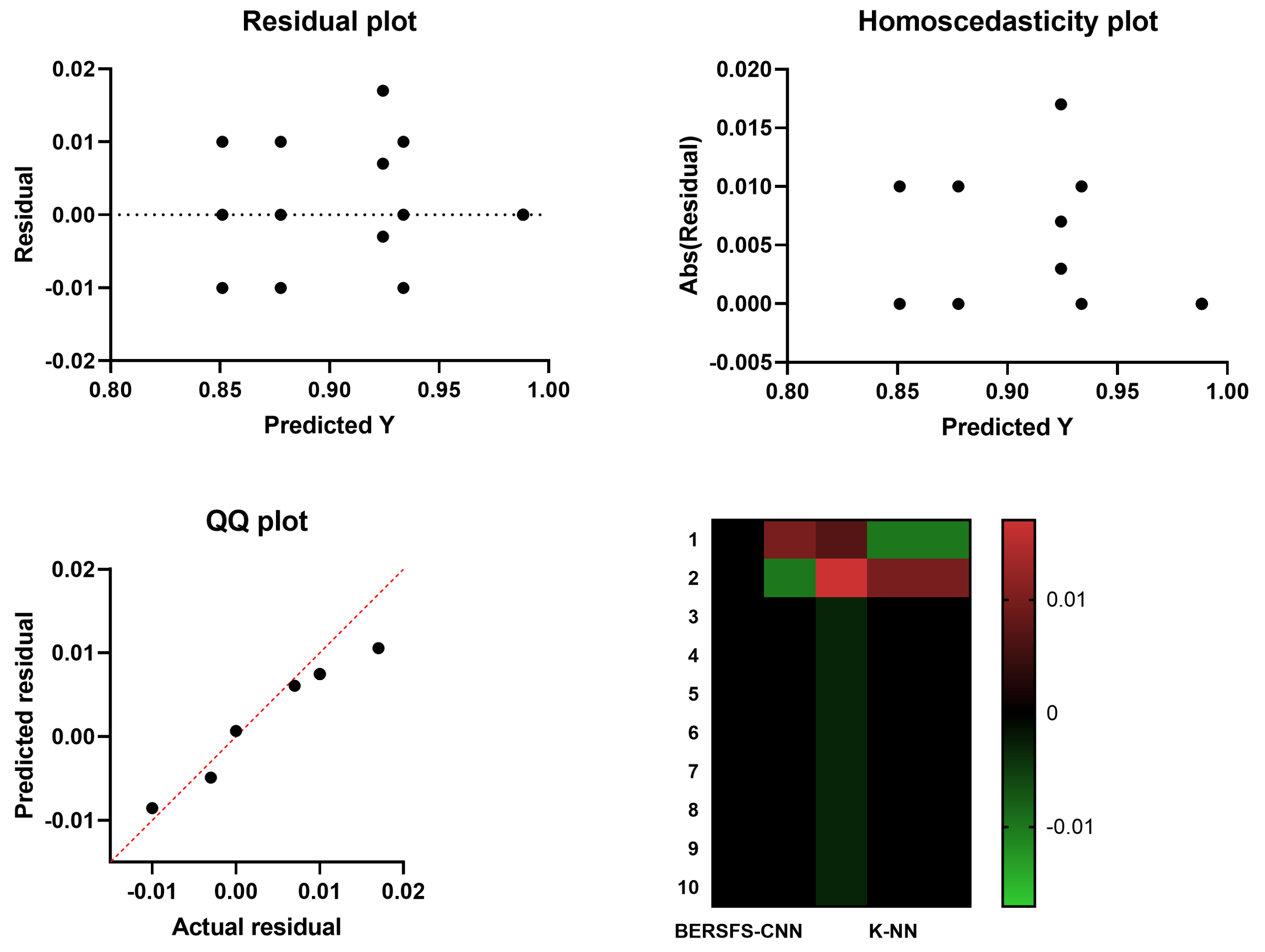
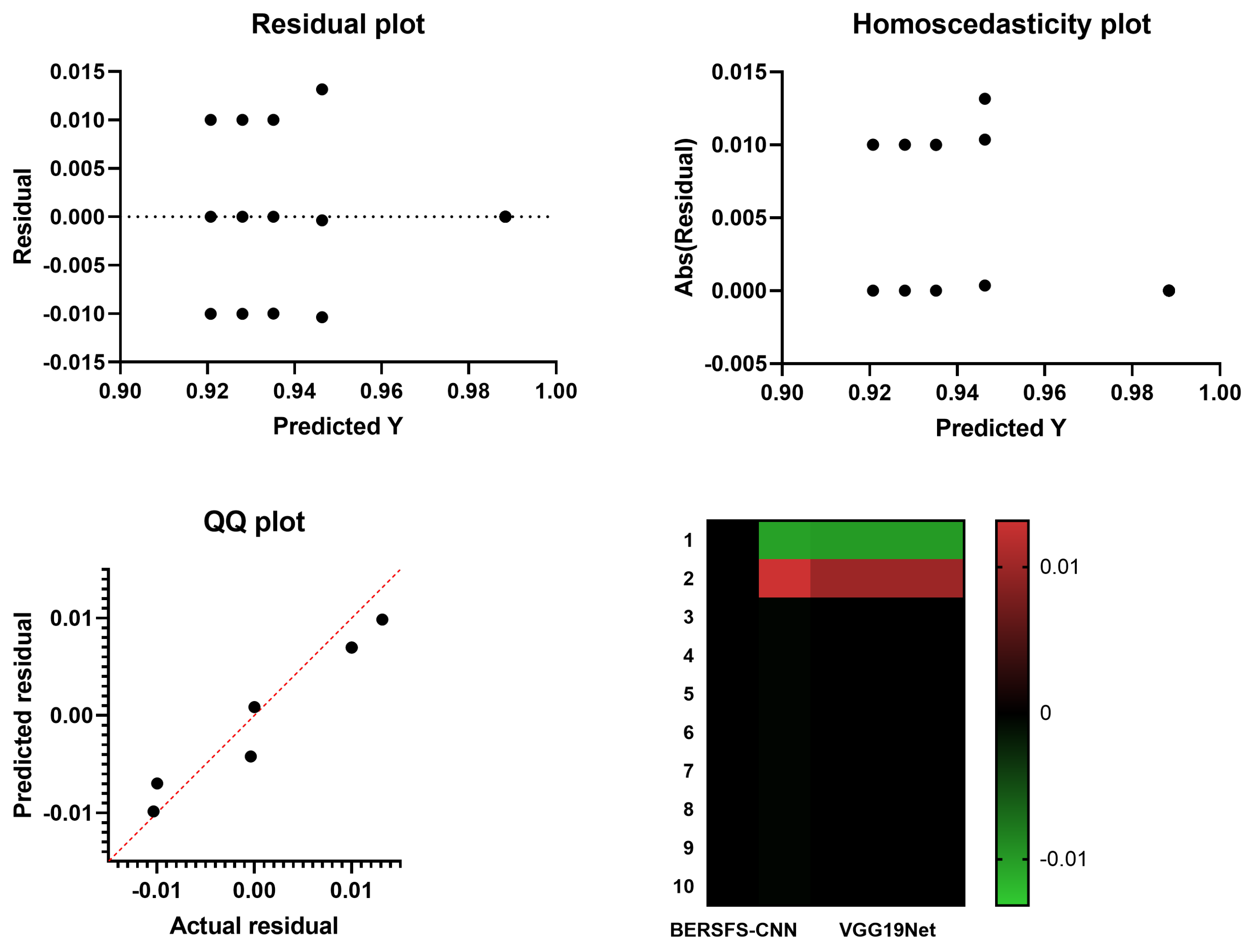
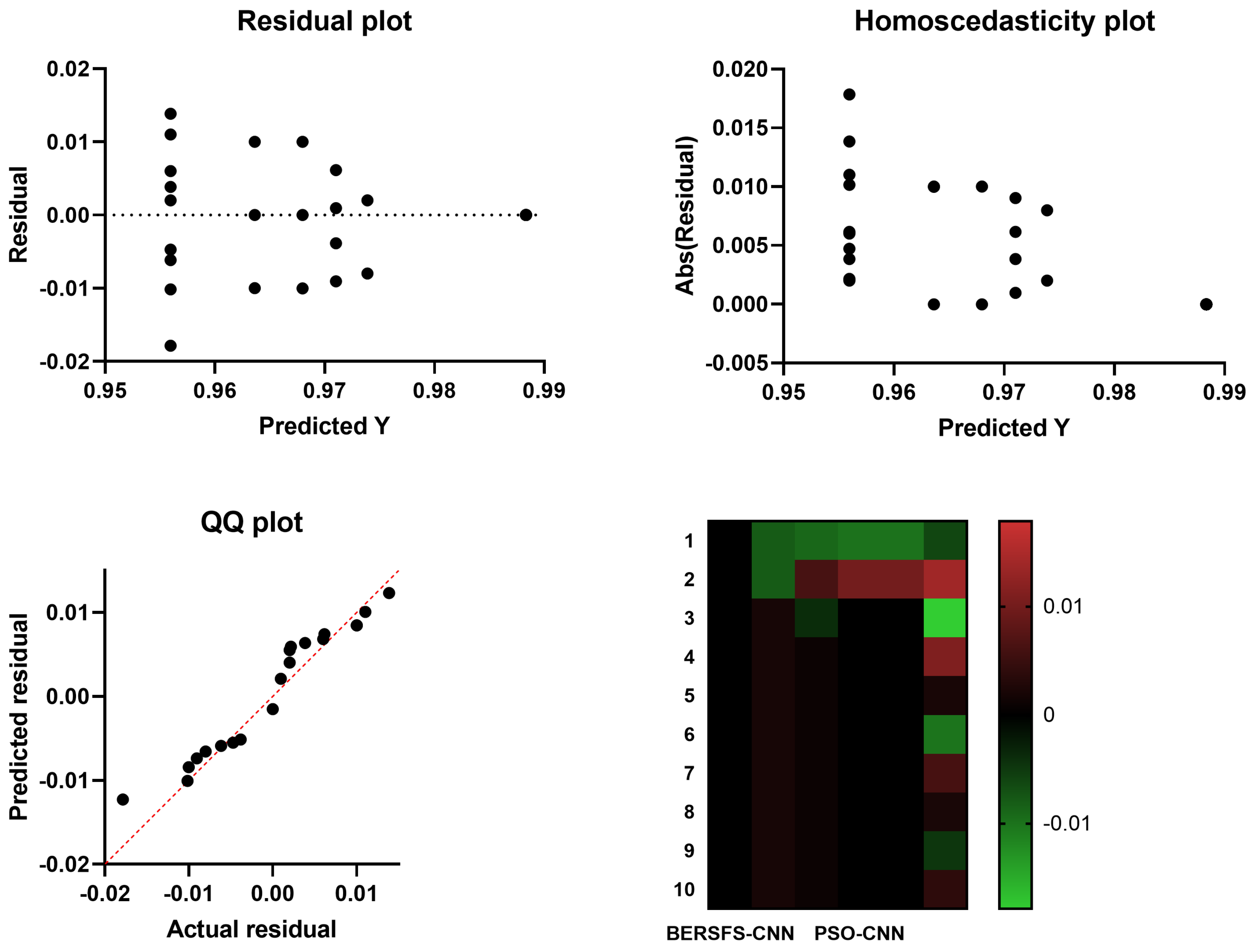
| Parameter | Value |
|---|---|
| Number of Agents | 10 |
| Number of Iterations | 80 |
| Number of Repetitions | 20 |
| ∈[0, 1] | |
| ∈[0, 1] | |
| Mutation probability | 0.5 |
| Exploration percentage | 70 |
| K (decreases from 2 to 0) | 1 |
| Parameter | Value |
|---|---|
| CNN training options (Default) Momentum Learn RateDropFactor L2Regularization LearnRateDropPeriod GradientThreshold GradientThresholdMethod ValidationData VerboseFrequency ValidationPatience ValidationFrequency ResetInputNormalization CNN training options (Custom) InitialLearnRate ExecutionEnvironment BatchSize MaxEpochs Verbose Shuffle LearnRateSchedule Optimizer | 0.9000 0.1000 1.0000 × 10 10 Inf l2norm imds 50 Inf 50 1 0.001 gpu 32 40 0 every-epoch piecwise BERSFS |
| No. Calculation | Metrics |
|---|---|
| Accuracy | |
| Sensitivity | |
| Specificity | |
| Precision (PPV) | |
| Negative Predictive Value (NPV) | |
| F1 Score |
| Accuracy | Sensitivity (TRP) | Specificity (TNP) | p Value (PPV) | N Value (NPV) | F1 Score | |
|---|---|---|---|---|---|---|
| BERSFS-CNN | 0.9883 | 0.8571 | 0.9921 | 0.7595 | 0.9959 | 0.8054 |
| CNN | 0.9337 | 0.7500 | 0.9693 | 0.8257 | 0.9524 | 0.7860 |
| SVM-Linear | 0.9213 | 0.8571 | 0.9231 | 0.2308 | 0.9959 | 0.3636 |
| K-NN | 0.8777 | 0.8000 | 0.9132 | 0.8081 | 0.9091 | 0.8040 |
| DT | 0.8510 | 0.7273 | 0.9132 | 0.8081 | 0.8696 | 0.7656 |
| SS | DF | MS | F (DFn, DFd) | p Value | |
|---|---|---|---|---|---|
| Treatment (between columns) | 0.1129 | 4 | 0.0282 | F (4, 45) = 1258 | p < 0.0001 |
| Residual (within columns) | 0.0010 | 45 | - | - | |
| Total | 0.1139 | 49 | - | - | - |
| BERSFS-CNN | CNN | SVM-Linear | K-NN | DT | |
|---|---|---|---|---|---|
| Theoretical median | 0 | 0 | 0 | 0 | 0 |
| Actual median | 0.9883 | 0.9337 | 0.9213 | 0.8777 | 0.8511 |
| Number of values | 10 | 10 | 10 | 10 | 10 |
| Wilcoxon signed-rank test | |||||
| Sum of signed ranks (W) | 55 | 55 | 55 | 55 | 55 |
| Sum of positive ranks | 55 | 55 | 55 | 55 | 55 |
| Sum of negative ranks | 0 | 0 | 0 | 0 | 0 |
| p value (two-tailed) | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Exact or estimate? | Exact | Exact | Exact | Exact | Exact |
| Significant (alpha = 0.05)? | Yes | Yes | Yes | Yes | Yes |
| How big is the discrepancy? | |||||
| Discrepancy | 0.9883 | 0.9337 | 0.9213 | 0.8777 | 0.8511 |
| Accuracy | Sensitivity (TRP) | Specificity (TNP) | p Value (PPV) | N Value (NPV) | F1 Score | |
|---|---|---|---|---|---|---|
| BERSFS-CNN | 0.9883 | 0.8571 | 0.9921 | 0.7595 | 0.9959 | 0.8054 |
| AlexNet | 0.9459 | 0.7143 | 0.9524 | 0.2941 | 0.9917 | 0.4167 |
| GoogLeNet | 0.9351 | 0.7143 | 0.9412 | 0.2500 | 0.9917 | 0.3704 |
| VGG19Net | 0.9280 | 0.7143 | 0.9339 | 0.2273 | 0.9917 | 0.3448 |
| ResNet-50 | 0.9208 | 0.6667 | 0.9266 | 0.1739 | 0.9917 | 0.2759 |
| SS | DF | MS | F (DFn, DFd) | p Value | |
|---|---|---|---|---|---|
| Treatment (between columns) | 0.0284 | 4 | 0.0071 | F (4, 45) = 363.3 | p < 0.0001 |
| Residual (within columns) | 0.0009 | 45 | - | - | |
| Total | 0.0293 | 49 | - | - | - |
| BERSFS-CNN | AlexNet | GoogLeNet | VGG19Net | ResNet-50 | |
|---|---|---|---|---|---|
| Theoretical median | 0 | 0 | 0 | 0 | 0 |
| Actual median | 0.9883 | 0.9459 | 0.9351 | 0.928 | 0.9208 |
| Number of values | 10 | 10 | 10 | 10 | 10 |
| Wilcoxon signed-rank test | |||||
| Sum of signed ranks (W) | 55 | 55 | 55 | 55 | 55 |
| Sum of positive ranks | 55 | 55 | 55 | 55 | 55 |
| Sum of negative ranks | 0 | 0 | 0 | 0 | 0 |
| p value (two-tailed) | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Exact or estimate? | Exact | Exact | Exact | Exact | Exact |
| Significant (alpha = 0.05)? | Yes | Yes | Yes | Yes | Yes |
| How big is the discrepancy? | |||||
| Discrepancy | 0.9883 | 0.9459 | 0.9351 | 0.928 | 0.9208 |
| Algorithm | Parameter (s) | Value (s) |
|---|---|---|
| BER | Mutation probability | 0.5 |
| Exploration percentage | 70 | |
| K (decreases from 2 to 0) | 1 | |
| SFS | ∈[0, 1] | |
| ∈[0, 1] | ||
| PSO | Acceleration constants | [2, 2] |
| Inertia , | [0.6, 0.9] | |
| Particles | 10 | |
| Iterations | 80 | |
| GWO | a | 2 to 0 |
| Iterations | 80 | |
| Wolves | 10 | |
| WOA | r | [0, 1] |
| Iterations | 80 | |
| Whales | 10 | |
| a | 2 to 0 |
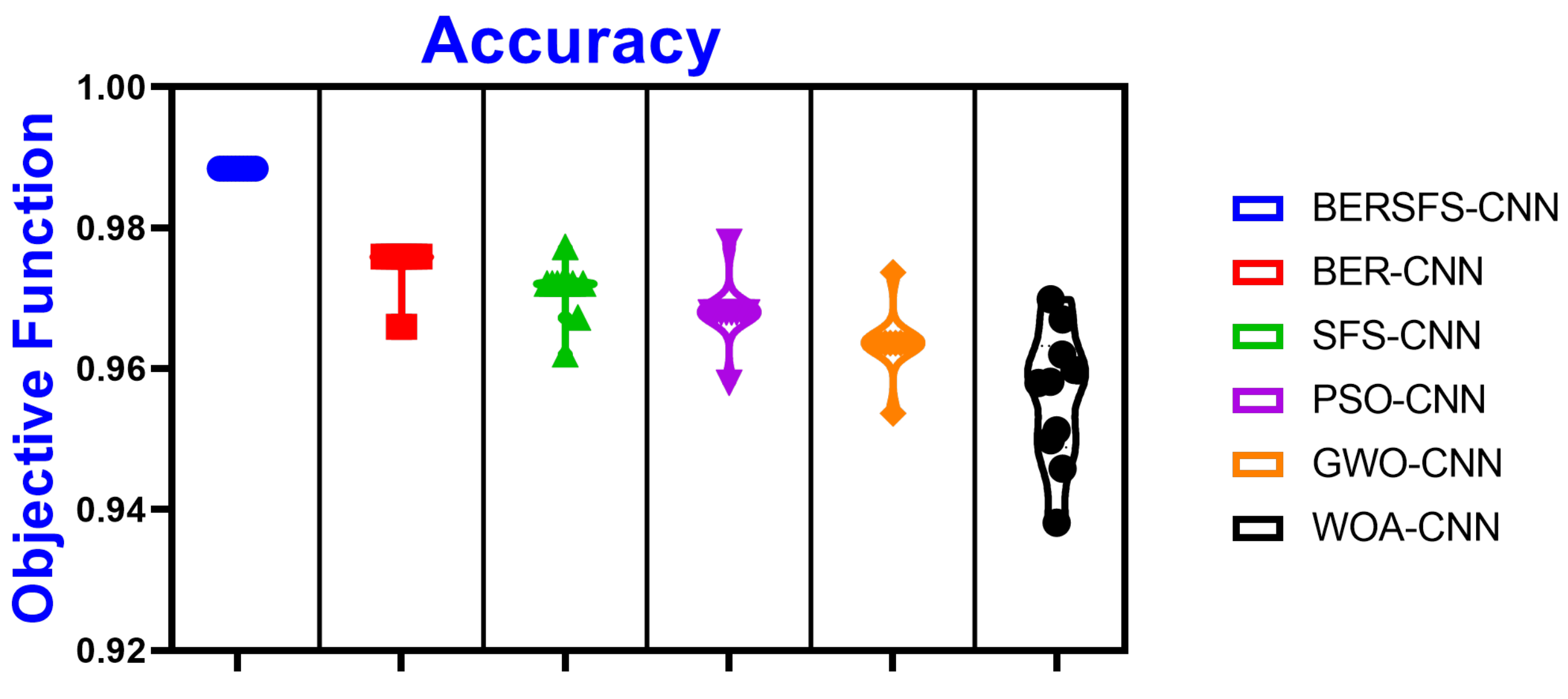
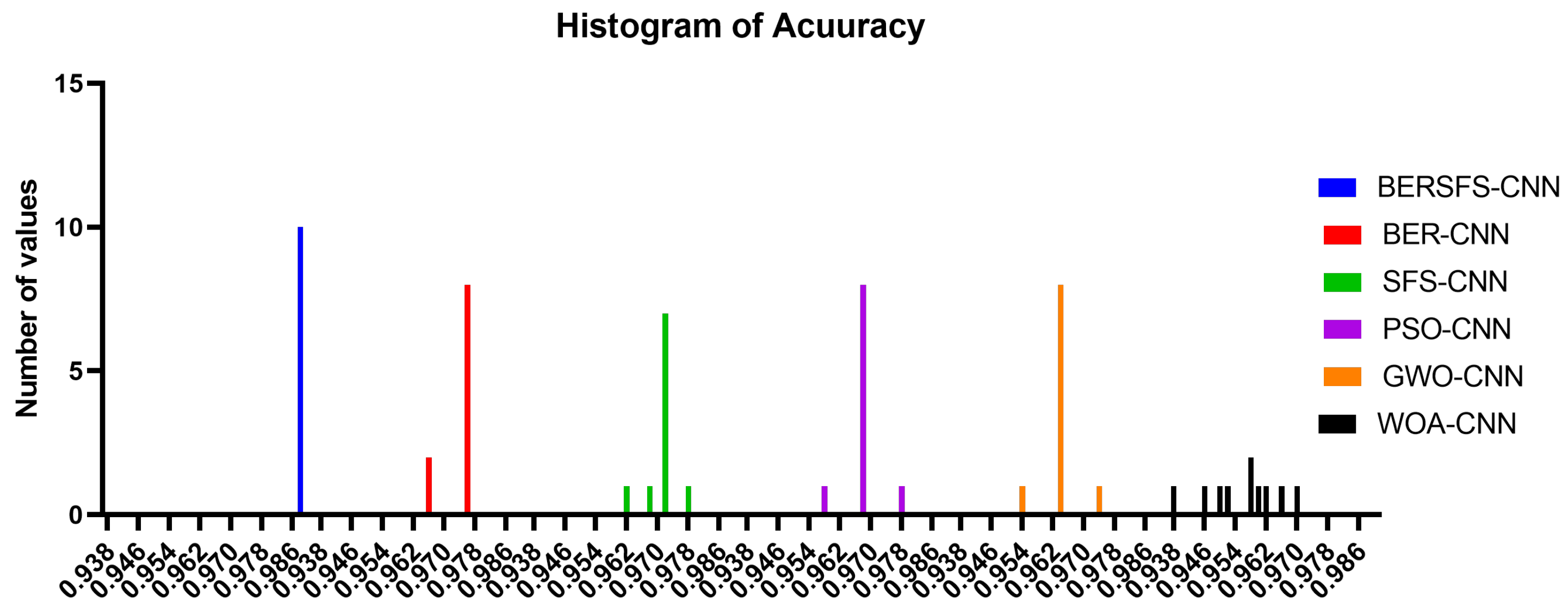
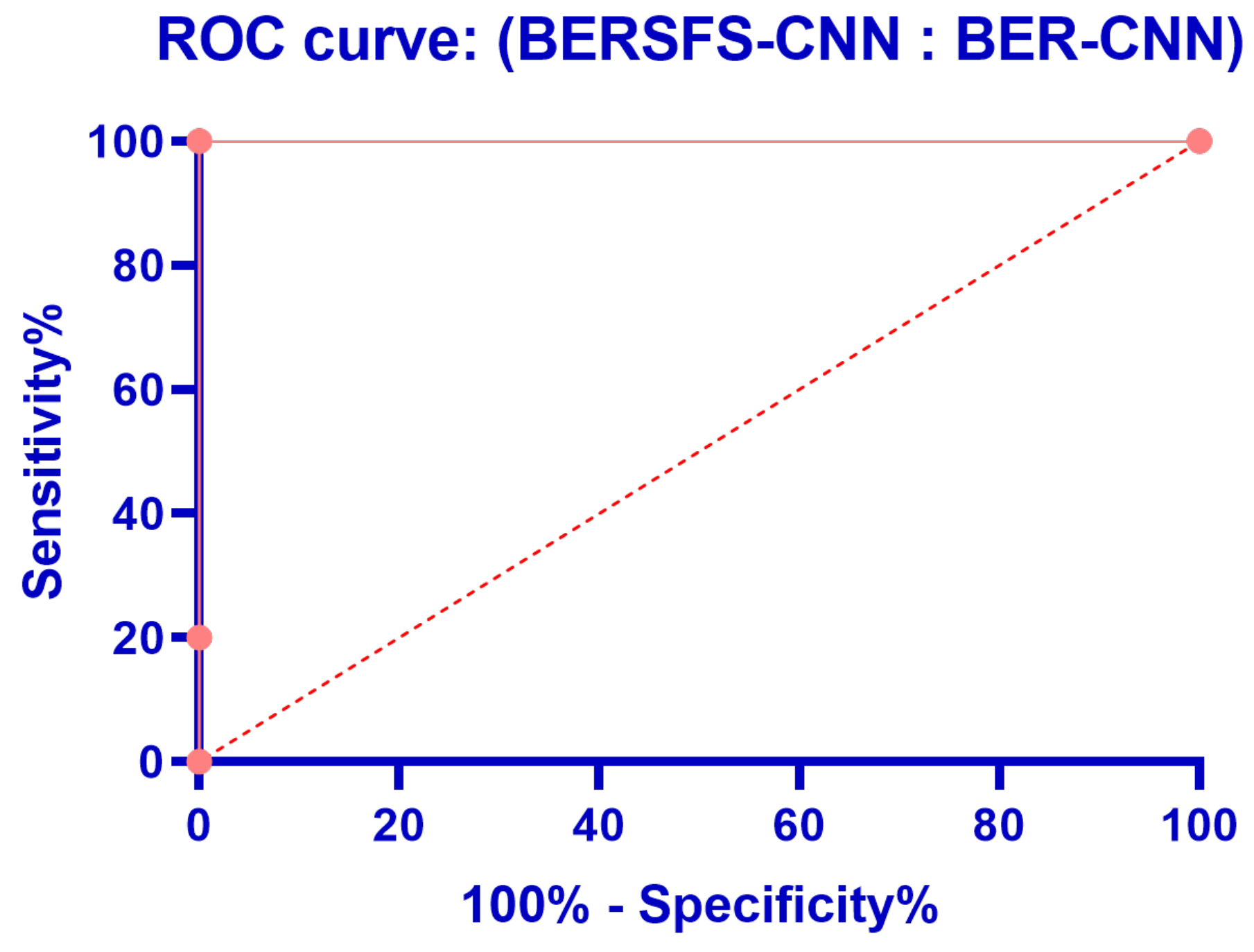
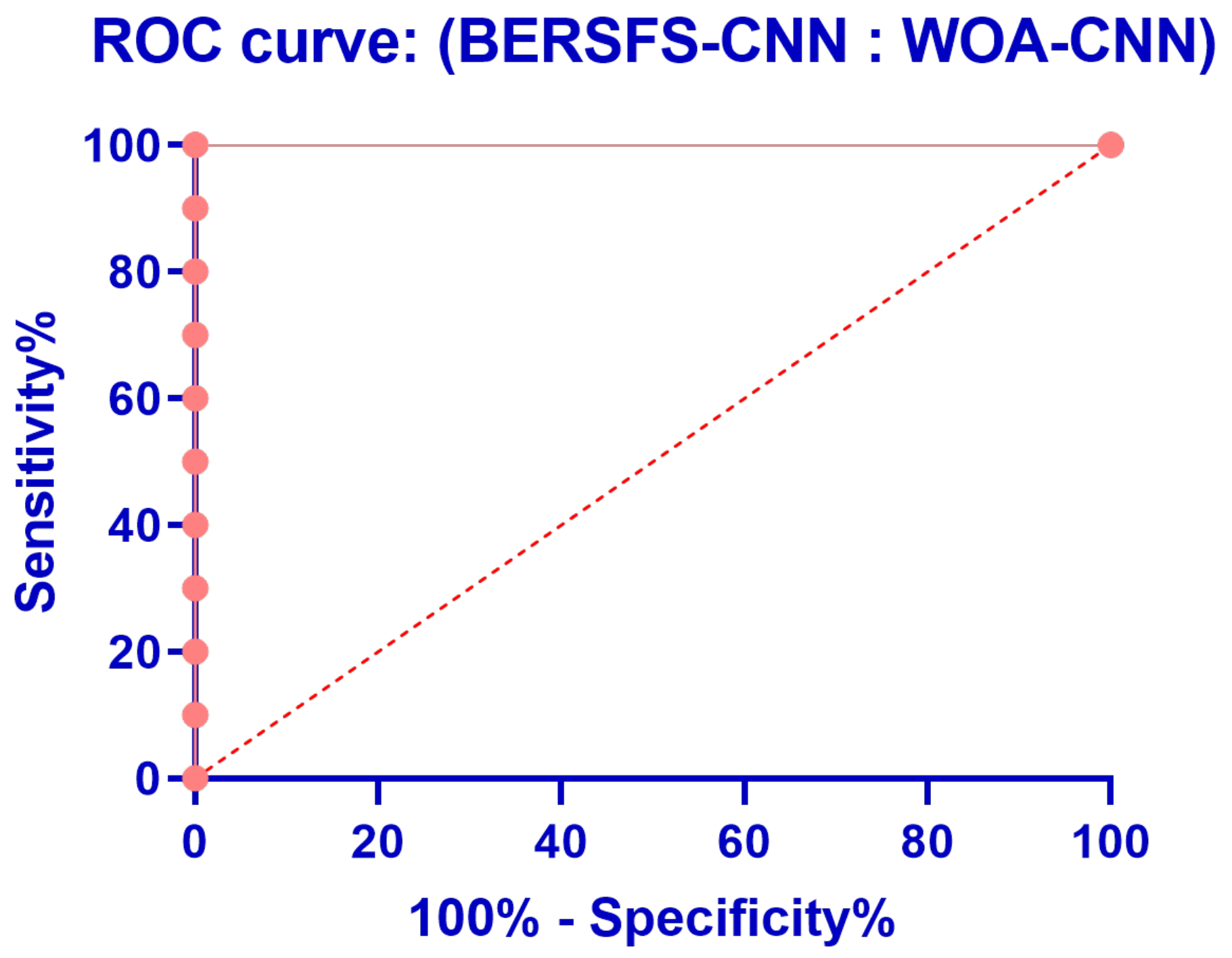
| Accuracy | Sensitivity (TRP) | Specificity (TNP) | p Value (PPV) | N Value (NPV) | F1 Score | |
|---|---|---|---|---|---|---|
| BERSFS-CNN | 0.9883 | 0.8571 | 0.9921 | 0.7595 | 0.9959 | 0.8054 |
| BER-CNN | 0.9759 | 0.7500 | 0.9796 | 0.3750 | 0.9959 | 0.5000 |
| SFS-CNN | 0.9720 | 0.6000 | 0.9796 | 0.3750 | 0.9917 | 0.4615 |
| PSO-CNN | 0.9680 | 0.4000 | 0.9796 | 0.2857 | 0.9877 | 0.3333 |
| GWO-CNN | 0.9636 | 0.4000 | 0.9767 | 0.2857 | 0.9859 | 0.3333 |
| WOA-CNN | 0.9598 | 0.7674 | 0.9655 | 0.3976 | 0.9929 | 0.5238 |
| SS | DF | MS | F (DFn, DFd) | p Value | |
|---|---|---|---|---|---|
| Treatment (between columns) | 0.0059 | 5 | 0.0012 | F (5, 54) = 41.27 | p < 0.0001 |
| Residual (within columns) | 0.0016 | 54 | - | - | |
| Total | 0.0075 | 59 | - | - | - |
| BERSFS-CNN | BER-CNN | SFS-CNN | PSO-CNN | GWO-CNN | WOA-CNN | |
|---|---|---|---|---|---|---|
| Theoretical median | 0 | 0 | 0 | 0 | 0 | 0 |
| Actual median | 0.9883 | 0.9759 | 0.972 | 0.968 | 0.9636 | 0.9581 |
| Number of values | 10 | 10 | 10 | 10 | 10 | 10 |
| Wilcoxon signed-rank test | ||||||
| Sum of signed ranks (W) | 55 | 55 | 55 | 55 | 55 | 55 |
| Sum of positive ranks | 55 | 55 | 55 | 55 | 55 | 55 |
| Sum of negative ranks | 0 | 0 | 0 | 0 | 0 | 0 |
| p value (two-tailed) | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Exact or estimate? | Exact | Exact | Exact | Exact | Exact | Exact |
| Significant (alpha = 0.05)? | Yes | Yes | Yes | Yes | Yes | Yes |
| How big is the discrepancy? | ||||||
| Discrepancy | 0.9883 | 0.9759 | 0.972 | 0.968 | 0.9636 | 0.9581 |
| BERSFS-CNN | BER-CNN | SFS-CNN | PSO-CNN | GWO-CNN | WOA-CNN | |
|---|---|---|---|---|---|---|
| Number of values | 10 | 10 | 10 | 10 | 10 | 10 |
| Minimum | 0.9883 | 0.9659 | 0.962 | 0.9580 | 0.9536 | 0.9381 |
| 25th percentile | 0.9883 | 0.9734 | 0.9708 | 0.9680 | 0.9636 | 0.9488 |
| Median | 0.9883 | 0.9759 | 0.972 | 0.9680 | 0.9636 | 0.9581 |
| 75th percentile | 0.9883 | 0.9759 | 0.972 | 0.9680 | 0.9636 | 0.9632 |
| Maximum | 0.9883 | 0.9759 | 0.9772 | 0.9780 | 0.9736 | 0.9698 |
| Range | 0 | 0.0100 | 0.0152 | 0.0200 | 0.0200 | 0.0317 |
| Mean | 0.9883 | 0.9739 | 0.9710 | 0.9680 | 0.9636 | 0.9560 |
| Std. deviation | 0 | 0.0042 | 0.0036 | 0.0047 | 0.0047 | 0.0097 |
| Std. error of mean | 0 | 0.0013 | 0.0013 | 0.0015 | 0.0015 | 0.0031 |
| Geometric mean | 0.9883 | 0.9739 | 0.9710 | 0.9680 | 0.9636 | 0.9559 |
| Geometric SD factor | 1 | 1.0040 | 1.0040 | 1.0050 | 1.0050 | 1.0100 |
| Sum | 9.8830 | 9.7390 | 9.7100 | 9.6800 | 9.6360 | 9.5600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khafaga, D.S.; Ibrahim, A.; El-Kenawy, E.-S.M.; Abdelhamid, A.A.; Karim, F.K.; Mirjalili, S.; Khodadadi, N.; Lim, W.H.; Eid, M.M.; Ghoneim, M.E. An Al-Biruni Earth Radius Optimization-Based Deep Convolutional Neural Network for Classifying Monkeypox Disease. Diagnostics 2022, 12, 2892. https://doi.org/10.3390/diagnostics12112892
Khafaga DS, Ibrahim A, El-Kenawy E-SM, Abdelhamid AA, Karim FK, Mirjalili S, Khodadadi N, Lim WH, Eid MM, Ghoneim ME. An Al-Biruni Earth Radius Optimization-Based Deep Convolutional Neural Network for Classifying Monkeypox Disease. Diagnostics. 2022; 12(11):2892. https://doi.org/10.3390/diagnostics12112892
Chicago/Turabian StyleKhafaga, Doaa Sami, Abdelhameed Ibrahim, El-Sayed M. El-Kenawy, Abdelaziz A. Abdelhamid, Faten Khalid Karim, Seyedali Mirjalili, Nima Khodadadi, Wei Hong Lim, Marwa M. Eid, and Mohamed E. Ghoneim. 2022. "An Al-Biruni Earth Radius Optimization-Based Deep Convolutional Neural Network for Classifying Monkeypox Disease" Diagnostics 12, no. 11: 2892. https://doi.org/10.3390/diagnostics12112892
APA StyleKhafaga, D. S., Ibrahim, A., El-Kenawy, E.-S. M., Abdelhamid, A. A., Karim, F. K., Mirjalili, S., Khodadadi, N., Lim, W. H., Eid, M. M., & Ghoneim, M. E. (2022). An Al-Biruni Earth Radius Optimization-Based Deep Convolutional Neural Network for Classifying Monkeypox Disease. Diagnostics, 12(11), 2892. https://doi.org/10.3390/diagnostics12112892















