Retrospective Clinical Trial to Evaluate the Effectiveness of a New Tanner–Whitehouse-Based Bone Age Assessment Algorithm Trained with a Deep Neural Network System
Abstract
1. Introduction
2. Materials and Methods
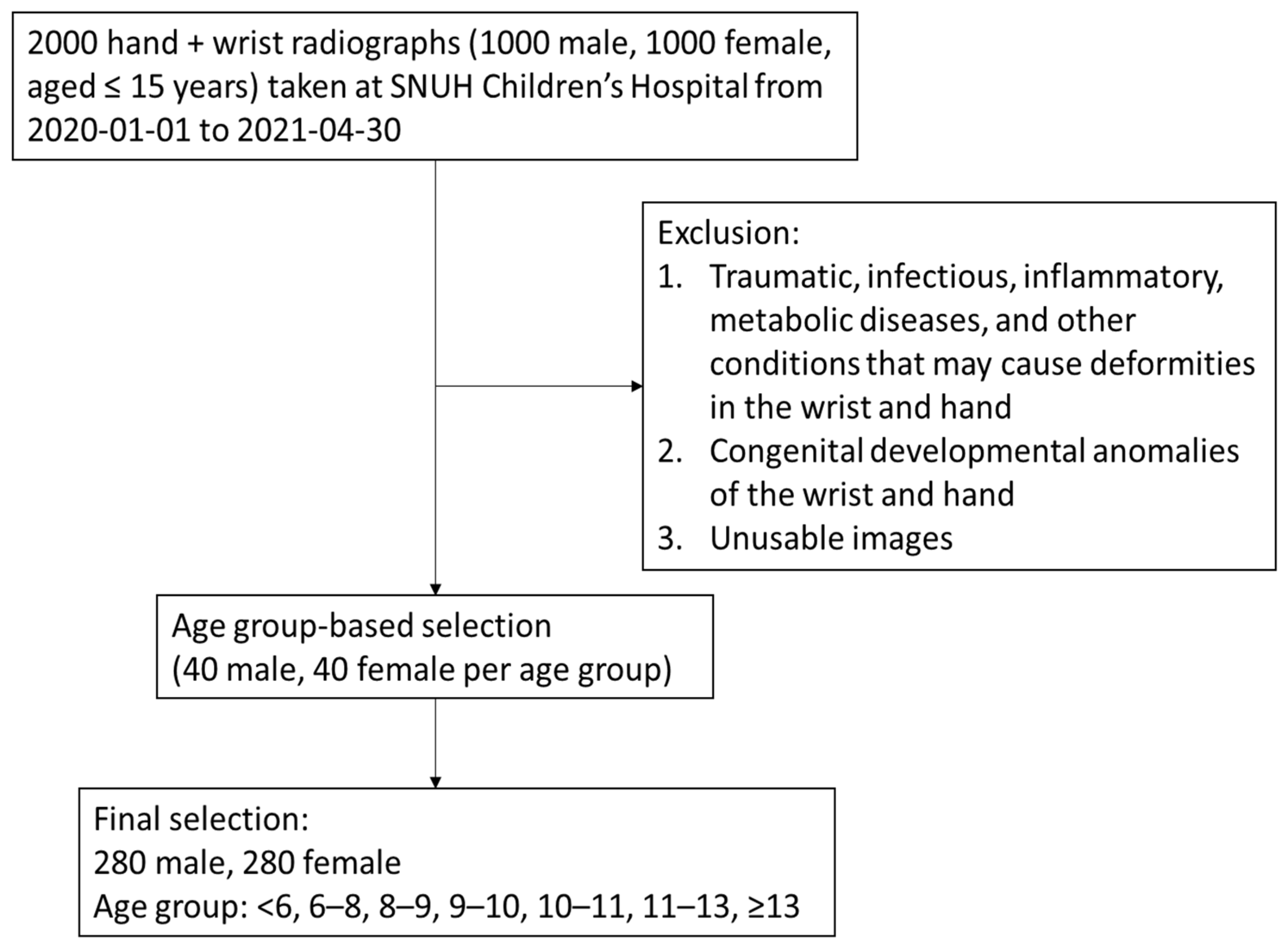
2.1. Selection of Study Participants
2.2. Bone Age Assessment by Radiologists
2.3. Bone Age Assessment by AI
2.4. Outcomes
2.5. Statistical Analysis
3. Results
3.1. Characteristics of Study Participants
3.2. Comparison of Bone Age Measurements Between the TW3-Based Model and Radiologists
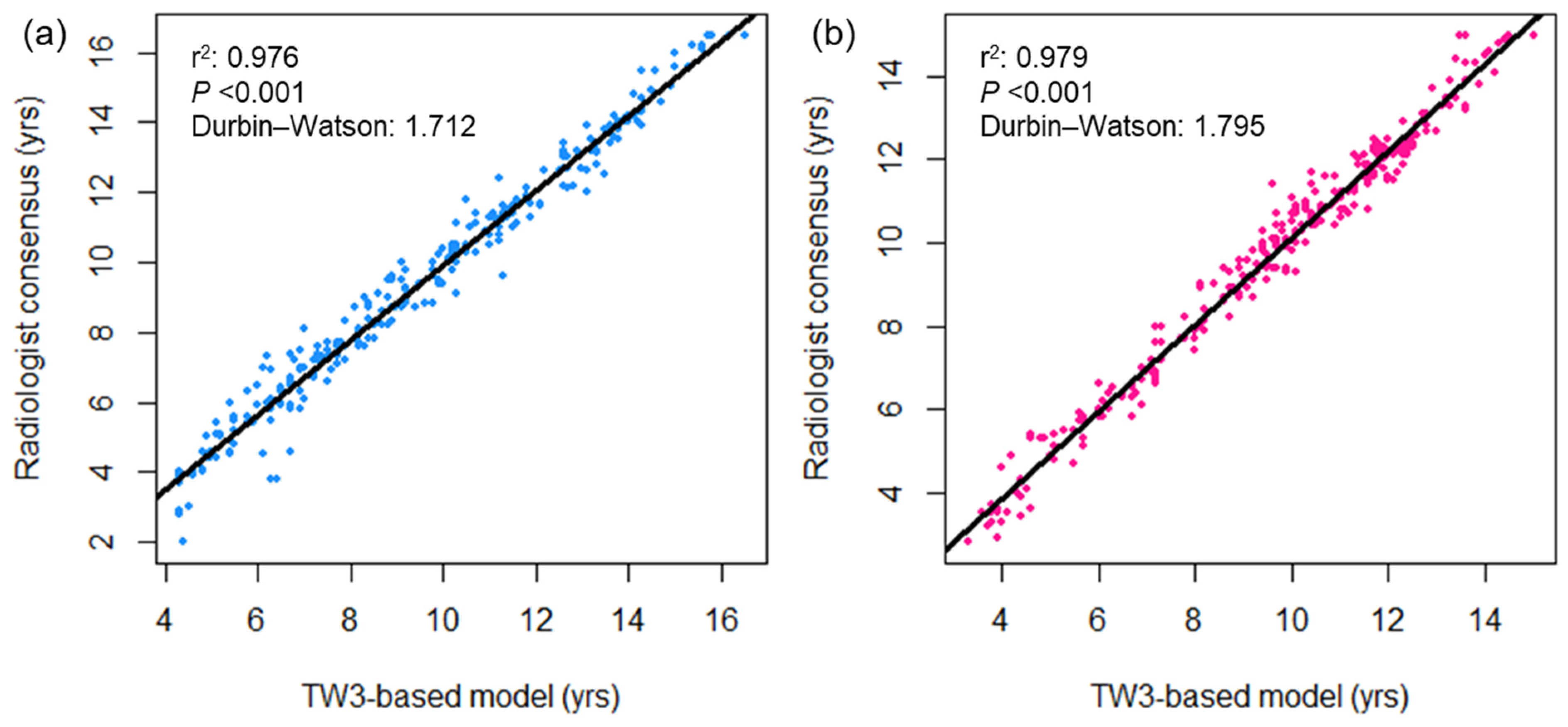
3.3. Linear Regression Analysis of Bone Age Measurements
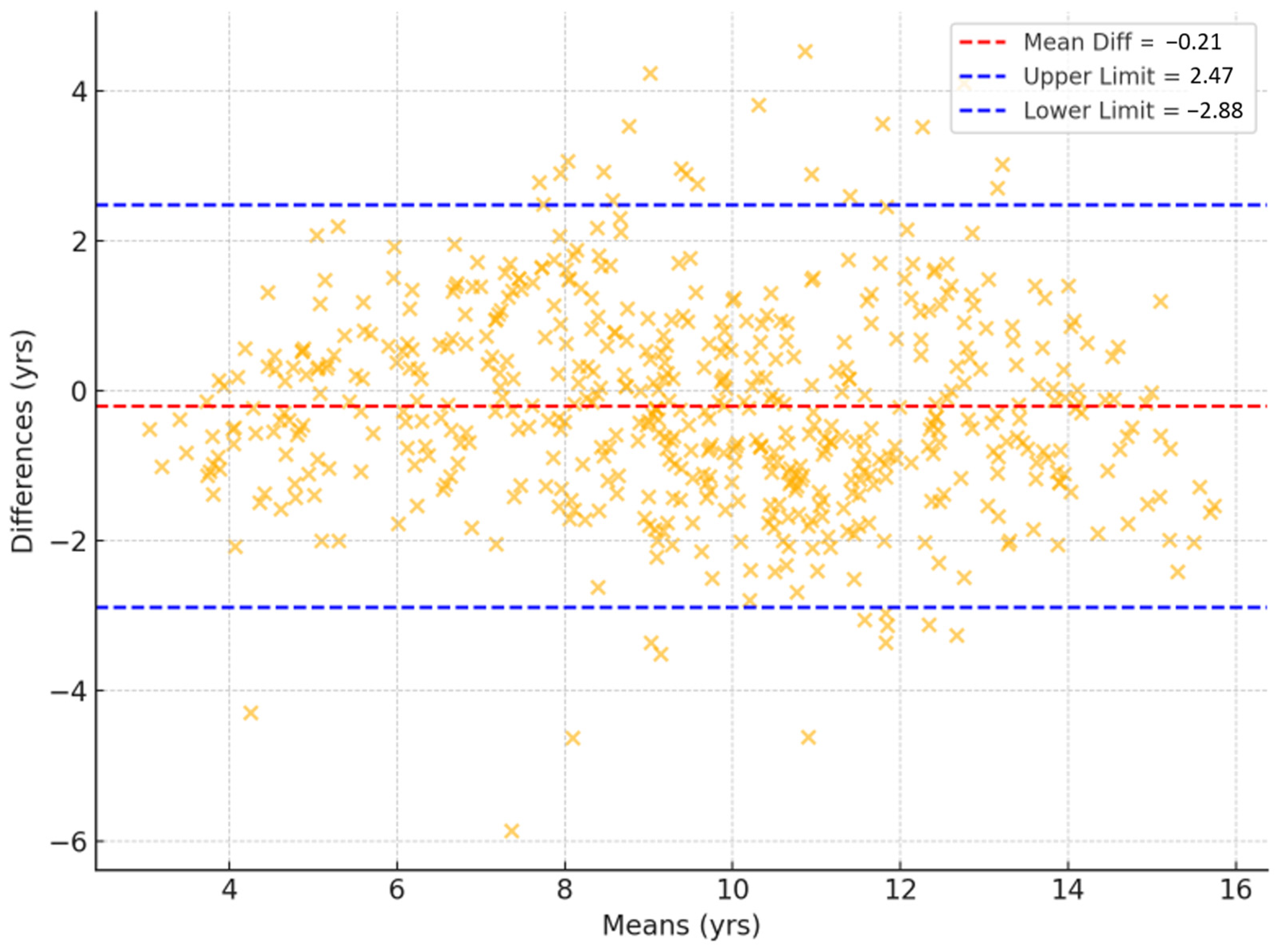
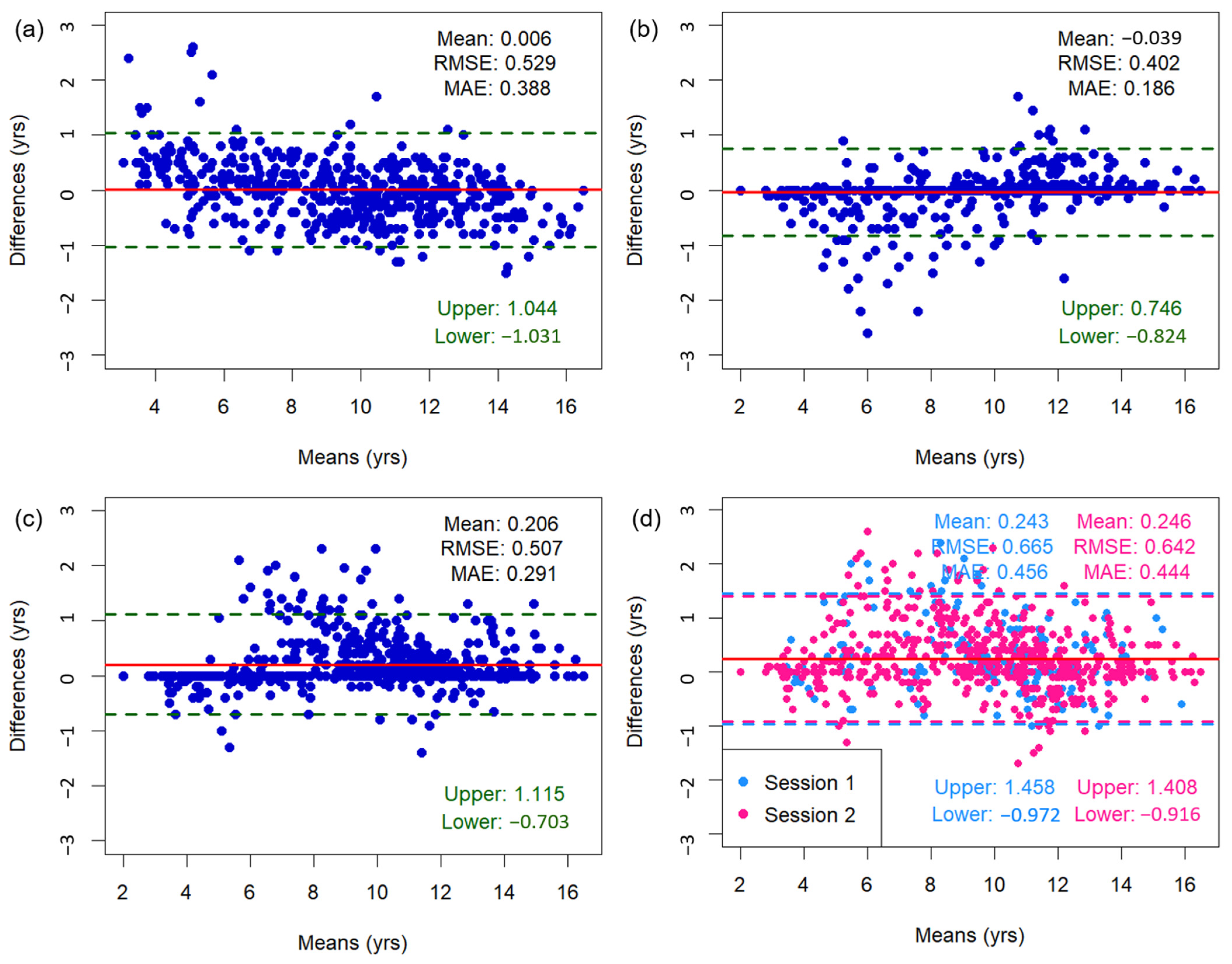
3.4. Bland–Altman Analysis of Bone Age Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| ROI 1 | Radiologist 1 | Radiologist 2 | Interobserver |
|---|---|---|---|
| Ulna | 0.993 | 0.991 | 0.927–0.936 |
| Radius | 0.986 | 0.975 | 0.820–0.845 |
| 3rd Distal Phalanx | 0.995 | 0.994 | 0.890–0.896 |
| 3rd Mid Phalanx | 0.992 | 0.988 | 0.878–0.882 |
| 3rd Proximal Phalanx | 0.983 | 0.991 | 0.920–0.924 |
| 3rd Metacarpal Bone | 0.998 | 0.948 | 0.763–0.792 |
| 5th Distal Phalanx | 0.991 | 0.997 | 0.861–0.871 |
| 5th Mid Phalanx | 0.980 | 0.994 | 0.845–0.852 |
| 5th Proximal Phalanx | 0.992 | 0.981 | 0.863–0.865 |
| 5th Metacarpal Bone | 0.992 | 0.963 | 0.725–0.752 |
| 1st Distal Phalanx | 0.991 | 0.990 | 0.828–0.839 |
| 1st Proximal Phalanx | 0.994 | 0.995 | 0.881–0.885 |
| 1st Metacarpal Bone | 0.992 | 0.991 | 0.861–0.872 |
| Total | 0.991 | 0.986 | 0.862–0.872 |
| Age (yrs) | Female | Male | Total |
|---|---|---|---|
| <6 | 8 (20.0%) | 18 (45.0%) | 26 (32.5%) |
| 6–8 | 4 (10.0%) | 7 (17.5%) | 11 (13.8%) |
| 8–9 | 11 (27.5%) | 6 (15.0%) | 17 (21.3%) |
| 9–10 | 5 (12.5%) | 6 (15.0%) | 11 (13.8%) |
| 10–11 | 4 (10.0%) | 10 (25.0%) | 14 (17.5%) |
| 11–13 | 2 (5.0%) | 1 (2.5%) | 3 (3.8%) |
| >13 | 8 (20.0%) | 9 (22.5%) | 17 (21.3%) |
| Total | 42 (15.0%) | 57 (20.4%) | 99 (17.7%) |
References
- Cavallo, F.; Mohn, A.; Chiarelli, F.; Giannini, C. Evaluation of Bone Age in Children: A Mini-Review. Front. Pediatr. 2021, 9, 580314. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Cho, S.Y.; Maeng, S.H.; Yi, E.S.; Jung, Y.J.; Park, S.W.; Sohn, Y.B.; Jin, D.K. Diagnosis and constitutional and laboratory features of Korean girls referred for precocious puberty. Korean J. Pediatr. 2012, 55, 481–486. [Google Scholar] [CrossRef] [PubMed]
- Creo, A.L.; Schwenk, W.F., 2nd. Bone Age: A Handy Tool for Pediatric Providers. Pediatrics 2017, 140, e20171486. [Google Scholar] [CrossRef]
- Kelly, P.M.; Dimeglio, A. Lower-limb growth: How predictable are predictions? J. Child. Orthop. 2008, 2, 407–415. [Google Scholar] [CrossRef]
- Greulich, W.W.; Pyle, S.I. Radiographic Atlas of Skeletal Development of the Hand and Wrist, 2nd ed.; Stanford University Press: Redwood City, CA, USA, 1999. [Google Scholar]
- Martin, D.D.; Wit, J.M.; Hochberg, Z.; Savendahl, L.; van Rijn, R.R.; Fricke, O.; Cameron, N.; Caliebe, J.; Hertel, T.; Kiepe, D.; et al. The use of bone age in clinical practice—Part 1. Horm. Res. Paediatr. 2011, 76, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Roche, A.F.; Rohmann, C.G.; French, N.Y.; Davila, G.H. Effect of training on replicability of assessments of skeletal maturity (Greulich-Pyle). Am. J. Roentgenol. Radium Ther. Nucl. Med. 1970, 108, 511–515. [Google Scholar] [CrossRef]
- Berst, M.J.; Dolan, L.; Bogdanowicz, M.M.; Stevens, M.A.; Chow, S.; Brandser, E.A. Effect of knowledge of chronologic age on the variability of pediatric bone age determined using the Greulich and Pyle standards. AJR Am. J. Roentgenol. 2001, 176, 507–510. [Google Scholar] [CrossRef]
- Tanner, J.M.; Healy, M.J.R.; Cameron, N.; Goldstein, H. Assessment of Skeletal Maturity and Prediction of Adult Height (TW3 Method), W.B.; Saunders: Philadelphia, PA, USA, 2001. [Google Scholar]
- Andersen, E. Comparison of Tanner-Whitehouse and Greulich-Pyle methods in a large scale Danish Survey. Am. J. Phys. Anthropol. 1971, 35, 373–376. [Google Scholar] [CrossRef]
- King, D.G.; Steventon, D.M.; O’Sullivan, M.P.; Cook, A.M.; Hornsby, V.P.; Jefferson, I.G.; King, P.R. Reproducibility of bone ages when performed by radiology registrars: An audit of Tanner and Whitehouse II versus Greulich and Pyle methods. Br. J. Radiol. 1994, 67, 848–851. [Google Scholar] [CrossRef]
- Spampinato, C.; Palazzo, S.; Giordano, D.; Aldinucci, M.; Leonardi, R. Deep learning for automated skeletal bone age assessment in X-ray images. Med. Image Anal. 2017, 36, 41–51. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; van der Laak, J.; van Ginneken, B.; Sanchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed]
- Hwang, E.J.; Park, C.M. Clinical Implementation of Deep Learning in Thoracic Radiology: Potential Applications and Challenges. Korean J. Radiol. 2020, 21, 511–525. [Google Scholar] [CrossRef] [PubMed]
- McKinney, S.M.; Sieniek, M.; Godbole, V.; Godwin, J.; Antropova, N.; Ashrafian, H.; Back, T.; Chesus, M.; Corrado, G.S.; Darzi, A.; et al. International evaluation of an AI system for breast cancer screening. Nature 2020, 577, 89–94. [Google Scholar] [CrossRef]
- Wang, K.; Mamidipalli, A.; Retson, T.; Bahrami, N.; Hasenstab, K.; Blansit, K.; Bass, E.; Delgado, T.; Cunha, G.; Middleton, M.S.; et al. Automated CT and MRI Liver Segmentation and Biometry Using a Generalized Convolutional Neural Network. Radiol. Artif. Intell. 2019, 1, 180022. [Google Scholar] [CrossRef]
- Yuan, R.; Janzen, I.; Devnath, L.; Khattra, S.; Myers, R.; Lam, S.; MacAulay, C. Predicting future lung cancer risk with low-dose screening CT using an artificial intelligence model. J. Thorac. Oncol. 2023, 18, S174. [Google Scholar] [CrossRef]
- Booz, C.; Yel, I.; Wichmann, J.L.; Boettger, S.; Al Kamali, A.; Albrecht, M.H.; Martin, S.S.; Lenga, L.; Huizinga, N.A.; D’Angelo, T.; et al. Artificial intelligence in bone age assessment: Accuracy and efficiency of a novel fully automated algorithm compared to the Greulich-Pyle method. Eur. Radiol. Exp. 2020, 4, 6. [Google Scholar] [CrossRef]
- Kim, J.R.; Shim, W.H.; Yoon, H.M.; Hong, S.H.; Lee, J.S.; Cho, Y.A.; Kim, S. Computerized Bone Age Estimation Using Deep Learning Based Program: Evaluation of the Accuracy and Efficiency. AJR Am. J. Roentgenol. 2017, 209, 1374–1380. [Google Scholar] [CrossRef]
- Lee, H.; Tajmir, S.; Lee, J.; Zissen, M.; Yeshiwas, B.A.; Alkasab, T.K.; Choy, G.; Do, S. Fully Automated Deep Learning System for Bone Age Assessment. J. Digit. Imaging 2017, 30, 427–441. [Google Scholar] [CrossRef]
- Shin, N.Y.; Lee, B.D.; Kang, J.H.; Kim, H.R.; Oh, D.H.; Lee, B.I.; Kim, S.H.; Lee, M.S.; Heo, M.S. Evaluation of the clinical efficacy of a TW3-based fully automated bone age assessment system using deep neural networks. Imaging Sci. Dent. 2020, 50, 237–243. [Google Scholar] [CrossRef]
- Tajmir, S.H.; Lee, H.; Shailam, R.; Gale, H.I.; Nguyen, J.C.; Westra, S.J.; Lim, R.; Yune, S.; Gee, M.S.; Do, S. Artificial intelligence-assisted interpretation of bone age radiographs improves accuracy and decreases variability. Skelet. Radiol. 2019, 48, 275–283. [Google Scholar] [CrossRef]
- Dallora, A.L.; Anderberg, P.; Kvist, O.; Mendes, E.; Diaz Ruiz, S.; Sanmartin Berglund, J. Bone age assessment with various machine learning techniques: A systematic literature review and meta-analysis. PLoS ONE 2019, 14, e0220242. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ouyang, L.; Wu, W.; Zhou, X.; Huang, K.; Wang, Z.; Song, C.; Chen, Q.; Su, Z.; Zheng, R.; et al. Validation of an established TW3 artificial intelligence bone age assessment system: A prospective, multicenter, confirmatory study. Quant. Imaging Med. Surg. 2024, 14, 144–159. [Google Scholar] [CrossRef]
- Zhou, X.L.; Wang, E.G.; Lin, Q.; Dong, G.P.; Wu, W.; Huang, K.; Lai, C.; Yu, G.; Zhou, H.C.; Ma, X.H.; et al. Diagnostic performance of convolutional neural network-based Tanner-Whitehouse 3 bone age assessment system. Quant. Imaging Med. Surg. 2020, 10, 657–667. [Google Scholar] [CrossRef] [PubMed]
- Maratova, K.; Zemkova, D.; Sedlak, P.; Pavlikova, M.; Amaratunga, S.A.; Krásničanová, H.; Souček, O.; Sumnik, Z. A comprehensive validation study of the latest version of BoneXpert on a large cohort of Caucasian children and adolescents. Front. Endocrinol. 2023, 14, 1130580. [Google Scholar] [CrossRef]
- Son, S.J.; Song, Y.; Kim, N.; Do, Y.; Kwak, N.; Lee, M.S.; Lee, B.D. TW3-based fully automated bone age assessment system using deep neural networks. IEEE Access 2019, 7, 33346–33358. [Google Scholar] [CrossRef]
- Lee, B.D.; Lee, M.S. Automated Bone Age Assessment Using Artificial Intelligence: The Future of Bone Age Assessment. Korean J. Radiol. 2021, 22, 792–800. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.R.; Lee, Y.S.; Yu, J. Assessment of bone age in prepubertal healthy Korean children: Comparison among the Korean standard bone age chart, Greulich–Pyle method, and Tanner–Whitehouse method. Korean J. Radiol. 2015, 16, 201–205. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16×16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhang, J.; Chen, W.; Joshi, T.; Zhang, X.; Loh, P.L.; Jog, V.; Bruce, R.J.; Garrett, J.W.; McMillan, A.B. BAE-ViT: An efficient multimodal vision transformer for bone age estimation. Tomography 2024, 10, 2058–2072. [Google Scholar] [CrossRef]
- Kim, P.H.; Yoon, H.M.; Kim, J.R.; Hwang, J.Y.; Choi, J.H.; Hwang, J.; Lee, J.; Sung, J.; Jung, K.H.; Bae, B.; et al. Bone Age Assessment Using Artificial Intelligence in Korean Pediatric Population: A Comparison of Deep-Learning Models Trained with Healthy Chronological and Greulich-Pyle Ages as Labels. Korean J. Radiol. 2023, 24, 1151–1163. [Google Scholar] [CrossRef]
- Ontell, F.K.; Ivanovic, M.; Ablin, D.S.; Barlow, T.W. Bone age in children of diverse ethnicity. AJR Am. J. Roentgenol. 1996, 167, 1395–1398. [Google Scholar] [CrossRef] [PubMed]

| Female | Male | p-Value | |
|---|---|---|---|
| N | 280 | 280 | |
| Age (mean ± SD, yrs) | |||
| Overall | 9.42 ± 2.86 | 9.45 ± 2.98 | 0.895 |
| <6 | 4.63 ± 0.98 | 4.51 ± 0.88 | 0.554 |
| 6–8 | 7.11 ± 0.59 | 6.98 ± 0.55 | 0.301 |
| 8–9 | 8.60 ± 0.30 | 8.52 ± 0.34 | 0.258 |
| 9–10 | 9.47 ± 0.28 | 9.58 ± 0.31 | 0.113 |
| 10–11 | 10.45 ± 0.27 | 10.49 ± 0.32 | 0.544 |
| 11–13 | 11.90 ± 0.67 | 12.06 ± 0.55 | 0.240 |
| >13 | 13.76 ± 0.64 | 14.02 ± 0.62 | 0.070 |
| Age (yrs) | Mean ± SD 1 | TW3-Based Model | Radiologists 2 | p-Value 3 |
|---|---|---|---|---|
| Overall | 9.43 ± 2.93 | 9.64 ± 3.05 | 9.64 ± 3.26 | 0.874 |
| <6 | 4.57 ± 0.94 | 5.22 ± 1.27 | 4.73 ± 1.44 | <0.001 |
| 6–8 | 7.04 ± 0.58 | 7.09 ± 1.41 | 7.08 ± 1.51 | 0.737 |
| 8–9 | 8.56 ± 0.33 | 8.70 ± 1.36 | 8.79 ± 1.59 | 0.093 |
| 9–10 | 9.52 ± 0.30 | 9.76 ± 1.47 | 9.80 ± 1.54 | 0.301 |
| 10–11 | 10.47 ± 0.30 | 10.94 ± 1.36 | 10.91 ± 1.46 | 0.584 |
| 11–13 | 11.98 ± 0.62 | 12.15 ± 1.38 | 12.15 ± 1.50 | 0.976 |
| >13 | 13.89 ± 0.65 | 13.65 ± 1.63 | 14.00 ± 1.63 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Choi, Y.-H.; Lee, S.-B.; Choi, J.-W.; Lee, S.; Hwang, J.-Y.; Cheon, J.-E.; Hong, S.; Kim, J.; Cho, Y.-J. Retrospective Clinical Trial to Evaluate the Effectiveness of a New Tanner–Whitehouse-Based Bone Age Assessment Algorithm Trained with a Deep Neural Network System. Diagnostics 2025, 15, 993. https://doi.org/10.3390/diagnostics15080993
Lee M, Choi Y-H, Lee S-B, Choi J-W, Lee S, Hwang J-Y, Cheon J-E, Hong S, Kim J, Cho Y-J. Retrospective Clinical Trial to Evaluate the Effectiveness of a New Tanner–Whitehouse-Based Bone Age Assessment Algorithm Trained with a Deep Neural Network System. Diagnostics. 2025; 15(8):993. https://doi.org/10.3390/diagnostics15080993
Chicago/Turabian StyleLee, Meesun, Young-Hun Choi, Seul-Bi Lee, Jae-Won Choi, Seunghyun Lee, Jae-Yeon Hwang, Jung-Eun Cheon, SungHyuk Hong, Jeonghoon Kim, and Yeon-Jin Cho. 2025. "Retrospective Clinical Trial to Evaluate the Effectiveness of a New Tanner–Whitehouse-Based Bone Age Assessment Algorithm Trained with a Deep Neural Network System" Diagnostics 15, no. 8: 993. https://doi.org/10.3390/diagnostics15080993
APA StyleLee, M., Choi, Y.-H., Lee, S.-B., Choi, J.-W., Lee, S., Hwang, J.-Y., Cheon, J.-E., Hong, S., Kim, J., & Cho, Y.-J. (2025). Retrospective Clinical Trial to Evaluate the Effectiveness of a New Tanner–Whitehouse-Based Bone Age Assessment Algorithm Trained with a Deep Neural Network System. Diagnostics, 15(8), 993. https://doi.org/10.3390/diagnostics15080993






