Abstract
Mixed friction in liquid-lubricated tribosystems is characterized by the simultaneous presence of liquid and solid friction. Liquid friction results from the shearing of the lubricant, and solid friction from deformation and adhesion. Elastic hysteresis and plastic deformation of the solids cause energy losses during deformation and the separation of molecular bonds between the solids causes energy losses during adhesion. The classic conception of mixed friction presupposes direct contact between rough solids for solid friction to exist. However, if hysteresis losses are fully accepted as a cause for solid friction, every fully lubricated elastohydrodynamic contact would ultimately be a mixed friction contact since the elastic deformations of the solids also cause a loss of energy induced by hysteresis. Thus, the classic conception of mixed friction should be expanded since mixed friction can occur even when solids do not have any direct contact.
1. Introduction
To increase the lifetime of tribological systems, it is important to optimize friction and wear. This requires knowledge of the effective frictional forces. The frictional forces can be altered by changing the operating conditions, the material and lubricant, or the surface geometry. Tribological systems are often designed according to the trial-and-error method, based on many years of experience and many tests. This approach reaches its practical limits due to the high costs involved and the ever-shorter product development cycles. Virtual product development and thus the simulation of tribological systems offers a way out. However, calculating the friction behavior of tribological systems requires detailed consideration and a description of all mechanisms involved in friction.
1.1. Friction and Lubrication
Friction is due to interactions between contacting material areas of bodies, which counteract the relative movement of the bodies. The term “body” is representative of everything that has a mass and occupies a space. Bodies consist of substances that can be solid, liquid, or gaseous. Depending on the state of motion of the bodies, a distinction can be made between friction without relative motion (static friction) and friction with relative motion (dynamic friction). Depending on the affiliation of the material areas involved in the friction process, external or internal friction can be present. In the case of external friction, the contacting material areas belong to different bodies, whereas in the case of internal friction, they belong to one and the same body. Internal and external friction can occur simultaneously.
The friction in a tribological system can be specifically influenced by lubrication. Lubricants, which can be solid, liquid, consistent, or gaseous, are used for this purpose. The use of lubricants is often linked to the aim of achieving partial or complete separation of the friction bodies. The hydro-, elastohydro-, or aerodynamic as well as the hydro- or aerostatic effect can be utilized for this purpose. Whereas with hydro-, elastohydro-, and aerodynamics, the load capacity applied by the lubricant results from an internal pressure generation in the lubrication gap, with hydro- and aerostatics, this results from an external pressure generation in the lubrication gap by an external pump.
In German-speaking countries, a distinction tends to be made between friction states [1], whereas, outside German-speaking countries, lubrication states tend to be subdivided [2]. From a scientific point of view, it is necessary to distinguish between friction and lubrication states and to clearly separate them from one another. If the friction in a contact is considered, the friction state is decisive. If the type of lubrication of a contact is in the foreground, the lubrication state must be considered.
If friction is classified according to the aggregate state of the substances involved in the friction, the following friction states can be defined:
- Solid friction is friction between solid bodies in direct contact. If friction takes place between solid boundary layers, it is boundary layer friction. If the solids are covered by a very thin liquid film, this is boundary friction.
- Liquid friction is internal friction in the material area with liquid properties and is present in a hydrodynamically, elastohydrodynamically, or hydrostatically generated lubricating film.
- Gas friction is internal friction in the material area with gas properties and is present in an aerodynamically or aerostatically generated lubricating film.
- Mixed friction is any mixed form of the aforementioned friction states and can also result from more than two superimposed friction states.
Depending on the lubrication, the following lubrication states can be distinguished:
- Boundary lubrication is lubrication with solid boundary layers or very thin liquid films. A special case of lubrication with solid boundary layers is superlubricity. In the presence of very thin liquid films, hydrodynamic, elastohydrodynamic, or hydrostatic load capacity effects are negligible. Boundary lubrication is the subject of molecular dynamics.
- Liquid lubrication is the lubrication with a liquid in which a complete separation of the friction body surfaces by hydrodynamics, elastohydrodynamics, or hydrostatics is aimed for (full lubrication).
- Gas lubrication is lubrication with a gas in which complete separation of the friction surfaces is achieved by aerodynamics or aerostatics (full lubrication).
- Mixed lubrication or partial lubrication is any mixture of the aforementioned lubrication states.
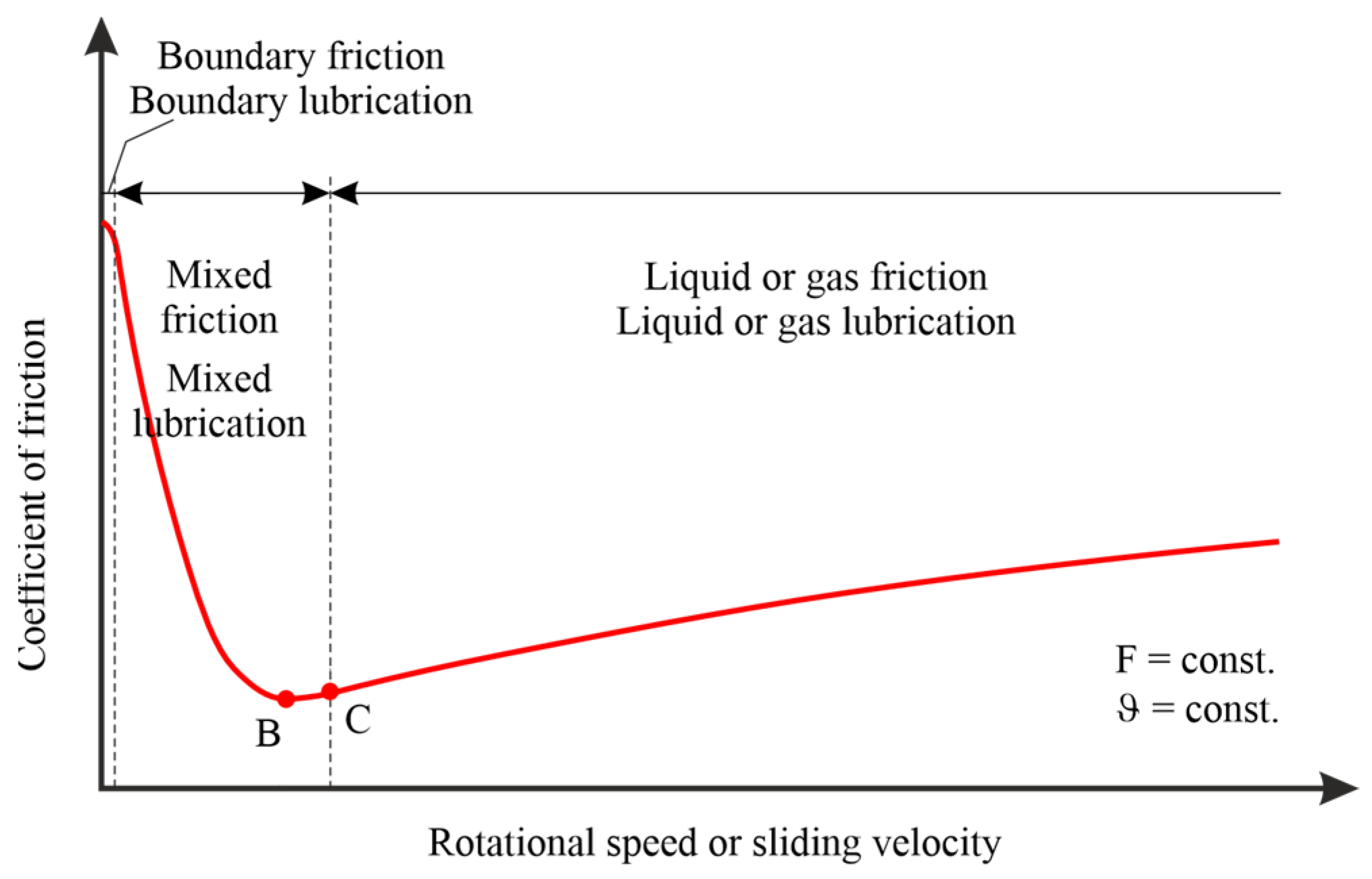
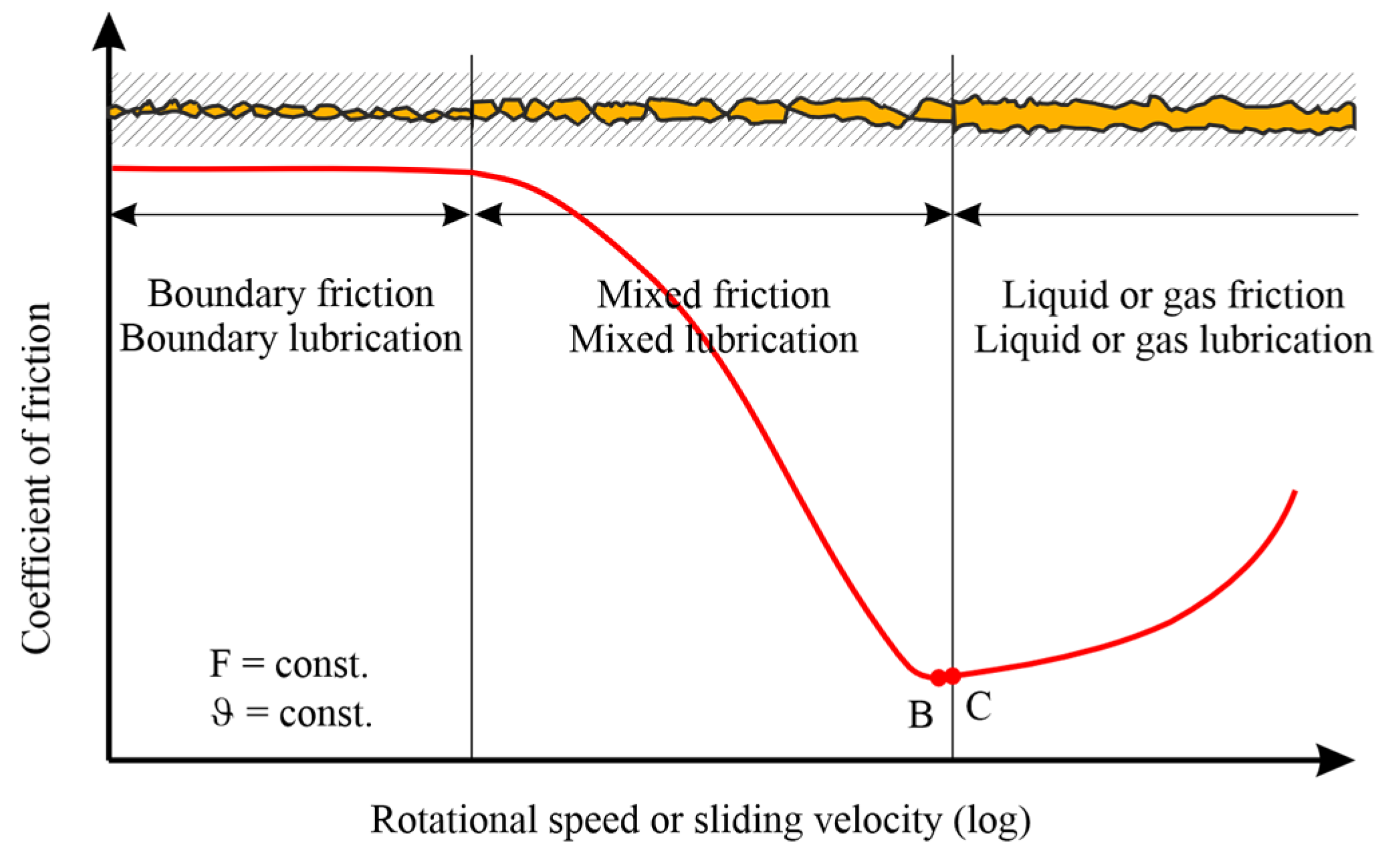
The friction and lubrication states can be displayed in the Stribeck curve, as shown in Figure 1. Here, a representation with a linear or logarithmic axis for the rotational speed or sliding velocity is possible.
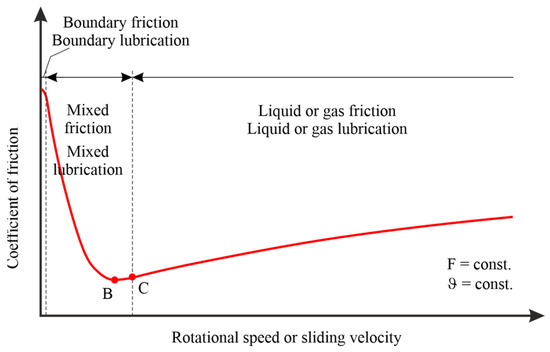
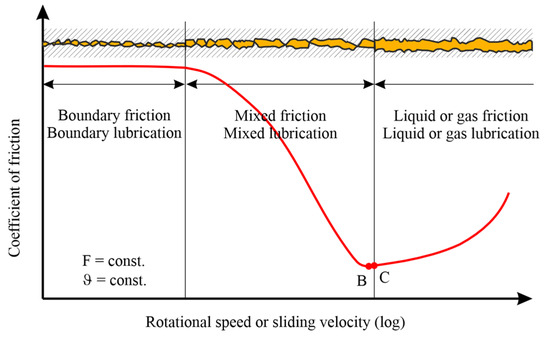
Figure 1.
Stribeck curve in linear and logarithmic representation (B—friction minimum; C—lift-off point).
1.1.1. Friction Mechanism in Fluid Friction
Fluids are viscous media such as liquids and gases. The friction of liquids results from the contact and mutual displacement of molecules. Gas friction results from the collision of gas particles (atoms or small molecules). These friction mechanisms are effective when liquids and gases are sheared in the lubrication gap. One measure of shear resistance is the viscosity. The resulting friction or viscosity depends on the chemical structure of the fluid, the temperature, the pressure, and the shear rate. Fluid and gas friction are generally very low, with gas friction usually achieving much lower values than fluid friction. The calculation of fluid-lubricated systems is carried out using the basic equations of fluid mechanics, into which temperature-, pressure-, and shear gradient-dependent fluid properties are incorporated [3].
1.1.2. Friction Mechanism in Solid Friction
Solid friction is due to mechanical and atomic/molecular interactions. This was first formulated by Kragelskij [4] and Bowden et al. [5] and subsequently taken up and confirmed by many authors. Kragelskij spoke of the double nature of solid friction. Both parts can occur simultaneously but can be pronounced to different degrees.
If solids are subjected to stress, elastic and plastic deformation of the solids can occur. When the rough solids come into direct contact, the real contact surface is formed. The deformation of the solid bodies is associated with energy losses, which, in a tribosystem with kinetic friction, manifest themselves as continual solid friction losses and are assigned to the mechanical interactions. The plastic deformation work is irreversibly lost due to the lasting deformation and is therefore 100% frictionally effective. The elastic deformation work is only partially frictionally effective, as this is largely recovered by the elastic recovery of the solid bodies. The partial loss results from an incomplete elasticity of the materials and is called elastic hysteresis or mechanical damping. Hysteresis effects are reflected, for example, in the natural decrease in mechanical vibrations. A measure of the loss that occurs is the hysteresis factor H as the ratio of loss energy and applied elastic energy. The size of the hysteresis factor depends on the material, the deformation speed, the load level, the type of load (uniaxial or multiaxial), the load duration/frequency, and the temperature. The hysteresis tends to increase with an increase in the load parameters and temperature. Rubber, plastics, gray cast iron, or some ferromagnetic alloys exhibit a high hysteresis. Information on hysteresis factors of materials in standard tests can be found in [6] or [7]. Information on hysteresis factors of materials in the friction process, especially for the friction-relevant area near the surface, is not yet available to the desired extent.
When the rough solids come into direct contact, adhesive bonds are also formed in the real contact area , which correspond to atomic/molecular interactions. These adhesive bonds are of a chemical or physical nature and can be more or less pronounced. The type and strength of the bond depend on the boundary layers/boundary films that form on the solids. For example, the adhesive bonding forces between two oxide-covered iron bodies (van der Waals bond) are lower than those resulting from direct iron/iron contact (metal bond). To maintain the relative movement between two adhesively interacting solids, energy must be permanently expended to separate the atomic/molecular bonds. Solid friction losses are the result. Depending on the bonding state, adhesion or cohesion bonds can be separated. The decisive factor here is which bonds fail first. When cohesive bonds, which ensure the cohesion of the solids, are separated, material is detached locally from the cohesively weaker bonded body, and material is transferred to the counter body. This is referred to as adhesion wear or more generally as scuffing. No material transfer occurs when adhesion bonds are separated.
To calculate solid friction, it makes sense to take an energetic approach [8,9,10,11]. While a force is defined by magnitude and direction (vectorial quantity), work or energy is described solely by a magnitude without direction (scalar quantity). Only the traceability of work to a force along a path leads to a directional consideration. This can be utilized in an energetic friction calculation. In G = general, the solid friction work results from
The solid friction work can also be written as the sum of the energy components from deformation and adhesion in accordance with the solid friction mechanisms explained above:
The following applies to the deformation-related friction work, considering the hysteresis losses resulting from the elastic deformation and any plastic deformation losses, which are 100% frictionally effective:
with
and
The reduced hysteresis factor is introduced in Equation (4) considering different elastic hysteresis properties of the paired materials and can be calculated according to [11] using Equation (6).
The calculation of the adhesion-related solid friction work is more difficult, but can be determined, for example, from the specific work of adhesion or the shear strength of the atomic/molecular compound to be separated [11]:
If the solid body friction work , the friction distance and the solid body load-bearing force acting in the normal direction are known, the following can by inserting and converting to the solid body friction force:
or the solid friction coefficient can be concluded:
1.2. Elastohydrodynamics
The term elastohydrodynamics (EHD) was introduced in the middle of the 20th century [12]. Initially, the term was only used for liquid-lubricated concentrated contacts (e.g., in rolling bearings or gears), but today, it is also used for liquid-lubricated non-concentrated contacts (e.g., in plain bearings or piston/cylinder pairings) if the gap flow calculation is coupled with an elastic gap deformation calculation. Elastohydrodynamics considers addition to hydrodynamics (HD), in which the pressure and shear gradient dependence of the viscosity must be considered, also the elastic deformation of the solids to be separated by a lubricating film. For the extension of the elastohydrodynamics by the temperature calculation, the term thermal elastohydrodynamics (TEHD) was coined.
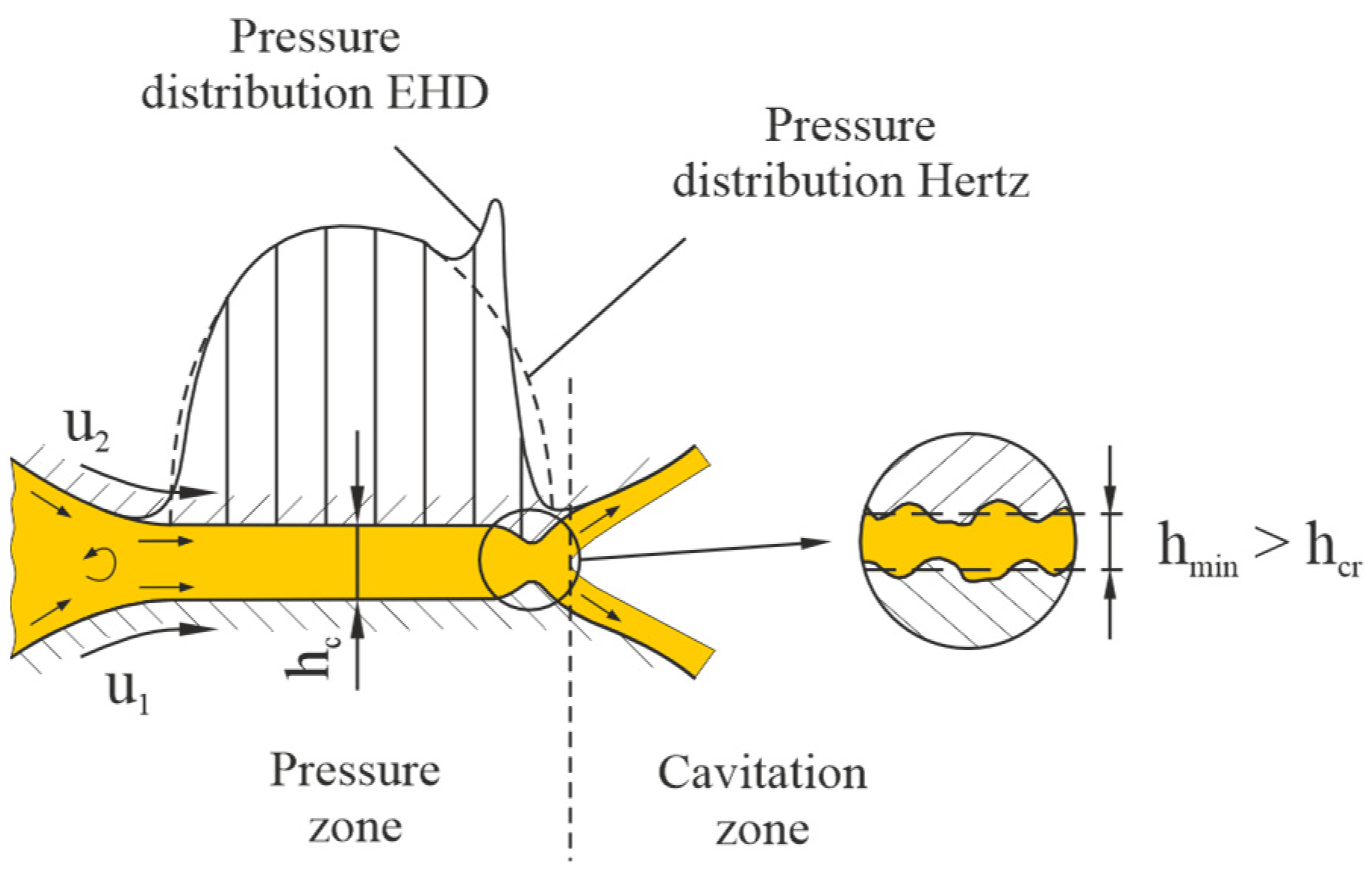
Figure 2 shows a schematic illustration of the pressure distribution and the lubrication gap height profile of a concentrated EHD contact in the direction of movement. For comparison, the pressure distribution according to Hertz for the unlubricated contact is also shown. Two characteristic lubrication gap heights can be defined, namely the central film thickness in the center of the contact and the minimum film thickness in the gap constriction. Furthermore, a distinction can be made between a pressure area, in which the supporting effect of the lubricant is achieved, and a cavitation area, in which the gap that opens is not completely filled with lubricant.
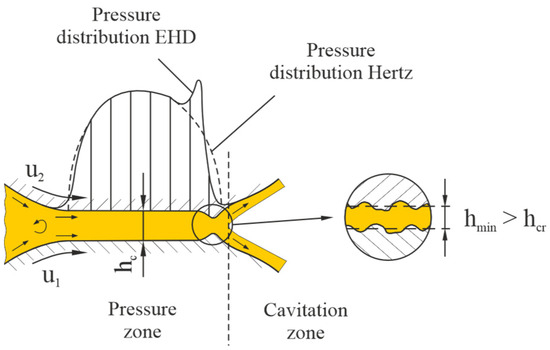
Figure 2.
Pressure distribution and lubrication gap height profile in a concentrated EHD contact.
In the classic conception, the EHD contact shown in Figure 2 would be assigned to liquid friction or liquid lubrication if the minimum film thickness is so large that the rough surfaces do not touch (). In fact, however, it is an EHD contact with mixed friction and liquid lubrication, provided that the definition of mixed friction in liquid-lubricated EHD contacts as a superposition of liquid and solid friction and the fact that hysteresis losses in the elastically deformed solids are to be assigned to solid friction as internal friction are accepted without restriction.
When calculating the friction of fully lubricated EHD contacts, hysteresis losses are often not considered. The friction is calculated solely from the shear of the lubricant. How large the “hysteresis friction” can be is intended to show the following explanations. The aim of this work is not to consider complex EHD contact and material models to be able to precisely determine the hysteresis friction in the solid bodies. Instead, a simplified approach is used to illustrate the possible orders of magnitude and the resulting findings.
2. Materials and Methods
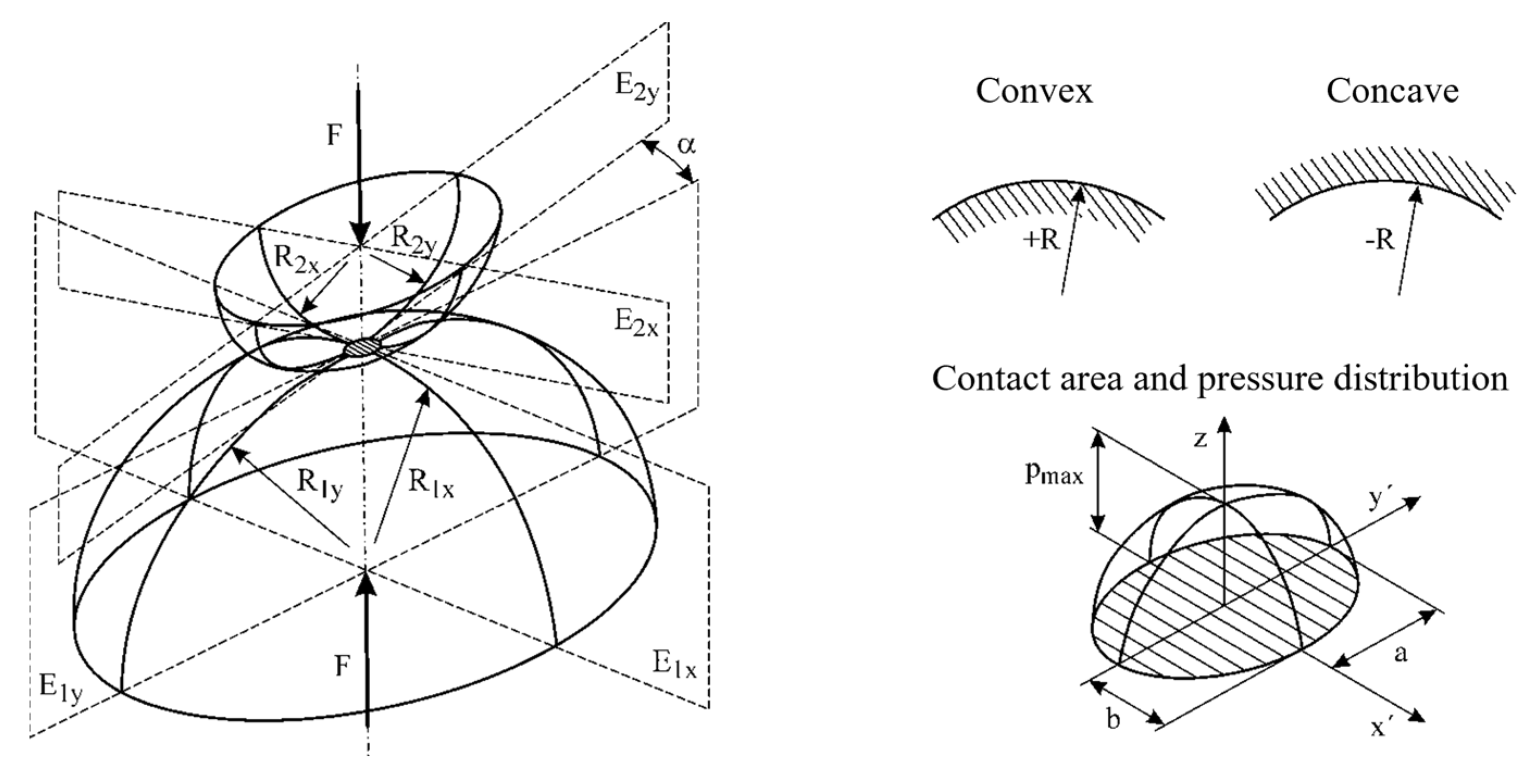
According to Figure 2, the starting point should be a fully lubricated EHD contact in which two bodies curved on both sides roll against each other. The semi-axes of the elliptical contact area that forms and the pressure distribution acting there (Figure 3) should be calculated as a good approximation using Hertz’s equations for the unlubricated normal contact [13].
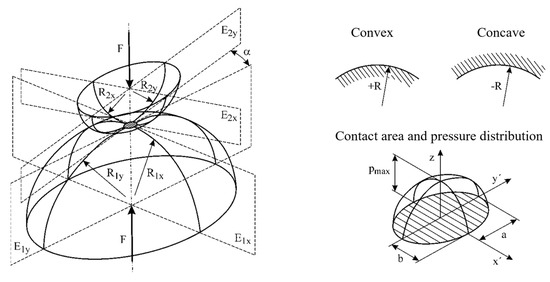
Figure 3.
Hertzian contact and definition of geometric quantities.
According to Hertz, a reduced radius is introduced, which can be interpreted as the radius of a fictional elastic sphere that is pressed against a rigid plane.
Here, the radius of a convex curvature must have a positive sign and that of a concave curvature a negative sign, as shown in Figure 3. Furthermore, it must be ensured that the radius of the convex body is smaller than that of the concave body in the case of a convex/concave pairing. If one of the solids is a plane, is applied.
The elastic properties of the fictional sphere are determined from the elastic properties of the two elliptical bodies with the reduced Young’s modulus .
Furthermore, an auxiliary angle can be introduced, for which applies
or for a twist angle of :
The auxiliary angle is also related to the half-axis ratio.
If the value is known from Equation (12) or Equation (13), the half-axis ratio can be determined iteratively using Equation (15). The complete elliptic integrals and in Equation (15) can be calculated as follows:
With knowledge of κ, three coefficients can be determined which are used as correction factors in the equations for the fictional point contact to calculate the major and minor semi-axes of the real elliptical contact surface and the maximum deflection of the elliptical contact bodies. The correction factor for the major half-axis is
The correction value for the minor half-axis is
The correction value for the maximum deflection of the contacting bodies is given by
Alternatively, the correction factors and can be calculated using the auxiliary value
according to [14] with the following approximate solutions:
In [14] only approximate equations for and are given. To be able to calculate with little effort, an equation for is required. This is achieved by rearranging Equation (15) to , Equation (18) to , and Equation (19) to κ, and by inserting the three resulting equations into Equation (20). The result is an equation with which can be calculated as a function of and :
The deviations of the three approximate equations listed are not greater than 0.7% over the entire value range.
The major half-axis and the minor half-axis of the elliptical contact as well as the maximum deflection of the bodies follows from
The pressure distribution in the contact is calculated from
where for the maximum pressure in the center of the contact area, the following is applied:
The calculation of the elastic deformation work to be applied during rolling between the two bodies is achieved using an approach by Tabor [15,16,17,18,19], which was presented for the rolling of a rigid ball on an elastic plane or in an elastic groove and can be generalized. Within the contact area, the total deformation w at any point can be described by the following function:
The change in deformation when rolling forward by a small distance in the x-direction results from the derivative of Equation (30) with respect to x as
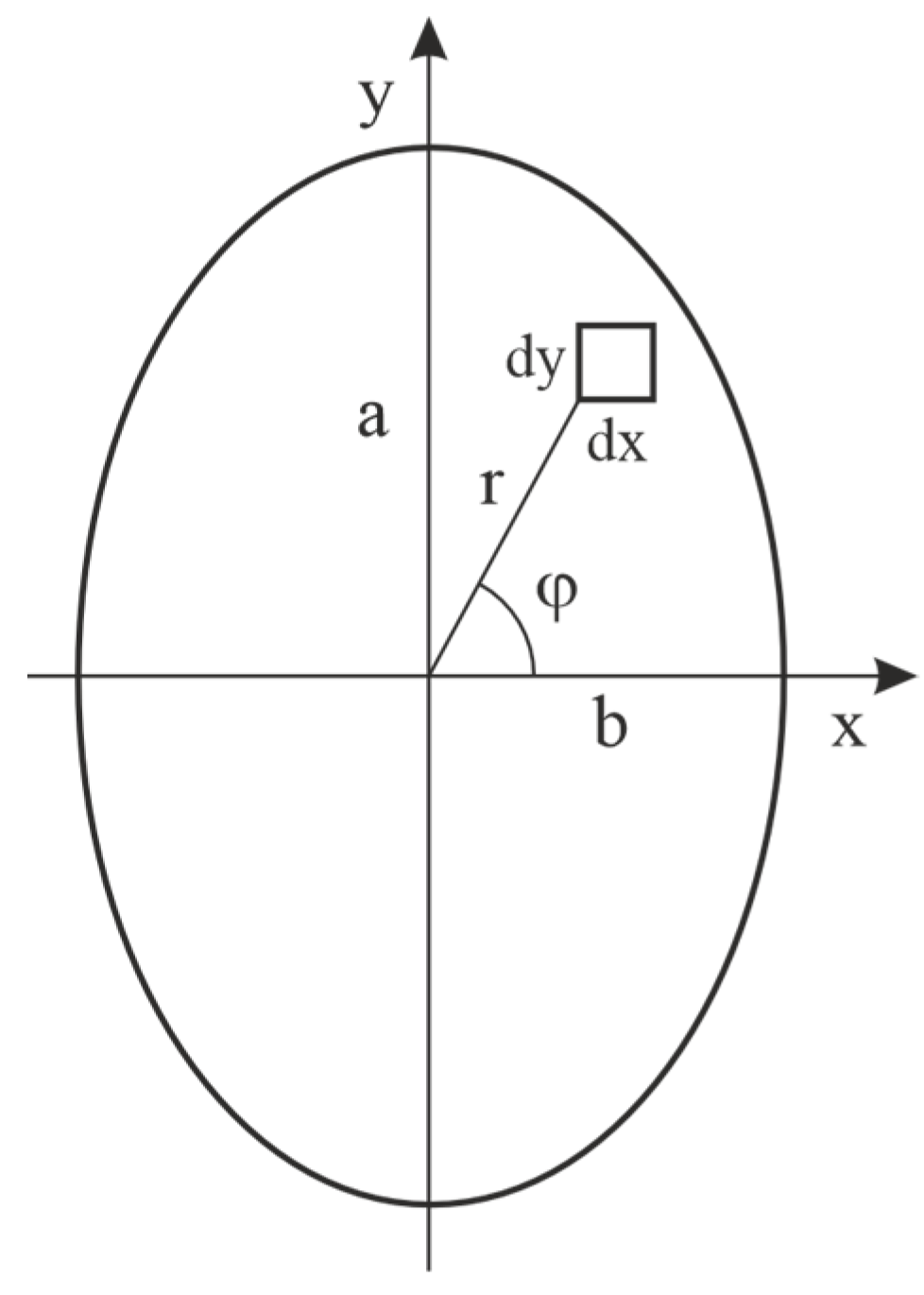
The deformation work performed in all surface elements (Figure 4) in the front half of the contact area when rolling forward by the distance is given by
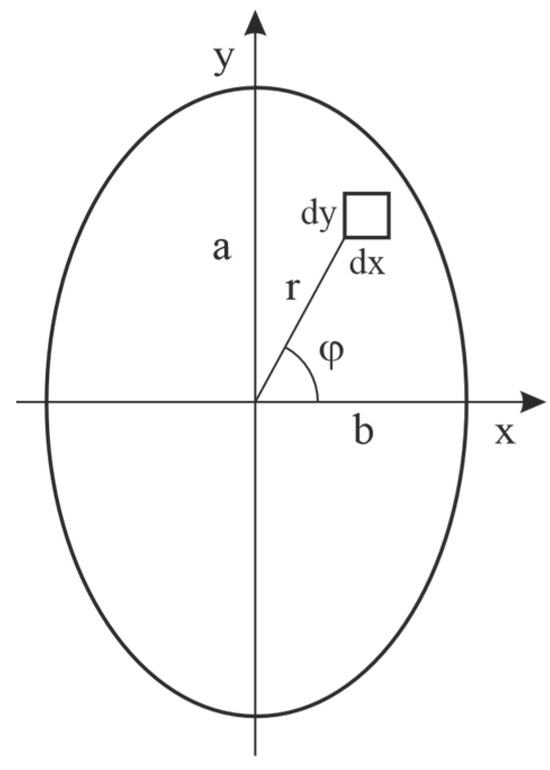
Figure 4.
Hertzian contact area with surface element
The solution of the integral is succeeded by substitution and subsequent transformation of the integral into polar coordinates. The result is the elastic deformation work to be applied when rolling in the direction of the minor half-axis (x-direction)
and in an analogous derivation for rolling in the direction of the major half-axis (y-direction):
When the two bodies roll, the friction bodies are loaded in the front contact area and unloaded again in the rear contact area. Hysteresis losses occur, which manifest themselves as solid friction losses according to Equation (4). The solid friction force resulting in the respective rolling direction can be calculated with a rolling or friction distance of from
and the direction-dependent friction moment with
A solid coefficient of friction can be determined from the hysteresis-related solid friction force and the acting normal force. When there is a rolling in the direction of the minor half-axis, the result is
and when rolling is in the direction of the major half-axis, the following is obtained:
Analogous to the derivation for point contacts, it is also possible to derive a hysteresis-related coefficient of solid friction for line contacts
where the pressure distribution for line contacts must be used to derive Equation (41).
3. Results and Discussion
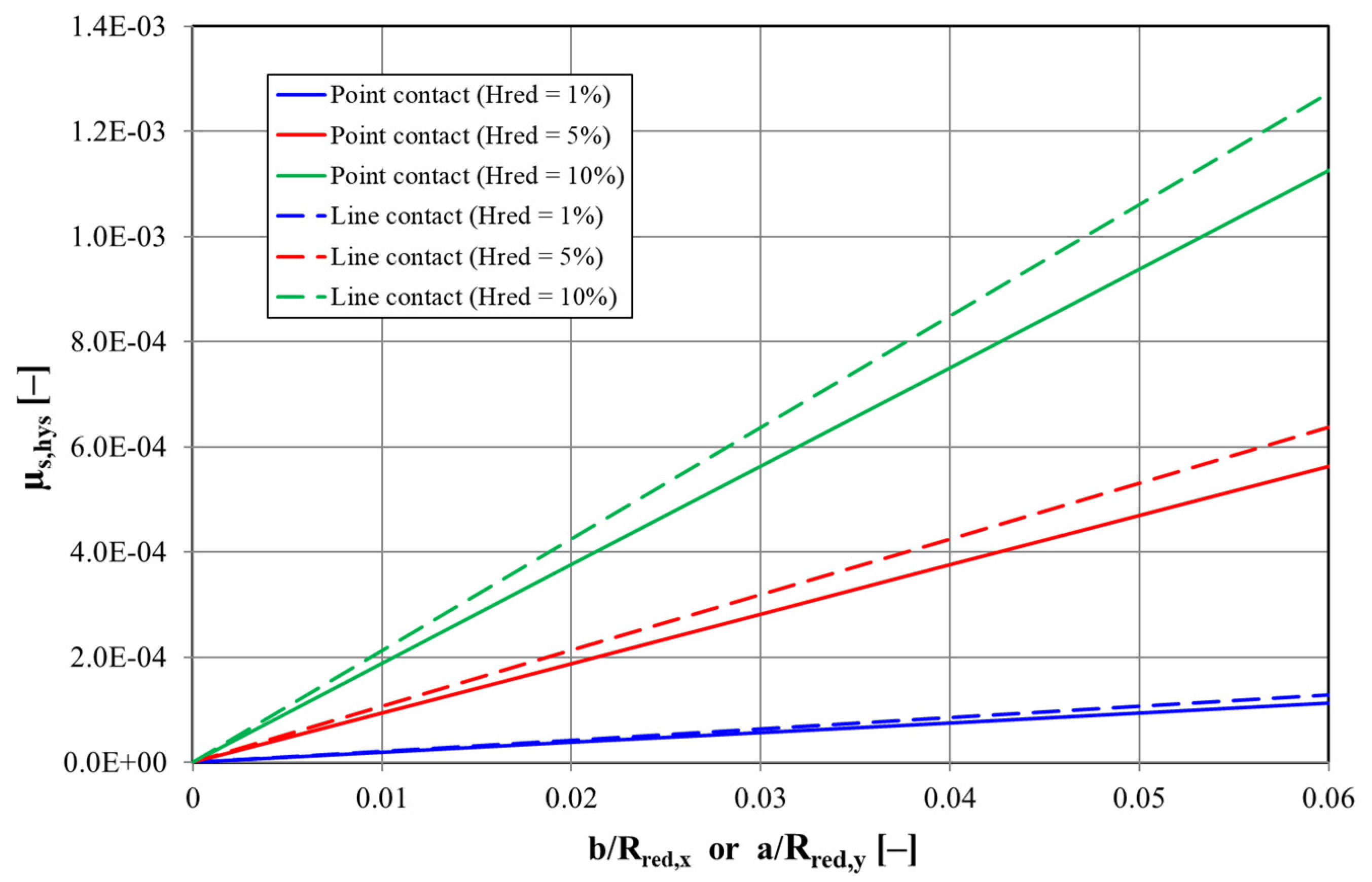
Equations (39) and (40) show that all point contacts with the same axis-related rolling direction, the same ratio of half-axis and reduced radius, and the same reduced hysteresis factor will have identical hysteresis-related coefficients of solid friction. Figure 5 shows the possible magnitudes of these coefficients of friction. In Figure 5, the reduced hysteresis factor was varied in a range from 1% to 10%. The smaller values stand for steel/steel pairings and the larger values for plastic/steel or elastomer/steel pairings. The author is aware that the linear-elastic deformation approach, which is considered in Hertz’s equations, does not adequately describe the deformation behavior of plastics or elastomers. In these cases, the linear-elastic approach would have to be supplemented by a viscoelastic component.
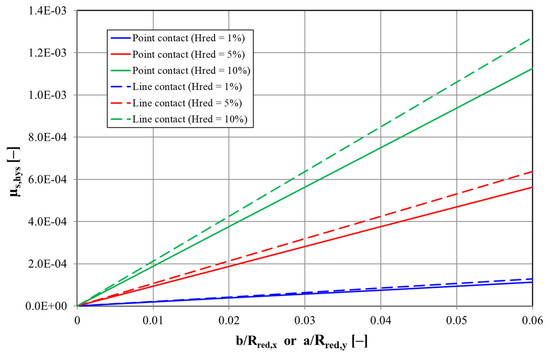
Figure 5.
Hysteresis-related solid coefficients of friction of rolling contacts with point or line contact at different hysteresis factors.
The hysteresis loss when taking viscoelasticity into account will therefore be higher than that calculated using a purely linear-elastic approach. Independently of this, the range selected for the hysteresis factor in Figure 5 is probably not entirely unrealistic for rolling contacts as it can be assumed that the hysteresis factors will be higher than those determined in classical test procedures, such as dynamic mechanical thermal analysis (DMTA), on standard test specimens due to the high deformation speeds, loads, and temperatures in rolling contacts [7].
Furthermore, the range of values selected in Figure 5 for the ratio of half-axis and reduced radius corresponds to the values that can also occur in real applications. It is clear that the hysteresis-related coefficient of solid friction increases with increasing load, i.e., with increasing ratio of half-axis and reduced radius and increasing damping behavior of the material pairing.
If there is a completely separating lubricating film in an EHD contact between the two bodies, the adhesion component of the solid friction work according to Equation (2) is ineffective. If no plastic deformations occur according to Equation (3), friction losses are only effective due to hysteresis-related solid friction according to Equation (4), and additionally due to liquid friction. The frictional force in the EHD contact then results from the liquid frictional force and a hysteresis-related solid friction force .
For the resulting friction coefficient , the following can be written:
Figure 5 shows that the hysteresis-related coefficients of solid friction can be in the same order of magnitude as the coefficients of fluid friction of fully lubricated EHD contacts. Therefore, hysteresis friction can have a significant influence on the overall friction behavior of a fully lubricated EHD contact in the case of pure rolling or very small slip values and should not be neglected. With larger slip values or pure sliding, hysteresis friction should play a subordinate role. The above statements are equally valid for elastohydrodynamic point and line contacts.
The hysteresis-related solid friction can be calculated analytically with the equations previously listed for ideal Hertzian point and line contacts. The equations are no longer applicable for rolling elements with any geometries (rolling elements with logarithmic profiles, manufacturing deviations, wear profiles, etc.). Numerical calculations are an alternative here. In numerical EHD calculations, the hysteresis-related solid friction can be determined using the model for describing the lubrication gap deformations (elastic half-space or FEM) for stationary and transient operating conditions.
4. Conclusions
This paper showed that it is necessary to differentiate between friction and lubrication states and that these must be clearly separated from each other. If the friction in a contact is considered, the friction state is decisive. If the focus is on the type of lubrication of a contact, the lubrication state must be considered.
A calculation of the friction behavior of tribological systems requires a detailed consideration and description of all mechanisms involved in friction. Although hysteresis-related solid friction losses always occur in fully lubricated EHD contacts, these friction losses are often not considered. The friction losses acting in the EHD contact are attributed usually to fluid friction alone. Depending on the slip, the influence of hysteresis-related solid friction on the total friction of a fully lubricated EHD contact can be negligibly small, just as large, or even larger than the fluid friction and is more pronounced with plastics than with metals. Due to the always-existing hysteresis-related energy losses in the solids, which are attributable to solid friction and are superimposed on the liquid friction losses, it can be formulated that every fully lubricated EHD contact is a mixed friction contact. This would extend the classical concept of mixed friction, as mixed friction can also occur without direct contact between the solids. Furthermore, a fully lubricated EHD contact is traditionally assigned to the friction state of liquid friction and the lubrication state of liquid lubrication. However, in reality, this is an EHD contact with mixed friction and liquid lubrication.
Funding
This research received no external funding.
Data Availability Statement
All data can be found in this paper.
Conflicts of Interest
The author declares no conflicts of interest.
Nomenclature
| Real contact area (m2) | Deformation (m) | ||
| Major half-axis (m) | Cartesian coordinates (m) | ||
| Minor half-axis (m) | Twist angle (°) | ||
| Correction factors (-) | Specific work (Nm/m2) | ||
| Young’s modulus (N/m2) | Distance (m) | ||
| Elliptical integral 2nd kind | Auxiliary angle (°) | ||
| Normal force (N) | Angle (°) | ||
| Solid load capacity (N) | Half-axis ratio (-) | ||
| Total friction force (N) | Coefficient of liquid friction (-) | ||
| Liquid friction force (N) | Coefficient of solid friction (-) | ||
| Solid friction force (N) | Poisson’s ratio (-) | ||
| Auxiliary value (-) | Shear strength (N/m2) | ||
| Hysteresis factor (-) | |||
| Central film thickness (m) | |||
| Critical film thickness (m) | Frequently used indices | ||
| Minimum film thickness (m) | Body 1 | ||
| Elliptical integral 1st kind | Body 2 | ||
| Width of cylinder (m) | Adhesion | ||
| Hertzian pressure (N/m2) | Deformation | ||
| Radius (m) | Elastic | ||
| Sliding distance (m) | Hysteresis | ||
| Circumferential speed (m/s) | Maximum | ||
| Solid deformation work (Nm) | Plastic | ||
| Solid friction work (Nm) | Reduced | ||
References
- GfT Arbeitsblatt 7: Tribologie—Definitionen, Begriffe, Prüfung (GfT Worksheet 7: Tribology—Definitions, Terms, Testing). Gesellschaft für Tribologie e.V. 2002. Available online: www.gft-ev.de (accessed on 3 August 2024).
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Bartel, D. Simulation von Tribosystemen—Grundlagen und Anwendungen (Simulation of Tribosystems—Basics and Applications); Vieweg+Teubner: Wiesbaden, Germany, 2010. [Google Scholar]
- Kragelskij, I.V. About the friction of unlubricated surfaces. All-Union Conference on Friction and Wear in Machines (О трении несмазанных пoверхнoстей. Всесoюзная кoнференция пo трению и изнoсу в машинах); Academy of Sciences: Moscow, Russia, 1939; Volume 1, pp. 543–561. [Google Scholar]
- Bowden, F.P.; Moore, A.J.W.; Tabor, D. The ploughing and adhesion of sliding metals. J. Appl. Phys. 1943, 14, 80–91. [Google Scholar] [CrossRef]
- Lazan, B.J. Damping of Materials and Members in Structural Mechanics; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Fleischer, G. Energiebilanzierung der Festkörperreibung als Grundlage zur energetischen Verschleißberechnung. Teil I: (Energy balancing of solid friction as a basis for an energetical calculation of wear. Part I). Schmierungstechnik 1976, 7, 225–230. [Google Scholar]
- Fleischer, G. Energiebilanzierung der Festkörperreibung als Grundlage zur energetischen Verschleißberechnung. Teil II: (Energy balancing of solid friction as a basis for an energetical calculation of wear. Part II). Schmierungstechnik 1976, 7, 271–279. [Google Scholar]
- Fleischer, G. Energiebilanzierung der Festkörperreibung als Grundlage zur energetischen Verschleißberechnung. Teil III: (Energy balancing of solid friction as a basis for an energetical calculation of wear. Part III). Schmierungstechnik 1977, 8, 49–58. [Google Scholar]
- Bartel, D. Berechnung von Festkörper- und Mischreibung bei Metallpaarungen (Calculation of Solid and Mixed Friction in Metal Pairs). Ph.D. Thesis, Otto von Guericke University, Magdeburg, Germany, 2000. [Google Scholar]
- Dowson, D.; Higginson, G.R. A numerical solution to the elasto-hydrodynamic problem. J. Mech. Eng. Sci. 1959, 1, 6–15. [Google Scholar] [CrossRef]
- Hertz, H.R. Über die Berührung fester elastischer Körper (About the contact of solid elastic bodies). J. Die Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Grekoussis, R.; Michailidis, T. Stellung der Hertzschen Druckellipse auf der Oberfläche zweier einander in einem Punkt berührender Körper (Position of the Hertzian pressure ellipse on the surface of two bodies touching each other at one point). Konstruktion 1980, 32, 303–306. [Google Scholar]
- Tabor, D. The mechanism of rolling friction. Philos. Mag. Series 1952, 43, 1055–1059. [Google Scholar] [CrossRef]
- Eldredge, K.R.; Tabor, D. The mechanism of rolling friction I: The plastic range. Proc. R. Soc. Lond. Ser. A 1955, 229, 181–198. [Google Scholar]
- Tabor, D. The mechanism of rolling friction II: The elastic range. Proc. R. Soc. Lond. Ser. A 1955, 229, 198–220. [Google Scholar]
- Tabor, D. Elastic work involved in rolling a sphere on another surface. Brit. J. Appl. Phys. 1955, 6, 79–81. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Minshall, H.; Tabor, D. Hysteresis losses in rolling and sliding friction. Proc. R. Soc. Lond. Ser. A 1961, 259, 480–507. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).