Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part I: Basic Relations
Abstract
:1. Introduction
2. Materials and Methods
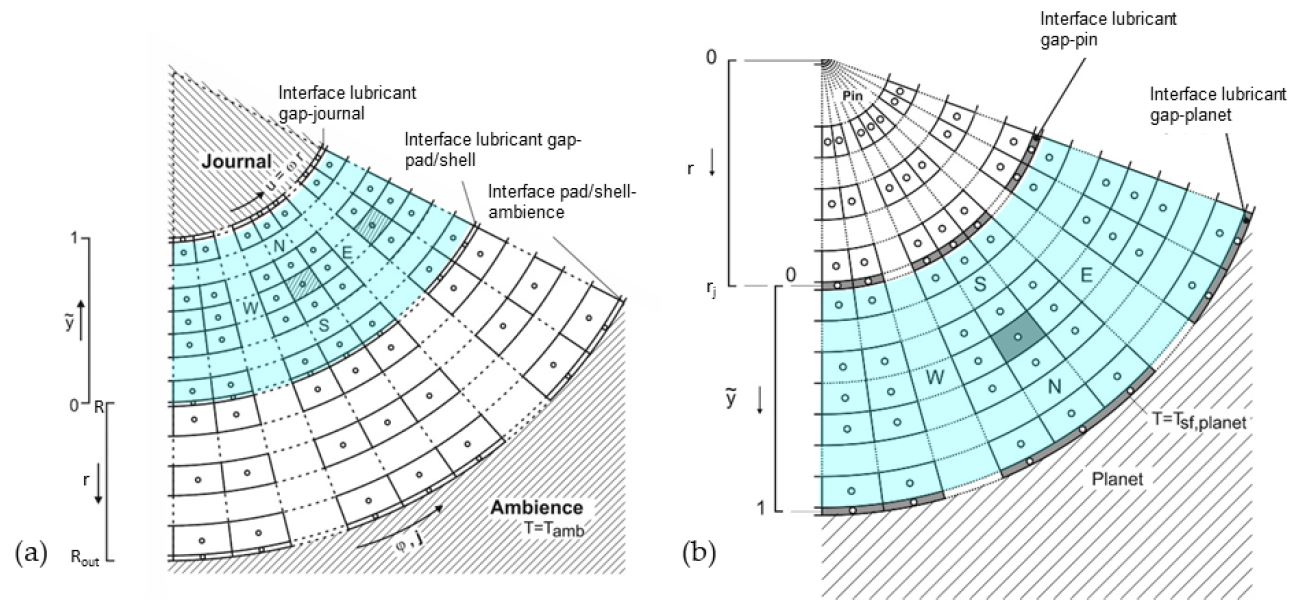
2.1. Governing Equations and Bearing Model
2.2. Verification of the Numerical Procedure
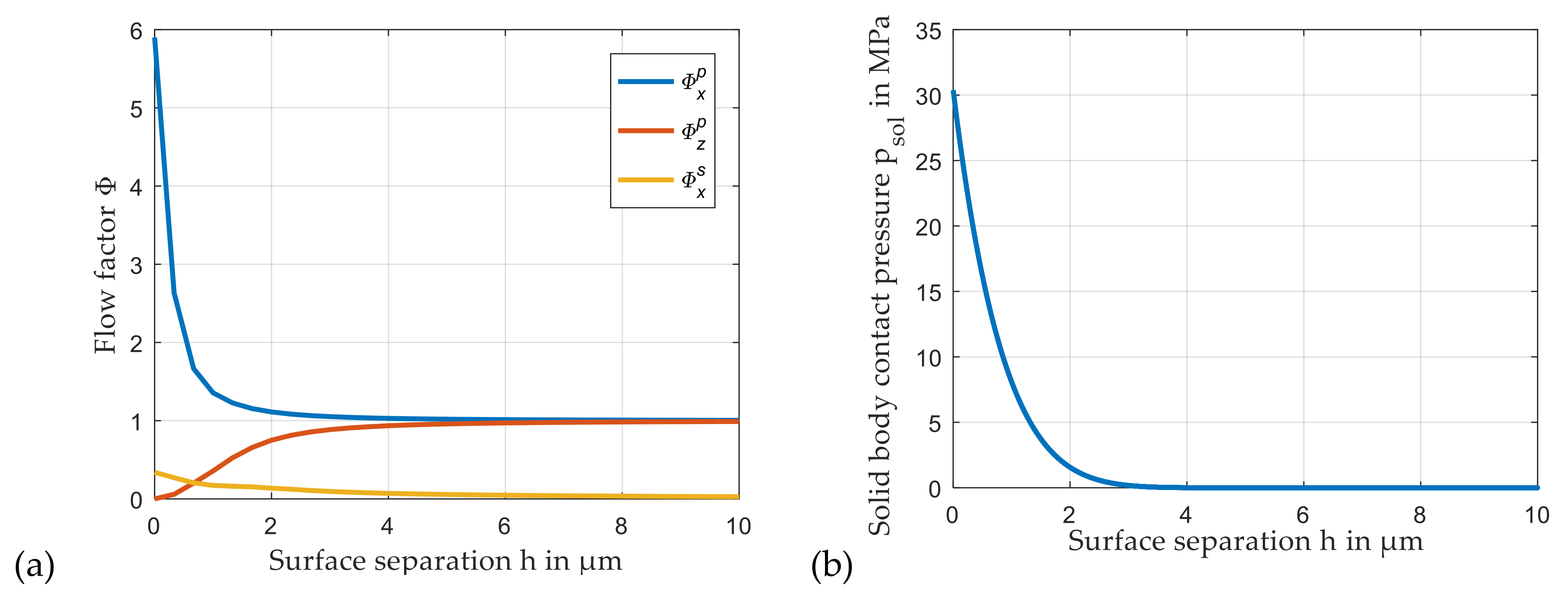
2.3. Flow Factors and Solid Contact Pressure
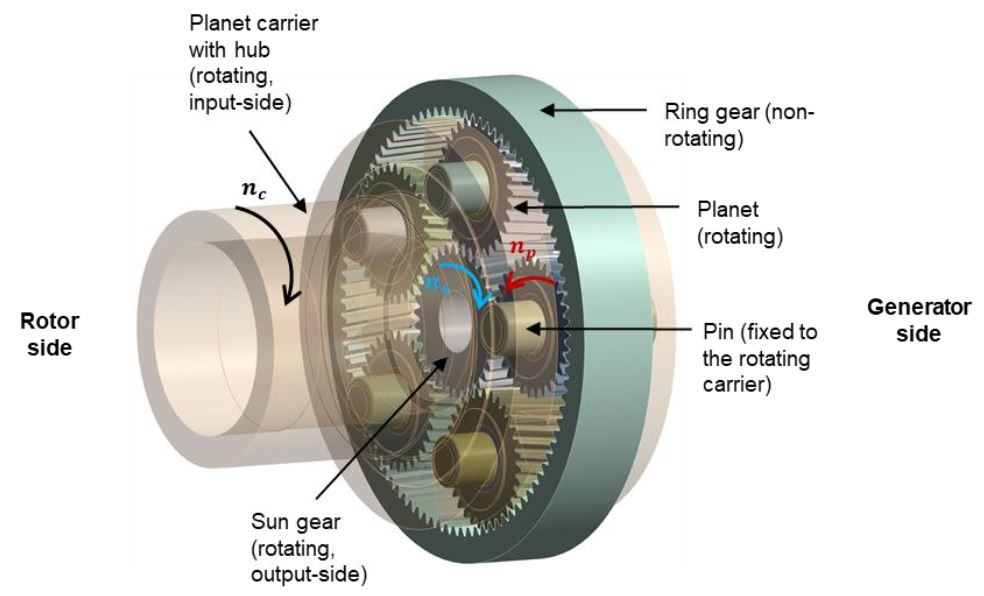
2.4. Investigated Sliding Planet Gear Bearing
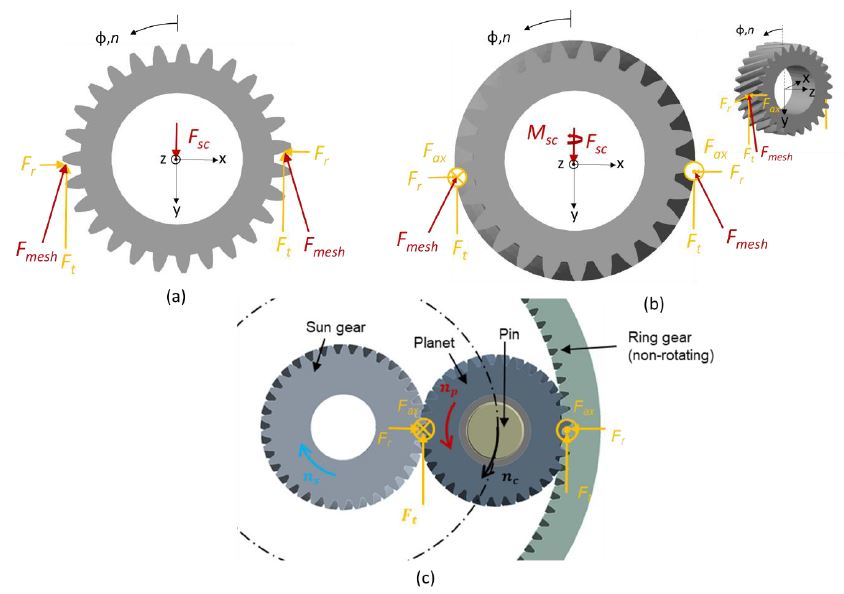
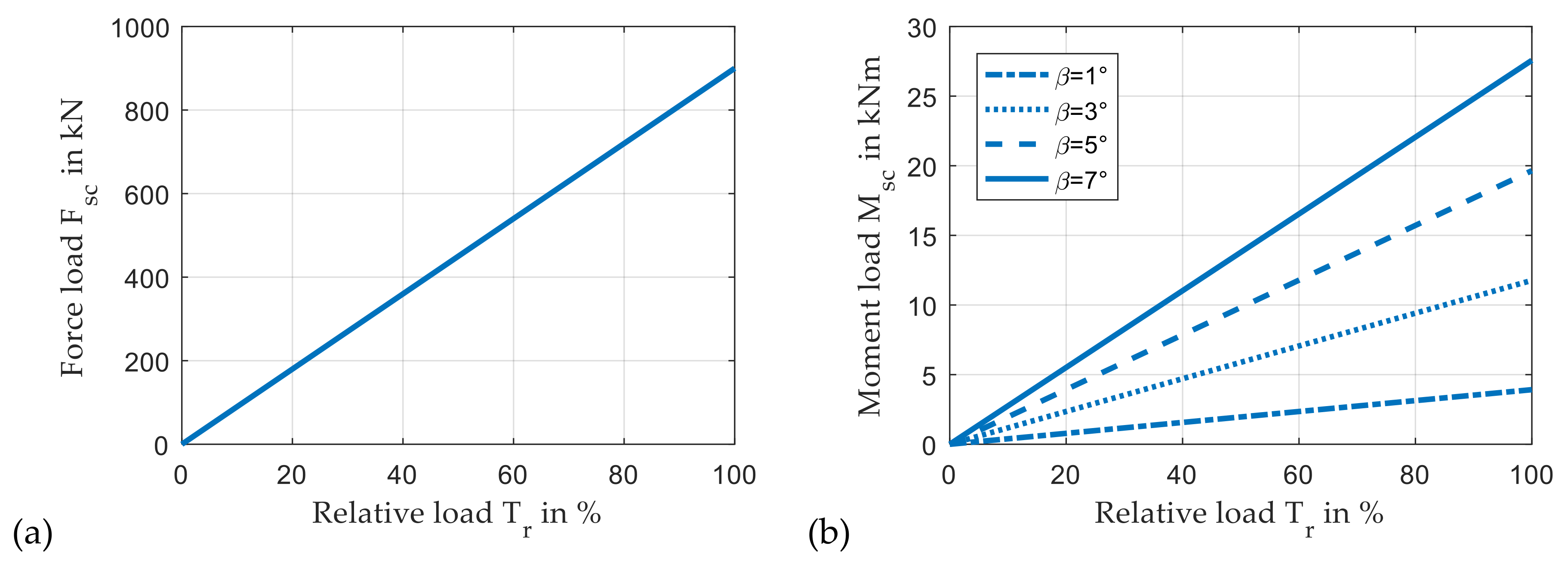
2.5. Bearing Loads Due to Mesh Forces
3. Results
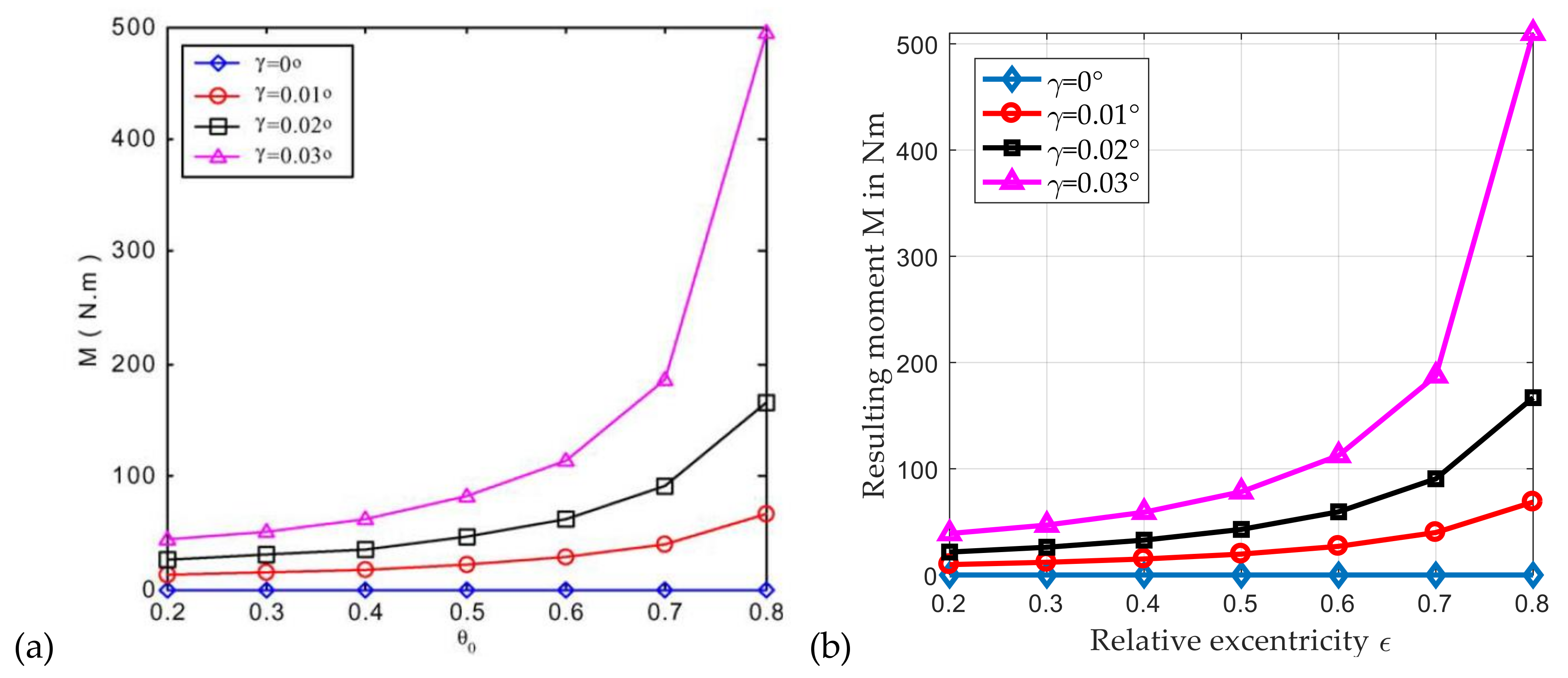
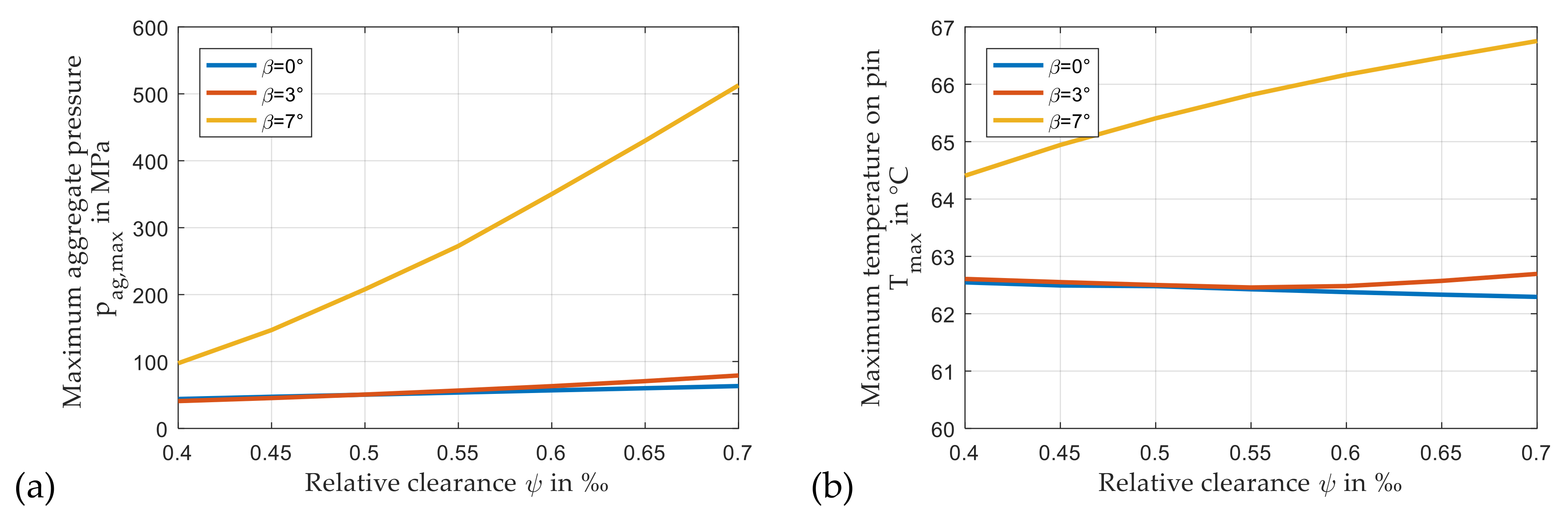
3.1. Impact of Helix Angle of the Helical Gear on Operating Conditions in the Lubricant Gap
3.2. Impact of Radial Clearance on Load Carrying Capacity
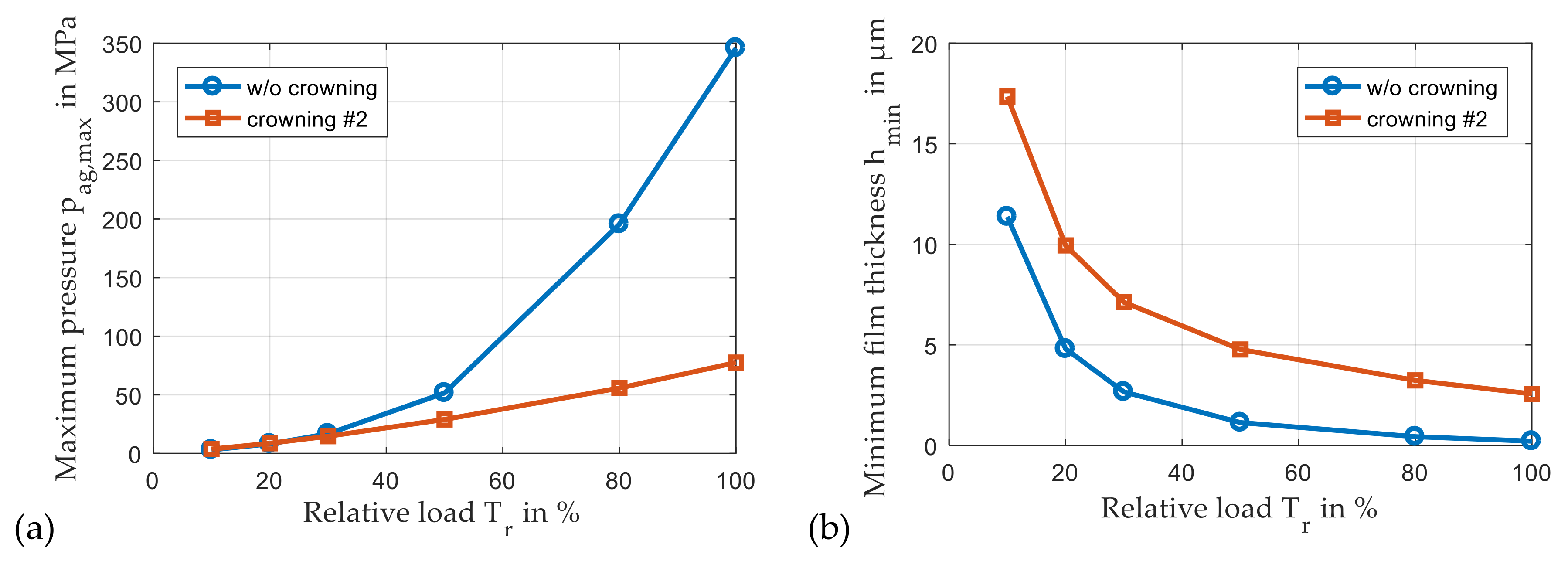
3.3. Impact of Axial Profiling
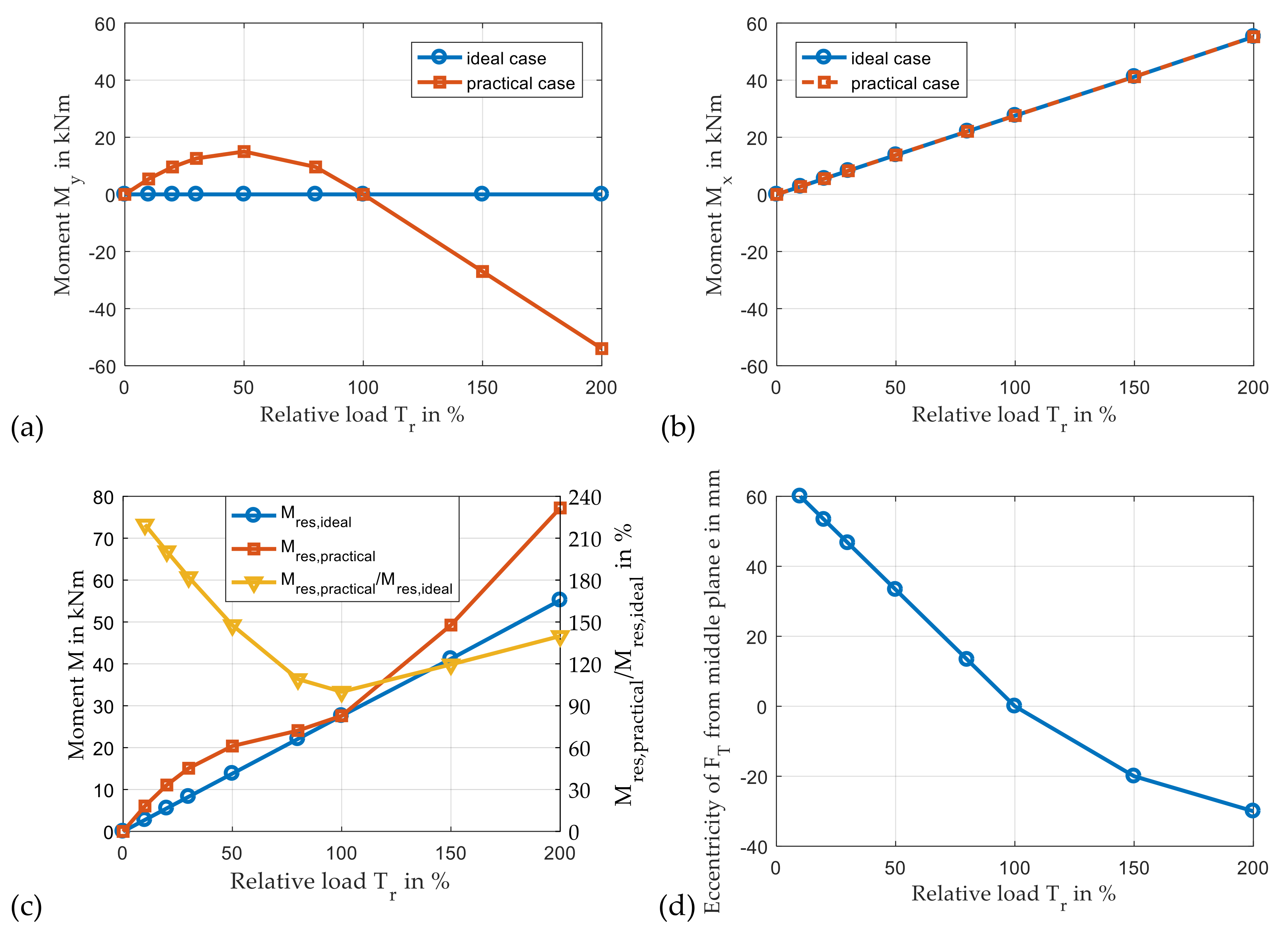
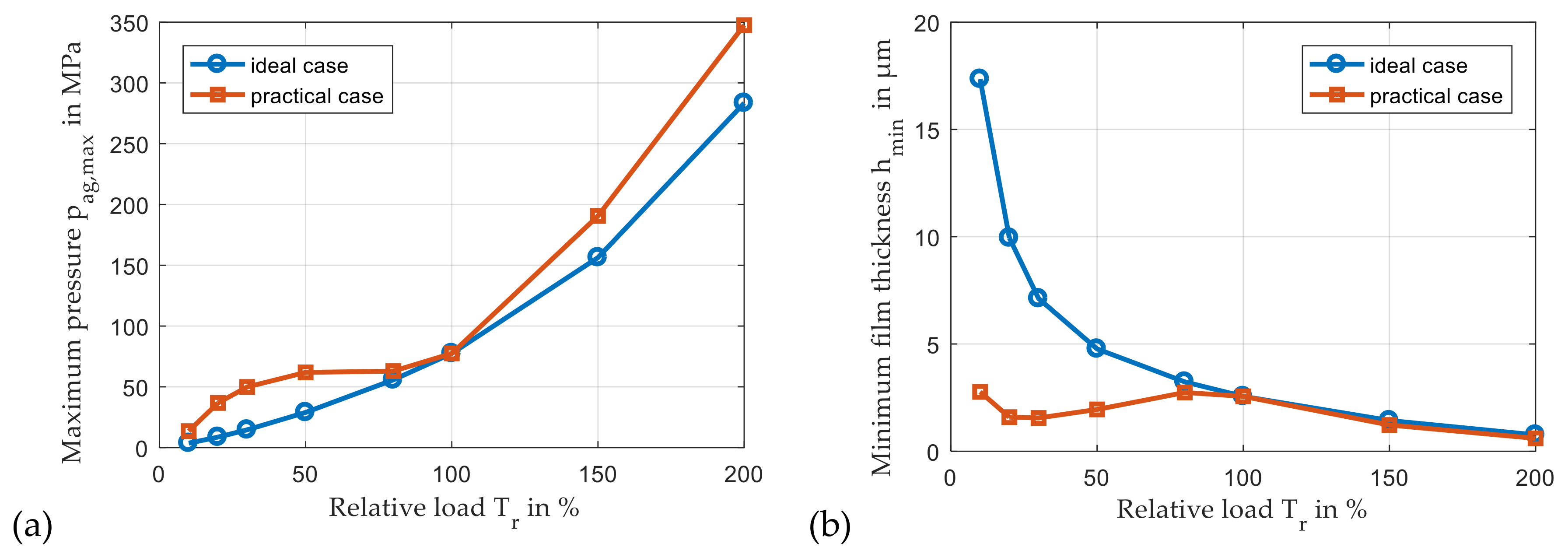
3.4. Operation at Part-Load and Over-Load Conditions
3.4.1. Part-Load Conditions for Homogenous Load Distribution on Tooth Flank
3.4.2. Part-Load and Over-Load Conditions for Constant Tooth Flank Geometry
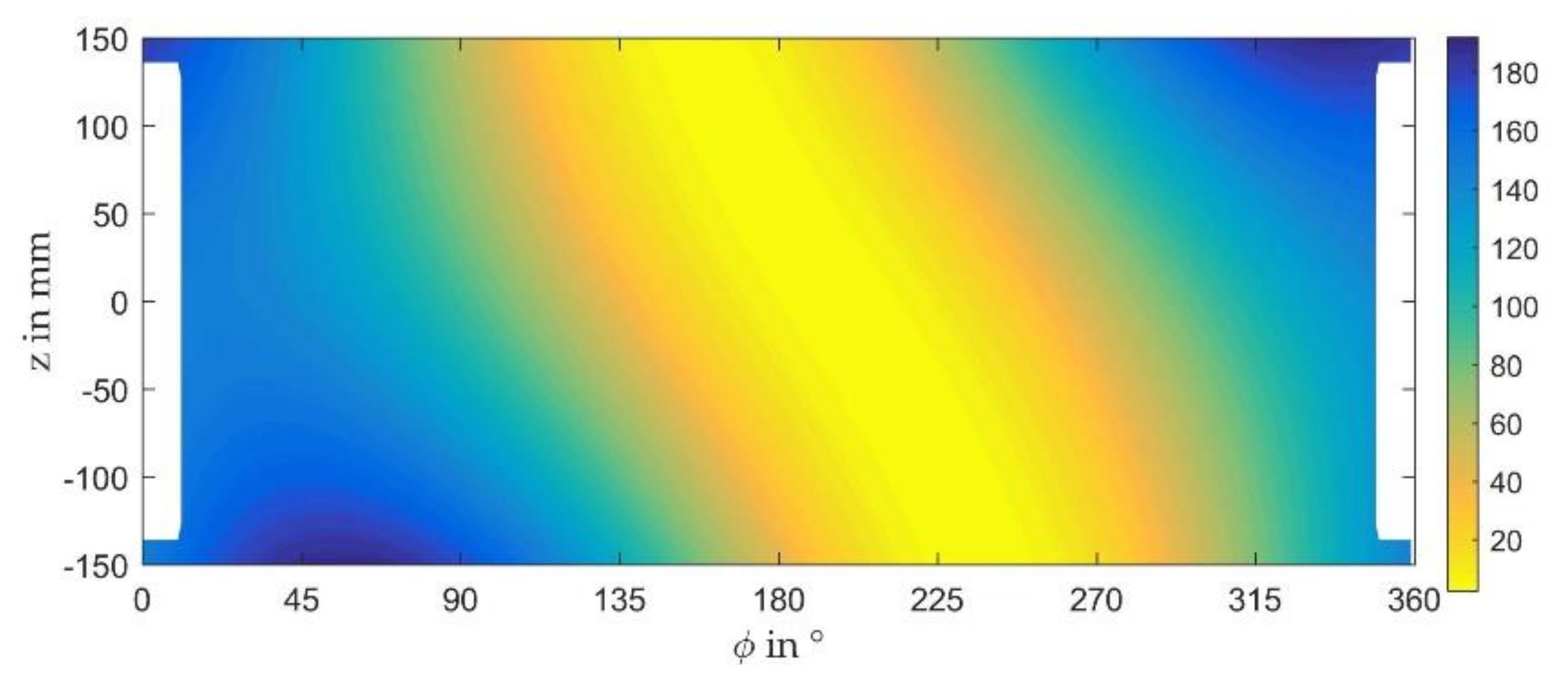
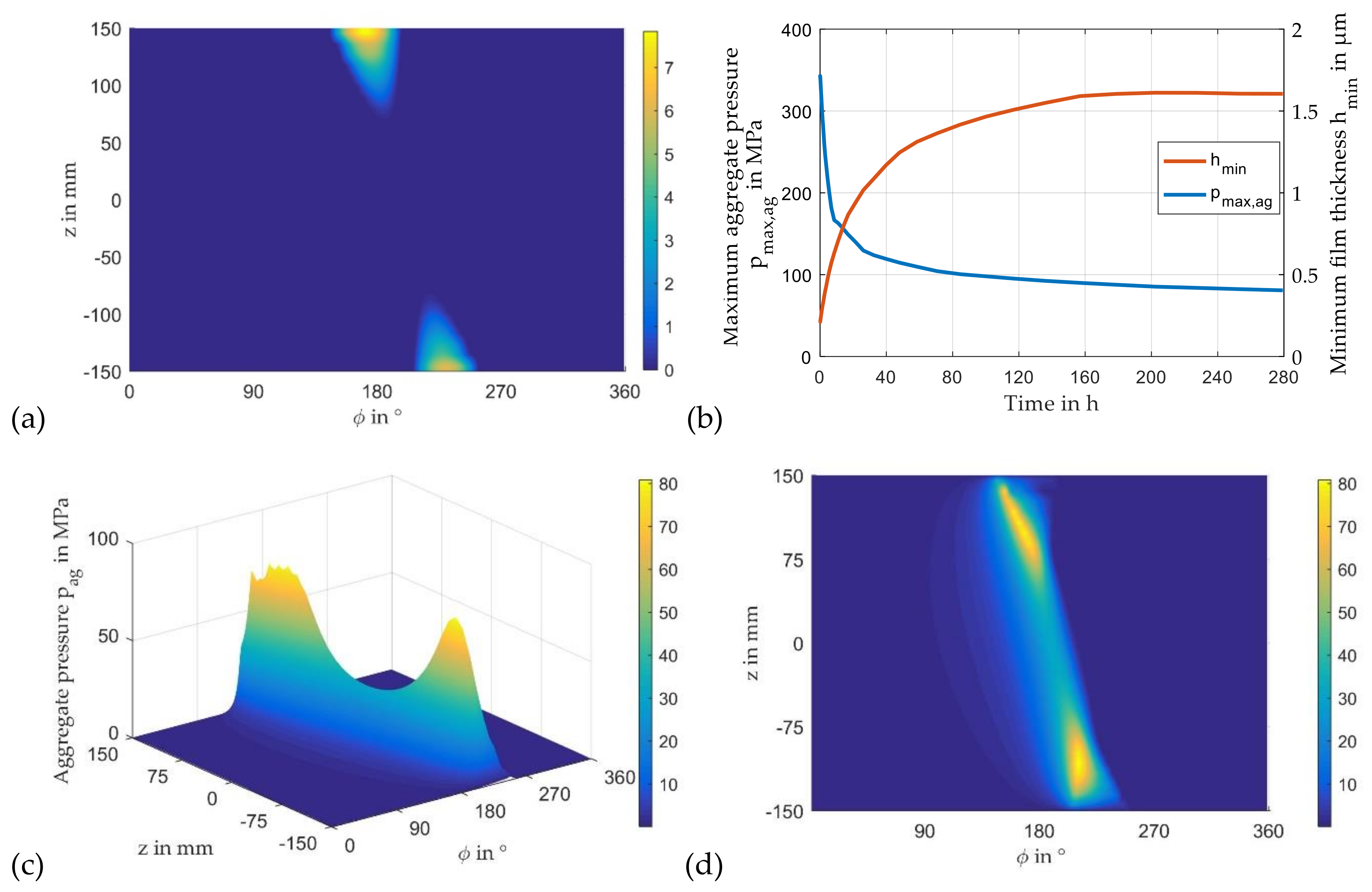
3.5. Modification of the Lubricant Gap by Wear
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| c | lubricant specific heat |
| CR | radial clearance |
| d1 | pitch diameter |
| e | Eccentricity between pin and planet |
| F0, F1, F2 | viscosity factors |
| F | force |
| h | film thickness |
| M | moment |
| n | rotor speed |
| p | pressure |
| Rq | root mean square surface roughness |
| T | temperature, torque |
| U | surface speed |
| u, v, w | flow velocities |
| x, y, z | Cartesian coordinates |
| X,Y | translational displacement relative to equilibrium position |
| Θ | lubricant density ratio |
| γ | attitude angle |
| η | lubricant dynamic viscosity |
| λ | lubricant conductivity |
| ρ | lubricant density |
| φx, φy | alignment angle about x-,y-axis |
| φX, φY | alignment angle about x-,y-axis relative to equilibrium position |
| ϕ | angular coordinate |
| ϕx,ϕzp | pressure flow factors |
| ΦxS | shear flow factor |
References
- Ragheb, A.; Ragheb, M. Wind turbine gearbox technologies. In Proceedings of the 2010 1st International Nuclear & Renewable Energy Conference (INREC), Amman, Jordan, 21–24 March 2010; pp. 1–8. [Google Scholar]
- Tavner, P.J.; Xiang, J.; Spinato, F. Reliability analysis for wind turbines. Wind Energy 2007, 10, 1–18. [Google Scholar] [CrossRef]
- Ribrant, J.; Bertling, L. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997–2005. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Qiao, W.; Lu, D. A survey on wind turbine condition monitoring and fault diagnosis—Part I: Components and subsystems. IEEE Trans. Ind. Electron. 2015, 62, 6536–6545. [Google Scholar] [CrossRef]
- Jones, A.; Harris, T.A. Analysis of a Rolling-Element Idler Gear Bearing Having a Deformable Outer-Race Structure. J. Basic Eng. 1963, 85, 273–278. [Google Scholar] [CrossRef]
- Fingerle, A.; Hochrein, J.; Otto, M.; Stahl, K. Theoretical Study on the Influence of Planet Gear Rim Thickness and Bearing Clearance on Calculated Bearing Life. J. Mech. Des. 2019, 142, 031102. [Google Scholar] [CrossRef]
- Bouyer, J.; Fillon, M. An Experimental Analysis of Misalignment Effects on Hydrodynamic Plain Journal Bearing Performances. J. Tribol. 2001, 124, 313–319. [Google Scholar] [CrossRef]
- Sun, J.; Changlin, G. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation. Tribol. Int. 2004, 37, 841–848. [Google Scholar] [CrossRef]
- Hili, M.A.; Bouaziz, S.; Maatar, M.; Fakhfakh, T.; Haddar, M. Hydrodynamic and Elastohydrodynamic Studies of a Cylindrical Journal Bearing. J. Hydrodyn. 2010, 22, 155–163. [Google Scholar] [CrossRef]
- Hagemann, T.; Kukla, S.; Schwarze, H. Measurement and prediction of the static operating conditions of a large turbine tilting-pad bearing under high circumferential speeds and heavy loads. In Proceedings of the ASME Turbo Expo 2013, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Prölß, M. Berechnung Langsam Laufender und Hoch Belasteter Gleitlager in Planetengetrieben unter Mischreibung, Verschleiß und Deformationen. Ph.D. Thesis, Clausthal University of Technology, Clausthal-Zellerfeld, Germany, 2020. [Google Scholar]
- Hagemann, T.; Schwarze, H. A Model for Oil Flow and Fluid Temperature Inlet Mixing in Hydrodynamic Journal Bearings. J. Tribol. 2018, 141, 021701. [Google Scholar] [CrossRef]
- Muzakkir, S.M.; Hirani, H.; Thakre, G.D. Lubricant for Heavily Loaded Slow-Speed Journal Bearing. Tribol. Trans. 2013, 56, 1060–1068. [Google Scholar] [CrossRef]
- Linjamaa, A.; Lehtovaara, A.; Larsson, R.; Kallio, M.; Söchting, S. Modelling and analysis of elastic and thermal deformations of a hybrid journal bearing. Tribol. Int. 2018, 118, 451–457. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Wang, J.; Ni, X. Coupling transient mixed lubrication and wear for journal bearing modeling. Tribol. Int. 2019, 138, 1–15. [Google Scholar] [CrossRef]
- Garabedian, N.T.; Gould, B.J.; Doll, G.L.; Burris, D.L. The Cause of Premature Wind Turbine Bearing Failures: Overloading or Underloading? Tribol. Trans. 2018, 61, 850–860. [Google Scholar] [CrossRef]
- Hagemann, T.; Ding, H.; Radtke, E.; Schwarze, H. Operating behavior of sliding planet gear bearings in wind turbine gearbox applications—Part II: Impact of structure deformation. Lubricants 2021, in press. [Google Scholar]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Falz, E. Grundzüge der Schmierungstechnik; Springer: Berlin/Heidelberg, Germany, 1931. [Google Scholar]
- Elrod, H.G. A Cavitation Algorithm. J. Lubr. Technol. 1981, 103, 350–354. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 1980; ISBN 9781315275130. [Google Scholar]
- Waltermann, H. Optimierte Thermo-Elasto-Hydrodynamische Berechnungsverfahren für Gleitlager. Ph.D. Thesis, Rheinisch-Westfälisch Technische Hochschule Aachen, Aachen, Germany, 1992. [Google Scholar]
- Hagemann, T.; Zemella, P.; Pfau, B.; Schwarze, H. Experimental and theoretical investigations on transition of lubrication conditions for a five-pad tilting-pad journal bearing with eccentric pivot up to highest surface speeds. Tribol. Int. 2020, 142, 106008. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The Contact of Two Nominally Flat Rough Surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Prölß, M.; Schwarze, H.; Hagemann, T.; Zemella, P.; Winking, P. Theoretical and Experimental Investigations on Transient Run-Up Procedures of Journal Bearings Including Mixed Friction Conditions. Lubricants 2018, 6, 105. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Cheng, H.S.; Arai, T.; Kobayashi, Y.; Aoyama, S. Numerical Simulation of Piston Ring in Mixed Lubrication—A Nonaxisymmetrical Analysis. J. Tribol. 1994, 116, 470–478. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Geometrical properties | |
| Number of pads, - | 1 |
| Nominal diameter, mm | 60 |
| Bearing width, mm | 66 |
| Radial clearance, µm | 30 |
| Pad sliding surface preload, - | 0.0 |
| Static analysis parameters | |
| Rotational speed, rpm | 3000 |
| Lubricant properties | |
| Lubricant dynamic viscosity, mPas | 9.0 |
| Parameter | Value |
|---|---|
| Geometrical properties | |
| Number of pads, - | 1 |
| Nominal diameter, mm | 250 |
| Pitch circle diameter, mm | 499 |
| Bearing width, mm | 300 |
| Angular span of lube oil pocket, degrees | 20.5 |
| Width of lube oil pocket, mm | 260 |
| Radial clearance, µm | 138 |
| Pad sliding surface preload, - | 0.0 |
| Static analysis parameters | |
| Nominal rotational speed, rpm | 30 |
| Nominal bearing load, kN | 900 |
| Lubricant supply temperature, °C | 60 |
| Lube oil supply pressure, MPa | 0.2 |
| Lubricant properties | |
| Lubricant | ISO VG 320 |
| Lubricant density kg/m3 | 865 @ 40 °C |
| Lubricant specific heat capacity kJ/(kg·K) | 2.0 @ 20 °C |
| Lubricant thermal conductivity, W/(m·K) | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagemann, T.; Ding, H.; Radtke, E.; Schwarze, H. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part I: Basic Relations. Lubricants 2021, 9, 97. https://doi.org/10.3390/lubricants9100097
Hagemann T, Ding H, Radtke E, Schwarze H. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part I: Basic Relations. Lubricants. 2021; 9(10):97. https://doi.org/10.3390/lubricants9100097
Chicago/Turabian StyleHagemann, Thomas, Huanhuan Ding, Esther Radtke, and Hubert Schwarze. 2021. "Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part I: Basic Relations" Lubricants 9, no. 10: 97. https://doi.org/10.3390/lubricants9100097
APA StyleHagemann, T., Ding, H., Radtke, E., & Schwarze, H. (2021). Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part I: Basic Relations. Lubricants, 9(10), 97. https://doi.org/10.3390/lubricants9100097







