Prediction and Deformation Mechanism Analysis of High Porosity in U–10Mo Monolithic Fuels at High Burnup
Abstract
:1. Introduction
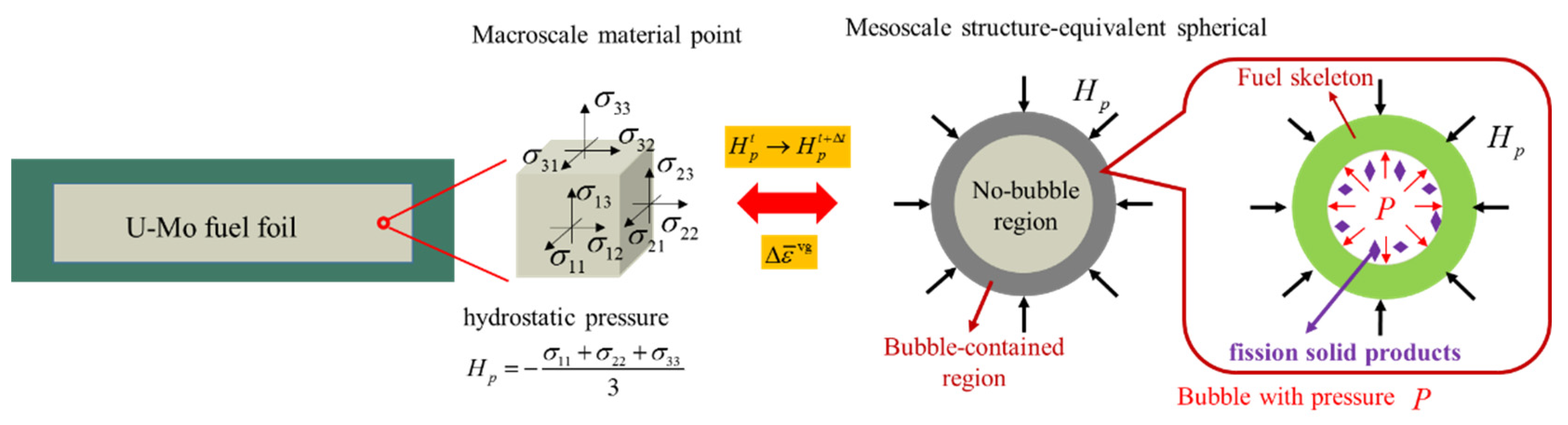
2. Improved Fuel Skeleton Creep-Based Volume Growth Model for U–Mo Fuels
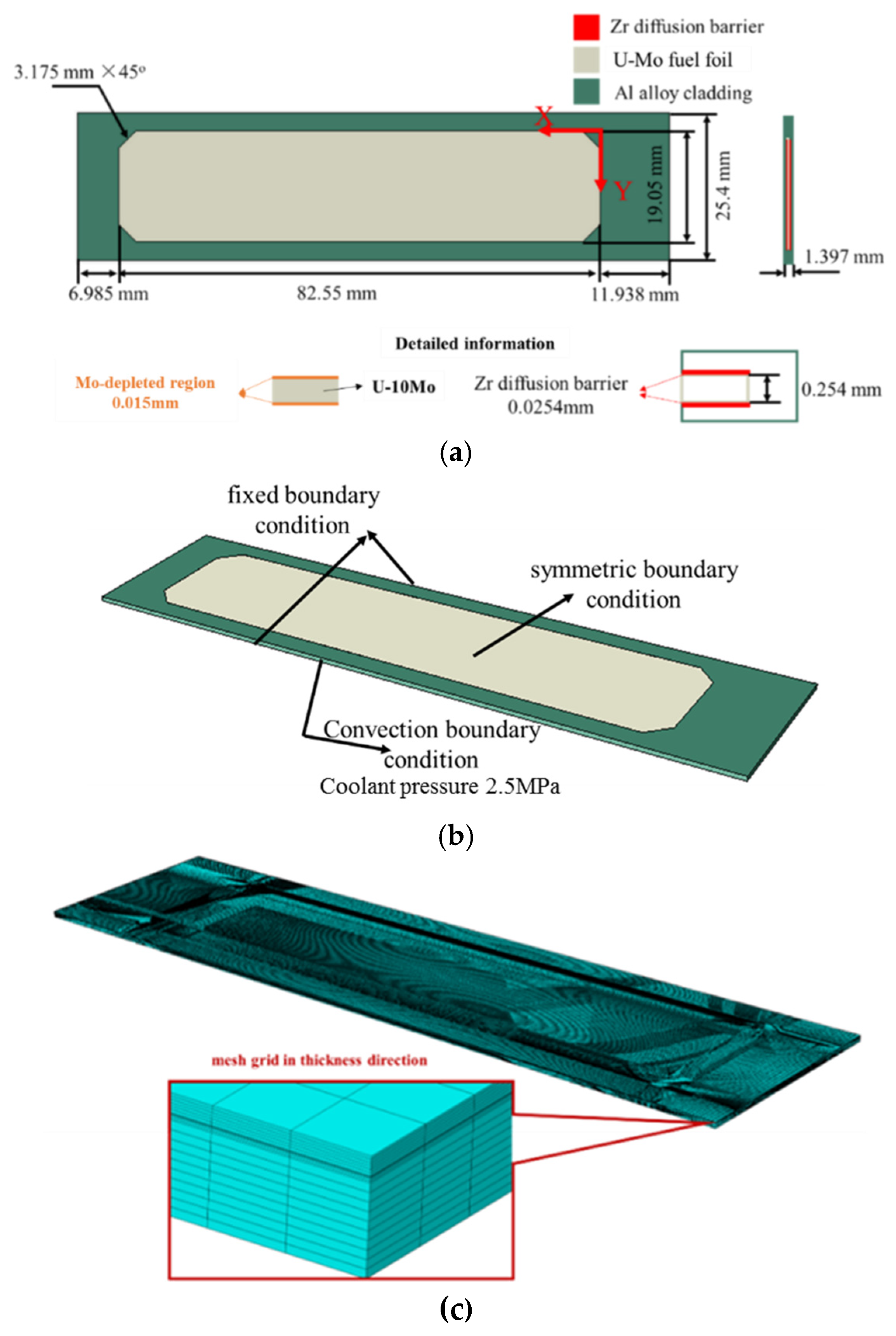
3. Finite Element Modeling of the In-Pile Thermo-Mechanical Coupling Behaviors in the Fuel Plate L1P7A0
3.1. Finite Element Model
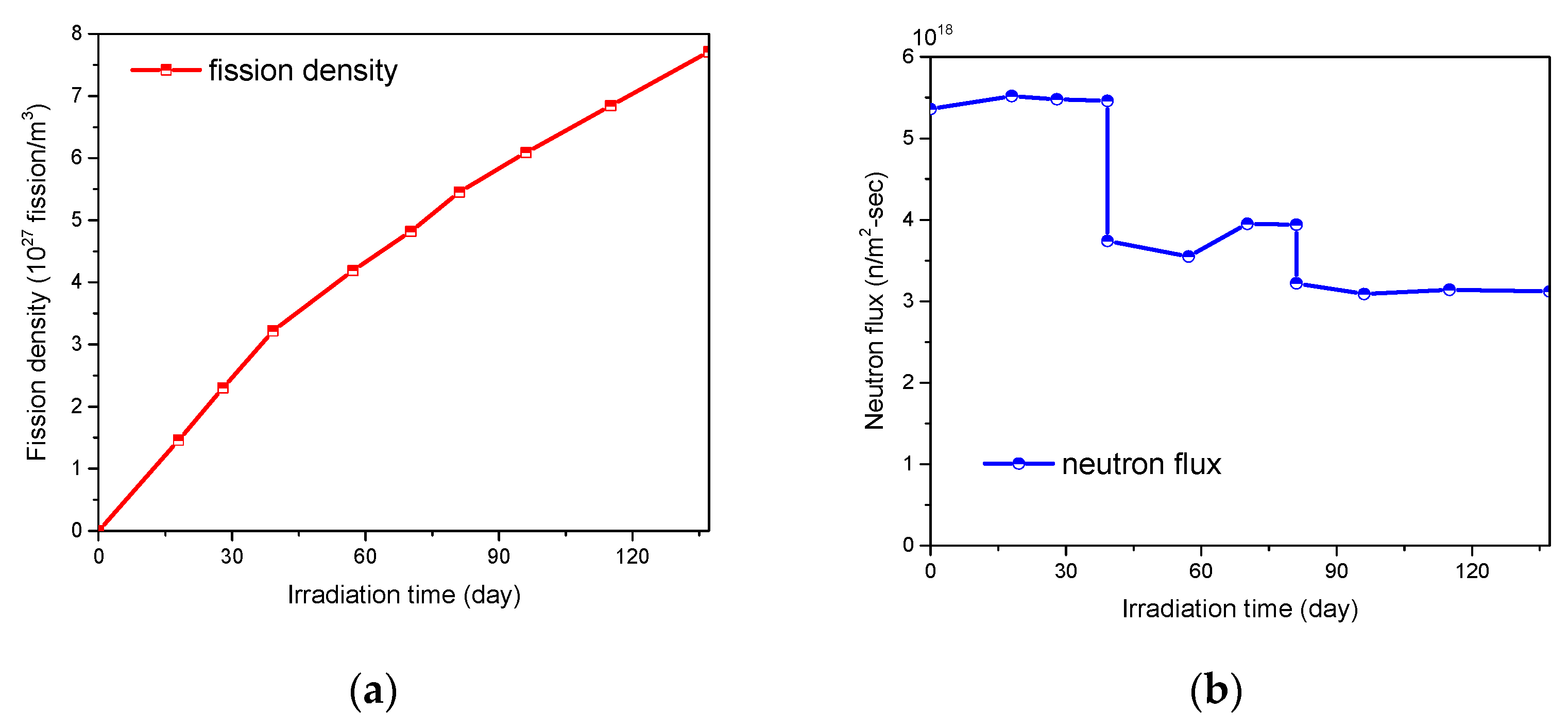
3.2. Modeling Approach
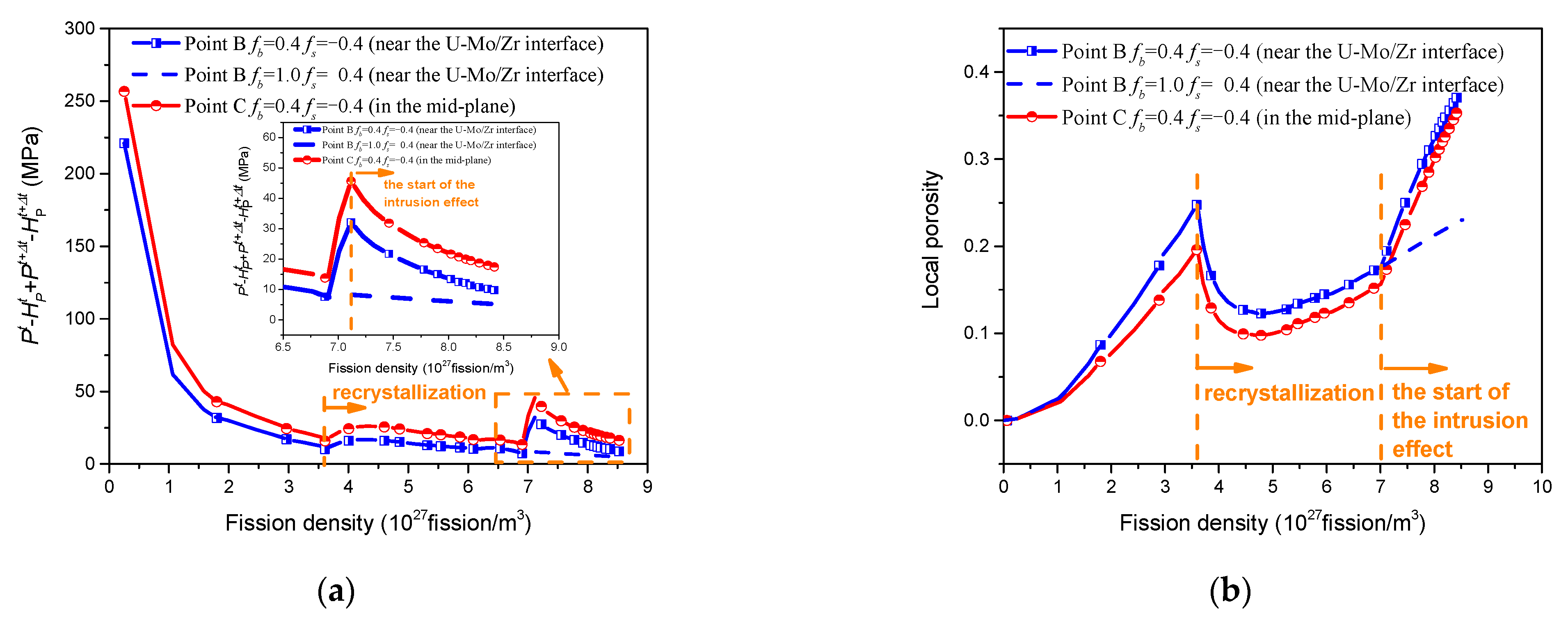
4. Results and Discussion
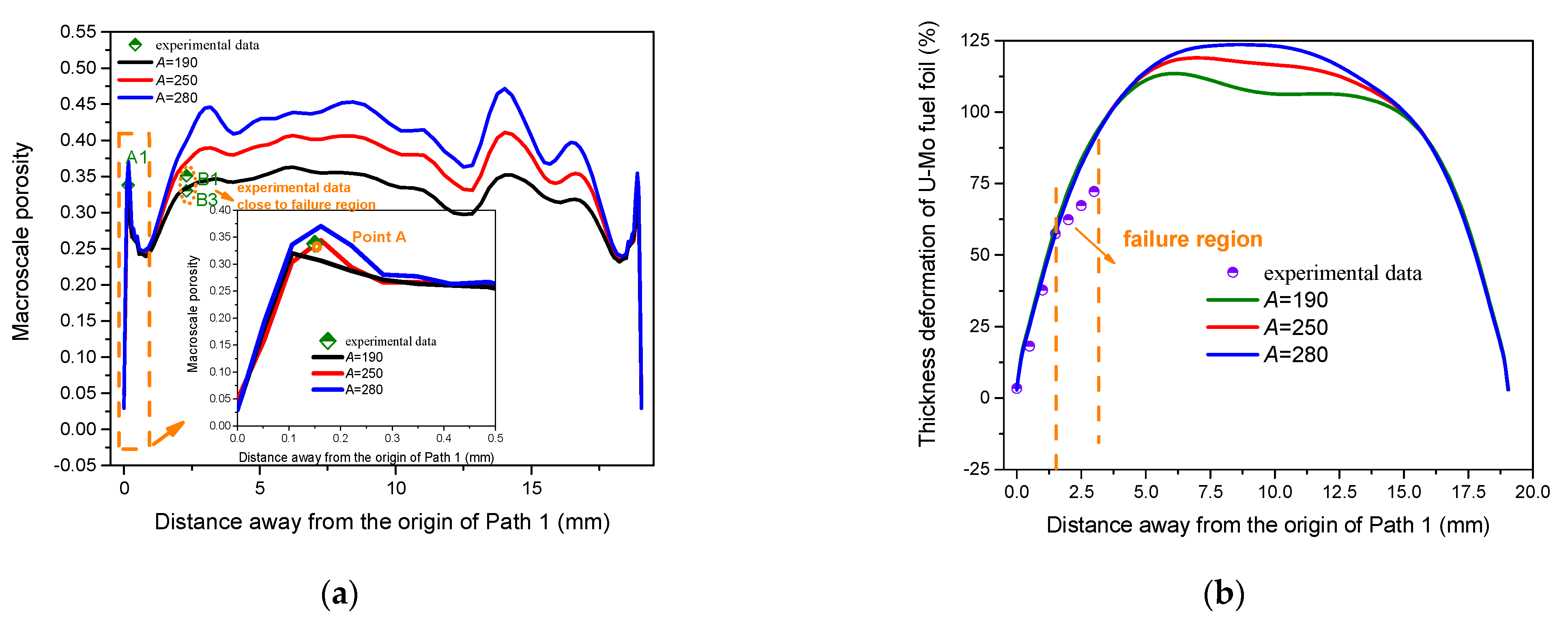
4.1. Predictions of the Macroscale Porosity and the Thickness Deformation for the Fuel Foil
4.2. The Underlying Deformation Mechanism of Higher Porosity of the Fuel Foil at High Burnup
5. Conclusions
- (1)
- The simulation results produce the best-fit creep rate coefficient of 250 × 10−22 mm3/(fission·Mpa) for the Mo-depleted region, and the parameters of fb = 0.4 and fs = −0.4 for the improved bubble growth model, by comparing the predicted results of macroscale porosities and thickness deformation of the U–Mo fuel foil with the experimental results.
- (2)
- The intrusion of solid fission products, leading to the extra differences between the bubble pressure and the external pressure, is the dominant factor to induce the high porosity in most regions of heavily irradiated fuel foil.
- (3)
- The locally enhanced fuel skeleton creep ability is responsible for the higher porosities near the U–Mo/Zr interface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mao, S.-X.; Song, J.-Y.; Zhu, W.-S.; Li, H.-M.; Pang, J.-Y.; Dang, D.-B.; Bai, Y. Heterogeneous oxidative desulfurization of fuels using amphiphilic mesoporous phosphomolybdate-based poly(ionic liquid) over a wide temperature range. Fuel 2023, 352, 128982. [Google Scholar] [CrossRef]
- Li, N.; Xue, J.; Wu, S.; Qin, K.; Liu, N. Research on Coal and Gangue Recognition Model Based on CAM-Hardswish with Effi-cientNetV2. Appl. Sci. 2023, 13, 8887. [Google Scholar] [CrossRef]
- Pascaris, A.S.; Pearce, J.M. U.S. Greenhouse Gas Emission Bottlenecks: Prioritization of Targets for Climate Liability. Energies 2020, 13, 3932. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Z.; Yun, D. Cladding Failure Modelling for Lead-Based Fast Reactors: A Review and Prospects. Metals 2023, 13, 1524. [Google Scholar] [CrossRef]
- Meyer, M.; Hofman, G.; Hayes, S.; Clark, C.; Wiencek, T.; Snelgrove, J.; Strain, R.; Kim, K.-H. Low-temperature irradiation behavior of uranium–molybdenum alloy dispersion fuel. J. Nucl. Mater. 2002, 304, 221–236. [Google Scholar] [CrossRef]
- Park, J.-M.; Kim, K.-H.; Kim, C.-K.; Meyer, M.K.; Hofman, G.L.; Strain, R.V. The irradiation behavior of atomized U-Mo alloy fuels at high temperature. Met. Mater. Int. 2001, 7, 151–157. [Google Scholar] [CrossRef]
- Lee, D.B.; Kim, K.H.; Kim, C.K. Thermal compatibility studies of unirradiated U-Mo alloys dispersed in aluminum. J. Nucl. Mater. 1997, 250, 79–82. [Google Scholar] [CrossRef]
- Smith, C.; Jue, J.-F.; Keiser, D.; Trowbridge, T.; Miller, B.; Robinson, A.; Winston, A.; Giglio, J. An investigation of the failure modes in U-10Mo monolithic fuel irradiated to high burnup. J. Nucl. Mater. 2023, 575, 154202. [Google Scholar] [CrossRef]
- Keiser, D.; Jue, J.; Miller, B.; Gan, J.; Robinson, A.; Madden, J. Observed Changes in As-Fabricated U-10Mo Monolithic Fuel Mi-crostructures after Irradiation in the Advanced Test Reactor. JOM 2017, 69, 2538–2545. [Google Scholar] [CrossRef]
- Rice, F.; Williams, W.; Robinson, A.; Harp, J.; Meyer, M.; Rabin, B. RERTR-12 Post-Irradiation Examination Summary Report; Idaho National Laboratory: Idaho Falls, ID, USA, 2015. [Google Scholar] [CrossRef]
- Schulthess, J.L.; Lloyd, W.R.; Rabin, B.; Wheeler, K.; Walters, T.W. Mechanical properties of irradiated U Mo alloy fuel. J. Nucl. Mater. 2018, 515, 91–106. [Google Scholar] [CrossRef]
- Burkes, D.E.; Casella, A.M.; Casella, A.J.; Buck, E.C.; Pool, K.N.; MacFarlan, P.J.; Edwards, M.K.; Smith, F.N. Thermal proper-ties of U-Mo alloys irradiated to moderate burnup and power. J. Nucl. Mater. 2015, 464, 331–341. [Google Scholar] [CrossRef]
- Burkes, D.E.; Schwerdt, I.J.; Huber, T.K.; Breitkreutz, H.; Reiter, C.; Petry, W.; Schulthess, J.L.; Casella, A.M.; Casella, A.J.; Buck, E.C.; et al. Thermal properties of U-Mo alloys irradiated under high fis-sion power density. J. Nucl. Mater. 2021, 547, 152823. [Google Scholar] [CrossRef]
- Burkes, D.E.; Prabhakaran, R.; Jue, J.; Rice, F.J. Mechanical Properties of DU-xMo Alloys with x = 7 to 12 Weight Percent. Metall. Mater. Trans. A 2009, 40, 1069–1079. [Google Scholar] [CrossRef]
- Leenaers, A.; Wight, J.; Berghe, S.; Ryu, H.J.; Valery, J.F. U-Mo Based Fuel System. Compr. Nucl. Mater. 2020, 5, 499–530. [Google Scholar]
- Rest, J.; Kim, Y.S.; Hofman, G.L.; Meyer, M.K.; Hayes, S.L. U-Mo Fuels Handbook; Argonne National Laboratory Report ANL-09/31; Argonne National Laboratory: Chicago, IL, USA, 2009. [Google Scholar]
- Kim, Y.S.; Hofman, G.; Cheon, J.; Robinson, A.; Wachs, D. Fission induced swelling and creep of U–Mo alloy fuel. J. Nucl. Mater. 2013, 437, 37–46. [Google Scholar] [CrossRef]
- Jian, X.; Kong, X.; Ding, S. A mesoscale stress model for irradiated U 10Mo monolithic fuels based on evolution of volume fraction/radius/internal pressure of bubbles. Nucl. Eng. Technol. 2019, 51, 1575–1588. [Google Scholar] [CrossRef]
- Jian, X.; Zhang, J.; Li, Y.; Ding, S. Skeleton-creep based bubble growth model and multi-scale mechanical constitutive model for U-10Mo fuels under irradiation. Int. J. Plast. 2023, 163, 103557. [Google Scholar] [CrossRef]
- Jian, X.; Yan, F.; Kong, X.; Li, Y.; Ding, S. Further development of the fission gas swelling model for U-10Mo fuels. J. Nucl. Mater. 2022, 565, 153769. [Google Scholar] [CrossRef]
- Rest, J. A model for the effect of the progression of irradiation-induced recrystallization from initiation to completion on swelling of UO2 and U–10Mo nuclear fuels. J. Nucl. Mater. 2005, 346, 226–232. [Google Scholar] [CrossRef]
- Kim, Y.S.; Hofman, G.; Cheon, J. Recrystallization and fission-gas-bubble swelling of U–Mo fuel. J. Nucl. Mater. 2013, 436, 14–22. [Google Scholar] [CrossRef]
- Spino, J.; Stalios, A.D.; Cruz, H.S.; Baron, D. Stereological evolution of the rim structure in PWR-fuels at prolonged irra-diation: Dependencies with burn-up and temperature. J. Nucl. Mater. 2006, 354, 66–84. [Google Scholar] [CrossRef]
- Perez, D.M.; Chang, G.S.; Wachs, D.M.; Roth, G.A.; Woolstenhulme, N.E. RERTR-12 Insertion 2 Irradiation Summary Report; Idaho National Laboratory: Idaho Falls, ID, USA, 2012. [Google Scholar] [CrossRef]
- Meyer, M.K. Investigation of the Cause of Low Blister Threshold Temperatures in the RERTR-12 and AFIP-4 Experiments; Idaho National Laboratory: Idaho Falls, ID, USA, 2012. [Google Scholar]
- Meyer, M.; Gan, J.; Jue, J.; Keiser, D.; Perez, E.; Robinson, A.; Wachs, D.; Woolstenhulme, N.; Hofman, G.; Kim, Y. Irradiation Performance of U-Mo Monolithic Fuel. Nucl. Eng. Technol. 2014, 46, 169–182. [Google Scholar] [CrossRef]
- Marchbanks, M.F. ANS Materials Databook; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1995. [Google Scholar]
- Ozaltun, H.; Shen, M.-H.H.; Medvedev, P. Assessment of residual stresses on U10Mo alloy based monolithic mini-plates during Hot Isostatic Pressing. J. Nucl. Mater. 2011, 419, 76–84. [Google Scholar] [CrossRef]
- Macdonald, P.E.; Thomson, L.B. MATPRO-version 10: A Handbook of Materials Properties for Use in the Analysis of Light Water Reactor Fuel Rod Behavior; Idaho National Laboratory: Idaho Falls, ID, USA, 1978. [Google Scholar]
- Hagrman, D.T.; Allison, C.M.; Berna, G.A. SCDAP/RELAP5/MOD 3.1 Code Manual: MATPRO; A Library of Materials Proper-ties for Light-Water-Reactor Accident Analysis, Idaho National Engineering and Environmental Laboratory: Idaho Falls, ID, USA, 2003. [Google Scholar]
- Suzuki, M.; Saitou, H. Light Water Reactor Fuel Analysis Code FEMAXI-6; Version 1; JAEA-Data/Code; Japan Atomic Energy Agency: Tsuruga-shi, Fukui, Japan, 2005. [Google Scholar]
- Dienst, W. Irradiation induced creep of ceramic nuclear fuels. J. Nucl. Mater. 1977, 65, 1–8. [Google Scholar] [CrossRef]
- Salvato, D.; Smith, C.; Ye, B.; Mei, Z.-G.; Yacout, A.; Van Eyken, J.; Miller, B.; Keiser, D.; Glagolenko, I.; Giglio, J.; et al. Impact of SEM acquisition parameters on the porosity analysis of irradiated U-Mo fuel. Nucl. Mater. Energy 2023, 36, 101469. [Google Scholar] [CrossRef]
- Di Lemma, F.; Jue, J.; Trowbridge, T.; Smith, C.; Miller, B.; Keiser, D.; Giglio, J.; Cole, J. Annealing influence on the microstructure of irradiated U-Mo monolithic fuel foils. Nucl. Mater. Energy 2023, 35, 101436. [Google Scholar] [CrossRef]
- Tang, Y.; Shan, Z.; Yin, G.; Miao, L.; Wang, S.; Zhang, Z. Low-Field Nuclear Magnetic Resonance Investigation on Early Hydra-tion Characterization of Cement Paste Mixed with Mineral Admixtures. Buildings 2023, 13, 2318. [Google Scholar] [CrossRef]
- Gao, S.; Wang, H.; Huang, H.; Kang, R. Molecular simulation of the plastic deformation and crack formation in single grit grinding of 4H-SiC single crystal. Int. J. Mech. Sci. 2023, 247, 108147. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, K.; Zhang, H.; Tian, X.; Jiang, Q.; Murugadoss, V.; Hou, H. Dislocation motion in plastic deformation of nano polycrystalline metal materials: A phase field crystal method study. Adv. Compos. Hybrid Mater. 2022, 5, 2546–2556. [Google Scholar] [CrossRef]
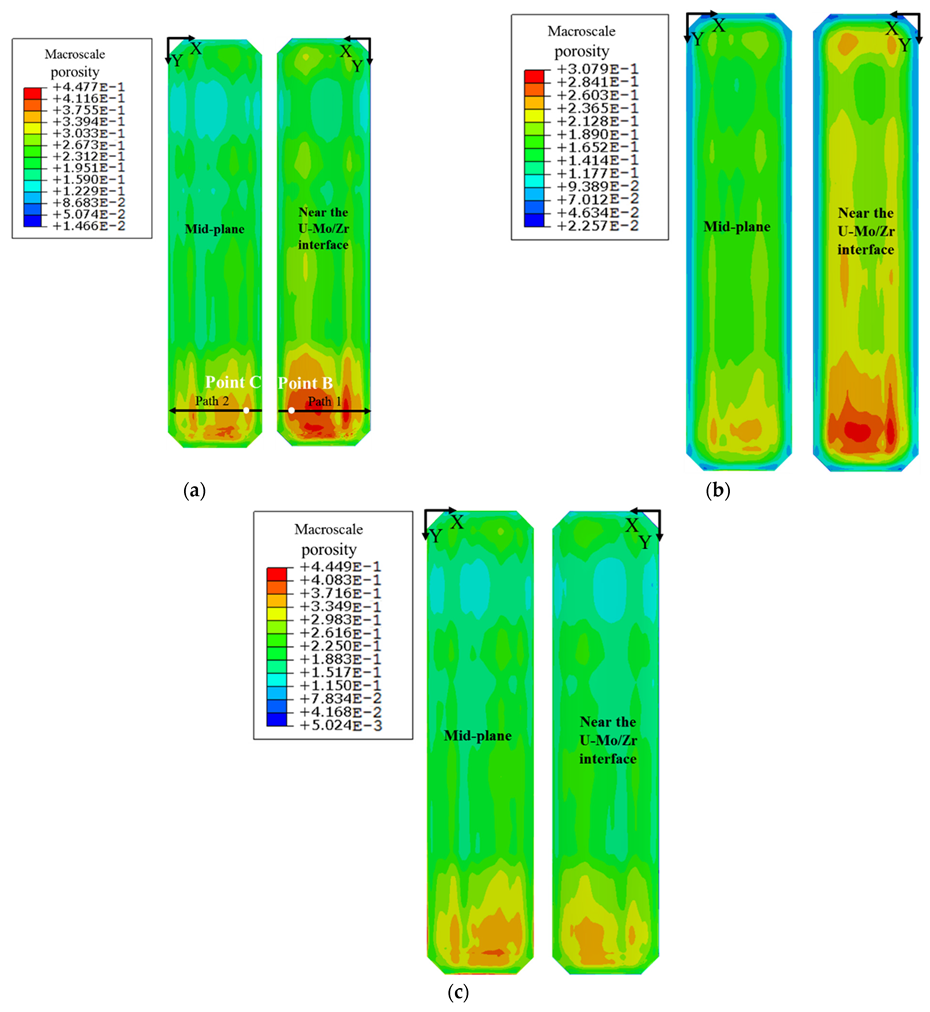
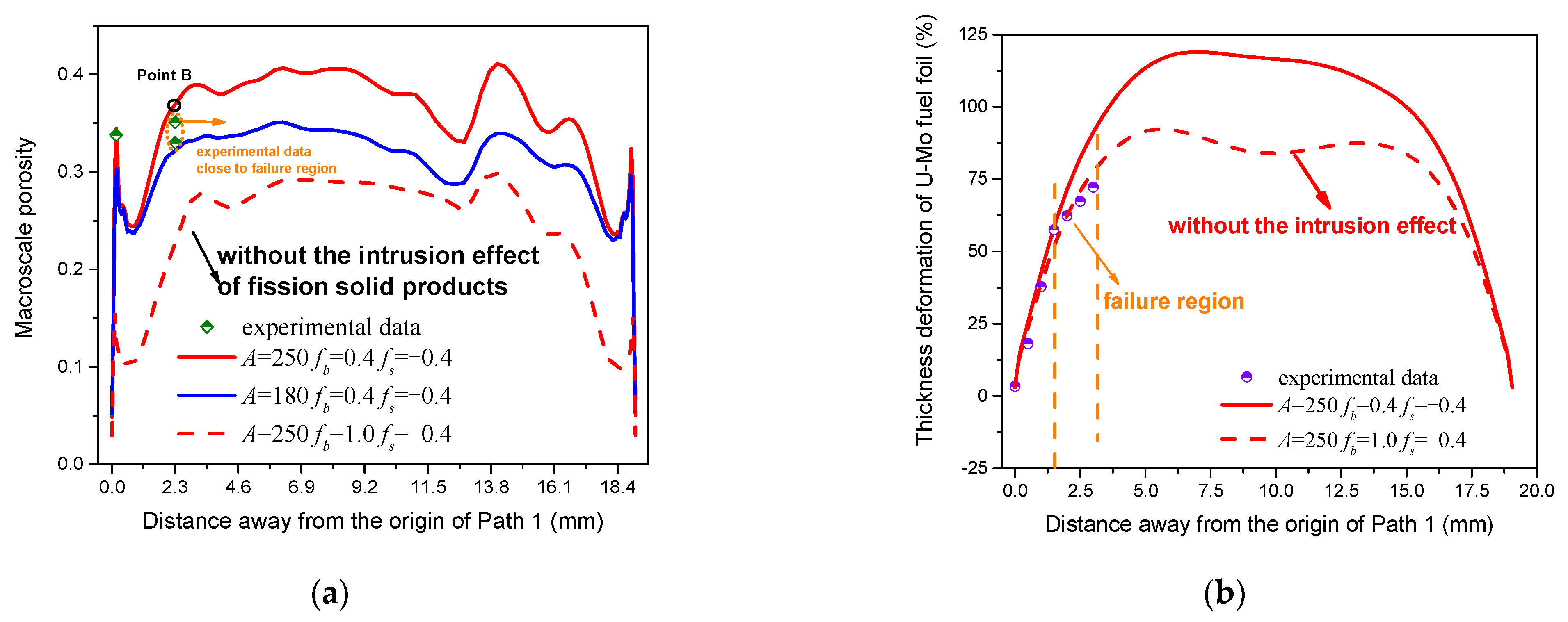
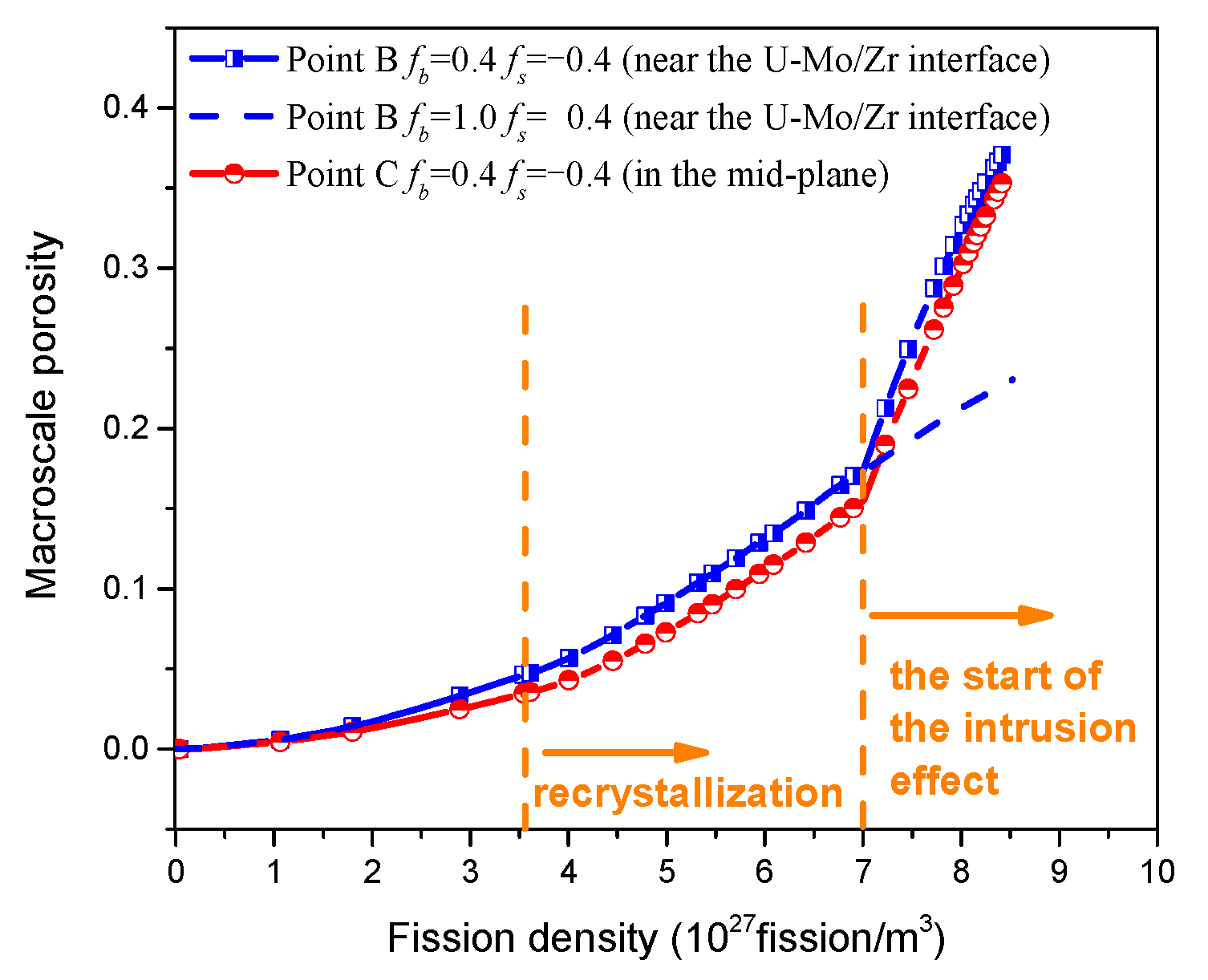
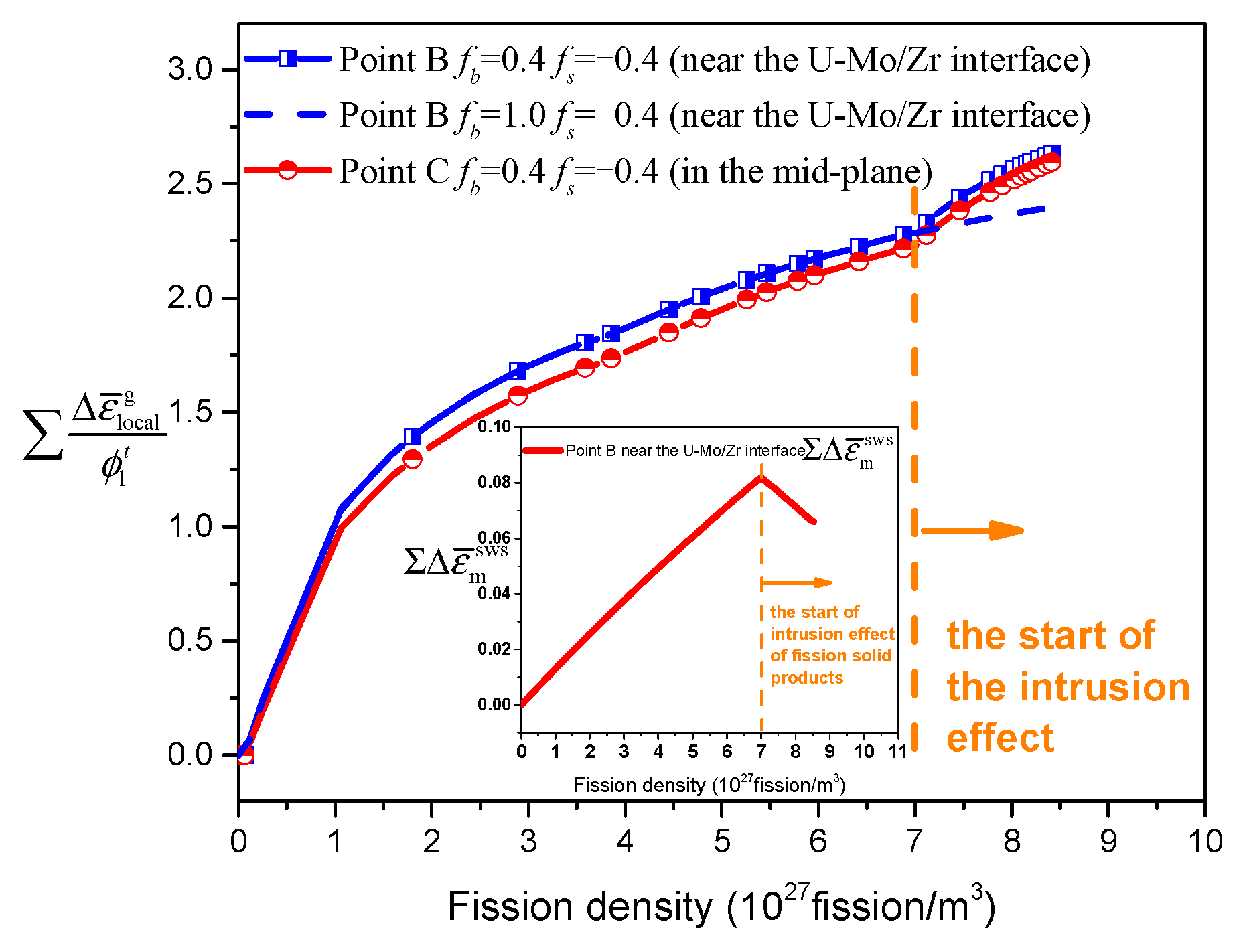
| Parameter | Point B | Point C |
|---|---|---|
| Bubble volume (10−20 m3) | 3.99047 | 0.14677 |
| Local porosity (%) | 4.10474 | 0.150874 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jian, X.; Zhao, Y.; Ding, S. Prediction and Deformation Mechanism Analysis of High Porosity in U–10Mo Monolithic Fuels at High Burnup. Metals 2023, 13, 1693. https://doi.org/10.3390/met13101693
Jian X, Zhao Y, Ding S. Prediction and Deformation Mechanism Analysis of High Porosity in U–10Mo Monolithic Fuels at High Burnup. Metals. 2023; 13(10):1693. https://doi.org/10.3390/met13101693
Chicago/Turabian StyleJian, Xiaobin, Yunmei Zhao, and Shurong Ding. 2023. "Prediction and Deformation Mechanism Analysis of High Porosity in U–10Mo Monolithic Fuels at High Burnup" Metals 13, no. 10: 1693. https://doi.org/10.3390/met13101693







