Exergy Analysis of Transcritical CO2 Air-Source Heat Pump with Honeycomb Gas Cooler
Abstract
:1. Introduction
2. Model of CO2 Heat Pump System
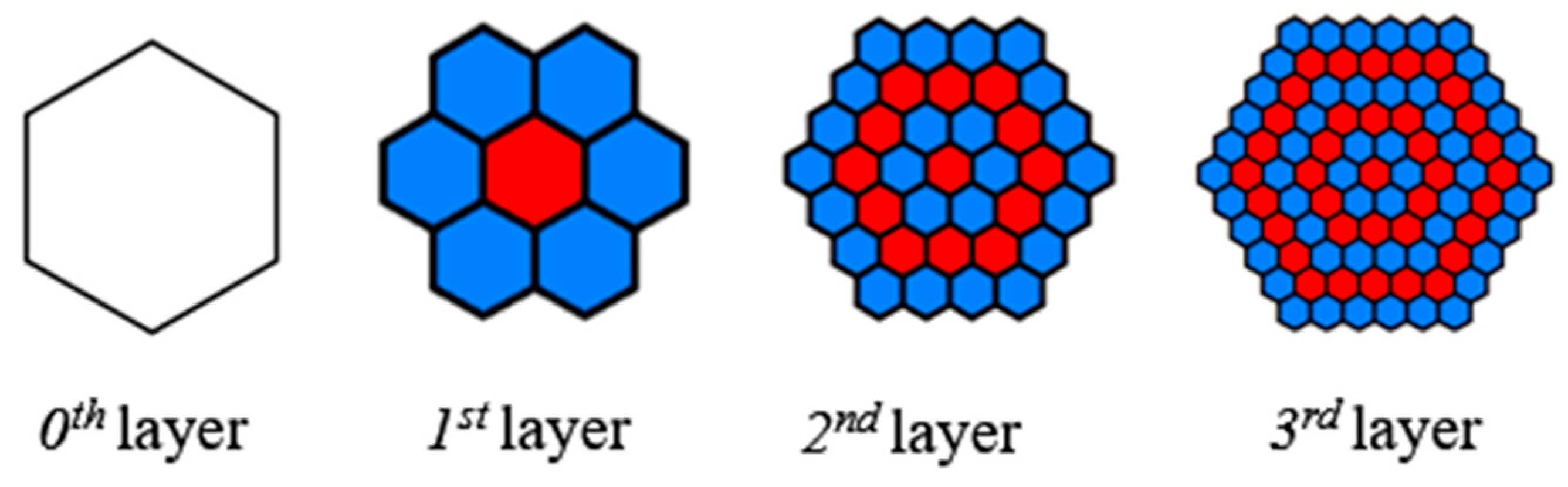
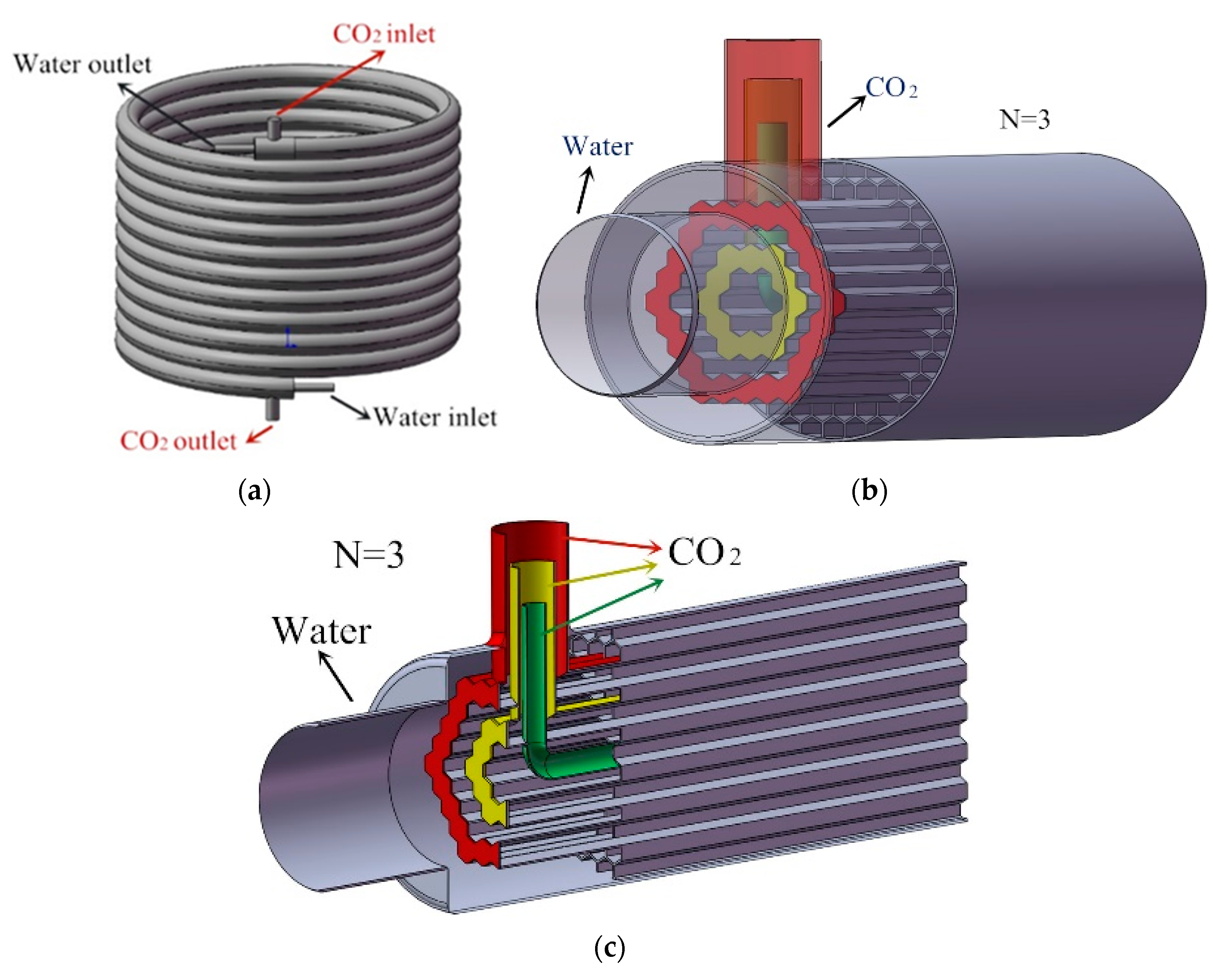
2.1. Introduction of Biomimetic Honeycomb Gas Cooler
- Each hexagonal unit of this honeycomb structure uses the walls of its surrounding units as its own heat transfer ribs, increasing the heat transfer area, and the monolithic honeycomb plays an intensive effect, enhancing the heat transfer capacity of individual units and significantly improving the heat transfer effect of the whole heat exchanger.
- The structure makes the hot and cold fluids in the heat exchange in reverse cross-cut not only to facilitate heat transfer but also to have a self-scouring effect to prevent fluid scaling in the heat exchanger wall.
- The honeycomb unit can make the cross-sectional flow velocity in the direction of fluid flow converge while driving the cross-sectional temperature gradient to tend to be uniform with the ideal field synergy effect, improving the efficiency of heat transfer.
- The honeycomb structure has strong pressure-bearing capacity and has the characteristics of periodic topological distribution. Honeycomb can absorb the energy of load action through the bending deformation of the cell wall with excellent stiffness, strength, and energy absorption performance.
2.2. System Model
- Compression process 1′–2: low-temperature and low-pressure CO2 was compressed to high-temperature and high-pressure state; in this process, due to the compressor’s unequal entropy compression, the actual outlet temperature of the compressor was greater than the temperature of equal entropy compression.
- Cooling process 2–3: CO2 was cooled from high-temperature and high-pressure state to low-temperature and high-pressure state in the gas cooler.
- Internal heat exchange processes 3–3′ and 1–1′: the CO2 from the gas cooler and the CO2 from the evaporator heat exchanged and were used to reduce the CO2 temperature at the throttle valve inlet and to increase the CO2 temperature at compressor suction.
- Throttling process 3′–4: CO2 in a high-pressure state moved through the throttle valve, throttling into low-pressure two-phase state.
- Evaporation process 4–1: the two-phase CO2 evaporated in the evaporator and became saturated or superheated.
- The CO2 heat pump water heater was in steady-state operation.
- Neglected the heat exchange between the system piping, compressor, etc., and the external environment.
- Ignored the pressure drop in the elbow and the piping connected between the components.
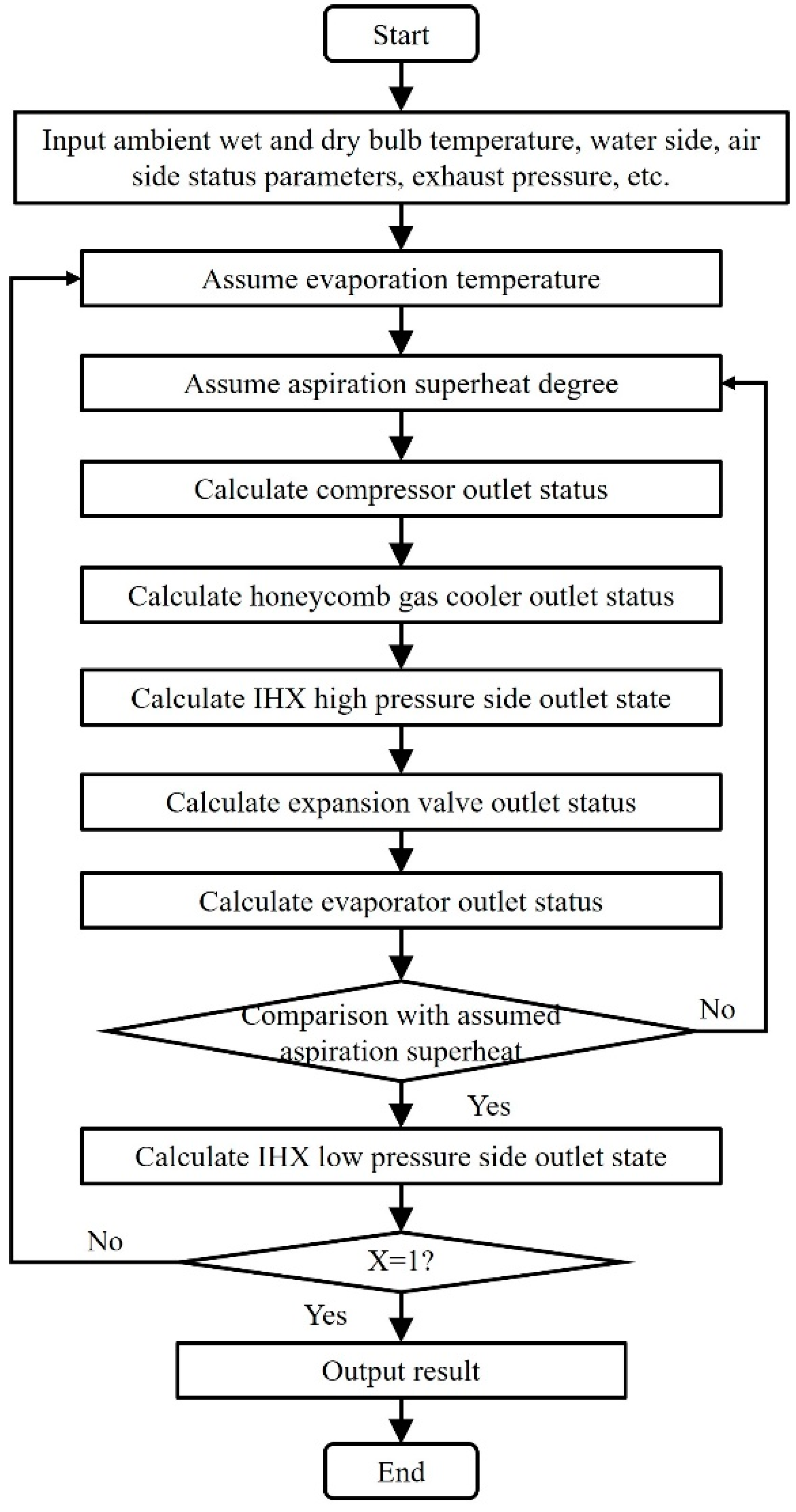
- The inlet flow rate of each component should be equal to the outlet flow rate of the previous component. The calculation flow of this procedure is shown in Figure 4.
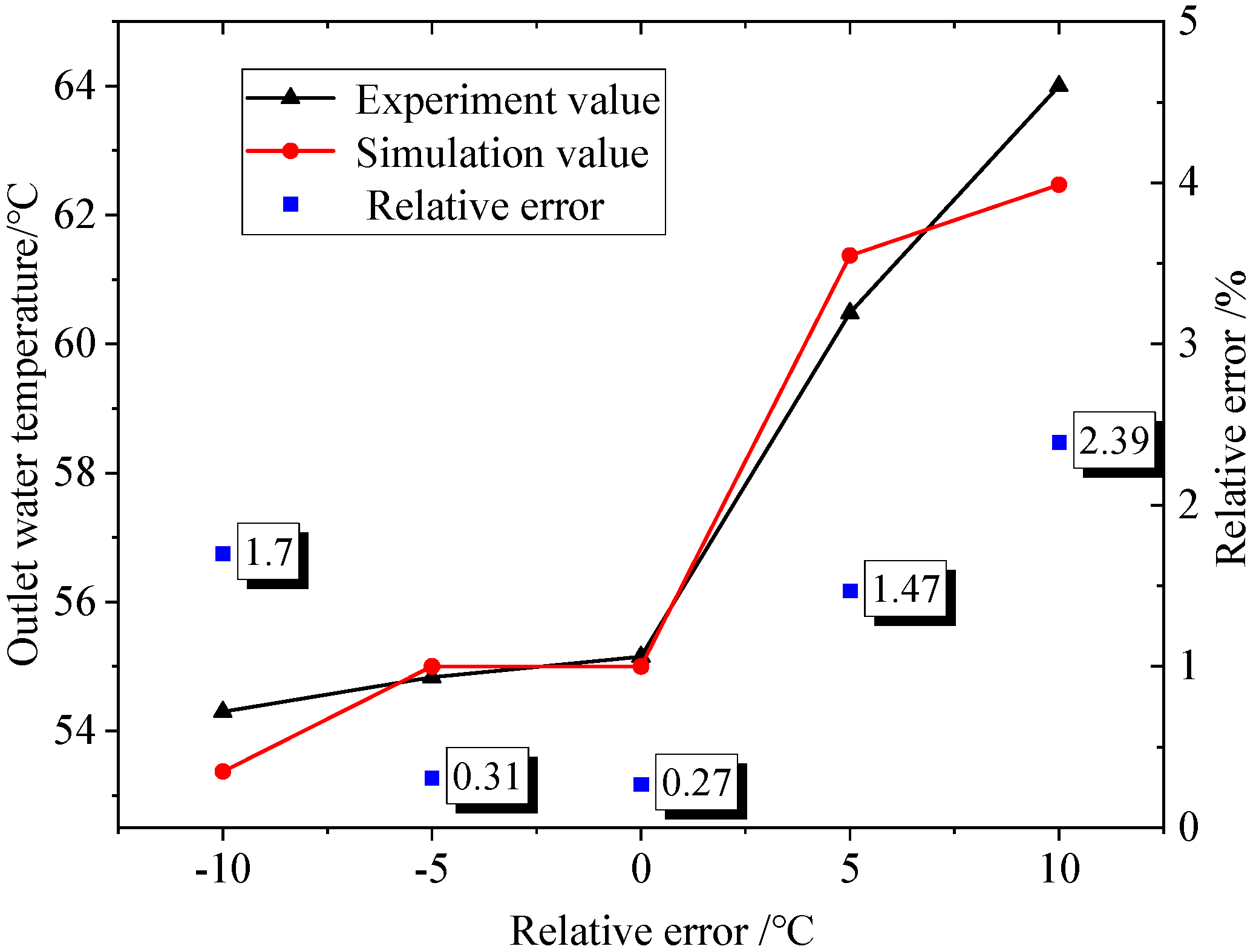
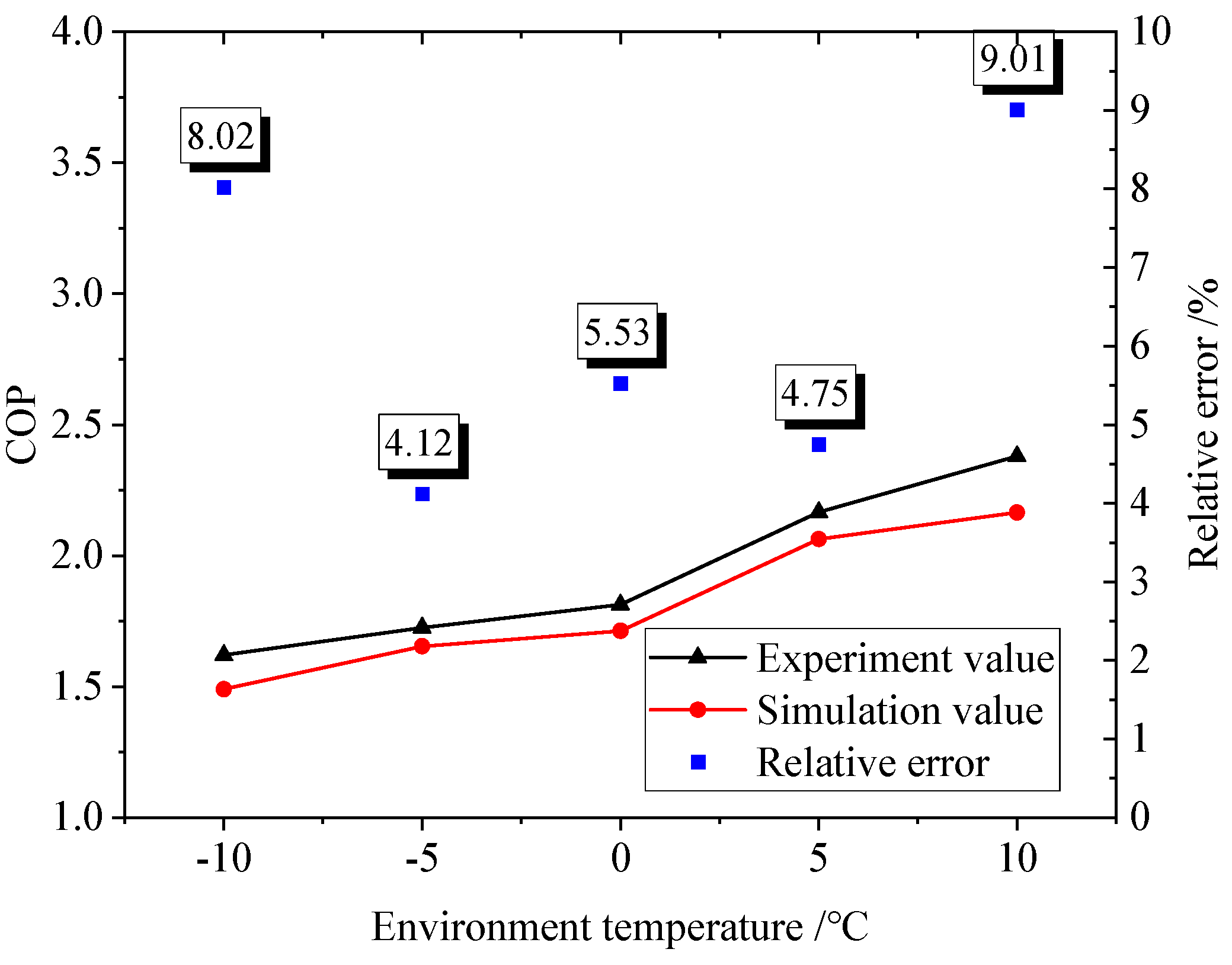
2.3. Model Validation
3. Exergy Analysis Model
3.1. Theoretical Basis
3.2. Exergy Modeling
4. Results and Discussion
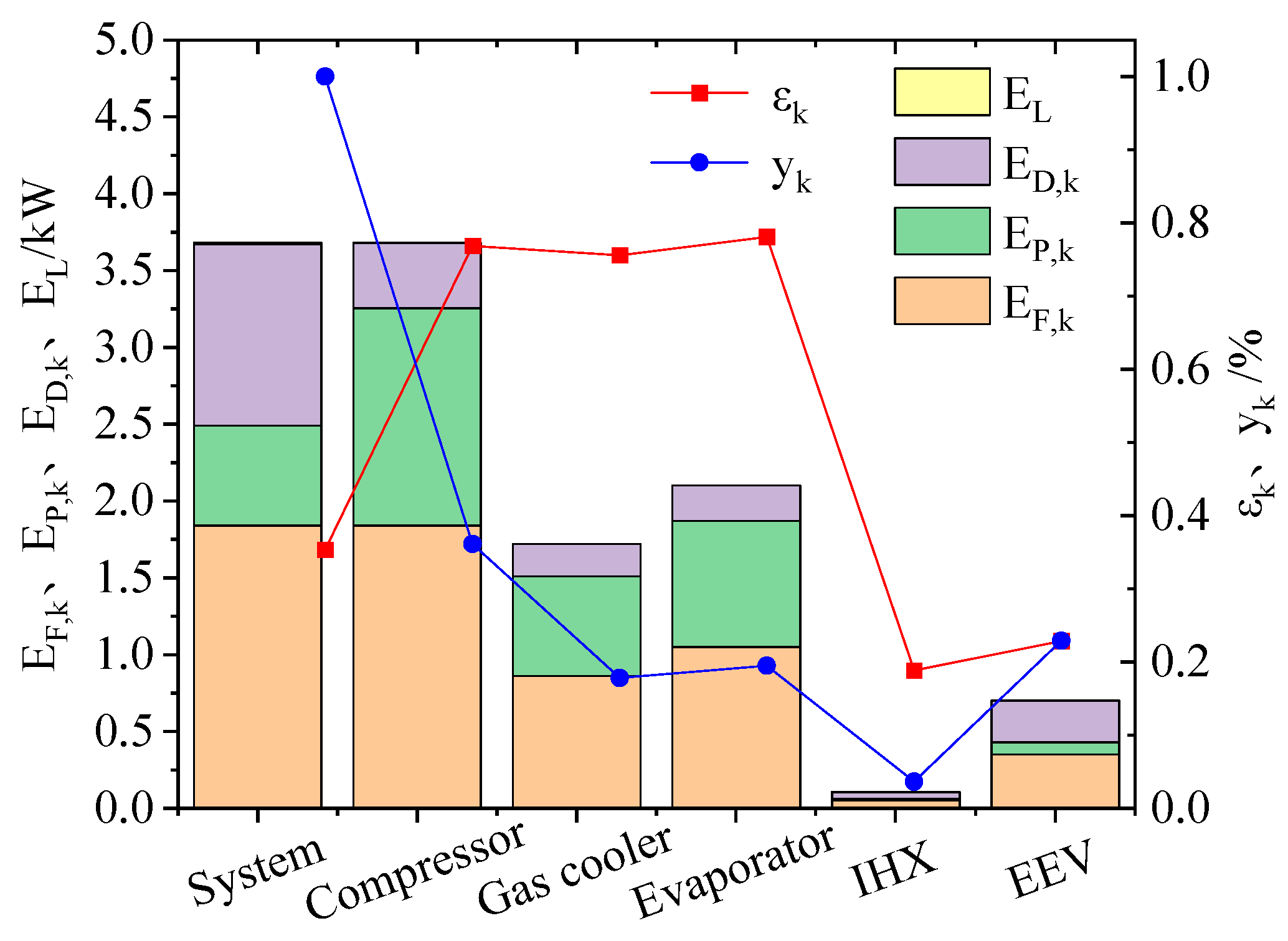
4.1. Exergy Destruction and Exergy Efficiency of the System and Each Component
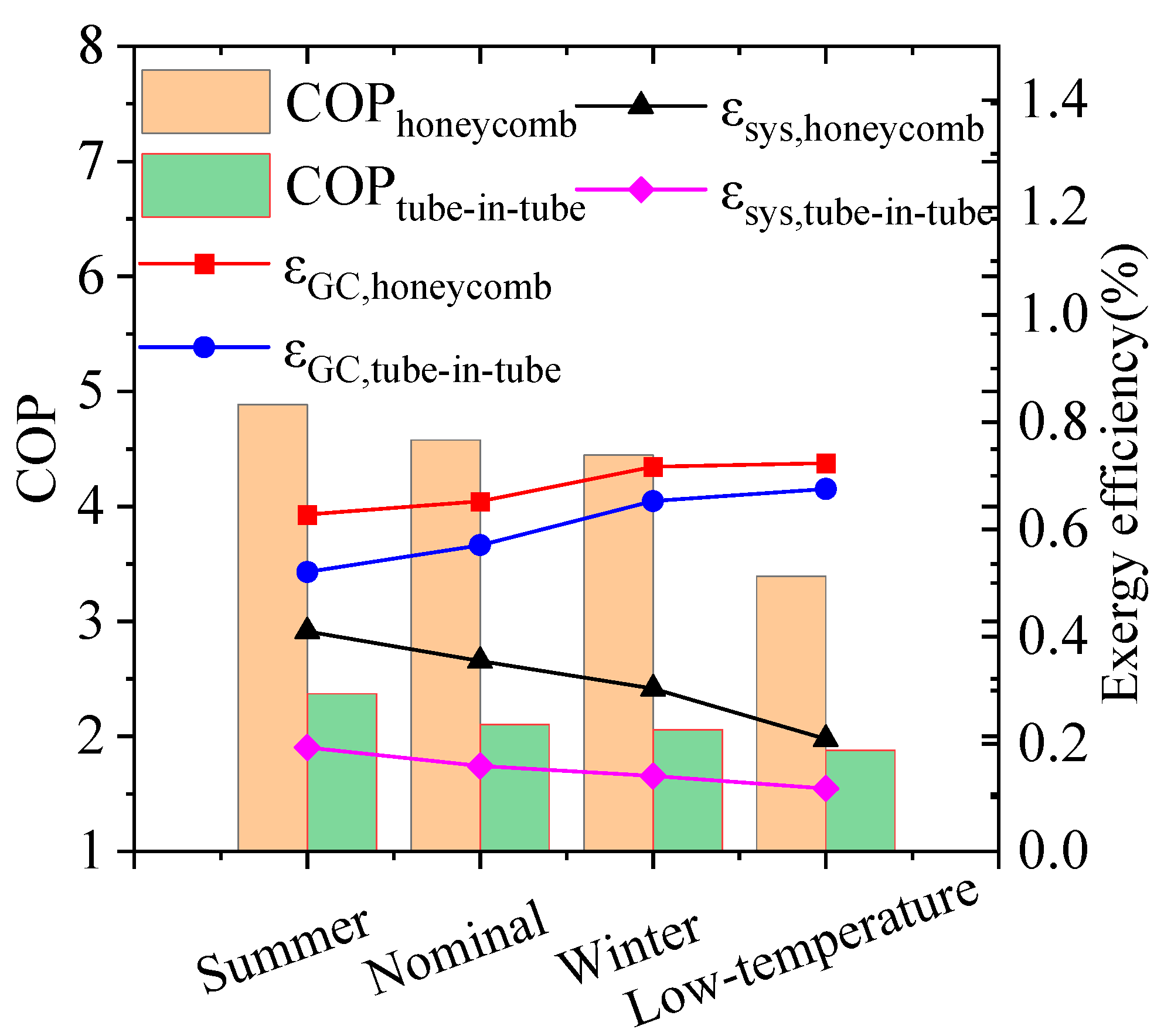
4.2. Effect of Different Forms of Gas Coolers on Exergy Destruction and Exergy Efficiency of Each Component
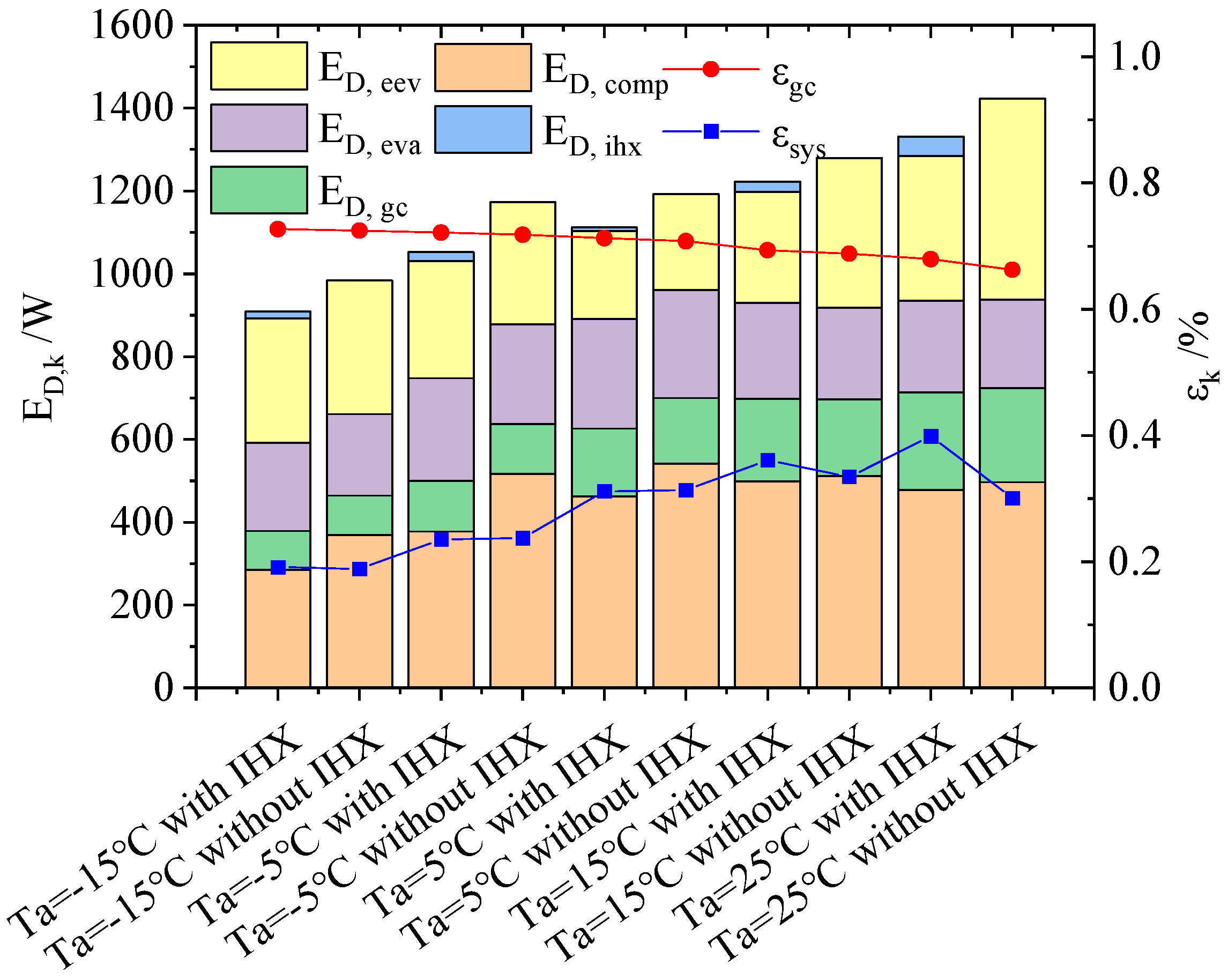
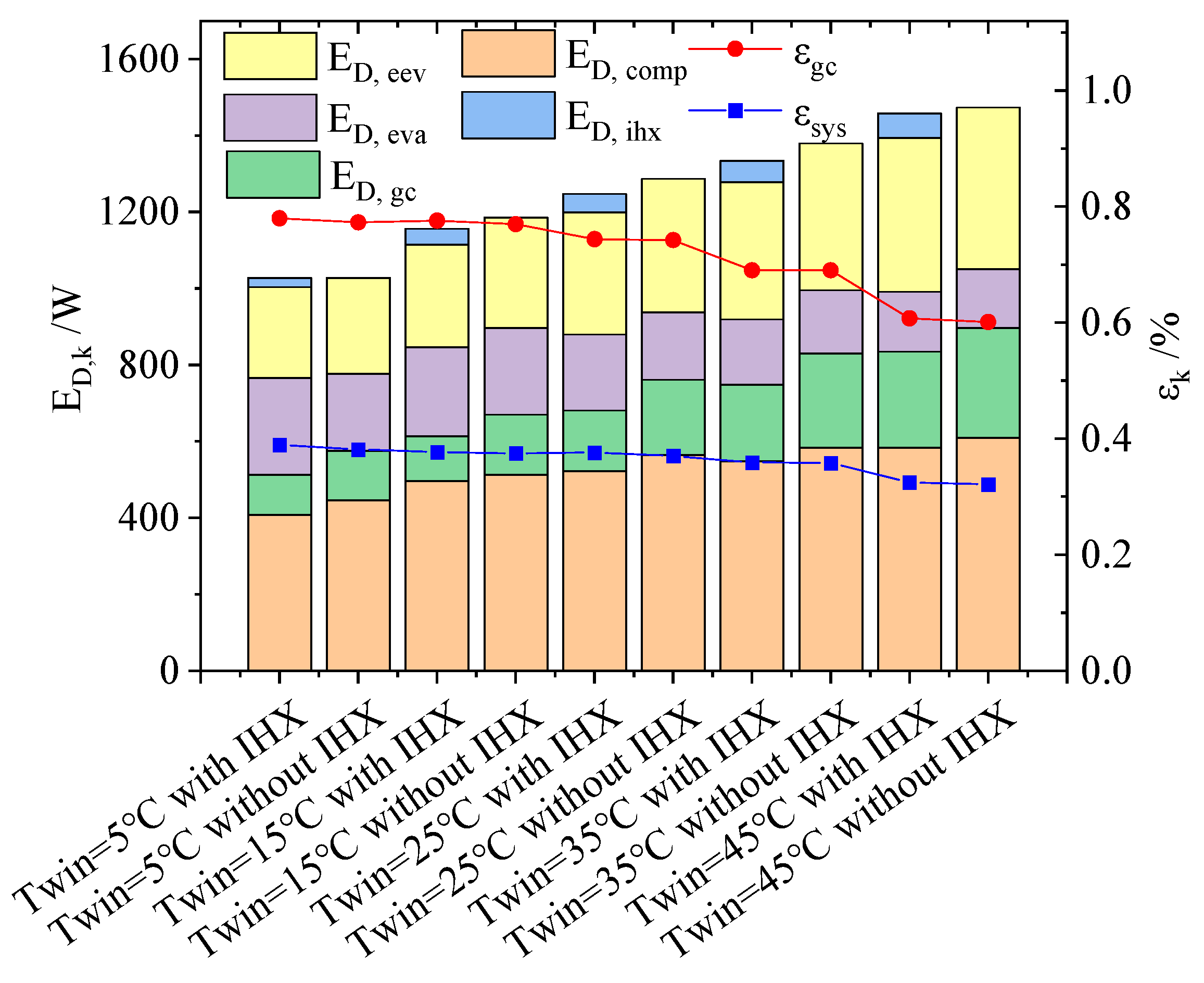
4.3. Effect of Different Working Conditions on Exergy Destruction and Exergy Efficiency of Each Component
4.4. System Improvement and Optimization Suggestions
5. Conclusions
- The system exergy efficiency is 35.33% under nominal operating conditions, which has a large potential for improvement in energy utilization. The three components with the largest exergy destruction percentage are the compressor, throttle valve, and evaporator in the order of 36.13%, 22.90%, and 19.51%, respectively.
- Under the same conditions, the COP of the heat pump with the honeycomb gas cooler is significantly higher than that of the heat pump with the tube-in-tube gas cooler. The exergy efficiency of the honeycomb gas cooler is 20.51%, 14.34%, 9.76%, and 7.20% higher than that of the gas cooler type under the four typical operating conditions. The system exergy efficiencies are 52.78%, 55.19%, 53.68%, and 43.89% higher, respectively. This implies that the honeycomb gas cooler has higher energy utilization.
- Suggestions for the improvement and optimization of the key components are made: The compressor is the key object of system improvement, and the exergy destruction of the compressor can be reduced by improving the structural design, using higher-quality lubricating oil, etc. Next is the throttle valve; common measures include structural optimization or using an expander or injector instead. The exergy destruction of the evaporator is mainly caused by the heat exchange temperature difference in the heat exchanger; the exergy efficiency can be improved by increasing the heat exchange area and reducing the heat exchange temperature difference.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Heat exchange area, m2 |
| cp | Specific heat capacity, J/kg·K |
| ED | Exergy destruction, kW |
| EF | Fuel exergy, kW |
| EP | Product exergy, kW |
| P | Pressure of CO2, MPa |
| Q | Heat transfer capacity, kW |
| V | Gas delivery volume of the compressor, m3/r |
| W | Compressor power consumption, kW |
| h | Enthalpy, kJ/ kg |
| m | Mass flow rate, kg/s |
| n | Number of layers in the honeycomb CO2 gas cooler |
| t | Temperature of fluid, °C |
| y | Exergy destruction percentage, % |
| Ω | Exergy destruction coefficient, % |
| α | Heat transfer coefficient, W/(m2·K) |
| δ | Wall thickness, m |
| ε | Exergy efficiency, % |
| η | Efficiency, % |
| λ | Thermal conductivity, W/(m·K) |
| ρ | Fluid density, kg/m3 |
Abbreviations
| EEV | Electronic expansion valve |
| IHX | Internal heat exchanger |
Subscript
| a | Air |
| com | Compressor |
| eev | Electronic expansion valve |
| eva | Evaporator |
| gc | Gas cooler |
| ihx | Internal heat exchanger |
| k | Component |
| f | Fluid |
| in | Inlet |
| is | Isentropic |
| j | Microelement |
| out | Outlet |
| r | Refrigerant |
| sys | System |
| w | Water |
| wall | Tube wall |
References
- Liu, S.C.; Zheng, L.; Dai, B.M.; Zhong, Z.; Li, H.; Song, M.; Sun, Z. Energetic, economic and environmental analysis of air source transcritical CO2 heat pump system for residential heating in China. Appl. Therm. Eng. 2019, 148, 1425–1439. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Wang, S.N.; Shao, W.; Hao, J. Feasible distributed energy supply options for household energy use in China from a carbon neutral perspective. Int. J. Environ. Res. Public Health 2021, 18, 12992. [Google Scholar] [CrossRef]
- Barta, R.B.; Groll, E.A.; Ziviani, D. Review of stationary and transport CO2 refrigeration and air conditioning technologies. Appl. Therm. Eng. 2021, 185, 116422. [Google Scholar] [CrossRef]
- Nawaz, K.; Shen, B.; Elatar, A.; Baxter, V.; Abdelaziz, O. Performance optimization of CO2 heat pump water heater. Int. J. Refrig. 2018, 85, 213–228. [Google Scholar] [CrossRef]
- Wang, J.; Belusko, M.; Semsarilar, H.; Evans, M.; Liu, M.; Bruno, F. An optimisation study on a real-world transcritical CO2 heat pump system with a flash gas bypass. Energy Convers. Manag. 2022, 251, 114995. [Google Scholar] [CrossRef]
- Cao, F.; Ye, Z.L.; Wang, Y.K. Experimental investigation on the influence of internal heat exchanger in a transcritical CO2 heat pump water heater. Appl. Therm. Eng. 2020, 168, 114855. [Google Scholar] [CrossRef]
- Wang, J.; Belusko, M.; Evans, M.; Liu, M.; Zhao, C.; Bruno, F. A comprehensive review and analysis on CO2 heat pump water heaters. Energy Convers. Manag. X 2022, 15, 100277. [Google Scholar] [CrossRef]
- Cui, C.; Zong, S.; Song, Y.L.; Yin, X.; Cao, F. Experimental investigation of the extreme seeking control on a transcritical CO2 heat pump water heater. Int. J. Refrig. 2022, 133, 111–122. [Google Scholar] [CrossRef]
- Wang, Y.K.; Ye, Z.L.; Song, Y.L.; Yin, X.; Cao, F. Energy, exergy, economic and environmental analysis of refrigerant charge in air source transcritical carbon dioxide heat pump water heater. Energy Convers. Manag. 2020, 223, 113209. [Google Scholar] [CrossRef]
- Wang, Z.H.; Li, G.C.; Wang, F.H. Performance analysis and operation optimization of air-to-water CO2 heat pump with phase change thermal storage. Energy Build. 2020, 209, 109738. [Google Scholar] [CrossRef]
- Dai, B.; Liu, C.; Liu, S.; Wang, D.; Wang, Q.; Zou, T.; Zhou, X. Life cycle techno-enviro-economic assessment of dual-temperature evaporation transcritical CO2 high-temperature heat pump systems for industrial waste heat recovery. Appl. Therm. Eng. 2023, 219, 119570. [Google Scholar] [CrossRef]
- Illán-Gómez, F.; Sena-Cuevas, V.F.; García-Cascales, J.R.; Velasco, F.J. Analysis of the optimal gas cooler pressure of a CO2 heat pump with gas bypass for hot water generation. Appl. Therm. Eng. 2021, 182, 116110. [Google Scholar] [CrossRef]
- Peng, X.; Wang, D.B.; Wang, G.H.; Yang, Y.; Xiang, S. Numerical investigation on the heating performance of a transcritical CO2 vapor-injection heat pump system. Appl. Therm. Eng. 2020, 166, 114656. [Google Scholar] [CrossRef]
- Wu, Z.X.; Zhang, Y.F.; Sheng, Y. Energy, exergy, economic(3E) analysis and multi-objective optimization of a novel dual functional integration system. Energy Convers. Manag. 2019, 199, 111962. [Google Scholar] [CrossRef]
- Sun, Z.L.; Wang, Q.F.; Xie, Z.Y.; Liu, S.; Su, D.; Cui, Q. Energy and exergy analysis of low GWP refrigerants in cascade refrigeration system. Energy 2019, 170, 1170–1180. [Google Scholar] [CrossRef]
- Patil, O.S.; Shet, S.A.; Jadhao, M.; Agrawal, N. Energetic and exergetic studies of modified CO2 transcritical refrigeration cycles. Int. J. Low Carbon Technol. 2021, 16, 171–180. [Google Scholar] [CrossRef]
- Wu, J.X.; Sun, S.J.; Song, Q.L.; Sun, D.; Wang, D.; Li, J. Energy, exergy, exergoeconomic and environmental (4E) analysis of cascade heat pump, recuperative heat pump and carbon dioxide heat pump with different temperature lifts. Renew. Energy 2023, 207, 407–421. [Google Scholar] [CrossRef]
- Li, Y.M.; Wang, C.C. Investigation of the performance of a transcritical CO2 heat pump system subject to heated water conditions: Perspective from the second law. Appl. Therm. Eng. 2021, 193, 116999. [Google Scholar] [CrossRef]
- Liu, R.J.; Gao, F.L.; Liang, K.F.; Wang, L.; Wang, M.; Mi, G.; Li, Y. Thermodynamic Evaluation of Transcritical CO2 Heat Pump Considering Temperature Matching under the Constraint of Heat Transfer Pinch Point. J. Therm. Sci. 2021, 30, 869–879. [Google Scholar] [CrossRef]
- Maddah, S.; Safaei, M.R. Determination of the optimal discharge pressure of the transcritical CO2 heat pump cycles for heating and cooling performances based on new correlation. J. Therm. Anal. Calorim. Int. Forum Therm. Stud. 2021, 145, 1537–1546. [Google Scholar] [CrossRef]
- Wang, Y.K.; Ye, Z.L.; Yin, X.; Song, Y.; Cao, F. Energy, exergy and exergoeconomic evaluation of the air source transcritical CO2 heat pump with internal heat exchanger for space heating. Int. J. Refrig. 2021, 130, 14–26. [Google Scholar] [CrossRef]
- Ghazizade-Ahsaee, H.; Ameri, M. Effects of using expander and internal heat exchanger on carbon dioxide direct-expansion geothermal heat pump. Appl. Therm. Eng. 2018, 136, 389–407. [Google Scholar] [CrossRef]
- Wang, Y.; He, Y.; Song, Y.; Yin, X.; Cao, F.; Wang, X. Energy and exergy analysis of the air source transcritical CO2 heat pump water heater using CO2-based mixture as working fluid. Energies 2021, 14, 4470. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Wei, X.L.; Qin, X. Experimental study on energy, exergy, and exergoeconomic analyses of a novel compression/ejector transcritical CO2 heat pump system with dual heat sources. Energy Convers. Manag. 2022, 271, 116343. [Google Scholar] [CrossRef]
- Wang, Z.H.; Li, G.C.; Zhang, Y.J.; Wang, F.; Jiang, X.; Ma, Z. Flow and heat transfer investigation of supercritical carbon dioxide in a novel biomimetic honeycomb fractal gas cooler of transcritical CO2 heat pumps. Therm. Sci. Eng. Prog. 2023, 37, 101533. [Google Scholar] [CrossRef]
- Li, G.C.; Wang, Z.H.; Wang, F.H.; Zhang, Y. Numerical investigation on the performance characteristics of a novel biomimetic honeycomb fractal gas cooler of transcritical CO2 heat pump. J. Build. Eng. 2022, 59, 105091. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wang, Z.H.; Jiang, X.; Xu, K.; Ma, Z.; Dou, W. Heat transfer and performance enhancement investigation of biomimetic honeycomb gas coolers in transcritical CO2 heat pumps. Appl. Therm. Eng. 2023, 230, 120645. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, F.H.; Li, G.C.; Song, M.; Ma, Z.; Ren, H.; Li, K. Experimental investigation on thermal characteristics of transcritical CO2 heat pump unit combined with thermal energy storage for residential heating. Appl. Therm. Eng. 2020, 165, 114505. [Google Scholar] [CrossRef]
- Ma, Y.T.; Wang, P.; Zhang, Q.C.; Li, M.X.; Cai, S.Q. Development status of CO2 heat pump water heaters. Refrig. Air Cond. 2018, 18, 67–71. (In Chinese) [Google Scholar]



| Components | Type | Structural Parameters |
|---|---|---|
| Compressor | Rotor compressor | Motor frequency: 50 Hz Power: 2.19 kW Theoretical volume: 1.44 m3/h |
| Gas cooler | Coaxial tube-in-tube type of heat exchanger | Inner tube: 22.2 mm diameter, 1.2 mm wall thickness, made of stainless steel Inner tube: 19 mm diameter, 0.9 mm wall thickness, made of copper Length of heat exchange section: 18.57 m |
| Evaporator | Finned-tube heat exchanger | Tube diameter: 7.94 mm Tube wall thickness: 0.7 mm Tube material: copper Fin thickness: 0.11 mm Fin material: aluminum sleeve Fin spacing: 2.0 mm Number of tubes in a single row: 30 Number and length of loops: 5/14.4 m |
| IHX | Coaxial casing type of heat exchanger | Outer tube: 22 mm diameter, made of copper Inner tube: tube diameter of 12.7 mm, material is copper Length of heat exchange section: 1.2 m |
| Expansion valve | CO2 heat pump cross-critical cycle special electronic expansion valve | Valve orifice diameter: Ø 1.4 mm Maximum pressure limit: 14 MPa |
| Working Condition | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| Ambient temperature/°C | −10 | −5 | 0 | 5 | 10 |
| Water flow/m3·h−1 | 0.2 | ||||
| Inlet water temperature/°C | 35 | ||||
| Component | Fuel Exergy | Product Exergy | Exergy Destruction |
|---|---|---|---|
| Compressor | |||
| Gas cooler | |||
| Evaporator | |||
| IHX | |||
| EEV | |||
| System |
| Component | /kW | /kW | /kW | /kW | /% | /% | |
|---|---|---|---|---|---|---|---|
| Compressor | 1.840 | 1.414 | 0.426 | - | 76.85 | 23.15 | 36.13 |
| Gas cooler | 0.860 | 0.650 | 0.210 | - | 75.58 | 11.41 | 17.81 |
| Evaporator | 1.050 | 0.820 | 0.230 | - | 78.10 | 12.50 | 19.51 |
| IHX | 0.053 | 0.010 | 0.043 | - | 18.87 | 2.34 | 3.65 |
| EEV | 0.350 | 0.080 | 0.270 | - | 22.86 | 14.67 | 22.90 |
| System | 1.840 | 0.650 | 1.179 | 0.011 | 35.33 | 64.08 | 100.00 |
| Condition | Water Inlet Temperature/°C | Water Outlet Temperature/°C | Air Dry-Bulb Temperature/°C | Air Wet-Bulb Temperature/°C |
|---|---|---|---|---|
| Summer | 24 ± 1.0 | 65 ± 2 | 25 ± 1.0 | 21 ± 1.0 |
| Nominal | 17 ± 1.0 | 65 ± 2 | 16 ± 1.0 | 12 ± 1.0 |
| Winter | 9 ± 1.0 | 65 ± 2 | 7 ± 1.0 | 6 ± 1.0 |
| Low temperature | 5 ± 1.0 | 65 ± 2 | −12 ± 1.0 | −14 ± 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Z.; Zhang, P.; Jiang, X.; Wang, F.; Huan, C.; Ma, Z. Exergy Analysis of Transcritical CO2 Air-Source Heat Pump with Honeycomb Gas Cooler. Buildings 2023, 13, 2147. https://doi.org/10.3390/buildings13092147
Zhang Y, Wang Z, Zhang P, Jiang X, Wang F, Huan C, Ma Z. Exergy Analysis of Transcritical CO2 Air-Source Heat Pump with Honeycomb Gas Cooler. Buildings. 2023; 13(9):2147. https://doi.org/10.3390/buildings13092147
Chicago/Turabian StyleZhang, Yujia, Zhihua Wang, Pengfei Zhang, Xin Jiang, Fenghao Wang, Chao Huan, and Zhenjun Ma. 2023. "Exergy Analysis of Transcritical CO2 Air-Source Heat Pump with Honeycomb Gas Cooler" Buildings 13, no. 9: 2147. https://doi.org/10.3390/buildings13092147
APA StyleZhang, Y., Wang, Z., Zhang, P., Jiang, X., Wang, F., Huan, C., & Ma, Z. (2023). Exergy Analysis of Transcritical CO2 Air-Source Heat Pump with Honeycomb Gas Cooler. Buildings, 13(9), 2147. https://doi.org/10.3390/buildings13092147










